Lecture_Notes/Dijkstra Article.md

Problem Statement

Recently, Riya won the scholarship to attend the Linux Open Source Conference in Paris. She was very excited to be a part of it. On the day of the conference, she got late and now she wants to quickly know whats the shortest path she needs to follow in order to reach the conference venue as early as possible. She used maps in order to search for it but while exploring the maps application she wondered how exactly the application is computing the shortest path from her location to the destination to easily and effectively.

Brute Force Solution

The brute force solution to find the shortest path from a source node can be to explore all possible paths that exist between source to the destination node. But this will lead to exponential time complexity.

Dijkstra Algorithm

Dijkstra’s algorithm is an algorithm that maps the shortest path between two nodes on a graph.

The best example to depict the application of Dijkstra’s algorithm is Google Maps. It gives you number of ways from one destination to the other. But, it primarily focuses on the shortest path between the 2 places.

Dijkstra’s algorithm can be used to determine the shortest path from one node in a graph to every other node within the same graph data structure, provided that the nodes are reachable from the starting node.!

Dijkstra’s algorithm follows somehow the principle of Dynamic Programming as well. Consider the shortest path from s to some vertex w. It traverses a sequence of vertices, with a final vertex v that then connects to w to finish the shortest path to w. The key observation is that the path up to v must be a shortest path to v. Because if it weren't, we could replace that path to v with a shorter path, which would also shorten the path to w, which would contradict the claim that we have a shortest path to w. Dijkstra's algorithm was that it is basically an efficient version of breadth-first search on a different graph.

Specifically, given a graph G with positive integer edge-weights, one could construct a new unweighted graph H (with the same vertices in G and some additional ones), by replacing each weighted edge with a number of edges equivalent to its weight. So, for example, if you had an edge (u,v) with weight 10 in G, you'd replace this edge by a series of 10 edges between u and v (with new intermediate vertices of course) in H.

Now, the distances between the vertices that were originally from G are preserved, but we've converted the weighted graph into an unweighted graph that we can run BFS on.

At this point, you might realize that you don't really care about the distances to these new intermediate vertices, and you'd only want to enqueue/visit the vertices that were originally from G, which gets you to the idea of a priority queue.

Algorithm

• We assume that all the nodes are unvisited and all the nodes are at infinite distance from starting node.

• Choose the node which is closest to chosen starting node, say node ‘ i ‘ and mark it as visited.

• Update the distance of all the node adjacent to ‘ i ‘, if the path is shorter than the present distance.

Let’s Just discuss this in details:

• Take a boolean array and initialize all the elements to 0 (0 = unvisited, 1 = visited)

• Create an array v[ ], which holds the distance of the nodes from starting node and initialize it to infinity (INT_MAX)

• Equate v[starting node] to 0 (because shortest distance to node from itself is 0)

• Pick the node which is not visited and is at the minimum distance from starting node(unvisited and smallest in v[ ]), say node ‘ u ‘ and mark it as visited (spt[u]=1).

• Update distance value of all adjacent vertices of u. To update the distance values, iterate through all adjacent vertices.

• For every adjacent vertex v, if sum of distance value of u (from source) and weight of edge u-v, is less than the distance value of v, then update the distance value of v.

Dry Run

Pseudocode

def dijkstra(self, source, dest):
        assert source in self.vertices, 'Such source node doesn't exist'

        # 1. Mark all nodes unvisited and store them.
        # 2. Set the distance to zero for our initial node 
        # and to infinity for other nodes.
        distances = {vertex: inf for vertex in self.vertices}
        previous_vertices = {
            vertex: None for vertex in self.vertices
        }
        distances[source] = 0
        vertices = self.vertices.copy()

        while vertices:
            # 3. Select the unvisited node with the smallest distance, 
            # it's current node now.
            current_vertex = min(
                vertices, key=lambda vertex: distances[vertex])

            # 6. Stop, if the smallest distance 
            # among the unvisited nodes is infinity.
            if distances[current_vertex] == inf:
                break

            # 4. Find unvisited neighbors for the current node 
            # and calculate their distances through the current node.
            for neighbour, cost in self.neighbours[current_vertex]:
                alternative_route = distances[current_vertex] + cost

                # Compare the newly calculated distance to the assigned 
                # and save the smaller one.
                if alternative_route < distances[neighbour]:
                    distances[neighbour] = alternative_route
                    previous_vertices[neighbour] = current_vertex

            # 5. Mark the current node as visited 
            # and remove it from the unvisited set.
            vertices.remove(current_vertex)


        path, current_vertex = deque(), dest
        while previous_vertices[current_vertex] is not None:
            path.appendleft(current_vertex)
            current_vertex = previous_vertices[current_vertex]
        if path:
            path.appendleft(current_vertex)
        return path

Time Complexity

The bottleneck of Dijkstra's algorithm is finding the next closest, unvisited node/vertex. Using LinkedList this has a complexity of O(numberOfEdges), since in the worst case scenario we need to go through all the edges of the node to find the one with the smallest weight.

To make this better, we can use Java's heap data structure - PriorityQueue. Using a PriorityQueue guarantees us that the next closest, unvisited node (if there is one) will be the first element of the PriorityQueue. So now finding the next closest node is done in constant (O(1)) time, however, keeping the PriorityQueue sorted (removing used edges and adding new ones) takes O(log(numberOfEdges)) time. This is still much better than O(numberOfEdges).

Further, we have O(numberOfNodes) iterations and therefore as many deletions from the PriorityQueue (that take O(log(numberOfEdges)) time), and adding all of our edges also takes O(log(numberOfEdges)) time. This gives us a total of O((numberOfEdges + numberOfNodes) * log(numberOfEdges)) complexity when using PriorityQueue.

Problems with Dijkstra

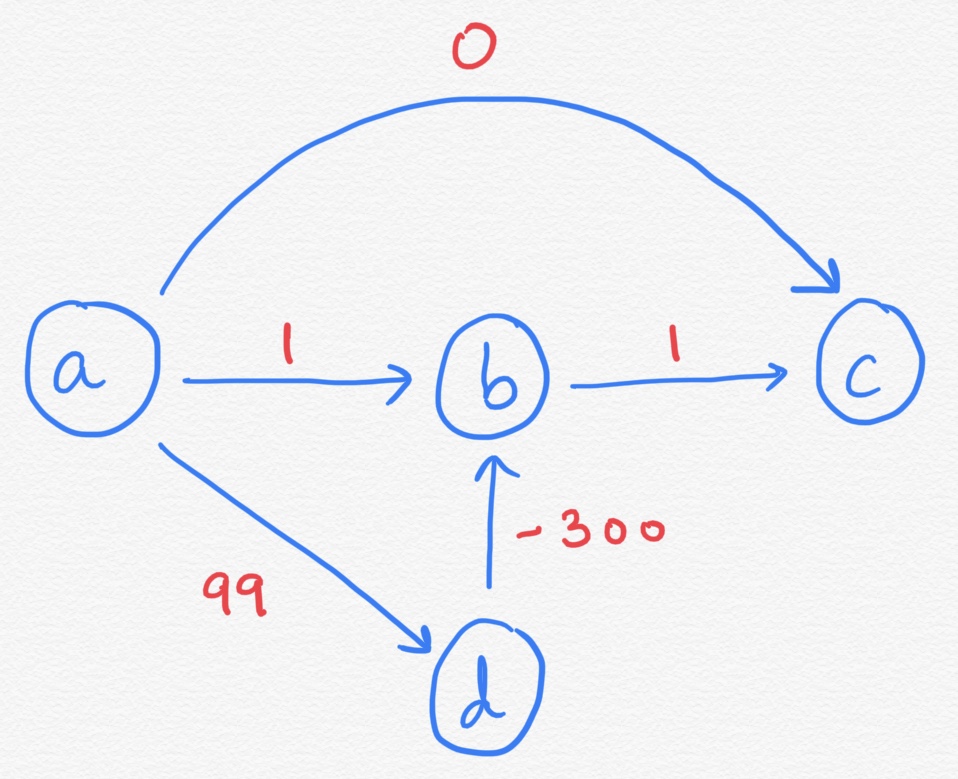
Dijkstra algorithm does not work with graphs having negative weight edges. The below image is a classic example of Dijsktra algorithm being unsuccessful with negative weight edges.

Dijkstra follows a simple rule that if all edges have non negative weights, adding an edge will never make the path smaller. That's why it follows the greedy strategy and picks up the shortest path and in turn which turns out optimal.

Let's start with A. A -> A will be marked as 0, everything else from A will be infinity. In next turn A -> B will be 1. A -> D will be 99. A -> C will be 0.

No changes will be there if you expand vertices B and C. When you expand D, that will change A -> B to -201.
Still A -> C is 0, when there is a shorter path from A -> D -> B -> C costing -200.

Dijsktra will not be able to find out this and it fails.