Notes/Lecture_Notes
1
0
Fork 0
mirror of https://github.com/dholerobin/Lecture_Notes.git synced 2025-09-13 05:42:12 +00:00
Code Issues Packages Projects Releases Wiki Activity

Initial Commit

Browse Source
This commit is contained in:
gparidhi51
2024-03-15 16:00:07 +05:30
committed by GitHub
parent 8662d179cf
commit 16e65a901d
98 changed files with 52995 additions and 0 deletions
Download Patch File Download Diff File Expand all files Collapse all files

480
Academy DSA Typed Notes/Intermediate/Intermediate DSA Arrays 2D Matrices.md Normal file
View File

@@ -0,0 +1,480 @@
# 2D Matrices
### Definition
A 2D matrix is a specific type of 2D array that has a rectangular grid of numbers, where each number is called an element. It is a mathematical structure that consists of a set of numbers arranged in rows and columns.
2D matrix can be declared as:
```
int mat[N][M];
```
*int* is the datatype.
*mat* is the matrix name.
*N* is the number of rows in matrix.
*M* is the number of columns in matrix.
*mat[i][j]* represents the element present in the *i-th* row of *j-th* column.
Below is the pictorial representation of 2D matrix.
![](https://i.imgur.com/s1UeTtc.png)
**Note:** A matrix having *N* rows and *M* columns can store **N*M** elements.
### Question
Given a matrix of size NxM. What will be the index of the top right cell?
Choose the correct answer
**Choices**
- [ ] 0,0
- [ ] 0,M
- [ ] M-1,0
- [x] 0,M-1
### Question
Given a matrix of size NxM. What will be the index of the bottom right cell?
Choose the correct answer
**Choices**
- [ ] N,M
- [ ] M,N
- [x] N-1,M-1
- [ ] M-1,N-1
### Question 1 : Given a matrix print row-wise sum
**Problem Statement**
Given a 2D matrix mat[N][M], print the row-wise sum.
#### TestCase
**Input:**
```
mat[3][4] = {
{1,2,3,4},
{5,6,7,8},
{9,10,11,12}
}
```
**Output:**
```
10
26
42
```
### Approach
The approach is to traverse each row and while traversing take the sum of all the elements present in that row.
### Pseudocode:
```cpp
function SumRow(int mat[N][M]) {
for (int i = 0; i < N; i++) {
int sum = 0;
for (int j = 0; j < M; j++) {
sum = sum + mat[i][j];
}
print(sum);
}
}
```
### Question
What is the time and space complexity of to calculate row-wise sum for a matrix of size N*M?
Choose the correct answer
**Choices**
- [ ] TC: O(N^2), SC: O(n)
- [ ] TC: O(N^2), SC: O(1)
- [ ] TC: O(N^M), SC: O(n)
- [x] TC: O(N*M), SC: O(1)
Since we are iterating over all the elements just once, hence
Time Complexity: **O(N*M)**.
We are not using any extra space,
Space Complextiy: **O(1)**.
### Question 2 : Given a matrix print col-wise sum
Given a 2D matrix mat[N][M], print the column-wise sum.
**TestCase**
```
mat[3][4] = {
{1,2,3,4},
{5,6,7,8},
{9,10,11,12}
}
```
**Output**
```
15 18 21 24
```
:::warning
Please take some time to think about the solution approach on your own before reading further.....
:::
### Approach
While traversing each column, we can calculate sum of all the elements present in that column.
### Pseudocode
```cpp
function SumColumn(int mat[N][M]) {
for (int j = 0; j < M; j++) {
int sum = 0;
for (int i = 0; i < N; i++) {
sum = sum + mat[i][j];
}
print(sum);
}
}
```
#### Complexity
Time Complexity: **O(N*M)**.
Space Complextiy: **O(1)**.
### Question 3 : Given a square matrix print diagonals
Given a matrix 2D square matrix mat[N][N], print diagonals.
How many main Diagonals are there in a square matrix?
$2.$
1. **Principal Diagonal:** From top left to bottom right.
3. **Anti Diagonal:** From top right to bottom left.
![](https://i.imgur.com/aJ4chji.png)
First, let's print **Principal Diagonal**
**TestCase**
```
mat[3][3] = {
{1,2,3},
{5,6,7},
{9,10,11}
}
```
**Output:**
```
1 6 11
```
### Question 3 Approach
#### Pseudocode:
```cpp
function PrintDiagonal(int mat[N][N]) {
int i = 0;
while (i < N) {
print(mat[i][i]);
i = i + 1;
}
}
```
### Question
Given a matrix of size NxN. What will be the time complexity to print the diagonal elements?
Chose the correct answer
**Choices**
- [ ] O(N*sqrt(N))
- [x] O(N)
- [ ] O(N^2)
- [ ] O(NlogN)
Since i starts at 0 and goes till N-1, hence there are total N iterations.
Time Complexity: **O(N)**.
Space Complextiy: **O(1)**.
### Given square matrix, print **Anti-diagonal**
**TestCase**
```
mat[3][3] = {
{1,2,3},
{5,6,7},
{9,10,11}
}
```
**Output:**
```
3 6 9
```
### Pseudocode:
```cpp
function PrintDiagonal(int mat[N][N]) {
int i = 0, j = N - 1;
while (i < N) {
print(mat[i][j]);
i++;
j--;
}
}
```
### Complexity
Time Complexity: **O(N)**.
Space Complextiy: **O(1)**.
### Question 4 Print diagonals in a matrix (right to left)
**Problem Statement**
Given a 2D matrix mat print all the elements diagonally from right to left
**TestCase**
```
mat[3][4] = {
{1,2,3,4},
{5,6,7,8},
{9,10,11,12}
}
```
**Output:**
```
1
2 5
3 6 9
4 7 10
8 11
12
```
### Question
Given a matrix of size N*M, how many Right to Left diagonals will be there?
Choose the correct Options
**Choices**
- [ ] N*M
- [ ] N+M
- [x] N+M-1
- [ ] N+M+1
1. M diagonals are starting from first row.
2. N diagonals start from last column.
3. There is a common diagonal at index 0, M-1.
So, total count = N+M-1 Let's take an example as shown below:
![](https://i.imgur.com/FLZq9TI.png)
### Question
Given a matrix of size 4x5, how many Right to Left diagonals will be there?
Choose the correct answer
**Choices**
- [x] 8
- [ ] 11
- [ ] 9
- [ ] 10
### Question 4 Approach
:::warning
Please take some time to think about the solution approach on your own before reading further.....
:::
* For every start of the diagonal, how do the indices change when we iterate over it?
Row number increments by 1 and column number decrements by 1 as shown in the diagram.
![](https://i.imgur.com/2cR3BTh.png)
### Pseudocode
```cpp
function print_diagonal_elements(A[N][M]) {
//print all diagonals starting from 0th row
i = 0
for (j = 0; j < M; j++) {
s = i;
e = j;
while (s < N && e >= 0) {
print(A[s][e])
s++
e—
}
print(“\n”)
}
//print all diagonals starting from last column
j = M - 1
for (i = 1; i < N; i++) {
s = i;
e = j;
while (s < N && e >= 0) {
print(A[s][e])
s++
e—
}
print(“\n”)
}
}
```
### Question
Time Complexity of printing all the diagonals of a matrix of dimensions N X M?
Choose the correct answer
**Choices**
- [ ] O(N^2 * M^2)
- [ ] O(N^2 + M^2)
- [ ] O(N + M)
- [x] O(N * M)
### Question 5 : Transpose of a square matrix
**Problem Statement**
Given a square 2D matrix mat[N][N], find transpose.
**Transpose of matrix**
The transpose of a matrix is a new matrix obtained by interchanging the rows and columns of the original matrix.
**TestCase**
```
mat[3][3] = {
{1,2,3},
{5,6,7},
{9,10,11}
}
```
**Output:**
```
{
{1,5,9},
{2,6,10},
{3,7,11}
}
```
:::warning
Please take some time to think about the solution approach on your own before reading further.....
:::
### Question 5 Approach
#### Observation
* After performing the transpose, what is same in the original matix and its transpose ?
The diagonal that starts from (0,0) is same.
![](https://i.imgur.com/9Xu3SYE.png)
* Along the diagonals, the elements have swapped their positions with corresponding elements.
#### PseudoCode
```cpp
function find_transpose(matrix[N][N]){
for(int i = 0; i < N; i++){
for(int j = i + 1; j < N; j++){
swap(matrix[i][j],matrix[j][i]);
}
}
}
```
**Note:** If we start j at 0, the matrix will come back to its original position.
### Question
What is the time and space complexity to find transpose of a square matrix?
Chose the correct answer
**Choices**
- [ ] TC: O(N), SC: O(n)
- [ ] TC: O(N^2), SC: O(n)
- [x] TC: O(N^2), SC: O(1)
- [ ] O(N), SC: O(1)
**Complexity**
Time Complexity: **O(N^2)**.
Space Complextiy: **O(1)**.
### Question 6 Rotate a matrix to 90 degree clockwise
**Problem Statement**
Given a matrix mat[N][N], rotate it to 90 degree clockwise.
**TestCase**
```
{
{1,2,3},
{4,5,6},
{7,8,9}
}
```
**Output**
```
{
{7,4,1},
{8,5,2},
{9,6,3}
}
```
### Question 6 Approach
### Hint:
* What if we first find the transpose of the matrix?
* Is there any relation between rotated matrix and transposed matrix ?
:::warning
Using the Hints, please take some time to think about the solution approach on your own before reading further.....
:::
### Observation:
Yes, if we reverse all the rows, then it will become rotated matrix.
The rotated matrix looks like:
![](https://i.imgur.com/B4p4avm.png)
**Transpose and rotated matrix:**
![](https://i.imgur.com/ZfdZaor.png)
#### PseudoCode
```cpp
Function rotate(int mat[N][N]) {
mat = transpose(mat);
for (int i = 0; i < N; i++) {
reverse(mat[i]);
}
return mat;
}
```
#### Complexity
Time Complexity: **O(N*N)**.
Space Complextiy: **O(1)**.

393
Academy DSA Typed Notes/Intermediate/Intermediate DSA Arrays Sliding Window & Contribution Technique.md Normal file
View File

@@ -0,0 +1,393 @@
# Sliding Window & Contribution Technique
## Problem 1 : Find the max sum out of all possible subarray of the array
### Problem Statement
Given an array of integers, find the total sum of all possible subarrays.
**#Note:** This question has been previously asked in *Google* and *Facebook*.
### Solution
* We can use the previous approach, where we calculated all sum subarray using Carry Forward technique.
* Instead of keeping track of maximum, we can simply add the sums in a variable.
### Pseudocode
```cpp
int sumOfAllSubarraySums(int arr[], int n) {
int total_sum = 0;
for (int i = 0; i < n; i++) {
int subarray_sum = 0;
for (int j = i; j < n; j++) {
subarray_sum += arr[j];
total_sum += subarray_sum;
}
}
return total_sum;
}
```
### Time and Space Complexity
* TC - O(n^2)
* SC - O(1)
## Problem 2 : Contribution Technique
We can optimize the above solution further by observing a pattern in the subarray sums.
Let's take the example array ``[1, 2, 3]``. The subarrays and their sums are:
```
[1] -> 1
[1, 2] -> 3
[1, 2, 3] -> 6
[2] -> 2
[2, 3] -> 5
[3] -> 3
Total Sum = 1+3+6+2+5+3 = 20
```
Instead of generating all subarrays, we can check that a particular element appears in how many subarrays and add its contribution that many times to the answer.
* the first element 1 appears in 3 subarrays: [1], [1, 2], and [1, 2, 3].
* the second element 2 appears in 4 subarrays: [2], [1, 2], [2, 3], and [1, 2, 3].
* the third element 3 appears in 3 subarrays: [3], [2, 3], and [1, 2, 3].
Total = $(1*3) + (2*4) + (3*3) = 20$
:::warning
Please take some time to think about "How to calculate the number of subarrays in which A[i] appears?" on your own before reading further.....
:::
### Question
In how many subarrays, the element at index 1 will be present?
A: [3, -2, 4, -1, 2, 6 ]
**Choices**
- [ ] 6
- [ ] 3
- [x] 10
- [ ] 8
**Explanation:** The subarrays in which the element at index 1 is present are -
[3, -2], [3, -2, 4], [3, -2, 4, -1], [3, -2, 4, -1, 2], [3, -2, 4, -1, 2, 6], [-2], [-2, 4], [-2, 4, -1], [-2, 4, -1, 2], [-2, 4, -1, 2, 6 ]. There are total 10 such subarrays.
### Question
In how many subarrays, the element at index 2 will be present?
A: [3, -2, 4, -1, 2, 6 ]
**Choices**
- [ ] 6
- [x] 12
- [ ] 10
- [ ] 8
**Explanation:** The subarrays in which the element at index 1 is present are -
[3, -2, 4], [3, -2, 4, -1], [3, -2, 4, -1, 2], [3, -2, 4, -1, 2, 6], [-2, 4], [-2, 4, -1], [-2, 4, -1, 2], [-2, 4, -1, 2, 6], [4], [4, -1], [4, -1, 2], [4, -1, 2, 6 ]. There are total 12 such subarrays.
### Find sum of all Subarrays sums continued
**Generalized Calculation -**
The start of such subarrays can be $0, 1, ..i$
The end of such subarrays can be $i, i+1, i+2, ...n-1$
Elements in range [0 i] = $i+1$
Elements in range [i n-1] = $n-1-i+1 = n-i$
Thus, the total number of subarrays containing arr[i] is i+1 multiplied by n-i.
This gives us the expression `(i+1) * (n-i)`.
We can use this pattern to compute the total sum of all subarrays in O(n) time complexity. The steps are as follows:
* Initialize a variable total_sum to zero.
* Iterate over all elements of the input array arr. For each element arr[i], compute `arr[i] * (i+1) * (n-i)` and add it to total_sum.
* Return total_sum as the output of the function.
#### Pseudocode
```cpp
int sumOfAllSubarraySums(arr[]) {
int n = arr.size();
int total_sum = 0;
// Iterate over all elements of the array and compute the sum of all subarrays containing that element
for (int i = 0; i < n; i++) {
total_sum += arr[i] * (i + 1) * (n - i);
}
return total_sum;
}
```
#### Time and Space Complexity
* TC - O(n)
* SC - O(1)
### Total number of subarrays of length K
Number of subarrays of length K = Total number of start indices of subarrays of length K.
| length (K) | start of first window | start of last window |
| -------- | -------- | -------- |
| 1 | 0 | N-1 |
| 2 | 0 | N-2 |
| 3 | 0 | N-3 |
| 4 | 0 | N-4 |
| K | 0 | N-K |
All start positions for length K, will be within range **[0 N-K]**. Therefore total is N-K+1.
Hence, total number of subarrays of length K = **N-K+1**.
### Question
Given N=7, K=4, what will be the total number of subarrays of len K?
**Choices**
- [ ] 3
- [x] 4
- [ ] 5
- [ ] 6
## Problem 3 Given an array, print start and end indices of subarrays of length K.
Given an array of size N, print start and end indices of subarrays of length K.
**Example**
If N=8, K=3
All start and end indices are
| start | end |
| ----- | ----- |
| 0 | 2 |
| 1 | 3 |
| 2 | 4 |
| 3 | 5 |
| 4 | 6 |
| 5 | 7 |
[start end] = K
end - start + 1 = K
end = K + start - 1
#### Pseudocode
```cpp=
//Iterate over all the start indices
for (int i = 0; i <= N - K; i++) {
int j = K + i - 1;
print(i, j);
}
```
> Note: Now we know how to iterate over windows of length K.
## Problem 4 : Given an array, print maximum subarray sum with length K
Given an array of N elements. Print maximum subarray sum for subarrays with length = K.
**Example**
```
N=10 K=5
```
| -3 | 4 | -2 | 5 | 3 | -2 | 8 | 2 | -1 | 4 |
| --- | --- | --- | --- | --- | --- | --- | --- | --- |:---:|
**Explanation**
| s | e | sum |
| -------- | -------- | -------- |
| 0 | 4 | 7 |
| 1 | 5 | 8 |
| 2 | 6 | 12 |
| 3 | 7 | 16 |
| 4 | 8 | 10 |
| 5 | 9 | 11 |
Maximum: **16**
:::warning
Please take some time to think about the solution approach on your own before reading further.....
:::
### Problem 4 : Bruteforce Approach
We have to calculate the sum of all subarrays of size k and find the maximum out of them
#### Pseudeocode
```cpp
function maxSubarrayOfLengthK(A[], N, K) {
ans = INT_MIN
//first window
i = 0
j = k - 1
while (j < N) {
sum = 0
for (idx = start; idx <= end; idx++) {
sum += A[idx]
}
ans = max(sum, ans)
//going to next subarray of length k
i++
j++
}
print(ans)
}
```
#### Complexity
For what value of k will the iterations be highest ?
![](https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/031/030/original/1.png?1681232198)
:::warning
Please take some time to think about the optimised solution approach on your own before reading further.....
:::
## Problem 4 : Optimized Approach using Prefix Sum Array
We can use **Prefix Sum Array** since we have to find sum within a range.
### Pseudeocode
```cpp
function maxSubarrayOfLengthK(A[], N, K) {
// calculate prefix sum array
pf[N]
pf[0] = A[0]
for (idx = 1; idx < N; idx++) {
pf[idx] = pf[idx - 1] + A[idx];
}
ans = INT_MIN
i = 0
j = K - 1
// calculate for each pair of indicies
while (j < N) {
sum = pf[j] - (i == 0 ? 0 : pf[i - 1])
ans = max(sum, ans)
i++
j++
}
print(ans)
}
```
### Question
What is Time Complexity and Space Complexity respectively?
**Choices**
- [ ] O(N^2) and O(N)
- [x] O(N) and O(N)
- [ ] O(N) and O(N^2)
- [ ] O(1) and O(N)
---
### Problem 4 Optimized Approach : using Sliding Window
We want to reduce the space complexity without modifying the given array, but how?
#### Observations
* We can get sum of next subarray using current subarray sum as follows:-
* By adding a new element to current sum.
* By subtracting the first element of current subarray.
Given array :-
| -3 | 4 | -2 | 5 | 3 | -2 | 8 | 2 | -1 | 4 |
| --- | --- | --- | --- | --- | --- | --- | --- | --- |:---:|
First subarray from 0 to 4:-
| -3 | 4 | -2 | 5 | 3 |
| --- | --- | --- | --- | --- |
Converting first to second subarray :-
| <span style="color:red"> ~~-3~~ </span> | 4 | -2 | 5 | 3 | <span style="color:green"> -2 </span> |
| --- | --- | --- | --- | --- | --- |
Based upon above observation can we say:-
<div class="alert alert-block alert-warning">
sum of all elements of next subarray = sum of elements of current subarray - first element of current subarray + new element
</div>
This approach is known as **Sliding window approach**.
#### Dry Run
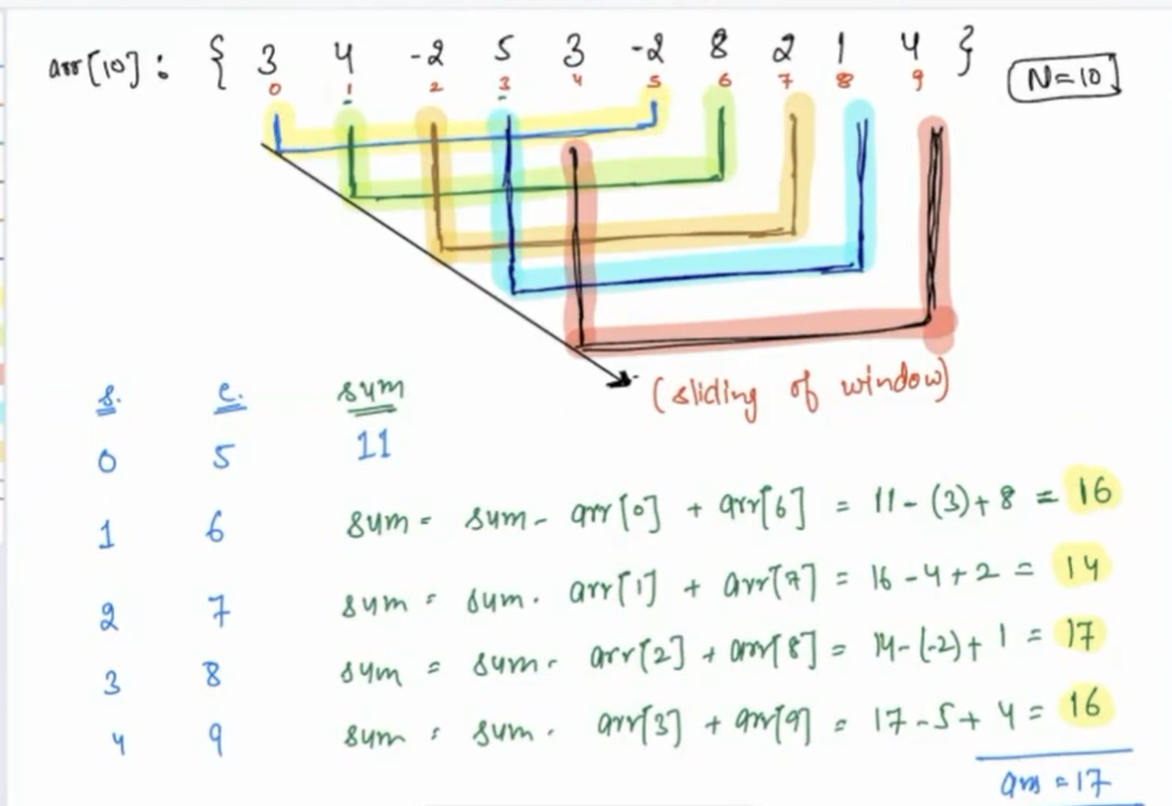
![](https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/031/066/original/Screenshot_%286%29.png?1681239141)
**We can clearly observe the window sliding in above run.**
#### Pseudeocode
```cpp
function maxSubarrayOfLengthK(A[], N, K) {
ans = INT_MIN
i = 0
j = K - 1
sum = 0 // here k iterations
for (int idx = i; idx <= j; idx++) {
sum += A[idx]
}
ans = max(sum, ans)
j++
i++
while (j < N) {
sum = sum + A[j] - A[i - 1]
ans = max(sum, ans)
// here N-k iterations
i++
j++
}
print(ans)
}
```
***Time Complexity : O(N)**
**Space Complexity : O(1)***
## Observations for solving problems on Subarrays.
### Observations
Following are the observations that can be useful when solving problems related to subarrays:
* Subarrays can be visualized as contiguous part of an array, where the starting and ending indices determine the subarray.
* The total number of subarrays in an array of length n is n*(n+1)/2.
* To print all possible subarrays, O(n^3) time complexity is required.
* The sum of all subarrays can be computed in O(n^2) time complexity and O(1) space complexity by using Carry Forward technique.
* The sum of all subarrays can be computed in O(n^2) time complexity and O(n) space complexity using the prefix sum technique.
* The number of subarrays containing a particular element arr[i] can be computed in O(n) time complexity and O(1) space complexity using the formula (i+1)*(n-i). This method is called `Contribution Technique`.

400
Academy DSA Typed Notes/Intermediate/Intermediate DSA Arrays - Carry Forward & Subarrays.md Normal file
View File

@@ -0,0 +1,400 @@
# Carry Forward & Subarrays
## Problem 1 : Count of Pairs ag
Given a string **s** of lowercase characters, return the **count of pairs (i,j)** such that **i < j** and **s[ i ] is 'a'** and **s[ j ] is 'g'**.
### Example 1
```plaintext
String s = "abegag"
Ans = 3
```
### Explanation:
Here, [i,j] such that i<j and s[i] is 'a' and s[j] is 'g' are [0,3], [0,5] and [4,5]. So ans would be 3.
### Question
What is the count of **a,g** pairs in the array:-
s = **"acgdgag"**
**Choices**
- [x] 4
- [ ] 3
- [ ] 5
- [ ] 2
**Explanation:**
Here, [i,j] such that i<j and s[i] is 'a' and s[j] is 'g' are [0,2], [0,4], [0,6] and [5,6]. So ans would be 4.
### Question
How many **ag** pairs are in this string?
s = **"bcaggaag"**
**Choices**
- [x] 5
- [ ] 4
- [ ] 3
- [ ] 6
**Explanation:**
Here, [i,j] such that i<j and s[i] is 'a' and s[j] is 'g' are [2,3], [2,4], [2,7], [5,7] and [6,7]. So ans would be 5.
:::warning
Please take some time to think about the brute force approach on your own before reading further.....
:::
### Problem 1 : Brute Force Solution
For every **'a'**, we need to find the count of **g's** on the right side of **a**. So, we need to have nested loops.
**Pseudocode**
```cpp
int count_ag(string s) {
int result = 0;
for (int i = 0; i < n; i++) {
if (s[i] == 'a') {
for (int j = i + 1; j < n; j++) {
if (s[j] == 'g') {
result++;
}
}
}
}
return result;
}
```
#### Time and Space Complexity
-- TC - $O(n^2)$
-- SC - $O(1)$
### Problem 1 Optimised solution
#### Observation:
* For every **'g'**, we need to know the count of **'a'** on left side of **'g'**.
* We will store the count of **'a'** and whenever **'g'** is encountered, we will add the count of **'a'** to the result.
#### Dry Run
Example: **"acbagkagg"**
![reference link](https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/032/986/original/dry.jpeg?1682663462)
#### Pseudocode
```cpp
int count_ag(string s) {
int result = 0;
int count_a = 0;
for (int i = 0; i < n; i++) {
if (s[i] == 'a') {
count_a++;
} else if (s[i] == 'g') {
result += count_a;
}
}
return result;
}
```
#### Time and Space Complexity
What will be T.C and S.C for this approach?
-- TC - $O(n)$
-- SC - $O(1)$
## Introduction to Subarrays
### Definition
A subarray is a contiguous part of an array. It is formed by selecting a range of elements from the array. A subarray can have one or more elements and must be a contiguous part of the original array.
### Example
Consider the following array of integers:
| 4 | 1 | 2 | 3 | -1 | 6 | 9 | 8 | 12 |
| - | - | - | - | - | - | - | - | - |
* `2, 3, -1, 6` is a subarray of length 4.
* `9` is a subarray of single element.
* `4, 1, 2, 3, -1, 6, 9, 8, 12` is a subarray consisting of all the array elements.
* `4, 12` is **not** a subarray because loop does not count as subarray.
* `1, 2, 6` is **not** a subarray beacuse the array elements must be contiguous.
* `3, 2, 1, 4` is **not** a subarray because order of the elements in a subarray should be same as in the array.
### Question
A[] = { 2, 4, 1, 6, -3, 7, 8, 4}
Which of the following is a valid subarray?
**Choices**
- [ ] {1, 6, 8}
- [ ] {1, 4}
- [ ] {6, 1, 4, 2}
- [x] {7, 8, 4}
**Explanation:** {1, 6, 8} & {1, 4} are not contiguous parts of array. {6, 1, 4, 2} is not in the same order as in original array. Only {7, 8, 4} is a valid subarray.
### Representation of a Subarray
#### Representation of a Subarray
A Subarray can be uniquely represented in following ways:
1. By specifying the `start` and `end` index of the subarray.
2. By specifying the `start` index and `length` of the subarray.
If we consider the same array from the above example,
| 4 | 1 | 2 | 3 | -1 | 6 | 9 | 8 | 12 |
| - | - | - | - | - | - | - | - | - |
The subarray `2, 3, -1, 6` can be represented as
* the range of elements starting at index `2` and ending at index `5` (0-based indexing).
* the range of elements having length of `4` with start index as `2`.
### Question
How many subarrays of the following array start from index 0
[4, 2, 10, 3, 12, -2, 15]
**Choices**
- [ ] 6
- [x] 7
- [ ] 21
- [ ] 36
[4] (starting from index 0)
[4, 2]
[4, 2, 10]
[4, 2, 10, 3]
[4, 2, 10, 3, 12]
[4, 2, 10, 3, 12, -2]
[4, 2, 10, 3, 12, -2, 15]
Therefore, there are a total of 7 subarrays that start from index 0.
### Question
How many subarrays of the following array start from index 1
[4, 2, 10, 3, 12, -2, 15]
**Choices**
- [x] 6
- [ ] 7
- [ ] 21
- [ ] 36
[2] (starting from index 1)
[2, 10]
[2, 10, 3]
[2, 10, 3, 12]
[2, 10, 3, 12, -2]
[2, 10, 3, 12, -2, 15]
Therefore, there are a total of 6 subarrays that start from index 1.
### Formula to count no. of subarrays
No. of subarrays starting from index 0 = n
No. of subarrays starting from index 1 = n-1
No. of subarrays starting from index 2 = n-2
No. of subarrays starting from index 3 = n-3
...........
...........
No. of subarrays starting from index n-1 = 1
So, Using the formula for the sum of an arithmetic series, total number of subarrays = n + (n-1) + (n-2) + (n-3) + . . . . . . + 3 + 2 + 1 = n(n+1)/2.
``` cpp
total = n(n + 1) / 2
```
### Print the subarray of the array that starts from the start index and ends at the end index
#### Problem Statement
Given an array of integers and two indices, a start index and an end index, we need to print the subarrays of the array that starts from the start index and ends at the end index (both inclusive).
#### Solution
To solve this problem, we can simply iterate over the elements of the array from the start index to the end index (both inclusive) and print each element.
#### Pseudocode
```cpp
void printSubarray(int arr[], int start, int end) {
for (int i = start; i <= end; i++) {
cout << arr[i] << " ";
}
cout << endl;
}
```
#### Time and Space Complexity
What will be T.C and S.C for the above approach?
* TC - O(n)
* SC - O(1)
### Print all possible subarrays of the array
**Problem Statement:**
Given an array of integers, we need to print all possible subarrays of the array.
**Example**
```cpp
Input: [1, 2, 3]
Output:
[1]
[1, 2]
[1, 2, 3]
[2]
[2, 3]
[3]
```
#### Solution
To solve this problem, we can generate all possible subarrays of the array using two nested loops.
* The outer loop iterates over the starting index of the subarray.
* The inner loop iterates over the ending index of the subarray.
* At each iteration, we print the subarray from the starting index to the ending index.
#### Pseudocode
```cpp
void printSubarrays(int arr[], int n) {
// Generate all possible subarrays
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
// Print the current subarray
for (int k = i; k <= j; k++) {
cout << arr[k] << " ";
}
cout << endl;
}
}
}
```
#### TC & SC:
TC - O(N^3)
SC - O(1)
### Problem 2 : Max And Min
**Given an array of N integers, return the length of smallest subarray which contains both maximum and minimum element of the array.**
### Question
What is the length of the smallest subarray which has both, the max and the min of the array?
| 2 | 2 | 6 | 4 | 5 | 1 | 5 | 2 | 6 | 4 | 1|
| --| --| --| --| --| --| --| --| --| --| --|
**Choices**
- [ ] 4
- [ ] 5
- [ ] 2
- [x] 3
Here, minimum element is 1 and maximum is 6. Smallest subarray which contains both is from index 8 to index 10 which is of length 10-8+1=3.
**Another Example**
```plaintext
A[ ] = { 1, 2, 3, 1, 3, 4, 6, 4, 6, 3}
Ans = 4
```
**Explanation:**
Here, minimum element is 1 and maximum is 6. Smallest subarray which contains both is from index 3 to index 6 which is of length 6-3+1=4.
:::warning
Please take some time to think about the brute force approach on your own before reading further.....
:::
### Problem 2 : Brute Force Solution
Check all subarrays and find the answer.
-- TC - $O(n^3)$
-- SC - $O(1)$
Note: It can be reduced to $O(n^2)$ since we can check miniumum and maximum in a subarray in second loop itself.
### Problem 2 : Optimised Solution Observation
* The answer subarray must have exactly one instance of minimum element and one instance of maximum element since we want the length to be minimum.
* The minimum and maximum value must be present at the corners of the subarray.
* So, basically we are looking for subarray **which starts with maximum value and ends with closest minimum value or which starts with minimum value and ends with closest maximum value.**
**NOTE:**
1. We can search a **min** for a **max** or vice versa, only in a single direction.
1. We don't have to consider all the pairs of min and max but look for closest pair, since we want to find smallest such subarray.
2. So we can keep track of the last found min and a last found max index.
#### Dry Run
```plaintext
A[ ] = { 2, 2, 6, 4, 5, 1, 5, 2, 6, 4, 1 }
```
Initially,
last_min_index = **-1**
last_max_index = **-1**
ans = **INT_MAX**
minValue = **1**
maxValue = **6**
| i | A[i] | last_min_index |last_max_index|ans|
| -------- | -------- | -------- |-------- |-------- |
| 0| 2| -1| -1| INT_MAX |
| 1| 2| -1| -1| INT_MAX |
| 2| 6| -1| 2| INT_MAX |
| 3| 4| -1| 2| INT_MAX |
| 4| 5| -1| 2| INT_MAX |
| 5| 1| 5| 2| 5-2+1 = 4|
| 6| 5| 5| 2| 4|
| 7| 2| 5| 2| 4|
| 8| 6| 5| 8| 4|
| 9| 4| 5| 8| 4|
| 10| 1| 10| 8|10-8+1 = 3|
**So final ans would be 3.**
#### Pseudocode
```cpp
int minSubarray(int A[], int n) {
// find maximum and minimum
// values in the array
int minValue = minOfArray(A);
int maxValue = maxOfArray(A);
int last_min_index = -1, last_max_index = -1, ans = INT_MAX;
for (int i = 0; i < N; i++) {
if (A[i] == minValue) {
last_min_index = i;
if (last_max_index != -1) {
ans = min(ans, i - last_max_index + 1);
}
}
if (A[i] == maxValue) {
last_max_index = i;
if (last_min_index != -1) {
ans = min(ans, i - last_min_index + 1);
}
}
}
return ans;
}
```
#### Time and Space Complexity
What will be T.C and S.C for this approach?
-- TC - $O(n)$
-- SC - $O(1)$

599
Academy DSA Typed Notes/Intermediate/Intermediate DSA Arrays - Prefix Sum.md Normal file
View File

@@ -0,0 +1,599 @@
# Prefix Sum
## Problem Description
Given N elements and Q queries. For each query, calculate sum of all elements from L to R [0 based index].
### Example:
A[ ] = [-3, 6, 2, 4, 5, 2, 8, -9, 3, 1]
Queries (Q)
| L | R | Solution |
| -------- | -------- | -------- |
| 4 | 8 | 9 |
| 3 | 7 | 10 |
| 1 | 3 | 12 |
| 0 | 4 | 14 |
| 7 | 7 | -9 |
:::info
Before moving forward, think about the brute force solution approach.....
:::
## Brute Force Approach
For each query Q, we iterate and calculate the sum of elements from index L to R
### Pseudocode
```cpp
Function querySum(Queries[][], Array[], querySize, size) {
for (i = 0; i < Queries.length; i++) {
L = Queries[i][0]
R = Queries[i][1]
sum = 0
for (j = L; j <= R; j++) {
sum += Array[j]
}
print(sum)
}
}
```
***Time Complexity : O(N * Q)**
**Space Complexity : O(1)***
>Since Time complexity of this approach is O(N * Q) then in a case where there are 10^5 elements & 10^5 queries where each query is (L=0 and R=10^5-1) we would encounter **TLE** hence this approach is Inefficient
### Question
Given the scores of the 10 overs of a cricket match
2, 8, 14, 29, 31, 49, 65, 79, 88, 97
How many runs were scored in just 7th over?
**Choices**
- [x] 16
- [ ] 20
- [ ] 18
- [ ] 17
Total runs scored in over 7th : 65 - 49 = 16
(score[7]-score[6])
### Question
Given the scores of the 10 overs of a cricket match
2, 8, 14, 29, 31, 49, 65, 79, 88, 97
How many runs were scored from 6th to 10th over(both included)?
**Choices**
- [x] 66
- [ ] 72
- [ ] 68
- [ ] 90
Total runs scored in over 6th to 10th : 97 - 31 = 66
(score[10]-score[5])
### Question
Given the scores of the 10 overs of a cricket match
2, 8, 14, 29, 31, 49, 65, 79, 88, 97
How many runs were scored in just 10th over?
**Choices**
- [ ] 7
- [ ] 8
- [x] 9
- [ ] 10
Total runs scored in over 6th to 10th : 97 - 88 = 9
(score[10]-score[9])
### Question
Given the scores of the 10 overs of a cricket match
2, 8, 14, 29, 31, 49, 65, 79, 88, 97
How many runs were scored from 3rd to 6th over(both included)?
**Choices**
- [ ] 70
- [ ] 40
- [ ] 9
- [x] 41
Total runs scored in over 3rd to 6th : 49-8 = 41
(score[6]-score[2])
### Question
Given the scores of the 10 overs of a cricket match
2, 8, 14, 29, 31, 49, 65, 79, 88, 97
How many runs were scored from 4th to 9th over(both included)?
**Choices**
- [ ] 75
- [ ] 80
- [x] 74
- [ ] 10
Total runs scored in over 4th to 9th : 88 - 14 = 74
(score[9]-score[3])
:::success
What do you observe from above cricket example ? Take some time and think about it....
:::
### Observation for Optimised Solution
#### Observation
* On observing cricket board score, we can say that queries can be answered in just constant time since we have cummulative scores.
* In the similar manner, if we have cummulative sum array for the above problem, we should be able to answer it in just constant time.
* We need to create cumulative sum or <B>prefix sum array</B> for above problem.
</div>
## How to create Prefix Sum Array ?
### Definition
pf[i] = sum of all elements from 0 till ith index.
<!-- </div> -->
### Example
Step1:-
Provided the intial array:-
| 2 | 5 | -1 | 7 | 1 |
| --- | --- | --- | --- | --- |
We'll create prefix sum array of size 5 i.e. size equal to intial array.
`Initialise pf[0] = initialArray[0]`
| 2 | - | - | - | - |
| --- | --- | --- | --- | --- |
| 2 | 7 | - | - | - |
| --- | --- | --- | --- | --- |
| 2 | 7 | 6 | - | - |
| --- | --- | --- | --- | --- |
| 2 | 7 | 6 | 13 | - |
| --- | --- | --- | --- | --- |
| 2 | 7 | 6 | 13 | 14 |
| --- | --- | --- | --- | --- |
Finally we have the prefix sum array :-
| 2 | 7 | 6 | 13 | 14 |
| --- | --- | --- | --- | --- |
### Question
Calculate the prefix sum array for following array:-
| 10 | 32 | 6 | 12 | 20 | 1 |
| --- | --- | --- | --- | --- |:---:|
**Choices**
- [x] `[10,42,48,60,80,81]`
- [ ] `[10,42,49,60,79,81]`
- [ ] `[42,48,60,80,81,10]`
- [ ] `[15,43,58,61,70,82]`
### Brute Force Code to create Prefix Sum Array and observation for Optimisation
```cpp
pf[N]
for (i = 0; i < N; i++) {
sum = 0;
for (int j = 0; j <= i; j++) {
sum = sum + A[j]
}
pf[i] = sum;
}
```
## Observation for Optimising Prefix Sum array calculations
pf[0] = A[0]
pf[1] = A[0] + A[1]
pf[2] = A[0] + A[1] + A[2]
pf[3] = A[0] + A[1] + A[2] + A[3]
pf[4] = A[0] + A[1] + A[2] + A[3] + A[4]
* Can we observe that we are making redundant calculations?
* We could utilise the previous sum value.
* pf[0] = A[0]
* pf[1] = pf[0] + A[1]
* pf[2] = pf[1] + A[2]
* pf[3] = pf[2] + A[3]
* pf[4] = pf[3] + A[4]
* **Generalised Equation is:** ```pf[i] = pf[i-1] + A[i]```
## Optimised Code:
```cpp
pf[N]
pf[0] = A[0];
for (i = 1; i < N; i++) {
pf[i] = pf[i - 1] + A[i];
}
```
* Time Complexity: O(N)
### How to answer the Queries ?
:::success
Now that we have created prefix sum array...finally how can we answer the queries ? Let's think for a while...
:::
A[ ] = [-3, 6, 2, 4, 5, 2, 8, -9, 3, 1]
pf[ ] =[-3, 3, 5, 9, 14, 16, 24, 15, 18, 19]
| L | R | Solution | |
| -------- | -------- | -------- | -------- |
| 4 | 8 | pf[8] - pf[3] | 18 - 9 = 9 |
| 3 | 7 | pf[7] - pf[2] |15 - 5 = 10 |
| 1 | 3 | pf[3] - pf[0] |9 - (-3) = 12 |
| 0 | 4 | pf[4] |14 |
| 7 | 7 | pf[7] - pf[6] |15 - 24 = -9 |
### Generalised Equation to find Sum:
sum[L R] = pf[R] - pf[L-1]
Note: if L==0, then sum[L R] = pf[R]
### Complete code for finding sum of queries using Prefix Sum array:
```cpp
Function querySum(Queries[][], Array[], querySize, size) {
//calculate pf array
pf[N]
pf[0] = A[0];
for (i = 1; i < N; i++) {
pf[i] = pf[i - 1] + A[i];
}
//answer queries
for (i = 0; i < Queries.length; i++) {
L = Queries[i][0];
R = Queries[i][1];
if (L == 0) {
sum = pf[R]
} else {
sum = pf[R] - pf[L - 1];
}
print(sum);
}
}
```
***Time Complexity : O(N+Q)**
**Space Complexity : O(N)***
### Space Complexity can be further optimised if you modify the given array.
```cpp
Function prefixSumArrayInplace(Array[], size) {
for (i = 1; i < size; i++) {
Array[i] = Array[i - 1] + Array[i];
}
}
```
***Time Complexity : O(N)**
**Space Complexity : O(1)***
### Problem 1 : Sum of even indexed elements
Given an array of size N and Q queries with start (s) and end (e) index. For every query, return the sum of all **even indexed elements** from **s to e**.
**Example**
```plaintext
A[ ] = { 2, 3, 1, 6, 4, 5 }
Query :
1 3
2 5
0 4
3 3
Ans:
1
5
7
0
```
### Explanation:
* From index 1 to 3, sum: A[2] = 1
* From index 2 to 5, sum: A[2]+A[4] = 5
* From index 0 to 4, sum: A[0]+A[2]+A[4] = 7
* From index 3 to 3, sum: 0
### Brute Force
How many of you can solve it in $O(N*Q)$ complexity?
**Idea:** For every query, Iterate over the array and generate the answer.
:::warning
Please take some time to think about the Optimised approach on your own before reading further.....
:::
### Problem 1 : Observation for Optimisation
Whenever range sum query is present, we should think in direction of **Prefix Sum**.
**Hint 1:** Should we find prefix sum of entire array?
**Expected:** No, it should be only for even indexed elements.
**We can assume that elements at odd indices are 0 and then create the prefix sum array.**
Consider this example:-
```
A[] = 2 3 1 6 4 5
PSe[] = 2 2 3 3 7 7
```
> Note: PSe</sub>[i] denotes sum of all even indexed elements from 0 to ith index.
If **i is even** we will use the following equation :-
<div class="alert alert-block alert-warning">
PSe</sub>[i] = PSe</sub>[i-1] + A[i]
</div>
If **i is odd** we will use the following equation :-
<div class="alert alert-block alert-warning">
PSe[i] = PSe[i-1]
</div>
### Question
Construct the Prefix Sum for even indexed elements for the given array
[2, 4, 3, 1, 5]
**Choices**
- [ ] 1, 6, 9, 10, 15
- [x] 2, 2, 5, 5, 10
- [ ] 0, 4, 4, 5, 5
- [ ] 0, 4, 7, 8, 8
We will assume elements at odd indices to be 0 and create a prefix sum array taking this assumption.
So ```2 2 5 5 10``` will be the answer.
### Problem 1 : Pseudocode
```cpp
void sum_of_even_indexed(int A[], int queries[][], int N) {
// prefix sum for even indexed elements
int PSe[N];
if (A[0] % 2 == 0) PSe[0] = A[0];
else PSe[0] = 0;
for (int i = 0; i < N; i++) {
if (i % 2 == 0) {
PSe[i] = PSe[i - 1] + A[i];
} else {
PSe[i] = PSe[i - 1];
}
}
for (int i = 0; i < queries.size(); i++) {
s = queries[i][0]
e = queries[i][1]
if (s == 0) {
print(PSe[e])
} else {
print(PSe[e] - PSe[s - 1])
}
}
}
```
### Complexity
-- TC - $O(n)$
-- SC - $O(n)$
### Problem 1 Extension : Sum of all odd indexed elements
If we have to calculate the sum of all ODD indexed elements from index **s** to **e**, then Prefix Sum array will be created as follows -
> if i is odd
<div class="alert alert-block alert-warning">
PSo[i] = PSo[i-1] + array[i]
</div>
> and if i is even :-
<div class="alert alert-block alert-warning">
PSo[i] = PSo[i-1]
</div>
### Problem 2 : Special Index
Given an array of size N, count the number of special index in the array.
**Note:** **Special Indices** are those after removing which, sum of all **EVEN** indexed elements is equal to sum of all **ODD** indexed elements.
**Example**
```plaintext
A[ ] = { 4, 3, 2, 7, 6, -2 }
Ans = 2
```
We can see that after removing 0th and 2nd index **S<sub>e</sub>** and **S<sub>o</sub>** are equal.
| i | A[i] | S<sub>e</sub> | S<sub>o</sub> |
| --- |------------------| ----- | ----- |
| 0 | { 3, 2, 7, 6, -2 } | 8 | 8 |
| 1 | { 4, 2, 7, 6, -2 } | 9 | 8 |
| 2 | { 4, 3, 7, 6, -2 } | 9 | 9 |
| 3 | { 4, 3, 2, 6, -2 } | 4 | 9 |
| 4 | { 4, 3, 2, 7, -2 } | 4 | 10 |
| 5 | { 4, 3, 2, 7, 6 } | 12 | 10 |
**Note: Please keep a pen and paper with you for solving quizzes.**
### Question
What will be the sum of elements at **ODD indices** in the resulting array after removal of **index 2** ?
A[ ] = [ 4, 1, 3, 7, 10 ]
**Choices**
- [ ] 8
- [ ] 14
- [x] 11
- [ ] 9
After removal of element at **index 2**, elements after index 2 has changed their positions:
Sum of elements at **ODD** indices from **[0 to 1]** + Sum of elements at **EVEN** indices from **[3 to 4]** =
1 + 10 = 11
### Question
What will be the sum of elements at **ODD indices** in the resulting array after removal of **index 3** ?
A[ ] = { 2, 3, 1, 4, 0, -1, 2, -2, 10, 8 }
**Choices**
- [ ] 8
- [x] 15
- [ ] 12
- [ ] 21
**Explanation:**
After removal of element at index 3, elements after index 3 has changed their positions:
Sum of elements at **ODD** indices from **[0 to 2]** index + Sum of elements at **EVEN** indices from **[4 to 9]** = A[1]+A[4]+A[6]+A[8] = **3+0+2+10 = 15**
### Question
What will be the sum of elements at EVEN indices in the resulting array after removal of index 3 ?
[2, 3, 1, 4, 0, -1, 2, -2, 10, 8]
**Choices**
- [ ] 15
- [x] 8
- [ ] 10
- [ ] 12
After removal of element at index 3, elements are after index 3 has changed their positions:
Sum of elements at **EVEN** indices from **[0 to 2]** index + Sum of elements at **ODD** indices from **[4 to 9]** = A[0]+A[2]+A[5]+A[7]+A[9] = 2+1+(-1)+(-2)+8 = 8
:::warning
Please take some time to think about the optimised solution approach on your own before reading further.....
:::
### Problem 2 : Observation for Optimised Approach
* Suppose, we want to check if **i** is a **Special Index**.
* Indices of elements present on the left side of i will remain intact while indices of elements present on the right side of element i will get changed.
* Elements which were placed on odd indices will shift on even indices and vice versa.
For example:
```plaintext
A[ ] = { 2, 3, 1, 4, 0, -1, 2, -2, 10, 8 }
```
Sum of **ODD** indexed elements after removing element at index 3 =
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/033/820/original/oddsum.png?1683629378" width=500 />
Sum of **EVEN** indexed elements after removing element at index 3 =
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/033/822/original/evensum.png?168362945" width=500 />
### Approach
* Create **Prefix Sum** arrays for **ODD** and **EVEN** indexed elements.
* Run a loop for $i$ from 0 to n – 1, where n is the size of the array.
* For every element check whether **So** is equal to **Se** or not using the above equations.
* Increment the count if Se is equal to So.
**NOTE:** Handle the case of $i=0$.
### Pseudocode
```cpp
int count_special_index(int arr[], int n) {
// prefix sum for even indexed elements
int PSe[n];
// prefix sum for odd indexed elements
int PSo[n];
//Say we have already calculated PSe and PSo
//Code to find Special Indices
int count = 0;
for (int i = 0; i < n; i++) {
int Se, So;
if (i == 0) {
Se = PSo[n - 1] - PSo[i]; //sum from [i+1 n-1]
So = PSe[n - 1] - PSe[i]; //sum from [i+1 n-1]
} else {
Se = PSe[i - 1] + PSo[n - 1] - PSo[i]; //sum even from [0 to i-1] and odd from [i+1 n-1]
So = PSo[i - 1] + PSe[n - 1] - PSe[i]; //sum odd from [0 to i] and even from [i+1 n-1]
}
if (Se == So) {
count++;
}
}
return count;
}
```
### Complexity
-- TC - $O(n)$
-- SC - $O(n)$

484
Academy DSA Typed Notes/Intermediate/Intermediate DSA Bit Manipulations Basics.md Normal file
View File

@@ -0,0 +1,484 @@
# Bit Manipulation Basics
## Decimal Number System
* The decimal system, also known as the base-10 system, is the number system we use in our everyday lives.
* It is called base-10 because a single digit can take 10 values from 0 to 9.
The position of each digit in a decimal number represents a different power of 10.
For example,
```cpp
342 = 300 + 40 + 2 = 3*10^2 + 4*10^1 + 2*10^0
```
```cpp
2563 = 2000 + 500 + 60 + 3 = 2*10^3 + 5*10^2 + 6*10^1 + 3*10^0
```
---
## Binary Number System
* The binary system, also known as the base-2 system, is used in digital electronics and computing.
* It has only two digits, which are 0 and 1.
In the binary system, each digit represents a different power of 2.
For example,
```cpp
110 = 1*2^2 + 1*2^1 + 0*2^0 = 4 + 2 + 0 = 6
```
```cpp
1011 = 1*2^3 + 0*2^2 1*2^1 + 1*2^0 = 8 + 0 + 2 + 1 = 11
```
---
### Binary to Decimal Conversion
For this conversion, we need to multiply each digit of the binary number by the corresponding power of 2, and then add up the results.
**Example 1:**
Convert binary number 1101 to decimal number.
```
Starting from the rightmost digit, we have:
1 * 2^0 = 1
0 * 2^1 = 0
1 * 2^2 = 4
1 * 2^3 = 8
Adding up the results, we get:
1 + 0 + 4 + 8 = 13
Therefore, the decimal equivalent of the binary number 1101 is 13.
```
**Example 2:**
Convert binary number 10101 to decimal number.
- Starting from the rightmost digit, we have:
```
1 * 2^0 = 1
0 * 2^1 = 0
1 * 2^2 = 4
0 * 2^3 = 0
1 * 2^4 = 16
```
- Adding up the results, we get:
```
1 + 0 + 4 + 0 + 16 = 21
```
Therefore, the decimal equivalent of the binary number 10101 is 21.
---
### Question
What is the decimal representation of this binary number: 1011010
**Choices**
- [ ] 45
- [x] 90
- [ ] 94
- [ ] 130
**Explanation:**
Starting from the rightmost digit, we have:
0 * 2^0 = 0
1 * 2^1 = 2
0 * 2^2 = 0
1 * 2^3 = 8
1 * 2^4 = 16
0 * 2^5 = 0
1 * 2^6 = 64
Adding up the results, we get: 0 + 2 + 0 + 8 + 16 + 0 + 64 = 90
Therefore, the decimal representation of the binary number 1011010 is 90.
---
### Decimal to Binary Conversion
We can solve it using long division method, for which we need to repeatedly divide the decimal number by 2 and record the remainder until the quotient becomes 0.
**Example:**
Convert decimal number 20 to binary number.
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/034/146/original/bitmanipulationimage1.png?1683885852" width="40%" height="20%">
---
### Question
What is the binary representation of 45 ?
**Choices**
- [ ] 101100
- [ ] 101110
- [ ] 101111
- [x] 101101
**Explanation:** Here are the steps to convert decimal number 45 to binary:
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/034/147/original/bitmanipulationimage2.png?1683885879" width="40%" height="20%">
---
### Addition of Decimal Numbers
**Example -**
```cpp
Calculate => (368 + 253)
```
<img
src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/033/817/original/Screenshot_2023-05-09_at_3.57.38_PM.png?1683628220" width="30%" >
**Explanation:**
* Start by adding the rightmost digits: 8 + 3 = 11 (digit = 11%10 = 1, carry 11/10 = 1)
* Next column: 1 + 6 + 5 = 12 (digit = 12%10 = 2, carry 12/10 = 1)
* Final column: 1 + 3 + 4 = 8 (digit = 8%10 = 8, carry 8/10 = 0)
Therefore, answer is 821.
---
### Addition of Binary Numbers
**Example 1:**
| | 1 | 0 | 1 | 0 | 1 |
|---|---|---|---|---|---|
| + | | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 |
**Explanation:**
d = answer digit, c = carry
* From right, 1 + 1 = 2 (d = 2%2=0, c = 2/2 = 1)
* Next: 1 + 0 + 0 = 1 (d = 1%2=1, c = 1/2 = 0)
* Next: 0 + 1 + 1 = 2 (d = 2%2=0, c = 2/2 = 1)
* Next: 1 + 0 + 1= 2 (d = 2%2=0, c = 2/2 = 1)
* Final: 1 + 1 = 2 (d = 2%2=0, c = 2/2 = 1)
* Finally, 1 carry is remaining, so write 1.
The result is 100010 in binary.
**Example 2:**
| | 1 | 1 | 0 | 1 | 0 | 1 |
|---|---|---|---|---|---|---|
| + | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 |
**Explanation:**
d = answer digit, c = carry
* From Right: 1 + 0 = 1 (d: 1%2 = 1, c: 1/2 = 0)
* Next column: 0 + 0 + 1 = 1 (d: 1%2 = 1, c: 1/2 = 0)
* Next column: 0 + 1 + 1 = 2 (d: 2%2 = 0, c: 2/2 = 1)
* Next column: 1 + 0 + 0 = 1 (d: 1%2 = 1, c: 1/2 = 0)
* Next column: 0 + 1 + 0 = 1 (d: 1%2 = 1, c: 1/2 = 0)
* Next column: 0 + 1 + 1 = 2 (d: 2%2 = 0, c: 2/2 = 1)
* Finally, 1 carry is remaining, so write 1.
The result is 1011011 in binary.
---
### Question
What is the sum of these binary numbers: 10110 + 00111
**Choices**
- [ ] 11111
- [ ] 10101
- [ ] 11011
- [x] 11101
**Explanation:**
d = answer digit, c = carry
* Start by adding the rightmost bits: 0 + 1 = 1 (d: 1%2 = 1, c: 1/2 = 0)
* Next column: 0 + 1 + 1 = 2 (d: 2%2 = 0, c: 2/2 = 1)
* Next column: 1 + 1 + 1 = 3 (d: 3%2 = 1, c: 3/2 = 1)
* Next column: 1 + 0 + 0 = 1 (d: 1%2 = 1, c: 1/2 = 0)
* Final column: 0 + 1 + 0 = 1 (d: 1%2 = 1, c: 1/2 = 0)
The result is 11101 in binary.
---
### Bitwise Operators
* Bitwise operators are used to perform operations on individual bits of binary numbers.
* They are often used in computer programming to manipulate binary data.
* In bitwise operations, `0 -> false/unset` and `1 -> true/set`
#### AND (&)
* This operator takes two binary numbers and performs a logical AND operation on each pair of corresponding bits.
* The resulting bit in the output is 1 if and only if both the corresponding bits in the input are 1. Otherwise, the resulting bit is 0.
* The symbol for AND operator is '&'.
``` cpp
0 & 0 = 0
1 & 0 = 0
0 & 1 = 0
1 & 1 = 1
```
#### OR (|)
* This operator takes two binary numbers and performs a logical OR operation on each pair of corresponding bits.
* The resulting bit in the output is 1 if either one or both of the corresponding bits in the input are 1. Otherwise, the resulting bit is 0.
* The symbol for OR operator is '|'.
``` cpp
0 | 0 = 0
1 | 0 = 1
0 | 1 = 1
1 | 1 = 1
```
#### XOR (^)
* This operator takes two binary numbers and performs a logical XOR (exclusive OR) operation on each pair of corresponding bits.
* The resulting bit in the output is 1 if the corresponding bits in the input are different. Otherwise, the resulting bit is 0.
* The symbol for XOR operator is '^'.
``` cpp
0 ^ 0 = 0
1 ^ 0 = 1
0 ^ 1 = 1
1 ^ 1 = 0
```
#### NOT(!/~)
* This operator takes a single binary number and performs a logical NOT operation on each bit.
* The resulting bit in the output is the opposite of the corresponding bit in the input.
* The symbols for NOT operator are '~' or '!'.
``` cpp
~0 = 1
~1 = 0
```
---
### Bitwise Operations Example
**Example 1:**
```cpp
5 & 6
//Binary representation
5 -> 101
6 -> 110
// Bitwise AND operation
101 & 110 = 100 = 4
```
**Example 2:**
```cpp
20 & 45
//Binary representation
20 -> 010100
45 -> 101101
// Bitwise AND operation
010100 & 101101 = 111101 = 61
```
**Example 3:**
```cpp
92 & 154
//Binary representation
92 -> 01011100
154 -> 10011010
// Bitwise OR operation
01011100 | 10011010 = 11011110 = 222
```
**Example 4**:
```cpp
~01011100
//Binary representation
92 -> 01011100
// Bitwise NOT operation
~01011100 = 10100011 = 163
```
**Example 5:**
```cpp
92 ^ 154
//Binary representation
92 -> 01011100
154 -> 10011010
// Bitwise XOR operation
01011100 ^ 10011010 = 11000110 = 198
```
---
### Question
What is the value of A ^ B (i.e. A XOR B) where, A = 20 and B = 45?
**Choices**
- [ ] 4
- [ ] 20
- [x] 57
- [ ] 61
**Explanation:**
* A = 20 = 00010100 (in binary)
* B = 45 = 00101101 (in binary)
Performing XOR on each pair of bits, we get:
```
00010100 ^ 00101101 = 00111001
```
Therefore, the value of A XOR B is 00111001, which is 57 in decimal format.
---
### Binary Representation of Negative numbers
To convert a negative number to its binary representation, we can use two's complement representation.
It works as follows -
* Convert the absolute value of number to Binary representation.
* Invert all the bits of number obtained in step 1.
* Add 1 to the number obtained in step 2.
Example of converting the negative number $-5$ to its $8-bit$ binary representation:
1. 5 to binary representation:```0000 0101```
2. Invert all the bits:`0000 0101 -> 1111 1010`
3. Add 1 to the inverted binary representation:
`1111 1010 + 0000 0001 = 1111 1011`
**Note:**
1. The MSB has a negative base and that is where the negative sign comes from.
2. In case of positive number, MSB is always 0 and in case of negative number, MSB is 1.
---
### Question
What is the binary representation of -3 in 8-bit signed integer format?
Choose the correct answer
**Choices**
- [x] 11111101
- [ ] 01111101
- [ ] 00000011
- [ ] 10101010
---
### Question
What is the binary representation of -10 in 8-bit signed integer format?
Choose the correct answer
**Choices**
- [x] 11110110
- [ ] 11110111
- [ ] 11111110
- [ ] 10101010
---
### Range of Data Types
What is the minimum & maximum no. that can be stored in the given no. of bits?
![](https://hackmd.io/_uploads/B1K61joE3.png)
Generalisation for N Bits:
![](https://hackmd.io/_uploads/Hk1JbioE2.png)
So, in general we can say that the {minimum,maximum} number in n-bit number is **{-2<sup>N-1</sup> , 2<sup>N-1</sup>-1}**.
#### Integer(32-bit number)
Integer is the 32 bit number. Its range is **{-2<sup>32-1</sup> , 2<sup>32-1</sup>-1}**.
#### Long(64-bit number)
Long is the 64 bit number. Its range is **{-2<sup>64-1</sup> , 2<sup>64-1</sup>-1}**.
### Approximation
Approximation is done to better approximate the range of values that can be stored in integer or long.
For integer,
![](https://hackmd.io/_uploads/SkjvJPtEn.png)
For long,
![](https://hackmd.io/_uploads/rJjtkwY4n.png)
---
### Importance of Constraints
Let's understand the importance of constraints using example.
Suppose we have two integers as
```
a = 10^5
b = 10^6
```
What will be the value of c ?
#### TRY 1:
```
int c = a*b
```
It will Overflow, i.e **c** will contain wrong value.
**Fails, the Reason:**
* The calculation happens at ALU.
* If we provide ALU with two INT, it calculates result in INT.
* Therefore, $a*b$ will overflow before even getting stored in c.
#### TRY 2:
Say, we change the data type of c to long, what will be the value of c?
```
long c = a*b
```
**Fails, the Reason:**
**c** would contain overflowed value since $a*b$ will overflow at the time of calculation, therefore there's no use to change datatype of **c** from INT to LONG.
#### TRY 3:
What if we typecast $a*b$ to long as below?
```
long c = long (a*b)
```
**Fails, the Reason:**
Already overflown, hence no use to typecast later.
#### TRY 4:
What if we change the equation as shown below?
```
long c = (long) a * b
```
This is the correct way to store.
**WORKS, the Reason:**
* Here, we have typecasted **a** to long before multiplying with **b**.
* If we send one INT and one LONG, ALU calculates answer in LONG.
### Question
Given an array of size N, calculate the sum of array elements.
**Constraints:**
1 <= N <= 10<sup>5</sup>
1 <= A[i] <= 10<sup>6</sup>
Is the following code correct ?
```
int sum = 0;
for (int i = 0; i < N; i++) {
sum = sum + A[i];
}
print(sum)
```
**We should look at constraints.**
As per constraint, range of sum will be as follows -
**1 <= sum <= 10<sup>11</sup>**
The above code is incorrect since sum can be as big as 10<sup>11</sup> which can't be stored in INTEGER.
Hence, we should change dataType of "sum" to LONG.

541
Academy DSA Typed Notes/Intermediate/Intermediate DSA Interview Problems.md Normal file
View File

@@ -0,0 +1,541 @@
# Interview Problems
## Analyzing constraints
### Tips on Problem Constraints
* Analyzing the constraints can help you determine which time complexity and data structure or algorithm to use for a given problem.
* It is important to look at the constraints whenever we are solving a problem.
Note: In Interviews, don't ask the constraints directly. Rather, tell your approach and ask the interviewer if you need to optimize further.
If,
| Constraint | Possible Time Complexities |
| ----------------------- | ------------------------------ |
| n <= 10^6 | O(n), O(nlogn) |
| n <= 20 | O(n!), O(2^n) |
| n <= 10^10 | O(logn), O(sqrt(n)) |
Note: These are just general guidelines. The actual time complexity can vary based on the specific problem and implementation.
It's always important to analyze the problem and determine the best approach for your specific solution.
---
### Problem 1 Find the maximum number of consecutive 1's after replacement
#### Problem Statement
Given an array of 1's and 0's, you are allowed to replace only one 0 with 1. Find the maximum number of consecutive 1's that can be obtained after making the replacement.
**Example 1**
```cpp
Input = [1, 1, 0, 1, 1, 0, 1, 1]
Output = 5
```
**Explanation:**
If we replace 0 at 2nd index or 0 at 5th index with 1, in both cases we get 5 consecutes 1's.
### Question
Find the maximum number of consecutive 1's that can be obtained after replacing only one 0 with 1.
A[] = [ 1, 1, 0, 1, 1, 0, 1, 1, 1 ]
**Choices**
- [ ] 4
- [ ] 5
- [x] 6
- [ ] 7
* If we replace 0 at 2nd index with 1 we get 5 consecutes 1's.
* If we replace 0 at 5th index with 1 we get 6 consecutes 1's.
Hence, the maximum is 6 consecutive 1's.
---
### Question
Find the maximum number of consecutive 1's that can be obtained after replacing only one 0 with 1.
A[] = [0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0]
**Choices**
- [ ] 4
- [ ] 5
- [x] 6
- [ ] 7
* If we replace 0 at 0th index with 1 we get 4 consecutes 1's.
* If we replace 0 at 4th index with 1 we get 6 consecutes 1's.
* If we replace 0 at 7th index with 1 we get 5 consecutes 1's.
* If we replace 0 at last index with 1 we get 3 consecutes 1's.
Hence, the maximum is 6 consecutive 1's.
---
:::warning
Please take some time to think about the solution approach on your own before reading further.....
:::
### Solution Approach
* Maintain a variable say "ans", which keeps track of the maximum consecutive 1's encountered.
* Initialize it with 0.
* Iterate through the input array. When we encounter a zero at an index, we do the following:
* Count no. of consecutive 1's on left: **l**
* Count no. of consecutive 1's on right: **r**
* If (**l+r+1** > ans), replace ans with (**l+r+1**).
**Edge case**: When all the array elements are `1's`, then return the length of the whole array.
#### Pseudocode
```cpp
int findMaxConsecutiveOnes(int nums[]) {
int n = nums.size();
int maxCount = 0;
int totalOnes = 0;
for (int i = 0; i < n; i++) {
if (nums[i] == 1)
totalOnes++;
}
if (totalOnes == n)
return n;
for (int i = 0; i < n; i++) {
if (nums[i] == 0) {
int l = 0, r = 0, j = i + 1;
// calculate the maximum consecutive ones after replacing this zero
while (j < n && nums[j] == 1) {
r++;
j++;
}
j = i - 1;
while (j >= 0 && nums[j] == 1) {
l++;
j--;
}
maxCount = max(l + r + 1, count);
}
}
return maxCount;
}
```
---
### Question
What will be the TC of this approach ?
**Choices**
- [x] O(n)
- [ ] O(n^2)
- [ ] O(n^3)
- [ ] O(n^4)
**Explanation:**
The time complexity of the above solution is O(n) because it performs a single pass over the input array and every element will get accessed at maximum of 3 times.
> ![](https://hackmd.io/_uploads/rk-sTkprh.png)
---
## Variation of Problem 1
### Coding Question 2
#### Problem Statement
Given an array of 1's and 0's, find the maximum number of consecutive 1's that can be obtained by SWAPPING at most one 0 with 1(already present in the string).
**Example 1**
```cpp
Input: [1, 0, 1, 1, 0, 1]
Output: 5
```
#### Explanation:
We can swap zero at index 4 with 1 to get the array [1, 0, 1, 1, 1, 1], which has 5 consecutive 1s.
---
### Question
find the maximum number of consecutive 1’s that can be obtained by swapping at most one 0 with 1.
A[] = [1, 1, 0, 1, 1, 1]
**Choices**
- [ ] 2
- [ ] 4
- [x] 5
- [ ] 6
**Explanation:**
We can swap the zero at index 2 with 1 at either index 0 or index 5 to get the array which has 5 consecutive 1s.
---
### Problem 1 variation continues
#### Solution
* The solution is very similar to solution to previous problem except for some modifications.
* We iterate through the input array. When we encounter a zero at an index, we do the following:
* Count no. of consecutive 1's on left -> l.
* Count no. of consecutive 1's on right -> r.
* If (l+r) is equal to total no. of 1's in the array, then currMax = (l+r), else currMax = (l+r+1).
* If (currMax > ans), replace ans with (currMax)
**Edge case**: When all the array elements are `1's`, then return the length of the whole array.
#### Pseudocode
```cpp
int findMaxConsecutiveOnes(int nums[]) {
int n = nums.size();
int maxCount = 0;
int totalOnes = 0;
for (int i = 0; i < n; i++) {
if (nums[i] == 1)
totalOnes++;
}
if (totalOnes == n)
return n;
for (int i = 0; i < n; i++) {
if (nums[i] == 0) {
int l = 0, r = 0, j = i + 1, currMax;
// calculate the maximum consecutive ones after swapping this zero
while (j < n && nums[j] == 1) {
r++;
j++;
}
j = i - 1;
while (j >= 0 && nums[j] == 1) {
l++;
j--;
}
if (l + r == totalOnes)
currMax = l + r;
else
currMax = l + r + 1
maxCount = max(currMax, count);
}
}
return maxCount;
}
```
#### Time and Space Complexity
* TC - O(n)
* SC - O(1)
---
### Problem 2 Majority Element
Given an array of N integers, find the **majority element.**
The **majority element** is the element that occurs more than n/2 times where n is size of the array.
**Example 1**
```plaintext
A[ ] = { 2, 1, 4 }
Ans = No Majority element
```
### Explanation
Here, none of the elements have frequency more than n/2 where n is 3.
**Example 2**
```plaintext
A[ ] = { 3, 4, 3, 2, 4, 4, 4, 4}
Ans = 4
```
#### Explanation
Here, frequency of 4 is more than n/2 that is 5 where n is 8. So 4 will be the majority element.
**Example 3**
```plaintext
A[ ] = { 3, 3, 4, 2, 4, 4, 2, 4}
Ans = No Majority element
```
#### Explanation:
Here, none of the elements have frequency more than n/2 where n is 8.
---
### Question
What is the majority element in this array?
3, 4, 3, 6, 1, 3, 2, 5, 3, 3, 3
**Choices**
- [ ] 1
- [x] 3
- [ ] 2
- [ ] 6
Here, 3 has frequency > n/2 where n is 11.
### Question
What is the majority element in the following array?
4, 6, 5, 3, 4, 5, 6, 4, 4, 4
**Choices**
- [ ] 3
- [ ] 4
- [ ] 6
- [x] No Majority Element
**Explanation:**
Here, none of the elements have frequency more than n/2 where n is 10.
---
### Question
At max how many majority elements can be there in an array?
**Choices**
- [x] 1
- [ ] 2
- [ ] n-1
- [ ] n
Suppose there is an array of size n. If frequency of an element is greater than n/2, then there cannot exist an element in remaining elements whose frequency is greater than n/2 .
Hence, there can be only one majority element.
---
### Problem 2 Brute Force
Iterate through every element in the array, count the number of times each element appears, and return the element that appears more than n/2 times.
#### Pseudocode
```cpp
void findMajority(int arr[], int n) {
int maxCount = 0;
int index = -1;
for (int i = 0; i < n; i++) {
int count = 0;
for (int j = 0; j < n; j++) {
if (arr[i] == arr[j])
count++;
}
if (count > maxCount) {
maxCount = count;
index = i;
}
}
if (maxCount > n / 2)
print(arr[index])
else
print("No Majority Element")
}
```
#### Complexity
-- TC - $O(n^2)$
-- SC - $O(1)$
:::warning
Please take some time to think about the Optimised approach on your own before reading further.....
:::
---
### Problem 2 Optimised Approach using Moore’s Voting Algorithm
#### Observation 1:
There can only be **one majority element** in the array.
#### Proof:
We will prove it by contradiction.
* Let's say there are two majority elements, say m1 and m2.
* frequency(m1) > n/2 and frequency(m2) > n/2
* Adding both sides,
* frequency(m1) + frequency(m2) > n **[it not possible]**
* Hence, Prooved.
#### Observation 2:
If we **remove any two distinct elements, the majority element remains the same.**
**Explanation 1:**
> Consider array of 13 blocks.
First **7 blocks** are filled with **GREEN colour**.
Next **6 blocks** are filled with **RED colour**.
**Majority** is **GREEN**.
If we remove 2 distinct blocks, 1 from GREEN and 1 from RED, we will be left with 11 elements.
**Majority** is still **GREEN**.
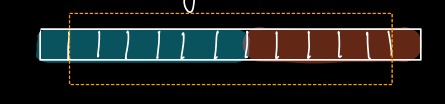
![](https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/032/886/original/e1.jpeg?1682577851)
> Again, If we remove 2 distinct elements, 1 from GREEN and 1 from RED, we will be left with 9 elements.
**Majority** is still **GREEN**.
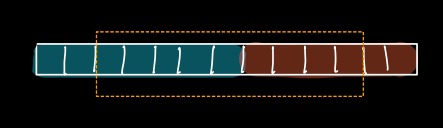
![reference link](https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/032/887/original/e2.jpeg?1682578235)
> If we continue this process we will get GREEN as MAJORITY element.
**Explanation 2:**
Suppose there are **4 parties** participating in an **election**.
* First: ORANGE party(OP) with **9** candidates.
* Second: YELLOW party(YP) with **3** candidates.
* Third: RED party(RP) with **2** candidates.
* Fourth: GREEN party(GP) with **3** candidates.
Currently, the **WINNER is ORANGE**
![](https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/032/666/original/elect.jpeg?1682430684)
| Remove | Orange | Yellow | Red | Green | Winner|
| --- |--- | ---| ----- | ------| ---|
|1 OP and 1 YP | 8 | 2 | 2 | 3 |Orange
|1 OP and 1 GP | 7 | 2 | 2 | 2 |Orange
|1 OP and 1 RP | 6 | 2 | 1 | 2 |Orange
|1 YP and 1 RP | 6 | 1 | 0 | 2 |Orange
|1 YP and 1 GP | 6 | 0 | 0 | 1 |Orange
|1 OP and 1 GP | 5 | 0 | 0 | 0 |Orange
We can observe that after removing 2 distinct party votes every time, majority is maintained at every point.
**Note:** We cannot remove same party votes twice.
---
### Problem 2 Moore’s Voting Algorithm Approach and Dry Run
#### Approach
* Iterate through each element of the array, keeping track of the majority element's count and index.
* If the next element is the same as the current majority element, increase the count; otherwise, decrease the count.
* If the count becomes zero, update the majority index to the current element and reset the count to 1.
* After the iteration, go through the array once again and determine the count of the majority element found.
* If count > N/2, return majority elsement; else majority element doesn't exist.
#### Dry Run
Please **dry run** for the following example:
```plaintext
A[ ] = { 3, 4, 3, 6, 1, 3, 2, 5, 3, 3, 3 }
```
#### Pseudocode
```cpp
int findCandidate(int a[], int size) {
int maj_index = 0, count = 1;
for (int i = 1; i < size; i++) {
if (count == 0) {
maj_index = i;
count = 1;
} else {
if (a[maj_index] == a[i])
count++;
else
count--;
}
}
//check if the candidate
//occurs more than n/2 times
int count = 0;
for (int i = 0; i < size; i++) {
if (a[i] == a[maj_index])
count++;
}
if (count > size / 2)
return a[maj_index];
else
return -1;
}
```
#### Time and Space Complexity
What will be T.C and S.C for this approach?
-- TC - $O(n)$
-- SC - $O(1)$
---
### Problem 3 Row to Column Zero
You are given a 2D integer matrix A, make all the elements in a row or column zero if the A[i][j] = 0. Specifically, make entire ith row and jth column zero.
**Example**
**Input:**
[1,2,3,4]
[5,6,7,0]
[9,2,0,4]
**Output:**
[1,2,0,0]
[0,0,0,0]
[0,0,0,0]
**Explanation:**
A[2][4] = A[3][3] = 0, so make 2nd row, 3rd row, 3rd column and 4th column zero
#### Observation
If you start row wise and make one row completely zero if it has 0 then you will loose information for making columns zero.
**Note:** None element is negative so see if you may use this for not loosing info.
#### Approach
* Let's start row wise first.
* Select rows one by one and make all the elements of that row -1(except which are 0), if any element in that row is 0.
* Similariy you have to do the same thing for columns.
* Now, before returning traverse the matrix and make all the -1 elements 0.
#### Pseudocode
```cpp
int n = A.size(), m = A[0].size();
for (int i = 0; i < n; i++) {
int flag = 0;
for (int j = 0; j < m; j++) {
if (A[i][j] == 0) flag = 1;
}
if (flag == 1) {
for (int j = 0; j < m; j++) {
if (A[i][j] != 0) A[i][j] = -1;
}
}
}
for (int j = 0; j < m; j++) {
int flag = 0;
for (int i = 0; i < n; i++) {
if (A[i][j] == 0) flag = 1;
}
if (flag == 1) {
for (int i = 0; i < n; i++) {
if (A[i][j] != 0) A[i][j] = -1;
}
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (A[i][j] == -1) A[i][j] = 0;
}
}
return A;
```

477
Academy DSA Typed Notes/Intermediate/Intermediate DSA Introduction to Arrays.md Normal file
View File

@@ -0,0 +1,477 @@
# Introduction To Arrays
## Space Complexity
* Space complexity is the max space(worst case) that is utilised at any point in time during running the algorithm.
* We also determine Space Complexity using **Big O**.
Consider the following example:
```pseudocode
func(int N) { // 4 bytes
int x; // 4 bytes
int y; // 4 bytes
long z; // 8 bytes
}
```
* We only consider the space utilised by our program and not the Input Space since it is not in our control, hence we'll ignore space taken by "int N".
* The above code takes total **16B** of memory.
* Hence, we say the **Space Complexity** of the above code is **O(1)** (1 resembles constant).
### Question
Find the Space Complexity [Big(O)] of the below program.
```pseudocode
func(int N) { // 4 bytes
int arr[10]; // 40 Bytes
int x; // 4 bytes
int y; // 4 bytes
long z; // 8 bytes
int[] arr = new int[N]; // 4 * N bytes
}
```
**Choices**
- [x] N
- [ ] 4N + 60
- [ ] Constant
- [ ] N^2
### Question
Find the Space Complexity [Big(O)] of the below program.
```pseudocode
func(int N) { // 4 bytes
int x = N; // 4 bytes
int y = x * x; // 4 bytes
long z = x + y; // 8 bytes
int[] arr = new int[N]; // 4 * N bytes
long[][] l = new long[N][N]; // 8 * N * N bytes
}
```
**Choices**
- [ ] N
- [ ] 4N + 60
- [ ] Constant
- [x] N^2
### Question on Space Complexity
Find the Space Complexity [Big(O)] of the below program.
```cpp
int maxArr(int arr[], int N) {
int ans = arr[0];
for(i from 1 to N-1) {
ans = max(ans, arr[i]);
}
return ans;
}
```
### Space complexity: O(1)
* Don't consider the space acquired by the input size. Space complexity is the order of extra space used by the algorithm.
* **arr[]** is already given to us, we didn't create it, hence it'll not be counted in the Space Complexity.
* **int N** will also not be counted in space but since it is contant hence doesn't matter.
* Additional space is also called **computational or auxiliary space.**
* The above code finds the max element of the Array.
### Introduction To Arrays
#### Definition
Array is the collection of same types of data. The datatype can be of any type i.e, int, float, char, etc. Below is the declaration of the array:
```
int arr[n];
```
Here, ‘int’ is the datatype, ‘arr’ is the name of the array and ‘n’ is the size of an array.
We can access all the elements of the array as arr[0], arr[1] ….. arr[n-1].
**Note:** Array indexing starts with 0.
##### Why indexing starts at 0 ?
An array arr[i] is interpreted as *(arr+i). Here, arr denotes the address of the first array element or the 0 index element. So *(arr+i) means the element at i distance from the first element of the array.
### Question
What will be the indices of the first and last elements of an array of size **N**?
Choose the correct answer
**Choices**
- [ ] 1,N
- [x] 0,N-1
- [ ] 1,N-1
- [ ] 0,N
## Introduction to Arrays Continued
### Print all elements of the array
The elements of arrays can be printed by simply traversing all the elements. Below is the pseudocode to print all elements of array.
```
void print_array(int arr[],int n){
for(int i=0;i<n;i++){
print(arr[i]);
}
}
```
### Question
What is the time complexity of accessing element at the ith index in an array of size **N**?
**Choices**
- [ ] O(N)
- [x] O(1)
- [ ] O(N*N)
- [ ] O(log(N)).
### Question
int arr[5] = {5,-4,8,9,10}
Print sum of 1st and 5th element
Choose the correct answer
**Choices**
- [ ] print(arr[0]+arr[5])
- [x] print(arr[0]+arr[4])
- [ ] print(arr[1]+arr[5])
- [ ] print(arr[1]+arr[4])
### Question 1 Reverse the array
Given an array 'arr' of size 'N'. Reverse the entire array.
#### TestCase:
#### Input:
```
N = 5
arr = {1,2,3,4,5}
```
#### Output:
```
arr = {5,4,3,2,1}
```
:::warning
Please take some time to think about the solution approach on your own before reading further.....
:::
#### Approach
The simplest approach to solve the problem is to keep two pointers at the end, traverse the array till middle element and swap first element with last element, second with second last, third with third last and so on.
![](https://i.imgur.com/xUDocWR.png)
**What should be the stopping condition?**
Say N = 6
| i | j | swap |
| -------- | -------- | -------- |
| 0 | 5 | A[0] & A[5] |
| 1 | 4 | A[1] & A[4] |
| 2 | 3 | A[2] & A[3] |
| 3 | 2 | STOP |
Say N = 5
| i | j | swap |
| -------- | -------- | -------- |
| 0 | 4 | A[0] & A[4] |
| 1 | 3 | A[1] & A[3] |
| 2 | 2 | STOP |
We can stop as soon as $i>=j$
### Pseudocode
```cpp
Function reverse(int arr[], int N) {
int i = 0, j = N - 1;
while (i < j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
i++;
j--;
}
}
```
#### Complexity:
**Time Complexity - O(N).
Space Complexity - O(1).**
### Question 2 Reverse in a range
Given an array 'arr' of size 'N' and integers 'l' and 'r'. Reverse the array from 'l' to 'r'.
#### TestCase:
#### Input:
```
N = 5
arr = {1,2,3,4,5}
[0 based index]
l = 1
r = 3
```
#### Output:
```
arr = {1,4,3,2,5}
```
#### Pseudocode
```cpp
Function reverse(int arr[], int N, int l, int r) {
while (l < r) {
int temp = arr[l];
arr[l] = arr[r];
arr[r] = temp;
l++;
r--;
}
}
```
#### Complexity:
**Time Complexity - O(N).
Space Complexity - O(1).**
### Question 3 Rotate K times
Given an array 'arr' of size 'N'. Rotate the array from right to left 'K' times. (i.e, if K = 1, last element will come at first position,...)
#### TestCase:
#### Input:
```
N = 5
arr = {1,2,3,4,5}
k = 2
```
#### Output:
```
arr = {4,5,1,2,3}
```
#### Explanation:
Initially the array is:
| 1 | 2 | 3 | 4 | 5 |
After 1st rotation:
| 5 | 1 | 2 | 3 | 4 |
After 2nd rotation:
| 4 | 5 | 1 | 2 | 3 |
:::warning
Please take some time to think about the solution approach on your own before reading further.....
:::
### BruteForce Approach
Simple approach is to rotate the array one element at a time.
#### Pseudocode
```cpp
Function rotateK(int arr[], int N, int K) {
for (int i = 0; i < K; i++) {
int temp = arr[N - 1];
for (int j = N - 1; j >= 1; j--) {
arr[j] = arr[j - 1];
}
arr[0] = temp;
}
}
```
#### Complexity:
**Time Complexity - O(N*K).
Space Complexity - O(1).**
### Optimized Approach
:::success
Please take some time to think about the optimised solution approach on your own before reading further.....
:::
#### Optimized Appraoch Observations
* After K rotations, last K elements become 1st K elements and rest elements will go at back.
For example - Suppose we have an array arr as shown below and k = 3.
`1 2 3 4 5 6 7`
After 1st rotation, k=1:
`7 1 2 3 4 5 6`
After 2nd rotation, k=2:
`6 7 1 2 3 4 5`
After 3rd rotation, k=3:
`5 6 7 1 2 3 4`
So, we have observed that last 3(K=3) elements i.e, `5 6 7` comes in front and rest elements appear at the end.
Therefore, we will first reverse the entire array, then reverse first K elements individually and then next N-K elements individually.
```
1 2 3 4 5 6 7 //Given Array, K=3
7 6 5 4 3 2 1 //Reversed Entire Array
5 6 7 4 3 2 1 //Reversed first K elements
5 6 7 1 2 3 4 //Reversed last N-K elements
```
#### Pseudocode
```cpp
Function countgreater(int arr[], int N, int k) {
reverse(arr, N, 0, N - 1);
reverse(arr, N, 0, K - 1);
reverse(arr, N, K, N - 1);
}
```
#### Edge Case
K might be very large but if we observe carefully then after N rotations the array comes to its initial state.
Hence, K rotation is equivalent to K%N rotations.
Suppose we have an array:
`1 2 3 4`
After 1st rotation, the array becomes:
`2 3 4 1`
After 2nd rotation, the array becomes:
`3 4 1 2`
After 3rd rotation, the array becomes:
`4 1 2 3`
Afer 4th rotation, the array becomes:
`1 2 3 4`
Hence, we have concluded that after **N** rotations, the array become same as before 1st rotation.
### Final Pseudocode
```cpp
Function countgreater(int arr[], int N, int K) {
K = k % N;
reverse(arr, N, 0, N - 1);
reverse(arr, N, 0, K - 1);
reverse(arr, N, K, N - 1);
}
```
#### Complexity:
**Time Complexity - O(N).
Space Complexity - O(1).**
## Dynamic Arrays
### Question:
What is the drawback of normal arrays?
#### Issue:
The size has to be declared before hand.
### Dynamic Arrays
* A dynamic array is an array with a big improvement: automatic resizing.
* It expands as you add more elements. So you don't need to determine the size ahead of time.
### Strengths:
**Fast lookups:** Just like arrays, retrieving the element at a given index takes
O(1) time.
**Variable size:** You can add as many items as you want, and the dynamic array will expand to hold them.
### Weaknesses:
**Slow worst-case appends:**
* Usually, adding a new element at the end of the dynamic array takes O(1) time.
* But if the dynamic array doesn't have any room for the new item, it'll need to expand, which takes O(n) time.
* It is because we have to take a new array of bigger size and copy all the elements to a new array and then add a new element.
* So, Time Complexity to add a new element to Dynamic array is **O(1) amortised**.
* Amortised means when most operations take **O(1)** but some operations take **O(N)**.
### Dynamic Arrays in Different Languages
#### Java
```
ArrayList<String> al = new ArrayList<>(); //Arraylist is created
```
```
al.add("50"); //50 is inserted at the end
```
```
al.clear(); // al={}
```
```
for (int i = 0; i < al.size(); i++) {
System.out.print(al.get(i) + " ");
} //iterating the Arraylist
```
#### C++
```
vector<int> a; //vector is created
```
```
a.push_back(60);
//a = {10, 20, 30, 40, 50, 60} after insertion at end
```
```
a.clear(); // a={}
```
```
for(int i=0; i<a.size(); i++) {
cout<<a[i];
} //iterating the vector
```
#### Python
```
thislist = [] //created list
```
```
thislist.append("orange") //added orange at end
```
```
thislist.clear() //cleared the list
```
```
for i in range(len(thislist)):
print(thislist[i]) //iterating on the list
```

420
Academy DSA Typed Notes/Intermediate/Intermediate DSA Introduction to Problem Solving.md Normal file
View File

@@ -0,0 +1,420 @@
# Introduction to Problem Solving
---
Notes Description
---
* Introduction to Problem Solving
* Time Complexity
* Introduction to Arrays
* Prefix Sum
* Carry Forward
* Subarrays
* 2D Matrices
* Sorting Basics
* Hashing Basics
* Strings Basics
* Bit Manipulation Basics
* Interview Problems
**Following will be covered in the notes!**
1. Count the Factors
2. Optimisation for counting the Factors
3. Check if a number is Prime
4. Sum of N Natural Numbers
5. Definition of AP & GP
6. How to find the number of a times a piece of code runs, i.e, number of Iterations.
7. How to compare two Algorithms.
## Count of factors of a number N
Q. What is a factor?
A. We say i is a factor of N if i divides N completely, i.e the remainder is 0.
How to programmatically check if i is a factor of N ?
We can use % operator which gives us the remainder.
=> **N % i == 0**
**Question 1:**
Given N, we have to count the factors of N.
**Note:** N > 0
**Question 2:**
Number of factors of the number 24.
**Choices**
- [ ] 4
- [ ] 6
- [x] 8
- [ ] 10
**Explanation:**
1, 2, 3, 4, 6, 8, 12, and 24 are the factors.
**Question 3:**
Number of factors of the number 10.
**Choices**
- [ ] 1
- [ ] 2
- [ ] 3
- [x] 4
**Explanation:**
1, 2, 5, and 10 are the factors.
:::warning
Please take some time to think about the solution approach on your own before reading further.....
:::
### Counting Factors Brute force solution
What is the minimum factor of a number ?
=> 1
What is the maximum factor of a number ?
=> The number itself
So, we can find all factors of N from 1 to N.
### Pseudocode
```cpp
function countfactors (N):
fac_count = 0
for i = 1 till N:
if N % i == 0:
fac = fac + 1
return fac
```
### Observations for Optimised Solution
* Now, your code runs on servers.
* When you submit your code, do you expect some time within which it should return the Output ?
* You wouldn't want to wait when you even don't know how long to wait for ?
* Just like that one friend who says, 'Just a little more time, almost there.' And you feel annoyed, not knowing how much longer you'll have to wait.
Servers have the capability of running ~10^8 Iterations in 1 sec.
|N| Iterations| Execution Time|
|-|----------|---------- |
|10^8| 10^8 iterations| 1 sec |
|10^9| 10^9 iterations| 10 sec |
|10^18| 10^18 iterations| 317 years |
### Optimisation for Counting Factors
**Optimization:**
i * j = N -> {i and j are factors of N}
=> j = N / i -> {i and N / i are factors of N}
For example, N = 24
|i| N / i|
|-|----------|
|1| 24|
|2| 12|
|3| 8|
|4| 6|
|6| 4|
|8| 3|
|12| 2|
|24| 1|
Q. Can we relate these values?
A. We are repeating numbers after a particular point. Here, that point is from 5th row.
Now, repeat the above process again for N = 100.
|i| N / i|
|-|----------|
|1| 100|
|2| 50|
|4| 25|
|5| 20|
|10| 10|
|20| 5|
|25| 4|
|50| 2|
|100| 1|
:::warning
Please take some time to think about the solution approach on your own before reading further.....
:::
The factors are repeating from 6th row. After a certain point factors start repeating, so we need to find a point till we have to iterate.
We need to only iterate till -
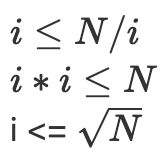
![](https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/043/846/original/upload_b7d89a4e3534f96005e65eaec0681e2a.png?1692787858)
### Pseudocode
```cpp
function countfactors (N):
fac_count = 0
for i = 1 till sqrt(N):
if N % i == 0:
fac = fac + 2
return fac
```
Q. Will the above work in all the cases?
A. No, not for perfect squares. Explain this for N = 100, what mistake we are doing. We will count 10 twice.
**Observation:** Using the above example, we need to modify the code for perfect squares.
### Pseudocode with Edge Case Covered
```cpp
function countfactors (N):
fac_count = 0
for i = 1 till sqrt(N):
if N % i == 0:
if i == N / i:
fac = fac + 1
else:
fac = fac + 2
return fac
```
Dry run the above code for below examples,
N = 24, 100, 1.
|N| Iterations| Execution Time|
|-|----------|---------- |
|10^18| 10^9 iterations| 10 secs |
To implement sqrt(n) , replace the condition i <= sqrt(N) by i * i <= N.
### Follow Up Question
Given N, You need to check if it is prime or not.
**Question**
How many prime numbers are there?
10, 11, 23, 2, 25, 27, 31
**Choices**
- [ ] 1
- [ ] 2
- [ ] 3
- [x] 4
**Explanation:**
Q. What is a prime Number?
A. Number which has only 2 factors, 1 and N itself.
So, 11, 23, 2, and 31 are the only prime numbers since they all have exactly 2 factors.
## Prime Check
Our original question was to check if a number is prime or not. For that, we can just count the number of factors to be 2.
```cpp
function checkPrime(N):
if countfactors(N) == 2:
return true
else:
return false
```
For N = 1, it will return false, which is correct. Since, 1 is neither prime nor composite.
---
**Question**
1 + 2 + 3 + 4 + 5 + 6 + .. 100 = ?
**Choices**
- [ ] 1010
- [x] 5050
- [ ] 5100
- [ ] 1009
**Explanation:**
![](https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/034/347/original/ytbMtMR.png?1684220222)
Generalize this for the first N natural numbers.
![](https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/034/348/original/iqYoobK.png?1684220244)
## Some basic math properties:
1. `[a,b]` - This type of range means that a and b are both inclusive.
2. `(a,b)` - This type of range means that a and b are both excluded.
**Question**
How many numbers are there in the range [3,10]?
**Choices**
- [ ] 7
- [ ] 6
- [x] 8
- [ ] 10
**Explanation:**
The range [3,10] includes all numbers from 3 to 10, inclusive. Inclusive means that both the lower bound (3) and the upper bound (10) are included in the range. Thus the numbers that are included are 3 4 5 6 7 8 9 10.
**Question**
How many numbers are there in the range [a,b]?
**Choices**
- [ ] b-a
- [x] b-a+1
- [ ] b-a-1
**Explanation:**
To find the number of numbers in a given range, we can subtract the lower bound from the upper bound and then add 1. Mathematically, this can be expressed as:
```
Number of numbers in the range
= Upper bound - Lower bound + 1
```
### What do we mean by Iteration?
The number of times a loop runs, is known as Iteration.
**Question**
How many times will the below loop run ?
```cpp
for(i=1; i<=N; i++)
{
if(i == N) break;
}
```
**Choices**
- [ ] N - 1
- [x] N
- [ ] N + 1
- [ ] log(N)
**Question**
How many iterations will be there in this loop ?
```cpp
for(int i = 0; i <= 100; i++){
s = s + i + i^2;
}
```
**Choices**
- [ ] 100 - 1
- [ ] 100
- [x] 101
- [ ] 0
**Question**
How many iterations will be there in this loop?
```cpp
func(){
for(int i = 1; i <= N; i++){
if(i % 2 == 0){
print(i);
}
}
for(int j = 1; j <= M; j++){
if(j % 2 == 0){
print(j);
}
}
}
```
**Choices**
- [ ] N
- [ ] M
- [ ] N * M
- [x] N + M
**Explanation:**
We are executing loops one after the other. Let's say we buy first 5 apples and then we buy 7 apples, the total apples will be 12, so correct ans is N + M
## Geometric Progression (G.P.)
> **Example for intution:**
```
5 10 20 40 80 ..
```
In these type of series, the common ratio is same. In the given example the common ratio r is
= 10/5
= 20/10
= 40/20
= 80/40
= 2
**Generic Notation:**
a, a * r, a * r^2, ...
### Sum of first N terms of a GP
**Sum of first N terms of GP:**
=![](https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/043/847/original/upload_7d7368fe780e904c2836a90ed74e5b1e.png?1692787881)
r cannot be equal to 1 because the denominator cannot be zero.
**Note:**
When r is equal to 1, the sum is given by a * n.
## How to compare two algorithms?
**Story**
There was a contest going on to SORT the array and 2 people took part in it (say Gaurav and Shila).
They had to sort the array in ascending order.
arr[5] = {3, 2, 6, 8, 1} -> {1, 2, 3, 6, 8}
Both of them submitted their algorithms and they are being run on the same input.
### Discussion
**Can we use execution time to compare two algorithms?**
Say initially **Algo1** took **15 sec** and **Algo2** took **10sec**.
This implies that **Shila's Algo 1** performed better, but then Gaurav pointed out that he was using **Windows XP** whereas Shila was using **MAC**, hence both were given the same laptops.........
![](https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/034/050/original/time-complexity-2-image-1.png?1683815146)
### Conclusion
We can't evaluate algorithm's performance using **execution time** as it depends on a lot of factors like operating system, place of execution, language, etc.
**Question**
How can we compare two algorithms?
Which measure doesn't depend on any factor?
**Answer:** Number of Iterations
**Why?**
* The number of iterations of an algorithm remains the same irrespective of Operating System, place of execution, language, etc.

523
Academy DSA Typed Notes/Intermediate/Intermediate DSA Memory Management.md Normal file
View File

@@ -0,0 +1,523 @@
# Beginner : Memory Management
---
## Introduction to stack
### Idli Maker Examples
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/051/250/original/Screenshot_2023-09-26_at_5.39.11_PM.png?1695922237" alt= “” width ="700" height="300">
### Stack
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/051/251/original/Screenshot_2023-09-26_at_5.37.44_PM.png?1695922271" alt= “” width ="600" height="300">
:::success
There are a lot of quizzes in this session, please take some time to think about the solution on your own before reading further.....
:::
---
### Introduction to call stack
#### Example 1
Consider the below code:
```java
int add(int x, int y) {
return x + y;
}
int product(int x, int y) {
return x * y;
}
int subtract(int x, int y) {
return x - y;
}
public static void main() {
int x = 10;
int y = 20;
int temp1 = add(x, y);
int temp2 = product(x, y);
int temp3 = subtract(x, y);
System.out.println(temp1 + temp2 + temp3);
}
```
Following is the call stack execution for above code:
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/051/252/original/Screenshot_2023-09-26_at_5.41.09_PM.png?1695922314" alt= “” width ="200" height="400">
**Ouput:** 220
#### Example 2
Consider the below code:
```java
int add(int x, int y) {
return x + y;
}
public static void main() {
int x = 10;
int y = 20;
int temp1 = add(x, y);
int temp2 = add(temp1, 30);
int temp3 = add(temp2, 40);
System.out.println(temp3);
}
```
Following is the call stack execution for above code:
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/067/735/original/explanation.png?1710154203" alt= “” width ="200" height="400">
**Output:** 100
#### Example 3
Consider the below code:
```java
int add(int x, int y) {
return x + y;
}
static int fun(int a, int b) {
int sum = add(a, b);
int ans = sum * 10;
return ans;
}
static void extra(int w){
System.out.println("Hello");
System.out.println(w);
}
public static void main() {
int x = 10;
int y = 20;
int z = fun(x, y);
System.out.println(z);
extra(z);
}
```
Following is the call stack execution for above code:
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/050/828/original/Screenshot_2023-09-26_at_5.36.25_PM.png?1695730007" alt= “” width ="150" height="450">
**Output:**
```plaintext
300
Hello
310
```
---
### Types of Memory in Java
Following are the types of memory present in Java -
1. **Stack** -<br> All the primitive data type and reference will be stored in stack.
2. **Heap** -<br> Container of that reference is stored in heap. Arrays, ArrayList, Objects are created inside heap.
**Example 1**
Consider the below code:
```java
public static void main() {
int x = 10;
int[] ar = new int[3];
System.out.println(ar); // #ad1
System.out.println(ar[2]); // 0
ar[1] = 7;
}
```
Now, lets analyze the given code -
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/051/253/original/upload_db1be0d6807a0107d3b4a49f92083d10.png?1695922800" alt= “” width ="400" height="400">
**Note**:
1. **Primitive data types:** [int, float, double, char, boolean, long] memory will be assigned in stack.
2. **Reference/ address of the container:** will be stored in stack.
3. **Container:** [Array/ Arraylist] will be stored in heap.
**Example 2**
Consider the below code:
```java
public static void main() {
int x = 10;
int[] ar = new int[3];
int[] ar2 = ar;
System.out.println(ar); // 4k
System.out.println(ar2); // 4k
}
```
Now, lets analyze the given code -
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/051/253/original/upload_db1be0d6807a0107d3b4a49f92083d10.png?1695922800" alt= “” width ="300" height="300">
**Example 3**
Consider the below code:
```java
public static void main() {
int[] ar = new int[3];
System.out.println(ar); // 5k
ar[1] = 9;
ar[2] = 5;
ar = new int[5];
System.out.println(ar); // 7k
}
```
Now, lets analyze the given code -
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/051/254/original/upload_838ad761524ff3f484346b1762d842ab.png?1695923038" alt= “” width ="300" height="300">
**Example 4**
Consider the below code:
```java
static void fun(int[] a){
System.out.println(a); // 9k
a[1] = 5;
}
public static void main() {
int[] ar = new int[3];
System.out.println(ar); // 9k
ar[0] = 90;
ar[1] = 50;
fun(ar);
System.out.println(ar[1]); // 5
}
```
Now, lets analyze the given code -
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/051/255/original/upload_96b9617bf2562ab2cf70308c14562662.png?1695923094" alt= “” width ="300" height="300">
**Example 5**
Consider the below code:
```java
public static void main() {
float y = 7.84f;
int[][] mat = new int[3][4];
System.out.println(mat); // 9k
System.out.println(mat[1]); // 3k
System.out.println(mat[1][3]); // 0
}
```
Now, lets analyze the given code -
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/051/256/original/upload_d6ef6f285e8852ea6483735ea9b275ff.png?1695923118" alt= “” width ="300" height="300">
**Example 6**
Consider the below code:
```java
static void sum(int[][] mat){
System.out.println(mat); // 2k
System.out.println(mat[0][0] + mat[1][0]); // 40
}
public static void main() {
int[][] mat = new int[2][3];
mat[0][0] = 15;
mat[1][0] = 25;
sum(mat);
}
```
Now, lets analyze the given code -
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/051/258/original/upload_60fffb5badb5839f531e4a4b49d50280.png?1695923213" alt= “” width ="300" height="300">
**Example 7**
Consider the below code:
```java
static int sumOfRow(int[] arr){
System.out.println(arr); // 7k
int sum = 0;
for (int i = 0; i < arr.length; i++){
sum = sum + arr[i];
}
return sum;
}
public static void main() {
int[][] mat = new int[2][3];
mat[0][0] = 9;
mat[0][1] = 5;
mat[0][2] = 1;
int ans = sumOfRow(mat[0]); // 7k
System.out.println(ans); // 15
}
```
Now, lets analyze the given code -
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/051/259/original/upload_ebc077e9eb41f97f24666a4fc1c97c6c.png?1695923287" alt= “” width ="300" height="400">
### Question
Predict the Output :
```Java
static void change(int a) {
a = 50;
}
public static void main(String args[]) {
int a = 10;
change(a);
System.out.println(a);
}
```
**Choices**
- [x] 10
- [ ] 50
- [ ] Error
**Explanation**
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/051/260/original/upload_88f3bbcc4fd367434b74cf4b394cebe8.png?1695923386" alt= “” width ="200" height="300">
* The parameter variable 'a' of change function is reassigned to the value of 50, because both the functions have their own variables, so the variable "a" of main function is different than of variable "a" in change function.
* Stack changes are temporary.
---
### Question
Predict the output :
```java
static void change(int[]a) {
a[0] = 50;
}
public static void main(String args[]) {
int[]a = {10};
change(a);
System.out.println(a[0]);
}
```
**Choices**
- [ ] 10
- [x] 50
- [ ] Error
---
**Explanation:**
* The array a in change method and main method both refer to the same array object in the heap.
* Heap changes are permanent changes.
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/051/261/original/upload_b6a922583fd12618a2bb53d4233d6569.png?1695923456" alt= “” width ="200" height="300">
---
### Question
Predict the output :
```java
static void test(int[]a) {
a = new int[1];
a[0] = 50;
}
public static void main(String args[]) {
int[]a = {10};
test(a);
System.out.println(a[0]);
}
```
**Choices**
- [x] 10
- [ ] 50
- [ ] Error
---
**Explanation:**
Inside the test method, a new integer array with length 1 is allocated on the heap memory, and the reference to this array is assigned to the parameter variable a. Hence, now the variable 'a' inside test function and main function point to different references.Heap changes are permanent.
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/051/262/original/upload_2880b16a60cdc943bbd8deb67bc51f87.png?1695923573" alt= “” width ="200" height="300">
---
### Question
Predict the output:
```java
static void fun(int[] a) {
a = new int[1];
a[0] = 100;
}
public static void main() {
int[] a = {10, 20, 30};
fun(a);
System.out.println(a[0]);
}
```
**Choices**
- [x] 10
- [ ] 100
- [ ] Error
- [ ] inky pinky po
**Explanation:**
Inside the fun method, a new integer array with length 1 is allocated on the heap memory, and the reference to this array is assigned to the parameter variable a. Hence, now the variable 'a' inside test function and main function point to different references.
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/051/263/original/upload_fe68bae5077ef0992c9d7cec41e6c8cb.png?1695923634" alt= “” width ="300" height="300">
---
### Question
Predict the output :
```java
static void swap(int a,int b) {
int temp = a;
a = b;
b = temp;
}
public static void main(String args[]) {
int a = 10;
int b = 20;
swap(a,b);
System.out.println(a + " " + b);
}
```
**Choices**
- [x] 10 20
- [ ] 20 10
- [ ] 10 10
- [ ] Error
**Explanation:**
* Swap function is called by value not by reference.
* So, the changes made in the swap function are temporary in the memory stack.
* Once we got out of the swap function, the changes will go because they are made in temporary variables.
* Hence no swapping is done and variable have the same value as previous.
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/051/264/original/upload_95a36c6cecdaa3e8eb1fa455c50dd9b0.png?1695923691" alt= “” width ="200" height="300">
---
### Question
Predict the output :
```java
static void swap(int[]a,int[]b) {
int temp = a[0];
a[0] = b[0];
b[0] = temp;
}
public static void main(String args[]) {
int[]a = {10};
int[]b = {20};
swap(a,b);
System.out.println(a[0] + " " + b[0]);
}
```
**Choices**
- [ ] 10 20
- [x] 20 10
- [ ] 10 10
- [ ] Error
**Explanation:**
Inside swap function, the array variables 'a' & 'b' are passed by reference, so they are pointing to same references in the heap memory as of 'a' & 'b' variables inside main function.
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/051/265/original/upload_30b26edaf41f106c5f23c653f55b87bd.png?1695923815" alt= “” width ="300" height="300">
---
### Question
Predict the output :
```java
static int[] fun(int[]a) {
a = new int[2];
a[0] = 50; a[1] = 60;
return a;
}
public static void main(String args[]) {
int[]a = {10,20,30};
a = fun(a);
System.out.println(a[0]);
}
```
**Choices**
- [ ] 10
- [x] 50
- [ ] Error
**Explanation:**
* When fun method is called on array a, then a new integer array is allocated on the heap memory.
* But since, we are returning the new array in the main method, so now the changes done in fun method persists.
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/051/266/original/upload_ee2fe92543bb6f84908886e2144ef3d2.png?1695923985" alt= “” width ="300" height="300">
---
### Question
Predict the output :
```java
static void test(int[]a) {
a = new int[2];
a[0] = 94;
}
public static void main(String args[]) {
int[]a = {10,20,30};
test(a);
System.out.println(a[0]);
}
```
**Choices**
- [x] 10
- [ ] 94
- [ ] Error
**Explanation:**
Inside the test function, a new integer array with length 2 is allocated on the heap memory, and the reference to this array is assigned to the parameter variable a. Hence, now the variable 'a' inside test function and main function point to different references.
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/051/267/original/upload_4bebf48ccf793236b9b7077d14c2b3c5.png?1695924086" alt= “” width ="300" height="300">

454
Academy DSA Typed Notes/Intermediate/Intermediate DSA Sorting Basics.md Normal file
View File

@@ -0,0 +1,454 @@
# Sorting
## Introduction
**Sorting** is an arrangement of data in particular order on the basis of some parameter
### Example 1:
```
A[ ] = { 2, 3, 9, 12, 17, 19 }
```
The above example is sorted in ascending order on the basis of magnitude.
### Example 2:
```
A[ ] = { 19, 6, 5, 2, -1, -19 }
```
The above example is sorted in descending order on the basis of magnitude.
### Question
Is the array { 1, 13, 9 , 6, 12 } sorted ?
**Choices**
- [x] Yes
- [ ] No
In the above quiz, array is sorted in ascending order on the basis of count of factors. Count of factors for the above array is { 1, 2, 3, 4, 6 }.
**Sorting** is essential for organizing, analyzing, searching, and presenting data efficiently and effectively in various applications and contexts.
### Problem 1 : Minimize the cost to empty array
Given an array of **n** integers, minimize the cost to empty given array where cost of removing an element is equal to **sum of all elements left in an array**.
### Example 1
```plaintext
A[ ] = { 2, 1, 4 }
Ans = 11
```
**Explanation**
After removing 4 cost = 4+2+1 = 7
After removing 2 cost = 2+1 = 3
After removing 1 cost = 1 = 1
Total cost = 11
### Question
Minimum cost to remove all elements from array {4, 6, 1} ?
**Choices**
- [ ] 11
- [ ] 15
- [x] 17
- [ ] 21
After removing 6 cost = 4+6+1 = 11
After removing 4 cost = 4+1 = 5
After removing 1 cost = 1 = 1
Total cost = 17
### Question
Minimum cost to remove all elements from array[] = {3, 5, 1, -3}
**Choices**
- [ ] 4
- [x] 2
- [ ] 0
- [ ] 18
After removing 5 cost = 5+3+1+(-3) = 6
After removing 3 cost = 3+1+(-3) = 1
After removing 1 cost = 1+(-3) = -2
After removing -3 cost = -3) = -3
Total cost = 2
:::warning
Please take some time to think about the solution approach on your own before reading further.....
:::
### Problem 1 Solution Approach
**Observation**
* Start removing from the largest element.
![](https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/031/455/original/remove.jpeg?1681489808)
Here we can see if we have to minimise the cost we should add the largest number minimum number of times, that implies it should be the first one to be removed.
The formula would be **$\sum$(i+1)\*arr[i]** where **i** is the index.
Follow the below steps to solve the problem.
* **Sort** the data in descending order.
* Initialise the **ans** equal to 0.
* Run a loop for i from 0 to **n** – 1, where **n** is the size of the array.
* For every element add **arr[i]\*i** to the ans.
#### Pseudocode
```cpp
int calculate_cost(int arr[], int n) {
reverse_sort(arr);
int ans = 0;
for (int i = 0; i < n; i++) {
ans += i * arr[i];
}
return ans;
}
```
#### Time and Space Complexity
-- TC - O(nlogn)
-- SC - O(n)
### Problem 2 : Find count of Noble Integers
Given an array of distinct elements of size n, find the count of **noble integers**.
> Note: arr[i] is **noble** if count of elements smaller than arr[i] is equal to arr[i] where arr[i] is element at index i.
**Example 1**
```plaintext
A[ ] = { 1, -5, 3, 5, -10, 4}
Ans = 3
```
**Explanation**
For arr[2] there are three elements less than 3 that is 1, -5 and -10. So arr[0] is noble integer.
For arr[3] there are five elements less than 5 that is 1, 3, 4, 5, -5 and -10. So arr[3] is noble integer.
For arr[5] there are four elements less than 4 that is 1, 3, -5 and -10. So arr[5] is noble integer.
In total there are 3 noble elements.
### Question
Count the number of noble integers in the array. A = { -3, 0, 2 , 5 }
**Choices**
- [ ] 0
- [x] 1
- [ ] 2
- [ ] 3
**Explanation:**
For arr[2] there are two elements less than 2 that is -3 and 0. So arr[2] is noble integer.
In total there are 2 noble elements.
:::warning
Please take some time to think about the Brute Force solution approach on your own before reading further.....
:::
### Problem 2 : Bruteforce Solution
#### Observation
Iterate through every element in the array, for every element count the number of smaller elements.
#### Pseudocode
```cpp
int find_nobel_integers(int arr[], int n) {
int ans = 0;
for (int i = 0; i < n; i++) {
int count = 0;
for (int j = 0; j < n; j++) {
if (arr[j] < arr[i])
count++;
}
if (count == arr[i]) {
ans++;
}
}
return ans;
}
```
#### Time and Space Complexity
-- TC - O(N^2)
-- SC - O(1)
### Problem 1 Optimised Solution
#### Optimised Solution - 1
* Hint 1: What is the extra work being done?
Expected: For every element, we are using an extra loop for calculating the count of smaller elements.
* Hint 2: Can sorting the array help here?
#### Observation:
If we sort the data all elements smaller than the element at index i will be on from index **0 to i-1**. So total number of smaller elements will be equal to **i**.
#### Pseudocode
```cpp
int find_nobel_integers(int arr[], int n) {
sort(arr);
int ans = 0;
for (int i = 0; i < n; i++) {
if (arr[i] == i) {
ans = ans + 1;
}
}
return ans;
}
```
#### Time and Space Complexity
-- TC - O(nlogn)
-- SC - O(1)
### Problem 3 Find count of nobel integers (Not Distinct)
Given an array of size n, find the count of noble integers.
> Note: Same as previous question, but all elements need not to be distinct
### Question
Count the no of noble integers in the array. A = { -10, 1, 1, 3, 100 }
**Choices**
- [ ] 1
- [x] 3
- [ ] 2
- [ ] 4
**Explanation:**
For arr[1] and arr[2] there is one element less than 1. So arr[1] and arr[2] are noble integers.
Similarly arr[3] will be the npble lement as there are 3 elements less than 3.
So in total 3 elements are noble integers.
### Question
Count the no of noble integers in the array
A = { -10, 1, 1, 2, 4, 4, 4, 8, 10 }
**Choices**
- [ ] 4
- [x] 5
- [ ] 6
- [ ] 7
**Explanation:**
arr[1], arr[2], arr[4], arr[5], arr[6] are the noble elements here.
### Question
Count the no of noble integers in the array
A = { -3, 0, 2, 2, 5, 5, 5, 5, 8, 8, 10, 10, 10, 14 }
**Choices**
- [ ] 4
- [ ] 5
- [ ] 6
- [x] 7
**Explanation:**
For arr[8] and arr[9] there are eight elements less than 8 that is -3, 0, 2, 5. So arr[8] and arr[9] are noble integers.
Similarly arr[9], arr[10], arr[11], ar[12] are noble elements.
So in total 6 elements are noble integers.
:::warning
Please take some time to think about the solution approach on your own before reading further.....
:::
### Problem 3 Solution
#### Observation
* If the current element is same as previous element then the total number of smaller elements will be same as previous element.
* If current element is not equal to previous element then the total number of smaller elements is equal to its index.
#### Pseudocode
```cpp
int find_nobel_integers(int arr[], int n) {
sort(arr);
int count = 0, ans = 0;
if (arr[0] == 0) ans++;
for (int i = 1; i < n; i++) {
if (arr[i] != arr[i - 1])
count = i;
if (count == arr[i])
ans++;
}
return ans;
}
```
#### Time and Space Complexity
-- TC - O(nlogn)
-- SC - O(1)
## Sorting Algorithm - Selection Sort
A sorting algorithm is a method of reorganizing the elements in a meaningful order.
> Imagine this. You are asked to arrange students according to their increasing heights.
**Divide the queue of students into two parts – arranged and unarranged.**
1. To begin with, place all the students in the unarranged queue.
2. From this unarranged queue, search for the shortest student and place him/her in the list of arranged students.
3. Again, from the unarranged queue, select the second-shortest student. Place this student in the arranged queue, just after the smallest student.
4. Repeat the above-given steps until all the students are placed into the arranged queue.
**Did you see what we just did here?**
We used the selection sort algorithm to arrange all the students in a height-wise order.
**To better understand selection sort, let's consider a list of Integers 5, 6, 4, 2.**
The steps to sort this list would involve –
![](https://hackmd.io/_uploads/ByRkDJIR2.png)
#### Pseudocode:
```cpp
void selectionSort(int arr[], int size) {
int i, j, minIndex;
for (i = 0; i < size - 1; i++) {
// set minIndex equal to the first unsorted element
minIndex = i;
//iterate over unsorted sublist and find the minimum element
for (j = i + 1; j < size; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
// swapping the minimum element with the element at minIndex to place it at its correct position
swap(arr[minIndex], arr[i]);
}
}
```
#### TC & SC
**Time Complexity:** O(N<sup>2</sup>) since we have to iterate entire list to search for a minimum element everytime.
For 1 element, N iterations,
For N elements, N<sup>2</sup> iterations.
**Space Complexity:** O(1)
## Sorting Algorithm - Insertion Sort
**Insertion Sort** is one of the simplest sorting techniques which you might have used in your daily lives while arranging a deck of cards.
> So without going into how this algorithm works, let’s think about how you would usually go about arranging the deck of cards?
**Say you are given 10 cards, 1 to 10 of spades, all shuffled, and you want to sort these cards.**
1. You would basically pick any random card(e.g. 7), and place it into your left hand, assuming the left hand is meant to carry the sorted cards.
2. Then you would pick another random card, say 2, and place 2 in the correct position on your left hand, i.e. before 7.
3. Then again if you pick 5, you would place it between 2 and 7 on your left hand, and this way we know we are able to sort our deck of cards. Since we insert one element at a time in its correct position, hence its name “Insertion Sort”.
#### Dry Run
E.g. if elements were in order:
```3, 5, 2```
You can start by picking 3, and since there is no element to the left of 3, we can assume it is in the correct place.
Array:
```3, 5, 2```
You can pick 5, you compare 5 with 3, and you find 5 is in the correct order amongst the array of [3, 5].
Array:
```3, 5, 2```
Then you pick 2, you find the place in the left side array of [3,5] to place this 2. Since 2 must come before 3, we insert 2 before 3.
Array:
```2, 3, 5 →```
Which is a sorted order.
#### Approach
Line 2: We don’t process the first element, as it has nothing to compare against.
Line 3: Loop from i=1 till the end, to process each element.
Line 4: Extract the element at position i i.e. array[i]. Let it be called E.
Line 5: To compare E with its left elements, loop j from i-1 to 0
Line 6, 7: Compare E with the left element, if E is lesser, then move array[j] to right by 1.
Line 8: Once we have found the position for E, place it there.
#### Pseudocode
```cpp
void insertionSort(int arr[], int n) {
for (int i = 1; i < n; i++) { // Start from 1 as arr[0] is always sorted
Int currentElement = arr[i];
Int j = i - 1;
// Move elements of arr[0..i-1], that are greater than key,
// to one position ahead of their current position
while (j >= 0 && arr[j] > currentElement) {
arr[j + 1] = arr[j];
j = j - 1;
}
// Finally place the Current element at its correct position.
arr[j + 1] = currentElement;
}
}
```
#### TC & SC
**Time Complexity:**
**Worst Case:** O(N^2), when the array is sorted in reverse order.
**Best Case:** O(N), when the data is already sorted in desied order, in that case there will be no swap.
Space Complexity: O(1)
**Note**
1. Both Selection & Insertion are in-place sorting algorithms, means they don't need extra space.
2. Since the time complexity of both can go to O(N^2), it is only useful when we have a lesser number of elements to sort in an array.

382
Academy DSA Typed Notes/Intermediate/Intermediate DSA Strings.md Normal file
View File

@@ -0,0 +1,382 @@
# String
A string can be defined as a sequence of characters or in other words we can say that it is an array of characters.
**Example**
Below are the examples of string:
```
"Welcome to Scaler"
"Hello World!"
```
**Note:** String is represented using double quote i.e, `""`. All the characters of string must be inside this quote.
**Character**
A character is a single symbol that represents a letter, number, or other symbol in a computer's character set. Characters are used to represent textual data, and they are typically represented using its ASCII value.
**Example**
```
'a'
'B'
'1'
'_'
```
Computer store everything in binary. So, how do we store strings in computer?
Each character has corresponding decimal value associated to it which is known as ASCII value.
**'A' to 'Z'** have ASCII from **65 to 90**
**'a' to 'z'** have ASCII from **97 to 122**
**'0' to '9'** have ASCII from **48 to 57**
Each character '?', '!', '\*', ... has a corresponding ASCII associated with it.
### Some Operations:
**Note:** Characters can also be printed using its ascii value. for example, the ascii value of 'A' is 65, so it can be printed as
```CPP
char ch = (char)65;
print(ch);
/*
character 'A' gets printed; we are assigning Integer to Char,hence in some languages typecasting will be required.
*/
```
```cpp=
char ch = (char)('a' + 1);
/*
When we do arithmetic operations on characters, automatically computations happen on their ASCII values.
*/
print(ch); //'b' will get printed
```
```cpp=
int x = 'a';
/*
No need to typecast since we are assigning Char to Int (smaller data type to bigger, so it will not overflow)
*/
print(x); //97 will be printed
```
## Question 1 : Switch cases
Given a string consisting of only alphabets(either lowercase or uppercase). Print all the characters of string in such a way that for all lowercase character, print its uppercase character and for all uppercase character, print its lowercase character.
**TestCase**
**Input**
```
"Hello"
```
**Output**
```
"hELLO"
```
**Explanation**
Here, there is only one uppercase character present in the string i.e, 'H' so convert it to lowercase character. All other characters are in lowercase, hence they are converted into uppercase characters.
### Question
What is the output for String = "aDgbHJe" ?
**Choices**
- [ ] ADGBHJE
- [ ] aDgbHJe
- [x] AdGBhjE
- [ ] adgbhje
---
:::warning
Please take some time to think about the solution approach on your own before reading further.....
:::
**Observation**
The key observations are:
* Lowercase characters can be changed into uppercase by subtracting 32 from its ASCII values.
* Uppercase charactes can be changed into lowercase by adding 32 from its ASCII values.
The above points are derived from the fact that for every alphabet, the difference between its ascii value in lowercase and uppercase is 32.
#### Pseudocode
```cpp
Function toggle(char s[]) {
int n = s.size();
for (int i = 0; i < n; i++) {
if (s[i] >= 65 and s[i] <= 91) {
print(s[i] + 32);
} else {
print(s[i] - 32);
}
}
}
```
#### Complexity
Time Complexity- **O(N)**.
Space Complexity- **O(1)**.
## Substring
A substring is a contiguous sequence of characters within a string. A substring concept in string is similar to subarray concept in array.
**A substring can be:**
1. Continous part of string.
2. Full string can be a substring.
3. A single character can also be a subsring.
**Example**
Suppose, we have a string as
```
"abc"
```
There are total 6 substring can be formed from the above string. All substrings are
```
"a"
"b"
"c"
"ab"
"bc"
"abc"
```
### Question
How many total substrings will be there for the String "bxcd" ?
**Choices**
- [ ] 7
- [ ] 8
- [x] 10
- [ ] 9
---
**Explanation:**
All the substrings are as follows-
```
"b", "x", "c", "d", "bx", "xc", "cd", "bxc", "xcd", "bxcd"
```
We can also find the count using n*(n+1)/2.
### Question 2 Check Palindrome
Check whether the given substring of string **s** is palindrome or not.
A palindrome is the sequence of characters that reads the same forward and backward.for example, "nayan", "madam", etc.
**TestCase**
**Input**
```
s = "anamadamspe"
start = 3
end = 7
```
**Output**
```
true
```
**Explanation**
The substring formed from index 3 to 7 is "madam" which is palindrome.
### Question 2 Approach
#### Approach
Below is the simple algorithm to check whether the substring is palindrome or not:
* Initialize two indices *start* and *end* to point to the beginning and *end* of the string, respectively.
* While *start* is less than *end*, do the following:
* If the character at index *start* is not equal to the character at index *end*, the string is not a palindrome. Return false.
* Else, increment *start* and decrement *end*.
* If the loop completes without finding a non-matching pair, the string is a palindrome. Return true.
#### Pseudocode
```cpp
function ispalindrome(char s[], int start, int end) {
while (start < end) {
if (s[start] != s[end]) {
return false;
} else {
start++;
end--;
}
}
return true;
}
```
#### Complexity
Time Complexity- **O(N)**.
Space Complexity- **O(1)**.
## Question 3 : Longest Palindromic substring
Given a string **s**, calculate the length of longest palindromic substring in **s**.
**TestCase**
**Input**
```
"anamadamm"
```
**Output**
```
5
```
**Explanation**
The substring "madam" of size 5 is the longest palindromic substring that can be formed from given string.
### Question
What is the length of longest palindromic substring within string "feacabacabgf" ?
**Choices**
- [ ] 6
- [ ] 3
- [x] 7
- [ ] 10
### Question
What is the length of longest palindromic substring within string "a d a e b c d f d c b e t g g t e" ?
**Choices**
- [ ] 6
- [ ] 3
- [x] 9
- [ ] 10
:::warning
Please take some time to think about the brute force solution approach on your own before reading further.....
:::
### Question 4 Brute Force Approach
The naive approach is to for all the substring check whether the string is palindrome or not. if it is palindrome and its size is greater than the previous answer(which is initially 0), then update the answer.
#### Pseudocode
```cpp
function longestPalindrome(char s[]) {
int N = s.size();
int ans = 0;
for (int i = 0; i < N; i++) {
for (int j = i; j < N; j++) {
if (ispalindrome(s, i, j)) {
ans = max(ans, j - i + 1);
}
}
}
return ans;
}
```
#### Complexity
Time Complexity- **O(N^3)**.
Space Complexity- **O(1)**.
#### Idea
The key idea here is that:
* For odd length substring, take every character as a center and expand its center and gets maximum size palindromic substring.
* For even length substring, take every adjacent character as a center and expand its center and get maximum size palindromic substring.
#### Pseudocode
```cpp
function longestpalindrome(char s[]) {
int maxlength = 0;
int N = s.size();
for (int c = 0; c < N; c++) {
//odd length string
int left = c, right = c;
while (left >= 0 and right < N) {
if (s[left] != s[right]) {
break;
}
left--;
right++;
}
maxlength = max(maxlength, right - left - 1);
//even length string
left = c;
right = c + 1;
while (left >= 0 and right < N) {
if (s[left] != s[right]) {
break;
}
left--;
right++;
}
maxlength = max(maxlength, right - left - 1);
}
return maxlength;
}
```
#### Complexity
Time Complexity- **O(N^2)**.
Space Complexity- **O(1)**.
### Immutability of Strings
In languages like **Java, C#, JavaScript, Python and Go**, strings are immutable, which means it's **value can't be changed**.
```cpp=
String s1 = "Hello"; // String literal
String s2 = "Hello"; // String literal
String s3 = s1; // same reference
```
![](https://hackmd.io/_uploads/SkGyXywRh.png)
* As seen above, because strings with the same content share storage in a single pool, this minimize creating a copy of the same value.
* That is to say, once a String is generated, its content cannot be changed and hence changing content will lead to the creation of a new String.
```cpp=
//Changing the value of s1
s1 = "Java";
//Updating with concat() operation
s2.concat(" World");
//The concatenated String will be created as a new instance and an object should refer to that instance to get the concatenated value.
String newS3 = s3.concat(" Scaler");
System.out.println("s1 refers to " + s1);
System.out.println("s2 refers to " + s2);
System.out.println("s3 refers to " + s3);
System.out.println("newS3 refers to " + newS3);
```
**Output**
```cpp=
s1 refers to Java
s2 refers to Hello
s3 refers to Hello
news3 refers to Hello Scaler
```
![](https://hackmd.io/_uploads/BkzzEkPC3.png)
As shown above, considering the example:
* String s1 is updated with a new value and that's why a new instance is created. Hence, s1 reference changes to that newly created instance "Java".
* String s2 and s3 remain unchanged as their references were not changed to a new instance created after performing concat() operation.
* "Hello World" remains unreferenced to any object and lost in the pool as s2.concat() operation (in line number 5) is not assigned to any object. That's why there is a reference to its result.
* String newS3 refers to the instance of s3.concat() operation that is "Hello Scaler" as it is referenced to new object newS3.
**Hence, Strings are immutable and whenever we change the string only its reference is changed to the new instance.**

565
Academy DSA Typed Notes/Intermediate/Intermediate DSA Time Complexity.md Normal file
View File

@@ -0,0 +1,565 @@
# Time Complexity
**Topics covered :**
1. Log Basics + Iteration Problems
2. Comparing Iterations using Graph
3. Time Complexity - Definition and Notations (Asymptotic Analysis - Big O)
6. TLE
7. Importance of Constraints
:::success
There are a lot of quizzes in this session, please take some time to think about the solution on your own before reading further.....
:::
## Basics of Logarithm
Q. What is the meaning of LOG ?
A. Logarithm is the inverse of exponential function.
Q. How to read the statement "log<sub>b</sub>(a)"?
A. To what value we need to raise b, such that we get a.
If log<sub>b</sub>(a) = c, then it means b<sup>c</sup> = a.
**Examples**
1. log<sub>2</sub>(64) = 6
**How?** 2 raise to the power what is 64? It's 6 since 2<sup>6</sup> = 64
2. log<sub>3</sub>(27) = 3
3. log<sub>5</sub>(25) = 2
4. log<sub>2</sub>(32) = 5
Now, calculate the floor values of the following logarithms.
5. log<sub>2</sub>(10) = 3
6. log<sub>2</sub>(40) = 5
**Note:**
If 2<sup>k</sup> = N => log<sub>2</sub>(N) = k
Let's look at one more formula:
1. What is log<sub>2</sub>(2^6)?
A. 6
Explanation: To what power you should raise 2, such that it equates to 2^6.
2. What is log<sub>3</sub>(3^5)?
A. 5
Explanation: To what power you should raise 3, such that it equates to 3^5.
**Note:**
In general, log<sub>a</sub>(a^N) = N
**Question**:
Given a positive integer N, how many times do we need to divide it by 2 (Consider only integer part) until it reaches 1.
For example, N = 100
100 -> 50 -> 25 -> 12 -> 6 -> 3 -> 1
Hence, 6 times.
What if N = 324?
324 -> 162 -> 81 -> 40 -> 20 -> 10 -> 5 -> 2 -> 1
Hence, 8 times.
### **Question**
How many times we need to divide 9 by 2 till it reaches 1 ?
**Choices**
- [ ] 4
- [x] 3
- [ ] 5
- [ ] 2
**Explanation:**
N --> N/2 --> N/4 --> N/8 --> ...... 1
N/2^0 --> N/2^1 --> N/2^2 --> N/2^3 --> ...... N/2^K
N/2^K = 1
K = log<sub>2</sub>(N)
### **Question**
How many times we need to divide 27 by 2 till reaches 1 ?
**Choices**
- [ ] 5
- [x] 4
- [ ] 3
- [ ] 6 -->
### **Question**
How many iterations will be there in this loop ?
```pseudocode
N > 0
i = N;
while (i > 1) {
i = i / 2;
}
```
**Choices**
- [ ] N
- [ ] N/2
- [ ] sqrt(N)
- [x] log(N)
**Explanation:**
The given loop starts with the initial value of i as N and continues until i becomes less than or equal to 1, by repeatedly dividing i by 2 in each iteration.
Hence, Iterations are log(N)
### **Question**
How many iterations will be there in this loop
```
for(i=1; i<N; i=i*2)
{
...
}
```
**Choices**
- [ ] infinite
- [ ] sqrt(N)
- [ ] 0
- [x] log(N)
![](https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/031/486/original/AsFKtNz.png?1681540630)
### **Question**
How many iterations will be there in this loop ?
```pseudocode
N>=0
for(i=0; i<=N; i = i*2)
{
...
}
```
**Choices**
- [x] Infinite
- [ ] N/2
- [ ] 0
- [ ] log(N)
![](https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/031/485/original/DlI3rSU.png?1681540550)
### Question
How many iterations will be there in this loop
```
for(i=1; i<=10; i++){
for(j=1; j<=N; j++){
/ ......../
}
}
```
**Choices**
- [ ] N + N
- [ ] N^2
- [x] 10 * N
- [ ] N + 10
> Multiplying the loops each time might not be correct. In this case, it works.
### **Question**
How many iterations will be there in this loop
```
for(i=1; i<=N; i++){
for(j=1; j<=N; j++){
...
}
}
```
**Choices**
- [ ] 2 * N
- [x] N * N
- [ ] 10 * N
- [ ] N * sqrt(N)
**Explanation:**
The given loop consists of two nested loops. The outer loop iterates from i=1 to i=N, and the inner loop iterates from j=1 to j=N.
For each value of i in the outer loop, the inner loop will iterate N times. This means that for every single iteration of the outer loop, the inner loop will iterate N times.
Therefore, the correct answer is N * N.
### **Question**
How many iterations will be there in this loop
```
for(i=1; i <= N; i++){
for(j=1; j <= N; j = j*2){
...
}
}
```
**Choices**
- [ ] (N^2 + 2N + 1)/2
- [x] N * log(N)
- [ ] N^2
- [ ] N(N+1)/2
**Explanation:**
The given loop consists of two nested loops. The outer loop iterates from i=1 to i <= N, and the inner loop iterates from j=1 to j <= N, with j being incremented by a power of 2 in each iteration.
For each value of i in the outer loop, the inner loop iterates in powers of 2 for j. This means that the inner loop will iterate for j=1, 2, 4, 8,... up to the largest power of 2 less than or equal to N, which is log<sub>2</sub>(N).
Therefore, the correct answer is N * log<sub>2</sub>(N).
### **Question**
How many iterations will be there in this loop ?
```
for(i = 1; i <= 4; i++) {
for(j = 1; j <= i ; j++) {
//print(i+j)
}
}
```
**Choices**
- [ ] log(N)
- [ ] 2N
- [x] 10
- [ ] N -->
### **Question**
How many Iterations will be there in this loop ?
```
for(i = 1; i <= N; i++) {
for(j = 1; j <= i ; j++) {
//print(i+j)
}
}
```
**Choices**
- [ ] log(N)
- [x] N*(N+1)/2
- [ ] (N-1)/2
- [ ] N/2
### **Question**
How many iterations will be there in this loop
```
for(i=1; i<=N; i++){
for(j=1; j<=(2^i); j++)
{
...
}
}
```
**Choices**
- [ ] 2^N
- [x] 2 * (2^N - 1)
- [ ] 2 * (2N)
- [ ] infinite
![](https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/031/487/original/Cei0j2o.png?1681540943)
This is GP, where a=2, r=2 and no. of terms are N.
Consider two algorithms Algo1 and Algo2 given by Kushal and Ishani respectively.
Considering **N** to be the size of the input:
Algo|Number of Iterations
-|-
Algo1|100 * log(N)
Algo2|N / 10
Now, see the graph of the two algorithms based on N.
Graphs info:
* X-axis plots N (input size)
* Red line (Algo 1): **100 * log(N)**
* Blue line (Algo 2): **N/10**
![](https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/034/052/original/time-complexity-2-image-2.png?1683815171)
### Observations:
Assuming both graphs intersect at N = 3500, let's draw some observations.
For small input (N <= 3500), Ishani's algorithm performed better.
For large input (N > 3500), Kushal's algorithm performed better.
**In today's world data is huge**
* IndiaVSPak match viewership was **18M**.
* Baby Shark video has **2.8B** views.
Therefore, Kushal's algorithm won since it has lesser iterations for huge data value.
*We use **Asymptotic Analysis** to estimate the performance of an Algorithm when Input is huge.*
**Asymptotic Analysis** OR **Big(O)** simply means analysing perfomance of algorithms for **larger inputs**.
### Calculation of Big(O)
**Steps** for **Big O** calculation are as follows:
* Calculate **Iterations** based on **Input Size**
* Ignore **Lower Order Terms**
* Ignore **Constant Coefficients**
**Example-**
Kushal's algo took **100 * log<sub>2</sub>N** iterations: Big O is **O(log<sub>2</sub>N)**
Ishani's algo took **N / 10** iterations: Big O is **O(N)**
**For example**,
1. Iterations: 4N^2 + 3N + 1
2. Neglect lower order term: 3N + 1; Remaining Term: 4N^2
3. Neglect constant 4
Big O is O(N^2)
### Comparsion Order:
log(N) < sqrt(N) < N < N log(N) < N sqrt(N) < N^2 < N^3 < 2^(N) < N! < N^N
**Using an example**
N = 36
5 < 6 < 36 < 36\*5 < 36\*6 < 36<sup>2</sup> < 36<sup>3</sup> < 2<sup>36</sup> < 36! < 36<sup>36</sup>
**Ques:** What is the big notation time complexity of the following expression?
4N^2 + 3N + 6 sqrt(N) + 9 log_2(N) + 10
Ans = O(N^2)
### Question
F(N) = 4N + 3Nlog(N) + 1
O(F(N)) = ?
**Choices**
- [ ] N
- [x] N * logN
- [ ] Constant
- [ ] N^2
### Question
F(N) = 4NlogN + 3NSqrt(N) + 10^6
O(F(N)) = ?
**Choices**
- [ ] N
- [ ] N * logN
- [ ] N^2
- [x] N * Sqrt(N)
## Why do we neglect Lower Order Terms
Let's say the number of Iterations of an Algorithm are: N<sup>2</sup>+10N
N|Total Iterations = N<sup>2</sup>+10N|Lower Order Term = 10N|% of 10N in total iterations = 10N/(N<sup>2</sup>+10N)*100
-|-|-|-
10|200|100|50%
100|10<sup>4</sup>+10<sup>3</sup>|10<sup>3</sup>|Close to 9%
10000|10<sup>8</sup>+10<sup>5</sup>|10<sup>5</sup>|0.1%
## Conclusion
We can say that, as the **Input Size** increases, the contribution of **Lower Order Terms** decreases.
### Why do we neglect Constant Coefficients
When the comparison is on very larger input sizes, the constants do not matter after a certain point. For example,
| Algo 1(Nikhil)|Algo 2(Pooja)|Winner for Larger Input|
| -------- | -------- | -------- |
| 10 * log<sub>2</sub> N | N | Nikhil |
| 100 * log<sub>2</sub> N | N | Nikhil |
| 9 * N | N<sup>2</sup> | Nikhil |
| 10 * N | N<sup>2</sup> / 10| Nikhil |
| N * log<sub>2</sub> N | 100 * N | Pooja |
## Issues with Big(O)
### Issue 1
**We cannot always say that one algorithm will always be better than the other algorithm.**
**Example:**
* Algo1 (Iterations: 10<sup>3</sup> N) -> Big O: O(N)
* Algo2 (Iterations: N<sup>2</sup>) -> Big O: O(N<sup>2</sup>)
* Algo 1 is better than Algo 2 but only for large inputs, not for small input sizes.
|Input Size (N)| Algo 1 (10<sup>3</sup>) | Algo 2 (N<sup>2</sup>) | Optimised|
| --| --| --| --|
|N = 10| 10<sup>4</sup>| 10<sup>2</sup>|Algo 2|
|N = 100| 10<sup>5</sup>| 10<sup>4</sup>|Algo 2|
|N = 10<sup>3</sup>| 10<sup>6</sup>| 10<sup>6</sup>|Both are same|
|N = 10<sup>3</sup> + 1| (10<sup>3</sup>)*(10<sup>3</sup> + 1)| (10<sup>3</sup> + 1)*(10<sup>3</sup> + 1)|Algo 1|
|N = 10<sup>4</sup>| 10<sup>7</sup>| 10<sup>8</sup>|Algo 1|
**Claim:** For all large inputs >= 1000, Algo 1 will perform better than Algo 2.
### Issue 2
If 2 algorithms have same higher order terms, then Big O is not capable to identify algorithm with higher iterations.
Consider the following questions -
Count the number of odd elements from 1 to N
Code 1: Iterations: N
```pseudocode
for (int i = 1; i <= N; i++) {
if (i % 2 != 0) {
c = c + 1;
}
}
```
Code 2: Iterations: N/2
```pseudocode
for (int i = 1; i <= N; i = i + 2) {
c = c + 1;
}
```
In both, Big O is O(N) but we know second code is better.
## Time Limit Exceeded Error
* **Is it necessary to write the entire code and then test it to determine its correctness?**
* **Can we assess the logic's viability before writing any code?**
### Online Editors and Why TLE occurs
* Codes are executed on online servers of various platforms such as Codechef, Codeforces, etc.
* The **processing speed** of their server machines is **1 GHz** which means they can perform **10<sup>9</sup> instructions** per second.
* Generally, **codes should be executed in 1 second**.
Using this information, we can say at max our code should have at most **10<sup>9</sup> instructions**.
Instructions means any single operation such as multiplication, addition, function calling, single variable declaration, etc.
### Question
Consider the following code:
Find the total number of instructions in the code below (Note that the instructions involved in the loop part are repetitive)
![](https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/034/057/original/time-complexity-2-image-7.png?1683815308)
**Conclusion:**
Calculating Instructions is tedious job, rather we can make certain approximations in terms of number of Iterations.
### Approximation 1
Suppose the **code** has as small as **10 Instructions in 1 Iteration**.
Therefore,
| Instructions | Iterations |
| -------- | -------- |
| 10 | 1 |
| 10^9 | 10^8 |
In **1 sec**, we can have at max **10<sup>9</sup> Instructions** or **10<sup>8</sup> Iterations**, provided there are **10 Instructions / Iteration**.
### Approximation 2
Suppose the **code** has as huge as **100 Instructions in 1 Iteration**.
Therefore,
| Instructions | Iterations |
| -------- | -------- |
| 100 | 1 |
| 10^9 | 10^7 |
In **1 sec**, we can have at max **10<sup>9</sup> Instructions** or **10<sup>7</sup> Iterations**, provided there are **100 Instructions / Iteration**.
### Conclusion:
In general, our code can have **10<sup>7</sup>** to **10<sup>8</sup> Iterations** to be able to run in **1 sec**.
## General Structure to solve a question
### How to approach a problem?
* Read the **Question** and **Constraints** carefully.
* Formulate an **Idea** or **Logic**.
* Verify the **Correctness** of the Logic.
* Mentally develop a **Pseudocode** or rough **Idea of Loops**.
* Determine the **Time Complexity** based on the Pseudocode.
* Assess if the time complexity is feasible and won't result in **Time Limit Exceeded (TLE)** errors.
* **Re-evaluate** the **Idea/Logic** if the time constraints are not met; otherwise, proceed.
* **Code** the idea if it is deemed feasible.
### Importance of Constraints
#### Question
If 1 <= N <= 10<sup>5</sup>,
then which of the following Big O will work ?
| Complexity | Iterations | Works ? |
| -------- | -------- | -------- |
| O(N<sup>3</sup>) | (10<sup>5</sup>)<sup>3</sup> | No |
| O(N<sup>2</sup>) log N | (10<sup>10</sup>)*log 10<sup>5</sup> | No |
| O(N<sup>2</sup>) | (10<sup>5</sup>)<sup>2</sup> | No |
| O(N * log N) | (10<sup>5</sup>)*log 10<sup>5</sup> | Yes |
#### Question
If 1 <= N <= 10<sup>6</sup>,
then which of the following Big O will work ?
| Complexity | Iterations | Works ? |
| -------- | -------- | -------- |
| O(N<sup>3</sup>) | (10<sup>6</sup>)<sup>3</sup> | No |
| O(N<sup>2</sup>) log N | (10<sup>12</sup>)*log 10<sup>6</sup> | No |
| O(N<sup>2</sup>) | (10<sup>12</sup>) | No |
| O(N * log N) | (10<sup>6</sup>)*log 10<sup>6</sup> ~ 10<sup>7</sup> | May Be |
| O(N) | (10<sup>6</sup>) | Yes |
#### Question
If constraints are
1 <= N <= 100, N<sup>3</sup> will also pass.
If constraints are
1 <= N <= 20, 2<sup>N</sup> will also pass.
**Note:**
In Online Assessments, if we are not getting any other approach to a problem, try out the code; it may pass some test cases, which is better than nothing.