 +
+### XOR( ^ ) Operator
+**Left Shift Operator** can be used with the **XOR** operator to **FLIP(or TOGGLE)** the **ith** bit in the number.
+
+```
+N = (N ^ (1<
+
+### XOR( ^ ) Operator
+**Left Shift Operator** can be used with the **XOR** operator to **FLIP(or TOGGLE)** the **ith** bit in the number.
+
+```
+N = (N ^ (1< +
+
+### AND( & ) Operator
+**Left Shift Operator** can be used with **AND** operator to check whether the **ith** bit is set or not in the number.
+
+```
+X = (N & (1<
+
+
+### AND( & ) Operator
+**Left Shift Operator** can be used with **AND** operator to check whether the **ith** bit is set or not in the number.
+
+```
+X = (N & (1< +
+
+---
+### Problem 1 Check whether ith bit in **N** is SET or not
+
+Check whether the **ith** bit in **N** is SET or not.
+
+
+#### Approach
+
+Taking **AND with 1** can help us.
+0 & 1 = 0
+1 & 1 = 1
+
+1. We can shift 1 to the ith bit.
+2. If `X = (N & (1<
+
+
+---
+### Problem 1 Check whether ith bit in **N** is SET or not
+
+Check whether the **ith** bit in **N** is SET or not.
+
+
+#### Approach
+
+Taking **AND with 1** can help us.
+0 & 1 = 0
+1 & 1 = 1
+
+1. We can shift 1 to the ith bit.
+2. If `X = (N & (1<) +
+* Iterate on every bit.
+* If the count of numbers in which ith bit is set is a multiple of 3, then in answer ith bit is NOT SET.
+* If the count of numbers in which ith bit is of the form (3 * x) + 1, then in answer ith bit is SET.
+
+#### Pseudocode
+```cpp=
+int ans = 0;
+
+for (int i = 0; i < 32; i++) { // go to every bit one by one
+ int cnt = 0;
+
+ for (int j = 0; j < arr.size(); j++) { // iterate on array
+
+ // check if ith bit is set
+ if ((arr[j] & (1 << i)) cnt++;
+ }
+
+ if (cnt % 3 == 1) // If the count is not the multiple of 3
+ ans = ans | 1 << i; // set ith bit in ans
+ }
+
+ print(ans);
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(1)
+
+---
+### Problem 3 Single number 3
+
+Given an integer array, all the elements will occur twice except two. Find those two elements.
+
+**Input:** [4, 5, 4, 1, 6, 6, 5, 2]
+
+**Output:** 1, 2
+
+#### Hint:
+* Will finding XOR help ? May be!
+* What do we get if we XOR all numbers ? XOR of the two unique numbers!
+* From that can we identify/separate the two numbers ? Not Really! Why?
+ * Example: If XOR is 7, we aren't sure which 2 numbers are they. (2, 5), (1, 6), (3, 4), ... have xor = 7, so we won't be able to identify!
+
+
+***Is there any way in which we can identify the two numbers from their XOR ?***
+
+Suppose if two unique numbers are **a** and **b**. Their XOR is **c**.
+In **c** if say 0th bit is set, what does that tell about a and b ?
+In one of the numbers the bit is set and in other the bit is unset! So, can we identify the numbers based on that ?
+
+#### Idea:
+
+* We will find the position of any set bit in XOR c, it will denote that this bit is different in a and b.
+* Now, we divide the entire array in two groups, based upon whether that particular bit is set or not.
+* This way a and b will fall into different groups.
+* Now since every number repeats twice, they will cancel out when we take XOR of the two groups individually leaving a and b.
+
+
+#### Pseudocode
+```cpp
+int xorAll = 0;
+
+// XOR of all numbers in the array
+for (int i = 0; i < N; i++) {
+ xorAll ^= A[i];
+}
+
+// Find the rightmost set bit position
+// Note: Any other bit can be used as well
+int pos;
+
+for (pos = 0; pos < 32; pos++) {
+ if (checkbit(xorAll, pos))
+ break;
+}
+
+num1 = 0;
+num2 = 0;
+
+// Divide the array into two groups based on the rightmost set bit
+for (int i = 0; i < N; i++) {
+ if (checkbit(A[i], pos)) {
+ num1 ^= A[i];
+ } else {
+ num2 ^= A[i];
+ }
+}
+
+print(num1);
+print(num2);
+```
+
+---
+### Question
+What is the time complexity to find two unique elements where every element is present 2 times except for two unique elements?
+
+**Choices**
+- [ ] O(1)
+- [ ] O(log(N))
+- [x] O(N)
+- [ ] O(32 * N)
+
+---
+### Problem 4 Maximum AND pair
+
+Given N array elements, choose two indices(i, j) such that **(i != j)** and **(arr[i] & arr[j])** is maximum.
+
+**Input:** [5, 4, 6, 8, 5]
+
+**Output:** [0, 4]
+
+If we take the **&** of 5 with 5, we get 5 which is the maximum possible value here. The required answer would be their respective indices i.e. **0,4**
+
+---
+### Question
+Max & Pair in this array (arr[] = 21,18,24,17,16) is
+
+**Choices**
+- [x] 21&17
+- [ ] 24&21
+- [ ] 17&16
+- [ ] 24&18
+
+---
+### Question
+Max & Pair in this array (arr[] =5,4,3,2,1) is
+
+**Choices**
+- [x] 5&4
+- [ ] 1&2
+- [ ] 1&4
+- [ ] 4&3
+
+---
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+### Maximum AND pair Approach
+
+
+#### Brute Force
+Using two for loops and calculating **bitwise &** for all possible pairs and storing the maximum of all of them.
+
+#### Complexity
+**Time Complexity:** O(N^2)
+**Space Complexity:** O(1)
+
+#### Observation
+1. When bit is set in both the numbers, that bit in their **&** will be 1
+2. For answer to be maximum, we will want the set bit to be present towards as left as possible.
+3. This indicates that we should start processing the numbers from MSB.
+
+#### Optimized Solution
+
+* Iterate from the Most significant bit to Least significant bit and for all the numbers in the array, count the numbers for which that bit is set
+* If the count comes out to be greater than 1 then pairing is possible, so we include only the elements with that bit set into our vector. Also, set this bit in your answer.
+* If the count is 0 or 1, the pairing is not possible, so we continue with the same set and next bit position.
+
+#### Dry Run
+
+Example: { 26, 13, 23, 28, 27, 7, 25 }
+
+26: 1 1 0 1 0
+13: 0 1 1 0 1
+23: 1 0 1 1 1
+28: 1 1 1 0 0
+27: 1 1 0 1 1
+07: 0 0 1 1 1
+25: 1 1 0 0 1
+
+1. Let's start with MSB, **at position 4**, there are 5 numbers with set bits. Since count is >=2, we can form a pair. Therefore, in answer 1 will be present at this position.
+ans:
+
+| 1 | _ | _ | _ | _ |
+| -------- | -------- | -------- | -------- | -------- |
+
+
+
+* Iterate on every bit.
+* If the count of numbers in which ith bit is set is a multiple of 3, then in answer ith bit is NOT SET.
+* If the count of numbers in which ith bit is of the form (3 * x) + 1, then in answer ith bit is SET.
+
+#### Pseudocode
+```cpp=
+int ans = 0;
+
+for (int i = 0; i < 32; i++) { // go to every bit one by one
+ int cnt = 0;
+
+ for (int j = 0; j < arr.size(); j++) { // iterate on array
+
+ // check if ith bit is set
+ if ((arr[j] & (1 << i)) cnt++;
+ }
+
+ if (cnt % 3 == 1) // If the count is not the multiple of 3
+ ans = ans | 1 << i; // set ith bit in ans
+ }
+
+ print(ans);
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(1)
+
+---
+### Problem 3 Single number 3
+
+Given an integer array, all the elements will occur twice except two. Find those two elements.
+
+**Input:** [4, 5, 4, 1, 6, 6, 5, 2]
+
+**Output:** 1, 2
+
+#### Hint:
+* Will finding XOR help ? May be!
+* What do we get if we XOR all numbers ? XOR of the two unique numbers!
+* From that can we identify/separate the two numbers ? Not Really! Why?
+ * Example: If XOR is 7, we aren't sure which 2 numbers are they. (2, 5), (1, 6), (3, 4), ... have xor = 7, so we won't be able to identify!
+
+
+***Is there any way in which we can identify the two numbers from their XOR ?***
+
+Suppose if two unique numbers are **a** and **b**. Their XOR is **c**.
+In **c** if say 0th bit is set, what does that tell about a and b ?
+In one of the numbers the bit is set and in other the bit is unset! So, can we identify the numbers based on that ?
+
+#### Idea:
+
+* We will find the position of any set bit in XOR c, it will denote that this bit is different in a and b.
+* Now, we divide the entire array in two groups, based upon whether that particular bit is set or not.
+* This way a and b will fall into different groups.
+* Now since every number repeats twice, they will cancel out when we take XOR of the two groups individually leaving a and b.
+
+
+#### Pseudocode
+```cpp
+int xorAll = 0;
+
+// XOR of all numbers in the array
+for (int i = 0; i < N; i++) {
+ xorAll ^= A[i];
+}
+
+// Find the rightmost set bit position
+// Note: Any other bit can be used as well
+int pos;
+
+for (pos = 0; pos < 32; pos++) {
+ if (checkbit(xorAll, pos))
+ break;
+}
+
+num1 = 0;
+num2 = 0;
+
+// Divide the array into two groups based on the rightmost set bit
+for (int i = 0; i < N; i++) {
+ if (checkbit(A[i], pos)) {
+ num1 ^= A[i];
+ } else {
+ num2 ^= A[i];
+ }
+}
+
+print(num1);
+print(num2);
+```
+
+---
+### Question
+What is the time complexity to find two unique elements where every element is present 2 times except for two unique elements?
+
+**Choices**
+- [ ] O(1)
+- [ ] O(log(N))
+- [x] O(N)
+- [ ] O(32 * N)
+
+---
+### Problem 4 Maximum AND pair
+
+Given N array elements, choose two indices(i, j) such that **(i != j)** and **(arr[i] & arr[j])** is maximum.
+
+**Input:** [5, 4, 6, 8, 5]
+
+**Output:** [0, 4]
+
+If we take the **&** of 5 with 5, we get 5 which is the maximum possible value here. The required answer would be their respective indices i.e. **0,4**
+
+---
+### Question
+Max & Pair in this array (arr[] = 21,18,24,17,16) is
+
+**Choices**
+- [x] 21&17
+- [ ] 24&21
+- [ ] 17&16
+- [ ] 24&18
+
+---
+### Question
+Max & Pair in this array (arr[] =5,4,3,2,1) is
+
+**Choices**
+- [x] 5&4
+- [ ] 1&2
+- [ ] 1&4
+- [ ] 4&3
+
+---
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+### Maximum AND pair Approach
+
+
+#### Brute Force
+Using two for loops and calculating **bitwise &** for all possible pairs and storing the maximum of all of them.
+
+#### Complexity
+**Time Complexity:** O(N^2)
+**Space Complexity:** O(1)
+
+#### Observation
+1. When bit is set in both the numbers, that bit in their **&** will be 1
+2. For answer to be maximum, we will want the set bit to be present towards as left as possible.
+3. This indicates that we should start processing the numbers from MSB.
+
+#### Optimized Solution
+
+* Iterate from the Most significant bit to Least significant bit and for all the numbers in the array, count the numbers for which that bit is set
+* If the count comes out to be greater than 1 then pairing is possible, so we include only the elements with that bit set into our vector. Also, set this bit in your answer.
+* If the count is 0 or 1, the pairing is not possible, so we continue with the same set and next bit position.
+
+#### Dry Run
+
+Example: { 26, 13, 23, 28, 27, 7, 25 }
+
+26: 1 1 0 1 0
+13: 0 1 1 0 1
+23: 1 0 1 1 1
+28: 1 1 1 0 0
+27: 1 1 0 1 1
+07: 0 0 1 1 1
+25: 1 1 0 0 1
+
+1. Let's start with MSB, **at position 4**, there are 5 numbers with set bits. Since count is >=2, we can form a pair. Therefore, in answer 1 will be present at this position.
+ans:
+
+| 1 | _ | _ | _ | _ |
+| -------- | -------- | -------- | -------- | -------- |
+
+ +
+We will remove all numbers where 0 is present.
+[13 and 7 gets removed or are set to 0]
+
+
+
+We will remove all numbers where 0 is present.
+[13 and 7 gets removed or are set to 0]
+
+ +
+
+2. At position 3, there are 4 numbers with set bits(which haven't been cancelled). Since count is >=2, we can form a pair. Therefore, in answer 1 will be present at this position.
+ans:
+
+| 1 | 1 | _ | _ | _ |
+| -------- | -------- | -------- | -------- | -------- |
+
+We will remove all numbers where 0 is present.
+[23 gets removed or is set to 0]
+
+
+
+2. At position 3, there are 4 numbers with set bits(which haven't been cancelled). Since count is >=2, we can form a pair. Therefore, in answer 1 will be present at this position.
+ans:
+
+| 1 | 1 | _ | _ | _ |
+| -------- | -------- | -------- | -------- | -------- |
+
+We will remove all numbers where 0 is present.
+[23 gets removed or is set to 0]
+ +
+
+3. At position 2, there is 1 number with set bit. Since count is less than 2, we can't form a pair. Therefore, in answer 0 will be present at this position.
+ans:
+
+| 1 | 1 | 0 | _ | _ |
+| -------- | -------- | -------- | -------- | -------- |
+
+We will NOT remove any number.
+
+
+4. At position 1, there are 2 numbers with set bits. Since count is >=2, we can form a pair. Therefore, in answer 1 will be present at this position.
+
+ans:
+
+| 1 | 1 | 0 | 1 | _ |
+| -------- | -------- | -------- | -------- | -------- |
+
+We will remove all numbers where 0 is present.
+[28 and 25 gets removed or are set to 0]
+
+
+
+
+3. At position 2, there is 1 number with set bit. Since count is less than 2, we can't form a pair. Therefore, in answer 0 will be present at this position.
+ans:
+
+| 1 | 1 | 0 | _ | _ |
+| -------- | -------- | -------- | -------- | -------- |
+
+We will NOT remove any number.
+
+
+4. At position 1, there are 2 numbers with set bits. Since count is >=2, we can form a pair. Therefore, in answer 1 will be present at this position.
+
+ans:
+
+| 1 | 1 | 0 | 1 | _ |
+| -------- | -------- | -------- | -------- | -------- |
+
+We will remove all numbers where 0 is present.
+[28 and 25 gets removed or are set to 0]
+
+ +
+
+5. At position 0, there is 1 number with set bit. Since count is <2, we can't form a pair. Therefore, in answer 0 will be present at this position.
+
+ans:
+
+| 1 | 1 | 0 | 1 | 0 |
+| -------- | -------- | -------- | -------- | -------- |
+
+We will NOT remove any number.
+
+**We are done and answer final answer is present in variable ans**.
+
+---
+### Maximum AND pair Pseudocode
+#### Pseudocode
+```cpp
+ int ans = 0;
+
+ for (int i = 31; i >= 0; i--) {
+ //count no. of set bits at ith index
+ int count = 0;
+
+ for (int j = 0; j < n; j++) {
+ if (arr[j] & (1 << i))
+ cnt++;
+ }
+
+ //set that bit in ans if count >=2
+ if (count >= 2) {
+ ans = ans | (1 << i);
+
+ //set all numbers which have 0 bit at this position to 0
+ for (int j = 0; j < n; j++) {
+ if (arr[j] & (1 << i) == 0)
+ arr[j] = 0;
+ }
+
+ }
+ }
+
+ print(ans);
+
+//The numbers which cannot be choosen to form a pair have been made zero
+
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(1)
+
+
+
+Similarly, if we have to find maximum & of triplets then we will do for count>=3 and for quadruples as count >= 4 and so on ...
+
+
+---
+### Problem 5 Count of pairs with maximum AND
+
+Calculate the Count of Pairs for which bitwise & is maximum (GOOGLE Interview Question)
+
+#### Solution:
+
+Do exactly as above and then traverse on the array and find the number of elements which are greater than 0
+
+Required answer will be Nc2 or N(N-1)/2
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(1)
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA DP 1 One Dimentional.md b/Academy DSA Typed Notes/Advanced/DSA DP 1 One Dimentional.md
new file mode 100644
index 0000000..cc6e314
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA DP 1 One Dimentional.md
@@ -0,0 +1,342 @@
+# DP 1: One Dimentional
+
+---
+## Fibonacci Series
+
+`0 1 1 2 3 5 8 13 21 ...`
+
+### fibonacci Expresion
+* `fib(n) = fib(n-1) + fib(n-2)`
+* base case for the fibonacci expression -> `fib(0) = 0; fib(1) = 1`
+
+### Psuedocode
+```java
+int fib(n) {
+ if (n <= 1) return n;
+ return fib(n - 1) + (n - 2);
+}
+```
+> Time complexity for the above code : **O(2^N)**
+> Space Complexity for the above code : **O(N)**
+
+---
+### Problem 1 Fibonacci Series
+
+
+#### Properties of Dynamic Programming
+* **Optimal Substructure** - i.e. solving a problem by solving smaller subproblems
+* **Overlapping Subproblems** - solving some subproblems multiple times
+
+#### Solution for Dynamic Programming
+* Store the information about already solved sub-problem and use it
+
+
+#### Psuedocode of Fibonacci series using dynamic Programming
+```java
+int f[N + 1] // intialize it with -1
+
+int fib(n) {
+ if (N <= 1) return n;
+
+ // if already solved, don't repeat
+ if (f[N] != -1) return f[N];
+
+ // store it
+ f[N] = fib(n - 1) + (n - 2);
+ return f[N];
+}
+```
+**Two main operations performed in the above code of dynamic programming:**
+* If we have already solved a problem just return the solution, don't repeat the step
+* If not solved, solve and store the solution
+
+#### Dry Run
+
+
+
+
+5. At position 0, there is 1 number with set bit. Since count is <2, we can't form a pair. Therefore, in answer 0 will be present at this position.
+
+ans:
+
+| 1 | 1 | 0 | 1 | 0 |
+| -------- | -------- | -------- | -------- | -------- |
+
+We will NOT remove any number.
+
+**We are done and answer final answer is present in variable ans**.
+
+---
+### Maximum AND pair Pseudocode
+#### Pseudocode
+```cpp
+ int ans = 0;
+
+ for (int i = 31; i >= 0; i--) {
+ //count no. of set bits at ith index
+ int count = 0;
+
+ for (int j = 0; j < n; j++) {
+ if (arr[j] & (1 << i))
+ cnt++;
+ }
+
+ //set that bit in ans if count >=2
+ if (count >= 2) {
+ ans = ans | (1 << i);
+
+ //set all numbers which have 0 bit at this position to 0
+ for (int j = 0; j < n; j++) {
+ if (arr[j] & (1 << i) == 0)
+ arr[j] = 0;
+ }
+
+ }
+ }
+
+ print(ans);
+
+//The numbers which cannot be choosen to form a pair have been made zero
+
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(1)
+
+
+
+Similarly, if we have to find maximum & of triplets then we will do for count>=3 and for quadruples as count >= 4 and so on ...
+
+
+---
+### Problem 5 Count of pairs with maximum AND
+
+Calculate the Count of Pairs for which bitwise & is maximum (GOOGLE Interview Question)
+
+#### Solution:
+
+Do exactly as above and then traverse on the array and find the number of elements which are greater than 0
+
+Required answer will be Nc2 or N(N-1)/2
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(1)
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA DP 1 One Dimentional.md b/Academy DSA Typed Notes/Advanced/DSA DP 1 One Dimentional.md
new file mode 100644
index 0000000..cc6e314
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA DP 1 One Dimentional.md
@@ -0,0 +1,342 @@
+# DP 1: One Dimentional
+
+---
+## Fibonacci Series
+
+`0 1 1 2 3 5 8 13 21 ...`
+
+### fibonacci Expresion
+* `fib(n) = fib(n-1) + fib(n-2)`
+* base case for the fibonacci expression -> `fib(0) = 0; fib(1) = 1`
+
+### Psuedocode
+```java
+int fib(n) {
+ if (n <= 1) return n;
+ return fib(n - 1) + (n - 2);
+}
+```
+> Time complexity for the above code : **O(2^N)**
+> Space Complexity for the above code : **O(N)**
+
+---
+### Problem 1 Fibonacci Series
+
+
+#### Properties of Dynamic Programming
+* **Optimal Substructure** - i.e. solving a problem by solving smaller subproblems
+* **Overlapping Subproblems** - solving some subproblems multiple times
+
+#### Solution for Dynamic Programming
+* Store the information about already solved sub-problem and use it
+
+
+#### Psuedocode of Fibonacci series using dynamic Programming
+```java
+int f[N + 1] // intialize it with -1
+
+int fib(n) {
+ if (N <= 1) return n;
+
+ // if already solved, don't repeat
+ if (f[N] != -1) return f[N];
+
+ // store it
+ f[N] = fib(n - 1) + (n - 2);
+ return f[N];
+}
+```
+**Two main operations performed in the above code of dynamic programming:**
+* If we have already solved a problem just return the solution, don't repeat the step
+* If not solved, solve and store the solution
+
+#### Dry Run
+
+ +
+We're going to figure out what **`fib(5)`** is using a method called recursion, and we'll keep track of our answers in an array. Here's how it works, step by step:
+
+* **Starting Point:**
+We want to find out what fib(5) is. Our array, where we store our results, starts with -1 in every spot because we haven't calculated anything yet.
+
+* **Breaking it Down:**
+To get fib(5), we first need to know fib(4) and fib(3).
+
+* **Going Deeper:**
+For fib(4), we need fib(3) and fib(2). And for fib(3) (the one we saw earlier), we also need fib(2) and fib(1).
+
+* **Even Deeper:**
+To find fib(2), we look at fib(1) and fib(0).
+
+* **Simple Answers:**
+Now, fib(1) and fib(0) are easy; they are 1 and 0. We use these to find out fib(2), which is 1 (0 + 1). Store it before moving forward.
+
+* **Building Up:**
+We keep using these small answers to find the bigger ones. If we already know an answer (like fib(2)), we don't have to calculate it again; we just use the answer from our array.
+
+By the end, we'll have the answer to fib(5), and all the smaller fib numbers stored in our array!
+
+#### Time and Space Complexity
+
+**Time Complexity for the above code is O(N)** and **space complexity is O(N)**. Thus, we were able to reduce the time complexity from O(2^N) to O(N) using dynamic programing
+
+---
+### Dynamic Programming Types
+
+
+#### Types of DP Solution:
+*Dynamic programming solution can be of two types*:
+* **`Top-Down`** [Also know as **Memoization**]
+ * It is a recursive solution
+ * We start with the biggest problem and keep on breaking it till we reach the base case.
+ * Then store answers of already evaluated problems.
+
+* **`Bottom-Up`**
+ * It is an iterative solution
+ * We start with the smallest problem, solve it and store its result.
+ * Then we keep on moving to the bigger problems and use the already calculated results from sub-problems.
+
+
+#### Bottom Up Approach for Fibonacci series
+#### Psuedocode
+```java
+int fib[N + 1];
+
+fib[0] = 0;
+fib[1] = 1;
+
+for (i = 2, i <= N; i++) {
+ fib[i] = fib[i - 1] + fib[i - 2];
+}
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(N)
+
+> Through this approach we were able to eliminate recursive stack.
+
+#### Further optimising the Space Complexity
+
+If seen closely, the above approach can be optimised by using just simple variables instead of an array. In this way, we can further optimize the space.
+
+#### Pseudocode
+```java
+int a = 0;
+int b = 1;
+int c;
+for (int i = 2; i <= N; i++) {
+ c = a + b;
+ a = b;
+ b = c;
+}
+```
+> In the above code we were able to optimize the space complexity to O(1).
+
+---
+### Question
+What is the purpose of memoization in dynamic programming?
+
+**Choices**
+
+- [ ] To minimize the space complexity of the algorithm
+- [x] To store and reuse solutions to subproblems
+- [ ] To calculate results of all calls
+- [ ] To improve the readability of the code
+
+---
+### Question
+Which approach is considered as an iterative process?
+
+**Choices**
+
+- [ ] Top-down approach
+- [x] Bottom-up approach
+- [ ] Both are iterative
+- [ ] Neither is iterative
+
+
+---
+### Problem 2 Climbing Staircase
+
+
+
+*Calculate the number of ways to reach the Nth stair. You can take 1 step at a time or 2 steps at a time.*
+
+
+
+We're going to figure out what **`fib(5)`** is using a method called recursion, and we'll keep track of our answers in an array. Here's how it works, step by step:
+
+* **Starting Point:**
+We want to find out what fib(5) is. Our array, where we store our results, starts with -1 in every spot because we haven't calculated anything yet.
+
+* **Breaking it Down:**
+To get fib(5), we first need to know fib(4) and fib(3).
+
+* **Going Deeper:**
+For fib(4), we need fib(3) and fib(2). And for fib(3) (the one we saw earlier), we also need fib(2) and fib(1).
+
+* **Even Deeper:**
+To find fib(2), we look at fib(1) and fib(0).
+
+* **Simple Answers:**
+Now, fib(1) and fib(0) are easy; they are 1 and 0. We use these to find out fib(2), which is 1 (0 + 1). Store it before moving forward.
+
+* **Building Up:**
+We keep using these small answers to find the bigger ones. If we already know an answer (like fib(2)), we don't have to calculate it again; we just use the answer from our array.
+
+By the end, we'll have the answer to fib(5), and all the smaller fib numbers stored in our array!
+
+#### Time and Space Complexity
+
+**Time Complexity for the above code is O(N)** and **space complexity is O(N)**. Thus, we were able to reduce the time complexity from O(2^N) to O(N) using dynamic programing
+
+---
+### Dynamic Programming Types
+
+
+#### Types of DP Solution:
+*Dynamic programming solution can be of two types*:
+* **`Top-Down`** [Also know as **Memoization**]
+ * It is a recursive solution
+ * We start with the biggest problem and keep on breaking it till we reach the base case.
+ * Then store answers of already evaluated problems.
+
+* **`Bottom-Up`**
+ * It is an iterative solution
+ * We start with the smallest problem, solve it and store its result.
+ * Then we keep on moving to the bigger problems and use the already calculated results from sub-problems.
+
+
+#### Bottom Up Approach for Fibonacci series
+#### Psuedocode
+```java
+int fib[N + 1];
+
+fib[0] = 0;
+fib[1] = 1;
+
+for (i = 2, i <= N; i++) {
+ fib[i] = fib[i - 1] + fib[i - 2];
+}
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(N)
+
+> Through this approach we were able to eliminate recursive stack.
+
+#### Further optimising the Space Complexity
+
+If seen closely, the above approach can be optimised by using just simple variables instead of an array. In this way, we can further optimize the space.
+
+#### Pseudocode
+```java
+int a = 0;
+int b = 1;
+int c;
+for (int i = 2; i <= N; i++) {
+ c = a + b;
+ a = b;
+ b = c;
+}
+```
+> In the above code we were able to optimize the space complexity to O(1).
+
+---
+### Question
+What is the purpose of memoization in dynamic programming?
+
+**Choices**
+
+- [ ] To minimize the space complexity of the algorithm
+- [x] To store and reuse solutions to subproblems
+- [ ] To calculate results of all calls
+- [ ] To improve the readability of the code
+
+---
+### Question
+Which approach is considered as an iterative process?
+
+**Choices**
+
+- [ ] Top-down approach
+- [x] Bottom-up approach
+- [ ] Both are iterative
+- [ ] Neither is iterative
+
+
+---
+### Problem 2 Climbing Staircase
+
+
+
+*Calculate the number of ways to reach the Nth stair. You can take 1 step at a time or 2 steps at a time.*
+
+ +
+**`CASE 1: (number of stairs = 1)`**
+{1}
+
+
+**`CASE 1: (number of stairs = 1)`**
+{1}
+ +
+
+
+Number of ways to reach first stair : 1 (as shown in fig)
+
+
+**`CASE 2: (number of stairs = 2)`**
+
+{1, 1}
+{2}
+
+
+
+
+
+Number of ways to reach first stair : 1 (as shown in fig)
+
+
+**`CASE 2: (number of stairs = 2)`**
+
+{1, 1}
+{2}
+
+ +
+Number of ways to reach two stairs : 2 (as shown in fig)
+
+**`CASE 3: (number of stairs = 3)`**
+
+{1, 2}
+{1, 1, 1}
+{2, 1}
+
+
+
+Number of ways to reach two stairs : 2 (as shown in fig)
+
+**`CASE 3: (number of stairs = 3)`**
+
+{1, 2}
+{1, 1, 1}
+{2, 1}
+
+ +
+Number of ways to reach two stairs : 3 (as shown in fig)
+
+**`CASE 4: (number of stairs = 4)`**
+{1, 1, 2}
+{2, 2}
+{1, 2, 1}
+{1, 1, 1, 1}
+{2, 1, 1}
+
+
+
+---
+### Question
+In Stairs Problems, the result for N=4
+
+**Choices**
+- [ ] 4
+- [x] 5
+- [ ] 6
+- [ ] 7
+
+**Explanation:**
+
+To reach 1st staircase : 1 way
+To reach 2nd staircase : 2 ways
+To reach 3rd staircase : 3 ways
+To reach 4th staircase : 5 ways
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+### Problem 2 Climbing Staircase Approach
+#### Approach
+
+We can come to 4th stair from 2nd and 3rd step.
+* If I get to know #steps to reach stair 3, we can take length 1 step and reach stair 4.
+* Similarly, if I get to know #steps to reach stair 2, we can take length 2 step and reach stair 4.
+
+
+
+Number of ways to reach two stairs : 3 (as shown in fig)
+
+**`CASE 4: (number of stairs = 4)`**
+{1, 1, 2}
+{2, 2}
+{1, 2, 1}
+{1, 1, 1, 1}
+{2, 1, 1}
+
+
+
+---
+### Question
+In Stairs Problems, the result for N=4
+
+**Choices**
+- [ ] 4
+- [x] 5
+- [ ] 6
+- [ ] 7
+
+**Explanation:**
+
+To reach 1st staircase : 1 way
+To reach 2nd staircase : 2 ways
+To reach 3rd staircase : 3 ways
+To reach 4th staircase : 5 ways
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+### Problem 2 Climbing Staircase Approach
+#### Approach
+
+We can come to 4th stair from 2nd and 3rd step.
+* If I get to know #steps to reach stair 3, we can take length 1 step and reach stair 4.
+* Similarly, if I get to know #steps to reach stair 2, we can take length 2 step and reach stair 4.
+
+ +
+
+
+ +
+
+
+ +
+* Number of ways we can reach to the nth step is either by (n - 1) or (n - 2).
+* Answer will be summation of number of ways to reach (n - 1)th step + number of ways to reach (n - 2)th step
+
+We can see that the above has been deduced to fibonacii expression
+
+---
+### Problem 3 Get Minimum Squares
+
+*Find minimum number of perfect squares required to get sum = N. (duplicate squares are allowed)*
+
+*example 1 --> N = 6*
+
+sum 6 can be obtained by the addition of following squares:
+* `1^2+1^2+1^2+1^2+1^2+1^2`
+* `1^2+1^2+2^2` --> minimum number of squares is 3 in this case
+
+*example 2 --> N = 10*
+
+sum 10 can be obtained by the addition of following squares:
+* `1^2+1^2+..... 10 times`
+* `2^2 + 1^2..... 6 times`
+* `2^2 + 2^2 + 1^2 + 1^2`
+* `3^2 + 1^2 `--> minimum number of squares is 2 in this case
+
+*example 3 --> N = 9*
+
+sum 10 can be obtained by the addition of following squares:
+* `1^2+1^2+..... 9 times`
+* `2^2 + 1^2..... 5 times`
+* `2^2 + 2^2 + 1^2 `
+* `3^2` --> minimum number of squares is 1 in this case
+
+
+---
+### Question
+What is the minimum number of perfect squares required to get sum = 5. (duplicate squares are allowed)
+
+**Choices**
+- [ ] 5
+- [ ] 1
+- [x] 2
+- [ ] 3
+
+
+**Explanation**:
+
+sum 5 can be obtained by the addition of following squares:
+* `1^2 + 1^2 + 1^2 + 1^2 + 1^2`
+* `2^2 + 1^2` --> minimum number of squares is 2 in this case
+
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Get Minimum Squares Approach
+
+#### Approach 1
+* Can we simply do **`N - (nearest perfect square)`** ?
+
+ * Verifying approach 1 with example N=12
+ * 12-9 (closest square) = 3
+ * 3-1 = 2
+ * 2-1 = 1
+ * 1-1 = 0
+ * We are using 4 perfect squares, whereas the minimum number of square is 3 (2^2 + 2^2 +2^2) so approach 1 is not useful in this case
+
+#### Brute Force Approach
+* Try every possible way to form the sum using brute force to solve a example N = 12
+
+
+* Number of ways we can reach to the nth step is either by (n - 1) or (n - 2).
+* Answer will be summation of number of ways to reach (n - 1)th step + number of ways to reach (n - 2)th step
+
+We can see that the above has been deduced to fibonacii expression
+
+---
+### Problem 3 Get Minimum Squares
+
+*Find minimum number of perfect squares required to get sum = N. (duplicate squares are allowed)*
+
+*example 1 --> N = 6*
+
+sum 6 can be obtained by the addition of following squares:
+* `1^2+1^2+1^2+1^2+1^2+1^2`
+* `1^2+1^2+2^2` --> minimum number of squares is 3 in this case
+
+*example 2 --> N = 10*
+
+sum 10 can be obtained by the addition of following squares:
+* `1^2+1^2+..... 10 times`
+* `2^2 + 1^2..... 6 times`
+* `2^2 + 2^2 + 1^2 + 1^2`
+* `3^2 + 1^2 `--> minimum number of squares is 2 in this case
+
+*example 3 --> N = 9*
+
+sum 10 can be obtained by the addition of following squares:
+* `1^2+1^2+..... 9 times`
+* `2^2 + 1^2..... 5 times`
+* `2^2 + 2^2 + 1^2 `
+* `3^2` --> minimum number of squares is 1 in this case
+
+
+---
+### Question
+What is the minimum number of perfect squares required to get sum = 5. (duplicate squares are allowed)
+
+**Choices**
+- [ ] 5
+- [ ] 1
+- [x] 2
+- [ ] 3
+
+
+**Explanation**:
+
+sum 5 can be obtained by the addition of following squares:
+* `1^2 + 1^2 + 1^2 + 1^2 + 1^2`
+* `2^2 + 1^2` --> minimum number of squares is 2 in this case
+
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Get Minimum Squares Approach
+
+#### Approach 1
+* Can we simply do **`N - (nearest perfect square)`** ?
+
+ * Verifying approach 1 with example N=12
+ * 12-9 (closest square) = 3
+ * 3-1 = 2
+ * 2-1 = 1
+ * 1-1 = 0
+ * We are using 4 perfect squares, whereas the minimum number of square is 3 (2^2 + 2^2 +2^2) so approach 1 is not useful in this case
+
+#### Brute Force Approach
+* Try every possible way to form the sum using brute force to solve a example N = 12
+ +
+The above image shows all possiblities to achieve 12.
+
+Now, to get minimum sum of 12 we will find minimum square of 11 or minimum square of 8 or minimum square of 3 + 1.
+
+The above is a recursive problem where we can see overalapping subproblems, like for N=7.
+
+#### Dynamic Programming Approach
+Here optimal structure has been obtained as well as overlapping subproblems
+
+So, we can say that
+`square(i) = 1 + min{ squares(i - x^2) for all x^2 <= i} `and base case is square[0] = 0
+
+#### Psuedocode
+```java
+int dp[N + 1]; //initialise (-1)
+int psquares(int N, int dp[]) {
+ if (n == 0) return 0;
+ if (dp[N] != -1) return dp[N];
+ ans = int - max;
+ for (x = 1; x * x <= N; x++) {
+ ans = min(ans, psquares(N - x ^ 2)); // dp
+ }
+ dp[N] = 1 + ans;
+ return dp[N];
+}
+```
+Time complexity for the above code is O(N(sqrt(N))) and space complexity is O(N).
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA DP 2 Two Dimentional.md b/Academy DSA Typed Notes/Advanced/DSA DP 2 Two Dimentional.md
new file mode 100644
index 0000000..3045270
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA DP 2 Two Dimentional.md
@@ -0,0 +1,724 @@
+# DP 2: Two Dimensional
+
+---
+## Problem 1 Maximum Subsequence Sum
+
+Find maximum subsequence sum from a given array, where selecting adjacent element is not allowed.
+
+**Examples**
+Example 1: ar[] = {9, 4, 13}
+Output 1: 22. Since out of all possible non adjacent element subsequences, the subsequence (9, 13) will yield maximum sum.
+
+Example 2: ar[] = {9, 4, 13, 24}
+Output 2: 33 (24 + 9)
+
+
+---
+### Question
+Find maximum subsequence sum from `[10, 20, 30, 40]`, where selecting adjacent element is not allowed.
+
+**Choices**
+- [ ] 70
+- [x] 60
+- [ ] 100
+- [ ] 50
+
+**Explanation**:
+
+Maximum Subsequence is 60. Since, Out of all possible non adjacent element subsequences, the subsequence (20, 40) will yield maximum sum of 60.
+
+
+---
+### Maximum Subsequence Sum Brute Force Approach
+
+:::warning
+Please take some time to think about the brute force approach on your own before reading further.....
+:::
+
+#### Brute Force Approach
+- Consider all the valid subsequences **`(this a backtracking step)`**.
+- For creating subsequences, for every element we can make a choice, whether to select it or reject it.
+- Say, we start from right most element. If we keep it, then (n - 1)th element can't be considered, so jump to (n - 2)th. If we don't, then (n - 1)th element can be considered. So on...
+
+
+
+
+The above image shows all possiblities to achieve 12.
+
+Now, to get minimum sum of 12 we will find minimum square of 11 or minimum square of 8 or minimum square of 3 + 1.
+
+The above is a recursive problem where we can see overalapping subproblems, like for N=7.
+
+#### Dynamic Programming Approach
+Here optimal structure has been obtained as well as overlapping subproblems
+
+So, we can say that
+`square(i) = 1 + min{ squares(i - x^2) for all x^2 <= i} `and base case is square[0] = 0
+
+#### Psuedocode
+```java
+int dp[N + 1]; //initialise (-1)
+int psquares(int N, int dp[]) {
+ if (n == 0) return 0;
+ if (dp[N] != -1) return dp[N];
+ ans = int - max;
+ for (x = 1; x * x <= N; x++) {
+ ans = min(ans, psquares(N - x ^ 2)); // dp
+ }
+ dp[N] = 1 + ans;
+ return dp[N];
+}
+```
+Time complexity for the above code is O(N(sqrt(N))) and space complexity is O(N).
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA DP 2 Two Dimentional.md b/Academy DSA Typed Notes/Advanced/DSA DP 2 Two Dimentional.md
new file mode 100644
index 0000000..3045270
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA DP 2 Two Dimentional.md
@@ -0,0 +1,724 @@
+# DP 2: Two Dimensional
+
+---
+## Problem 1 Maximum Subsequence Sum
+
+Find maximum subsequence sum from a given array, where selecting adjacent element is not allowed.
+
+**Examples**
+Example 1: ar[] = {9, 4, 13}
+Output 1: 22. Since out of all possible non adjacent element subsequences, the subsequence (9, 13) will yield maximum sum.
+
+Example 2: ar[] = {9, 4, 13, 24}
+Output 2: 33 (24 + 9)
+
+
+---
+### Question
+Find maximum subsequence sum from `[10, 20, 30, 40]`, where selecting adjacent element is not allowed.
+
+**Choices**
+- [ ] 70
+- [x] 60
+- [ ] 100
+- [ ] 50
+
+**Explanation**:
+
+Maximum Subsequence is 60. Since, Out of all possible non adjacent element subsequences, the subsequence (20, 40) will yield maximum sum of 60.
+
+
+---
+### Maximum Subsequence Sum Brute Force Approach
+
+:::warning
+Please take some time to think about the brute force approach on your own before reading further.....
+:::
+
+#### Brute Force Approach
+- Consider all the valid subsequences **`(this a backtracking step)`**.
+- For creating subsequences, for every element we can make a choice, whether to select it or reject it.
+- Say, we start from right most element. If we keep it, then (n - 1)th element can't be considered, so jump to (n - 2)th. If we don't, then (n - 1)th element can be considered. So on...
+
+
+ +
+
+The above image shows tree which has all the choices of selection. Here we can see that the choices are overlapping.
+
+Moreover, as the problem can be broken into smaller problems and has overlapping sub problems, we can use **dynamic programming**.
+
+
+---
+### Maximum Subsequence Sum Top Down Approach
+
+#### Top Down Approach
+So for **maxSum(i)** there are two options:
+* either we can select element present at index i
+ * if we select that element we will include its value ie ar[i] and the recursive call will be **maxSum(i-2)**
+* or we cannot select the element present at index i
+ * so in this case we will not include its value and will make recursive call which is **maxSum(i-1)**
+
+`dp[i] = stores the maximum value that can be obtained by selecting 0 to ith toy.`
+
+The maximum of the choice we make will give us the final answer
+
+#### Psuedocode
+
+```cpp
+int dp[N] //initialize it with negative infinity
+
+// i will be initialised with N-1, i.e we start with the last element
+int maxSum(int[] arr, i, dp[N]) {
+ if (i < 0) {
+ return 0
+ }
+ if (dp[i] != -infinity) {
+ return dp[i]
+ }
+ //Don't consider the ith element, in this case we can consider (i-1)th element
+ f1 = maxSum(arr, i - 1, dp);
+
+ //Consider the ith element, in this case we can't consider (i-1)th element, so we jump to (i-2)th element
+ f2 = arr[i] + maxSum(arr, i - 2, dp);
+
+ ans = max(f1, f2)
+
+ dp[i] = ans;
+
+ return ans
+}
+```
+
+#### Time & Space Complexity
+
+**Time complexity:** O(N). As we are filling the DP array of size N linearly, it would take O(N) time.
+**Space complexity:** O(N), because of dp array of size N.
+
+
+---
+### Maximum Subsequence Sum Bottom Up Approach
+
+**Problem 1**
+**`dp[i] is defined as the maximum subsequence sum from [0 - i] provided no adjacent elements are selected`**
+
+arr = {9, 4, 13, 24}
+
+We can start from arr[0] and we have two choices: either we can select arr[0] or reject.
+* If we select it, the maximum value we can acheive is arr[0] = 9
+* If we reject it, the value which we will get is 0
+* So, we will store arr[0] in dp[0]
+
+* Now, we will look at arr[0] and arr[1] to find the maximum
+ * As arr[0] > arr[1], we will store arr[0] in dp[1]
+* Similary we will repeat the above steps to fill dp[].
+
+
+#### Psuedocode
+
+```cpp
+dp[N]
+for(i = 0; i < N; i++){
+ dp[i] = max(dp[i - 1], arr[i] + dp[i - 2])
+}
+return dp[N - 1]
+```
+
+
+#### Time & Space Complexity
+**Time complexity:** O(N). As we are filling the DP array of size N linearly, it would take O(N) time.
+**Space complexity:** O(N), because of dp array of size N.
+
+---
+### Problem 2 Count Unique Paths
+
+Given mat[n][m], find total number of ways from (0,0) to (n - 1, m - 1). We can move 1 step in horizontal direction or 1 step in vertical direction.
+
+
+
+
+The above image shows tree which has all the choices of selection. Here we can see that the choices are overlapping.
+
+Moreover, as the problem can be broken into smaller problems and has overlapping sub problems, we can use **dynamic programming**.
+
+
+---
+### Maximum Subsequence Sum Top Down Approach
+
+#### Top Down Approach
+So for **maxSum(i)** there are two options:
+* either we can select element present at index i
+ * if we select that element we will include its value ie ar[i] and the recursive call will be **maxSum(i-2)**
+* or we cannot select the element present at index i
+ * so in this case we will not include its value and will make recursive call which is **maxSum(i-1)**
+
+`dp[i] = stores the maximum value that can be obtained by selecting 0 to ith toy.`
+
+The maximum of the choice we make will give us the final answer
+
+#### Psuedocode
+
+```cpp
+int dp[N] //initialize it with negative infinity
+
+// i will be initialised with N-1, i.e we start with the last element
+int maxSum(int[] arr, i, dp[N]) {
+ if (i < 0) {
+ return 0
+ }
+ if (dp[i] != -infinity) {
+ return dp[i]
+ }
+ //Don't consider the ith element, in this case we can consider (i-1)th element
+ f1 = maxSum(arr, i - 1, dp);
+
+ //Consider the ith element, in this case we can't consider (i-1)th element, so we jump to (i-2)th element
+ f2 = arr[i] + maxSum(arr, i - 2, dp);
+
+ ans = max(f1, f2)
+
+ dp[i] = ans;
+
+ return ans
+}
+```
+
+#### Time & Space Complexity
+
+**Time complexity:** O(N). As we are filling the DP array of size N linearly, it would take O(N) time.
+**Space complexity:** O(N), because of dp array of size N.
+
+
+---
+### Maximum Subsequence Sum Bottom Up Approach
+
+**Problem 1**
+**`dp[i] is defined as the maximum subsequence sum from [0 - i] provided no adjacent elements are selected`**
+
+arr = {9, 4, 13, 24}
+
+We can start from arr[0] and we have two choices: either we can select arr[0] or reject.
+* If we select it, the maximum value we can acheive is arr[0] = 9
+* If we reject it, the value which we will get is 0
+* So, we will store arr[0] in dp[0]
+
+* Now, we will look at arr[0] and arr[1] to find the maximum
+ * As arr[0] > arr[1], we will store arr[0] in dp[1]
+* Similary we will repeat the above steps to fill dp[].
+
+
+#### Psuedocode
+
+```cpp
+dp[N]
+for(i = 0; i < N; i++){
+ dp[i] = max(dp[i - 1], arr[i] + dp[i - 2])
+}
+return dp[N - 1]
+```
+
+
+#### Time & Space Complexity
+**Time complexity:** O(N). As we are filling the DP array of size N linearly, it would take O(N) time.
+**Space complexity:** O(N), because of dp array of size N.
+
+---
+### Problem 2 Count Unique Paths
+
+Given mat[n][m], find total number of ways from (0,0) to (n - 1, m - 1). We can move 1 step in horizontal direction or 1 step in vertical direction.
+
+ +
+
+**Example**
+
+
+
+
+**Example**
+
+ +
+
+> `h` represents movement in horizontal direction and `v` represents movement in vertical direction
+
+**Ans:** 6
+
+
+
+---
+### Question
+Find the total number of ways to go from (0, 0) to (1, 2)
+
+| o | | |
+|---|---|---|
+| | | **o** |
+
+
+**Choices**
+- [ ] 1
+- [ ] 2
+- [x] 3
+- [ ] 4
+
+
+**Explanation**:
+
+The 2D matrix dp is
+
+| | 0 | 1 | 2 |
+|---|---|---|---|
+| 0 | 1 | 1 | 1 |
+| 1 | 1 | 2 | 3 |
+
+From here, the number of ways to go from (0, 0) to (1, 2) is 3.
+
+
+---
+### Count Unique Paths Brute Force Approach
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Brute Force Appoarch
+**Backtracking**, i.e., start from (0, 0) and try all possible scenarios to reach (n - 1, m - 1)
+
+#### Observation
+Can we break it into subproblems?
+- We can reach (n - 1, m - 1) in one step (by moving vertically) from (n - 2, m - 1)
+- We can reach (n - 1, m - 1) in one step (by moving horizontally) (n - 1, m - 2)
+
+
+
+
+> `h` represents movement in horizontal direction and `v` represents movement in vertical direction
+
+**Ans:** 6
+
+
+
+---
+### Question
+Find the total number of ways to go from (0, 0) to (1, 2)
+
+| o | | |
+|---|---|---|
+| | | **o** |
+
+
+**Choices**
+- [ ] 1
+- [ ] 2
+- [x] 3
+- [ ] 4
+
+
+**Explanation**:
+
+The 2D matrix dp is
+
+| | 0 | 1 | 2 |
+|---|---|---|---|
+| 0 | 1 | 1 | 1 |
+| 1 | 1 | 2 | 3 |
+
+From here, the number of ways to go from (0, 0) to (1, 2) is 3.
+
+
+---
+### Count Unique Paths Brute Force Approach
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Brute Force Appoarch
+**Backtracking**, i.e., start from (0, 0) and try all possible scenarios to reach (n - 1, m - 1)
+
+#### Observation
+Can we break it into subproblems?
+- We can reach (n - 1, m - 1) in one step (by moving vertically) from (n - 2, m - 1)
+- We can reach (n - 1, m - 1) in one step (by moving horizontally) (n - 1, m - 2)
+
+ +
+
+
+#### Recursive Relation
+
+**ways(i, j) = ways(i - 1, j) + ways(i, j - 1)**
+
+#### Base Condition
+- When i == 0, we have only one path to reach at the end, i.e., by moving vertically.
+- Similary, when j == 0, we have only one path to reach at the end, i.e., by moving horizontally.
+
+Therefore, **ways(0, j) = ways(i, 0) = 1**
+
+#### Pseudocode:
+```java
+int ways(i, j) {
+ if (i == 0 || j == 0) {
+ return 1;
+ }
+ return ways(i - 1, j) + ways(i, j - 1);
+}
+```
+
+Time Complexity: O(2 ^ (N * M)), as at every step we have two options, and there are total of N * M cells.
+
+
+---
+### Count Unique Paths Optimization
+
+#### Optimization using DP
+
+We can see the **optimal substructure** in this problem as it can be defined in terms of smaller subproblems.
+
+**Are there overlapping subproblems as well?**
+
+
+
+
+
+#### Recursive Relation
+
+**ways(i, j) = ways(i - 1, j) + ways(i, j - 1)**
+
+#### Base Condition
+- When i == 0, we have only one path to reach at the end, i.e., by moving vertically.
+- Similary, when j == 0, we have only one path to reach at the end, i.e., by moving horizontally.
+
+Therefore, **ways(0, j) = ways(i, 0) = 1**
+
+#### Pseudocode:
+```java
+int ways(i, j) {
+ if (i == 0 || j == 0) {
+ return 1;
+ }
+ return ways(i - 1, j) + ways(i, j - 1);
+}
+```
+
+Time Complexity: O(2 ^ (N * M)), as at every step we have two options, and there are total of N * M cells.
+
+
+---
+### Count Unique Paths Optimization
+
+#### Optimization using DP
+
+We can see the **optimal substructure** in this problem as it can be defined in terms of smaller subproblems.
+
+**Are there overlapping subproblems as well?**
+
+ +
+
+We can see that, `(i - 1, j - 1)` are the overlapping subproblems.
+
+***Since there is optimal substructure and overlapping subproblems, DP can be easily applied.***
+
+*Which type of array should be used?*
+Since two args (i and j) are varying in above method, 2-d storage is needed of size N x M.
+
+#### Top Down Approach
+
+**`dp[i][j] = It is defined as the total ways to reach from 0,0 to i,j`**
+
+#### Pseudocode
+```java
+int dp[N][M]; // initialized with -1
+int ways(i, j) {
+ if (i == 0 || j == 0) {
+ return 1;
+ }
+
+ if (dp[i][j] != -1) {
+ return dp[i][j];
+ }
+ ans = ways(i - 1, j, dp) + ways(i, j - 1, dp);
+ dp[i][j] = ans;
+ return ans;
+}
+```
+#### Complexity
+**Time Complexity:** O(N * M), as we are filling a matrix of size N * M.
+**Space Complexity:** O(N * M), as we have used dp matrix of size N * M.
+
+> *In how many ways can we reach (0, 0) starting from (0, 0)?*
+>
+> If you say 0, that means there is no way to reach (0, 0) or (0, 0) is unreachable. Hence, to reach (0, 0) from (0, 0), there is 1 way and not 0.
+
+#### Bottom Up Approach:
+Consider a 2D matrix `dp` of size N * M.
+`dp[i][j] = It is defined as the total ways to reach from 0,0 to i,j`
+
+In bottom up approach, we start from the smallest problem which is (0, 0) in this case.
+- No. of ways to move (0, 0) from (0, 0) = ways(0, 0) = 1
+- Similarly, ways(0, 1) = ways(0, 2) = . . . = 1
+- Also, ways(1, 0) = ways(2, 0) = . . . = 1
+- Now, ways(1, 1) = ways(1, 0) + ways(0, 1) = 2
+- Similarly, ways(1, 2) = ways(1, 1) + ways(0, 2) = 3, and so on.
+
+
+
+
+We can see that, `(i - 1, j - 1)` are the overlapping subproblems.
+
+***Since there is optimal substructure and overlapping subproblems, DP can be easily applied.***
+
+*Which type of array should be used?*
+Since two args (i and j) are varying in above method, 2-d storage is needed of size N x M.
+
+#### Top Down Approach
+
+**`dp[i][j] = It is defined as the total ways to reach from 0,0 to i,j`**
+
+#### Pseudocode
+```java
+int dp[N][M]; // initialized with -1
+int ways(i, j) {
+ if (i == 0 || j == 0) {
+ return 1;
+ }
+
+ if (dp[i][j] != -1) {
+ return dp[i][j];
+ }
+ ans = ways(i - 1, j, dp) + ways(i, j - 1, dp);
+ dp[i][j] = ans;
+ return ans;
+}
+```
+#### Complexity
+**Time Complexity:** O(N * M), as we are filling a matrix of size N * M.
+**Space Complexity:** O(N * M), as we have used dp matrix of size N * M.
+
+> *In how many ways can we reach (0, 0) starting from (0, 0)?*
+>
+> If you say 0, that means there is no way to reach (0, 0) or (0, 0) is unreachable. Hence, to reach (0, 0) from (0, 0), there is 1 way and not 0.
+
+#### Bottom Up Approach:
+Consider a 2D matrix `dp` of size N * M.
+`dp[i][j] = It is defined as the total ways to reach from 0,0 to i,j`
+
+In bottom up approach, we start from the smallest problem which is (0, 0) in this case.
+- No. of ways to move (0, 0) from (0, 0) = ways(0, 0) = 1
+- Similarly, ways(0, 1) = ways(0, 2) = . . . = 1
+- Also, ways(1, 0) = ways(2, 0) = . . . = 1
+- Now, ways(1, 1) = ways(1, 0) + ways(0, 1) = 2
+- Similarly, ways(1, 2) = ways(1, 1) + ways(0, 2) = 3, and so on.
+
+ +
+#### Pseudocode
+```java
+dp[N][M];
+// Initialize `dp` row - 0 and col - 0 with 1.
+for (i = 1; i <= N; i++) {
+ for (j = 1; j <= M; j++) {
+ dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
+ }
+}
+return dp[N - 1][M - 1];
+```
+
+Time Complexity: O(N * M)
+Space Complexity: O(N * M)
+
+
+#### Can we further optimize the space complexity?
+
+- The answer of every row is dependent upon its previous row.
+- So, essentially, we require two rows at a time - (1) current row (2) previous row. Thus, the space can be optimized to use just two 1-D arrays.
+
+
+---
+### Problem 3 Total number of ways to go to bottom right corner from top left corner
+
+
+Find the total number of ways to go to bottom right corner (N - 1, M - 1) from top left corner (0, 0) where cell with value 1 and 0 represents non-blocked and blocked cell respectively.
+We can either traverse one step down or one step right.
+
+
+
+#### Pseudocode
+```java
+dp[N][M];
+// Initialize `dp` row - 0 and col - 0 with 1.
+for (i = 1; i <= N; i++) {
+ for (j = 1; j <= M; j++) {
+ dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
+ }
+}
+return dp[N - 1][M - 1];
+```
+
+Time Complexity: O(N * M)
+Space Complexity: O(N * M)
+
+
+#### Can we further optimize the space complexity?
+
+- The answer of every row is dependent upon its previous row.
+- So, essentially, we require two rows at a time - (1) current row (2) previous row. Thus, the space can be optimized to use just two 1-D arrays.
+
+
+---
+### Problem 3 Total number of ways to go to bottom right corner from top left corner
+
+
+Find the total number of ways to go to bottom right corner (N - 1, M - 1) from top left corner (0, 0) where cell with value 1 and 0 represents non-blocked and blocked cell respectively.
+We can either traverse one step down or one step right.
+
+ +
+
+#### Solution
+
+
+
+| 1 | 1 | 1 | 1 |
+| - | - | - | - |
+| 1 | 0 | 1 | 0 |
+| 0 | 0 | 1 | 1 |
+| 0 | 0 | 1 | 2 |
+| 0 | 0 | 1 | 3 |
+
+
+The given problem is just a variation of above problem. Only advancement is that if cell value has 0, then there is no way to reach the bottom right cell.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Pseudocode (Recursive Approach)
+
+```cpp
+if (mat[i][j] != 0) {
+ ways(i, j) = ways(i - 1, j) + ways(i, j - 1);
+} else {
+ ways[i][j] = 0;
+}
+```
+
+Similar base condition can be added to top-down and bottom-up approach to optimize it using DP.
+
+
+---
+### Question
+How many unique paths in the grid from (0, 0) to (2, 2) ?
+
+| 1 | 1 | 1 |
+|-------|-------|-------|
+| **0** | **0** | **0** |
+| **1** | **1** | **1** |
+
+where cell with value 1 and 0 represents non-blocked and blocked cell respectively.
+
+**Choices**
+- [x] 0
+- [ ] 1
+- [ ] 2
+- [ ] 3
+
+
+**Explanation**:
+
+On the Grid, Row 1 is completely blocked. So there is no path from (0, 0) to (2, 2).
+
+Thus, the Total number of unique paths is 0.
+
+---
+### Problem 4 Dungeons and Princess
+
+
+Find the minimum health level of the prince to start with to save the princess, where the negative numbers denote a dragon and positive numbers denote red bull.
+
+Redbull will increase the health whereas the dragons will decrease the health.
+
+The prince can move either in horizontal right direction or vertical down direction.
+If health level <= 0, it means prince is dead.
+
+
+
+
+#### Solution
+
+
+
+| 1 | 1 | 1 | 1 |
+| - | - | - | - |
+| 1 | 0 | 1 | 0 |
+| 0 | 0 | 1 | 1 |
+| 0 | 0 | 1 | 2 |
+| 0 | 0 | 1 | 3 |
+
+
+The given problem is just a variation of above problem. Only advancement is that if cell value has 0, then there is no way to reach the bottom right cell.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Pseudocode (Recursive Approach)
+
+```cpp
+if (mat[i][j] != 0) {
+ ways(i, j) = ways(i - 1, j) + ways(i, j - 1);
+} else {
+ ways[i][j] = 0;
+}
+```
+
+Similar base condition can be added to top-down and bottom-up approach to optimize it using DP.
+
+
+---
+### Question
+How many unique paths in the grid from (0, 0) to (2, 2) ?
+
+| 1 | 1 | 1 |
+|-------|-------|-------|
+| **0** | **0** | **0** |
+| **1** | **1** | **1** |
+
+where cell with value 1 and 0 represents non-blocked and blocked cell respectively.
+
+**Choices**
+- [x] 0
+- [ ] 1
+- [ ] 2
+- [ ] 3
+
+
+**Explanation**:
+
+On the Grid, Row 1 is completely blocked. So there is no path from (0, 0) to (2, 2).
+
+Thus, the Total number of unique paths is 0.
+
+---
+### Problem 4 Dungeons and Princess
+
+
+Find the minimum health level of the prince to start with to save the princess, where the negative numbers denote a dragon and positive numbers denote red bull.
+
+Redbull will increase the health whereas the dragons will decrease the health.
+
+The prince can move either in horizontal right direction or vertical down direction.
+If health level <= 0, it means prince is dead.
+
+ +
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+#### Observation
+One might argue to solve it by finding the path with minimum sum or maximum sum.
+
+Let's check does it even work or not?
+
+#### Using path with minimum sum(fails)
+- For the above matrix, the path with minimum sum is -3 -> -6 -> -15 -> -7 -> 5 -> -3 -> -4, which yields sum as 33. So, minimum health level should be (3 + 6 + 15 + 7) + 1 = 32, right?
+- No because if we start with **health 4** and follow the path -3 -> 2 -> 4 -> -5 -> 6 -> -2 -> -4, we can definitely reach the princess with lesser initial health.
+- Thus, finding the path with minimum sum doesn't work/
+
+#### Using path with maximum sum(fails)
+
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+#### Observation
+One might argue to solve it by finding the path with minimum sum or maximum sum.
+
+Let's check does it even work or not?
+
+#### Using path with minimum sum(fails)
+- For the above matrix, the path with minimum sum is -3 -> -6 -> -15 -> -7 -> 5 -> -3 -> -4, which yields sum as 33. So, minimum health level should be (3 + 6 + 15 + 7) + 1 = 32, right?
+- No because if we start with **health 4** and follow the path -3 -> 2 -> 4 -> -5 -> 6 -> -2 -> -4, we can definitely reach the princess with lesser initial health.
+- Thus, finding the path with minimum sum doesn't work/
+
+#### Using path with maximum sum(fails)
+
+ +
+
+- For the above matrix, the path with maximum sum is -2 -> -8 -> 100 -> 1, which yields sum as 91. So, minimum health level should be (2 + 8) + 1 = 11, right?
+- No because if we start with **health 7** and follow the path -2 -> -1 -> -3 -> 1, we can definitely reach the princess with lesser initial health.
+- Similarly, finding the path with maximum sum doesn't work.
+
+> NOTE:
+> Finding the path with maximum or minimum sum is a greedy approach, which doesn't work for this problem.
+
+#### How to approach the problem then?
+Let's start with finding the smallest problem.
+
+***Where does smallest problem lie?* (0, 0) ?*** **NO**
+
+The smallest problem lies at **`(M - 1, N - 1)`**, because we need to find the minimum health to finally enter that cell to save the princess.
+
+***Now, what should be the minimum health to enter a cell?***
+
+Suppose the cell(M - 1, N - 1) has value -4, then to enter the cell needed is: minimum_health + (-4) > 0 => minimum_health + (-4) = 1 => minimum_health = 5
+
+
+
+
+- For the above matrix, the path with maximum sum is -2 -> -8 -> 100 -> 1, which yields sum as 91. So, minimum health level should be (2 + 8) + 1 = 11, right?
+- No because if we start with **health 7** and follow the path -2 -> -1 -> -3 -> 1, we can definitely reach the princess with lesser initial health.
+- Similarly, finding the path with maximum sum doesn't work.
+
+> NOTE:
+> Finding the path with maximum or minimum sum is a greedy approach, which doesn't work for this problem.
+
+#### How to approach the problem then?
+Let's start with finding the smallest problem.
+
+***Where does smallest problem lie?* (0, 0) ?*** **NO**
+
+The smallest problem lies at **`(M - 1, N - 1)`**, because we need to find the minimum health to finally enter that cell to save the princess.
+
+***Now, what should be the minimum health to enter a cell?***
+
+Suppose the cell(M - 1, N - 1) has value -4, then to enter the cell needed is: minimum_health + (-4) > 0 => minimum_health + (-4) = 1 => minimum_health = 5
+
+ +
+
+There are two ways to enter the cell:
+**(1)** via TOP **(2)** via LEFT.
+***Which one to choose?***
+
+We know, to enter the cell with value -4, the minimum health should be 5. Therefore, if we want to enter from top cell with value -2, then x + (-2) = 5; x = 7, where 'x' is minimum health to enter top cell.
+
+Similary, y + (-3) = 5; y = 8.
+
+
+
+
+There are two ways to enter the cell:
+**(1)** via TOP **(2)** via LEFT.
+***Which one to choose?***
+
+We know, to enter the cell with value -4, the minimum health should be 5. Therefore, if we want to enter from top cell with value -2, then x + (-2) = 5; x = 7, where 'x' is minimum health to enter top cell.
+
+Similary, y + (-3) = 5; y = 8.
+
+ +
+Hence, we should choose minimum of these and enter the cell via top.
+
+**What is the minimum health required to enter a cell (i, j) which has two options to move ahead?**
+
+
+
+Hence, we should choose minimum of these and enter the cell via top.
+
+**What is the minimum health required to enter a cell (i, j) which has two options to move ahead?**
+
+ +
+
+
+
+
+
+
+
+
+ +
+> If the minimum health evaluates to negative, we should consider 1 in place of that as with any health <= 0, the prince will die.
+
+Let's fill the matrix using the same approach.
+
+
+
+
+> If the minimum health evaluates to negative, we should consider 1 in place of that as with any health <= 0, the prince will die.
+
+Let's fill the matrix using the same approach.
+
+
+ +
+
+Here, `dp[i][j]` = min health with which prince should take the entry at (i, j) so that he can save the princess.
+
+---
+### Question
+What is the Time Complexity to find minimum cost path from (0,0) to (r-1, c-1)?
+
+**Choices**
+- [ ] O(max(r, c))
+- [ ] O(c )
+- [x] O(r * c)
+- [ ] O(r + c)
+
+---
+### Dungeons and Princess Algorithm and Pseudocode
+#### Algorithm
+```java
+arr[i][j] + x = min(dp[i + 1][j], dp[i][j + 1])
+x = min(dp[i + 1][j], dp[i][j + 1]) - arr[i][j]
+```
+
+Since `x` should be > 0
+
+```java
+x = max(1, min(dp[i + 1][j], dp[i][j + 1]) - arr[i][j])
+```
+
+#### Pseudocode:
+```java
+declare dp[N][M];
+if (arr[N - 1][M - 1] > 0) {
+ dp[N - 1][M - 1] = 1;
+} else {
+ dp[N - 1][M - 1] = 1 + abs(arr[N - 1][M - 1]);
+}
+
+// Fill the last column and last row
+
+for (i = N - 2; i >= 0; i--) {
+ for (j = M - 2; j >= 0; j--) {
+ x = max(1, min(dp[i + 1][j], dp[i][j + 1]) - arr[i][j]);
+ dp[i][j] = x;
+ }
+}
+
+return dp[0][0];
+```
+
+#### Complexity
+**Time Complexity:** O(N * M)
+**Space Complexity:** O(N * M)
+
+
+---
+### Catalan Numbers
+
+
+The Catalan numbers form a sequence of natural numbers that have numerous applications in combinatorial mathematics. Each number in the sequence is a solution to a variety of counting problems. The Nth Catalan number, denoted as Cn, can be used to determine:
+
+* The number of correct combinations of N pairs of parentheses.
+* The number of distinct binary search trees with N nodes, etc.
+
+Here is the sequence,
+```
+C0 = 1
+C1 = 1
+C2 = C0 * C1 + C1 * C0 = 2
+C3 = C0 * C2 + C1 * C1 + C2 * C0 = 5
+C4 = C0 * C3 + C1 * C2 + C2 * C1 + C3 * C0 = 14
+C5 = C0 * C4 + C1 * C3 + C2 * C2 + C3 * C1 + C4 * C0 = 42
+```
+
+#### Formula
+
+
+
+
+Here, `dp[i][j]` = min health with which prince should take the entry at (i, j) so that he can save the princess.
+
+---
+### Question
+What is the Time Complexity to find minimum cost path from (0,0) to (r-1, c-1)?
+
+**Choices**
+- [ ] O(max(r, c))
+- [ ] O(c )
+- [x] O(r * c)
+- [ ] O(r + c)
+
+---
+### Dungeons and Princess Algorithm and Pseudocode
+#### Algorithm
+```java
+arr[i][j] + x = min(dp[i + 1][j], dp[i][j + 1])
+x = min(dp[i + 1][j], dp[i][j + 1]) - arr[i][j]
+```
+
+Since `x` should be > 0
+
+```java
+x = max(1, min(dp[i + 1][j], dp[i][j + 1]) - arr[i][j])
+```
+
+#### Pseudocode:
+```java
+declare dp[N][M];
+if (arr[N - 1][M - 1] > 0) {
+ dp[N - 1][M - 1] = 1;
+} else {
+ dp[N - 1][M - 1] = 1 + abs(arr[N - 1][M - 1]);
+}
+
+// Fill the last column and last row
+
+for (i = N - 2; i >= 0; i--) {
+ for (j = M - 2; j >= 0; j--) {
+ x = max(1, min(dp[i + 1][j], dp[i][j + 1]) - arr[i][j]);
+ dp[i][j] = x;
+ }
+}
+
+return dp[0][0];
+```
+
+#### Complexity
+**Time Complexity:** O(N * M)
+**Space Complexity:** O(N * M)
+
+
+---
+### Catalan Numbers
+
+
+The Catalan numbers form a sequence of natural numbers that have numerous applications in combinatorial mathematics. Each number in the sequence is a solution to a variety of counting problems. The Nth Catalan number, denoted as Cn, can be used to determine:
+
+* The number of correct combinations of N pairs of parentheses.
+* The number of distinct binary search trees with N nodes, etc.
+
+Here is the sequence,
+```
+C0 = 1
+C1 = 1
+C2 = C0 * C1 + C1 * C0 = 2
+C3 = C0 * C2 + C1 * C1 + C2 * C0 = 5
+C4 = C0 * C3 + C1 * C2 + C2 * C1 + C3 * C0 = 14
+C5 = C0 * C4 + C1 * C3 + C2 * C2 + C3 * C1 + C4 * C0 = 42
+```
+
+#### Formula
+
+ +
+
+
+ +
+
+#### Psuedo Code
+
+```cpp
+int C[N + 1];
+
+C[0] = 1;
+C[1] = 1;
+
+for (int i = 2; i <= N; i++) {
+ for (int j = 0; j < i; j++) {
+ C[i] += C[j] * C[N - 1 - j];
+ }
+}
+```
+
+#### Complexity
+
+**Time Complexity:** O(N^2^)
+**Space Complexity:** O(N)
+
+Now, Let's look into a problem, which can be solved by finding the **Nth catalan number**.
+
+
+---
+### Problem 5 Total Number of Unique BSTs
+
+
+You are given a number N, Count Total number of Unique Binary Search Trees, that can be formed using N distinct numbers.
+
+**Example**
+
+**Input:**
+N = 3
+
+**Output:**
+5
+
+**Explanation:**
+
+The Unique binary Search Trees are
+```
+ 30 10 30 10 20
+ / \ / \ / \
+ 10 20 20 30 10 30
+ \ \ / /
+ 20 30 10 20
+```
+
+---
+### Question
+Count Total number of Unique Binary Search Trees, that can be formed using 2 distinct numbers
+
+**Choices**
+- [ ] 1
+- [x] 2
+- [ ] 5
+- [ ] 4
+
+**Explanation**:
+
+Lets take 2 distinct numbers as [10, 20]
+
+The possible BSTs are
+```
+ 20 10
+ / \
+ 10 20
+```
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Total Number of Unique BSTs Dryrun
+
+
+Lets take N = 5, the numbers are [10, 20, 30, 40, 50].
+
+Lets keep each number as the root! one by one.
+
+**10 as root**
+```
+ 10
+ \
+ \
+ \
+ 20, 30, 40, 50
+```
+
+Here we notice that, 20, 30, 40 and 50 can be structured by various sub-roots. So, lets denote by C4.
+
+Also on the right side, there is no elements. So denoting by C0.
+
+`10 as root => C0 * C1`
+
+
+**20 as root**
+```
+ 20
+ / \
+ / \
+ / \
+ 10 30, 40, 50
+```
+
+There are 1 element on the left side and 3 elements on the right side.
+
+`20 as root => C1 * C3`
+
+
+**30 as root**
+```
+ 30
+ / \
+ / \
+ / \
+ 10, 20 40, 50
+```
+
+
+There are 2 element on the left side and 2 elements on the right side.
+
+
+`30 as root => C2 * C2`
+
+
+**40 as root**
+```
+ 40
+ / \
+ / \
+ / \
+ 10, 20, 30 50
+```
+
+
+There are 3 element on the left side and 1 elements on the right side.
+
+
+`40 as root => C0 * C1`
+
+**50 as root**
+```
+ 50
+ /
+ /
+ /
+ 10, 20, 30, 40
+```
+
+There are 4 element on the left side and 1 elements on the right side.
+
+
+`10 as root => C4 * C0`
+
+C5 = C0 * C4 + C1 * C3 + C2 * C2 + C3 * C1 + C4 * C0
+
+which is 42.
+
+#### Solution
+
+The Solution for finding the total number of Unique BSTs is the **Nth Catalan Number**.
+
+
+
+---
+### Total Number of Unique BSTs Pseudo Code
+
+#### Psuedo Code
+
+The pseudo code is same as the Catalan Number Psuedo code.
+
+```cpp
+function findTotalUniqueBSTs(int N) {
+ int C[N + 1];
+
+ C[0] = 1;
+ C[1] = 1;
+
+ for (int i = 2; i <= N; i++) {
+ for (int j = 0; j < i; j++) {
+ C[i] += C[j] * C[N - 1 - j];
+ }
+ }
+
+ return C[N];
+}
+```
+
+#### Complexity
+
+**Time Complexity:** O(N^2^)
+**Space Complexity:** O(N)
+
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA DP 3 Knapsack.md b/Academy DSA Typed Notes/Advanced/DSA DP 3 Knapsack.md
new file mode 100644
index 0000000..155722f
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA DP 3 Knapsack.md
@@ -0,0 +1,312 @@
+# DP 3: Knapsack
+
+---
+## Knapsack Problem
+
+Given N objects with their values Vi profit/loss their weight Wi. A bag is given with capacity W that can be used to carry some objects such that the total sum of object weights W and sum of profit in the bag is maximized or sum of loss in the bag is minimized.
+
+We will try Knapsack when these combinations are given:
+* number of objects will be N
+* every object will have 2 attributes namingly value and weight
+* and capacity will be given
+
+---
+### Problem 1 Fractional Knapsack
+
+Given N cakes with their happiness and weight. Find maximum total happiness that can be kept in a bag with capacity = W (cakes can be divided)
+
+**Example**:
+N = 5; W = 40
+Happiness of the 5 cakes = [3, 8, 10, 2, 5]
+Weight of the 5 cakes = [10, 4, 20, 8, 15]
+Goal - happiness should be maximum possible and the total sum of weights should be <= 40.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+**Approach**
+
+**`Since we can divide the objects, hence they can be picked based on their value per unit weight.`**
+
+**`For per unit weight, below are the happiness values:`**
+* Cake 1: `happiness = 0.3`;
+* Cake 2: `happiness = 2`;
+* Cake 3: `happiness = 0.5`;
+* Cake 4: `happiness = 0.25`;
+* Cake 5: `happiness = 0.33`;
+
+
+
+
+#### Psuedo Code
+
+```cpp
+int C[N + 1];
+
+C[0] = 1;
+C[1] = 1;
+
+for (int i = 2; i <= N; i++) {
+ for (int j = 0; j < i; j++) {
+ C[i] += C[j] * C[N - 1 - j];
+ }
+}
+```
+
+#### Complexity
+
+**Time Complexity:** O(N^2^)
+**Space Complexity:** O(N)
+
+Now, Let's look into a problem, which can be solved by finding the **Nth catalan number**.
+
+
+---
+### Problem 5 Total Number of Unique BSTs
+
+
+You are given a number N, Count Total number of Unique Binary Search Trees, that can be formed using N distinct numbers.
+
+**Example**
+
+**Input:**
+N = 3
+
+**Output:**
+5
+
+**Explanation:**
+
+The Unique binary Search Trees are
+```
+ 30 10 30 10 20
+ / \ / \ / \
+ 10 20 20 30 10 30
+ \ \ / /
+ 20 30 10 20
+```
+
+---
+### Question
+Count Total number of Unique Binary Search Trees, that can be formed using 2 distinct numbers
+
+**Choices**
+- [ ] 1
+- [x] 2
+- [ ] 5
+- [ ] 4
+
+**Explanation**:
+
+Lets take 2 distinct numbers as [10, 20]
+
+The possible BSTs are
+```
+ 20 10
+ / \
+ 10 20
+```
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Total Number of Unique BSTs Dryrun
+
+
+Lets take N = 5, the numbers are [10, 20, 30, 40, 50].
+
+Lets keep each number as the root! one by one.
+
+**10 as root**
+```
+ 10
+ \
+ \
+ \
+ 20, 30, 40, 50
+```
+
+Here we notice that, 20, 30, 40 and 50 can be structured by various sub-roots. So, lets denote by C4.
+
+Also on the right side, there is no elements. So denoting by C0.
+
+`10 as root => C0 * C1`
+
+
+**20 as root**
+```
+ 20
+ / \
+ / \
+ / \
+ 10 30, 40, 50
+```
+
+There are 1 element on the left side and 3 elements on the right side.
+
+`20 as root => C1 * C3`
+
+
+**30 as root**
+```
+ 30
+ / \
+ / \
+ / \
+ 10, 20 40, 50
+```
+
+
+There are 2 element on the left side and 2 elements on the right side.
+
+
+`30 as root => C2 * C2`
+
+
+**40 as root**
+```
+ 40
+ / \
+ / \
+ / \
+ 10, 20, 30 50
+```
+
+
+There are 3 element on the left side and 1 elements on the right side.
+
+
+`40 as root => C0 * C1`
+
+**50 as root**
+```
+ 50
+ /
+ /
+ /
+ 10, 20, 30, 40
+```
+
+There are 4 element on the left side and 1 elements on the right side.
+
+
+`10 as root => C4 * C0`
+
+C5 = C0 * C4 + C1 * C3 + C2 * C2 + C3 * C1 + C4 * C0
+
+which is 42.
+
+#### Solution
+
+The Solution for finding the total number of Unique BSTs is the **Nth Catalan Number**.
+
+
+
+---
+### Total Number of Unique BSTs Pseudo Code
+
+#### Psuedo Code
+
+The pseudo code is same as the Catalan Number Psuedo code.
+
+```cpp
+function findTotalUniqueBSTs(int N) {
+ int C[N + 1];
+
+ C[0] = 1;
+ C[1] = 1;
+
+ for (int i = 2; i <= N; i++) {
+ for (int j = 0; j < i; j++) {
+ C[i] += C[j] * C[N - 1 - j];
+ }
+ }
+
+ return C[N];
+}
+```
+
+#### Complexity
+
+**Time Complexity:** O(N^2^)
+**Space Complexity:** O(N)
+
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA DP 3 Knapsack.md b/Academy DSA Typed Notes/Advanced/DSA DP 3 Knapsack.md
new file mode 100644
index 0000000..155722f
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA DP 3 Knapsack.md
@@ -0,0 +1,312 @@
+# DP 3: Knapsack
+
+---
+## Knapsack Problem
+
+Given N objects with their values Vi profit/loss their weight Wi. A bag is given with capacity W that can be used to carry some objects such that the total sum of object weights W and sum of profit in the bag is maximized or sum of loss in the bag is minimized.
+
+We will try Knapsack when these combinations are given:
+* number of objects will be N
+* every object will have 2 attributes namingly value and weight
+* and capacity will be given
+
+---
+### Problem 1 Fractional Knapsack
+
+Given N cakes with their happiness and weight. Find maximum total happiness that can be kept in a bag with capacity = W (cakes can be divided)
+
+**Example**:
+N = 5; W = 40
+Happiness of the 5 cakes = [3, 8, 10, 2, 5]
+Weight of the 5 cakes = [10, 4, 20, 8, 15]
+Goal - happiness should be maximum possible and the total sum of weights should be <= 40.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+**Approach**
+
+**`Since we can divide the objects, hence they can be picked based on their value per unit weight.`**
+
+**`For per unit weight, below are the happiness values:`**
+* Cake 1: `happiness = 0.3`;
+* Cake 2: `happiness = 2`;
+* Cake 3: `happiness = 0.5`;
+* Cake 4: `happiness = 0.25`;
+* Cake 5: `happiness = 0.33`;
+
+ +
+
+**Solution**
+
+**`Arrange the cakes in descending order with respect to happiness/weight and start picking the element`**
+* Select the 2nd cake (happiness = 2), reducing capacity to 36(40-4).
+* Choose the 3rd cake (happiness = 0.5), further reducing capacity to 16(36-20).
+* Opt for the 5th cake (happiness = 0.33), leaving a capacity of 1(16-15).
+* Take a part of the 1st cake (happiness = 0.3), using up the remaining capacity.
+* Total happiness achieved: 23.3 (8 + 10 + 5 + 0.3).
+
+**Time complexity** of the above solution is O(Nlog(N)) because it requires sorting with respect to `happiness/weight`.
+
+**Space complexity** of the above solution is O(1).*
+
+#### Pseudo Code
+```cpp
+public class Solution {
+ class Items {
+ double cost;
+ int weight, value, ind;
+ Items(int weight, int value, double cost) {
+ this.weight = weight;
+ this.value = value;
+ this.cost = cost;
+ }
+ }
+
+ public int solve(int[] A, int[] B, int C) {
+ Items[] iVal = new Items[A.length];
+ for (int i = 0; i < A.length; i++) {
+ double cost = (A[i] * 1.0) / B[i];
+ iVal[i] = new Items(B[i], A[i], cost);
+ }
+ Arrays.sort(iVal, new Comparator < Items > () {
+ @Override
+ public int compare(Items o1, Items o2) {
+ if (o1.cost >= o2.cost) {
+ return -1;
+ }
+ return 1;
+ }
+ });
+ double totalValue = 0.0;
+ for (int i = 0; i < A.length; i++) {
+ int curWt = iVal[i].weight;
+ int curVal = iVal[i].value;
+ if (C >= curWt) {
+ C = C - curWt;
+ totalValue += curVal;
+ } else {
+ totalValue += (C * iVal[i].cost);
+ break;
+ }
+ }
+
+ return (int)(totalValue * 100);
+
+ }
+}
+```
+
+---
+### Flipkart's Upcoming Special Promotional Event
+
+
+Flipkart is planning a special promotional event where they need to create an exclusive combo offer. The goal is to create a combination of individual items that together offer the highest possible level of customer satisfaction (indicating its popularity and customer ratings) while ensuring the total cost of the items in the combo does not exceed a predefined combo price.
+
+---
+### Problem 2 : 0-1 Knapsack
+
+## 0-1 Knapsack
+In this type of knapsack question, **division of object is not allowed.**
+
+### Question
+
+Given N toys with their happiness and weight. Find maximum total happiness that can be kept in a bag with capacity W. Division of toys are not allowed.
+
+---
+### Question
+In the Fractional Knapsack problem, what is the key difference compared to the 0/1 Knapsack?
+
+**Choices**
+- [ ] Items can only be fully included or excluded.
+- [x] Items can be partially included, allowing fractions.
+- [ ] The knapsack has infinite capacity.
+- [ ] The knapsack has a fixed capacity.
+
+
+
+**Explanation**
+
+ In the Fractional Knapsack problem, items can be included in fractions, enabling optimization of the total value based on weight.
+
+
+**Example**:
+N = 4; W = 7
+Happiness of the 4 toys = [4, 1, 5, 7]
+Weight of the 4 toys = [3, 2, 4, 5]
+
+> If we buy toys based on maximum happiness or maximum happiness/weight we may not get the best possible answer.
+
+:::warning
+Please take some time to think about the bruteforce approach on your own before reading further.....
+:::
+
+#### Brute Force Approach:
+* Consider all subsets of items and select the one with highest summation of happiness.
+
+Since there are in total 2^N^ subsequences and we have to consider each of them. Therefore the time complexity is:
+
+
+**Solution**
+
+**`Arrange the cakes in descending order with respect to happiness/weight and start picking the element`**
+* Select the 2nd cake (happiness = 2), reducing capacity to 36(40-4).
+* Choose the 3rd cake (happiness = 0.5), further reducing capacity to 16(36-20).
+* Opt for the 5th cake (happiness = 0.33), leaving a capacity of 1(16-15).
+* Take a part of the 1st cake (happiness = 0.3), using up the remaining capacity.
+* Total happiness achieved: 23.3 (8 + 10 + 5 + 0.3).
+
+**Time complexity** of the above solution is O(Nlog(N)) because it requires sorting with respect to `happiness/weight`.
+
+**Space complexity** of the above solution is O(1).*
+
+#### Pseudo Code
+```cpp
+public class Solution {
+ class Items {
+ double cost;
+ int weight, value, ind;
+ Items(int weight, int value, double cost) {
+ this.weight = weight;
+ this.value = value;
+ this.cost = cost;
+ }
+ }
+
+ public int solve(int[] A, int[] B, int C) {
+ Items[] iVal = new Items[A.length];
+ for (int i = 0; i < A.length; i++) {
+ double cost = (A[i] * 1.0) / B[i];
+ iVal[i] = new Items(B[i], A[i], cost);
+ }
+ Arrays.sort(iVal, new Comparator < Items > () {
+ @Override
+ public int compare(Items o1, Items o2) {
+ if (o1.cost >= o2.cost) {
+ return -1;
+ }
+ return 1;
+ }
+ });
+ double totalValue = 0.0;
+ for (int i = 0; i < A.length; i++) {
+ int curWt = iVal[i].weight;
+ int curVal = iVal[i].value;
+ if (C >= curWt) {
+ C = C - curWt;
+ totalValue += curVal;
+ } else {
+ totalValue += (C * iVal[i].cost);
+ break;
+ }
+ }
+
+ return (int)(totalValue * 100);
+
+ }
+}
+```
+
+---
+### Flipkart's Upcoming Special Promotional Event
+
+
+Flipkart is planning a special promotional event where they need to create an exclusive combo offer. The goal is to create a combination of individual items that together offer the highest possible level of customer satisfaction (indicating its popularity and customer ratings) while ensuring the total cost of the items in the combo does not exceed a predefined combo price.
+
+---
+### Problem 2 : 0-1 Knapsack
+
+## 0-1 Knapsack
+In this type of knapsack question, **division of object is not allowed.**
+
+### Question
+
+Given N toys with their happiness and weight. Find maximum total happiness that can be kept in a bag with capacity W. Division of toys are not allowed.
+
+---
+### Question
+In the Fractional Knapsack problem, what is the key difference compared to the 0/1 Knapsack?
+
+**Choices**
+- [ ] Items can only be fully included or excluded.
+- [x] Items can be partially included, allowing fractions.
+- [ ] The knapsack has infinite capacity.
+- [ ] The knapsack has a fixed capacity.
+
+
+
+**Explanation**
+
+ In the Fractional Knapsack problem, items can be included in fractions, enabling optimization of the total value based on weight.
+
+
+**Example**:
+N = 4; W = 7
+Happiness of the 4 toys = [4, 1, 5, 7]
+Weight of the 4 toys = [3, 2, 4, 5]
+
+> If we buy toys based on maximum happiness or maximum happiness/weight we may not get the best possible answer.
+
+:::warning
+Please take some time to think about the bruteforce approach on your own before reading further.....
+:::
+
+#### Brute Force Approach:
+* Consider all subsets of items and select the one with highest summation of happiness.
+
+Since there are in total 2^N^ subsequences and we have to consider each of them. Therefore the time complexity is:  +
+#### Dry Run of Brute Force Apporach
+
+
+
+#### Dry Run of Brute Force Apporach
+
+ +
+In the above figure each element is taken and its selection is determined based on happiness and weight.
+
+> Here we can notice optimal sub structure as well as overlapping sub problems.
+> *Thus we can use dynamic progamming in this case*
+
+If index and capacity can define one unique state total number of unique states are `O(N * (W + 1))` which is `O(N * W)`, as index will go from 0 to N - 1 and weight will go from 0 to W.
+
+```cpp
+dp[N][W] = max happiness (considering N objects and capacity W)
+```
+
+
+
+In the above figure each element is taken and its selection is determined based on happiness and weight.
+
+> Here we can notice optimal sub structure as well as overlapping sub problems.
+> *Thus we can use dynamic progamming in this case*
+
+If index and capacity can define one unique state total number of unique states are `O(N * (W + 1))` which is `O(N * W)`, as index will go from 0 to N - 1 and weight will go from 0 to W.
+
+```cpp
+dp[N][W] = max happiness (considering N objects and capacity W)
+```
+
+ +
+> Here taking N = i and W = j, we have two choices either to select dp[i][j] or to reject it. On selecting it will result into` h[i] + dp[i - 1][j - wt[i]]`(h[i]=happiness of i) and on rejecting it will be `dp[i - 1][j]`.
+
+#### Base Case
+* for all j when i = 0, dp[0][j] = 0
+* for all i when j = 0, dp[i][0] = 0
+
+#### Psuedocode
+
+```java
+//for all i,j dp[i][j]=0
+for (i--> 1 to N) { // 1based index for input
+ for (j--> 1 to W) {
+ if (wt[i] <= j) {
+ dp[i][j] = max(dp[i - 1][j], h[i] + dp(i - 1)(j - wt[i]))
+ } else {
+ dp[i][j] = dp[i - 1][j]
+ }
+ }
+}
+return dp[N][w]
+}
+```
+
+
+The dimensions should be (N + 1) * (W + 1) as the final answer would be at dp[N][W]
+
+#### Dry run
+taking the N = 4 and W = 7
+Happiness of the 4 toys = [4, 1, 5, 7]
+Weight of the 4 toys = [3, 2, 4, 5]
+
+
+
+> Here taking N = i and W = j, we have two choices either to select dp[i][j] or to reject it. On selecting it will result into` h[i] + dp[i - 1][j - wt[i]]`(h[i]=happiness of i) and on rejecting it will be `dp[i - 1][j]`.
+
+#### Base Case
+* for all j when i = 0, dp[0][j] = 0
+* for all i when j = 0, dp[i][0] = 0
+
+#### Psuedocode
+
+```java
+//for all i,j dp[i][j]=0
+for (i--> 1 to N) { // 1based index for input
+ for (j--> 1 to W) {
+ if (wt[i] <= j) {
+ dp[i][j] = max(dp[i - 1][j], h[i] + dp(i - 1)(j - wt[i]))
+ } else {
+ dp[i][j] = dp[i - 1][j]
+ }
+ }
+}
+return dp[N][w]
+}
+```
+
+
+The dimensions should be (N + 1) * (W + 1) as the final answer would be at dp[N][W]
+
+#### Dry run
+taking the N = 4 and W = 7
+Happiness of the 4 toys = [4, 1, 5, 7]
+Weight of the 4 toys = [3, 2, 4, 5]
+
+ +
+* Initially, we filled the `dp` matrix with zeros. Now, we will fill every position one by one.
+ - At i = 1, j = 1
+ wt[i] = wt[1] = 3
+ since wt[i] > j, dp[i][j] = dp[i - 1][j] => dp[1][1] = dp[0][1] = 0
+* At i = 1, j = 2
+ wt[i] = wt[1] = 3
+ since wt[i] > j, dp[i][j] = dp[i - 1][j] => dp[1][2] = dp[0][2] = 0
+* At i = 1, j = 3
+ wt[i] = wt[1] = 3
+ since wt[i] <= j, dp[i][j] = max(dp[i - 1][j], h[i] + dp[i - 1][j - wt[i]])
+ => dp[1][3] = max(dp[0][2], h[1] + dp[0][0]) = max(0, 4 + 0) = 4
+
+Similary we wil follow the above to fill the entire table.
+
+> Time complexity for the above code is O(N * W)
+
+> Space Complexity for the above code is O(N * W), we can furture optimize space complexity by using 2 rows. So the space complexity is O(2W) which can be written as O(W).
+
+---
+### Problem 3 Unbounded Knapsack
+
+## Unbounded Knapsack or 0-N Knapsack
+* objects cannot be divided
+* same object can be selected multiple times
+
+#### Question
+
+Given N toys with their happiness and weight. Find more total happiness that can be kept in a bag with capacity W. Division of toys are not allowed and infinite toys are available.
+
+#### Example
+
+N = 3; W = 8
+Happiness of the 3 toys = [2, 3, 5]
+Weight of the 3 toys = [3, 4, 7]
+
+*In this case we will select second index toy 2 times. Happiness we will be 6 and weight will be 8.*
+
+Now here as we do not have any limitation on which toy to buy index will not matter, only capacity will matter.
+
+:::warning
+Please take some time to think about the brute force approach on your own before reading further.....
+:::
+
+#### Dry Run for Brute Force Appoarch
+
+
+
+* Initially, we filled the `dp` matrix with zeros. Now, we will fill every position one by one.
+ - At i = 1, j = 1
+ wt[i] = wt[1] = 3
+ since wt[i] > j, dp[i][j] = dp[i - 1][j] => dp[1][1] = dp[0][1] = 0
+* At i = 1, j = 2
+ wt[i] = wt[1] = 3
+ since wt[i] > j, dp[i][j] = dp[i - 1][j] => dp[1][2] = dp[0][2] = 0
+* At i = 1, j = 3
+ wt[i] = wt[1] = 3
+ since wt[i] <= j, dp[i][j] = max(dp[i - 1][j], h[i] + dp[i - 1][j - wt[i]])
+ => dp[1][3] = max(dp[0][2], h[1] + dp[0][0]) = max(0, 4 + 0) = 4
+
+Similary we wil follow the above to fill the entire table.
+
+> Time complexity for the above code is O(N * W)
+
+> Space Complexity for the above code is O(N * W), we can furture optimize space complexity by using 2 rows. So the space complexity is O(2W) which can be written as O(W).
+
+---
+### Problem 3 Unbounded Knapsack
+
+## Unbounded Knapsack or 0-N Knapsack
+* objects cannot be divided
+* same object can be selected multiple times
+
+#### Question
+
+Given N toys with their happiness and weight. Find more total happiness that can be kept in a bag with capacity W. Division of toys are not allowed and infinite toys are available.
+
+#### Example
+
+N = 3; W = 8
+Happiness of the 3 toys = [2, 3, 5]
+Weight of the 3 toys = [3, 4, 7]
+
+*In this case we will select second index toy 2 times. Happiness we will be 6 and weight will be 8.*
+
+Now here as we do not have any limitation on which toy to buy index will not matter, only capacity will matter.
+
+:::warning
+Please take some time to think about the brute force approach on your own before reading further.....
+:::
+
+#### Dry Run for Brute Force Appoarch
+
+ +
+Step 1:
+* if we select toy with index 1, capacity left will be `8 - wt of toy 1 = 8 - 3 = 5`. And the happiness will be `h = 2`
+* Similarily if we select toy with index 2, capacity left will be `8 - wt of toy 2 = 8 - 4 = 4`. And the happiness will be `h = 3`
+* if we select toy with index 3, capacity left will be `8 - wt of toy 3 = 8 - 7 = 1`. And the happiness will be `h = 5`
+
+Step 2:
+After buying toy 1
+* Now if we buy toy 1, capacity will reduce to 2 and happiness will become 4
+* Similary if we buy toy 2, capacity will reduce to 1 and happiness will become 5
+* We cannot buy toy 3 as the capacity will be exceeded.
+
+
+We will follow similar steps to find all the possiblity.
+
+> We will pick the toy with maximum happiness that is 6 in this case after selecting toy 2 firstly and then selecting toy 2 again.
+
+Here we can notice optimal sub structure as well as overlapping sub problems. Thus we can apply dynamic programming.
+
+* Unqiue states here will be` W + 1 = O(W)` because the capacity can be from 0 to W
+
+Base case for the above question:
+* if capacity is 0, happiness is 0. So, `dp[0] = 0`
+
+Equation `dp[i] = max(h[i] + dp[i - wt[j]])` for all toys j
+
+#### Psuedocode
+```java
+for all i, dp[0] = 0
+for (i--> 1 to W) {
+ for (j--> 1 to N) {
+ if (wt[j] <= i)
+ dp[i] = max(h[i] + dp[i - wt[j]])
+ }
+}
+return dp[W]
+```
+
+#### Complexity
+**Time Complexity:** O(N * W)
+**Space Complexity:** O(W)
+
+---
+### Question
+We have Weight Capacity of 100
+- Values = {1, 30}
+- Weights = {1, 50}
+
+What is the maximum value you can have?
+
+**Choices**
+- [ ] 0
+- [x] 100
+- [ ] 60
+- [ ] 80
+
+**Explanation**
+There are many ways to fill knapsack.
+
+- 2 instances of 50 unit weight item.
+- 100 instances of 1 unit weight item.
+- 1 instance of 50 unit weight item and 50
+ instances of 1 unit weight items.
+
+We get maximum value with option 2, i.e **100**
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA DP 4 Applications of Knapsack.md b/Academy DSA Typed Notes/Advanced/DSA DP 4 Applications of Knapsack.md
new file mode 100644
index 0000000..9a07494
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA DP 4 Applications of Knapsack.md
@@ -0,0 +1,274 @@
+# DP 4: Applications of Knapsack
+
+---
+
+### Question
+Time Complexity of the unbounded 0-1 knapsack problem?
+- W : capacity of knapsack
+- N : no. of elements
+- K : Max weight of any item
+- P : max value of any item
+
+**Choices**
+Chose the correct answer
+- [x] O(NW)
+- [ ] O(NK)
+- [ ] O(NP)
+- [ ] O(WK)
+- [ ] O(WP)
+- [ ] O(KP)
+
+
+
+
+**Explanation**
+For every node, we need to go to its left, that's the only way we can reach the smallest one.
+
+---
+## Introduction to the knapsack and DP
+
+### What Is Dynamic Programming?
+In the context of dynamic programming, the ``knapsack problem`` refers to a classic optimization problem that can be solved using dynamic programming techniques.
+
+### Example
+Suppose we are working on solving the fibonacci series problesm, then we can break it into step by step as follows:
+
+
+
+Step 1:
+* if we select toy with index 1, capacity left will be `8 - wt of toy 1 = 8 - 3 = 5`. And the happiness will be `h = 2`
+* Similarily if we select toy with index 2, capacity left will be `8 - wt of toy 2 = 8 - 4 = 4`. And the happiness will be `h = 3`
+* if we select toy with index 3, capacity left will be `8 - wt of toy 3 = 8 - 7 = 1`. And the happiness will be `h = 5`
+
+Step 2:
+After buying toy 1
+* Now if we buy toy 1, capacity will reduce to 2 and happiness will become 4
+* Similary if we buy toy 2, capacity will reduce to 1 and happiness will become 5
+* We cannot buy toy 3 as the capacity will be exceeded.
+
+
+We will follow similar steps to find all the possiblity.
+
+> We will pick the toy with maximum happiness that is 6 in this case after selecting toy 2 firstly and then selecting toy 2 again.
+
+Here we can notice optimal sub structure as well as overlapping sub problems. Thus we can apply dynamic programming.
+
+* Unqiue states here will be` W + 1 = O(W)` because the capacity can be from 0 to W
+
+Base case for the above question:
+* if capacity is 0, happiness is 0. So, `dp[0] = 0`
+
+Equation `dp[i] = max(h[i] + dp[i - wt[j]])` for all toys j
+
+#### Psuedocode
+```java
+for all i, dp[0] = 0
+for (i--> 1 to W) {
+ for (j--> 1 to N) {
+ if (wt[j] <= i)
+ dp[i] = max(h[i] + dp[i - wt[j]])
+ }
+}
+return dp[W]
+```
+
+#### Complexity
+**Time Complexity:** O(N * W)
+**Space Complexity:** O(W)
+
+---
+### Question
+We have Weight Capacity of 100
+- Values = {1, 30}
+- Weights = {1, 50}
+
+What is the maximum value you can have?
+
+**Choices**
+- [ ] 0
+- [x] 100
+- [ ] 60
+- [ ] 80
+
+**Explanation**
+There are many ways to fill knapsack.
+
+- 2 instances of 50 unit weight item.
+- 100 instances of 1 unit weight item.
+- 1 instance of 50 unit weight item and 50
+ instances of 1 unit weight items.
+
+We get maximum value with option 2, i.e **100**
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA DP 4 Applications of Knapsack.md b/Academy DSA Typed Notes/Advanced/DSA DP 4 Applications of Knapsack.md
new file mode 100644
index 0000000..9a07494
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA DP 4 Applications of Knapsack.md
@@ -0,0 +1,274 @@
+# DP 4: Applications of Knapsack
+
+---
+
+### Question
+Time Complexity of the unbounded 0-1 knapsack problem?
+- W : capacity of knapsack
+- N : no. of elements
+- K : Max weight of any item
+- P : max value of any item
+
+**Choices**
+Chose the correct answer
+- [x] O(NW)
+- [ ] O(NK)
+- [ ] O(NP)
+- [ ] O(WK)
+- [ ] O(WP)
+- [ ] O(KP)
+
+
+
+
+**Explanation**
+For every node, we need to go to its left, that's the only way we can reach the smallest one.
+
+---
+## Introduction to the knapsack and DP
+
+### What Is Dynamic Programming?
+In the context of dynamic programming, the ``knapsack problem`` refers to a classic optimization problem that can be solved using dynamic programming techniques.
+
+### Example
+Suppose we are working on solving the fibonacci series problesm, then we can break it into step by step as follows:
+
+ +
+Let us now solve some questions related to dynamic programming.
+
+---
+### Problem 1 Cut the rod for maximum profit
+
+
+A rod of length `N` and an array `A` of length `N` is given. The elements (`i`) of the array contain the length of the rod (1-based indexing). Find the maximum values that can be obtained by cutting the rod into some pieces and selling them.
+
+**Example**
+Suppose we have the length on `N = 5` and we have to divide it then the division can be done as:
+
+
+
+Let us now solve some questions related to dynamic programming.
+
+---
+### Problem 1 Cut the rod for maximum profit
+
+
+A rod of length `N` and an array `A` of length `N` is given. The elements (`i`) of the array contain the length of the rod (1-based indexing). Find the maximum values that can be obtained by cutting the rod into some pieces and selling them.
+
+**Example**
+Suppose we have the length on `N = 5` and we have to divide it then the division can be done as:
+
+ +
+Now, we can see that $9$ is the maximum value that we can get.
+
+#### Solution
+A naive approach to solving this problem would involve considering all possible combinations of cutting the rod into pieces and calculating the total value for each combination. This can be achieved using recursion and backtracking, where for each possible cut, the value of the cut piece is added to the recursively calculated value of the remaining part of the rod. The maximum value obtained among all combinations is the desired result.
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Our Approach
+As we can visualize from the example, there is an overlapping subproblem and an optimal sub-structure. So, we should opt for the DP approach.
+
+> **Note**: We can observe three things here:
+ 1. The maximum capacity is the length of the order.
+ 2. `A[i]` is storing the length of the piece of the rod.
+ 3. The sum of the length of each piece must be less than or equal to ``N``
+The general observation that we can get here from these three things is that it is a knapsack problem.
+
+---
+### Question
+The cutting rod question is:
+
+**Choices**
+- [ ] Fractional Knapsack
+- [ ] `0-1` Knapsack
+- [x] Unbounded Knapsack (or `0-N` Knapsack)
+
+---
+### Cut the rod for maximum profit Approach
+
+#### Approach
+- First, define the state of the dp i.e. `dp[i]`, it will be the maximum value that can be received by the rod of length `i`.
+- The base case will be 0 in the case when the length of the rod is 0. This means `dp[0] = 0`.
+
+We will loop over the array, and then calculate the maximum profit, and finally store the maximum profit in the current dp state.
+
+Let us now see the pseudo-code for the problem.
+
+#### Pseudocode
+```cpp
+for all values of i: dp[i] = 0
+
+for (i = 1 to N) // length of rod to sell = i
+{
+ for (j = 1 to i) {
+ dp[i] = max(dp[i], A[j] + dp[i - j])
+ }
+}
+return dp[N]
+```
+
+#### Time and Space Complexity
+- **Time Complexity**: $O(N^2)$, as we are traversing the N-length array using nested for loops (Simply, we can also say that the capacity is `N` and the length of the array is also `N`).
+- **Space Complexity**: `O(N)`, as we are using an extra dp array to store the current state of profit.
+
+
+---
+### Problem 2 Count the number of ways using coins (ordered selection)
+
+
+In how many ways can the sum be equal to ``N`` by using coins given in the array? One coin can be used multiple times.
+
+**Example**
+There are 2 ways to solve this problem
+a. **Ordered selection of coin**
+
+Let us create the set of numbers that cummulate the value of `N`.
+
+
+
+Now, we can see that $9$ is the maximum value that we can get.
+
+#### Solution
+A naive approach to solving this problem would involve considering all possible combinations of cutting the rod into pieces and calculating the total value for each combination. This can be achieved using recursion and backtracking, where for each possible cut, the value of the cut piece is added to the recursively calculated value of the remaining part of the rod. The maximum value obtained among all combinations is the desired result.
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Our Approach
+As we can visualize from the example, there is an overlapping subproblem and an optimal sub-structure. So, we should opt for the DP approach.
+
+> **Note**: We can observe three things here:
+ 1. The maximum capacity is the length of the order.
+ 2. `A[i]` is storing the length of the piece of the rod.
+ 3. The sum of the length of each piece must be less than or equal to ``N``
+The general observation that we can get here from these three things is that it is a knapsack problem.
+
+---
+### Question
+The cutting rod question is:
+
+**Choices**
+- [ ] Fractional Knapsack
+- [ ] `0-1` Knapsack
+- [x] Unbounded Knapsack (or `0-N` Knapsack)
+
+---
+### Cut the rod for maximum profit Approach
+
+#### Approach
+- First, define the state of the dp i.e. `dp[i]`, it will be the maximum value that can be received by the rod of length `i`.
+- The base case will be 0 in the case when the length of the rod is 0. This means `dp[0] = 0`.
+
+We will loop over the array, and then calculate the maximum profit, and finally store the maximum profit in the current dp state.
+
+Let us now see the pseudo-code for the problem.
+
+#### Pseudocode
+```cpp
+for all values of i: dp[i] = 0
+
+for (i = 1 to N) // length of rod to sell = i
+{
+ for (j = 1 to i) {
+ dp[i] = max(dp[i], A[j] + dp[i - j])
+ }
+}
+return dp[N]
+```
+
+#### Time and Space Complexity
+- **Time Complexity**: $O(N^2)$, as we are traversing the N-length array using nested for loops (Simply, we can also say that the capacity is `N` and the length of the array is also `N`).
+- **Space Complexity**: `O(N)`, as we are using an extra dp array to store the current state of profit.
+
+
+---
+### Problem 2 Count the number of ways using coins (ordered selection)
+
+
+In how many ways can the sum be equal to ``N`` by using coins given in the array? One coin can be used multiple times.
+
+**Example**
+There are 2 ways to solve this problem
+a. **Ordered selection of coin**
+
+Let us create the set of numbers that cummulate the value of `N`.
+
+ +
+So, we can see that we have the value we get is $6$.
+
+Now, let's look at the selection tree of the coin selection. We can divide the number by selecting the choices of subraction.
+
+
+
+So, we can see that we have the value we get is $6$.
+
+Now, let's look at the selection tree of the coin selection. We can divide the number by selecting the choices of subraction.
+
+ +
+
+#### Solution - Ordered Selection of Coin
+The naive approach to solving this problem involves using a recursive approach with backtracking. For each coin value in the array, subtract it from the target sum N, and recursively find the number of ways to form the remaining sum using the same coin set. Repeat this process for all coins and sum up the results.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Approach
+As we can observe from the examples above, we have to calculate the number of ways of selection, it is similar to the unbounded knapsack problem (as one coin can be selected multiple times).
+
+---
+### Question
+What is the number of ways to get `sum = 0`
+
+**Choices**
+- [ ] 0
+- [x] 1
+- [ ] 2
+- [ ] Undefined
+
+---
+### Count the number of ways using coins Pseudocode
+#### Pseudocode
+```cpp
+for all values of i: dp[i] = 0
+dp[0] = 1
+
+for (i = 1 to N) {
+ for (j = 1 to(A.length - 1)) {
+ if (A[j] <= i) {
+ dp[i] += dp[i - A[j]]
+ }
+ }
+}
+
+return dp[N]
+```
+
+
+#### Time and Space Complexity
+- **Time Complexity**: $O(N * (length~ of ~the ~array))$.
+- **Space Complexity**: $O(N)$.
+
+---
+### Problem 3 Count the number of ways using coins (un-ordered selection)
+
+
+Given a set of coins and a target sum, find the number of ways to make the target sum using the coins, where each coin can only be used once.
+
+**Example**
+
+Suppose we have a situation same as the last one.
+N = 5 and coins we have [3, 1, 4].
+
+So here we have 3 possible ways.
+
+Now, let us try to arrage the coins to get the desired value.
+
+
+
+
+#### Solution - Ordered Selection of Coin
+The naive approach to solving this problem involves using a recursive approach with backtracking. For each coin value in the array, subtract it from the target sum N, and recursively find the number of ways to form the remaining sum using the same coin set. Repeat this process for all coins and sum up the results.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Approach
+As we can observe from the examples above, we have to calculate the number of ways of selection, it is similar to the unbounded knapsack problem (as one coin can be selected multiple times).
+
+---
+### Question
+What is the number of ways to get `sum = 0`
+
+**Choices**
+- [ ] 0
+- [x] 1
+- [ ] 2
+- [ ] Undefined
+
+---
+### Count the number of ways using coins Pseudocode
+#### Pseudocode
+```cpp
+for all values of i: dp[i] = 0
+dp[0] = 1
+
+for (i = 1 to N) {
+ for (j = 1 to(A.length - 1)) {
+ if (A[j] <= i) {
+ dp[i] += dp[i - A[j]]
+ }
+ }
+}
+
+return dp[N]
+```
+
+
+#### Time and Space Complexity
+- **Time Complexity**: $O(N * (length~ of ~the ~array))$.
+- **Space Complexity**: $O(N)$.
+
+---
+### Problem 3 Count the number of ways using coins (un-ordered selection)
+
+
+Given a set of coins and a target sum, find the number of ways to make the target sum using the coins, where each coin can only be used once.
+
+**Example**
+
+Suppose we have a situation same as the last one.
+N = 5 and coins we have [3, 1, 4].
+
+So here we have 3 possible ways.
+
+Now, let us try to arrage the coins to get the desired value.
+
+ +
+So, what we can observe out of it is:
+- The current state of dp, i.e. `dp[i]` is to select the number of ways to get the sum equal to i by selecting coins from L to R in the array.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Solution: Un-ordered Selection of Coin
+How we can solve it:
+- Initialize an array dp with all values set to 0. This array will be used to store the number of ways to make change for each possible sum from 0 to N.
+- Set the initial value of `dp[0]` to 1. This step indicates that there is one way to make change for an amount of 0, which is by not using any coins.
+- Iterate through the different coin denominations represented by the array A. This loop will consider each coin one by one.
+- For each coin denomination `A[j]`, iterate through the possible sums from 1 to N. This loop will consider each sum value from 1 to N and calculate the number of ways to make change for that sum.
+- Inside the inner loop, check if the current coin denomination `A[j]` is less than or equal to the current sum `i`. If it is, then it's possible to use this coin to make change for the current sum.
+- If the condition is met, update the `dp` array for the current sum i by adding the number of ways to make change for the remaining amount (`i - A[j]`). This is where dynamic programming comes into play, as you are building up the solutions for larger sums based on the solutions for smaller sums.
+- After both loops complete, the `dp[N]` value will represent the number of ways to make change for the desired amount N using the given coin denominations.
+- Finally, return the value stored in `dp[N]`.
+
+
+#### Pseudocode
+```cpp
+for all values of i: dp[i] = 0
+dp[0] = 1
+
+for (j = 0 to(A.length - 1)) // coins
+{
+ for (i = 1 to N) // sum
+ {
+ if (A[j] <= i) {
+ dp[i] += dp[i - A[j]]
+ }
+ }
+}
+
+return dp[N]
+```
+
+
+#### Time and Space Complexity
+- **Time Complexity**: $O(N * (length~ of~ the~ array))$.
+- **Space Complexity**: `O(N)`.
+
+
+
+---
+### Problem 4 Extended 0-1 Knapsack Problem
+
+We are given `N` toys with their happiness and weight. Find max total happiness that can be kept in a bag with the capacity `W`. Here, we cannot divide the toys.
+
+The constraints are:
+$- 1 <= N <= 500$
+$- 1 <= h[i] <= 50$
+$- 1 <= wt[i] <= 10^9$
+$- 1 <= W <= 10^9$
+
+
+---
+### Question
+What is the MAX value we can get for these items i.e. (weight, value) pairs in 0-1 knapsack of capacity W = 8.
+Items = [(3, 12), (6, 20), (5, 15), (2, 6), (4, 10)]
+
+Chose the correct answer
+
+
+**Choices**
+- [x] 27
+- [ ] 28
+- [ ] 29
+- [ ] 30
+
+**Explanation**
+
+Simple 0-1 Knapsack, after trying all combinations 27 is the highest value we can have inside the knapsack.
+
+---
+### Extended 0-1 Knapsack Problem Approach and Explanation
+
+#### Approach and Calculations
+
+
+
+So, what we can observe out of it is:
+- The current state of dp, i.e. `dp[i]` is to select the number of ways to get the sum equal to i by selecting coins from L to R in the array.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Solution: Un-ordered Selection of Coin
+How we can solve it:
+- Initialize an array dp with all values set to 0. This array will be used to store the number of ways to make change for each possible sum from 0 to N.
+- Set the initial value of `dp[0]` to 1. This step indicates that there is one way to make change for an amount of 0, which is by not using any coins.
+- Iterate through the different coin denominations represented by the array A. This loop will consider each coin one by one.
+- For each coin denomination `A[j]`, iterate through the possible sums from 1 to N. This loop will consider each sum value from 1 to N and calculate the number of ways to make change for that sum.
+- Inside the inner loop, check if the current coin denomination `A[j]` is less than or equal to the current sum `i`. If it is, then it's possible to use this coin to make change for the current sum.
+- If the condition is met, update the `dp` array for the current sum i by adding the number of ways to make change for the remaining amount (`i - A[j]`). This is where dynamic programming comes into play, as you are building up the solutions for larger sums based on the solutions for smaller sums.
+- After both loops complete, the `dp[N]` value will represent the number of ways to make change for the desired amount N using the given coin denominations.
+- Finally, return the value stored in `dp[N]`.
+
+
+#### Pseudocode
+```cpp
+for all values of i: dp[i] = 0
+dp[0] = 1
+
+for (j = 0 to(A.length - 1)) // coins
+{
+ for (i = 1 to N) // sum
+ {
+ if (A[j] <= i) {
+ dp[i] += dp[i - A[j]]
+ }
+ }
+}
+
+return dp[N]
+```
+
+
+#### Time and Space Complexity
+- **Time Complexity**: $O(N * (length~ of~ the~ array))$.
+- **Space Complexity**: `O(N)`.
+
+
+
+---
+### Problem 4 Extended 0-1 Knapsack Problem
+
+We are given `N` toys with their happiness and weight. Find max total happiness that can be kept in a bag with the capacity `W`. Here, we cannot divide the toys.
+
+The constraints are:
+$- 1 <= N <= 500$
+$- 1 <= h[i] <= 50$
+$- 1 <= wt[i] <= 10^9$
+$- 1 <= W <= 10^9$
+
+
+---
+### Question
+What is the MAX value we can get for these items i.e. (weight, value) pairs in 0-1 knapsack of capacity W = 8.
+Items = [(3, 12), (6, 20), (5, 15), (2, 6), (4, 10)]
+
+Chose the correct answer
+
+
+**Choices**
+- [x] 27
+- [ ] 28
+- [ ] 29
+- [ ] 30
+
+**Explanation**
+
+Simple 0-1 Knapsack, after trying all combinations 27 is the highest value we can have inside the knapsack.
+
+---
+### Extended 0-1 Knapsack Problem Approach and Explanation
+
+#### Approach and Calculations
+
+ +
+The normal approach to solve this problem would involve using a recursive or iterative algorithm to consider all possible combinations of toys and select the one with the maximum happiness that doesn't exceed the weight limit. However, due to the constraints provided (N up to 500, `wt[i]` up to $10^9$, ``W`` up to $10^9$), this approach would be extremely slow and inefficient.
+
+By employing dynamic programming, we can optimize the solution significantly. The DP approach allows us to break down the problem into subproblems and store the results of these subproblems in a table to avoid redundant calculations. In this case, we can use a 2-D DP table where `dp[i][w]` represents the maximum happiness that can be achieved with the first `i` toys and a weight constraint of `w`.
+
+DP offers a much faster solution, as it reduces the time complexity from exponential to polynomial time, making it suitable for large inputs like those in the given constraints. Therefore, opting for a DP approach is essential to meet the time and pace constraints of this problem.
diff --git a/Academy DSA Typed Notes/Advanced/DSA Graphs 1 Introduction, DFS & Cycle Detection.md b/Academy DSA Typed Notes/Advanced/DSA Graphs 1 Introduction, DFS & Cycle Detection.md
new file mode 100644
index 0000000..0b5fa6d
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Graphs 1 Introduction, DFS & Cycle Detection.md
@@ -0,0 +1,499 @@
+# Graphs 1: Introduction with BFS & DFS
+
+---
+## Graphs Introduction
+
+### Introduction
+
+**Graph**: It is a collection of nodes and edges.
+
+Some real life examples of Graph -
+1. Network of computers
+2. A Website
+3. Google Maps
+4. Social Media
+
+
+
+The normal approach to solve this problem would involve using a recursive or iterative algorithm to consider all possible combinations of toys and select the one with the maximum happiness that doesn't exceed the weight limit. However, due to the constraints provided (N up to 500, `wt[i]` up to $10^9$, ``W`` up to $10^9$), this approach would be extremely slow and inefficient.
+
+By employing dynamic programming, we can optimize the solution significantly. The DP approach allows us to break down the problem into subproblems and store the results of these subproblems in a table to avoid redundant calculations. In this case, we can use a 2-D DP table where `dp[i][w]` represents the maximum happiness that can be achieved with the first `i` toys and a weight constraint of `w`.
+
+DP offers a much faster solution, as it reduces the time complexity from exponential to polynomial time, making it suitable for large inputs like those in the given constraints. Therefore, opting for a DP approach is essential to meet the time and pace constraints of this problem.
diff --git a/Academy DSA Typed Notes/Advanced/DSA Graphs 1 Introduction, DFS & Cycle Detection.md b/Academy DSA Typed Notes/Advanced/DSA Graphs 1 Introduction, DFS & Cycle Detection.md
new file mode 100644
index 0000000..0b5fa6d
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Graphs 1 Introduction, DFS & Cycle Detection.md
@@ -0,0 +1,499 @@
+# Graphs 1: Introduction with BFS & DFS
+
+---
+## Graphs Introduction
+
+### Introduction
+
+**Graph**: It is a collection of nodes and edges.
+
+Some real life examples of Graph -
+1. Network of computers
+2. A Website
+3. Google Maps
+4. Social Media
+
+ +
+
+
+ +
+
+
+ +
+
+---
+### Types of Graph
+
+
+### Cyclic Graph
+
+A cyclic graph contains at least one cycle, which is a closed path that returns to the same vertex.
+Diagram:
+```javascript
+A -- B
+| |
+| |
+D -- C
+```
+
+### Acyclic Graph
+An acyclic graph has no cycles, meaning there are no closed paths in the graph.
+Diagram:
+```javascript
+A -- B
+| |
+D C
+```
+
+### Directed Graph (Digraph)
+In a directed graph, edges have a direction, indicating one-way relationships between vertices.
+Diagram:
+```javascript
+A --> B
+| |
+v v
+D --> C
+```
+
+### Undirected Graph
+In an undirected graph, edges have no direction, representing symmetric relationships between vertices.
+Diagram:
+```javascript
+A -- B
+| |
+| |
+D -- C
+```
+
+### Connected Graph
+A connected graph has a path between every pair of vertices, ensuring no isolated vertices.
+Diagram
+```javascript
+A -- B
+|
+D -- C
+```
+
+### Disconnected Graph
+A disconnected graph has at least two disconnected components, meaning there is no path between them.
+Diagram:
+```javascript
+A -- B C -- D
+| |
+E -- F G -- H
+```
+
+### Weighted Graph
+In a weighted graph, edges have associated weights or costs, often used to represent distances, costs, or other metrics.
+Diagram (Undirected with Weights):
+```javascript
+A -2- B
+| |
+1 3
+| |
+D -4- C
+```
+
+### Unweighted Graph
+An unweighted graph has no associated weights on its edges.
+Diagram (Undirected Unweighted):
+```javascript
+A -- B
+|
+D -- C
+```
+
+### Degree of a Vertex
+The degree of a vertex is the number of edges incident to it.
+Diagram:
+```javascript
+ B
+ |
+A--C--D
+```
+
+### Outdegree of a Vertex
+The outdegree of a vertex in a directed graph is the number of edges leaving that vertex.
+Diagram:
+```javascript
+A --> B
+| |
+v v
+D --> C
+```
+
+### Simple Graph
+A simple graph has no self-loops or multiple edges between the same pair of vertices.
+Diagram:
+```javascript
+A -- B
+|
+D -- C
+```
+
+
+
+---
+### How to store a graph
+
+
+### Graph:
+
+
+
+
+---
+### Types of Graph
+
+
+### Cyclic Graph
+
+A cyclic graph contains at least one cycle, which is a closed path that returns to the same vertex.
+Diagram:
+```javascript
+A -- B
+| |
+| |
+D -- C
+```
+
+### Acyclic Graph
+An acyclic graph has no cycles, meaning there are no closed paths in the graph.
+Diagram:
+```javascript
+A -- B
+| |
+D C
+```
+
+### Directed Graph (Digraph)
+In a directed graph, edges have a direction, indicating one-way relationships between vertices.
+Diagram:
+```javascript
+A --> B
+| |
+v v
+D --> C
+```
+
+### Undirected Graph
+In an undirected graph, edges have no direction, representing symmetric relationships between vertices.
+Diagram:
+```javascript
+A -- B
+| |
+| |
+D -- C
+```
+
+### Connected Graph
+A connected graph has a path between every pair of vertices, ensuring no isolated vertices.
+Diagram
+```javascript
+A -- B
+|
+D -- C
+```
+
+### Disconnected Graph
+A disconnected graph has at least two disconnected components, meaning there is no path between them.
+Diagram:
+```javascript
+A -- B C -- D
+| |
+E -- F G -- H
+```
+
+### Weighted Graph
+In a weighted graph, edges have associated weights or costs, often used to represent distances, costs, or other metrics.
+Diagram (Undirected with Weights):
+```javascript
+A -2- B
+| |
+1 3
+| |
+D -4- C
+```
+
+### Unweighted Graph
+An unweighted graph has no associated weights on its edges.
+Diagram (Undirected Unweighted):
+```javascript
+A -- B
+|
+D -- C
+```
+
+### Degree of a Vertex
+The degree of a vertex is the number of edges incident to it.
+Diagram:
+```javascript
+ B
+ |
+A--C--D
+```
+
+### Outdegree of a Vertex
+The outdegree of a vertex in a directed graph is the number of edges leaving that vertex.
+Diagram:
+```javascript
+A --> B
+| |
+v v
+D --> C
+```
+
+### Simple Graph
+A simple graph has no self-loops or multiple edges between the same pair of vertices.
+Diagram:
+```javascript
+A -- B
+|
+D -- C
+```
+
+
+
+---
+### How to store a graph
+
+
+### Graph:
+
+ +
+### Adjacency Matrix:
+All the edges in above graph has equal weights.
+In adjacency matrix, `mat[i][j] = 1`, if there is an edge between them else it will be 0.
+
+
+
+### Adjacency Matrix:
+All the edges in above graph has equal weights.
+In adjacency matrix, `mat[i][j] = 1`, if there is an edge between them else it will be 0.
+
+ +
+
+
+#### Pseudocode:
+
+```cpp
+int N, M
+int mat[N+1][M+1] = {0}
+
+for(int i=0; i < A.size(); i++) {
+ u = A[i][0];
+ v = A[i][1];
+
+ mat[u][v] = 1
+ mat[v][u] = 1
+}
+```
+
+Note: In case of weighted graph, we store weights in the matrix.
+
+**Advantage:** Easy to update new edges.
+
+**Disadvantage:** Space wastage because of also leaving space for non-exitent edges.
+Moreover,
+If N<=10^5, it won't be possible to create matrix of size 10^10.
+It is possible only if N <= 10^3
+
+
+**Space Complexity:** O(N^2^)
+
+### 2. Adjacency List:
+
+An adjacency list is a common way to represent a graph in computer science. It's used to describe which nodes (or vertices) in the graph are connected to each other. Here's how it works:
+
+#### Graph:
+
+
+
+
+
+#### Pseudocode:
+
+```cpp
+int N, M
+int mat[N+1][M+1] = {0}
+
+for(int i=0; i < A.size(); i++) {
+ u = A[i][0];
+ v = A[i][1];
+
+ mat[u][v] = 1
+ mat[v][u] = 1
+}
+```
+
+Note: In case of weighted graph, we store weights in the matrix.
+
+**Advantage:** Easy to update new edges.
+
+**Disadvantage:** Space wastage because of also leaving space for non-exitent edges.
+Moreover,
+If N<=10^5, it won't be possible to create matrix of size 10^10.
+It is possible only if N <= 10^3
+
+
+**Space Complexity:** O(N^2^)
+
+### 2. Adjacency List:
+
+An adjacency list is a common way to represent a graph in computer science. It's used to describe which nodes (or vertices) in the graph are connected to each other. Here's how it works:
+
+#### Graph:
+
+ +
+#### Adjacency List:
+
+Stores the list of nodes connected corresponding to every node.
+
+
+#### Adjacency List:
+
+Stores the list of nodes connected corresponding to every node.
+ +
+We can create map of
+
+We can create map of  +
+---
+### Question
+Time Complexity for DFS?
+
+**Choices**
+- [x] O(V + E)
+- [ ] O(V)
+- [ ] O(2E)
+
+**Explanation**:
+
+The time complexity of the DFS algorithm is O(V + E), where V is the number of vertices (nodes) in the graph, and E is the number of edges. This is because, in the worst case, the algorithm visits each vertex once and each edge once.
+
+**Space Complexity:** O(V)
+
+
+---
+### Problem 1 Detecting Cycles in a Directed Graph
+
+Check if given graph has a cycle?
+
+**Examples**
+
+1)
+
+
+---
+### Question
+Time Complexity for DFS?
+
+**Choices**
+- [x] O(V + E)
+- [ ] O(V)
+- [ ] O(2E)
+
+**Explanation**:
+
+The time complexity of the DFS algorithm is O(V + E), where V is the number of vertices (nodes) in the graph, and E is the number of edges. This is because, in the worst case, the algorithm visits each vertex once and each edge once.
+
+**Space Complexity:** O(V)
+
+
+---
+### Problem 1 Detecting Cycles in a Directed Graph
+
+Check if given graph has a cycle?
+
+**Examples**
+
+1)
+ +
+2)
+
+
+2)
+ +
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Approach
+
+Apply DFS, if a node in current path is encountered again, it means cycle is present!
+With this, we will have to keep track of the path.
+
+Example 1:
+
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Approach
+
+Apply DFS, if a node in current path is encountered again, it means cycle is present!
+With this, we will have to keep track of the path.
+
+Example 1:
+ +
+>Say we start at 0 -> 1 -> 3
+path[] = {0, 1, 3}
+Now, while coming back from 3, we can remove the 3 from path array.
+path[] = {0, 1}
+Now, 0 -> 1 -> 2 -> 3
+path[] = {0, 1, 2, 3} ***[Here, we came back to 3, but via different path, which is not an issue for us]***
+
+Example 2:
+
+
+>Say we start at 0 -> 1 -> 3
+path[] = {0, 1, 3}
+Now, while coming back from 3, we can remove the 3 from path array.
+path[] = {0, 1}
+Now, 0 -> 1 -> 2 -> 3
+path[] = {0, 1, 2, 3} ***[Here, we came back to 3, but via different path, which is not an issue for us]***
+
+Example 2:
+ +
+> Say we start at 0 -> 1 -> 2 -> 3
+path[] = {0, 1, 2, 3}
+Now, from 3, we come back to 1.
+path[] = {0, 1, 2, 3, 1} ***[But 1 is already a part of that path, which means cycle is present]***
+
+#### Pseudocode
+
+```javascript
+list < int > graph[] //filled
+bool visited[] = {0}
+int path[N] = {0}
+
+bool dfs(int u) {
+ visited[u] = true
+ path[u] = 1
+
+ for (int i = 0; i < graph[u].size(); i++) {
+ int v = graph[u][i]
+ if (path[v] == 1) return true
+ else if (!visited[v] && dfs(v)) {
+ return true
+ }
+ }
+ path[u] = 0;
+ return false;
+}
+```
+
+#### Complexity
+**Time Complexity:** O(V + E)
+**Space Complexity:** O(V)
+
+
+
+---
+### Problem 2 Number of Islands Statement and Approach
+
+
+You are given a 2D grid of '1's (land) and '0's (water). Your task is to determine the number of islands in the grid. An island is formed by connecting adjacent (horizontally or vertically) land cells. Diagonal connections are not considered.
+
+Given here if the cell values has 1 then there is land and 0 if it is water, and you may assume all four edges of the grid are all surrounded by water.
+
+
+
+> Say we start at 0 -> 1 -> 2 -> 3
+path[] = {0, 1, 2, 3}
+Now, from 3, we come back to 1.
+path[] = {0, 1, 2, 3, 1} ***[But 1 is already a part of that path, which means cycle is present]***
+
+#### Pseudocode
+
+```javascript
+list < int > graph[] //filled
+bool visited[] = {0}
+int path[N] = {0}
+
+bool dfs(int u) {
+ visited[u] = true
+ path[u] = 1
+
+ for (int i = 0; i < graph[u].size(); i++) {
+ int v = graph[u][i]
+ if (path[v] == 1) return true
+ else if (!visited[v] && dfs(v)) {
+ return true
+ }
+ }
+ path[u] = 0;
+ return false;
+}
+```
+
+#### Complexity
+**Time Complexity:** O(V + E)
+**Space Complexity:** O(V)
+
+
+
+---
+### Problem 2 Number of Islands Statement and Approach
+
+
+You are given a 2D grid of '1's (land) and '0's (water). Your task is to determine the number of islands in the grid. An island is formed by connecting adjacent (horizontally or vertically) land cells. Diagonal connections are not considered.
+
+Given here if the cell values has 1 then there is land and 0 if it is water, and you may assume all four edges of the grid are all surrounded by water.
+
+ +
+In this case we can see that our answer is 5.
+
+**Que: Do we need adjacency list ?**
+Ans: No, since the information is already present in form of matrix which can be utilised as it is.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Approach:
+
+**Set a Counter:** Start with a counter at zero for tracking island count.
+
+**Scan the Grid:** Go through each cell in the grid.
+
+**Search for Islands:** When you find a land cell ('1'), use either BFS or DFS to explore all connected land cells.
+
+**Mark Visited Cells:** Change each visited '1' to '0' during the search to avoid recounting.
+
+**Count Each Island:** Increase the counter by 1 for every complete search that identifies a new island.
+
+**Finish the Search:** Continue until all grid cells are checked.
+
+**Result:** The counter will indicate the total number of islands.
+
+
+---
+### Number of Islands Dry Run and Pseudocode
+
+#### Dry-Run:
+```java
+[
+ ['1', '1', '0', '0', '0'],
+ ['1', '1', '0', '0', '0'],
+ ['0', '0', '0', '0', '0'],
+ ['0', '0', '0', '1', '1']
+]
+```
+
+* Initialize variable islands = 0.
+* Start iterating through the grid:
+* At grid[0][0], we find '1'. Increment islands to 1 and call visitIsland(grid, 0, 0).
+* visitIsland will mark all connected land cells as '0', and we explore the neighboring cells recursively. After this, the grid becomes:
+
+
+```cpp-
+[
+ ['0', '0', '0', '0', '0'],
+ ['0', '0', '0', '0', '0'],
+ ['0', '0', '1', '0', '0'],
+ ['0', '0', '0', '1', '1']
+]
+```
+* Continue iterating through the grid:
+* At grid[2][2], we find '1'. Increment islands to 2 and call visitIsland(grid, 2, 2).
+* visitIsland will mark connected land cells as '0', and we explore the neighboring cells recursively. After this, the grid becomes:
+```java
+[
+ ['0', '0', '0', '0', '0'],
+ ['0', '0', '0', '0', '0'],
+ ['0', '0', '0', '0', '0'],
+ ['0', '0', '0', '1', '1']
+]
+```
+* Continue the iteration.
+* At grid[3][3], we find '1'. Increment islands to 3 and call visitIsland(grid, 3, 3).
+
+We can visit only 4 coordinates, considering them to be i, j; it means we can visit **(i,j-1), (i-1, j), (i, j+1), (i+1, j)**
+
+
+
+In this case we can see that our answer is 5.
+
+**Que: Do we need adjacency list ?**
+Ans: No, since the information is already present in form of matrix which can be utilised as it is.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Approach:
+
+**Set a Counter:** Start with a counter at zero for tracking island count.
+
+**Scan the Grid:** Go through each cell in the grid.
+
+**Search for Islands:** When you find a land cell ('1'), use either BFS or DFS to explore all connected land cells.
+
+**Mark Visited Cells:** Change each visited '1' to '0' during the search to avoid recounting.
+
+**Count Each Island:** Increase the counter by 1 for every complete search that identifies a new island.
+
+**Finish the Search:** Continue until all grid cells are checked.
+
+**Result:** The counter will indicate the total number of islands.
+
+
+---
+### Number of Islands Dry Run and Pseudocode
+
+#### Dry-Run:
+```java
+[
+ ['1', '1', '0', '0', '0'],
+ ['1', '1', '0', '0', '0'],
+ ['0', '0', '0', '0', '0'],
+ ['0', '0', '0', '1', '1']
+]
+```
+
+* Initialize variable islands = 0.
+* Start iterating through the grid:
+* At grid[0][0], we find '1'. Increment islands to 1 and call visitIsland(grid, 0, 0).
+* visitIsland will mark all connected land cells as '0', and we explore the neighboring cells recursively. After this, the grid becomes:
+
+
+```cpp-
+[
+ ['0', '0', '0', '0', '0'],
+ ['0', '0', '0', '0', '0'],
+ ['0', '0', '1', '0', '0'],
+ ['0', '0', '0', '1', '1']
+]
+```
+* Continue iterating through the grid:
+* At grid[2][2], we find '1'. Increment islands to 2 and call visitIsland(grid, 2, 2).
+* visitIsland will mark connected land cells as '0', and we explore the neighboring cells recursively. After this, the grid becomes:
+```java
+[
+ ['0', '0', '0', '0', '0'],
+ ['0', '0', '0', '0', '0'],
+ ['0', '0', '0', '0', '0'],
+ ['0', '0', '0', '1', '1']
+]
+```
+* Continue the iteration.
+* At grid[3][3], we find '1'. Increment islands to 3 and call visitIsland(grid, 3, 3).
+
+We can visit only 4 coordinates, considering them to be i, j; it means we can visit **(i,j-1), (i-1, j), (i, j+1), (i+1, j)**
+
+ +
+#### Pseudocode
+
+
+
+#### Pseudocode
+
+ +
+
+
+ +
+
+
+ diff --git a/Academy DSA Typed Notes/Advanced/DSA Graphs 2 BFS, Matrix Questions & Topological Sort.md b/Academy DSA Typed Notes/Advanced/DSA Graphs 2 BFS, Matrix Questions & Topological Sort.md
new file mode 100644
index 0000000..b14c1a7
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Graphs 2 BFS, Matrix Questions & Topological Sort.md
@@ -0,0 +1,417 @@
+# DSA: Graphs 2: BFS, Matrix Questions & Topological Sort
+
+---
+## BFS
+Breadth-First Search (BFS) is another graph traversal algorithm used to explore and navigate graphs or trees. It starts at a source node and explores all its neighbors at the current depth level before moving on to the next level. BFS uses a queue data structure to maintain the order of nodes to be visited.
+
+### Approach:
+* We use a queue to maintain the order of nodes to visit in a breadth-first manner.
+* We start with a vector visited to keep track of whether each node has been visited. Initially, all nodes are marked as unvisited (false).
+* We enqueue the startNode into the queue and mark it as visited.
+* We enter a loop that continues until the queue is empty.
+* In each iteration, we dequeue the front element (the current node) from the queue and process it. Processing can include printing the node or performing any other desired operation.
+* We then iterate through the neighbors of the current node. For each neighbor that hasn't been visited, we enqueue it into the queue and mark it as visited.
+* The BFS traversal continues until the queue is empty, visiting nodes level by level.
+
+
+### Example/Dry-Run
+```javascript
+ A --- B --- C
+ | |
+ +---------+
+ |
+ D
+```
+Suppose in this if we want to perform BFS then:
+
+* Start from the source node (City A).
+* Explore neighboring nodes level by level.
+* Use a queue to maintain the order.
+* Mark visited nodes (using adjaency list) to avoid repetition.
+* Stop when the target node (City D) is reached.
+* This guarantees the shortest path in unweighted graphs.
+
+
+#### Pseudocode:
+```javascript
+void bfs(int startNode) {
+ vector < bool > visited(MAX_NODES, false); // Initialize all nodes as unvisited
+ queue < int > q;
+
+ q.push(startNode); // Enqueue the start node
+ visited[startNode] = true; // Mark the start node as visited
+
+ while (!q.empty()) {
+ int currentNode = q.front();
+ q.pop();
+
+ // Process the current node (e.g., print or perform an operation)
+
+ for (int neighbor: graph[currentNode]) {
+ if (!visited[neighbor]) {
+ q.push(neighbor); // Enqueue unvisited neighbors
+ visited[neighbor] = true; // Mark neighbor as visited
+ }
+ }
+ }
+```
+
+#### Compexity
+**Time Complexity:** O(V + E)
+**Space Complexity:** O(V)
+
+
+---
+### Question
+
+Consider a graph with the following adjacency matrix:
+
+```
+[0, 1, 1, 0]
+[1, 0, 0, 0]
+[1, 0, 0, 1]
+[0, 0, 1, 0]
+```
+
+What is the order in which the nodes will be visited when performing a breadth-first search (BFS) starting from node 0?
+
+**Choices**
+- [x] 0, 1, 2, 3
+- [ ] 0, 1, 3, 2
+- [ ] 0, 2, 3, 1
+- [ ] 0, 1, 3, 1
+
+
+The correct answer is (a) 0, 1, 2, 3.
+
+BFS (Breadth-First Search) explores neighbor nodes first before moving to the next level. Starting from node 0, BFS visits its neighbors 1 and 2. It then moves to the next level and visits 1's neighbor 3. Finally, it moves to the next level but finds no more unvisited nodes. Therefore, the order of BFS traversal is 0, 1, 2, 3.
+
+---
+### Multisource BFS
+
+There are N number of nodes and multisource(S1,S2,S3), we need to find the length of shortest path for given destination node to any one of the source node{S1,S2,S3}.
+
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Graphs 2 BFS, Matrix Questions & Topological Sort.md b/Academy DSA Typed Notes/Advanced/DSA Graphs 2 BFS, Matrix Questions & Topological Sort.md
new file mode 100644
index 0000000..b14c1a7
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Graphs 2 BFS, Matrix Questions & Topological Sort.md
@@ -0,0 +1,417 @@
+# DSA: Graphs 2: BFS, Matrix Questions & Topological Sort
+
+---
+## BFS
+Breadth-First Search (BFS) is another graph traversal algorithm used to explore and navigate graphs or trees. It starts at a source node and explores all its neighbors at the current depth level before moving on to the next level. BFS uses a queue data structure to maintain the order of nodes to be visited.
+
+### Approach:
+* We use a queue to maintain the order of nodes to visit in a breadth-first manner.
+* We start with a vector visited to keep track of whether each node has been visited. Initially, all nodes are marked as unvisited (false).
+* We enqueue the startNode into the queue and mark it as visited.
+* We enter a loop that continues until the queue is empty.
+* In each iteration, we dequeue the front element (the current node) from the queue and process it. Processing can include printing the node or performing any other desired operation.
+* We then iterate through the neighbors of the current node. For each neighbor that hasn't been visited, we enqueue it into the queue and mark it as visited.
+* The BFS traversal continues until the queue is empty, visiting nodes level by level.
+
+
+### Example/Dry-Run
+```javascript
+ A --- B --- C
+ | |
+ +---------+
+ |
+ D
+```
+Suppose in this if we want to perform BFS then:
+
+* Start from the source node (City A).
+* Explore neighboring nodes level by level.
+* Use a queue to maintain the order.
+* Mark visited nodes (using adjaency list) to avoid repetition.
+* Stop when the target node (City D) is reached.
+* This guarantees the shortest path in unweighted graphs.
+
+
+#### Pseudocode:
+```javascript
+void bfs(int startNode) {
+ vector < bool > visited(MAX_NODES, false); // Initialize all nodes as unvisited
+ queue < int > q;
+
+ q.push(startNode); // Enqueue the start node
+ visited[startNode] = true; // Mark the start node as visited
+
+ while (!q.empty()) {
+ int currentNode = q.front();
+ q.pop();
+
+ // Process the current node (e.g., print or perform an operation)
+
+ for (int neighbor: graph[currentNode]) {
+ if (!visited[neighbor]) {
+ q.push(neighbor); // Enqueue unvisited neighbors
+ visited[neighbor] = true; // Mark neighbor as visited
+ }
+ }
+ }
+```
+
+#### Compexity
+**Time Complexity:** O(V + E)
+**Space Complexity:** O(V)
+
+
+---
+### Question
+
+Consider a graph with the following adjacency matrix:
+
+```
+[0, 1, 1, 0]
+[1, 0, 0, 0]
+[1, 0, 0, 1]
+[0, 0, 1, 0]
+```
+
+What is the order in which the nodes will be visited when performing a breadth-first search (BFS) starting from node 0?
+
+**Choices**
+- [x] 0, 1, 2, 3
+- [ ] 0, 1, 3, 2
+- [ ] 0, 2, 3, 1
+- [ ] 0, 1, 3, 1
+
+
+The correct answer is (a) 0, 1, 2, 3.
+
+BFS (Breadth-First Search) explores neighbor nodes first before moving to the next level. Starting from node 0, BFS visits its neighbors 1 and 2. It then moves to the next level and visits 1's neighbor 3. Finally, it moves to the next level but finds no more unvisited nodes. Therefore, the order of BFS traversal is 0, 1, 2, 3.
+
+---
+### Multisource BFS
+
+There are N number of nodes and multisource(S1,S2,S3), we need to find the length of shortest path for given destination node to any one of the source node{S1,S2,S3}.
+
+ +
+
+#### Solution
+Length = 2
+In the beginning, we need to push all source node at once and apply exact BFS,then return the distance of destination node.
+#### Time and Space Complexity
+* **TC -** O(N+E)
+* **SC -** O(N+E)
+
+---
+### Rotten Oranges
+
+There is given a matrix and there are 3 values where 0 means empty cell, 1 means fresh orange present and 2 means rotten orange prsent, we need to find the time when all oranges will become rotten.
+**Note:** If not possible, return - 1.
+
+
+
+
+#### Solution
+Length = 2
+In the beginning, we need to push all source node at once and apply exact BFS,then return the distance of destination node.
+#### Time and Space Complexity
+* **TC -** O(N+E)
+* **SC -** O(N+E)
+
+---
+### Rotten Oranges
+
+There is given a matrix and there are 3 values where 0 means empty cell, 1 means fresh orange present and 2 means rotten orange prsent, we need to find the time when all oranges will become rotten.
+**Note:** If not possible, return - 1.
+
+ +
+
+
+#### Solution
+
+
+
+
+
+#### Solution
+
+ +
+
+
+**Answer:** after 3 minutes all oranges will get rotten.
+* Initially, We need to insert all rotten oranges in Queue (where each element in queue is in a pair),
+* Then check if any fresh oranges has become rotten and if they did, return the time otherwise return -1.
+
+#### Pseudocode
+```java
+public class RottingOranges {
+ private static final int[] dx = {-1, 1, 0, 0};
+ private static final int[] dy = {0, 0, -1, 1};
+
+ public int orangesRotting(int[][] grid) {
+ int rowCount = grid.length;
+ int colCount = grid[0].length;
+ Queue< int[] > queue = new LinkedList< >();
+ int freshOranges = 0;
+ int minutes = 0;
+
+ // Count fresh oranges and add rotten oranges to the queue
+ for (int i = 0; i < rowCount; i++) {
+ for (int j = 0; j < colCount; j++) {
+ if (grid[i][j] == 2) {
+ queue.offer(new int[]{i, j, minutes});
+ } else if (grid[i][j] == 1) {
+ freshOranges++;
+ }
+ }
+ }
+ if (freshOranges == 0) {
+ // If there are no fresh oranges initially, they are already rotten.
+ return 0;
+ }
+
+ while (!queue.isEmpty()) {
+ int[] cell = queue.poll();
+ int x = cell[0];
+ int y = cell[1];
+ minutes = cell[2];
+
+ for (int i = 0; i < 4; i++) {
+ int newX = x + dx[i];
+ int newY = y + dy[i];
+
+ if (isValid(grid, newX, newY) && grid[newX][newY] == 1) {
+ grid[newX][newY] = 2;
+ freshOranges--;
+ queue.offer(new int[] {newX, newY, minutes + 1});
+ }
+ }
+ }
+
+ return (freshOranges == 0) ? minutes : -1;
+ }
+ private boolean isValid(int[][] grid, int x, int y) {
+ int rowCount = grid.length;
+ int colCount = grid[0].length;
+ return x >= 0 && x < rowCount && y >= 0 && y < colCount;
+ }
+
+
+```
+
+---
+### Possibility of finishing the courses
+
+
+Given N courses with pre-requisites, we have to check if it is possible to finish all the course ?
+
+**Example:**
+
+N = 5
+
+**Pre-requisites**
+1 ---> 2 & 3 [1 is pre-req for 2 and 3]
+2 ---> 3 & 5
+3 ---> 4
+4 ---> 2
+
+
+
+
+
+**Answer:** after 3 minutes all oranges will get rotten.
+* Initially, We need to insert all rotten oranges in Queue (where each element in queue is in a pair),
+* Then check if any fresh oranges has become rotten and if they did, return the time otherwise return -1.
+
+#### Pseudocode
+```java
+public class RottingOranges {
+ private static final int[] dx = {-1, 1, 0, 0};
+ private static final int[] dy = {0, 0, -1, 1};
+
+ public int orangesRotting(int[][] grid) {
+ int rowCount = grid.length;
+ int colCount = grid[0].length;
+ Queue< int[] > queue = new LinkedList< >();
+ int freshOranges = 0;
+ int minutes = 0;
+
+ // Count fresh oranges and add rotten oranges to the queue
+ for (int i = 0; i < rowCount; i++) {
+ for (int j = 0; j < colCount; j++) {
+ if (grid[i][j] == 2) {
+ queue.offer(new int[]{i, j, minutes});
+ } else if (grid[i][j] == 1) {
+ freshOranges++;
+ }
+ }
+ }
+ if (freshOranges == 0) {
+ // If there are no fresh oranges initially, they are already rotten.
+ return 0;
+ }
+
+ while (!queue.isEmpty()) {
+ int[] cell = queue.poll();
+ int x = cell[0];
+ int y = cell[1];
+ minutes = cell[2];
+
+ for (int i = 0; i < 4; i++) {
+ int newX = x + dx[i];
+ int newY = y + dy[i];
+
+ if (isValid(grid, newX, newY) && grid[newX][newY] == 1) {
+ grid[newX][newY] = 2;
+ freshOranges--;
+ queue.offer(new int[] {newX, newY, minutes + 1});
+ }
+ }
+ }
+
+ return (freshOranges == 0) ? minutes : -1;
+ }
+ private boolean isValid(int[][] grid, int x, int y) {
+ int rowCount = grid.length;
+ int colCount = grid[0].length;
+ return x >= 0 && x < rowCount && y >= 0 && y < colCount;
+ }
+
+
+```
+
+---
+### Possibility of finishing the courses
+
+
+Given N courses with pre-requisites, we have to check if it is possible to finish all the course ?
+
+**Example:**
+
+N = 5
+
+**Pre-requisites**
+1 ---> 2 & 3 [1 is pre-req for 2 and 3]
+2 ---> 3 & 5
+3 ---> 4
+4 ---> 2
+
+ +
+The pre-req information is represented in above directed graph.
+
+
+#### Explanantion:
+
+**Que:** Which course shall we complete first?
+The one having no pre-requisites. (say 1)
+
+
+
+The pre-req information is represented in above directed graph.
+
+
+#### Explanantion:
+
+**Que:** Which course shall we complete first?
+The one having no pre-requisites. (say 1)
+
+ +
+Next, which one shall we pick ?
+
+We can't pick any course because of the dependencies. Hence, it means we can't finish courses in above example.
+
+The reason is there's a cycle!
+Have you heard of the term deadlock ? [*For experience we need job, for job we need experience like scenario :p* ]
+
+**Conclusion:** If it's a cyclic graph, answer will always be false, else true.
+
+**Observation:** To solve the problem, we need directed acyclic graph!
+
+---
+### Possibility of finishing courses approach
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+**Example:**
+
+
+
+Next, which one shall we pick ?
+
+We can't pick any course because of the dependencies. Hence, it means we can't finish courses in above example.
+
+The reason is there's a cycle!
+Have you heard of the term deadlock ? [*For experience we need job, for job we need experience like scenario :p* ]
+
+**Conclusion:** If it's a cyclic graph, answer will always be false, else true.
+
+**Observation:** To solve the problem, we need directed acyclic graph!
+
+---
+### Possibility of finishing courses approach
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+**Example:**
+
+ +
+Pick ? 1 [not dependant on any other course]
+Next Pick ? 2
+Next Pick ? 3
+Next Pick ? 4
+Next Pick ? 5
+
+**Order:**
+1 2 3 4 5
+
+The above order is known as topological sort/ topological order.
+
+**Que:** For one graph, can we have only one topological order?
+
+
+
+Pick ? 1 [not dependant on any other course]
+Next Pick ? 2
+Next Pick ? 3
+Next Pick ? 4
+Next Pick ? 5
+
+**Order:**
+1 2 3 4 5
+
+The above order is known as topological sort/ topological order.
+
+**Que:** For one graph, can we have only one topological order?
+
+ +
+Is the order 1 2 3 4 5 valid ? YES!
+What about 1 3 2 4 5 ? YES!
+What about 1 3 4 2 5 ? YES!
+
+Hence, it is possible that we have multiple topological order for a given graph.
+
+#### Definition
+
+**Topological sort** is a linear ordering of the vertices (nodes) in a directed acyclic graph (DAG) such that for every directed edge (u, v), vertex u comes before vertex v in the ordering. In other words, it arranges the nodes in such a way that if there is a directed edge from node A to node B, then node A comes before node B in the sorted order.
+
+---
+## Topological Sort
+
+Let's find topological ordering of below graph!
+
+
+
+Is the order 1 2 3 4 5 valid ? YES!
+What about 1 3 2 4 5 ? YES!
+What about 1 3 4 2 5 ? YES!
+
+Hence, it is possible that we have multiple topological order for a given graph.
+
+#### Definition
+
+**Topological sort** is a linear ordering of the vertices (nodes) in a directed acyclic graph (DAG) such that for every directed edge (u, v), vertex u comes before vertex v in the ordering. In other words, it arranges the nodes in such a way that if there is a directed edge from node A to node B, then node A comes before node B in the sorted order.
+
+---
+## Topological Sort
+
+Let's find topological ordering of below graph!
+
+ +
+**Indegree:** The count of incoming nodes is known as indegree of a node.
+
+For above graph, the indegrees will be as follows -
+
+
+
+**Indegree:** The count of incoming nodes is known as indegree of a node.
+
+For above graph, the indegrees will be as follows -
+
+ +
+### Next Steps
+* Insert all the nodes with indegree=0 in a queue
+* Dequeue an element from the queue and update the indegree for all the neighbours, if the indegree for any nbr becomes 0 add that node in the queue.
+
+
+
+### Approach:
+* Create an array to store indegrees, initially set all values to zero.
+* Iterate through each node in the graph using a loop.
+* For each node, traverse its outgoing edges by iterating through its adjacency list.
+* For each neighboring node in the adjacency list, increment its indegree count by one.
+* Continue the loop until you've processed all nodes in the graph.
+* The array now contains the indegree of each node, where the value at index i represents the indegree of node i.
+
+**Example:**
+
+
+
+### Next Steps
+* Insert all the nodes with indegree=0 in a queue
+* Dequeue an element from the queue and update the indegree for all the neighbours, if the indegree for any nbr becomes 0 add that node in the queue.
+
+
+
+### Approach:
+* Create an array to store indegrees, initially set all values to zero.
+* Iterate through each node in the graph using a loop.
+* For each node, traverse its outgoing edges by iterating through its adjacency list.
+* For each neighboring node in the adjacency list, increment its indegree count by one.
+* Continue the loop until you've processed all nodes in the graph.
+* The array now contains the indegree of each node, where the value at index i represents the indegree of node i.
+
+**Example:**
+
+ +
+In the above photo we can refer the indegree of each of the nodes is written in green.
+
+#### Pseudocode:
+```java
+in [N], i, in [i] = 0;
+for (i = 0; i < n; i++) {
+ for (nbr: adj[i]) {
+ ibr[i] += 1;
+ }
+}
+```
+#### Complexity
+**Time Complexity:** O(N + E)
+**Space Complexity:** 0(N)
+
+---
+### Topological Sort (Right to Left)
+
+
+
+In a right-to-left topological order, you start from the "rightmost" vertex (i.e., a vertex with no outgoing edges) and proceed leftward. This approach can be useful in certain situations and can be thought of as a reverse topological ordering.
+
+Here's how you can approach it:
+
+#### Approach:
+* Identify a vertex with no outgoing edges (in-degree = 0). If there are multiple such vertices, you can choose any of them.
+* Remove that vertex from the graph along with all its outgoing edges. This removal may affect the in-degrees of other vertices.
+* Repeat steps 1 and 2 until all vertices are removed from the graph. The order in which you remove the vertices constitutes the right-to-left topological order.
+
+#### Example/Dry-Run:
+```java
+A -> B -> C
+| |
+v v
+D E
+```
+To find the right-to-left topological order:
+
+* Start with a vertex with no outgoing edges. In this case, you can start with vertex C.
+* Remove vertex C and its outgoing edge. The graph becomes:
+```java
+A -> B
+|
+v
+D E
+```
+Now, you can choose either B or E, both of which have no outgoing edges. Let's choose B and remove it:
+```java
+A
+|
+v
+D E
+```
+* Continue with the remaining vertices. Choose A next:
+```java
+|
+v
+D E
+```
+* Finally, remove D and E:
+```java
+|
+v
+| |
+```
+The order in which you removed the vertices is a right-to-left topological order: C, B, A, D, E.
+
+#### Pseudocode
+```java
+function topologicalSortRightToLeft(graph):
+ // Function to perform DFS and record nodes in the order they are finished
+ function dfs(node):
+ mark node as visited
+ for each neighbor in graph[node]:
+ if neighbor is not visited:
+ dfs(neighbor)
+ append node to order list
+
+ create an empty order list
+ initialize a visited array with False for all nodes
+
+ for each node in the graph:
+ if node is not visited:
+ dfs(node)
+
+ reverse the order list
+
+ return the reversed order list as the topological order (right-to-left)
+```
+
+#### Complexity
+**Time Complexity:** O(V+E)
+**Space Complexity:** O(V)
+
+---
+### Question
+Which of the following is correct topological order for this graph?
+
+
+
+In the above photo we can refer the indegree of each of the nodes is written in green.
+
+#### Pseudocode:
+```java
+in [N], i, in [i] = 0;
+for (i = 0; i < n; i++) {
+ for (nbr: adj[i]) {
+ ibr[i] += 1;
+ }
+}
+```
+#### Complexity
+**Time Complexity:** O(N + E)
+**Space Complexity:** 0(N)
+
+---
+### Topological Sort (Right to Left)
+
+
+
+In a right-to-left topological order, you start from the "rightmost" vertex (i.e., a vertex with no outgoing edges) and proceed leftward. This approach can be useful in certain situations and can be thought of as a reverse topological ordering.
+
+Here's how you can approach it:
+
+#### Approach:
+* Identify a vertex with no outgoing edges (in-degree = 0). If there are multiple such vertices, you can choose any of them.
+* Remove that vertex from the graph along with all its outgoing edges. This removal may affect the in-degrees of other vertices.
+* Repeat steps 1 and 2 until all vertices are removed from the graph. The order in which you remove the vertices constitutes the right-to-left topological order.
+
+#### Example/Dry-Run:
+```java
+A -> B -> C
+| |
+v v
+D E
+```
+To find the right-to-left topological order:
+
+* Start with a vertex with no outgoing edges. In this case, you can start with vertex C.
+* Remove vertex C and its outgoing edge. The graph becomes:
+```java
+A -> B
+|
+v
+D E
+```
+Now, you can choose either B or E, both of which have no outgoing edges. Let's choose B and remove it:
+```java
+A
+|
+v
+D E
+```
+* Continue with the remaining vertices. Choose A next:
+```java
+|
+v
+D E
+```
+* Finally, remove D and E:
+```java
+|
+v
+| |
+```
+The order in which you removed the vertices is a right-to-left topological order: C, B, A, D, E.
+
+#### Pseudocode
+```java
+function topologicalSortRightToLeft(graph):
+ // Function to perform DFS and record nodes in the order they are finished
+ function dfs(node):
+ mark node as visited
+ for each neighbor in graph[node]:
+ if neighbor is not visited:
+ dfs(neighbor)
+ append node to order list
+
+ create an empty order list
+ initialize a visited array with False for all nodes
+
+ for each node in the graph:
+ if node is not visited:
+ dfs(node)
+
+ reverse the order list
+
+ return the reversed order list as the topological order (right-to-left)
+```
+
+#### Complexity
+**Time Complexity:** O(V+E)
+**Space Complexity:** O(V)
+
+---
+### Question
+Which of the following is correct topological order for this graph?
+
+ +
+**Choices**
+- [x] TD,TA,TC,TB
+- [ ] TA,TD,TC,TB
+- [ ] TC,TA,TD,TB
+
+---
+### Another approach to BFS
+
+
+Find the minimum number of edges to reach v starting from u in undirected simple graph.
+
+**Graph:**
+
+
+
+**Choices**
+- [x] TD,TA,TC,TB
+- [ ] TA,TD,TC,TB
+- [ ] TC,TA,TD,TB
+
+---
+### Another approach to BFS
+
+
+Find the minimum number of edges to reach v starting from u in undirected simple graph.
+
+**Graph:**
+
+) +
+
+#### Approach
+
+Imagine you're playing a game where you have to find the quickest way from point A (vertex u) to point B (vertex v) in a giant maze. This is similar to using Breadth-First Search (BFS) in a graph.
+
+**Think of BFS as your strategy for exploring the maze:**
+
+**Start at Point A:** You're at the entrance of the maze (vertex u), ready to find the shortest path to the treasure (vertex v).
+
+**Explore Closest Paths First:** Just like deciding which paths to take in the maze, BFS first checks all the paths that are one step away from your current position, then moves to paths two steps away, and so on.
+
+**Layer by Layer:** It's like a ripple effect in a pond. You throw a stone (start at vertex u), and the ripples (paths) expand outward, reaching further away points one layer at a time.
+
+**Reaching Point B:** As you follow this method, the moment you step on point B (vertex v) in the maze, you know you've found the shortest route. In BFS, when you first reach vertex v, it guarantees the minimum steps taken, just like finding the quickest path out of the maze.
+
+So, by using BFS in our maze game (or graph), we ensure we're taking the most efficient route possible, avoiding any long detours or dead-ends. It's a smart and systematic way to reach our goal with the least amount of hassle!
diff --git a/Academy DSA Typed Notes/Advanced/DSA Graphs 3 MST (Prims Algo.) & Dijkstra Algo.md b/Academy DSA Typed Notes/Advanced/DSA Graphs 3 MST (Prims Algo.) & Dijkstra Algo.md
new file mode 100644
index 0000000..090f695
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Graphs 3 MST (Prims Algo.) & Dijkstra Algo.md
@@ -0,0 +1,239 @@
+# Graphs 3: MST & Dijkstra
+
+---
+### Challenges in Flipkart's Logistics and Delivery
+
+
+**Scenario:**
+Suppose Flipkart has N local distribution centers spread across a large metropolitan city. These centers need to be interconnected for efficient movement of goods. However, building and maintaining roads between these centers is costly. Flipkart's goal is to minimize these costs while ensuring every center is connected and operational.
+
+**Goal:** You are given number of centers and possible connections that can be made with their cost. Find minimum cost of constructing roads between centers such that it is possible to travel from one center to any other via roads.
+
+
+
+**Explanation**
+
+**Example:**
+
+
+
+
+#### Approach
+
+Imagine you're playing a game where you have to find the quickest way from point A (vertex u) to point B (vertex v) in a giant maze. This is similar to using Breadth-First Search (BFS) in a graph.
+
+**Think of BFS as your strategy for exploring the maze:**
+
+**Start at Point A:** You're at the entrance of the maze (vertex u), ready to find the shortest path to the treasure (vertex v).
+
+**Explore Closest Paths First:** Just like deciding which paths to take in the maze, BFS first checks all the paths that are one step away from your current position, then moves to paths two steps away, and so on.
+
+**Layer by Layer:** It's like a ripple effect in a pond. You throw a stone (start at vertex u), and the ripples (paths) expand outward, reaching further away points one layer at a time.
+
+**Reaching Point B:** As you follow this method, the moment you step on point B (vertex v) in the maze, you know you've found the shortest route. In BFS, when you first reach vertex v, it guarantees the minimum steps taken, just like finding the quickest path out of the maze.
+
+So, by using BFS in our maze game (or graph), we ensure we're taking the most efficient route possible, avoiding any long detours or dead-ends. It's a smart and systematic way to reach our goal with the least amount of hassle!
diff --git a/Academy DSA Typed Notes/Advanced/DSA Graphs 3 MST (Prims Algo.) & Dijkstra Algo.md b/Academy DSA Typed Notes/Advanced/DSA Graphs 3 MST (Prims Algo.) & Dijkstra Algo.md
new file mode 100644
index 0000000..090f695
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Graphs 3 MST (Prims Algo.) & Dijkstra Algo.md
@@ -0,0 +1,239 @@
+# Graphs 3: MST & Dijkstra
+
+---
+### Challenges in Flipkart's Logistics and Delivery
+
+
+**Scenario:**
+Suppose Flipkart has N local distribution centers spread across a large metropolitan city. These centers need to be interconnected for efficient movement of goods. However, building and maintaining roads between these centers is costly. Flipkart's goal is to minimize these costs while ensuring every center is connected and operational.
+
+**Goal:** You are given number of centers and possible connections that can be made with their cost. Find minimum cost of constructing roads between centers such that it is possible to travel from one center to any other via roads.
+
+
+
+**Explanation**
+
+**Example:**
+
+ +
+
+
+**Output:**
+
+
+
+
+
+**Output:**
+
+ +
+
+### Idea:
+
+To achieve the lowest cost in our scenario, consider these key points:
+
+1. **Aim for Fewer roads:** Minimizing the number of roads directly leads to reduced costs.
+
+2. **Opt for a Tree Structure:** Why a tree? Well, in the world of data structures, a tree uniquely stands out when it comes to minimal connections. For any given N nodes, a tree is the only structure that connects all nodes with exactly N - 1 edges. This is precisely what we need - the bare minimum of edges to connect all points, ensuring the lowest possible number of roads.
+
+
+**Another Example:**
+
+
+
+
+### Idea:
+
+To achieve the lowest cost in our scenario, consider these key points:
+
+1. **Aim for Fewer roads:** Minimizing the number of roads directly leads to reduced costs.
+
+2. **Opt for a Tree Structure:** Why a tree? Well, in the world of data structures, a tree uniquely stands out when it comes to minimal connections. For any given N nodes, a tree is the only structure that connects all nodes with exactly N - 1 edges. This is precisely what we need - the bare minimum of edges to connect all points, ensuring the lowest possible number of roads.
+
+
+**Another Example:**
+
+ +
+The end goal is that all centers should be connected.
+
+**Possible Solutions -**
+
+
+
+The end goal is that all centers should be connected.
+
+**Possible Solutions -**
+
+ +
+Here first is better because the sum of all edge weights is minimum.
+
+The tree which spans (covers) all the vertices with the minimum number of edges needed to connect them is known as **Spanning Tree**.
+
+### Minimum Spanning Tree
+
+The minimum spanning tree has all the properties of a spanning tree with an added constraint of having the minimum possible weights among all possible spanning trees.
+
+**Uniqueness of MST:** If all edge weights are unique, there's only one MST. If some weights are the same, multiple MSTs can exist.
+
+**Algorithms for MST:** Kruskal's and Prim's algorithms are used to find MSTs. The MST found can vary based on the choices made for edges with equal weights. Both algorithms solve for same problem having same time and space complexities.
+
+
+### Solution to Flipkart's problem
+
+**Application of MST:**
+* **Identify All Possible Connections:** First, identify all the possible routes that can connect these N centers. Imagine this as a network where each center is a node, and each possible road between two centers is an edge.
+
+* **Assign Costs:** Assign a cost to each potential road, based on factors like distance, traffic, or construction expenses. In real-life terms, shorter and more straightforward routes would generally cost less.
+
+* **Create the MST:** Now, apply the MST algorithm (like Kruskal's or Prim's). The algorithm will select routes that connect all the centers with the least total cost, without forming any loops or cycles.
+
+* **Outcome:** The result is a network of roads connecting all centers with the shortest total length or the lowest cost.
+
+---
+## Prim's Algorithm
+
+
+Let's consider the below **Graph:**
+
+
+
+Here first is better because the sum of all edge weights is minimum.
+
+The tree which spans (covers) all the vertices with the minimum number of edges needed to connect them is known as **Spanning Tree**.
+
+### Minimum Spanning Tree
+
+The minimum spanning tree has all the properties of a spanning tree with an added constraint of having the minimum possible weights among all possible spanning trees.
+
+**Uniqueness of MST:** If all edge weights are unique, there's only one MST. If some weights are the same, multiple MSTs can exist.
+
+**Algorithms for MST:** Kruskal's and Prim's algorithms are used to find MSTs. The MST found can vary based on the choices made for edges with equal weights. Both algorithms solve for same problem having same time and space complexities.
+
+
+### Solution to Flipkart's problem
+
+**Application of MST:**
+* **Identify All Possible Connections:** First, identify all the possible routes that can connect these N centers. Imagine this as a network where each center is a node, and each possible road between two centers is an edge.
+
+* **Assign Costs:** Assign a cost to each potential road, based on factors like distance, traffic, or construction expenses. In real-life terms, shorter and more straightforward routes would generally cost less.
+
+* **Create the MST:** Now, apply the MST algorithm (like Kruskal's or Prim's). The algorithm will select routes that connect all the centers with the least total cost, without forming any loops or cycles.
+
+* **Outcome:** The result is a network of roads connecting all centers with the shortest total length or the lowest cost.
+
+---
+## Prim's Algorithm
+
+
+Let's consider the below **Graph:**
+
+ +
+Say we start with **vertex 5**, now we can choose an edge originating out of 5.
+
+
+
+Say we start with **vertex 5**, now we can choose an edge originating out of 5.
+
+ +
+*Which one should we choose?*
+The one with minimum weight.
+
+We choose 5 ---- 3 with weight 2
+
+
+
+*Which one should we choose?*
+The one with minimum weight.
+
+We choose 5 ---- 3 with weight 2
+
+ +
+Now, after this, since 5 and 3 are part of the MST, we shall choose a min weighted edge originated from either 3 or 5. That edge should connect to a vertex which hasn't been visited yet.
+
+
+
+Now, after this, since 5 and 3 are part of the MST, we shall choose a min weighted edge originated from either 3 or 5. That edge should connect to a vertex which hasn't been visited yet.
+
+ +
+We choose 5 ---- 4 with weight 3
+
+
+
+We choose 5 ---- 4 with weight 3
+
+ +
+Now, same process follows i.e, we can select a min weighted edge originating from 3, 4, or 5 such that it should connect to a vertex that hasn't been visited yet.
+
+
+**After completing the entire process, we shall have below MST.**
+
+
+
+Now, same process follows i.e, we can select a min weighted edge originating from 3, 4, or 5 such that it should connect to a vertex that hasn't been visited yet.
+
+
+**After completing the entire process, we shall have below MST.**
+
+ +
+
+### Execution
+
+Say we have a black box(we'll name it later)
+
+Now, say we start with 5. From 5, via weight 3 we can visit 4, via weight 5 we can visit 6, via weight 2 we can visit 3.
+
+We'll information as - (weight, vertex)
+
+
+
+
+### Execution
+
+Say we have a black box(we'll name it later)
+
+Now, say we start with 5. From 5, via weight 3 we can visit 4, via weight 5 we can visit 6, via weight 2 we can visit 3.
+
+We'll information as - (weight, vertex)
+
+ +
+From this, we'll get vertex reachable via min weight, which data structure can be helpful ?
+**MIN HEAPS**
+
+Now, we remove (2, 3) from heaps and connect 3 to 5.
+
+From 3, the nodes that are reachable will be pushed to the heap.
+*We'll insert only those vertices which haven't been visited yet.*
+
+
+
+From this, we'll get vertex reachable via min weight, which data structure can be helpful ?
+**MIN HEAPS**
+
+Now, we remove (2, 3) from heaps and connect 3 to 5.
+
+From 3, the nodes that are reachable will be pushed to the heap.
+*We'll insert only those vertices which haven't been visited yet.*
+
+ +
+Select the minimum weighted -> (3, 4)
+
+Now, this shall continue.
+
+
+#### Pseudocode
+
+```java
+while (!heap.isEmpty()) {
+
+ Pair p = heap.getMin();
+
+ if (vis[v] == true)
+ continue;
+
+ // Add the vertex to the MST and accumulate the weight
+ vis[v] = true;
+ ans += p.first
+
+ // Now, you can optionally iterate through the adjacent vertices of 'v' and update the heap with new edges
+ for ((u, w) in adj[v]) {
+
+ if (!vis[u]) {
+ // Add the unvisited neighbor edges to the heap
+ heap.add({w,u});
+ }
+ }
+}
+```
+
+#### Complexity
+**Time Complexity:** O(E * logE)
+**Space Complexity:** O(V + E)
+
+---
+## Dijkstra’s Algorithm
+
+
+There are N cities in a country, you are living in city-1. Find minimum distance to reach every other city from city-1.
+
+We need to return the answer in the form of array
+
+
+
+Select the minimum weighted -> (3, 4)
+
+Now, this shall continue.
+
+
+#### Pseudocode
+
+```java
+while (!heap.isEmpty()) {
+
+ Pair p = heap.getMin();
+
+ if (vis[v] == true)
+ continue;
+
+ // Add the vertex to the MST and accumulate the weight
+ vis[v] = true;
+ ans += p.first
+
+ // Now, you can optionally iterate through the adjacent vertices of 'v' and update the heap with new edges
+ for ((u, w) in adj[v]) {
+
+ if (!vis[u]) {
+ // Add the unvisited neighbor edges to the heap
+ heap.add({w,u});
+ }
+ }
+}
+```
+
+#### Complexity
+**Time Complexity:** O(E * logE)
+**Space Complexity:** O(V + E)
+
+---
+## Dijkstra’s Algorithm
+
+
+There are N cities in a country, you are living in city-1. Find minimum distance to reach every other city from city-1.
+
+We need to return the answer in the form of array
+
+) +
+**Output:**
+
+
+
+**Output:**
+
+ +
+
+**Initialize Data Structures:**
+
+* Create an adjacency list (graph) to represent the cities and their distances.
+* Initialize a distances list with infinity for all cities except city-1 (set to 0).
+* Use a `Heap
+
+
+**Initialize Data Structures:**
+
+* Create an adjacency list (graph) to represent the cities and their distances.
+* Initialize a distances list with infinity for all cities except city-1 (set to 0).
+* Use a `Heap +
+
+```java
+ while (!hp.isEmpty()) {
+ Pair rp = hp.poll(); // Extract the minimum element
+
+ int d = rp.first; // Distance
+ int u = rp.second; // City
+
+ // Skip if this distance is greater than the known distance
+ if (d > dist[u]) {
+ continue;
+ }
+
+ // Explore neighbors of u and update distances
+ for ( /* Loop through neighbors */ ) {
+ int v = /* Neighbor city */ ;
+ int w = /* Weight to reach v from u */ ;
+
+ // Calculate the new distance via u
+ int new_dist = dist[u] + w;
+
+ // If the new distance is shorter, update dist and add to heap
+ if (new_dist < dist[v]) {
+ dist[v] = new_dist;
+ hp.add(new Pair(new_dist, v));
+ }
+ }
+ }
+ }
+```
+
+* The time complexity of the Dijkstra's algorithm implementation with a min-heap of pairs is $O((E + V) * log(V))$, where E is the number of edges, V is the number of vertices (cities), and log(V) represents the complexity of heap operations.
+* The space complexity of this implementation is O(V + E), where V is the space used to store the dist array (minimum distances) for all cities, and E is the space used to represent the graph (adjacency list).
+
+### Can Dijkstra's algorithm work on negative wieghts?
+
+Dijkstra's algorithm is not suitable for graphs with negative edge weights as it assumes non-negative weights to guarantee correct results. Negative weights can lead to unexpected behavior and incorrect shortest path calculations.
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Greedy.md b/Academy DSA Typed Notes/Advanced/DSA Greedy.md
new file mode 100644
index 0000000..a8835d4
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Greedy.md
@@ -0,0 +1,841 @@
+# Advanced DSA: Greedy
+
+---
+## Introduction on Greedy
+
+The greedy approach deals with maximizing our profit and minimizing our loss.
+
+
+
+**Example 1:**
+Suppose we want to buy an iPhone, and the price of an iPhone at Amazon is 1.3 lakhs, the price at Paytm at 1.2 lakhs and the price at Flipkart is 1.25 lakhs.
+So we will buy an iPhone from Paytm as it has a minimum price.
+Here we are considering only one factor i.e. the amount of an iphone.
+
+**Example 2:**
+
+Suppose we want to switch a company and we have three offer letters. The first company is given a 22 LPA offer, the second company is given a 25 LPA, and the third company is given a 28 LPA offer.
+
+So we are going to select 28 LPA offer company. Here we are again considering the money factor, we are not considering the factors:
+- Job is remote
+- Work culture
+- Timings
+- Growth
+
+But if 25 LPA company has other facilities better than 28 LPA offer company. 25 LPA company has flexible working hours, provides remote job and good work culture. Then we are going to choose 25 LPA offer company.
+
+If we involve only one factor then selection will become easier and if multiple factors are involved then the decision becomes a bit difficult.
+
+In this lecture, we are going to do questions which involve multiple factors.
+
+
+---
+### Problem 1 Flipkart's Challenge in Effective Inventory Management
+
+In the recent expansion into grocery delivery, Flipkart faces a crucial challenge in effective inventory management. Each grocery item on the platform carries its own expiration date and profit margin, represented by arrays A[i] (expiration date for the ith item) and B[i] (profit margin for the ith item). To mitigate potential losses due to expiring items, Flipkart is seeking a strategic solution. The objective is to identify a method to strategically promote certain items, ensuring they are sold before their expiration date, thereby maximizing overall profit. Can you assist Flipkart in developing an innovative approach to optimize their grocery inventory and enhance profitability?
+
+
+**A[i] -> expiration time for ith item**
+**B[i] -> profit gained by ith item**
+
+Time starts with **T = 0**, and it takes 1 unit of time to sell one item and the item **can only be sold if T < A[i].**
+
+Sell items such that the sum of the **profit by items is maximized.**
+
+**Example**
+
+**`A[] = [3 1 3 2 3]`**
+**`B[] = [6 5 3 1 9]`**
+**`index: 0 1 2 3 4`**
+
+
+### Idea 1 - Pick the highest profit item first
+
+
+- We will first sell the item with the highest profit.
+
+Initially T = 0
+
+- We have the maximum profit item at index 4, so will sell it and increment T by 1.
+
+
+| T | Item Index | Profit |
+|:---:|:---------:|:------:|
+| 1 | 4 | 9 |
+
+- Now the item at index 1 can't be sold as A[1] <= T. So we can not sell it.
+
+
+- Now we will sell the item at 0 index.
+
+| T | Item Index | Profit |
+|:---:|:---------:|:------:|
+| 1 | 4 | 9 |
+| 2 | 0 | 6 |
+
+
+
+- Now the item at index 3 can't be sold as A[3] <= T. So we can not sell it.
+
+
+- Now we will sell the item at 2 index.
+
+| T | Item Index | Profit |
+|:---:|:---------:|:------:|
+| 1 | 4 | 9 |
+| 2 | 0 | 6 |
+| 3 | 2 | 3 |
+
+So we have a total profit: 18.
+
+:bulb: **`But we can have a better answer than this answer. Let us try one more combination of selling items.`**
+
+**`A[] = [3 1 3 2 3]`**
+**`B[] = [6 5 3 1 9]`**
+**`index: 0 1 2 3 4`**
+
+Initially T = 0
+
+- We have sold the item at index 1 and increment T by 1.
+
+
+| T | Item Index | Profit |
+|:---:|:---------:|:------:|
+| 1 | 1 | 5 |
+
+- Now we have sold the item at index 4 and again increment T by 1.
+
+
+| T | Item Index | Profit |
+|:---:|:---------:|:------:|
+| 1 | 1 | 5 |
+| 2 | 4 | 9 |
+
+- Now the item at index 3 can't be sold as A[3] <= T. So we can not sell it.
+
+
+- Now have sold the item at 0 index.
+
+| T | Item Index | Profit |
+|:---:|:---------:|:------:|
+| 1 | 1 | 5 |
+| 2 | 4 | 9 |
+| 3 | 0 | 6 |
+
+
+- Now the item at index 2 can't be sold as A[2] <= T. So we can not sell it
+
+So we have a total profit 20.
+
+Here we are getting the total profit greater than the total profit of the previously sold combination of items.
+
+And we can achieve maximum profit 20.
+
+**The greedy approach is selecting the path by greedy approach, in greedy we will select one path based on some conditions by assuming that this path will give us the solution.**
+
+
+
+
+---
+### Question
+
+What is the maximum profit we can achieve if we have two items with expiration time in A and profit in B:
+
+A = [1, 2]
+B = [3, 1500]
+
+**Choices**
+
+- [ ] 3
+- [ ] 1500
+- [x] 1503
+- [ ] 0
+
+
+
+**Explanation**
+
+A = [1, 2]
+B = [3, 1500]
+
+
+
+Initially T = 0
+
+- We have selected the item at index 9 and incremented T by 1.
+
+
+|T|Item Index|Profit|
+|-|-|-|
+|1|0|3|
+
+- Now we have selected the item at index 1 and again increment T by 1.
+
+
+|T|Item Index|Profit|
+|-|-|-|
+|1|0|3|
+|2|1|1500|
+
+So we have a total profit 1503.
+
+
+---
+
+
+### Solution - Effective Inventory Management
+
+- Pick the highest profit item first approach is not giving us the maximum profit, so it will not work. We have to think of another approach.
+
+#### Idea: Sell Everything
+
+Our approach is always towards selling all the items so that we can achieve maximum profit.
+ So our approach is to first sell the item with the minimum end time.
+
+ For this, we have to sort the expiration time in ascending order.
+
+**Example:**
+
+A[] = [1, 3, 3, 3, 5, 5, 5, 8]
+B[] = [5, 2, 7, 1, 4, 3, 8, 1]
+
+
+Initially T = 0
+
+- We can sell an item available at index 0, as A[0] = 1, and T < A[0]
+
+| T | Item Index | Profit |
+|:---:|:---------:|:------:|
+| 1 | 0 | 5 |
+
+- We can sell an item available at index 1, as A[1] = 3, and T < A[1]
+
+| T | Item Index | Profit |
+|:---:|:---------:|:------:|
+| 1 | 0 | 5 |
+| 2 | 1 | 2 |
+
+- We can sell a item available at index 2, as A[2] = 3, and T < A[2]
+
+
+| T | Item Index | Profit |
+|:---:|:---------:|:------:|
+| 1 | 0 | 5 |
+| 2 | 1 | 2 |
+| 3 | 2 | 7 |
+
+- But we can not sell the item available at index 3, as A[3] = 3, and A[3] <= T, here the profit of the item at index 3 is 1, so we ignore it easily as it has very little profit.
+
+- We can sell a item available at index 4, as A[4] = 5, and T < A[4].
+
+
+| T | Item Index | Profit |
+|:---:|:---------:|:------:|
+| 1 | 0 | 5 |
+| 2 | 1 | 2 |
+| 3 | 2 | 7 |
+| 4 | 4 | 4 |
+
+- We can sell a item available at index 5, as A[5] = 5, and T < A[5].
+
+
+| T | Item Index | Profit |
+|:---:|:---------:|:------:|
+| 1 | 0 | 5 |
+| 2 | 1 | 2 |
+| 3 | 2 | 7 |
+| 4 | 4 | 4 |
+| 5 | 5 | 3 |
+
+- But we can not sell the item available at index 6, as A[6] = 5, and A[6] <= T. But we can say that we must have to select this item to get the maximum profit as it has the larger profit. But we are rejecting it.
+- To select the item available at index 6, we have to remove one of the previously selected items.
+- So we want to discard the item with the minimum profit among all the selected items.
+
+
+| T | Item Index | Profit |
+|:-----:|:---------:|:------:|
+| 1 | 0 | 5 |
+| ~~2~~ | ~~1~~ | ~~2~~ |
+| 3 | 2 | 7 |
+| 4 | 4 | 4 |
+| 5 | 5 | 3 |
+| 5 | 6 | 8 |
+
+
+
+- We can sell item available at index 7, as A[7] = 8, and T < A[7].
+
+
+|T|Item Index|Profit|
+|-|-|-|
+|1|0|5|
+|~~2~~|~~1~~|~~2~~|
+|3|2|7|
+|4|4|4|
+|5|5|3|
+|5|6|8|
+|6|7|1|
+
+
+So we have a total profit 28.
+
+
+**`At any point, if we weren't able to choose a item as T >= A[i] and realize we made a wrong choice before, we will get rid of the item with least profit we previously picked and choose the current one instead.`**
+
+
+#### Approach
+
+The solution to this question is just like the team selection. We have to select the strongest player, if we have any player who is stronger than the player in our team, then we will remove the weaker player from the team and add that player to our team.
+
+
+**Example**: Solving using min-heap
+
+| | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
+| -- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- |
+|A[ ]| 1 | 3 | 3 | 3 | 5 | 5 | 5 | 8 |
+|B[ ]| 5 | 2 | 7 | 1 | 4 | 3 | 8 | 1 |
+
+
+**Solution**
+
+Initially **T = 0** and we have a empty min-heap.
+
+
+
+
+```java
+ while (!hp.isEmpty()) {
+ Pair rp = hp.poll(); // Extract the minimum element
+
+ int d = rp.first; // Distance
+ int u = rp.second; // City
+
+ // Skip if this distance is greater than the known distance
+ if (d > dist[u]) {
+ continue;
+ }
+
+ // Explore neighbors of u and update distances
+ for ( /* Loop through neighbors */ ) {
+ int v = /* Neighbor city */ ;
+ int w = /* Weight to reach v from u */ ;
+
+ // Calculate the new distance via u
+ int new_dist = dist[u] + w;
+
+ // If the new distance is shorter, update dist and add to heap
+ if (new_dist < dist[v]) {
+ dist[v] = new_dist;
+ hp.add(new Pair(new_dist, v));
+ }
+ }
+ }
+ }
+```
+
+* The time complexity of the Dijkstra's algorithm implementation with a min-heap of pairs is $O((E + V) * log(V))$, where E is the number of edges, V is the number of vertices (cities), and log(V) represents the complexity of heap operations.
+* The space complexity of this implementation is O(V + E), where V is the space used to store the dist array (minimum distances) for all cities, and E is the space used to represent the graph (adjacency list).
+
+### Can Dijkstra's algorithm work on negative wieghts?
+
+Dijkstra's algorithm is not suitable for graphs with negative edge weights as it assumes non-negative weights to guarantee correct results. Negative weights can lead to unexpected behavior and incorrect shortest path calculations.
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Greedy.md b/Academy DSA Typed Notes/Advanced/DSA Greedy.md
new file mode 100644
index 0000000..a8835d4
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Greedy.md
@@ -0,0 +1,841 @@
+# Advanced DSA: Greedy
+
+---
+## Introduction on Greedy
+
+The greedy approach deals with maximizing our profit and minimizing our loss.
+
+
+
+**Example 1:**
+Suppose we want to buy an iPhone, and the price of an iPhone at Amazon is 1.3 lakhs, the price at Paytm at 1.2 lakhs and the price at Flipkart is 1.25 lakhs.
+So we will buy an iPhone from Paytm as it has a minimum price.
+Here we are considering only one factor i.e. the amount of an iphone.
+
+**Example 2:**
+
+Suppose we want to switch a company and we have three offer letters. The first company is given a 22 LPA offer, the second company is given a 25 LPA, and the third company is given a 28 LPA offer.
+
+So we are going to select 28 LPA offer company. Here we are again considering the money factor, we are not considering the factors:
+- Job is remote
+- Work culture
+- Timings
+- Growth
+
+But if 25 LPA company has other facilities better than 28 LPA offer company. 25 LPA company has flexible working hours, provides remote job and good work culture. Then we are going to choose 25 LPA offer company.
+
+If we involve only one factor then selection will become easier and if multiple factors are involved then the decision becomes a bit difficult.
+
+In this lecture, we are going to do questions which involve multiple factors.
+
+
+---
+### Problem 1 Flipkart's Challenge in Effective Inventory Management
+
+In the recent expansion into grocery delivery, Flipkart faces a crucial challenge in effective inventory management. Each grocery item on the platform carries its own expiration date and profit margin, represented by arrays A[i] (expiration date for the ith item) and B[i] (profit margin for the ith item). To mitigate potential losses due to expiring items, Flipkart is seeking a strategic solution. The objective is to identify a method to strategically promote certain items, ensuring they are sold before their expiration date, thereby maximizing overall profit. Can you assist Flipkart in developing an innovative approach to optimize their grocery inventory and enhance profitability?
+
+
+**A[i] -> expiration time for ith item**
+**B[i] -> profit gained by ith item**
+
+Time starts with **T = 0**, and it takes 1 unit of time to sell one item and the item **can only be sold if T < A[i].**
+
+Sell items such that the sum of the **profit by items is maximized.**
+
+**Example**
+
+**`A[] = [3 1 3 2 3]`**
+**`B[] = [6 5 3 1 9]`**
+**`index: 0 1 2 3 4`**
+
+
+### Idea 1 - Pick the highest profit item first
+
+
+- We will first sell the item with the highest profit.
+
+Initially T = 0
+
+- We have the maximum profit item at index 4, so will sell it and increment T by 1.
+
+
+| T | Item Index | Profit |
+|:---:|:---------:|:------:|
+| 1 | 4 | 9 |
+
+- Now the item at index 1 can't be sold as A[1] <= T. So we can not sell it.
+
+
+- Now we will sell the item at 0 index.
+
+| T | Item Index | Profit |
+|:---:|:---------:|:------:|
+| 1 | 4 | 9 |
+| 2 | 0 | 6 |
+
+
+
+- Now the item at index 3 can't be sold as A[3] <= T. So we can not sell it.
+
+
+- Now we will sell the item at 2 index.
+
+| T | Item Index | Profit |
+|:---:|:---------:|:------:|
+| 1 | 4 | 9 |
+| 2 | 0 | 6 |
+| 3 | 2 | 3 |
+
+So we have a total profit: 18.
+
+:bulb: **`But we can have a better answer than this answer. Let us try one more combination of selling items.`**
+
+**`A[] = [3 1 3 2 3]`**
+**`B[] = [6 5 3 1 9]`**
+**`index: 0 1 2 3 4`**
+
+Initially T = 0
+
+- We have sold the item at index 1 and increment T by 1.
+
+
+| T | Item Index | Profit |
+|:---:|:---------:|:------:|
+| 1 | 1 | 5 |
+
+- Now we have sold the item at index 4 and again increment T by 1.
+
+
+| T | Item Index | Profit |
+|:---:|:---------:|:------:|
+| 1 | 1 | 5 |
+| 2 | 4 | 9 |
+
+- Now the item at index 3 can't be sold as A[3] <= T. So we can not sell it.
+
+
+- Now have sold the item at 0 index.
+
+| T | Item Index | Profit |
+|:---:|:---------:|:------:|
+| 1 | 1 | 5 |
+| 2 | 4 | 9 |
+| 3 | 0 | 6 |
+
+
+- Now the item at index 2 can't be sold as A[2] <= T. So we can not sell it
+
+So we have a total profit 20.
+
+Here we are getting the total profit greater than the total profit of the previously sold combination of items.
+
+And we can achieve maximum profit 20.
+
+**The greedy approach is selecting the path by greedy approach, in greedy we will select one path based on some conditions by assuming that this path will give us the solution.**
+
+
+
+
+---
+### Question
+
+What is the maximum profit we can achieve if we have two items with expiration time in A and profit in B:
+
+A = [1, 2]
+B = [3, 1500]
+
+**Choices**
+
+- [ ] 3
+- [ ] 1500
+- [x] 1503
+- [ ] 0
+
+
+
+**Explanation**
+
+A = [1, 2]
+B = [3, 1500]
+
+
+
+Initially T = 0
+
+- We have selected the item at index 9 and incremented T by 1.
+
+
+|T|Item Index|Profit|
+|-|-|-|
+|1|0|3|
+
+- Now we have selected the item at index 1 and again increment T by 1.
+
+
+|T|Item Index|Profit|
+|-|-|-|
+|1|0|3|
+|2|1|1500|
+
+So we have a total profit 1503.
+
+
+---
+
+
+### Solution - Effective Inventory Management
+
+- Pick the highest profit item first approach is not giving us the maximum profit, so it will not work. We have to think of another approach.
+
+#### Idea: Sell Everything
+
+Our approach is always towards selling all the items so that we can achieve maximum profit.
+ So our approach is to first sell the item with the minimum end time.
+
+ For this, we have to sort the expiration time in ascending order.
+
+**Example:**
+
+A[] = [1, 3, 3, 3, 5, 5, 5, 8]
+B[] = [5, 2, 7, 1, 4, 3, 8, 1]
+
+
+Initially T = 0
+
+- We can sell an item available at index 0, as A[0] = 1, and T < A[0]
+
+| T | Item Index | Profit |
+|:---:|:---------:|:------:|
+| 1 | 0 | 5 |
+
+- We can sell an item available at index 1, as A[1] = 3, and T < A[1]
+
+| T | Item Index | Profit |
+|:---:|:---------:|:------:|
+| 1 | 0 | 5 |
+| 2 | 1 | 2 |
+
+- We can sell a item available at index 2, as A[2] = 3, and T < A[2]
+
+
+| T | Item Index | Profit |
+|:---:|:---------:|:------:|
+| 1 | 0 | 5 |
+| 2 | 1 | 2 |
+| 3 | 2 | 7 |
+
+- But we can not sell the item available at index 3, as A[3] = 3, and A[3] <= T, here the profit of the item at index 3 is 1, so we ignore it easily as it has very little profit.
+
+- We can sell a item available at index 4, as A[4] = 5, and T < A[4].
+
+
+| T | Item Index | Profit |
+|:---:|:---------:|:------:|
+| 1 | 0 | 5 |
+| 2 | 1 | 2 |
+| 3 | 2 | 7 |
+| 4 | 4 | 4 |
+
+- We can sell a item available at index 5, as A[5] = 5, and T < A[5].
+
+
+| T | Item Index | Profit |
+|:---:|:---------:|:------:|
+| 1 | 0 | 5 |
+| 2 | 1 | 2 |
+| 3 | 2 | 7 |
+| 4 | 4 | 4 |
+| 5 | 5 | 3 |
+
+- But we can not sell the item available at index 6, as A[6] = 5, and A[6] <= T. But we can say that we must have to select this item to get the maximum profit as it has the larger profit. But we are rejecting it.
+- To select the item available at index 6, we have to remove one of the previously selected items.
+- So we want to discard the item with the minimum profit among all the selected items.
+
+
+| T | Item Index | Profit |
+|:-----:|:---------:|:------:|
+| 1 | 0 | 5 |
+| ~~2~~ | ~~1~~ | ~~2~~ |
+| 3 | 2 | 7 |
+| 4 | 4 | 4 |
+| 5 | 5 | 3 |
+| 5 | 6 | 8 |
+
+
+
+- We can sell item available at index 7, as A[7] = 8, and T < A[7].
+
+
+|T|Item Index|Profit|
+|-|-|-|
+|1|0|5|
+|~~2~~|~~1~~|~~2~~|
+|3|2|7|
+|4|4|4|
+|5|5|3|
+|5|6|8|
+|6|7|1|
+
+
+So we have a total profit 28.
+
+
+**`At any point, if we weren't able to choose a item as T >= A[i] and realize we made a wrong choice before, we will get rid of the item with least profit we previously picked and choose the current one instead.`**
+
+
+#### Approach
+
+The solution to this question is just like the team selection. We have to select the strongest player, if we have any player who is stronger than the player in our team, then we will remove the weaker player from the team and add that player to our team.
+
+
+**Example**: Solving using min-heap
+
+| | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
+| -- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- |
+|A[ ]| 1 | 3 | 3 | 3 | 5 | 5 | 5 | 8 |
+|B[ ]| 5 | 2 | 7 | 1 | 4 | 3 | 8 | 1 |
+
+
+**Solution**
+
+Initially **T = 0** and we have a empty min-heap.
+
+ +
+All the items are sorted in the ascending order of expiration time.
+
+- We can sell a item available at index 0, as A[0] = 1, so here T < A[0], so we will sell the item available at index 0 and add its profit in min-heap.
+
+**T = 1**
+
+
+
+All the items are sorted in the ascending order of expiration time.
+
+- We can sell a item available at index 0, as A[0] = 1, so here T < A[0], so we will sell the item available at index 0 and add its profit in min-heap.
+
+**T = 1**
+
+ +
+- We can sell a item available at index 1, as A[1] = 3, so here T < A[1], so we will sell the item available at index 1 and add its profit in min-heap.
+
+**T = 2**
+
+
+
+- We can sell a item available at index 1, as A[1] = 3, so here T < A[1], so we will sell the item available at index 1 and add its profit in min-heap.
+
+**T = 2**
+
+ +
+- We can sell a item available at index 2, as A[2] = 3, so here T < A[2], so we will sell the item available at index 2 and add its profit in min-heap.
+
+**T = 3**
+
+
+
+
+- We can sell a item available at index 2, as A[2] = 3, so here T < A[2], so we will sell the item available at index 2 and add its profit in min-heap.
+
+**T = 3**
+
+
+ +
+- But we can not sell the item available at index 3, as A[3] = 3, and A[3] <= T. Now we will check if we have taken any incorrect steps in the past.
+- We check if we have any items in the heap with profit less than 1. So we have 2 minimum profit in the heap but 2 > 1, so it proves all our past decisions are correct. So we will skip the item available at index 3.
+
+
+- We can sell a item available at index 4, as A[4] = 5, and T < A[4] and add its profit in min-heap.
+
+**T = 4**
+
+
+
+- But we can not sell the item available at index 3, as A[3] = 3, and A[3] <= T. Now we will check if we have taken any incorrect steps in the past.
+- We check if we have any items in the heap with profit less than 1. So we have 2 minimum profit in the heap but 2 > 1, so it proves all our past decisions are correct. So we will skip the item available at index 3.
+
+
+- We can sell a item available at index 4, as A[4] = 5, and T < A[4] and add its profit in min-heap.
+
+**T = 4**
+
+ +
+- We can sell a item available at index 5, as A[5] = 5, so here T < A[5] and add its profit in min-heap.
+
+
+**T = 5**
+
+
+
+- We can sell a item available at index 5, as A[5] = 5, so here T < A[5] and add its profit in min-heap.
+
+
+**T = 5**
+
+ +
+- But we can not sell the item available at index 6, as A[6] = 5, and A[6] <= T. Now we will check if we have made any incorrect decisions in the past.
+- We have minimum profit 2 in the heap, so remove it from the heap and add the profit of the item available at index 6 in the heap.
+
+**T = 5**
+
+
+
+- But we can not sell the item available at index 6, as A[6] = 5, and A[6] <= T. Now we will check if we have made any incorrect decisions in the past.
+- We have minimum profit 2 in the heap, so remove it from the heap and add the profit of the item available at index 6 in the heap.
+
+**T = 5**
+
+ +
+
+- We can sell a item available at index 7, as A[7] = 8, so here T < A[7], so we will sell the item available at index 7 and add its profit in min-heap.
+
+
+**T = 6**
+
+
+
+
+- We can sell a item available at index 7, as A[7] = 8, so here T < A[7], so we will sell the item available at index 7 and add its profit in min-heap.
+
+
+**T = 6**
+
+ +
+- Now we can find the answer by removing one-by-one elements from the heap and adding them to the answer.
+
+So we have final answer = $1 + 3 + 4 + 5 + 7 + 8 = 28$
+
+
+#### PseudoCode
+```cpp
+1. Sort them in increasing order of time.
+2. Minheap heap:
+ T = 0
+for (i = 0; i < N; i++) {
+ if (T < A[i]) {
+ heap.insert(B[i])
+ T++
+ } else {
+ if (B[i] <= root of heap) -> ignore {
+
+ }
+ else {
+ extractMin()
+ heap.insert(B[i])
+ }
+ }
+}
+3. Remove all elements from the heap and add them to get the answer.
+```
+
+---
+### Question
+
+What is the time and space complexity of this question?
+
+**Choices**
+
+- [ ] TC: O(N), SC: O(N)
+- [x] TC: O(NlogN), SC: O(N)
+- [ ] TC: O(N$^2$), SC: O(N)
+- [ ] TC: O(N$^2$) , SC: O(N$^2$)
+
+
+---
+### Effective Inventory Management Complexity
+
+**Time Complexity**
+
+```cpp
+1. Sort them in increasing order of time.-- -> NlogN
+2. Minheap heap:
+ T = 0
+for (i = 0; i < N; i++) {
+ -- -> N
+ if (T < A[i]) {
+ heap.insert(B[i]) -- -> logN
+ T++
+ } else {
+ if (B[i] <= root of heap) -> ignore {
+
+ }
+ else {
+ extractMin() -- -> logN
+ heap.insert(B[i]) -- -> logN
+ }
+ }
+}
+3. Remove all elements from the heap and add them to get the answer.
+```
+
+So overall time complexity = O(NlogN) + O(NlogN)
+
+- **Time Complexity: O(NlogN)**
+- **Space Complexity: O(N)**
+
+
+---
+### Problem 2 Candy Distribution
+
+There are N students with their marks. The teacher has to give them candies such that
+a) Every student should have at least one candy
+b) Students with more marks than any of his/her neighbours have more candies than them.
+
+Find minimum candies to distribute.
+
+
+**Example**
+**Input:** [1, 5, 2, 1]
+**Explanation:** First we will give 1 candy to all students.
+|index|0|1|2|3|
+|-|-|-|-|-|
+|marks|1|5|2|1|
+|candy|1|1|1|1|
+
+Index 1 student has marks greater than their neighbours. So it must have candies greater than his neighbors.
+
+|index|0|1|2|3|
+|-|-|-|-|-|
+|marks|1|5|2|1|
+|candy|1|~~1~~ 2 |1|1|
+
+Index 2 student has marks greater than its right neighbour. So it must have candies greater than his right neighbour.
+
+|index|0|1|2|3|
+|-|-|-|-|-|
+|marks|1|5|2|1|
+|candy|1|~~1~~ 2 |~~1~~ 2 |1|
+
+Now index 1 student again has marks greater than both neighbors but its candies are not greater than its right neighbor's candies. So it must have candies greater than his both neighbors.
+
+|index|0|1|2|3|
+|-|-|-|-|-|
+|marks|1|5|2|1|
+|candy|1|~~1~~ ~~2~~ 3 |~~1~~ 2 |1|
+
+Now all the conditions of the question are satisfied, so total 7 candies are required to be distributed among students.
+
+**Output:** 7
+
+
+---
+### Question
+
+What is the minimum number of candies teacher has to use if the marks are: [4, 4, 4, 4, 4]
+
+**Choices**
+
+- [ ] 1
+- [x] 5
+- [ ] 10
+- [ ] 20
+
+
+**Explanation**
+
+[4, 4, 4, 4, 4]
+
+First, we will give 1 candy to all students.
+|index|0|1|2|3|4|
+|-|-|-|-|-|-|
+|marks|4|4|4|4|4|
+|candy|1|1|1|1|1|
+
+Now any student does not have marks greater than its neighbors. So our candy distribution is perfect.
+
+**So total 5 candies are required.**
+
+
+
+---
+### Candy Distribution Example
+
+**Example**
+
+**Input:** [8, 10, 6, 2]
+
+
+
+First, we will give 1 candy to all students.
+|index|0|1|2|3|
+|-|-|-|-|-|
+|marks|8|10|6|2|
+|candy|1|1|1|1|
+
+- Now student at index 2 has marks greater than its right neighbor, so it receive 2 candies.
+
+|index|0|1|2|3|
+|-|-|-|-|-|
+|marks|8|10|6|2|
+|candy|1|1|~~1~~ 2|1|
+
+- Student at index 1 has marks greater than both neighbours, so it must candies greater than both neighbours. So it receives 3 candies.
+
+|index|0|1|2|3|
+|-|-|-|-|-|
+|marks|8|10|6|2|
+|candy|1|~~1~~ 3|~~1~~ 2|1|
+
+So total 7 candies are required.
+
+**Output:** 7
+
+
+---
+### Question
+
+What is the minimum number of candies the teacher has to use if the marks are: [1, 6, 3, 1, 10, 12, 20, 5, 2]
+
+**Choices**
+
+- [ ] 15
+- [x] 19
+- [ ] 21
+- [ ] 20
+
+
+**Explanation**
+
+[1, 6, 3, 1, 10, 12, 20, 5, 2]
+
+First, we will give 1 candy to all students.
+| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
+|:-----:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|
+| marks | 1 | 6 | 3 | 1 | 10 | 12 | 20 | 5 | 2 |
+| candy | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
+
+First, let us consider the left nighbor of all the indexes.
+
+- Now a student at index 1 has marks greater than its left neighbour, so it should receive at least 2 candies.
+
+| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
+|:-----:| --- | ------- | --- | --- | --- | --- | --- | --- | --- |
+| marks | 1 | 6 | 3 | 1 | 10 | 12 | 20 | 5 | 2 |
+| candy | 1 | ~~1~~ 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
+
+- Now student at index 2, and 3 does not have marks greater than their left neighbour.
+
+- Student at index 4 has marks greater than its left neighbour, so it should receive at least 2 candies.
+
+| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
+|:-----:| --- | ------- | --- | --- | ------- | --- | --- | --- | --- |
+| marks | 1 | 6 | 3 | 1 | 10 | 12 | 20 | 5 | 2 |
+| candy | 1 | ~~1~~ 2 | 1 | 1 | ~~1~~ 2 | 1 | 1 | 1 | 1 |
+
+- Student at index 5 has marks greater than its left neighbour, so it should receive at least 3 candies.
+
+| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
+|:-----:| --- | ------- | --- | --- | ------- | ------- | --- | --- | --- |
+| marks | 1 | 6 | 3 | 1 | 10 | 12 | 20 | 5 | 2 |
+| candy | 1 | ~~1~~ 2 | 1 | 1 | ~~1~~ 2 | ~~1~~ 3 | 1 | 1 | 1 |
+
+- Student at index 6 has marks greater than its left neighbour, so it should receive at least 4 candies.
+
+| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
+|:-----:| --- | ------- | --- | --- | ------- | ------- | ------- | --- | --- |
+| marks | 1 | 6 | 3 | 1 | 10 | 12 | 20 | 5 | 2 |
+| candy | 1 | ~~1~~ 2 | 1 | 1 | ~~1~~ 2 | ~~1~~ 3 | ~~1~~ 4 | 1 | 1 |
+
+- Student at index 7 and index 8 does not have marks greater than their left neighbour.
+
+Now let us consider the right neighbour.
+
+
+- Student at index 7 has marks greater than its right neighbour, so it should receive at least 2 candies.
+
+| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
+|:-----:| --- | ------- | --- | --- | ------- | ------- | ------- | ------- | --- |
+| marks | 1 | 6 | 3 | 1 | 10 | 12 | 20 | 5 | 2 |
+| candy | 1 | ~~1~~ 2 | 1 | 1 | ~~1~~ 2 | ~~1~~ 3 | ~~1~~ 4 | ~~1~~ 2 | 1 |
+
+- Student at index 6 has marks greater than its right neighbour, so it should receive at least 3 candies but it has 4 candies already which is greater than its right neighbour candies, so it is fine.
+
+- Student at index 5, 4 and 3 do not have marks greater than their right neighbour.
+
+- Student at index 2 has marks greater than its right neighbour. So it receives at least 2 candies.
+
+
+|index|0|1|2|3|4|5|6|7|8|
+|-|-|-|-|-|-|-|-|-|-|
+|marks|1|6|3|1|10|12|20|5|2|
+|candy|1|~~1~~ 2|~~1~~ 2|1|~~1~~ 2|~~1~~ 3|~~1~~ 4|~~1~~ 2|1|
+
+- Student at index 1 has marks greater than its right neighbour. So it receives at least 3 candies.
+
+| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
+|:-----:| --- | ------------- | ------- | --- | ------- | ------- | ------- | ------- | --- |
+| marks | 1 | 6 | 3 | 1 | 10 | 12 | 20 | 5 | 2 |
+| candy | 1 | ~~1~~ ~~2~~ 3 | ~~1~~ 2 | 1 | ~~1~~ 2 | ~~1~~ 3 | ~~1~~ 4 | ~~1~~ 2 | 1 |
+
+- Student at index 0 does not have marks greater than its right neighbour.
+
+So a total 19 candies are required.
+
+**Output:** 19
+
+
+---
+
+### Candy Distribution - Solution
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+**Step 1:** Assign 1 candy to all the students.
+**Step 2:** For all the values of i, consider its left neighbour, if(A[i] > A[i - 1]) then C[i] > C[i - 1], means candy of ith index should be greater than (i-1)th index candy, so we will follow the greedy approach as we want to distribute a minimum number of candies, so we do `C[i] = C[i - 1] + 1`
+
+```cpp
+if(A[i] > A[i - 1]){
+ C[i] = C[i - 1] + 1
+}
+```
+
+**Step 3:** For all the values of i, consider its right neighbour, if(A[i] > A[i+1]) then C[i] > C[i + 1], means candy of ith index should be greater than (i+1)th index candy, so first we check it has candies greater than his right neighbour or not if not then we will follow the greedy approach as we want to distribute a minimum number of candies, then we do `C[i] = C[i + 1] + 1`
+
+```cpp
+if(A[i] > A[i + 1]){
+ if(C[i] < C[i + 1] + 1)
+ C[i] = C[i + 1] + 1
+}
+```
+
+#### PsuedoCode
+```cpp
+int C[N];
+for all i, C[i] = 1
+for (i = 1; i < N; i++) {
+ if (arr[i] > arr[i - 1]) {
+ C[i] = C[i - 1] + 1
+ }
+}
+for (i = N - 2; i >= 0; i--) {
+ if (arr[i] > arr[i + 1] && C[i] < C[i + 1] + 1) {
+ C[i] = C[i + 1] + 1
+ }
+}
+
+ans = sum of all values in C[]
+```
+#### Complexity
+
+- **Time Complexity:** O(N)
+- **Space Complexity:** O(N)
+
+
+---
+### Problem 3 Maximum jobs
+
+
+Given N jobs with their start and end times. Find the maximum number of jobs that can be completed if only one job can be done at a time.
+
+**Example**
+
+
+
+- Now we can find the answer by removing one-by-one elements from the heap and adding them to the answer.
+
+So we have final answer = $1 + 3 + 4 + 5 + 7 + 8 = 28$
+
+
+#### PseudoCode
+```cpp
+1. Sort them in increasing order of time.
+2. Minheap heap:
+ T = 0
+for (i = 0; i < N; i++) {
+ if (T < A[i]) {
+ heap.insert(B[i])
+ T++
+ } else {
+ if (B[i] <= root of heap) -> ignore {
+
+ }
+ else {
+ extractMin()
+ heap.insert(B[i])
+ }
+ }
+}
+3. Remove all elements from the heap and add them to get the answer.
+```
+
+---
+### Question
+
+What is the time and space complexity of this question?
+
+**Choices**
+
+- [ ] TC: O(N), SC: O(N)
+- [x] TC: O(NlogN), SC: O(N)
+- [ ] TC: O(N$^2$), SC: O(N)
+- [ ] TC: O(N$^2$) , SC: O(N$^2$)
+
+
+---
+### Effective Inventory Management Complexity
+
+**Time Complexity**
+
+```cpp
+1. Sort them in increasing order of time.-- -> NlogN
+2. Minheap heap:
+ T = 0
+for (i = 0; i < N; i++) {
+ -- -> N
+ if (T < A[i]) {
+ heap.insert(B[i]) -- -> logN
+ T++
+ } else {
+ if (B[i] <= root of heap) -> ignore {
+
+ }
+ else {
+ extractMin() -- -> logN
+ heap.insert(B[i]) -- -> logN
+ }
+ }
+}
+3. Remove all elements from the heap and add them to get the answer.
+```
+
+So overall time complexity = O(NlogN) + O(NlogN)
+
+- **Time Complexity: O(NlogN)**
+- **Space Complexity: O(N)**
+
+
+---
+### Problem 2 Candy Distribution
+
+There are N students with their marks. The teacher has to give them candies such that
+a) Every student should have at least one candy
+b) Students with more marks than any of his/her neighbours have more candies than them.
+
+Find minimum candies to distribute.
+
+
+**Example**
+**Input:** [1, 5, 2, 1]
+**Explanation:** First we will give 1 candy to all students.
+|index|0|1|2|3|
+|-|-|-|-|-|
+|marks|1|5|2|1|
+|candy|1|1|1|1|
+
+Index 1 student has marks greater than their neighbours. So it must have candies greater than his neighbors.
+
+|index|0|1|2|3|
+|-|-|-|-|-|
+|marks|1|5|2|1|
+|candy|1|~~1~~ 2 |1|1|
+
+Index 2 student has marks greater than its right neighbour. So it must have candies greater than his right neighbour.
+
+|index|0|1|2|3|
+|-|-|-|-|-|
+|marks|1|5|2|1|
+|candy|1|~~1~~ 2 |~~1~~ 2 |1|
+
+Now index 1 student again has marks greater than both neighbors but its candies are not greater than its right neighbor's candies. So it must have candies greater than his both neighbors.
+
+|index|0|1|2|3|
+|-|-|-|-|-|
+|marks|1|5|2|1|
+|candy|1|~~1~~ ~~2~~ 3 |~~1~~ 2 |1|
+
+Now all the conditions of the question are satisfied, so total 7 candies are required to be distributed among students.
+
+**Output:** 7
+
+
+---
+### Question
+
+What is the minimum number of candies teacher has to use if the marks are: [4, 4, 4, 4, 4]
+
+**Choices**
+
+- [ ] 1
+- [x] 5
+- [ ] 10
+- [ ] 20
+
+
+**Explanation**
+
+[4, 4, 4, 4, 4]
+
+First, we will give 1 candy to all students.
+|index|0|1|2|3|4|
+|-|-|-|-|-|-|
+|marks|4|4|4|4|4|
+|candy|1|1|1|1|1|
+
+Now any student does not have marks greater than its neighbors. So our candy distribution is perfect.
+
+**So total 5 candies are required.**
+
+
+
+---
+### Candy Distribution Example
+
+**Example**
+
+**Input:** [8, 10, 6, 2]
+
+
+
+First, we will give 1 candy to all students.
+|index|0|1|2|3|
+|-|-|-|-|-|
+|marks|8|10|6|2|
+|candy|1|1|1|1|
+
+- Now student at index 2 has marks greater than its right neighbor, so it receive 2 candies.
+
+|index|0|1|2|3|
+|-|-|-|-|-|
+|marks|8|10|6|2|
+|candy|1|1|~~1~~ 2|1|
+
+- Student at index 1 has marks greater than both neighbours, so it must candies greater than both neighbours. So it receives 3 candies.
+
+|index|0|1|2|3|
+|-|-|-|-|-|
+|marks|8|10|6|2|
+|candy|1|~~1~~ 3|~~1~~ 2|1|
+
+So total 7 candies are required.
+
+**Output:** 7
+
+
+---
+### Question
+
+What is the minimum number of candies the teacher has to use if the marks are: [1, 6, 3, 1, 10, 12, 20, 5, 2]
+
+**Choices**
+
+- [ ] 15
+- [x] 19
+- [ ] 21
+- [ ] 20
+
+
+**Explanation**
+
+[1, 6, 3, 1, 10, 12, 20, 5, 2]
+
+First, we will give 1 candy to all students.
+| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
+|:-----:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|
+| marks | 1 | 6 | 3 | 1 | 10 | 12 | 20 | 5 | 2 |
+| candy | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
+
+First, let us consider the left nighbor of all the indexes.
+
+- Now a student at index 1 has marks greater than its left neighbour, so it should receive at least 2 candies.
+
+| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
+|:-----:| --- | ------- | --- | --- | --- | --- | --- | --- | --- |
+| marks | 1 | 6 | 3 | 1 | 10 | 12 | 20 | 5 | 2 |
+| candy | 1 | ~~1~~ 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
+
+- Now student at index 2, and 3 does not have marks greater than their left neighbour.
+
+- Student at index 4 has marks greater than its left neighbour, so it should receive at least 2 candies.
+
+| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
+|:-----:| --- | ------- | --- | --- | ------- | --- | --- | --- | --- |
+| marks | 1 | 6 | 3 | 1 | 10 | 12 | 20 | 5 | 2 |
+| candy | 1 | ~~1~~ 2 | 1 | 1 | ~~1~~ 2 | 1 | 1 | 1 | 1 |
+
+- Student at index 5 has marks greater than its left neighbour, so it should receive at least 3 candies.
+
+| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
+|:-----:| --- | ------- | --- | --- | ------- | ------- | --- | --- | --- |
+| marks | 1 | 6 | 3 | 1 | 10 | 12 | 20 | 5 | 2 |
+| candy | 1 | ~~1~~ 2 | 1 | 1 | ~~1~~ 2 | ~~1~~ 3 | 1 | 1 | 1 |
+
+- Student at index 6 has marks greater than its left neighbour, so it should receive at least 4 candies.
+
+| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
+|:-----:| --- | ------- | --- | --- | ------- | ------- | ------- | --- | --- |
+| marks | 1 | 6 | 3 | 1 | 10 | 12 | 20 | 5 | 2 |
+| candy | 1 | ~~1~~ 2 | 1 | 1 | ~~1~~ 2 | ~~1~~ 3 | ~~1~~ 4 | 1 | 1 |
+
+- Student at index 7 and index 8 does not have marks greater than their left neighbour.
+
+Now let us consider the right neighbour.
+
+
+- Student at index 7 has marks greater than its right neighbour, so it should receive at least 2 candies.
+
+| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
+|:-----:| --- | ------- | --- | --- | ------- | ------- | ------- | ------- | --- |
+| marks | 1 | 6 | 3 | 1 | 10 | 12 | 20 | 5 | 2 |
+| candy | 1 | ~~1~~ 2 | 1 | 1 | ~~1~~ 2 | ~~1~~ 3 | ~~1~~ 4 | ~~1~~ 2 | 1 |
+
+- Student at index 6 has marks greater than its right neighbour, so it should receive at least 3 candies but it has 4 candies already which is greater than its right neighbour candies, so it is fine.
+
+- Student at index 5, 4 and 3 do not have marks greater than their right neighbour.
+
+- Student at index 2 has marks greater than its right neighbour. So it receives at least 2 candies.
+
+
+|index|0|1|2|3|4|5|6|7|8|
+|-|-|-|-|-|-|-|-|-|-|
+|marks|1|6|3|1|10|12|20|5|2|
+|candy|1|~~1~~ 2|~~1~~ 2|1|~~1~~ 2|~~1~~ 3|~~1~~ 4|~~1~~ 2|1|
+
+- Student at index 1 has marks greater than its right neighbour. So it receives at least 3 candies.
+
+| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
+|:-----:| --- | ------------- | ------- | --- | ------- | ------- | ------- | ------- | --- |
+| marks | 1 | 6 | 3 | 1 | 10 | 12 | 20 | 5 | 2 |
+| candy | 1 | ~~1~~ ~~2~~ 3 | ~~1~~ 2 | 1 | ~~1~~ 2 | ~~1~~ 3 | ~~1~~ 4 | ~~1~~ 2 | 1 |
+
+- Student at index 0 does not have marks greater than its right neighbour.
+
+So a total 19 candies are required.
+
+**Output:** 19
+
+
+---
+
+### Candy Distribution - Solution
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+**Step 1:** Assign 1 candy to all the students.
+**Step 2:** For all the values of i, consider its left neighbour, if(A[i] > A[i - 1]) then C[i] > C[i - 1], means candy of ith index should be greater than (i-1)th index candy, so we will follow the greedy approach as we want to distribute a minimum number of candies, so we do `C[i] = C[i - 1] + 1`
+
+```cpp
+if(A[i] > A[i - 1]){
+ C[i] = C[i - 1] + 1
+}
+```
+
+**Step 3:** For all the values of i, consider its right neighbour, if(A[i] > A[i+1]) then C[i] > C[i + 1], means candy of ith index should be greater than (i+1)th index candy, so first we check it has candies greater than his right neighbour or not if not then we will follow the greedy approach as we want to distribute a minimum number of candies, then we do `C[i] = C[i + 1] + 1`
+
+```cpp
+if(A[i] > A[i + 1]){
+ if(C[i] < C[i + 1] + 1)
+ C[i] = C[i + 1] + 1
+}
+```
+
+#### PsuedoCode
+```cpp
+int C[N];
+for all i, C[i] = 1
+for (i = 1; i < N; i++) {
+ if (arr[i] > arr[i - 1]) {
+ C[i] = C[i - 1] + 1
+ }
+}
+for (i = N - 2; i >= 0; i--) {
+ if (arr[i] > arr[i + 1] && C[i] < C[i + 1] + 1) {
+ C[i] = C[i + 1] + 1
+ }
+}
+
+ans = sum of all values in C[]
+```
+#### Complexity
+
+- **Time Complexity:** O(N)
+- **Space Complexity:** O(N)
+
+
+---
+### Problem 3 Maximum jobs
+
+
+Given N jobs with their start and end times. Find the maximum number of jobs that can be completed if only one job can be done at a time.
+
+**Example**
+
+ +
+**Answer:** 5
+
+We will select the jobs that are not overlapping:
+- We select job `9 am - 11 am`, then we can not select `10 am - 1 pm` and `10 am - 2 pm`
+- Then we select jobs `3 pm - 4 pm` and `4 pm - 6 pm`
+- Then we select job `4 pm - 8 pm` and `8 pm - 10 pm` but we do not select job `7 pm - 9 pm`
+
+
+
+
+
+**Answer:** 5
+
+We will select the jobs that are not overlapping:
+- We select job `9 am - 11 am`, then we can not select `10 am - 1 pm` and `10 am - 2 pm`
+- Then we select jobs `3 pm - 4 pm` and `4 pm - 6 pm`
+- Then we select job `4 pm - 8 pm` and `8 pm - 10 pm` but we do not select job `7 pm - 9 pm`
+
+
+
+ +
+
+#### Approach
+We have to select the job in such a way that the start time of a currently selected job is greater than or equal to the end time of the previous job.
+
+`S[i] >= E[i - 1]`
+
+
+---
+### Question
+
+What is the maximum number of jobs one person can do if only one job at a time is allowed, the start times and end times of jobs are:
+
+S = [1, 5, 8, 7, 12, 13]
+E = [2, 10, 10, 11, 20, 19]
+
+**Choices**
+
+- [ ] 2
+- [x] 3
+- [ ] 4
+- [ ] 5
+
+
+**Explanation**
+
+S = [1, 5, 8, 7, 12, 13]
+E = [2, 10, 10, 11, 20, 19]
+
+
+
+
+#### Approach
+We have to select the job in such a way that the start time of a currently selected job is greater than or equal to the end time of the previous job.
+
+`S[i] >= E[i - 1]`
+
+
+---
+### Question
+
+What is the maximum number of jobs one person can do if only one job at a time is allowed, the start times and end times of jobs are:
+
+S = [1, 5, 8, 7, 12, 13]
+E = [2, 10, 10, 11, 20, 19]
+
+**Choices**
+
+- [ ] 2
+- [x] 3
+- [ ] 4
+- [ ] 5
+
+
+**Explanation**
+
+S = [1, 5, 8, 7, 12, 13]
+E = [2, 10, 10, 11, 20, 19]
+
+ +
+We will pick jobs `1 - 2`, `5 - 10` and `12 - 20`. So we can pick total three jobs.
+
+
+
+We will pick jobs `1 - 2`, `5 - 10` and `12 - 20`. So we can pick total three jobs.
+
+ +
+
+---
+
+
+### Maximum jobs - Solution
+
+The first idea towards a solution is to first pick a job with minimum duration.
+
+#### Idea 1 - Greedy based on duration
+Pick the job in the ascending order of the minimum duration. Let us take an example:
+
+
+
+
+---
+
+
+### Maximum jobs - Solution
+
+The first idea towards a solution is to first pick a job with minimum duration.
+
+#### Idea 1 - Greedy based on duration
+Pick the job in the ascending order of the minimum duration. Let us take an example:
+
+ +
+In this case, if we select the minimum duration job first, then we will select the job `10 - 13`, then we can not select any other job because both overlap with it.
+
+But if we have not selected `10 - 13`, then we can select both other jobs, which means we can select two jobs.
+
+
+
+
+In this case, if we select the minimum duration job first, then we will select the job `10 - 13`, then we can not select any other job because both overlap with it.
+
+But if we have not selected `10 - 13`, then we can select both other jobs, which means we can select two jobs.
+
+
+ +
+So selecting a job in the ascending order of the duration will not always give us the maximum number of jobs.
+
+
+#### Idea 2 - Greedy based on start time
+Pick the job in the ascending order of the start time. Let us take an example:
+
+
+
+
+
+So selecting a job in the ascending order of the duration will not always give us the maximum number of jobs.
+
+
+#### Idea 2 - Greedy based on start time
+Pick the job in the ascending order of the start time. Let us take an example:
+
+
+
+ +
+
+In this case, if we select the minimum start time job first, then we will select the job `2 - 20`, then we can not select any other job because both overlap with it.
+
+But if we have not selected `2 - 20`, then we can select both other jobs, which means we can select two jobs.
+
+
+
+
+In this case, if we select the minimum start time job first, then we will select the job `2 - 20`, then we can not select any other job because both overlap with it.
+
+But if we have not selected `2 - 20`, then we can select both other jobs, which means we can select two jobs.
+
+ +
+So selecting a job in the ascending order of the start time will not always give us the maximum number of jobs.
+
+#### Observation
+We have to take a combination of the above approaches means we have to start early with the minimum duration job.
+
+start early + minimum duration
+
+A combination of both is nothing but simply means ending early.
+
+start early + minimum duration = end early
+
+#### Solution
+We have to be greedy based on the end time, so we have to select jobs in the ascending order of end times.
+
+**Example:**
+
+S = [1, 5, 8, 7, 12, 13]
+E = [2, 10, 10, 11, 20, 19]
+
+Sort these jobs based on the end time.
+
+
+S = [1, 5, 8, 7, 13, 12]
+E = [2, 10, 10, 11, 19, 20]
+
+Initially ans = 0.
+
+| Index | 0 | 1 | 2 | 3 | 4 | 5 |
+|:----------:| --- | --- | --- |:---:|:---:|:---:|
+| Start time | 1 | 5 | 8 | 7 | 13 | 12 |
+| end time | 2 | 10 | 10 | 11 | 19 | 20 |
+
+
+- We will start with the first job, which has an end time 2 but now the start time of any next job must be greater than the end time of this job.
+
+
+**So we need to keep track of the last end time.**
+
+Till now lastEndTime = 2
+ans+=1, ans = 1
+
+- Now the job at index 1 has start time = 5, lastEndTime <= start time, so can select this job and lastEndTime will be updated to the end time of the current job and the answer is incremented by 1.
+lastEndTime = 10
+ans+=1, ans = 2
+- Now the job at index 2 has start time = 8, lastEndTime > start time, so we can not select this job.
+- Now the job at index 3 has start time = 7, lastEndTime > start time, so we can not select this job.
+- Now the job at index 4 has start time = 13, lastEndTime <= start time, so can select this job and lastEndTime will be updated to the end time of the current job and the answer is incremented by 1.
+lastEndTime = 19
+ans+=1, ans = 3
+- Now the job at index 5 has start time = 20, lastEndTime > start time, so we can not select this job.
+
+**Answer:** 3
+
+#### PseudoCode
+```cpp
+1. Sort on the basis of end-time
+2. ans = 1, lastEndTime = E[0]
+ for( i = 1 ; i < N ; i++){
+ if(S[i] >= lastEndTime){
+ ans++;
+ lastEndTime = E[i];
+ }
+ }
+3. return ans;
+```
+
+#### Complexity
+
+- **Time Complexity:** O(NlogN)
+- **Space Complexity:** O(N)
diff --git a/Academy DSA Typed Notes/Advanced/DSA Hashing 1 Introduction.md b/Academy DSA Typed Notes/Advanced/DSA Hashing 1 Introduction.md
new file mode 100644
index 0000000..1d169d8
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Hashing 1 Introduction.md
@@ -0,0 +1,561 @@
+# Hashing 1: Introduction
+
+---
+
+## HashMap
+
+Let's take an example:-
+
+* Imagine we have a hotel called Reddison, which has 5 rooms.
+* How can we maintain information on the status of rooms provided the hotel is old and hasn't adapted to technology yet?
+
+Solution: The hotel may maintain a manual register for five rooms like:-
+
+| Room no | occupied |
+|:-------:|:--------:|
+| 1 | Yes |
+| 2 | No |
+| 3 | Yes |
+| 4 | No |
+| 5 | No |
+
+
+* After a few years, the hotel became a success, and the rooms increased to 1000.
+* Provided the hotel decided to adapt to technology, what is the programmatically most straightforward approach to maintain the status of rooms?
+ * An array can be maintained where the index can denote the room number.
+ * If there are N rooms, we'll create an array of size + 1 where true denotes that room is occupied, and false denotes unoccupied.
+
+* Pandemic hit, due to which footfall reduced significantly. Owner visits Numerologist who asks them to change room numbers to some random lucky numbers from [1-109]. How can we maintain the status of the rooms now?
+ * Maintain boolean array of length 109 + 1 `bool arr[10^9 + 1]`.
+ * **ISSUE:** Status can be checked in O(1), but just for 1000 rooms, we require an array of size 109.
+
+* **Solution:** HashMaps
+ * HashMap is a data structure that stores
+
+So selecting a job in the ascending order of the start time will not always give us the maximum number of jobs.
+
+#### Observation
+We have to take a combination of the above approaches means we have to start early with the minimum duration job.
+
+start early + minimum duration
+
+A combination of both is nothing but simply means ending early.
+
+start early + minimum duration = end early
+
+#### Solution
+We have to be greedy based on the end time, so we have to select jobs in the ascending order of end times.
+
+**Example:**
+
+S = [1, 5, 8, 7, 12, 13]
+E = [2, 10, 10, 11, 20, 19]
+
+Sort these jobs based on the end time.
+
+
+S = [1, 5, 8, 7, 13, 12]
+E = [2, 10, 10, 11, 19, 20]
+
+Initially ans = 0.
+
+| Index | 0 | 1 | 2 | 3 | 4 | 5 |
+|:----------:| --- | --- | --- |:---:|:---:|:---:|
+| Start time | 1 | 5 | 8 | 7 | 13 | 12 |
+| end time | 2 | 10 | 10 | 11 | 19 | 20 |
+
+
+- We will start with the first job, which has an end time 2 but now the start time of any next job must be greater than the end time of this job.
+
+
+**So we need to keep track of the last end time.**
+
+Till now lastEndTime = 2
+ans+=1, ans = 1
+
+- Now the job at index 1 has start time = 5, lastEndTime <= start time, so can select this job and lastEndTime will be updated to the end time of the current job and the answer is incremented by 1.
+lastEndTime = 10
+ans+=1, ans = 2
+- Now the job at index 2 has start time = 8, lastEndTime > start time, so we can not select this job.
+- Now the job at index 3 has start time = 7, lastEndTime > start time, so we can not select this job.
+- Now the job at index 4 has start time = 13, lastEndTime <= start time, so can select this job and lastEndTime will be updated to the end time of the current job and the answer is incremented by 1.
+lastEndTime = 19
+ans+=1, ans = 3
+- Now the job at index 5 has start time = 20, lastEndTime > start time, so we can not select this job.
+
+**Answer:** 3
+
+#### PseudoCode
+```cpp
+1. Sort on the basis of end-time
+2. ans = 1, lastEndTime = E[0]
+ for( i = 1 ; i < N ; i++){
+ if(S[i] >= lastEndTime){
+ ans++;
+ lastEndTime = E[i];
+ }
+ }
+3. return ans;
+```
+
+#### Complexity
+
+- **Time Complexity:** O(NlogN)
+- **Space Complexity:** O(N)
diff --git a/Academy DSA Typed Notes/Advanced/DSA Hashing 1 Introduction.md b/Academy DSA Typed Notes/Advanced/DSA Hashing 1 Introduction.md
new file mode 100644
index 0000000..1d169d8
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Hashing 1 Introduction.md
@@ -0,0 +1,561 @@
+# Hashing 1: Introduction
+
+---
+
+## HashMap
+
+Let's take an example:-
+
+* Imagine we have a hotel called Reddison, which has 5 rooms.
+* How can we maintain information on the status of rooms provided the hotel is old and hasn't adapted to technology yet?
+
+Solution: The hotel may maintain a manual register for five rooms like:-
+
+| Room no | occupied |
+|:-------:|:--------:|
+| 1 | Yes |
+| 2 | No |
+| 3 | Yes |
+| 4 | No |
+| 5 | No |
+
+
+* After a few years, the hotel became a success, and the rooms increased to 1000.
+* Provided the hotel decided to adapt to technology, what is the programmatically most straightforward approach to maintain the status of rooms?
+ * An array can be maintained where the index can denote the room number.
+ * If there are N rooms, we'll create an array of size + 1 where true denotes that room is occupied, and false denotes unoccupied.
+
+* Pandemic hit, due to which footfall reduced significantly. Owner visits Numerologist who asks them to change room numbers to some random lucky numbers from [1-109]. How can we maintain the status of the rooms now?
+ * Maintain boolean array of length 109 + 1 `bool arr[10^9 + 1]`.
+ * **ISSUE:** Status can be checked in O(1), but just for 1000 rooms, we require an array of size 109.
+
+* **Solution:** HashMaps
+ * HashMap is a data structure that stores  +
+* Here, since we are not allowed to consider pairs where i == j these diagonal elements (marked in red) will not be considered.
+* Now, as you can see the upper (blue) and lower (yellow) triangles represent the same pairs (order of pair doesn't matter here) our program would work with either one of these triangular parts.
+
+*Now, considering upper triangle -*
+#### Observation:
+
+| i | j loops from [i...(N - 1)] |
+|:---:|:------------------------:|
+| 0 | [0..N-1] |
+| 1 | [1..N-1] |
+| 2 | [2..N-1] |
+| 3 | [3..N-1] |
+| 4 | - |
+
+Here for every index of i, j loops from i to N - 1
+
+For an `arr[i]`, the target will be `K-arr[i]`
+
+#### Pseudocode:
+```kotlin
+boolean checkPair(int arr[], int K) {
+
+ int N = arr.length
+ for (int i = 0; i < N; i++) {
+ //target: K-arr[i]
+ for (int j = i; j < N; j++) {
+ if (arr[i] == K - arr[i]) {
+ return true;
+ }
+ }
+ }
+ return false;
+}
+
+```
+
+#### Complexity
+**Time Complexity:** O(N^2)
+**Space Complexity:** O(1)
+
+
+---
+### Problem 1 Optimization with HashSet(Doesn't Work)
+
+* We can insert all elements in the set initially.
+* Now, iterate over every arr[i] and check if K-arr[i] is present in the set. If yes, return tue, else false.
+
+
+
+
+* Here, since we are not allowed to consider pairs where i == j these diagonal elements (marked in red) will not be considered.
+* Now, as you can see the upper (blue) and lower (yellow) triangles represent the same pairs (order of pair doesn't matter here) our program would work with either one of these triangular parts.
+
+*Now, considering upper triangle -*
+#### Observation:
+
+| i | j loops from [i...(N - 1)] |
+|:---:|:------------------------:|
+| 0 | [0..N-1] |
+| 1 | [1..N-1] |
+| 2 | [2..N-1] |
+| 3 | [3..N-1] |
+| 4 | - |
+
+Here for every index of i, j loops from i to N - 1
+
+For an `arr[i]`, the target will be `K-arr[i]`
+
+#### Pseudocode:
+```kotlin
+boolean checkPair(int arr[], int K) {
+
+ int N = arr.length
+ for (int i = 0; i < N; i++) {
+ //target: K-arr[i]
+ for (int j = i; j < N; j++) {
+ if (arr[i] == K - arr[i]) {
+ return true;
+ }
+ }
+ }
+ return false;
+}
+
+```
+
+#### Complexity
+**Time Complexity:** O(N^2)
+**Space Complexity:** O(1)
+
+
+---
+### Problem 1 Optimization with HashSet(Doesn't Work)
+
+* We can insert all elements in the set initially.
+* Now, iterate over every arr[i] and check if K-arr[i] is present in the set. If yes, return tue, else false.
+
+
+ +
+
+---
+**ISSUE: (Edge Case)**
+
+* For even K value, say arr[i] is K/2 and only one occurrence of it is present.
+* Eg: A[] = {8, 9, 2, -1, 4, 5, 11, -6, 4}; K=4, we will end up considering 2(present at index 2) two times.
+
+
+
+
+---
+**ISSUE: (Edge Case)**
+
+* For even K value, say arr[i] is K/2 and only one occurrence of it is present.
+* Eg: A[] = {8, 9, 2, -1, 4, 5, 11, -6, 4}; K=4, we will end up considering 2(present at index 2) two times.
+
+ +
+
+We can see the above logic isn't working
+
+### Resolution:
+We need not insert all elements into set at once. Rather only insert from [0, i - 1].
+
+
+---
+### Problem 1 Optimization with HashSet(Works)
+
+At ith index: Hashset should contain all the elements:[0...i - 1]
+
+Let's take an example,
+
+
+
+
+We can see the above logic isn't working
+
+### Resolution:
+We need not insert all elements into set at once. Rather only insert from [0, i - 1].
+
+
+---
+### Problem 1 Optimization with HashSet(Works)
+
+At ith index: Hashset should contain all the elements:[0...i - 1]
+
+Let's take an example,
+
+ +
+
+
+* Initially set is empty.
+* For every element at ith index, search for target (arr[i] - K) in set.
+* If found, it means it must have been previously inserted. If not, we'll insert arr[i], because in future if we'll find a pair, we'll be able to get the current element.
+
+Let's take another example,
+
+
+
+
+
+
+* Initially set is empty.
+* For every element at ith index, search for target (arr[i] - K) in set.
+* If found, it means it must have been previously inserted. If not, we'll insert arr[i], because in future if we'll find a pair, we'll be able to get the current element.
+
+Let's take another example,
+
+
+ +
+
+
+#### Pseudocode:
+```kotlin
+boolean targetSum(int arr[], int K) {
+ int N = arr.length;
+ Hashset < int > bs;
+
+ for (int i = 0; i < N; i++) {
+ //target = K - arr[i]
+ if (bs.contains(K - arr[i])) {
+ return true;
+ } else {
+ bs.add(arr[i]);
+ }
+ }
+ return false;
+}
+```
+---
+### Question
+Count pairs(i, j) such that, arr[i] + arr[j] == K && i != j in the given array.
+A = [3, 5, 1, 2, 1, 2] and K = 3.
+
+
+**Choices**
+- [ ] 1
+- [ ] 2
+- [ ] 3
+- [x] 4
+
+
+
+In the given array A = [3, 5, 1, 2, 1, 2], pairs with sum = 3 are:
+
+| Pairs |
+| ------ |
+| {2, 3} |
+| {2, 5} |
+| {3, 4} |
+
+---
+### Problem 2 Count no. of pairs with sum K
+
+Given an `arr[n]`, count number of pairs such that
+```kotlin
+arr[i] + arr[j] = K && i != j
+```
+
+**Example**
+
+Provided we have an arr[8] and K = 10, we have
+| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
+|:------:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|
+| arr[8] | 2 | 5 | 2 | 5 | 8 | 5 | 2 | 8 |
+
+**Pairs:**
+
+| Pairs: 9 |
+|:--------:|
+| {0, 4} |
+| {0, 7} |
+| {1, 5} |
+| {1, 3} |
+| {2, 4} |
+| {2, 7} |
+| {3, 5} |
+| {4, 6} |
+| {6, 7} |
+
+Here (i, j) and (j, i) considered as same.
+
+:::warning
+Please take some time to think about the optimised approach on your own before reading further.....
+:::
+
+### Optimised Approach(Same as in previous question)
+* Similar to our previous problem, we'll be searching for our target.
+* This time we also need to consider the frequency of how many times a particular element appeared, so we shall be maintianing a map.
+
+
+
+
+
+
+
+#### Pseudocode:
+```kotlin
+boolean targetSum(int arr[], int K) {
+ int N = arr.length;
+ Hashset < int > bs;
+
+ for (int i = 0; i < N; i++) {
+ //target = K - arr[i]
+ if (bs.contains(K - arr[i])) {
+ return true;
+ } else {
+ bs.add(arr[i]);
+ }
+ }
+ return false;
+}
+```
+---
+### Question
+Count pairs(i, j) such that, arr[i] + arr[j] == K && i != j in the given array.
+A = [3, 5, 1, 2, 1, 2] and K = 3.
+
+
+**Choices**
+- [ ] 1
+- [ ] 2
+- [ ] 3
+- [x] 4
+
+
+
+In the given array A = [3, 5, 1, 2, 1, 2], pairs with sum = 3 are:
+
+| Pairs |
+| ------ |
+| {2, 3} |
+| {2, 5} |
+| {3, 4} |
+
+---
+### Problem 2 Count no. of pairs with sum K
+
+Given an `arr[n]`, count number of pairs such that
+```kotlin
+arr[i] + arr[j] = K && i != j
+```
+
+**Example**
+
+Provided we have an arr[8] and K = 10, we have
+| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
+|:------:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|
+| arr[8] | 2 | 5 | 2 | 5 | 8 | 5 | 2 | 8 |
+
+**Pairs:**
+
+| Pairs: 9 |
+|:--------:|
+| {0, 4} |
+| {0, 7} |
+| {1, 5} |
+| {1, 3} |
+| {2, 4} |
+| {2, 7} |
+| {3, 5} |
+| {4, 6} |
+| {6, 7} |
+
+Here (i, j) and (j, i) considered as same.
+
+:::warning
+Please take some time to think about the optimised approach on your own before reading further.....
+:::
+
+### Optimised Approach(Same as in previous question)
+* Similar to our previous problem, we'll be searching for our target.
+* This time we also need to consider the frequency of how many times a particular element appeared, so we shall be maintianing a map.
+
+
+
+ +
+
+
+### Pseudocode:
+```kotlin
+int countTargetSum(int arr[], int K) {
+ int N = arr.length;
+ Hashmap < int, int > hm;
+
+ int c = 0;
+
+ for (int i = 0; i < n; i++) {
+ //target = K-arr[i]
+ if (hm.contains(K - arr[i])) {
+ c = c + hm[K - arr[i]] //freq of target = pairs
+ }
+
+ //insert arr[i]
+ if (hm.contains(arr[i])) {
+ hm[arr[i]]++;
+ } else {
+ hm.put(arr[i], 1);
+ }
+ }
+ return c;
+}
+
+```
+
+### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(N)
+
+---
+### Problem 3 Subarray with Sum K
+Given an array arr[n] check if there exists a subarray with sum = K
+
+### Example:
+We have the following array
+
+| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
+|:------:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|
+| arr[7] | 2 | 3 | 9 | -4 | 1 | 5 | 6 | 2 | 5 |
+
+Possible subarrays for the following values of K are,
+* k = 11: {2 3 9 -4 1}, {5, 6}
+* k = 10: {2 3 9 -4}
+* k = 15: {-4, 1, 5, 6, 2, 5}
+
+---
+### Question
+Check if there exist a subarray with sum = 110 in the given array?
+A = [ 5, 10, 20, 100, 105 ]
+
+
+**Choices**
+- [x] No
+- [ ] YES
+
+
+---
+### Approach
+
+To get subarray sum for any subarray in constant time, we can create a prefix sum array.
+
+Now, a subarray sum `PF[i] - PF[j]` should be equal to `K`
+
+OR
+**a - b = K**
+
+We can fix `a` and get the corresponding pair for it, given by `a - K`
+
+> We can create a HashSet at the time of traversal simultaneously
+> Here, instead of creating prefix sum initially, we are calculating it while iterating through the array.
+
+
+
+
+
+### Pseudocode:
+```kotlin
+int countTargetSum(int arr[], int K) {
+ int N = arr.length;
+ Hashmap < int, int > hm;
+
+ int c = 0;
+
+ for (int i = 0; i < n; i++) {
+ //target = K-arr[i]
+ if (hm.contains(K - arr[i])) {
+ c = c + hm[K - arr[i]] //freq of target = pairs
+ }
+
+ //insert arr[i]
+ if (hm.contains(arr[i])) {
+ hm[arr[i]]++;
+ } else {
+ hm.put(arr[i], 1);
+ }
+ }
+ return c;
+}
+
+```
+
+### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(N)
+
+---
+### Problem 3 Subarray with Sum K
+Given an array arr[n] check if there exists a subarray with sum = K
+
+### Example:
+We have the following array
+
+| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
+|:------:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|
+| arr[7] | 2 | 3 | 9 | -4 | 1 | 5 | 6 | 2 | 5 |
+
+Possible subarrays for the following values of K are,
+* k = 11: {2 3 9 -4 1}, {5, 6}
+* k = 10: {2 3 9 -4}
+* k = 15: {-4, 1, 5, 6, 2, 5}
+
+---
+### Question
+Check if there exist a subarray with sum = 110 in the given array?
+A = [ 5, 10, 20, 100, 105 ]
+
+
+**Choices**
+- [x] No
+- [ ] YES
+
+
+---
+### Approach
+
+To get subarray sum for any subarray in constant time, we can create a prefix sum array.
+
+Now, a subarray sum `PF[i] - PF[j]` should be equal to `K`
+
+OR
+**a - b = K**
+
+We can fix `a` and get the corresponding pair for it, given by `a - K`
+
+> We can create a HashSet at the time of traversal simultaneously
+> Here, instead of creating prefix sum initially, we are calculating it while iterating through the array.
+
+ +
+
+
+**Edge case:**
+If subarray from index 0 has sum = K.
+Say, K = 10
+a = 10, b = 10-10=0, now 0 won't be present in the array.
+Please take below example:
+
+
+
+
+
+**Edge case:**
+If subarray from index 0 has sum = K.
+Say, K = 10
+a = 10, b = 10-10=0, now 0 won't be present in the array.
+Please take below example:
+
+ +
+
+**To resolve this, take 0 in the set initially.**
+
+
+
+
+**To resolve this, take 0 in the set initially.**
+
+ +
+
+#### Pseudocode:
+```kotlin
+boolean targetSubarray(int arr[], int K) {
+ int N = arr.length;
+ long a = 0;
+
+ //cumulative sum, long -> to avoid overflow
+ HashSet < long > hs;
+ hs.add(0);
+ for (int i = 0; i < N; i++) {
+ a = a + arr[i];
+
+ //cumulative sum = target = a - k
+ if (hs.contains(a - K)) {
+ //subarray exists
+ return true;
+ } else {
+ hs.add(a);
+
+ }
+
+ }
+ return false;
+}
+
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(N)
+
+
+---
+### Problem 4 Distinct elements in every window of size K
+
+Given an array of integers and a number, K. Find the count of distinct elements in every window of size K in the array.
+
+**Example**
+
+```java
+// Input:
+Array = [1, 2, 1, 3, 4, 2, 3]
+K = 4
+
+// Output:
+[3, 4, 4, 3]
+```
+
+- In the first window `[1, 2, 1, 3]`, there are 3 distinct elements: 1, 2, and 3.
+- In the second window `[2, 1, 3, 4]`, there are 4 distinct elements: 2, 1, 3, and 4.
+- In the third window `[1, 3, 4, 2]`, there are again 4 distinct elements: 1, 3, 4, and 2.
+- In the fourth window `[3, 4, 2, 3]`, there are 3 distinct elements: 3, 4, and 2.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+#### Approach - Using HashSet
+
+- The code iterates through each possible window of size K in the given array.
+- For each window, a temporary HashSet (`distinctSet`) is created to store the distinct elements within that window.
+- Within the inner loop, the code adds each element of the window to the HashSet.
+- After processing the entire window, the size of the HashSet is calculated using `distinctSet.size()`, which represents the count of distinct elements.
+- The count is then added to the result list.
+- This process is repeated for all possible windows in the array.
+- The result list contains the count of distinct elements in each window
+
+#### Pseudocode
+
+```java
+//Pseudo code for 'countDistinctElements' function
+function countDistinctElements(arr, k):
+ result = empty list
+
+ for i = 0 to length of arr - k:
+ distinctSet = empty set
+
+ for j = i to i + k - 1:
+ add arr[j] to distinctSet
+
+ add size of distinctSet to result
+
+ return result
+```
+
+#### Complexity
+**Time Complexity:** `O((N-K+1) * K)`
+
+Considering the values of `K` as N/2, 1, and N.
+**When K = N/2:**
+ If `K` is about half of `N`, then the expression simplifies to `O((N/2 + 1) * N/2)`, which further simplifies to `O((N^2 + N) / 4)`. In this case, the primary factor is `N^2`, leading to a time complexity of approximately `O(N^2)`.
+**When K = 1:**
+ When `K` is set to 1, the expression becomes `O((N - 1 + 1) * 1)`, which straightforwardly simplifies to `O(N)`. It's important to note that this doesn't align with the original statement of the time complexity being `O(N^2)`.
+**When K = N:**
+ If `K` is equal to `N`, then the expression becomes `O((N - N + 1) * N)`, which further simplifies to `O(N^2)`.
+
+**Space Complexity:** O(K)
+
+---
+### Problem 4 Sliding Window - Map
+
+Sliding Window suggests to insert all elements of the first window in the set. Now slide the window, throw the prev element out and insert new adjacent element in the set.
+
+But we can't use Set here, since it is possible that the element just thrown out may be present in the current window.
+
+We will also need to maintain the frequency of elements, hence we will use Hashmap.
+
+- Maintain a HashMap to track the frequency of elements within the current subarray.
+- Initially, the algorithm populates the HashMap with the elements of the first subarray, counting distinct elements.
+- Then, as the window slides one step at a time:
+ - The algorithm updates the HashMap by updating frequency of the element leaving the window and increasing frequency of the new element entering the window.
+- The distinct element count for each subarray is determined by the size of the HashMap.
+
+#### Pseudocode
+
+```java
+void subfreq(int ar[], int k) {
+ int N = ar.length;
+
+ HashMap < int, int > hm;
+
+ // Step 1: Insert 1st subarray [0, k-1]
+ for (int i = 0; i < k; i++) {
+ //Increase frequecy by 1
+ if (hm.contains(ar[i])) {
+ int val = hm.get(ar[i]);
+ hm.put(ar[i], val + 1);
+ } else {
+ hm.put(ar[i], 1);
+ }
+
+ print(hm.size());
+ }
+
+ //step 2: Iterate all other subarrays
+ int s = 1, e = k;
+
+ while (e < N) {
+ //Remove ar[s-1]
+ int val = hm[ar[s - 1]];
+ hm[ar[s - 1]]--;
+
+ if (hm.get[ar[s - 1]] == 0) {
+ hm.remove(ar[s - 1]);
+ }
+
+ //add ar[e]
+ if (hm.contains(ar[e])) {
+ //Inc freq by 1
+ int val = hm[ar[e]];
+ hm[ar[e]]++;
+ } else {
+ hm.put(ar[e], 1);
+ }
+
+ print(hm.size());
+ s++
+
+ }
+}
+
+```
+#### Complexity
+**Time Complexity**: `O(n)`
+**Space Complexity**: `O(n)`
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Hashing 3 Internal Implementation & Problems.md b/Academy DSA Typed Notes/Advanced/DSA Hashing 3 Internal Implementation & Problems.md
new file mode 100644
index 0000000..4d84e85
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Hashing 3 Internal Implementation & Problems.md
@@ -0,0 +1,459 @@
+# Hashmap Implementation
+
+---
+## Check if given element exists in Q queries
+
+
+Given an array of size N and Q queries. In each query, an element is given. We have to check whether that element exists or not in the given array.
+
+**Example**
+
+A [ ] = {`2, 4, 11, 15 , 6, 8, 14, 9`}
+
+`4 Queries`
+`K = 4` (return true)
+`K = 10` (return false)
+`K = 17` (return false)
+`K = 14` (return true)
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Brute Force Approach
+
+For every query, loop through the given array to check the presence.
+
+Time Complexity - **O(N * Q)**
+Space Complexity - **O(1)**
+
+#### Observation
+
+We can create an array to mark the presence of an element against that particular index.
+
+A [ ] = {`2, 4, 11, 15 , 6, 8, 14, 9`}
+
+For example we can mark presence of
+2 at index 2
+4 at index 4 and so on....
+
+To execute that, we'll need to have indices till 15(max of Array).
+The array size needed is 16.
+
+Let's call that array as - DAT (Direct Access Table)
+int dat[16] = {0}; //initally assuming an element is not present
+
+| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
+| -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- |
+| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
+
+
+Let's mark the presence.
+```cpp
+for(int i = 0; i < N; i++) {
+ dat[A[i]] = 1;
+}
+```
+
+Below is how that array looks like -
+
+| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
+| -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- |
+| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
+
+#### Advantage of using DAT
+
+1. Time Complexity of Insertion - `O(1)`
+2. Time Complexity of Deletion - `O(1)`
+3. Time Complexity of Search - `O(1)`
+
+#### Issues with such a representation
+
+**1. Wastage of Space**
+* Say array is `A[] = {23, 60, 37, 90}`; now just to store presence of 4 elements, we'll have to construct an array of `size 91`.
+
+**2. Inability to create big Arrays**
+* If values in array are as big as $10^{15}$, then we will not be able to create this big array. At max array size possible is 10^6^(around)
+
+**3. Storing values other than positive Integers**
+* We'll have to make some adjustments to store negative numbers or characters. (It'll be possible but needs some work-around)
+
+---
+### Overcome Issues while retaining Advantages
+
+
+Let's say we have restriction of creating only array of size 10.
+
+Given Array -
+A [ ] = {`21, 42, 37, 45 , 99, 30`}
+
+**How can we do so ?**
+
+In array of size 10, we'll have indices from 0 to 9. How can we map all the values within this range ?
+
+**Basically, we can take a mod with 10.**
+
+21 % 10 = 1 (presence of 21 can be marked at index 1)
+
+42 % 10 = 2 (presence of 42 can be marked at index 2)
+
+37 % 10 = 7 (presence of 37 can be marked at index 7)
+
+45 % 10 = 5 (presence of 45 can be marked at index 5)
+
+99 % 10 = 9 (presence of 99 can be marked at index 9)
+
+30 % 10 = 0 (presence of 30 can be marked at index 0)
+
+| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
+| -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- |
+| 30 | 21 | 42 | 0 | 0 | 45 | 0 | 37 | 0 | 99 |
+
+
+#### What Have We Done ?
+
+* We have basically done Hashing. Hashing is a process where we pass our data through the Hash Funtion which gives us the hash value(index) to map our data to.
+* In this case, the hash function used is **MOD**. This is the simplest hash function. Usually, more complex hash functions are used.
+* The DAT that we created is known as **Hash Table** in terms of Hashing.
+
+
+
+#### Issue with Hashing ?
+
+**COLLISION!**
+
+Say given array is as follows -
+
+A [ ] = {21, 42, 37, 45, 77, 99, 31}
+
+Here, 21 & 31 will map to the same index => 1
+37 & 77 map to same index => 7
+
+
+**Can we completely avoid collision ?**
+
+`Not Really!`
+
+No matter how good a hash function is, we can't avoid collision!
+
+**Why ?**
+
+We are trying to map big values to a smaller range, collisions are bound to happen.
+
+Moreover, this can be explained using `Pigeon Hole Principle!`
+
+**Example -**
+
+Say we have 11 pigeons and we have only 8 holes to keep them. Now, provided holes are less, atleast 2 pigeons need to fit in a single hole.
+
+But, we can find some resolutions to collision.
+
+---
+### Collision Resolution Techniques
+
+
+
+
+
+>From Interview Perspective, Open Hashing is Important hence, we'll dive into that.
+
+
+
+---
+### Chaining
+
+
+Let's take the above problem where collision happened!
+
+A [ ] = {`21, 42, 37, 45, 77, 99, 31`}
+
+Here, 21 & 31 will map to the same index => 1
+37 & 77 map to same index => 7
+
+**How can we resolve Collision here?**
+
+We can somehow store both 21 & 31 at the same index.
+
+Basically we can have a linked list at every index.
+i.e, Array of Linked List
+
+
+Every index shall have head node of Linked List.
+
+
+
+**The above method is known as Chaining.**
+
+* **Chaining** is a technique used in data structures, particularly hash tables, to resolve collisions. When multiple items hash to the same index, chaining stores them in a linked list or another data structure at that index.
+
+**What will be the Time Complexity of Insertion ?**
+
+* First we will pass the given element to Hash Function, which will return an index. Now, we will simply add that element to the Linked List at that index.
+* If we insert at **tail** => `O(N)`
+* If we insert at **head** => `O(1)`
+Since order of Insertion doesn't matter to us, so we can **simply insert at head**.
+
+**What will be the Time Complexity of Deletion and Searching ?**
+
+
+* Time Complexity on average is always less than $\lambda$. $\lambda$ is known as lamda.
+
+* Time Complexity in worst case is still O(N)
+
+---
+### What is lamda
+
+
+There is a lamba($\lambda$) function which is nothing but a ratio of (number of elements inserted / size of the array).
+
+**Example:**
+
+
+
+Table size(Array size) = 8
+Inserted Elements = 6
+
+$\lambda$ = $\frac{6}{8}$ = 0.75
+
+Let's assume the predefined threshold is 0.7. The load factor is exceeding this value, so we will need to rehash the table.
+
+**Rehashing:**
+
+* Create a new hash table with double the size of the original hash table. In this case, the new size will be
+* 8×2=16
+* Redistribute the existing elements to their new positions in the larger hash table using a new hash function.
+* The load factor is now recalculated for the new hash table:
+*
+$\lambda$ = $\frac{6}{16} = 0.375$ (within the threshold of 0.7)
+
+---
+### Code Implementation
+
+#### Declaring the HashMap Class
+
+Let's go through the code implementation of a hashmap:
+
+* The HashMap class is defined with generic types `K` and `V` for keys and values.
+* The inner class `HMNode` represents a node containing a key-value pair.
+* `buckets` is an array of ArrayLists to store key-value pairs.
+* `size` keeps track of the number of key-value pairs in the hashmap.
+* The `initbuckets()` method initializes the array of buckets with a default size of 4.
+
+```java
+import java.util.ArrayList;
+
+class HashMap < K, V > {
+
+ private class HMNode {
+ K key;
+ V value;
+
+ public HMNode(K key, V value) {
+ this.key = key;
+ this.value = value;
+ }
+ }
+
+ private ArrayList < HMNode > [] buckets;
+ private int size; // number of key-value pairs
+
+ public HashMap() {
+ initbuckets();
+ size = 0;
+ }
+
+ private void initbuckets() {
+ buckets = new ArrayList[4];
+ for (int i = 0; i < 4; i++) {
+ buckets[i] = new ArrayList < > ();
+ }
+ }
+```
+
+#### Put Method
+* The `put` method adds a key-value pair to the hashmap.
+* It calculates the bucket index (`bi`) using the `hash` method and finds the data index within the bucket using `getIndexWithinBucket`.
+* If the key is found in the bucket, it updates the value. Otherwise, it inserts a new node.
+* After inserting, it checks the load factor (`lambda`) and triggers rehashing if the load factor exceeds 2.0.
+
+```java
+ public void put(K key, V value) {
+ int bi = hash(key);
+ int di = getIndexWithinBucket(key, bi);
+
+ if (di != -1) {
+ // Key found, update the value
+ buckets[bi].get(di).value = value;
+ } else {
+ // Key not found, insert new key-value pair
+ HMNode newNode = new HMNode(key, value);
+ buckets[bi].add(newNode);
+ size++;
+
+ // Check for rehashing
+ double lambda = size * 1.0 / buckets.length;
+ if (lambda > 2.0) {
+ rehash();
+ }
+ }
+ }
+```
+
+#### Hash Method
+* The `hash` method calculates the bucket index using the hash code of the key and takes the modulus to ensure it stays within the array size.
+```java
+ private int hash(K key) {
+ int hc = key.hashCode();
+ int bi = Math.abs(hc) % buckets.length;
+ return bi;
+ }
+```
+
+#### Get Index within Bucket
+* The `getIndexWithinBucket` method searches for the data index (`di`) of a key within a specific bucket. It returns -1 if the key is not found
+```java
+ private int getIndexWithinBucket(K key, int bi) {
+ int di = 0;
+ for (HMNode node: buckets[bi]) {
+ if (node.key.equals(key)) {
+ return di; // Key found
+ }
+ di++;
+ }
+ return -1; // Key not found
+ }
+```
+
+#### Rehash Method
+
+* The `rehash` method is called when the load factor exceeds 2.0.
+* It creates a new array of buckets, initializes the size to 0, and iterates through the old buckets, reinserting each key-value pair into the new array.
+*
+```java
+ private void rehash() {
+ ArrayList < HMNode > [] oldBuckets = buckets;
+ initbuckets();
+ size = 0;
+
+ for (ArrayList < HMNode > bucket: oldBuckets) {
+ for (HMNode node: bucket) {
+ put(node.key, node.value);
+ }
+ }
+ }
+```
+
+#### Get Method
+
+* The `get` method retrieves the value associated with a given key. It calculates the bucket index and searches within the bucket to find the key.
+```java
+ public V get(K key) {
+ int bi = hash(key);
+ int di = getIndexWithinBucket(key, bi);
+
+ if (di != -1) {
+ return buckets[bi].get(di).value;
+ } else {
+ return null;
+ }
+ }
+```
+
+#### Contains Key Method
+
+* The `containsKey` method checks if a given key exists in the hashmap by calculating the bucket index and checking the data index within the bucket.
+
+```java
+ public boolean containsKey(K key) {
+ int bi = hash(key);
+ int di = getIndexWithinBucket(key, bi);
+
+ return di != -1;
+ }
+```
+
+#### Remove Method
+
+* The `remove` method removes a key-value pair from the hashmap. If the key is found, it returns the value; otherwise, it returns null
+
+```java
+ public V remove(K key) {
+ int bi = hash(key);
+ int di = getIndexWithinBucket(key, bi);
+
+ if (di != -1) {
+ // Key found, remove and return value
+ size--;
+ return buckets[bi].remove(di).value;
+ } else {
+ return null; // Key not found
+ }
+ }
+```
+
+#### Size Method
+The `size` method returns the total number of key-value pairs in the hashmap.
+
+```java
+ public int size() {
+ return size;
+ }
+```
+
+#### Key Set Method
+
+* The `keyset` method returns an ArrayList containing all the keys in the hashmap by iterating through the buckets and nodes.
+
+```java
+ public ArrayList < K > keyset() {
+ ArrayList < K > keys = new ArrayList < > ();
+ for (ArrayList < HMNode > bucket: buckets) {
+ for (HMNode node: bucket) {
+ keys.add(node.key);
+ }
+ }
+ return keys;
+ }
+ }
+```
+
+---
+### Question
+What is the time complexity of the brute-force approach for checking the existence of an element in the array for Q queries?
+
+**Choices**
+- [ ] O(N)
+- [ ] O(Q)
+- [x] O(N * Q)
+- [ ] O(1)
+
+---
+### Question
+What advantage does the Direct Access Table (DAT) provide in terms of time complexity for insertion, deletion, and search operations?
+
+**Choices**
+- [x] O(1) for all operations
+- [ ] O(N) for all operations
+- [ ] O(1) for insertion and deletion, O(N) for search
+- [ ] O(N) for insertion and deletion, O(1) for search
+
+---
+### Question
+What is the purpose of the load factor (lambda) in a hashmap?
+
+**Choices**
+- [ ] It represents the number of elements in the hashmap.
+- [ ] It is used to calculate the hash code of a key.
+- [x] It determines when to trigger rehashing.
+- [ ] It controls the size of the hashmap.
+
+
+---
+### Question
+What does the rehashing process involve in a hashmap?
+
+**Choices**
+- [ ] Reducing the size of the hashmap
+- [x] Creating a new hash table with double the size and redistributing elements
+- [ ] Deleting all elements from the hashmap
+- [ ] Removing collision resolution techniques
diff --git a/Academy DSA Typed Notes/Advanced/DSA Heaps 1 Introduction.md b/Academy DSA Typed Notes/Advanced/DSA Heaps 1 Introduction.md
new file mode 100644
index 0000000..ca30a99
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Heaps 1 Introduction.md
@@ -0,0 +1,557 @@
+# Advanced DSA: Heaps 1: Introduction
+
+---
+## Problem 1 Connecting the ropes
+
+We are given an array that represents the size of different ropes. In a single operation, you can connect two ropes. Cost of connecting two ropes is sum of the length of ropes you are connecting. Find the minimum cost of connecting all the ropes.
+
+**`To illustrate:`**
+
+**Example 1**:
+
+int A[] = {2, 5, 3, 2, 6}
+
+
+
+
+#### Pseudocode:
+```kotlin
+boolean targetSubarray(int arr[], int K) {
+ int N = arr.length;
+ long a = 0;
+
+ //cumulative sum, long -> to avoid overflow
+ HashSet < long > hs;
+ hs.add(0);
+ for (int i = 0; i < N; i++) {
+ a = a + arr[i];
+
+ //cumulative sum = target = a - k
+ if (hs.contains(a - K)) {
+ //subarray exists
+ return true;
+ } else {
+ hs.add(a);
+
+ }
+
+ }
+ return false;
+}
+
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(N)
+
+
+---
+### Problem 4 Distinct elements in every window of size K
+
+Given an array of integers and a number, K. Find the count of distinct elements in every window of size K in the array.
+
+**Example**
+
+```java
+// Input:
+Array = [1, 2, 1, 3, 4, 2, 3]
+K = 4
+
+// Output:
+[3, 4, 4, 3]
+```
+
+- In the first window `[1, 2, 1, 3]`, there are 3 distinct elements: 1, 2, and 3.
+- In the second window `[2, 1, 3, 4]`, there are 4 distinct elements: 2, 1, 3, and 4.
+- In the third window `[1, 3, 4, 2]`, there are again 4 distinct elements: 1, 3, 4, and 2.
+- In the fourth window `[3, 4, 2, 3]`, there are 3 distinct elements: 3, 4, and 2.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+#### Approach - Using HashSet
+
+- The code iterates through each possible window of size K in the given array.
+- For each window, a temporary HashSet (`distinctSet`) is created to store the distinct elements within that window.
+- Within the inner loop, the code adds each element of the window to the HashSet.
+- After processing the entire window, the size of the HashSet is calculated using `distinctSet.size()`, which represents the count of distinct elements.
+- The count is then added to the result list.
+- This process is repeated for all possible windows in the array.
+- The result list contains the count of distinct elements in each window
+
+#### Pseudocode
+
+```java
+//Pseudo code for 'countDistinctElements' function
+function countDistinctElements(arr, k):
+ result = empty list
+
+ for i = 0 to length of arr - k:
+ distinctSet = empty set
+
+ for j = i to i + k - 1:
+ add arr[j] to distinctSet
+
+ add size of distinctSet to result
+
+ return result
+```
+
+#### Complexity
+**Time Complexity:** `O((N-K+1) * K)`
+
+Considering the values of `K` as N/2, 1, and N.
+**When K = N/2:**
+ If `K` is about half of `N`, then the expression simplifies to `O((N/2 + 1) * N/2)`, which further simplifies to `O((N^2 + N) / 4)`. In this case, the primary factor is `N^2`, leading to a time complexity of approximately `O(N^2)`.
+**When K = 1:**
+ When `K` is set to 1, the expression becomes `O((N - 1 + 1) * 1)`, which straightforwardly simplifies to `O(N)`. It's important to note that this doesn't align with the original statement of the time complexity being `O(N^2)`.
+**When K = N:**
+ If `K` is equal to `N`, then the expression becomes `O((N - N + 1) * N)`, which further simplifies to `O(N^2)`.
+
+**Space Complexity:** O(K)
+
+---
+### Problem 4 Sliding Window - Map
+
+Sliding Window suggests to insert all elements of the first window in the set. Now slide the window, throw the prev element out and insert new adjacent element in the set.
+
+But we can't use Set here, since it is possible that the element just thrown out may be present in the current window.
+
+We will also need to maintain the frequency of elements, hence we will use Hashmap.
+
+- Maintain a HashMap to track the frequency of elements within the current subarray.
+- Initially, the algorithm populates the HashMap with the elements of the first subarray, counting distinct elements.
+- Then, as the window slides one step at a time:
+ - The algorithm updates the HashMap by updating frequency of the element leaving the window and increasing frequency of the new element entering the window.
+- The distinct element count for each subarray is determined by the size of the HashMap.
+
+#### Pseudocode
+
+```java
+void subfreq(int ar[], int k) {
+ int N = ar.length;
+
+ HashMap < int, int > hm;
+
+ // Step 1: Insert 1st subarray [0, k-1]
+ for (int i = 0; i < k; i++) {
+ //Increase frequecy by 1
+ if (hm.contains(ar[i])) {
+ int val = hm.get(ar[i]);
+ hm.put(ar[i], val + 1);
+ } else {
+ hm.put(ar[i], 1);
+ }
+
+ print(hm.size());
+ }
+
+ //step 2: Iterate all other subarrays
+ int s = 1, e = k;
+
+ while (e < N) {
+ //Remove ar[s-1]
+ int val = hm[ar[s - 1]];
+ hm[ar[s - 1]]--;
+
+ if (hm.get[ar[s - 1]] == 0) {
+ hm.remove(ar[s - 1]);
+ }
+
+ //add ar[e]
+ if (hm.contains(ar[e])) {
+ //Inc freq by 1
+ int val = hm[ar[e]];
+ hm[ar[e]]++;
+ } else {
+ hm.put(ar[e], 1);
+ }
+
+ print(hm.size());
+ s++
+
+ }
+}
+
+```
+#### Complexity
+**Time Complexity**: `O(n)`
+**Space Complexity**: `O(n)`
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Hashing 3 Internal Implementation & Problems.md b/Academy DSA Typed Notes/Advanced/DSA Hashing 3 Internal Implementation & Problems.md
new file mode 100644
index 0000000..4d84e85
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Hashing 3 Internal Implementation & Problems.md
@@ -0,0 +1,459 @@
+# Hashmap Implementation
+
+---
+## Check if given element exists in Q queries
+
+
+Given an array of size N and Q queries. In each query, an element is given. We have to check whether that element exists or not in the given array.
+
+**Example**
+
+A [ ] = {`2, 4, 11, 15 , 6, 8, 14, 9`}
+
+`4 Queries`
+`K = 4` (return true)
+`K = 10` (return false)
+`K = 17` (return false)
+`K = 14` (return true)
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Brute Force Approach
+
+For every query, loop through the given array to check the presence.
+
+Time Complexity - **O(N * Q)**
+Space Complexity - **O(1)**
+
+#### Observation
+
+We can create an array to mark the presence of an element against that particular index.
+
+A [ ] = {`2, 4, 11, 15 , 6, 8, 14, 9`}
+
+For example we can mark presence of
+2 at index 2
+4 at index 4 and so on....
+
+To execute that, we'll need to have indices till 15(max of Array).
+The array size needed is 16.
+
+Let's call that array as - DAT (Direct Access Table)
+int dat[16] = {0}; //initally assuming an element is not present
+
+| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
+| -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- |
+| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
+
+
+Let's mark the presence.
+```cpp
+for(int i = 0; i < N; i++) {
+ dat[A[i]] = 1;
+}
+```
+
+Below is how that array looks like -
+
+| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
+| -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- |
+| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
+
+#### Advantage of using DAT
+
+1. Time Complexity of Insertion - `O(1)`
+2. Time Complexity of Deletion - `O(1)`
+3. Time Complexity of Search - `O(1)`
+
+#### Issues with such a representation
+
+**1. Wastage of Space**
+* Say array is `A[] = {23, 60, 37, 90}`; now just to store presence of 4 elements, we'll have to construct an array of `size 91`.
+
+**2. Inability to create big Arrays**
+* If values in array are as big as $10^{15}$, then we will not be able to create this big array. At max array size possible is 10^6^(around)
+
+**3. Storing values other than positive Integers**
+* We'll have to make some adjustments to store negative numbers or characters. (It'll be possible but needs some work-around)
+
+---
+### Overcome Issues while retaining Advantages
+
+
+Let's say we have restriction of creating only array of size 10.
+
+Given Array -
+A [ ] = {`21, 42, 37, 45 , 99, 30`}
+
+**How can we do so ?**
+
+In array of size 10, we'll have indices from 0 to 9. How can we map all the values within this range ?
+
+**Basically, we can take a mod with 10.**
+
+21 % 10 = 1 (presence of 21 can be marked at index 1)
+
+42 % 10 = 2 (presence of 42 can be marked at index 2)
+
+37 % 10 = 7 (presence of 37 can be marked at index 7)
+
+45 % 10 = 5 (presence of 45 can be marked at index 5)
+
+99 % 10 = 9 (presence of 99 can be marked at index 9)
+
+30 % 10 = 0 (presence of 30 can be marked at index 0)
+
+| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
+| -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- | -------- |
+| 30 | 21 | 42 | 0 | 0 | 45 | 0 | 37 | 0 | 99 |
+
+
+#### What Have We Done ?
+
+* We have basically done Hashing. Hashing is a process where we pass our data through the Hash Funtion which gives us the hash value(index) to map our data to.
+* In this case, the hash function used is **MOD**. This is the simplest hash function. Usually, more complex hash functions are used.
+* The DAT that we created is known as **Hash Table** in terms of Hashing.
+
+
+
+#### Issue with Hashing ?
+
+**COLLISION!**
+
+Say given array is as follows -
+
+A [ ] = {21, 42, 37, 45, 77, 99, 31}
+
+Here, 21 & 31 will map to the same index => 1
+37 & 77 map to same index => 7
+
+
+**Can we completely avoid collision ?**
+
+`Not Really!`
+
+No matter how good a hash function is, we can't avoid collision!
+
+**Why ?**
+
+We are trying to map big values to a smaller range, collisions are bound to happen.
+
+Moreover, this can be explained using `Pigeon Hole Principle!`
+
+**Example -**
+
+Say we have 11 pigeons and we have only 8 holes to keep them. Now, provided holes are less, atleast 2 pigeons need to fit in a single hole.
+
+But, we can find some resolutions to collision.
+
+---
+### Collision Resolution Techniques
+
+
+
+
+
+>From Interview Perspective, Open Hashing is Important hence, we'll dive into that.
+
+
+
+---
+### Chaining
+
+
+Let's take the above problem where collision happened!
+
+A [ ] = {`21, 42, 37, 45, 77, 99, 31`}
+
+Here, 21 & 31 will map to the same index => 1
+37 & 77 map to same index => 7
+
+**How can we resolve Collision here?**
+
+We can somehow store both 21 & 31 at the same index.
+
+Basically we can have a linked list at every index.
+i.e, Array of Linked List
+
+
+Every index shall have head node of Linked List.
+
+
+
+**The above method is known as Chaining.**
+
+* **Chaining** is a technique used in data structures, particularly hash tables, to resolve collisions. When multiple items hash to the same index, chaining stores them in a linked list or another data structure at that index.
+
+**What will be the Time Complexity of Insertion ?**
+
+* First we will pass the given element to Hash Function, which will return an index. Now, we will simply add that element to the Linked List at that index.
+* If we insert at **tail** => `O(N)`
+* If we insert at **head** => `O(1)`
+Since order of Insertion doesn't matter to us, so we can **simply insert at head**.
+
+**What will be the Time Complexity of Deletion and Searching ?**
+
+
+* Time Complexity on average is always less than $\lambda$. $\lambda$ is known as lamda.
+
+* Time Complexity in worst case is still O(N)
+
+---
+### What is lamda
+
+
+There is a lamba($\lambda$) function which is nothing but a ratio of (number of elements inserted / size of the array).
+
+**Example:**
+
+
+
+Table size(Array size) = 8
+Inserted Elements = 6
+
+$\lambda$ = $\frac{6}{8}$ = 0.75
+
+Let's assume the predefined threshold is 0.7. The load factor is exceeding this value, so we will need to rehash the table.
+
+**Rehashing:**
+
+* Create a new hash table with double the size of the original hash table. In this case, the new size will be
+* 8×2=16
+* Redistribute the existing elements to their new positions in the larger hash table using a new hash function.
+* The load factor is now recalculated for the new hash table:
+*
+$\lambda$ = $\frac{6}{16} = 0.375$ (within the threshold of 0.7)
+
+---
+### Code Implementation
+
+#### Declaring the HashMap Class
+
+Let's go through the code implementation of a hashmap:
+
+* The HashMap class is defined with generic types `K` and `V` for keys and values.
+* The inner class `HMNode` represents a node containing a key-value pair.
+* `buckets` is an array of ArrayLists to store key-value pairs.
+* `size` keeps track of the number of key-value pairs in the hashmap.
+* The `initbuckets()` method initializes the array of buckets with a default size of 4.
+
+```java
+import java.util.ArrayList;
+
+class HashMap < K, V > {
+
+ private class HMNode {
+ K key;
+ V value;
+
+ public HMNode(K key, V value) {
+ this.key = key;
+ this.value = value;
+ }
+ }
+
+ private ArrayList < HMNode > [] buckets;
+ private int size; // number of key-value pairs
+
+ public HashMap() {
+ initbuckets();
+ size = 0;
+ }
+
+ private void initbuckets() {
+ buckets = new ArrayList[4];
+ for (int i = 0; i < 4; i++) {
+ buckets[i] = new ArrayList < > ();
+ }
+ }
+```
+
+#### Put Method
+* The `put` method adds a key-value pair to the hashmap.
+* It calculates the bucket index (`bi`) using the `hash` method and finds the data index within the bucket using `getIndexWithinBucket`.
+* If the key is found in the bucket, it updates the value. Otherwise, it inserts a new node.
+* After inserting, it checks the load factor (`lambda`) and triggers rehashing if the load factor exceeds 2.0.
+
+```java
+ public void put(K key, V value) {
+ int bi = hash(key);
+ int di = getIndexWithinBucket(key, bi);
+
+ if (di != -1) {
+ // Key found, update the value
+ buckets[bi].get(di).value = value;
+ } else {
+ // Key not found, insert new key-value pair
+ HMNode newNode = new HMNode(key, value);
+ buckets[bi].add(newNode);
+ size++;
+
+ // Check for rehashing
+ double lambda = size * 1.0 / buckets.length;
+ if (lambda > 2.0) {
+ rehash();
+ }
+ }
+ }
+```
+
+#### Hash Method
+* The `hash` method calculates the bucket index using the hash code of the key and takes the modulus to ensure it stays within the array size.
+```java
+ private int hash(K key) {
+ int hc = key.hashCode();
+ int bi = Math.abs(hc) % buckets.length;
+ return bi;
+ }
+```
+
+#### Get Index within Bucket
+* The `getIndexWithinBucket` method searches for the data index (`di`) of a key within a specific bucket. It returns -1 if the key is not found
+```java
+ private int getIndexWithinBucket(K key, int bi) {
+ int di = 0;
+ for (HMNode node: buckets[bi]) {
+ if (node.key.equals(key)) {
+ return di; // Key found
+ }
+ di++;
+ }
+ return -1; // Key not found
+ }
+```
+
+#### Rehash Method
+
+* The `rehash` method is called when the load factor exceeds 2.0.
+* It creates a new array of buckets, initializes the size to 0, and iterates through the old buckets, reinserting each key-value pair into the new array.
+*
+```java
+ private void rehash() {
+ ArrayList < HMNode > [] oldBuckets = buckets;
+ initbuckets();
+ size = 0;
+
+ for (ArrayList < HMNode > bucket: oldBuckets) {
+ for (HMNode node: bucket) {
+ put(node.key, node.value);
+ }
+ }
+ }
+```
+
+#### Get Method
+
+* The `get` method retrieves the value associated with a given key. It calculates the bucket index and searches within the bucket to find the key.
+```java
+ public V get(K key) {
+ int bi = hash(key);
+ int di = getIndexWithinBucket(key, bi);
+
+ if (di != -1) {
+ return buckets[bi].get(di).value;
+ } else {
+ return null;
+ }
+ }
+```
+
+#### Contains Key Method
+
+* The `containsKey` method checks if a given key exists in the hashmap by calculating the bucket index and checking the data index within the bucket.
+
+```java
+ public boolean containsKey(K key) {
+ int bi = hash(key);
+ int di = getIndexWithinBucket(key, bi);
+
+ return di != -1;
+ }
+```
+
+#### Remove Method
+
+* The `remove` method removes a key-value pair from the hashmap. If the key is found, it returns the value; otherwise, it returns null
+
+```java
+ public V remove(K key) {
+ int bi = hash(key);
+ int di = getIndexWithinBucket(key, bi);
+
+ if (di != -1) {
+ // Key found, remove and return value
+ size--;
+ return buckets[bi].remove(di).value;
+ } else {
+ return null; // Key not found
+ }
+ }
+```
+
+#### Size Method
+The `size` method returns the total number of key-value pairs in the hashmap.
+
+```java
+ public int size() {
+ return size;
+ }
+```
+
+#### Key Set Method
+
+* The `keyset` method returns an ArrayList containing all the keys in the hashmap by iterating through the buckets and nodes.
+
+```java
+ public ArrayList < K > keyset() {
+ ArrayList < K > keys = new ArrayList < > ();
+ for (ArrayList < HMNode > bucket: buckets) {
+ for (HMNode node: bucket) {
+ keys.add(node.key);
+ }
+ }
+ return keys;
+ }
+ }
+```
+
+---
+### Question
+What is the time complexity of the brute-force approach for checking the existence of an element in the array for Q queries?
+
+**Choices**
+- [ ] O(N)
+- [ ] O(Q)
+- [x] O(N * Q)
+- [ ] O(1)
+
+---
+### Question
+What advantage does the Direct Access Table (DAT) provide in terms of time complexity for insertion, deletion, and search operations?
+
+**Choices**
+- [x] O(1) for all operations
+- [ ] O(N) for all operations
+- [ ] O(1) for insertion and deletion, O(N) for search
+- [ ] O(N) for insertion and deletion, O(1) for search
+
+---
+### Question
+What is the purpose of the load factor (lambda) in a hashmap?
+
+**Choices**
+- [ ] It represents the number of elements in the hashmap.
+- [ ] It is used to calculate the hash code of a key.
+- [x] It determines when to trigger rehashing.
+- [ ] It controls the size of the hashmap.
+
+
+---
+### Question
+What does the rehashing process involve in a hashmap?
+
+**Choices**
+- [ ] Reducing the size of the hashmap
+- [x] Creating a new hash table with double the size and redistributing elements
+- [ ] Deleting all elements from the hashmap
+- [ ] Removing collision resolution techniques
diff --git a/Academy DSA Typed Notes/Advanced/DSA Heaps 1 Introduction.md b/Academy DSA Typed Notes/Advanced/DSA Heaps 1 Introduction.md
new file mode 100644
index 0000000..ca30a99
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Heaps 1 Introduction.md
@@ -0,0 +1,557 @@
+# Advanced DSA: Heaps 1: Introduction
+
+---
+## Problem 1 Connecting the ropes
+
+We are given an array that represents the size of different ropes. In a single operation, you can connect two ropes. Cost of connecting two ropes is sum of the length of ropes you are connecting. Find the minimum cost of connecting all the ropes.
+
+**`To illustrate:`**
+
+**Example 1**:
+
+int A[] = {2, 5, 3, 2, 6}
+
+ +
+**Example 2**:
+
+**`Initial Ropes: [2, 5, 6, 3]`**
+
+Connect 2 and 5 (Cost = 2 + 5 = 7)
+Total Cost: 7
+New Ropes: [7, 6, 3]
+Next Step: [7, 6, 3]
+
+Connect 7 and 6 (Cost = 7 + 6 = 13)
+Total Cost: 7 + 13 = 20
+New Ropes: [13, 3]
+Final Step: [13, 3]
+
+Connect 13 and 3 (Cost = 13 + 3 = 16)
+Total Cost: 20 + 16 = 36
+Final Rope: [16]
+
+This is one of the options for finding the cost of connecting all ropes, but we need to find the minimum cost of connecting all the ropes.
+
+
+#### Observation
+Say, we have 3 ropes, **`x < y < z`**
+Which 2 ropes should we connect first ?
+
+| Case | 1 | 2 |3|
+| --------| -------- | -------- |--|
+| Step 1 | x+y | x+z |y+z|
+| Step 2 | (x+y) + z | (x+z) + y |(y+z) + x|
+
+Comparing case 1 and 2, y and z are different, now since y < z, we can say cost of 1 < cost of 2.
+
+
+Comparing case 2 and 3, x and y are different, now since x < y, we can say cost of 2 < cost of 3.
+
+**`Conclusion:`** Connecting smaller length ropes gives us lesser cost.
+
+#### Process:
+
+**`Initial Setup:`** Start with an array of rope lengths, e.g., [2, 2, 3, 5, 6]. First, sort the array.
+
+**`Combining Ropes:`**
+
+- Continuously pick the two smallest ropes.
+- Combine these ropes, adding their lengths to find the cost.
+- Insert the combined rope back into the array at its correct position in sorted array.
+- Repeat until only one rope remains.
+
+We are basically applying **`insertion sort`**.
+
+**`Example Steps:`**
+
+- Combine ropes 2 and 2 (cost = 4). New array: [3, 4, 5, 6]. Total cost: 4.
+- Combine ropes 3 and 4 (cost = 7). New array: [5, 6, 7]. Total cost: 11.
+- Combine ropes 5 and 6 (cost = 11). New array: [7, 11]. Total cost: 22.
+- Combine ropes 7 and 11 (cost = 18). Final rope: 18. Total cost: 40.
+
+
+#### Complexity
+**Time Complexity:** O(N^2^)
+**Space Complexity:** O(1)
+
+---
+### Question
+What is the minimum cost of connecting all the ropes for the array [1, 2, 3, 4]?
+
+**Choices**
+- [x] 19
+- [ ] 20
+- [ ] 10
+- [ ] 0
+
+
+
+**Explanation**:
+
+**Always pick two of the smallest ropes and combine them.**
+
+After combining the two smallest ropes at every step, we need to sort an array again to get the two minimum-length ropes.
+
+1, 2, 3, 4; cost = 3
+3, 3, 4; sort: 3, 3, 4; cost = 6
+6, 4; sort: 4, 6; cost = 10
+
+Final Length: 10
+Total Cost = (3 + 6 + 10) = 19
+
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Connecting the ropes optimisation
+
+
+Heaps efficiently perform the necessary operations:
+
+- Insertion of elements in **`O(log n)`** time.
+- Extraction of the minimum element in **`O(log n)`** time.
+
+**`NOTE: We'll understand how we can achive the above complexities, for now assume heap to be a black box solving the above requirements for us in lesser time.`**
+
+Heap returns the min or max value depending upon it is a min heap or max heap.
+
+Say, for above problem, we use a min heap. At every step, it will give us the 2 small length ropes. Please note below steps for solving above problem.
+
+
+
+**Example 2**:
+
+**`Initial Ropes: [2, 5, 6, 3]`**
+
+Connect 2 and 5 (Cost = 2 + 5 = 7)
+Total Cost: 7
+New Ropes: [7, 6, 3]
+Next Step: [7, 6, 3]
+
+Connect 7 and 6 (Cost = 7 + 6 = 13)
+Total Cost: 7 + 13 = 20
+New Ropes: [13, 3]
+Final Step: [13, 3]
+
+Connect 13 and 3 (Cost = 13 + 3 = 16)
+Total Cost: 20 + 16 = 36
+Final Rope: [16]
+
+This is one of the options for finding the cost of connecting all ropes, but we need to find the minimum cost of connecting all the ropes.
+
+
+#### Observation
+Say, we have 3 ropes, **`x < y < z`**
+Which 2 ropes should we connect first ?
+
+| Case | 1 | 2 |3|
+| --------| -------- | -------- |--|
+| Step 1 | x+y | x+z |y+z|
+| Step 2 | (x+y) + z | (x+z) + y |(y+z) + x|
+
+Comparing case 1 and 2, y and z are different, now since y < z, we can say cost of 1 < cost of 2.
+
+
+Comparing case 2 and 3, x and y are different, now since x < y, we can say cost of 2 < cost of 3.
+
+**`Conclusion:`** Connecting smaller length ropes gives us lesser cost.
+
+#### Process:
+
+**`Initial Setup:`** Start with an array of rope lengths, e.g., [2, 2, 3, 5, 6]. First, sort the array.
+
+**`Combining Ropes:`**
+
+- Continuously pick the two smallest ropes.
+- Combine these ropes, adding their lengths to find the cost.
+- Insert the combined rope back into the array at its correct position in sorted array.
+- Repeat until only one rope remains.
+
+We are basically applying **`insertion sort`**.
+
+**`Example Steps:`**
+
+- Combine ropes 2 and 2 (cost = 4). New array: [3, 4, 5, 6]. Total cost: 4.
+- Combine ropes 3 and 4 (cost = 7). New array: [5, 6, 7]. Total cost: 11.
+- Combine ropes 5 and 6 (cost = 11). New array: [7, 11]. Total cost: 22.
+- Combine ropes 7 and 11 (cost = 18). Final rope: 18. Total cost: 40.
+
+
+#### Complexity
+**Time Complexity:** O(N^2^)
+**Space Complexity:** O(1)
+
+---
+### Question
+What is the minimum cost of connecting all the ropes for the array [1, 2, 3, 4]?
+
+**Choices**
+- [x] 19
+- [ ] 20
+- [ ] 10
+- [ ] 0
+
+
+
+**Explanation**:
+
+**Always pick two of the smallest ropes and combine them.**
+
+After combining the two smallest ropes at every step, we need to sort an array again to get the two minimum-length ropes.
+
+1, 2, 3, 4; cost = 3
+3, 3, 4; sort: 3, 3, 4; cost = 6
+6, 4; sort: 4, 6; cost = 10
+
+Final Length: 10
+Total Cost = (3 + 6 + 10) = 19
+
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Connecting the ropes optimisation
+
+
+Heaps efficiently perform the necessary operations:
+
+- Insertion of elements in **`O(log n)`** time.
+- Extraction of the minimum element in **`O(log n)`** time.
+
+**`NOTE: We'll understand how we can achive the above complexities, for now assume heap to be a black box solving the above requirements for us in lesser time.`**
+
+Heap returns the min or max value depending upon it is a min heap or max heap.
+
+Say, for above problem, we use a min heap. At every step, it will give us the 2 small length ropes. Please note below steps for solving above problem.
+
+ +
+#### Time & Space Complexity
+For every operation, we are removing 2 elements and inserting one back, hence it is 3 * log N. For N operations, **`the time complexity will be O(N * log N)`**
+
+**`Space Complexity is O(N)`**
+
+---
+## Heap Data Structure
+
+The heap data structure is a binary tree with two special properties.
+- First property is based on structure.
+ - **Complete Binary Tree:** All levels are completely filled. The last level can be the exception but is should also be filled from left to right.
+- Second property is based on the order of elements.
+ - **Heap Order Property:** In the case of max heap, the value of the parent is greater than the value of the children. And in the case of min heap, the value of the parent is less than the value of the children.
+
+
+**Examples**
+
+**`Example 1:`**
+
+
+
+#### Time & Space Complexity
+For every operation, we are removing 2 elements and inserting one back, hence it is 3 * log N. For N operations, **`the time complexity will be O(N * log N)`**
+
+**`Space Complexity is O(N)`**
+
+---
+## Heap Data Structure
+
+The heap data structure is a binary tree with two special properties.
+- First property is based on structure.
+ - **Complete Binary Tree:** All levels are completely filled. The last level can be the exception but is should also be filled from left to right.
+- Second property is based on the order of elements.
+ - **Heap Order Property:** In the case of max heap, the value of the parent is greater than the value of the children. And in the case of min heap, the value of the parent is less than the value of the children.
+
+
+**Examples**
+
+**`Example 1:`**
+
+ +
+- This is the complete binary tree as all the levels are filled and the last level is filled from left to right.
+- Heap Order Property is also valid at every point in the tree, as 5 is less than 12 and 20, 12 is less than 25 and 13, 20 is less than 24 and 22, 25 is less than 35 and 34.
+- Hence, it is a **min-heap**
+
+
+**`Example 2:`**
+
+
+
+- This is the complete binary tree as all the levels are filled and the last level is filled from left to right.
+- Heap Order Property is also valid at every point in the tree, as 5 is less than 12 and 20, 12 is less than 25 and 13, 20 is less than 24 and 22, 25 is less than 35 and 34.
+- Hence, it is a **min-heap**
+
+
+**`Example 2:`**
+
+ +
+- This is the complete binary tree as all the levels are filled and the last level is filled from left to right.
+- Heap Order Property is also valid at every point in the tree, as 58 is greater than 39 and 26, 39 is greater than 34 and 12, 26 is greater than 3 and 9, 34 is greater than 16 and 1.
+- Hence, it is a **max-heap.**
+
+---
+### Array Implementation of Trees(Complete Binary Tree)
+
+
+
+
+- This is the complete binary tree as all the levels are filled and the last level is filled from left to right.
+- Heap Order Property is also valid at every point in the tree, as 58 is greater than 39 and 26, 39 is greater than 34 and 12, 26 is greater than 3 and 9, 34 is greater than 16 and 1.
+- Hence, it is a **max-heap.**
+
+---
+### Array Implementation of Trees(Complete Binary Tree)
+
+
+ +
+- We shall store elements in the array in level order wise.
+- Such an array representation of tree is only possible if it is a complete binary tree.
+
+
+
+- We shall store elements in the array in level order wise.
+- Such an array representation of tree is only possible if it is a complete binary tree.
+
+ +
+- Index 0 has its children at index 1 and 2
+- Index 1 has its children at index 3 and 4
+- Index 2 has its children at index 5 and 6
+- Index 3 has its children at index 7 and 8
+
+**`For the particular node stored at the i index, the left child is at (i * 2 + 1 ) and the right child is at (i * 2 + 2 )`**.
+
+**`For any node i, its parent is at (i-1)/2.`**
+
+
+
+- Index 0 has its children at index 1 and 2
+- Index 1 has its children at index 3 and 4
+- Index 2 has its children at index 5 and 6
+- Index 3 has its children at index 7 and 8
+
+**`For the particular node stored at the i index, the left child is at (i * 2 + 1 ) and the right child is at (i * 2 + 2 )`**.
+
+**`For any node i, its parent is at (i-1)/2.`**
+
+ +
+---
+### Insertion in min heap
+
+
+
+
+---
+### Insertion in min heap
+
+
+ +
+|0|1|2|3|4|5|6|7|
+|-|-|-|-|-|-|-|-|
+|5|12|20|25|13|24|22|35|
+
+
+**Example 1**: Insert 10
+
+In an array, if we will insert 10 at index 8, then our array becomes,
+
+|0|1|2|3|4|5|6|7|8|
+|-|-|-|-|-|-|-|-|-|
+|5|12|20|25|13|24|22|35|10|
+
+
+
+And the tree becomes,
+
+
+
+|0|1|2|3|4|5|6|7|
+|-|-|-|-|-|-|-|-|
+|5|12|20|25|13|24|22|35|
+
+
+**Example 1**: Insert 10
+
+In an array, if we will insert 10 at index 8, then our array becomes,
+
+|0|1|2|3|4|5|6|7|8|
+|-|-|-|-|-|-|-|-|-|
+|5|12|20|25|13|24|22|35|10|
+
+
+
+And the tree becomes,
+
+ +
+Now tree satisfies the complete binary tree property but the tree does not satisfy the min-heap property, as here 25 > 10.
+
+In this case, we shall start with the inserted node and compare the parent with the child and keep swapping until the property is satisfied.
+
+Let us assume the node inserted at index `i` and the index of its parent is `pi`.
+```cpp
+if(arr[pi] > arr[i]) swap
+```
+
+> i = 8
+pi = (8-1)/2 = 3
+Since, (arr[3] > arr[8]) swap
+
+
+
+Now tree satisfies the complete binary tree property but the tree does not satisfy the min-heap property, as here 25 > 10.
+
+In this case, we shall start with the inserted node and compare the parent with the child and keep swapping until the property is satisfied.
+
+Let us assume the node inserted at index `i` and the index of its parent is `pi`.
+```cpp
+if(arr[pi] > arr[i]) swap
+```
+
+> i = 8
+pi = (8-1)/2 = 3
+Since, (arr[3] > arr[8]) swap
+
+ +
+|0|1|2|3|4|5|6|7|8|
+|-|-|-|-|-|-|-|-|-|
+|5|12|20|10|13|24|22|35|25|
+
+
+
+Now again we need to confirm whether the heap order property is satisfied or not by checking with its parent again.
+
+> i = 3
+pi = (3-1)/2 = 1
+Since, (arr[1] > arr[3]) swap
+
+
+
+|0|1|2|3|4|5|6|7|8|
+|-|-|-|-|-|-|-|-|-|
+|5|12|20|10|13|24|22|35|25|
+
+
+
+Now again we need to confirm whether the heap order property is satisfied or not by checking with its parent again.
+
+> i = 3
+pi = (3-1)/2 = 1
+Since, (arr[1] > arr[3]) swap
+
+ +
+|0|1|2|3|4|5|6|7|8|
+|-|-|-|-|-|-|-|-|-|
+|5|10|20|12|13|24|22|35|25|
+
+Now again we need to confirm whether the heap order property is satisfied or not by checking with its parent again.
+
+> i = 1
+pi = (3-1)/2 = 0
+Since, (arr[0] < arr[1]) no need to swap
+
+STOP
+
+Now this tree satisfies the min-heap order property.
+|0|1|2|3|4|5|6|7|8|
+|-|-|-|-|-|-|-|-|-|
+|5|10|20|12|13|24|22|35|25|
+
+
+
+|0|1|2|3|4|5|6|7|8|
+|-|-|-|-|-|-|-|-|-|
+|5|10|20|12|13|24|22|35|25|
+
+Now again we need to confirm whether the heap order property is satisfied or not by checking with its parent again.
+
+> i = 1
+pi = (3-1)/2 = 0
+Since, (arr[0] < arr[1]) no need to swap
+
+STOP
+
+Now this tree satisfies the min-heap order property.
+|0|1|2|3|4|5|6|7|8|
+|-|-|-|-|-|-|-|-|-|
+|5|10|20|12|13|24|22|35|25|
+
+ +
+**Example 2**: Insert 3
+
+First insert 3 at index 9.
+
+|0|1|2|3|4|5|6|7|8|9|
+|-|-|-|-|-|-|-|-|-|-|
+|5|10|20|12|13|24|22|35|25|3|
+
+- Compare index 9 and parent index ((9-1)/2)= 4 value, as arr[4] > arr[9], swap.
+- Now again compare index 4 and , parent index((4-1)/2)=1 arr[1]>arr[4], swap again.
+- Now again compare index 1 and , parent index((1-1)/2)=0 arr[0]>arr[1], swap again.
+- Now zero index does not have any parent so stop.
+
+
+
+
+**Example 2**: Insert 3
+
+First insert 3 at index 9.
+
+|0|1|2|3|4|5|6|7|8|9|
+|-|-|-|-|-|-|-|-|-|-|
+|5|10|20|12|13|24|22|35|25|3|
+
+- Compare index 9 and parent index ((9-1)/2)= 4 value, as arr[4] > arr[9], swap.
+- Now again compare index 4 and , parent index((4-1)/2)=1 arr[1]>arr[4], swap again.
+- Now again compare index 1 and , parent index((1-1)/2)=0 arr[0]>arr[1], swap again.
+- Now zero index does not have any parent so stop.
+
+
+ +
+|0|1|2|3|4|5|6|7|8|9|
+|-|-|-|-|-|-|-|-|-|-|
+|3|5|20|12|10|24|22|35|25|13|
+
+
+**`NOTE: The maximum swap we can perform for any element to be inserted is equal to the height of the tree.`**
+
+---
+### Question
+
+Time Complexity of inserting an element in a heap having n nodes?
+
+**Choices**
+
+- [ ] O(1)
+- [x] O(log n)
+- [ ] O(sqrt n)
+- [ ] O(n)
+
+
+---
+### Inserting in min heap pseudocode
+#### Pseudocode
+```cpp
+heap[];
+heap.insert(val); // inserting at last
+i = heap.size - 1;
+while (i > 0) {
+ pi = (i - 1) / 2;
+ if (heap[pi] > heap[i]) {
+ swap(heap, pi, i);
+ i = pi;
+ } else {
+ break;
+ }
+}
+```
+
+#### Complexity
+**Time Complexity:** O(height of tree) = O(logN)
+
+
+---
+### Extract Min
+
+
+**`Min Heap -`**
+
+
+|0|1|2|3|4|5|6|7|8|9|
+|-|-|-|-|-|-|-|-|-|-|
+|3|5|20|12|10|24|22|35|25|13|
+
+
+**`NOTE: The maximum swap we can perform for any element to be inserted is equal to the height of the tree.`**
+
+---
+### Question
+
+Time Complexity of inserting an element in a heap having n nodes?
+
+**Choices**
+
+- [ ] O(1)
+- [x] O(log n)
+- [ ] O(sqrt n)
+- [ ] O(n)
+
+
+---
+### Inserting in min heap pseudocode
+#### Pseudocode
+```cpp
+heap[];
+heap.insert(val); // inserting at last
+i = heap.size - 1;
+while (i > 0) {
+ pi = (i - 1) / 2;
+ if (heap[pi] > heap[i]) {
+ swap(heap, pi, i);
+ i = pi;
+ } else {
+ break;
+ }
+}
+```
+
+#### Complexity
+**Time Complexity:** O(height of tree) = O(logN)
+
+
+---
+### Extract Min
+
+
+**`Min Heap -`**
+ +
+|0|1|2|3|4|5|6|7|8|
+|-|-|-|-|-|-|-|-|-|
+|2|4|5|11|6|7|8|20|12|
+
+
+In this tree, we have a minimum element at the root. First we swap the first and last elements, then remove the last index element of an array virtually, i.e. consider your array from index 0 to N-2.
+
+
+
+|0|1|2|3|4|5|6|7|8|
+|-|-|-|-|-|-|-|-|-|
+|2|4|5|11|6|7|8|20|12|
+
+
+In this tree, we have a minimum element at the root. First we swap the first and last elements, then remove the last index element of an array virtually, i.e. consider your array from index 0 to N-2.
+
+ +
+
+
+ +
+But the tree is not satisfying the heap-order property. To regain this heap-order property, first check 12, 4 and 5, the minimum is 4, so swap 12 with 4.
+
+
+
+But the tree is not satisfying the heap-order property. To regain this heap-order property, first check 12, 4 and 5, the minimum is 4, so swap 12 with 4.
+
+ +
+- Now check the index 1(12) value, it greater than index 3(11) and index 4(6), so we need to swap this value with the minimum of left and right child i.e. 6.
+
+
+
+- Now check the index 1(12) value, it greater than index 3(11) and index 4(6), so we need to swap this value with the minimum of left and right child i.e. 6.
+
+ +
+- Now index 4(12) does not have any child, so we will stop here. **`Now the heap-order property is regained.`**
+
+
+
+- Now index 4(12) does not have any child, so we will stop here. **`Now the heap-order property is regained.`**
+
+ +
+**`NOTE to Instructor: Perform extract-min again for more clarity on above tree.`**
+
+
+#### Pseudocode
+```cpp
+swap(heap, 0, heap - size() - 1)
+heap.remove(heap.size() - 1)
+heapify(heap[], 0);
+
+void heapify(heap[], i) {
+ while (2 i + 1 < N) { //need to handle the edge case when left child is there but not the right child
+ x = min(heap[i], heap[2 i + 1], heap[2 i + 2])
+
+ if (x == heap[i]) {
+ break
+ } else if (x == heap[2 i + 1]) {
+ swap(heap, i, 2 i + 1)
+ i = 2 i + 1
+ } else {
+ swap(heap, i, 2 i + 2)
+ i = 2 i + 2
+ }
+ }
+}
+```
+
+
+#### Complexity
+**Time Complexity:** O(log N)
+
+
+---
+### Build a heap
+
+We have an array of values, we want to make a heap of it.
+**`[5, 13, -2, 11, 27, 31, 0, 19]`**
+
+#### Idea 1
+Sort the array.
+[-2, 0, 5, 11, 13, 19, 27, 31]
+
+Looking at the tree below, we can see this is a heap.
+
+
+
+**`NOTE to Instructor: Perform extract-min again for more clarity on above tree.`**
+
+
+#### Pseudocode
+```cpp
+swap(heap, 0, heap - size() - 1)
+heap.remove(heap.size() - 1)
+heapify(heap[], 0);
+
+void heapify(heap[], i) {
+ while (2 i + 1 < N) { //need to handle the edge case when left child is there but not the right child
+ x = min(heap[i], heap[2 i + 1], heap[2 i + 2])
+
+ if (x == heap[i]) {
+ break
+ } else if (x == heap[2 i + 1]) {
+ swap(heap, i, 2 i + 1)
+ i = 2 i + 1
+ } else {
+ swap(heap, i, 2 i + 2)
+ i = 2 i + 2
+ }
+ }
+}
+```
+
+
+#### Complexity
+**Time Complexity:** O(log N)
+
+
+---
+### Build a heap
+
+We have an array of values, we want to make a heap of it.
+**`[5, 13, -2, 11, 27, 31, 0, 19]`**
+
+#### Idea 1
+Sort the array.
+[-2, 0, 5, 11, 13, 19, 27, 31]
+
+Looking at the tree below, we can see this is a heap.
+
+ +
+
+**`Time Complexity: O(N * logN)`**
+
+
+#### Idea 2
+Call insert(arr[i]) for every element of an array.
+
+**Explanation:**
+When insert(val) is called, at every insert we shall make sure heap property is being satisfied.
+
+It will take N * logN, as for each element, we will take O(log N) as heapify shall be called.
+
+**`Time Complexity:O(N * logN)`**
+
+--
+### Build a heap Idea 3
+
+#### Idea to build in linear time
+
+We have an array
+**`[7, 3, 5, 1, 6, 8, 10, 2, 13, 14, -2]`**
+
+We can represent this array in the form of a tree.
+
+
+
+
+**`Time Complexity: O(N * logN)`**
+
+
+#### Idea 2
+Call insert(arr[i]) for every element of an array.
+
+**Explanation:**
+When insert(val) is called, at every insert we shall make sure heap property is being satisfied.
+
+It will take N * logN, as for each element, we will take O(log N) as heapify shall be called.
+
+**`Time Complexity:O(N * logN)`**
+
+--
+### Build a heap Idea 3
+
+#### Idea to build in linear time
+
+We have an array
+**`[7, 3, 5, 1, 6, 8, 10, 2, 13, 14, -2]`**
+
+We can represent this array in the form of a tree.
+
+ +
+- In the above tree, the heap-order property is automatically valid for the leaf node, hence no need to heapify them.
+- Rather, we shall start with the first non-leaf node.
+- The first non-leaf is nothing but the parent of the last leaf node of the tree and the index of the last node is $n-1$, so the index of the first non-leaf is $((n-1-1)/2)=((n-2)/2)=(n/2)-1$.
+- We will call heapify() starting from for $(n/2)-1$ index to index 0.
+
+```cpp
+for (int i = (n / 2) - 1; i >= 0; i--) {
+ heapify(heap[], i);
+}
+```
+
+
+- Firstly it will call for i = 4(6), `heapfiy(heap[], 4)`, minimum of 6, 14, -2 is -2 so 6 and -2 will be swapped.
+
+
+- In the above tree, the heap-order property is automatically valid for the leaf node, hence no need to heapify them.
+- Rather, we shall start with the first non-leaf node.
+- The first non-leaf is nothing but the parent of the last leaf node of the tree and the index of the last node is $n-1$, so the index of the first non-leaf is $((n-1-1)/2)=((n-2)/2)=(n/2)-1$.
+- We will call heapify() starting from for $(n/2)-1$ index to index 0.
+
+```cpp
+for (int i = (n / 2) - 1; i >= 0; i--) {
+ heapify(heap[], i);
+}
+```
+
+
+- Firstly it will call for i = 4(6), `heapfiy(heap[], 4)`, minimum of 6, 14, -2 is -2 so 6 and -2 will be swapped.
+ +
+ - Now 6 does not have any children so we will stop here.
+
+- Call heapify for i = 3(1), now we will check minimum of 1, 2, 13 is 1, so here min-heap property is already satisfied.
+
+- Call heapify for i = 2(5), minimum of 5, 8, 10 is 5 and it is at index 2, so here min-heap property is already satisfied.
+
+- Call heapify for i = 1, minimum of 3, 1, -2 is -2 and so swap.
+
+
+ - Now 6 does not have any children so we will stop here.
+
+- Call heapify for i = 3(1), now we will check minimum of 1, 2, 13 is 1, so here min-heap property is already satisfied.
+
+- Call heapify for i = 2(5), minimum of 5, 8, 10 is 5 and it is at index 2, so here min-heap property is already satisfied.
+
+- Call heapify for i = 1, minimum of 3, 1, -2 is -2 and so swap.
+ +
+ - Now we will again check for 3, and 3 is less than 14 and 6, so here heap-order property is valid here.
+
+- Call heapify for i = 0, here also heap-order property is not satisfied as -2 is less than 7, so swap.
+
+
+ - Now we will again check for 3, and 3 is less than 14 and 6, so here heap-order property is valid here.
+
+- Call heapify for i = 0, here also heap-order property is not satisfied as -2 is less than 7, so swap.
+ +
+ - Now again check for 7, here minimum of 7, 1 and 3 is 1, so again swap it.
+
+
+ - Now again check for 7, here minimum of 7, 1 and 3 is 1, so again swap it.
+ +
+
+ - Now again check for minimum of 7, 2 and 13 is 2, so again swap it.
+
+
+
+ - Now again check for minimum of 7, 2 and 13 is 2, so again swap it.
+ +
+- Now 7 does not have any child so stop here.
+- Now all the nodes has valid heap-order property.
+
+
+#### Time Complexity
+
+
+
+- Now 7 does not have any child so stop here.
+- Now all the nodes has valid heap-order property.
+
+
+#### Time Complexity
+
+ +
+Total Number of elements in tree = N
+Elements at last level = N/2
+
+
+
+Total Number of elements in tree = N
+Elements at last level = N/2
+
+ +
+- We are not calling heapify() for the last level(leaf node), So for the leaf node, total swaps are 0.
+- For the last second level, we have N/4 nodes and at maximum, there can be 1 swap for these nodes i.e. with the last level.
+- And maximum swaps for N/8 level nodes 2.
+- Similar, for the root node, maximum swaps can be equal to the height of the tree.
+
+
+
+- We are not calling heapify() for the last level(leaf node), So for the leaf node, total swaps are 0.
+- For the last second level, we have N/4 nodes and at maximum, there can be 1 swap for these nodes i.e. with the last level.
+- And maximum swaps for N/8 level nodes 2.
+- Similar, for the root node, maximum swaps can be equal to the height of the tree.
+
+ +
+
+
+
+
+ +
+Here it is an Arithmetic Geometric progression. We need to find the sum of
+
+
+Here it is an Arithmetic Geometric progression. We need to find the sum of
+ +
+Multiply both sides by 1/2
+
+
+Multiply both sides by 1/2
+ +
+Now subtract the above two equations
+
+
+
+Now subtract the above two equations
+
+ +
+Here we are using the formula of the sum of GP.
+
+And put the value of the sum in this equation
+
+
+Here we are using the formula of the sum of GP.
+
+And put the value of the sum in this equation
+ +
+Then
+(N/2) * 2
+Here both will cancel out with each other and so our overall time complexity for building a heap is **O(N)**
+
+---
+### Question
+What is the time complexity for building a heap with N nodes?
+
+**Choices**
+- [ ] O(1)
+- [ ] O(N$^2$)
+- [x] O(N)
+- [ ] O(logN)
+
+
+
+---
+
+
+### Merge N-sorted arrays
+a - [2, 3, 11, 15, 20]
+b - [1, 5, 7, 9]
+c - [0, 2, 4]
+d - [3, 4, 5, 6, 7, 8]
+e - [-2, 5, 10, 20]
+
+We have to merge these sorted arrays.
+
+#### Idea
+- If we want to merge two sorted arrays then we need two pointers.
+- If we want to merge three sorted arrays then we need three pointers.
+- If we want to merge N sorted arrays then we need N pointers, in which complexity becomes very high and we need to keep track of N pointers.
+
+---
+### Question
+For merging N sorted arrays, which data structure would be the most efficient for this task ?
+
+**Choices**
+- [ ] Linked List
+- [ ] Array
+- [x] Min-Heap
+- [ ] Hash Table
+
+**Explanation:**
+
+A Min-Heap is an efficient data structure choice. The Min-Heap ensures that the smallest element among all the elements in the arrays is always at the front. This allows for constant-time access to the minimum element, making it efficient to extract and merge elements in sorted order.
+
+:::warning
+Please take some time to think about the optimised approach on your own before reading further.....
+:::
+
+#### Optimized Solution
+- First, we need to compare the 0th index element of every array.
+- Now we use heap here.
+- We will add an index 0 element of every array in the heap, in the form of element value, array number and Index of the element in particular.
+
+
+
+Then
+(N/2) * 2
+Here both will cancel out with each other and so our overall time complexity for building a heap is **O(N)**
+
+---
+### Question
+What is the time complexity for building a heap with N nodes?
+
+**Choices**
+- [ ] O(1)
+- [ ] O(N$^2$)
+- [x] O(N)
+- [ ] O(logN)
+
+
+
+---
+
+
+### Merge N-sorted arrays
+a - [2, 3, 11, 15, 20]
+b - [1, 5, 7, 9]
+c - [0, 2, 4]
+d - [3, 4, 5, 6, 7, 8]
+e - [-2, 5, 10, 20]
+
+We have to merge these sorted arrays.
+
+#### Idea
+- If we want to merge two sorted arrays then we need two pointers.
+- If we want to merge three sorted arrays then we need three pointers.
+- If we want to merge N sorted arrays then we need N pointers, in which complexity becomes very high and we need to keep track of N pointers.
+
+---
+### Question
+For merging N sorted arrays, which data structure would be the most efficient for this task ?
+
+**Choices**
+- [ ] Linked List
+- [ ] Array
+- [x] Min-Heap
+- [ ] Hash Table
+
+**Explanation:**
+
+A Min-Heap is an efficient data structure choice. The Min-Heap ensures that the smallest element among all the elements in the arrays is always at the front. This allows for constant-time access to the minimum element, making it efficient to extract and merge elements in sorted order.
+
+:::warning
+Please take some time to think about the optimised approach on your own before reading further.....
+:::
+
+#### Optimized Solution
+- First, we need to compare the 0th index element of every array.
+- Now we use heap here.
+- We will add an index 0 element of every array in the heap, in the form of element value, array number and Index of the element in particular.
+
+ +
+Now take the minimum element and insert it in the resultant array,
+
+- Now insert the next element of the list for which the minimum element is selected, like first, we have taken the fourth list element, so now insert the next element of the fourth list.
+
+
+
+Now take the minimum element and insert it in the resultant array,
+
+- Now insert the next element of the list for which the minimum element is selected, like first, we have taken the fourth list element, so now insert the next element of the fourth list.
+
+ +
+- Now again extract-min() from the heap and insert the next element of that list to which the minimum element belongs.
+- And keep repeating this until we have done with all the elements.
+
+#### Time Complexity
+**Time Complexity:** (XlogN)
+Here X is a total number of elements of all arrays.
\ No newline at end of file
diff --git a/Academy DSA Typed Notes/Advanced/DSA Heaps 2 Problems.md b/Academy DSA Typed Notes/Advanced/DSA Heaps 2 Problems.md
new file mode 100644
index 0000000..1f2099f
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Heaps 2 Problems.md
@@ -0,0 +1,567 @@
+# Advanced DSA: Heaps 2: Problems
+
+---
+## Problem 1 Sort an Array
+
+We want to sort an array in increasing order using a heap.
+
+
+
+### Idea
+We can use min-heap, and we need to call `extract-min()`/`remove(`) repeatedly many times, `extract-min()` will every time give the minimum element among all the available elements.
+1. Build a min-heap.
+2. `extract-min()` and store the returned value in the `ans` array until all the elements are not deleted.
+
+
+---
+### Question
+
+What is the time Complexity to convert an array to a heap?
+
+**Choices**
+
+- [ ] O(1)
+- [ ] O(log n)
+- [x] O(n)
+- [ ] O(nlog(n))
+
+
+
+---
+### Question
+Root element in a heap is ?
+
+**Choices**
+- [ ] min element of the array
+- [ ] max element of the array
+- [x] either min or max depending upon whether it is min or max heap
+- [ ] random element of the array
+
+**Explanation**:
+
+Either min or max depending upon whether it is min or max heap. Min-Heap has minimum element at the root node, where as Max-Heap has maximum element at the root node.
+
+
+
+---
+### Sort an Array Complexity and Solution Approach
+
+#### Complexity of sorting an array using heap
+1. Build a min-heap -> **Complexity:** `O(n)`
+2. `extract-min()` and store the returned value in the `ans` array until all the elements are not deleted.
+3. Complexity of `extract-min()` is `O(logn)` and we are calling `N` times, so the overall complexity is `O(NlogN)`.
+
+#### Complexity
+- **Time Complexity:** O(NlogN)
+- **Space Complexity:** O(N), as we are using another array for building the heap.
+
+#### Can we optimize the space complexity?
+
+**`Hint: Try to solve by using `max-heap`.`**
+
+- Let us take an example of `max-heap`
+
+>
+
+- Now again extract-min() from the heap and insert the next element of that list to which the minimum element belongs.
+- And keep repeating this until we have done with all the elements.
+
+#### Time Complexity
+**Time Complexity:** (XlogN)
+Here X is a total number of elements of all arrays.
\ No newline at end of file
diff --git a/Academy DSA Typed Notes/Advanced/DSA Heaps 2 Problems.md b/Academy DSA Typed Notes/Advanced/DSA Heaps 2 Problems.md
new file mode 100644
index 0000000..1f2099f
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Heaps 2 Problems.md
@@ -0,0 +1,567 @@
+# Advanced DSA: Heaps 2: Problems
+
+---
+## Problem 1 Sort an Array
+
+We want to sort an array in increasing order using a heap.
+
+
+
+### Idea
+We can use min-heap, and we need to call `extract-min()`/`remove(`) repeatedly many times, `extract-min()` will every time give the minimum element among all the available elements.
+1. Build a min-heap.
+2. `extract-min()` and store the returned value in the `ans` array until all the elements are not deleted.
+
+
+---
+### Question
+
+What is the time Complexity to convert an array to a heap?
+
+**Choices**
+
+- [ ] O(1)
+- [ ] O(log n)
+- [x] O(n)
+- [ ] O(nlog(n))
+
+
+
+---
+### Question
+Root element in a heap is ?
+
+**Choices**
+- [ ] min element of the array
+- [ ] max element of the array
+- [x] either min or max depending upon whether it is min or max heap
+- [ ] random element of the array
+
+**Explanation**:
+
+Either min or max depending upon whether it is min or max heap. Min-Heap has minimum element at the root node, where as Max-Heap has maximum element at the root node.
+
+
+
+---
+### Sort an Array Complexity and Solution Approach
+
+#### Complexity of sorting an array using heap
+1. Build a min-heap -> **Complexity:** `O(n)`
+2. `extract-min()` and store the returned value in the `ans` array until all the elements are not deleted.
+3. Complexity of `extract-min()` is `O(logn)` and we are calling `N` times, so the overall complexity is `O(NlogN)`.
+
+#### Complexity
+- **Time Complexity:** O(NlogN)
+- **Space Complexity:** O(N), as we are using another array for building the heap.
+
+#### Can we optimize the space complexity?
+
+**`Hint: Try to solve by using `max-heap`.`**
+
+- Let us take an example of `max-heap`
+
+>  +
+- Create an array for this max-heap.
+
+>
+
+- Create an array for this max-heap.
+
+>  +
+- Say, we extract an element, which element will we get? The Maximum!
+Now, the maximum element can be swapped with the last index. This way, maximum element will come at its correct position in sorted array.
+
+>
+
+- Say, we extract an element, which element will we get? The Maximum!
+Now, the maximum element can be swapped with the last index. This way, maximum element will come at its correct position in sorted array.
+
+>  +
+- Now we will virtually remove the last element, which means we consider an array till the second last element of an array.
+
+- Now, since the tree is not satisfying the heap order property, so we will call `heapify()` for index 0.
+
+- So when we call `heapify()`, firstly 3 is swapped with 13(maximum of 13 and 10).
+
+>
+
+- Now we will virtually remove the last element, which means we consider an array till the second last element of an array.
+
+- Now, since the tree is not satisfying the heap order property, so we will call `heapify()` for index 0.
+
+- So when we call `heapify()`, firstly 3 is swapped with 13(maximum of 13 and 10).
+
+>  +
+- Now again 3 is swapped with 7.
+
+>
+
+- Now again 3 is swapped with 7.
+
+>  +
+- Now 3 is the maximum among 3, 2 and 1. Hence, no further swaps are needed.
+Now we have an array,
+
+>
+
+- Now 3 is the maximum among 3, 2 and 1. Hence, no further swaps are needed.
+Now we have an array,
+
+>  +
+- As we know now a maximum of all available elements is present at root, call `extract-max()`, swap maximum element with the last index element(index 8) and then we will call heapify for the value 1.
+
+>
+
+- As we know now a maximum of all available elements is present at root, call `extract-max()`, swap maximum element with the last index element(index 8) and then we will call heapify for the value 1.
+
+>  +
+- 1 is swapped with 10, then swapped with 8, after that 1 will reach to its correct position.
+
+>
+
+- 1 is swapped with 10, then swapped with 8, after that 1 will reach to its correct position.
+
+>  +
+- Again extract the maximum and swap it with the last(7th) index element. Then call Heapify for it.
+
+In this way, repeat these steps we completed with all the elements of the tree.
+
+
+---
+### Sort an Array PseudoCode
+
+#### PseudoCode
+```cpp
+Build max - heap-- -> TC: O(N)
+j = N - 1;
+while (j > 0) {
+ swap(A[0], A[j]);
+ j--;
+ heapify(0, arr[], j)
+}
+```
+
+#### Complexity
+
+- **Time Complexity:** O(NlogN)
+- **Space Complexity:** O(1), we are not taking an extra array, we are converting the max heap into sorted array.
+
+
+#### Is heap sort an in-place sorting algorithm?
+**Answer:** Yes it is in-place as we are sorting an array using heap sort in constant time in the above question.
+
+#### Is heap sort a stable sorting algorithm?
+**Answer:** No heap sort is not stable.
+**Explanation:** Heap sort is not stable because operations in the heap can change the relative order of equivalent keys.
+
+---
+### Problem 2 kth Largest Element
+
+Given arr[N], find the kth largest element.
+
+
+**Example**
+**Input:**
+arr[] = [8, 5, 1, 2, 4, 9, 7]
+k = 3
+
+
+**Output:**
+7
+
+**Explanation:**
+In the above array,
+- First largest element = 9
+- Second largest element = 8
+- Third largest element = 7
+
+We need to return the third largest element.
+
+
+---
+### Question
+
+What is the 5th largest element of an array `[1, 2, 3, 4, 5]`?
+
+**Choices**
+
+- [ ] 5
+- [ ] 3
+- [x] 1
+- [ ] 2
+
+
+**Explanation**
+In the above array,
+- First largest element = 5
+- Second largest element = 4
+- Third largest element = 3
+- Fourth largest element = 2
+- Fifth largest element = 1
+
+We need to return the fifth largest element.
+
+
+---
+### kth Largest Element solution approach
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### :bulb: Idea 1(by sorting)
+Sort an array and simply return arr[N-K].
+
+**Example:**
+arr[] = [8, 5, 1, 2, 4, 9, 7]
+k = 3
+
+**Solution**
+Sort an array, [1, 2, 4, 5, 7, 8, 9]
+Now return arr[N-K] element i.e. arr[7-3] = arr[4] = 7
+
+**Time Complexity:** O(NlogN), **Space Complexity:** O(1).
+
+### :bulb: Idea 2(Using binary search)
+
+We can find the kth largest element by applying binary search just like we have used in the kth smallest element.
+**Time Complexity:** O(Nlog(max-min))
+
+### :bulb: Idea 3(Using heap sort)
+
+1. Build a max-heap.
+2. Call extract-max() k-1 times to remove K-1 elements(for first largest we need zero removals, for second largest we need 1 removal, in this way for kth largest we need k-1 removals)
+
+### Complexity
+**Time Complexity:** O(N + KlogN)
+**Space Complexity:** O(1)
+
+---
+### kth Largest Element Using min-heap
+
+### :bulb: Idea 4(Using min-heap)
+
+Let us take an example, we want to create a cricket team of 4 batsmen and we have 8 batsmen i.e. b1, b2, b3, b4, b5, b6, b7 and b8, and every batsman is given only 1 over and everyone tries to achieve maximum run in that over.
+
+Firstly, 4 batsmen played and scored
+|b1|b2|b3|b4|
+|-|-|-|-|
+|12|8|4|6|
+
+We have recently incorporated four batsmen into our team with respective scores of **`12, 8, 4, and 6`**. When batsman **`B5 joins, scoring 7`**, we opt to replace the player with the lowest score to maintain team quality. Since we use a min heap to track scores, we **`remove the batsman with a score of 4 and include B5`**, updating our heap to **[12, 8, 7, 6]**.
+
+Later, batsman **`B6 arrives, earning 3 runs`**. However, his score **`doesn't surpass our team's minimum`**, so he isn't added. Then, batsman **`B7 steps in, scoring a notable 10 runs`**. Outperforming our lowest score, **`B7's addition leads us to drop the current minimum`** scorer and update the heap to **[12, 8, 7, 10]**.
+
+Following this, batsman **`B8 enters with a score of 9`**. Exceeding the lowest score in our lineup, we **`incorporate B8 by removing the now lowest scorer`**, refining our heap to **[12, 8, 9, 10]**.
+
+Thus, in this dynamic team selection process, the minimum element in our heap represents the fourth-highest score among our players.
+
+#### Example:
+To find the 3rd largest element in an array using a min-heap of size 3:
+
+Given array: **`arr = [8, 5, 1, 2, 4, 9, 7] and k=3`**.
+
+- Initialize an empty min-heap.
+- Add the first three elements of the array to the heap: [8, 5, 1].
+- Iterate over the remaining elements. If an element is greater than the heap's minimum, remove the minimum and insert the new element.
+- After processing elements 2, 4, 9, and 7, the heap evolves as follows:
+ - [8, 5, 2] (after adding 2)
+ - [8, 5, 4] (after adding 4)
+ - [8, 5, 9] (after adding 9)
+ - [8, 7, 9] (after adding 7)
+- The 3rd largest element is the minimum in the heap: 7.
+
+#### PseudoCode
+```cpp
+Build min-heap with first k elements. -> O(K)
+Iterate on the remaining elements. -> (N-K)
+ for every element, check
+ if(curr element > min element in heap){
+ extractMin()
+ insert(current element)
+ }
+ans = getMin()
+```
+
+#### Complexity
+- **Time Complexity:** O(K+(N-K)logK)
+- **Space Complexity:** O(K)
+
+:bulb: What should we use for finding k-th smallest?
+- A max-heap of size K.
+
+
+---
+### Problem 2 kth Largest Element for all windows
+
+Find the kth largest element for all the windows of an array starting from 0 index.
+
+**Example**
+**Input:**
+arr[] = `[10, 18, 7, 5, 16, 19, 3]`
+k = 3
+
+
+**Solution:**
+
+- We need atleast 3 elements in a window, so we will consider first window from index 0 to k-1, we have elements in that `[10, 18, 7]`; third largest is 7, ans=`[7]`.
+- Window 0 to 3 `[10, 18, 7, 5]`,third largest = 7, ans=`[7, 7]`.
+- Window 0 to 4 `[10, 18, 7, 5, 16]`,third largest = 10, ans=`[7, 7, 10]`.
+- Window 0 to 5 `[10, 18, 7, 5, 16, 19]`,third largest = 16, ans=`[7, 7, 10, 16]`.
+- Window 0 to 6 `[10, 18, 7, 5, 16, 19, 3]`,third largest = 16, ans=`[7, 7, 10, 16, 16]`.
+
+---
+### Question
+Find the kth largest element for all the windows of an array starting from 0 index.
+
+arr[] = `[5, 4, 1, 6, 7]`
+k = 2
+
+**Choices**
+- [x] [4, 4, 5, 6]
+- [ ] [6, 6, 6, 6]
+- [ ] [5, 4, 1, 6]
+- [ ] [4, 1, 6, 7]
+
+
+
+**Explanation**:
+To find the second largest element in each window of a given size in an array:
+
+- Start with the first window (from index 0 to k-1). For example, in [5, 4], the second largest is 4. Answer array starts as [4].
+- Shift the window one element at a time and find the second largest in each new window.
+ - Window [5, 4, 1] gives second largest 4. Answer array becomes [4, 4].
+ - Window [5, 4, 1, 6] gives second largest 5. Answer array becomes [4, 4, 5].
+ - Window [5, 4, 1, 6, 7] gives second largest 6. Answer array becomes [4, 4, 5, 6].
+
+---
+### kth Largest Element for all windows Idea
+
+To find the k-largest elements in an array using a min-heap:
+
+- **Initialize Min-Heap**: Start with a min-heap and add the first k elements from the array to it.
+- **Compare and Update**: For each remaining array element, if it's larger than the heap's minimum, replace the minimum with this element.
+- **Track Minimums**: After each update, record the heap's minimum. This shows the evolving k-th largest element.
+
+#### Pseudocode
+```java
+Build min-heap with first K elements. -> O(K)
+ans.add(extractMin())
+
+Iterate on the remaining elements. -> (N-K)
+ for every element, check {
+ if(curr element > min element in heap){
+ extractMin()
+ insert(current element)
+ ans.add(extractMin())
+ }
+ }
+```
+
+---
+### Problem 3 Sort the nearly sorted array
+
+
+Given a nearly sorted array. You need to sort the array.
+
+> Nearly sorted array definition - Every element is shifted away from its correct position by at most k-steps.
+
+**Example**
+Sorted array can be `[11, 13, 20, 22, 31, 45, 48, 50, 60]`
+We are given,
+**Input:**
+arr[] = `[13, 22, 31, 45, 11, 20, 48, 60, 50]`
+k = 4
+
+Every element is not more than 4 distance away from its position.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### :bulb: Idea 1(Sorting)
+Sort an Array
+**Time Complexity:** O(NlogN)
+
+#### :bulb: Idea 2
+
+An element can be shifted by at most k steps, so the **`element at index 0 can only be shifted till index (k)`**, so the **`minimum element lies from index 0 to k`**.
+- So we need to choose a minimum of first k+1 elements.
+- We will take a min-heap of size k+1.
+- Add first k+1 elements into a heap, heap = `[13, 22, 31, 45, 11]`.
+- extractMin()(heap = `[13, 22, 31, 45]`) will give a first element of a sorted array, ans = `[11]`, now add the next element from an input array, into a heap, heap = `[13, 22, 31, 45, 20]`.
+- Again extractMin(), it will give a second of a sorted array, ans = `[11, 13]`, again add the next element of the input array, again extractMin(), in this way do until we reach the last index, and then remove minimum element from array one-by-one and add it to ans array.
+
+
+#### PseudoCode
+```cpp
+1. build min-heap with the first (k + 1) elements.
+2. for(i = k + 1 ; i < N ; i ++){
+ extractMin(); -> put it into ans[] array
+ insert( arr[i] )
+ }
+ while(minHeap is not empty){
+ extractMin() -> put it into ans[] array
+ }
+3. return ans;
+```
+
+#### Compexity
+**Time Complexity:** O(K + N.logK)
+**Space Complexity:** O(K)
+
+
+---
+### Flipkart's Delivery Time Estimation Challenge
+
+
+*Flipkart is currently dealing with the difficulty of precisely estimating and displaying the expected delivery time for orders to a specific pin code.*
+
+*The existing method relies on historical delivery time data for that pin code, using the median value as the expected delivery time.*
+
+*As the order history expands with new entries, Flipkart aims to enhance this process by dynamically updating the expected delivery time whenever a new delivery time is added. The objective is to find the expected delivery time after each new element is incorporated into the list of delivery times.*
+
+**End Goal:** With every addition of new delivery time, requirement is to find the median value.
+
+**Why Median ?**
+The median is calculated because it provides a more robust measure of the expected delivery time
+
+The median is less sensitive to outliers or extreme values than the mean. In the context of delivery times, this is crucial because occasional delays or unusually fast deliveries (outliers) can skew the mean significantly, leading to inaccurate estimations.
+
+---
+### Problem 4 Find the median
+
+Given an infinite stream of integers. Find the median of the current set of elements
+
+>### Median
+>Median is the Middle element in a sorted array.
+
+>The median of [1, 2, 5, 4, 3, 6]
+First, we need to sort an array [1, 2, 3, 4, 5, 6]
+We have two middle values as the size of the array is even i.e. 3, 4.
+So to find the median, we need to take the average of both middle values, median = (3+4)/2 = 3.5
+
+---
+### Question
+
+The median of [1, 2, 4, 3]
+
+**Choices**
+
+- [ ] 2
+- [ ] 4
+- [ ] 3
+- [x] 2.5
+
+**Explanation**:
+
+The median of [1, 2, 4, 3]
+First, we need to sort an array [1, 2, 3, 4]
+We have two middle values as the size of the array is even i.e. 2, 3.
+So to find the median, we need to take the average of both middle values,
+
+Median = (2+3)/2 = 2.5
+
+---
+### Find the median Brute Force Approach
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Understanding the question
+We have an infinite stream of elements.
+1. First we have one element.
+6, then median = 6.
+2. Next element if 3
+6, 3, then median = 4.5
+3. 6, 3, 8, then median = 6
+4. 6, 3, 8, 11, then median = 7
+5. 6, 3, 8, 11, 10 then median = 8
+
+
+#### Brute Force Idea
+For every incoming value, include the value and sort an array. Find the middle point/average of 2 middle points.
+**Time Complexity:** O(N^2^logN)
+
+
+---
+### Find the median solution approach
+
+#### Idea(Using Insertion Sort)
+Every time find the correct position of the upcoming element i.e. Insertion Sort
+
+**Time Complexity:** O(N^2^)
+
+#### Idea(Using heap)
+
+To find the median in an array by dividing it into two parts - one with smaller elements and the other with larger elements:
+
+Consider an array, **`for example, [6, 3, 8, 11]`**. We divide it such that **`6, 3 are on the smaller side`** and **`8, 11 on the larger side`**, as shown in the image:
+
+
+- Again extract the maximum and swap it with the last(7th) index element. Then call Heapify for it.
+
+In this way, repeat these steps we completed with all the elements of the tree.
+
+
+---
+### Sort an Array PseudoCode
+
+#### PseudoCode
+```cpp
+Build max - heap-- -> TC: O(N)
+j = N - 1;
+while (j > 0) {
+ swap(A[0], A[j]);
+ j--;
+ heapify(0, arr[], j)
+}
+```
+
+#### Complexity
+
+- **Time Complexity:** O(NlogN)
+- **Space Complexity:** O(1), we are not taking an extra array, we are converting the max heap into sorted array.
+
+
+#### Is heap sort an in-place sorting algorithm?
+**Answer:** Yes it is in-place as we are sorting an array using heap sort in constant time in the above question.
+
+#### Is heap sort a stable sorting algorithm?
+**Answer:** No heap sort is not stable.
+**Explanation:** Heap sort is not stable because operations in the heap can change the relative order of equivalent keys.
+
+---
+### Problem 2 kth Largest Element
+
+Given arr[N], find the kth largest element.
+
+
+**Example**
+**Input:**
+arr[] = [8, 5, 1, 2, 4, 9, 7]
+k = 3
+
+
+**Output:**
+7
+
+**Explanation:**
+In the above array,
+- First largest element = 9
+- Second largest element = 8
+- Third largest element = 7
+
+We need to return the third largest element.
+
+
+---
+### Question
+
+What is the 5th largest element of an array `[1, 2, 3, 4, 5]`?
+
+**Choices**
+
+- [ ] 5
+- [ ] 3
+- [x] 1
+- [ ] 2
+
+
+**Explanation**
+In the above array,
+- First largest element = 5
+- Second largest element = 4
+- Third largest element = 3
+- Fourth largest element = 2
+- Fifth largest element = 1
+
+We need to return the fifth largest element.
+
+
+---
+### kth Largest Element solution approach
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### :bulb: Idea 1(by sorting)
+Sort an array and simply return arr[N-K].
+
+**Example:**
+arr[] = [8, 5, 1, 2, 4, 9, 7]
+k = 3
+
+**Solution**
+Sort an array, [1, 2, 4, 5, 7, 8, 9]
+Now return arr[N-K] element i.e. arr[7-3] = arr[4] = 7
+
+**Time Complexity:** O(NlogN), **Space Complexity:** O(1).
+
+### :bulb: Idea 2(Using binary search)
+
+We can find the kth largest element by applying binary search just like we have used in the kth smallest element.
+**Time Complexity:** O(Nlog(max-min))
+
+### :bulb: Idea 3(Using heap sort)
+
+1. Build a max-heap.
+2. Call extract-max() k-1 times to remove K-1 elements(for first largest we need zero removals, for second largest we need 1 removal, in this way for kth largest we need k-1 removals)
+
+### Complexity
+**Time Complexity:** O(N + KlogN)
+**Space Complexity:** O(1)
+
+---
+### kth Largest Element Using min-heap
+
+### :bulb: Idea 4(Using min-heap)
+
+Let us take an example, we want to create a cricket team of 4 batsmen and we have 8 batsmen i.e. b1, b2, b3, b4, b5, b6, b7 and b8, and every batsman is given only 1 over and everyone tries to achieve maximum run in that over.
+
+Firstly, 4 batsmen played and scored
+|b1|b2|b3|b4|
+|-|-|-|-|
+|12|8|4|6|
+
+We have recently incorporated four batsmen into our team with respective scores of **`12, 8, 4, and 6`**. When batsman **`B5 joins, scoring 7`**, we opt to replace the player with the lowest score to maintain team quality. Since we use a min heap to track scores, we **`remove the batsman with a score of 4 and include B5`**, updating our heap to **[12, 8, 7, 6]**.
+
+Later, batsman **`B6 arrives, earning 3 runs`**. However, his score **`doesn't surpass our team's minimum`**, so he isn't added. Then, batsman **`B7 steps in, scoring a notable 10 runs`**. Outperforming our lowest score, **`B7's addition leads us to drop the current minimum`** scorer and update the heap to **[12, 8, 7, 10]**.
+
+Following this, batsman **`B8 enters with a score of 9`**. Exceeding the lowest score in our lineup, we **`incorporate B8 by removing the now lowest scorer`**, refining our heap to **[12, 8, 9, 10]**.
+
+Thus, in this dynamic team selection process, the minimum element in our heap represents the fourth-highest score among our players.
+
+#### Example:
+To find the 3rd largest element in an array using a min-heap of size 3:
+
+Given array: **`arr = [8, 5, 1, 2, 4, 9, 7] and k=3`**.
+
+- Initialize an empty min-heap.
+- Add the first three elements of the array to the heap: [8, 5, 1].
+- Iterate over the remaining elements. If an element is greater than the heap's minimum, remove the minimum and insert the new element.
+- After processing elements 2, 4, 9, and 7, the heap evolves as follows:
+ - [8, 5, 2] (after adding 2)
+ - [8, 5, 4] (after adding 4)
+ - [8, 5, 9] (after adding 9)
+ - [8, 7, 9] (after adding 7)
+- The 3rd largest element is the minimum in the heap: 7.
+
+#### PseudoCode
+```cpp
+Build min-heap with first k elements. -> O(K)
+Iterate on the remaining elements. -> (N-K)
+ for every element, check
+ if(curr element > min element in heap){
+ extractMin()
+ insert(current element)
+ }
+ans = getMin()
+```
+
+#### Complexity
+- **Time Complexity:** O(K+(N-K)logK)
+- **Space Complexity:** O(K)
+
+:bulb: What should we use for finding k-th smallest?
+- A max-heap of size K.
+
+
+---
+### Problem 2 kth Largest Element for all windows
+
+Find the kth largest element for all the windows of an array starting from 0 index.
+
+**Example**
+**Input:**
+arr[] = `[10, 18, 7, 5, 16, 19, 3]`
+k = 3
+
+
+**Solution:**
+
+- We need atleast 3 elements in a window, so we will consider first window from index 0 to k-1, we have elements in that `[10, 18, 7]`; third largest is 7, ans=`[7]`.
+- Window 0 to 3 `[10, 18, 7, 5]`,third largest = 7, ans=`[7, 7]`.
+- Window 0 to 4 `[10, 18, 7, 5, 16]`,third largest = 10, ans=`[7, 7, 10]`.
+- Window 0 to 5 `[10, 18, 7, 5, 16, 19]`,third largest = 16, ans=`[7, 7, 10, 16]`.
+- Window 0 to 6 `[10, 18, 7, 5, 16, 19, 3]`,third largest = 16, ans=`[7, 7, 10, 16, 16]`.
+
+---
+### Question
+Find the kth largest element for all the windows of an array starting from 0 index.
+
+arr[] = `[5, 4, 1, 6, 7]`
+k = 2
+
+**Choices**
+- [x] [4, 4, 5, 6]
+- [ ] [6, 6, 6, 6]
+- [ ] [5, 4, 1, 6]
+- [ ] [4, 1, 6, 7]
+
+
+
+**Explanation**:
+To find the second largest element in each window of a given size in an array:
+
+- Start with the first window (from index 0 to k-1). For example, in [5, 4], the second largest is 4. Answer array starts as [4].
+- Shift the window one element at a time and find the second largest in each new window.
+ - Window [5, 4, 1] gives second largest 4. Answer array becomes [4, 4].
+ - Window [5, 4, 1, 6] gives second largest 5. Answer array becomes [4, 4, 5].
+ - Window [5, 4, 1, 6, 7] gives second largest 6. Answer array becomes [4, 4, 5, 6].
+
+---
+### kth Largest Element for all windows Idea
+
+To find the k-largest elements in an array using a min-heap:
+
+- **Initialize Min-Heap**: Start with a min-heap and add the first k elements from the array to it.
+- **Compare and Update**: For each remaining array element, if it's larger than the heap's minimum, replace the minimum with this element.
+- **Track Minimums**: After each update, record the heap's minimum. This shows the evolving k-th largest element.
+
+#### Pseudocode
+```java
+Build min-heap with first K elements. -> O(K)
+ans.add(extractMin())
+
+Iterate on the remaining elements. -> (N-K)
+ for every element, check {
+ if(curr element > min element in heap){
+ extractMin()
+ insert(current element)
+ ans.add(extractMin())
+ }
+ }
+```
+
+---
+### Problem 3 Sort the nearly sorted array
+
+
+Given a nearly sorted array. You need to sort the array.
+
+> Nearly sorted array definition - Every element is shifted away from its correct position by at most k-steps.
+
+**Example**
+Sorted array can be `[11, 13, 20, 22, 31, 45, 48, 50, 60]`
+We are given,
+**Input:**
+arr[] = `[13, 22, 31, 45, 11, 20, 48, 60, 50]`
+k = 4
+
+Every element is not more than 4 distance away from its position.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### :bulb: Idea 1(Sorting)
+Sort an Array
+**Time Complexity:** O(NlogN)
+
+#### :bulb: Idea 2
+
+An element can be shifted by at most k steps, so the **`element at index 0 can only be shifted till index (k)`**, so the **`minimum element lies from index 0 to k`**.
+- So we need to choose a minimum of first k+1 elements.
+- We will take a min-heap of size k+1.
+- Add first k+1 elements into a heap, heap = `[13, 22, 31, 45, 11]`.
+- extractMin()(heap = `[13, 22, 31, 45]`) will give a first element of a sorted array, ans = `[11]`, now add the next element from an input array, into a heap, heap = `[13, 22, 31, 45, 20]`.
+- Again extractMin(), it will give a second of a sorted array, ans = `[11, 13]`, again add the next element of the input array, again extractMin(), in this way do until we reach the last index, and then remove minimum element from array one-by-one and add it to ans array.
+
+
+#### PseudoCode
+```cpp
+1. build min-heap with the first (k + 1) elements.
+2. for(i = k + 1 ; i < N ; i ++){
+ extractMin(); -> put it into ans[] array
+ insert( arr[i] )
+ }
+ while(minHeap is not empty){
+ extractMin() -> put it into ans[] array
+ }
+3. return ans;
+```
+
+#### Compexity
+**Time Complexity:** O(K + N.logK)
+**Space Complexity:** O(K)
+
+
+---
+### Flipkart's Delivery Time Estimation Challenge
+
+
+*Flipkart is currently dealing with the difficulty of precisely estimating and displaying the expected delivery time for orders to a specific pin code.*
+
+*The existing method relies on historical delivery time data for that pin code, using the median value as the expected delivery time.*
+
+*As the order history expands with new entries, Flipkart aims to enhance this process by dynamically updating the expected delivery time whenever a new delivery time is added. The objective is to find the expected delivery time after each new element is incorporated into the list of delivery times.*
+
+**End Goal:** With every addition of new delivery time, requirement is to find the median value.
+
+**Why Median ?**
+The median is calculated because it provides a more robust measure of the expected delivery time
+
+The median is less sensitive to outliers or extreme values than the mean. In the context of delivery times, this is crucial because occasional delays or unusually fast deliveries (outliers) can skew the mean significantly, leading to inaccurate estimations.
+
+---
+### Problem 4 Find the median
+
+Given an infinite stream of integers. Find the median of the current set of elements
+
+>### Median
+>Median is the Middle element in a sorted array.
+
+>The median of [1, 2, 5, 4, 3, 6]
+First, we need to sort an array [1, 2, 3, 4, 5, 6]
+We have two middle values as the size of the array is even i.e. 3, 4.
+So to find the median, we need to take the average of both middle values, median = (3+4)/2 = 3.5
+
+---
+### Question
+
+The median of [1, 2, 4, 3]
+
+**Choices**
+
+- [ ] 2
+- [ ] 4
+- [ ] 3
+- [x] 2.5
+
+**Explanation**:
+
+The median of [1, 2, 4, 3]
+First, we need to sort an array [1, 2, 3, 4]
+We have two middle values as the size of the array is even i.e. 2, 3.
+So to find the median, we need to take the average of both middle values,
+
+Median = (2+3)/2 = 2.5
+
+---
+### Find the median Brute Force Approach
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Understanding the question
+We have an infinite stream of elements.
+1. First we have one element.
+6, then median = 6.
+2. Next element if 3
+6, 3, then median = 4.5
+3. 6, 3, 8, then median = 6
+4. 6, 3, 8, 11, then median = 7
+5. 6, 3, 8, 11, 10 then median = 8
+
+
+#### Brute Force Idea
+For every incoming value, include the value and sort an array. Find the middle point/average of 2 middle points.
+**Time Complexity:** O(N^2^logN)
+
+
+---
+### Find the median solution approach
+
+#### Idea(Using Insertion Sort)
+Every time find the correct position of the upcoming element i.e. Insertion Sort
+
+**Time Complexity:** O(N^2^)
+
+#### Idea(Using heap)
+
+To find the median in an array by dividing it into two parts - one with smaller elements and the other with larger elements:
+
+Consider an array, **`for example, [6, 3, 8, 11]`**. We divide it such that **`6, 3 are on the smaller side`** and **`8, 11 on the larger side`**, as shown in the image:
+ +
+To find the median:
+
+- If both sides have an equal number of elements, take the average of the largest element on the smaller side and the smallest element on the larger side.
+- If the sizes are unequal, choose the largest element from the smaller side if it's larger, or the smallest from the larger side otherwise.
+
+**The key is to use two heaps:** a min-heap for the larger elements and a max-heap for the smaller elements. This approach maintains a balanced partition of the array for efficient median calculation.
+
+**Example**
+arr = [6, 3, 8, 11, 20, 2, 10, 8, 13, 50, _ _ _ ]
+
+Take two heaps, min-heap and max-heap
+
+
+To find the median:
+
+- If both sides have an equal number of elements, take the average of the largest element on the smaller side and the smallest element on the larger side.
+- If the sizes are unequal, choose the largest element from the smaller side if it's larger, or the smallest from the larger side otherwise.
+
+**The key is to use two heaps:** a min-heap for the larger elements and a max-heap for the smaller elements. This approach maintains a balanced partition of the array for efficient median calculation.
+
+**Example**
+arr = [6, 3, 8, 11, 20, 2, 10, 8, 13, 50, _ _ _ ]
+
+Take two heaps, min-heap and max-heap
+ +
+Smaller side elements are stored in max-heap and Greater side elements are stored in min-heap
+
+
+1. First element is 6, simply add it in max-heap
+
+
+Smaller side elements are stored in max-heap and Greater side elements are stored in min-heap
+
+
+1. First element is 6, simply add it in max-heap
+ +**The median is 6.**
+
+
+2. Second element is 3; compare with h1.getMax(), if 3<6 then it must be included in h1.
+
+**The median is 6.**
+
+
+2. Second element is 3; compare with h1.getMax(), if 3<6 then it must be included in h1.
+ +but now both the heaps do not have half-half elements. Remove the maximum element from max-heap and insert it into h2.
+
+but now both the heaps do not have half-half elements. Remove the maximum element from max-heap and insert it into h2.
+ +Now we have an equal number of elements in both heaps, so the median is the average of the largest value of h1 and the smallest value of h2.
+**Median is 4.5**
+
+
+3. Next element is 8.
+Compare it with h1.getMax(), 8>3 so 8 will go to h2.
+
+Now we have an equal number of elements in both heaps, so the median is the average of the largest value of h1 and the smallest value of h2.
+**Median is 4.5**
+
+
+3. Next element is 8.
+Compare it with h1.getMax(), 8>3 so 8 will go to h2.
+ +size(h2) is greater by 1
+**Median is 6**
+
+
+4. Next element is 11.
+Compare it with h1.getMax(), 11>3 so 11 will go to h2.
+
+size(h2) is greater by 1
+**Median is 6**
+
+
+4. Next element is 11.
+Compare it with h1.getMax(), 11>3 so 11 will go to h2.
+ +But now both heap does not have nearly half elements.
+So remove the minimum element and add it to h1.
+
+But now both heap does not have nearly half elements.
+So remove the minimum element and add it to h1.
+ +**Median is average of 6,8 = (6+8)/2 = 7**
+
+
+5. Next element is 20.
+Compare it with h1.getMax(), 20>6 so 20 will go to h2.
+
+**Median is average of 6,8 = (6+8)/2 = 7**
+
+
+5. Next element is 20.
+Compare it with h1.getMax(), 20>6 so 20 will go to h2.
+ +size(h2) is greater by 1
+**The median is 8.**
+
+In this way we will do for all the elements of an array, and find the median at every step, we need to take care that the |h1.size()-h2.size()|<=1.
+
+After adding all the medians in an array, we will get an answer: [6, 4.5, 6, 7, 8, 7, 8, 8, 8, _ _ _ ]
+
+
+---
+#### PseudoCode
+```cpp
+ h1, h2
+ h1.insert(arr[0])
+ print(arr[0])
+ for (int i = 1; i < N; i++) {
+ if (arr[i] > h1.getMax()) {
+ h2.insert(arr[i]);
+ } else {
+ h1.insert(arr[i]);
+ }
+ diff = | h1.size() - h2.size() |
+ if (diff > 1) {
+ if (h1.size() > h2.size()) {
+ h2.insert(h1.getMax());
+ } else {
+ h1.insert(h2.getMin());
+ }
+ }
+ if (h1.size() > h2.size()) {
+ print(h1.getMax());
+ } else if (h2.size() > h1.size()) {
+ print(h2.getMin())
+ } else {
+ print((h1.getMax() + h2.getMin()) / 2.0);
+ }
+ }
+```
+
+#### Complexity
+
+**Time Complexity:** O(NlogN)
+**Space Complexity:** O(N)
diff --git a/Academy DSA Typed Notes/Advanced/DSA Interview Problems.md b/Academy DSA Typed Notes/Advanced/DSA Interview Problems.md
new file mode 100644
index 0000000..f78bae7
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Interview Problems.md
@@ -0,0 +1,351 @@
+# DSA 4 - Interview Problems
+
+---
+### Problem 1 Target Sum
+
+You are given a set of non-negative integers and a target sum. The task is to determine whether there exists a subset of the given set whose sum is equal to the target sum.
+
+
+**Examples**
+**Input**: set = {3, 34, 4, 12, 5, 2}, sum = 9
+**Output**: True
+**Explanation**: There is a subset (4, 5) with a sum of 9.
+
+:::warning
+Please take some time to think about the brute force approach on your own before reading further.....
+:::
+
+#### Approach: Brute Force
+The brute force approach involves exploring all possible subsets of the given set. This is achieved through a recursive function named isSubsetSum(set, n, sum). The function explores two possibilities for each element: including it in the subset or excluding it. The base cases check if the sum is zero or if there are no more elements to consider.
+
+
+#### Code
+```java
+boolean isSubsetSum(int[] set, int n, int sum) {
+ if (sum == 0) return true;
+ if (n == 0 && sum != 0) return false;
+
+ // Explore two possibilities: include the current element or exclude it
+ return isSubsetSum(set, n - 1, sum) || isSubsetSum(set, n - 1, sum - set[n - 1]);
+}
+
+```
+
+#### Complexity Analysis
+* **Time complexity**: O(2^n) - Exponential
+* **Space complexity**: O(1)
+
+---
+### Target Sum Dynamic Programming Approach
+#### Approach:
+To optimize the solution, dynamic programming is employed. A 2D array `dp` is used to store results of subproblems. The value `dp[i][j]` represents whether it's possible to obtain a sum of `j` using the first `i` elements of the set.
+
+#### Code
+```java
+boolean isSubsetSum(int[] set, int n, int sum) {
+ boolean[][] dp = new boolean[n + 1][sum + 1];
+
+ // Initialize the first column as true, as sum 0 is always possible
+ for (int i = 0; i <= n; i++) dp[i][0] = true;
+
+ // Fill the dp array using a bottom-up approach
+ for (int i = 1; i <= n; i++) {
+ for (int j = 1; j <= sum; j++) {
+ dp[i][j] = dp[i - 1][j];
+ if (j >= set[i - 1]) dp[i][j] = dp[i][j] || dp[i - 1][j - set[i - 1]];
+ }
+ }
+
+ return dp[n][sum];
+}
+
+```
+
+#### Complexity Analysis
+* **Time complexity**: O(n * sum)
+* **Space complexity**: O(n * sum)
+
+---
+### Problem 2 Minimum Jumps to Reach End
+
+You are given a 0-indexed array of integers nums of length n. You are initially positioned at nums[0].
+
+Each element nums[i] represents the maximum length of a forward jump from index i. In other words, if you are at nums[i], you can jump to any nums[i + j] where:
+* 0 <= j <= nums[i]
+* i + j < n
+
+Return the minimum number of jumps to reach nums[n - 1]. The test cases are generated such that you can reach nums[n - 1].
+
+
+#### Example 1
+**Input**: nums = [2,3,1,1,4]
+**Output**: 2
+**Explanation**: The minimum number of jumps to reach the last index is 2. Jump 1 step from index 0 to 1, then 3 steps to the last index.
+
+#### Example 2
+**Input**: nums = [2,3,0,1,4]
+**Output**: 2
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Intuition
+
+The code utilizes a greedy approach, aiming to minimize the number of jumps by selecting the jump that maximizes the range of reachable positions at each step.
+
+#### Approach
+* Initialize a counter to keep track of the number of jumps (counter).
+* Use a while loop to iterate through the array until the end is reached.
+* In each iteration:
+ * Calculate the range of positions that can be reached from the current position (range).
+ * If the calculated range includes the last position or exceeds it, exit the loop.
+ * Find the position within the current range that maximizes the next reachable position (temp).
+ * Update the current position to the selected position (temp).
+ * Increment the jump counter (counter).
+* Repeat the process until the end is reached.
+
+#### Code
+```java
+class Solution {
+ public int jump(int[] nums) {
+ int i = 0;
+ int counter = 0;
+
+ // If the array has only one element, no jumps are needed
+ if (nums.length == 1)
+ return 0;
+
+ while (i < nums.length) {
+ counter++;
+ int range = i + nums[i];
+
+ // If the range includes the last position or exceeds it, exit the loop
+ if (range >= nums.length - 1)
+ break;
+
+ int max = 0;
+ int temp = 0;
+
+ // Find the position within the current range that maximizes the next reachable position
+ for (int k = i + 1; k <= range; k++) {
+ if (nums[k] + k >= max) {
+ max = nums[k] + k;
+ temp = k;
+ }
+ }
+ i = temp;
+ }
+ return counter;
+ }
+}
+
+```
+
+#### Complexity Analysis
+**Time complexity**: O(n)
+* The algorithm iterates through each element of the array once.
+* The inner loop within each iteration also traverses a limited number of positions.
+
+**Space complexity**: O(1)
+* The algorithm uses a constant amount of extra space.
+* The space requirements do not depend on the size of the input array.
+
+---
+### Problem 3 N digit numbers
+
+Find out the number of A digit positive numbers, whose digits on being added equals to a given number B.
+
+Note that a valid number starts from digits 1-9 except the number 0 itself. i.e. leading zeroes are not allowed.
+
+Since the answer can be large, output answer modulo 1000000007
+
+:::warning
+Please take some time to think about the brute force approach on your own before reading further.....
+:::
+
+### Brute Force Approach
+#### Objective
+Count the number of A-digit positive numbers whose digit sum equals a given number B.
+
+#### Idea
+* Generate all possible A-digit numbers
+* For each number, check if the sum of its digits equals B.
+* Keep track of the count of valid numbers.
+
+
+#### Code
+```cpp
+int bruteForceCount(int A, int B) {
+ int count = 0;
+ for (int num = pow(10, A - 1); num < pow(10, A); ++num) {
+ int digitSum = 0;
+ int temp = num;
+ while (temp > 0) {
+ digitSum += temp % 10;
+ temp /= 10;
+ }
+ if (digitSum == B) {
+ count++;
+ }
+ }
+ return count;
+}
+```
+
+---
+### N digit numbers optimization using Recursion
+#### Observation
+The brute force approach involves iterating through all A digit numbers and checking the count of numbers whose digit sum equals B.
+
+#### Optimized Recursive Approach
+
+**Recursive Function Definition**
+
+* The recursive function `countWays(id, sum)` is defined to represent the count of A-digit numbers with a digit sum equal to sum.
+* The base cases are as follows:
+ * If sum becomes negative, it implies that the digit sum has exceeded the target, so the count is 0.
+ * If id becomes 0, meaning all digits have been considered, the count is 1 if sum is 0 (indicating the target sum has been achieved), and 0 otherwise.
+ * Memoization is used to store and retrieve previously calculated values, preventing redundant computations.
+
+**Memoization Table**
+
+* The memo vector is a 2D table of size (A + 1) x (B + 1) initialized with -1 to represent uncalculated states.
+* The value `memo[id][sum]` stores the count of A-digit numbers with a digit sum of sum that has already been calculated.
+
+
+**Recursive Part**
+
+* The function explores all possible digits from 0 to 9 in a loop.
+* For each digit, it recursively calls `countWays(id - 1, sum - digit, memo)` to calculate the count of (A-1)-digit numbers with the updated digit sum.
+* The results are summed up, and the modulus operation is applied to avoid integer overflow.
+
+
+#### Optimized Recursive Code
+
+```cpp
+int memoizationCount(int A, int B) {
+ vector
+size(h2) is greater by 1
+**The median is 8.**
+
+In this way we will do for all the elements of an array, and find the median at every step, we need to take care that the |h1.size()-h2.size()|<=1.
+
+After adding all the medians in an array, we will get an answer: [6, 4.5, 6, 7, 8, 7, 8, 8, 8, _ _ _ ]
+
+
+---
+#### PseudoCode
+```cpp
+ h1, h2
+ h1.insert(arr[0])
+ print(arr[0])
+ for (int i = 1; i < N; i++) {
+ if (arr[i] > h1.getMax()) {
+ h2.insert(arr[i]);
+ } else {
+ h1.insert(arr[i]);
+ }
+ diff = | h1.size() - h2.size() |
+ if (diff > 1) {
+ if (h1.size() > h2.size()) {
+ h2.insert(h1.getMax());
+ } else {
+ h1.insert(h2.getMin());
+ }
+ }
+ if (h1.size() > h2.size()) {
+ print(h1.getMax());
+ } else if (h2.size() > h1.size()) {
+ print(h2.getMin())
+ } else {
+ print((h1.getMax() + h2.getMin()) / 2.0);
+ }
+ }
+```
+
+#### Complexity
+
+**Time Complexity:** O(NlogN)
+**Space Complexity:** O(N)
diff --git a/Academy DSA Typed Notes/Advanced/DSA Interview Problems.md b/Academy DSA Typed Notes/Advanced/DSA Interview Problems.md
new file mode 100644
index 0000000..f78bae7
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Interview Problems.md
@@ -0,0 +1,351 @@
+# DSA 4 - Interview Problems
+
+---
+### Problem 1 Target Sum
+
+You are given a set of non-negative integers and a target sum. The task is to determine whether there exists a subset of the given set whose sum is equal to the target sum.
+
+
+**Examples**
+**Input**: set = {3, 34, 4, 12, 5, 2}, sum = 9
+**Output**: True
+**Explanation**: There is a subset (4, 5) with a sum of 9.
+
+:::warning
+Please take some time to think about the brute force approach on your own before reading further.....
+:::
+
+#### Approach: Brute Force
+The brute force approach involves exploring all possible subsets of the given set. This is achieved through a recursive function named isSubsetSum(set, n, sum). The function explores two possibilities for each element: including it in the subset or excluding it. The base cases check if the sum is zero or if there are no more elements to consider.
+
+
+#### Code
+```java
+boolean isSubsetSum(int[] set, int n, int sum) {
+ if (sum == 0) return true;
+ if (n == 0 && sum != 0) return false;
+
+ // Explore two possibilities: include the current element or exclude it
+ return isSubsetSum(set, n - 1, sum) || isSubsetSum(set, n - 1, sum - set[n - 1]);
+}
+
+```
+
+#### Complexity Analysis
+* **Time complexity**: O(2^n) - Exponential
+* **Space complexity**: O(1)
+
+---
+### Target Sum Dynamic Programming Approach
+#### Approach:
+To optimize the solution, dynamic programming is employed. A 2D array `dp` is used to store results of subproblems. The value `dp[i][j]` represents whether it's possible to obtain a sum of `j` using the first `i` elements of the set.
+
+#### Code
+```java
+boolean isSubsetSum(int[] set, int n, int sum) {
+ boolean[][] dp = new boolean[n + 1][sum + 1];
+
+ // Initialize the first column as true, as sum 0 is always possible
+ for (int i = 0; i <= n; i++) dp[i][0] = true;
+
+ // Fill the dp array using a bottom-up approach
+ for (int i = 1; i <= n; i++) {
+ for (int j = 1; j <= sum; j++) {
+ dp[i][j] = dp[i - 1][j];
+ if (j >= set[i - 1]) dp[i][j] = dp[i][j] || dp[i - 1][j - set[i - 1]];
+ }
+ }
+
+ return dp[n][sum];
+}
+
+```
+
+#### Complexity Analysis
+* **Time complexity**: O(n * sum)
+* **Space complexity**: O(n * sum)
+
+---
+### Problem 2 Minimum Jumps to Reach End
+
+You are given a 0-indexed array of integers nums of length n. You are initially positioned at nums[0].
+
+Each element nums[i] represents the maximum length of a forward jump from index i. In other words, if you are at nums[i], you can jump to any nums[i + j] where:
+* 0 <= j <= nums[i]
+* i + j < n
+
+Return the minimum number of jumps to reach nums[n - 1]. The test cases are generated such that you can reach nums[n - 1].
+
+
+#### Example 1
+**Input**: nums = [2,3,1,1,4]
+**Output**: 2
+**Explanation**: The minimum number of jumps to reach the last index is 2. Jump 1 step from index 0 to 1, then 3 steps to the last index.
+
+#### Example 2
+**Input**: nums = [2,3,0,1,4]
+**Output**: 2
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Intuition
+
+The code utilizes a greedy approach, aiming to minimize the number of jumps by selecting the jump that maximizes the range of reachable positions at each step.
+
+#### Approach
+* Initialize a counter to keep track of the number of jumps (counter).
+* Use a while loop to iterate through the array until the end is reached.
+* In each iteration:
+ * Calculate the range of positions that can be reached from the current position (range).
+ * If the calculated range includes the last position or exceeds it, exit the loop.
+ * Find the position within the current range that maximizes the next reachable position (temp).
+ * Update the current position to the selected position (temp).
+ * Increment the jump counter (counter).
+* Repeat the process until the end is reached.
+
+#### Code
+```java
+class Solution {
+ public int jump(int[] nums) {
+ int i = 0;
+ int counter = 0;
+
+ // If the array has only one element, no jumps are needed
+ if (nums.length == 1)
+ return 0;
+
+ while (i < nums.length) {
+ counter++;
+ int range = i + nums[i];
+
+ // If the range includes the last position or exceeds it, exit the loop
+ if (range >= nums.length - 1)
+ break;
+
+ int max = 0;
+ int temp = 0;
+
+ // Find the position within the current range that maximizes the next reachable position
+ for (int k = i + 1; k <= range; k++) {
+ if (nums[k] + k >= max) {
+ max = nums[k] + k;
+ temp = k;
+ }
+ }
+ i = temp;
+ }
+ return counter;
+ }
+}
+
+```
+
+#### Complexity Analysis
+**Time complexity**: O(n)
+* The algorithm iterates through each element of the array once.
+* The inner loop within each iteration also traverses a limited number of positions.
+
+**Space complexity**: O(1)
+* The algorithm uses a constant amount of extra space.
+* The space requirements do not depend on the size of the input array.
+
+---
+### Problem 3 N digit numbers
+
+Find out the number of A digit positive numbers, whose digits on being added equals to a given number B.
+
+Note that a valid number starts from digits 1-9 except the number 0 itself. i.e. leading zeroes are not allowed.
+
+Since the answer can be large, output answer modulo 1000000007
+
+:::warning
+Please take some time to think about the brute force approach on your own before reading further.....
+:::
+
+### Brute Force Approach
+#### Objective
+Count the number of A-digit positive numbers whose digit sum equals a given number B.
+
+#### Idea
+* Generate all possible A-digit numbers
+* For each number, check if the sum of its digits equals B.
+* Keep track of the count of valid numbers.
+
+
+#### Code
+```cpp
+int bruteForceCount(int A, int B) {
+ int count = 0;
+ for (int num = pow(10, A - 1); num < pow(10, A); ++num) {
+ int digitSum = 0;
+ int temp = num;
+ while (temp > 0) {
+ digitSum += temp % 10;
+ temp /= 10;
+ }
+ if (digitSum == B) {
+ count++;
+ }
+ }
+ return count;
+}
+```
+
+---
+### N digit numbers optimization using Recursion
+#### Observation
+The brute force approach involves iterating through all A digit numbers and checking the count of numbers whose digit sum equals B.
+
+#### Optimized Recursive Approach
+
+**Recursive Function Definition**
+
+* The recursive function `countWays(id, sum)` is defined to represent the count of A-digit numbers with a digit sum equal to sum.
+* The base cases are as follows:
+ * If sum becomes negative, it implies that the digit sum has exceeded the target, so the count is 0.
+ * If id becomes 0, meaning all digits have been considered, the count is 1 if sum is 0 (indicating the target sum has been achieved), and 0 otherwise.
+ * Memoization is used to store and retrieve previously calculated values, preventing redundant computations.
+
+**Memoization Table**
+
+* The memo vector is a 2D table of size (A + 1) x (B + 1) initialized with -1 to represent uncalculated states.
+* The value `memo[id][sum]` stores the count of A-digit numbers with a digit sum of sum that has already been calculated.
+
+
+**Recursive Part**
+
+* The function explores all possible digits from 0 to 9 in a loop.
+* For each digit, it recursively calls `countWays(id - 1, sum - digit, memo)` to calculate the count of (A-1)-digit numbers with the updated digit sum.
+* The results are summed up, and the modulus operation is applied to avoid integer overflow.
+
+
+#### Optimized Recursive Code
+
+```cpp
+int memoizationCount(int A, int B) {
+ vector +
+### Iterable Interface
+* This is the root interface for the entire collection framework. The collection interface extends the iterable interface. Therefore, inherently, all the interfaces and classes implement this interface. The main functionality of this interface is to provide an iterator for the collections. Therefore, this interface contains only one abstract method which is the iterator. It returns the
+```
+Iterator iterator();
+```
+
+---
+
+
+### Collection Interface
+
+* The Collection interface is the root interface of the Java Collections Framework. It is the foundation upon which the collection framework is built. It declares the core methods that all collections will have. The
+* Collection interface is a part of the java.util package.
+* The JDK does not provide any direct implementations of this interface: it provides implementations of more specific sub-interfaces like Set and List. This interface is typically used to pass collections around and manipulate them where maximum generality is desired.
+* The Collection interface is not directly implemented by any class. However, it is implemented indirectly via its subtypes or subinterfaces like List, Queue, and Set. For Example, the HashSet class implements the Set interface which is a subinterface of the Collection interface.
+* It implements the Iterable interface.
+
+### Methods of Collection Interface
+
+The Collection interface includes various methods that can be used to perform different operations on objects. These methods are available in all its subinterfaces.
+
+* **add()** - inserts the specified element to the collection
+* **size()** - returns the size of the collection
+* **remove()** - removes the specified element from the collection
+* **iterator()** - returns an iterator to access elements of the collection
+* **addAll()** - adds all the elements of a specified collection to the collection
+* **removeAll()** - removes all the elements of the specified collection from the collection
+* **clear()** - removes all the elements of the collection
+
+
+---
+
+### Interfaces that extend the Collections Interface
+
+We are going to learn about the following SubInterfaces that extends the Collections Interface :
+1. **List :** This interface is dedicated to the data of the list type in which we can store all the ordered collection of the objects. This also allows duplicate data to be present in it.
+2. **Set:** A set is an unordered collection of objects in which duplicate values cannot be stored. This collection is used when we wish to avoid the duplication of the objects and wish to store only the unique objects.
+3. **SortedSet:** This interface is very similar to the set interface. The only difference is that this interface has extra methods that maintain the ordering of the elements. The sorted set interface extends the set interface and is used to handle the data which needs to be sorted.
+4. **Map** : A map is a data structure that supports the key-value pair for mapping the data. This interface doesn’t support duplicate keys because the same key cannot have multiple mappings, however, it allows duplicate values in different keys. A map is useful if there is data and we wish to perform operations on the basis of the key.
+5. **Queue:** As the name suggests, a queue interface maintains the FIFO(First In First Out) order similar to a real-world queue line. This interface is dedicated to storing all the elements where the order of the elements matter. For example, whenever we try to book a ticket, the tickets are sold at the first come first serve basis. Therefore, the person whose request arrives first into the queue gets the ticket.
+6. **Deque:** This is a very slight variation of the queue data structure. Deque, also known as a double-ended queue, is a data structure where we can add and remove the elements from both the ends of the queue. This interface extends the queue interface.
+
+Let's start going through each one in details one by one.
+
+---
+
+
+### List Interface
+
+* The **List** interface is a child of **Collection** Interface.The List interface is found in **java.util** package and inherits the Collection interface.
+* It is an ordered collection of objects in which duplicate values can be stored. Since List preserves the insertion order, it allows positional access and insertion of elements.
+* The implementation classes of the List interface are ArrayList, LinkedList, Vector and Stack. ArrayList and LinkedList are widely used in Java programming.
+
+* ### Declaration of Java List Interface
+ ```
+ public interface List
+
+### Iterable Interface
+* This is the root interface for the entire collection framework. The collection interface extends the iterable interface. Therefore, inherently, all the interfaces and classes implement this interface. The main functionality of this interface is to provide an iterator for the collections. Therefore, this interface contains only one abstract method which is the iterator. It returns the
+```
+Iterator iterator();
+```
+
+---
+
+
+### Collection Interface
+
+* The Collection interface is the root interface of the Java Collections Framework. It is the foundation upon which the collection framework is built. It declares the core methods that all collections will have. The
+* Collection interface is a part of the java.util package.
+* The JDK does not provide any direct implementations of this interface: it provides implementations of more specific sub-interfaces like Set and List. This interface is typically used to pass collections around and manipulate them where maximum generality is desired.
+* The Collection interface is not directly implemented by any class. However, it is implemented indirectly via its subtypes or subinterfaces like List, Queue, and Set. For Example, the HashSet class implements the Set interface which is a subinterface of the Collection interface.
+* It implements the Iterable interface.
+
+### Methods of Collection Interface
+
+The Collection interface includes various methods that can be used to perform different operations on objects. These methods are available in all its subinterfaces.
+
+* **add()** - inserts the specified element to the collection
+* **size()** - returns the size of the collection
+* **remove()** - removes the specified element from the collection
+* **iterator()** - returns an iterator to access elements of the collection
+* **addAll()** - adds all the elements of a specified collection to the collection
+* **removeAll()** - removes all the elements of the specified collection from the collection
+* **clear()** - removes all the elements of the collection
+
+
+---
+
+### Interfaces that extend the Collections Interface
+
+We are going to learn about the following SubInterfaces that extends the Collections Interface :
+1. **List :** This interface is dedicated to the data of the list type in which we can store all the ordered collection of the objects. This also allows duplicate data to be present in it.
+2. **Set:** A set is an unordered collection of objects in which duplicate values cannot be stored. This collection is used when we wish to avoid the duplication of the objects and wish to store only the unique objects.
+3. **SortedSet:** This interface is very similar to the set interface. The only difference is that this interface has extra methods that maintain the ordering of the elements. The sorted set interface extends the set interface and is used to handle the data which needs to be sorted.
+4. **Map** : A map is a data structure that supports the key-value pair for mapping the data. This interface doesn’t support duplicate keys because the same key cannot have multiple mappings, however, it allows duplicate values in different keys. A map is useful if there is data and we wish to perform operations on the basis of the key.
+5. **Queue:** As the name suggests, a queue interface maintains the FIFO(First In First Out) order similar to a real-world queue line. This interface is dedicated to storing all the elements where the order of the elements matter. For example, whenever we try to book a ticket, the tickets are sold at the first come first serve basis. Therefore, the person whose request arrives first into the queue gets the ticket.
+6. **Deque:** This is a very slight variation of the queue data structure. Deque, also known as a double-ended queue, is a data structure where we can add and remove the elements from both the ends of the queue. This interface extends the queue interface.
+
+Let's start going through each one in details one by one.
+
+---
+
+
+### List Interface
+
+* The **List** interface is a child of **Collection** Interface.The List interface is found in **java.util** package and inherits the Collection interface.
+* It is an ordered collection of objects in which duplicate values can be stored. Since List preserves the insertion order, it allows positional access and insertion of elements.
+* The implementation classes of the List interface are ArrayList, LinkedList, Vector and Stack. ArrayList and LinkedList are widely used in Java programming.
+
+* ### Declaration of Java List Interface
+ ```
+ public interface List +
+* it has a data section where the data is present
+* a next pointer which points to next element of the linked list
+
+### Structure of Linked List
+
+```java
+class Node{
+ int data;
+ Node next;
+ Node(int x){
+ data = x;
+ next = null;
+ }
+}
+```
+**Example of Linked List**
+
+
+
+* it has a data section where the data is present
+* a next pointer which points to next element of the linked list
+
+### Structure of Linked List
+
+```java
+class Node{
+ int data;
+ Node next;
+ Node(int x){
+ data = x;
+ next = null;
+ }
+}
+```
+**Example of Linked List**
+
+ +
+
+
++ +
 +
+* the first node of the linked list is called head
+* any linked list is represented by its first node
+
+---
+### Question
+Where will the "next" pointer of the last node point to?
+
+**Choices**
+- [ ] First Node
+- [ ] Any Node
+- [ ] Middle Node
+- [x] Null
+
+
+---
+### Question
+From which node can we travel the entire linked list ?
+
+**Choices**
+- [ ] Middle
+- [x] First
+- [ ] Last
+- [ ] Any Node
+
+
+---
+### Operation on Linked List
+
+### 1. Access kth element(k = 0; k is the first element)
+
+```java
+Node temp = Head // temp is a compy
+for i -> 1 to k {
+ temp = temp.next
+}
+return temp.data // never update head otherwise the first node is lost
+```
+> Time complexity to access the kth element is O(K). Here we can see that linked list takes more time compared to array as it would take constant time to access the kth element.
+
+### 2. Check for value X (searching)
+We can simply iterate and check if value X exists of not.
+```java
+temp = Head
+while (temp != null){
+ if(temp.data == X)
+ return true
+ temp = temp.next
+}
+return false
+```
+> Here if the Linked List is empty i.e if `Head = NULL`, if we try to access head.next it will give null pointer expection error.
+
+Time Complexity for searching in Linked list is O(N).
+
+> In linked list we cannot perform binary search because we have to travel to the middle element. We cannot jump to the middle element unlike array.
+
+---
+### Question
+What is the time complexity to search any node in the linked list?
+
+**Choices**
+- [ ] O(1)
+- [ ] O(log(N))
+- [x] O(N)
+- [ ] O(N ^2)
+
+
+---
+### Question
+What is the time complexity to access the Kth element of the linked list? [index K is valid]
+
+
+**Choices**
+- [ ] O(1)
+- [ ] O(log(N))
+- [ ] O(N)
+- [x] O(K)
+
+
+---
+### Problem 1 Insert a New Node with Data
+
+### Insert a New Node with Data
+
+Insert a new node with data **v** at index **p** in the linked list
+>Though indexing doesn't exist is LL, but for our understanding, let's say Node 1 is at index 0, Node 2 at index 1, etc.
+
+**Testcase 1**
+v = 60 and p = 3
+
+
+
+* the first node of the linked list is called head
+* any linked list is represented by its first node
+
+---
+### Question
+Where will the "next" pointer of the last node point to?
+
+**Choices**
+- [ ] First Node
+- [ ] Any Node
+- [ ] Middle Node
+- [x] Null
+
+
+---
+### Question
+From which node can we travel the entire linked list ?
+
+**Choices**
+- [ ] Middle
+- [x] First
+- [ ] Last
+- [ ] Any Node
+
+
+---
+### Operation on Linked List
+
+### 1. Access kth element(k = 0; k is the first element)
+
+```java
+Node temp = Head // temp is a compy
+for i -> 1 to k {
+ temp = temp.next
+}
+return temp.data // never update head otherwise the first node is lost
+```
+> Time complexity to access the kth element is O(K). Here we can see that linked list takes more time compared to array as it would take constant time to access the kth element.
+
+### 2. Check for value X (searching)
+We can simply iterate and check if value X exists of not.
+```java
+temp = Head
+while (temp != null){
+ if(temp.data == X)
+ return true
+ temp = temp.next
+}
+return false
+```
+> Here if the Linked List is empty i.e if `Head = NULL`, if we try to access head.next it will give null pointer expection error.
+
+Time Complexity for searching in Linked list is O(N).
+
+> In linked list we cannot perform binary search because we have to travel to the middle element. We cannot jump to the middle element unlike array.
+
+---
+### Question
+What is the time complexity to search any node in the linked list?
+
+**Choices**
+- [ ] O(1)
+- [ ] O(log(N))
+- [x] O(N)
+- [ ] O(N ^2)
+
+
+---
+### Question
+What is the time complexity to access the Kth element of the linked list? [index K is valid]
+
+
+**Choices**
+- [ ] O(1)
+- [ ] O(log(N))
+- [ ] O(N)
+- [x] O(K)
+
+
+---
+### Problem 1 Insert a New Node with Data
+
+### Insert a New Node with Data
+
+Insert a new node with data **v** at index **p** in the linked list
+>Though indexing doesn't exist is LL, but for our understanding, let's say Node 1 is at index 0, Node 2 at index 1, etc.
+
+**Testcase 1**
+v = 60 and p = 3
+
+ +
+
+
+**Solution to Testcase 1**
+* Iterate to the node having index p-1 where p-1>=0 from start of linked list. Here p is 3 so we iterate till 2
+* On reaching index 2 we create a new node riz with data v i.e. 60
+* Set **riz.next = t.next** and set **t.next = riz**
+
+
+
+
+**Solution to Testcase 1**
+* Iterate to the node having index p-1 where p-1>=0 from start of linked list. Here p is 3 so we iterate till 2
+* On reaching index 2 we create a new node riz with data v i.e. 60
+* Set **riz.next = t.next** and set **t.next = riz**
+ +
+
+**Testcase 2**
+
+
+
+**Testcase 2**
+ +
+**Solution to Testcase 2**
+**We can do the dry run similar to testcase 1 here is the final result**
+
+
+**Solution to Testcase 2**
+**We can do the dry run similar to testcase 1 here is the final result**
+ +
+---
+### Question
+Insert a new node with data **10** at index **2** in the Given linked list.
+
+Head -> 1 -> 6 -> 7 -> 9 -> Null
+
+Choose the correct LinkedList after insertion.
+
+**Choices**
+- [ ] Head -> 1 -> 6 -> 7 -> 9 -> **10** -> Null
+- [x] Head -> 1 -> 6 -> **10** -> 7 -> 9 -> Null
+- [ ] Head -> 1 -> **10** -> 6 -> 7 -> 9 -> Null
+- [ ] Head -> 10 -> 1 -> 6 -> 7 -> 9 -> Null
+
+
+---
+### Insert a New Node with Data Approach
+
+#### Approach
+
+* Traverse till **(p - 1)th** node. Let's call it **t**.
+* Create a new node **newNode**, with data **v**.
+* Set **newNode.next** equals to **t.next**.
+* Set **t.next** to reference of **newNode**.
+
+
+#### Pseudocode 1
+```cpp
+Function insertAtIndex(p, v, Node head) {
+ Node t = head
+ for (i = 1; i < p; i++) // iterating updating t, p-1 times
+ {
+ t = t.next
+ }
+
+ // create a new node
+ Node newNode = Node(v)
+
+ // Inserting the Node
+ newNode.next = t.next
+ t.next = newNode
+}
+```
+>Again there is an edge case to above solution can anyone figure it out ?
+
+#### Edge Case
+
+If p = 0 then where to insert the node ?
+=> At head of the list.
+
+
+
+---
+### Question
+Insert a new node with data **10** at index **2** in the Given linked list.
+
+Head -> 1 -> 6 -> 7 -> 9 -> Null
+
+Choose the correct LinkedList after insertion.
+
+**Choices**
+- [ ] Head -> 1 -> 6 -> 7 -> 9 -> **10** -> Null
+- [x] Head -> 1 -> 6 -> **10** -> 7 -> 9 -> Null
+- [ ] Head -> 1 -> **10** -> 6 -> 7 -> 9 -> Null
+- [ ] Head -> 10 -> 1 -> 6 -> 7 -> 9 -> Null
+
+
+---
+### Insert a New Node with Data Approach
+
+#### Approach
+
+* Traverse till **(p - 1)th** node. Let's call it **t**.
+* Create a new node **newNode**, with data **v**.
+* Set **newNode.next** equals to **t.next**.
+* Set **t.next** to reference of **newNode**.
+
+
+#### Pseudocode 1
+```cpp
+Function insertAtIndex(p, v, Node head) {
+ Node t = head
+ for (i = 1; i < p; i++) // iterating updating t, p-1 times
+ {
+ t = t.next
+ }
+
+ // create a new node
+ Node newNode = Node(v)
+
+ // Inserting the Node
+ newNode.next = t.next
+ t.next = newNode
+}
+```
+>Again there is an edge case to above solution can anyone figure it out ?
+
+#### Edge Case
+
+If p = 0 then where to insert the node ?
+=> At head of the list.
+
+ +
+#### Pseudocode 2
+
+```cpp
+Function insertAtIndex(p, v, Node head) {
+ // create a new node
+ Node newNode = Node(v)
+
+ Node t = head
+
+ if (p == 0) { // edge case
+ newNode.next = head
+ head = newNode
+ }
+
+ for (i = 1; i < p; i++) { // iterating updating t p-1 times
+ t = t.next
+ }
+
+ // Inserting the Node
+ newNode.next = t.next
+ t.next = newNode
+}
+```
+
+
+### Time Complexity for Insertion
+O(K)
+
+
+---
+
+### Deletion in Linked List
+
+*Delete the first occurrence of value X in the given linked list. If element is not present, leave as is.*
+
+**Example 1:**
+```java
+List: 1 -> 8 -> 4 -> -2 -> 12
+X = -2
+
+Ans:
+List: 1 -> 8 -> 4 -> 12
+-2 has been deleted from the list.
+```
+
+**Example 2:**
+```java
+List: 1 -> 8 -> 4 -> -2 -> 4 -> 12
+X = 4
+
+Ans:
+List: 1 -> 8 -> -2 -> 4 -> 12
+The first occurrence of 4 has been deleted from the list.
+```
+
+#### Cases:
+1. **Empty list i.e., head = null**
+
+```java
+List: null
+X = 4
+
+Ans:
+List: null
+```
+2. **head.data = X i.e., delete head**
+
+```java
+List: 4
+X = 4
+
+Ans:
+List: null
+```
+
+3. **X is somewhere in between the list, find and delete node with value X**
+```java
+List: 1 -> 8 -> 4 -> -2 -> 4 -> 12
+X = 4
+
+Ans:
+List: 1 -> 8 -> -2 -> 4 -> 12 (removed first occurrence)
+```
+4. **X is not in the list, simply return**
+```java
+List: 1 -> 8 -> -2 -> 7 -> 12
+X = 4
+
+Ans:
+List: 1 -> 8 -> -2 -> 7 -> 12
+```
+
+---
+### Question
+Delete the first occurrence of value **X** in the given linked list. If element is not present, leave as is.
+
+Linked List : ```5 -> 4 -> 7 -> 1 -> NULL```
+X (to Delete) : 1
+
+**Choices**
+- [ ] 5 -> 4 -> 7 -> 1 -> NULL
+- [x] 5 -> 4 -> 7 -> NULL
+- [ ] 4 -> 7 -> 1 -> NULL
+- [ ] 5 -> 7 -> NULL
+
+
+
+**Explanation:**
+
+The Value 1 is not present in the Linked List. So leave as it is.
+
+Thus, the final Linked List is 5 -> 4 -> 7 -> -1 -> NULL
+
+
+---
+### Deletion in Linked List Approach and Pseudocode
+#### Approach
+
+- Check if the list is empty; if so, return it as is.
+- If the target value X is at the head, update the head to the next node.
+- Otherwise, iterate through the list while looking for X.
+- When X is found, skip the node containing it by updating the next reference of the previous node.
+- Return the modified head (which may or may not have changed during the operation).
+
+#### Pseudocode
+
+```java
+if (head == null) return head
+if (head.data == X) {
+ tmp = head
+ free(tmp) //automatically done in java, whereas have to do manually for c++ and other languages.
+ head = Head.next
+ return head
+}
+temp = head
+while (temp.next != null) {
+ if (temp.next.data == X) {
+ tmp = temp.next
+ temp.next = temp.next.next
+ free(tmp)
+ return head
+ }
+ temp = temp.next
+}
+return head
+```
+#### Time complexity for Deletion
+**O(N)**
+
+> It can be seen that every operation in linked list takes linear time complexity unlike arrays.
+
+---
+### Problem 3 Reverse the linked list
+
+
+**Note:** We can't use extra space. Manipulate the pointers only.
+
+**Example**
+
+
+#### Pseudocode 2
+
+```cpp
+Function insertAtIndex(p, v, Node head) {
+ // create a new node
+ Node newNode = Node(v)
+
+ Node t = head
+
+ if (p == 0) { // edge case
+ newNode.next = head
+ head = newNode
+ }
+
+ for (i = 1; i < p; i++) { // iterating updating t p-1 times
+ t = t.next
+ }
+
+ // Inserting the Node
+ newNode.next = t.next
+ t.next = newNode
+}
+```
+
+
+### Time Complexity for Insertion
+O(K)
+
+
+---
+
+### Deletion in Linked List
+
+*Delete the first occurrence of value X in the given linked list. If element is not present, leave as is.*
+
+**Example 1:**
+```java
+List: 1 -> 8 -> 4 -> -2 -> 12
+X = -2
+
+Ans:
+List: 1 -> 8 -> 4 -> 12
+-2 has been deleted from the list.
+```
+
+**Example 2:**
+```java
+List: 1 -> 8 -> 4 -> -2 -> 4 -> 12
+X = 4
+
+Ans:
+List: 1 -> 8 -> -2 -> 4 -> 12
+The first occurrence of 4 has been deleted from the list.
+```
+
+#### Cases:
+1. **Empty list i.e., head = null**
+
+```java
+List: null
+X = 4
+
+Ans:
+List: null
+```
+2. **head.data = X i.e., delete head**
+
+```java
+List: 4
+X = 4
+
+Ans:
+List: null
+```
+
+3. **X is somewhere in between the list, find and delete node with value X**
+```java
+List: 1 -> 8 -> 4 -> -2 -> 4 -> 12
+X = 4
+
+Ans:
+List: 1 -> 8 -> -2 -> 4 -> 12 (removed first occurrence)
+```
+4. **X is not in the list, simply return**
+```java
+List: 1 -> 8 -> -2 -> 7 -> 12
+X = 4
+
+Ans:
+List: 1 -> 8 -> -2 -> 7 -> 12
+```
+
+---
+### Question
+Delete the first occurrence of value **X** in the given linked list. If element is not present, leave as is.
+
+Linked List : ```5 -> 4 -> 7 -> 1 -> NULL```
+X (to Delete) : 1
+
+**Choices**
+- [ ] 5 -> 4 -> 7 -> 1 -> NULL
+- [x] 5 -> 4 -> 7 -> NULL
+- [ ] 4 -> 7 -> 1 -> NULL
+- [ ] 5 -> 7 -> NULL
+
+
+
+**Explanation:**
+
+The Value 1 is not present in the Linked List. So leave as it is.
+
+Thus, the final Linked List is 5 -> 4 -> 7 -> -1 -> NULL
+
+
+---
+### Deletion in Linked List Approach and Pseudocode
+#### Approach
+
+- Check if the list is empty; if so, return it as is.
+- If the target value X is at the head, update the head to the next node.
+- Otherwise, iterate through the list while looking for X.
+- When X is found, skip the node containing it by updating the next reference of the previous node.
+- Return the modified head (which may or may not have changed during the operation).
+
+#### Pseudocode
+
+```java
+if (head == null) return head
+if (head.data == X) {
+ tmp = head
+ free(tmp) //automatically done in java, whereas have to do manually for c++ and other languages.
+ head = Head.next
+ return head
+}
+temp = head
+while (temp.next != null) {
+ if (temp.next.data == X) {
+ tmp = temp.next
+ temp.next = temp.next.next
+ free(tmp)
+ return head
+ }
+ temp = temp.next
+}
+return head
+```
+#### Time complexity for Deletion
+**O(N)**
+
+> It can be seen that every operation in linked list takes linear time complexity unlike arrays.
+
+---
+### Problem 3 Reverse the linked list
+
+
+**Note:** We can't use extra space. Manipulate the pointers only.
+
+**Example**
+ +
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Approach:
+- Check for Empty List:
+ - If head is null, return it as is.
+- Handle Single Node List:
+ - If head.next is null, return head. (This line is optional and can be omitted without affecting the core functionality.)
+- Reverse the Linked List:
+ - Initialize cur as head, pre as null, and a temporary variable nxt.
+ - While cur is not null, do the following:
+ - Store the next node in nxt.
+ - Reverse the next pointer of cur to point to pre.
+ - Update pre to cur.
+ - Move cur to the next node (nxt).
+- Update head:
+ - After the loop, set head to pre, making the reversed list the new head.
+
+#### Dry Run
+**Initialize the pointers**
+
+prev = null
+curr = 2 -> 5 -> 8 -> 7 -> 3 -> null
+nxt = null
+
+#### Iteration 1:
+**Store the next node in nxt**
+```java
+nxt = curr.next; nxt = 5 -> 8 -> 7 -> 3 -> null
+```
+**Reverse the next pointer of the current node**
+```java
+curr.next = prev
+```
+**Update the previous and current pointers**
+```java
+prev = curr
+curr = nxt
+prev = 2 -> null
+curr = 5 -> 8 -> 7 -> 3 -> null
+```
+#### Iteration 2:
+**Store the next node in nxt**
+```java
+nxt = curr.next; nxt = 8 -> 7 -> 3 -> null
+```
+**Reverse the next pointer of the current node**
+```java
+curr.next = prev
+```
+**Update the previous and current pointers**
+```java
+prev = curr
+curr = nxt
+prev = 5 -> 2 -> null
+curr = 8 -> 7 -> 3 -> null
+```
+
+#### Iteration 3:
+**Store the next node in nxt**
+```java
+nxt = curr.next; nxt = 7 -> 3 -> null
+```
+**Reverse the next pointer of the current node**
+```java
+curr.next = prev
+```
+**Update the previous and current pointers**
+```javascript
+prev = curr
+curr = nxt
+prev = 8 -> 5 -> 2 -> null
+curr = 7 -> 3 -> null
+```
+
+#### Iteration 4:
+**Store the next node in nxt**
+```java
+nxt = curr.next; nxt = 3->null
+```
+**Reverse the next pointer of the current node**
+```java
+curr.next = prev
+```
+**Update the previous and current pointers**
+```java
+prev = curr
+curr = nxt
+prev = 7 -> 8 -> 5 -> 2 -> null
+curr = 3 -> null
+```
+**Iteration 5**:
+
+**Store the next node in nxt**
+```java
+nxt = curr.next; nxt = null
+```
+**Reverse the next pointer of the current node**
+```java
+curr.next = prev
+```
+**Update the previous and current pointers**
+```java
+prev = curr
+curr = nxt
+prev = 3 -> 7 -> 8 -> 5 -> 2 -> null
+curr = null
+```
+
+The **loop terminates** because **curr is now null**
+
+Final state of the linked list:
+```java
+prev = 3 -> 7 -> 8 -> 5 -> 2 -> null
+curr = null
+The head of the linked list is now prev, which is the reversed linked list:
+
+3 7 8 5 2
+```
+
+---
+### Question
+Reverse the given Linked List.
+
+Linked List : 5 -> 6 -> 7 -> 8 -> 9
+
+**Choices**
+- [ ] 5 -> 6 -> 7 -> 8 -> 9
+- [x] 5 <- 6 <- 7 <- 8 <- 9
+- [ ] 9 -> 6 -> 7 -> 8 -> 5
+- [ ] 5 <- 6 -> 7 <- 8 <- 9
+
+
+
+
+---
+### Reverse the LinkedList Psuedo code and Time Complexity
+#### Psuedocode
+```java
+if (head == null)
+ return head;
+
+if (head.next == null)
+ return head;
+
+cur = head;
+pre = null;
+
+while (cur != null) {
+ next = cur.next;
+ cur.next = pre;
+ pre = cur;
+ cur = next;
+}
+
+head = pre;
+```
+#### TC & SC
+**Time complexity -** O(N)
+**Space complexity -** O(1)
+
+--
+### Problem 2 Check Palindrome
+
+Given a Linked List, check if it is a palindrome.
+
+**Example:**
+maam, racecar, never, 121, 12321
+
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Approach:
+- Check for Empty List:
+ - If head is null, return it as is.
+- Handle Single Node List:
+ - If head.next is null, return head. (This line is optional and can be omitted without affecting the core functionality.)
+- Reverse the Linked List:
+ - Initialize cur as head, pre as null, and a temporary variable nxt.
+ - While cur is not null, do the following:
+ - Store the next node in nxt.
+ - Reverse the next pointer of cur to point to pre.
+ - Update pre to cur.
+ - Move cur to the next node (nxt).
+- Update head:
+ - After the loop, set head to pre, making the reversed list the new head.
+
+#### Dry Run
+**Initialize the pointers**
+
+prev = null
+curr = 2 -> 5 -> 8 -> 7 -> 3 -> null
+nxt = null
+
+#### Iteration 1:
+**Store the next node in nxt**
+```java
+nxt = curr.next; nxt = 5 -> 8 -> 7 -> 3 -> null
+```
+**Reverse the next pointer of the current node**
+```java
+curr.next = prev
+```
+**Update the previous and current pointers**
+```java
+prev = curr
+curr = nxt
+prev = 2 -> null
+curr = 5 -> 8 -> 7 -> 3 -> null
+```
+#### Iteration 2:
+**Store the next node in nxt**
+```java
+nxt = curr.next; nxt = 8 -> 7 -> 3 -> null
+```
+**Reverse the next pointer of the current node**
+```java
+curr.next = prev
+```
+**Update the previous and current pointers**
+```java
+prev = curr
+curr = nxt
+prev = 5 -> 2 -> null
+curr = 8 -> 7 -> 3 -> null
+```
+
+#### Iteration 3:
+**Store the next node in nxt**
+```java
+nxt = curr.next; nxt = 7 -> 3 -> null
+```
+**Reverse the next pointer of the current node**
+```java
+curr.next = prev
+```
+**Update the previous and current pointers**
+```javascript
+prev = curr
+curr = nxt
+prev = 8 -> 5 -> 2 -> null
+curr = 7 -> 3 -> null
+```
+
+#### Iteration 4:
+**Store the next node in nxt**
+```java
+nxt = curr.next; nxt = 3->null
+```
+**Reverse the next pointer of the current node**
+```java
+curr.next = prev
+```
+**Update the previous and current pointers**
+```java
+prev = curr
+curr = nxt
+prev = 7 -> 8 -> 5 -> 2 -> null
+curr = 3 -> null
+```
+**Iteration 5**:
+
+**Store the next node in nxt**
+```java
+nxt = curr.next; nxt = null
+```
+**Reverse the next pointer of the current node**
+```java
+curr.next = prev
+```
+**Update the previous and current pointers**
+```java
+prev = curr
+curr = nxt
+prev = 3 -> 7 -> 8 -> 5 -> 2 -> null
+curr = null
+```
+
+The **loop terminates** because **curr is now null**
+
+Final state of the linked list:
+```java
+prev = 3 -> 7 -> 8 -> 5 -> 2 -> null
+curr = null
+The head of the linked list is now prev, which is the reversed linked list:
+
+3 7 8 5 2
+```
+
+---
+### Question
+Reverse the given Linked List.
+
+Linked List : 5 -> 6 -> 7 -> 8 -> 9
+
+**Choices**
+- [ ] 5 -> 6 -> 7 -> 8 -> 9
+- [x] 5 <- 6 <- 7 <- 8 <- 9
+- [ ] 9 -> 6 -> 7 -> 8 -> 5
+- [ ] 5 <- 6 -> 7 <- 8 <- 9
+
+
+
+
+---
+### Reverse the LinkedList Psuedo code and Time Complexity
+#### Psuedocode
+```java
+if (head == null)
+ return head;
+
+if (head.next == null)
+ return head;
+
+cur = head;
+pre = null;
+
+while (cur != null) {
+ next = cur.next;
+ cur.next = pre;
+ pre = cur;
+ cur = next;
+}
+
+head = pre;
+```
+#### TC & SC
+**Time complexity -** O(N)
+**Space complexity -** O(1)
+
+--
+### Problem 2 Check Palindrome
+
+Given a Linked List, check if it is a palindrome.
+
+**Example:**
+maam, racecar, never, 121, 12321
+
+ +
+
+---
+### Question
+Check the Given linked list is Palindrome or not.
+
+Linked List : ```Head -> 1 -> Null```
+
+**Choices**
+- [x] YES
+- [ ] NO
+
+
+**Explanation:**
+
+Yes, The Given Linked List is an Palindrome, Because it reads the same in reverse order as well.
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+### Check Palindrome Solution
+
+
+**Solution 1 :**
+Create a copy of linked list. Reverse it and Compare
+
+**Complexity**
+**Time Complexity -** O(N)
+**Space Complexity -** O(N).
+
+
+**Solution 2 :**
+1. Find middle element of linked list
+2. Reverse second half of linked list
+3. Compare first half and compare second half
+
+**Step wise solution:**
+
+1. **Find length of linked list**
+```java
+n = 0
+temp = Head
+while(temp != null){
+ n++
+ temp = temp.next
+}
+```
+2. **Go to the middle element**
+// If n = 10(even), we'll reverse from 6th node.
+// If n = 9(odd), then also we'll reverse from 6th node.(**5th node will be middle one that need not be compared with any node**)
+
+So, regardless of even/odd, we can skip (n + 1) / 2 nodes.
+```java
+temp Head
+(for i --> 1 to (n + 1) / 2){
+ temp =temp.next
+}
+//temp middle
+```
+3. Now reverse the linked list from $((n+1)/2 + 1)th$ node.
+4. Compare both the linked list
+
+#### T.C & S.C
+
+Total time complexity for checking palindrome is O(N) and space complexity is O(N).
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Linked List 2 Sorting and Detecting Loop.md b/Academy DSA Typed Notes/Advanced/DSA Linked List 2 Sorting and Detecting Loop.md
new file mode 100644
index 0000000..13691b3
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Linked List 2 Sorting and Detecting Loop.md
@@ -0,0 +1,503 @@
+# Linked List 2: Sorting and Detecting Loop
+
+---
+### Question
+What is the time complexity needed to delete a node from a linked list?
+
+**Choices**
+- [ ] O(1)
+- [ ] O(log(N))
+- [x] O(N)
+- [ ] O(N^2)
+
+#### Explanation
+
+To delete a node from the linked list we need to traverse till that node. In the worst case, the time-complexity would be O(N).
+
+---
+
+### Question
+What is the time complexity needed to insert a node as the head of a linked list?
+
+
+**Choices**
+- [x] O(1)
+- [ ] O(log(N))
+- [ ] O(N)
+- [ ] O(N$^2$)
+
+
+**Explanation**
+
+No traversal is needed to reach the head node. Therefore the time complexity needed is constant i.e. O(1).
+
+---
+### Question
+
+What is the time complexity needed to delete the last node from a linked list?
+
+**Choices**
+- [ ] O(1)
+- [ ] O(log(N))
+- [x] O(N)
+- [ ] O(N$^2$)
+
+**Explanation:**
+
+To delete the last node from the linked list we need to traverse till that node. In that case, the time-complexity would be O(N).
+
+---
+### Question
+
+Can we do Binary Search in a sorted Linked List?
+
+**Choices**
+- [ ] Yes
+- [x] No
+
+
+**Explanation:**
+
+Binary search relies on random access to elements, which is not possible in a linked list.
+
+
+
+---
+### Problem 1 Find the middle element.
+
+Given a Linked List, Find the middle element.
+
+**Examples**
+
+Following 0 based indexing: The middle node is the node having the index (n / 2), where n is the number of nodes.
+
+```cpp
+Input: [1 -> 2 -> 3 -> 4 -> 5]
+Output: [3]
+
+Here 3 is the middle element
+
+```
+
+```cpp
+Input: [1 -> 2 -> 3 -> 4]
+Output: [2]
+
+There are two middle elements here: 2 and 3 respectively.
+
+```
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+### Find the middle element Solution
+#### Solution
+
+* First, We will find the length of the linked-list.
+* Now we will traverse half the length to find the middle node
+
+
+
+#### Pseudocode
+```cpp
+function findMiddle(head)
+ if head is null
+ return null
+
+ count = 0
+ current = head
+ while current is not null
+ count = count + 1
+ current = current.next
+
+ middleIndex = count / 2
+ current = head
+ for i = 0 to middleIndex - 1
+ current = current.next
+
+ return current
+}
+```
+
+#### Complexity
+**Time Complexity:** O(n * 2) = O(n)
+**Space Complexity:** O(1)
+
+#### Optimized Solution
+We can optimize the solution using the **Two Pointers** technique.
+* Take two pointers initially pointing at the head of the Linked List and name them slowPointer and fastPointer respectively.
+* The fastPointer will travel two nodes at a time, whereas the slowPointer will traverse a single node at a time
+* When the fastPointer reaches the end node, the slowPointer must necessarily be pointing at the middle node
+
+
+
+
+---
+### Question
+Check the Given linked list is Palindrome or not.
+
+Linked List : ```Head -> 1 -> Null```
+
+**Choices**
+- [x] YES
+- [ ] NO
+
+
+**Explanation:**
+
+Yes, The Given Linked List is an Palindrome, Because it reads the same in reverse order as well.
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+### Check Palindrome Solution
+
+
+**Solution 1 :**
+Create a copy of linked list. Reverse it and Compare
+
+**Complexity**
+**Time Complexity -** O(N)
+**Space Complexity -** O(N).
+
+
+**Solution 2 :**
+1. Find middle element of linked list
+2. Reverse second half of linked list
+3. Compare first half and compare second half
+
+**Step wise solution:**
+
+1. **Find length of linked list**
+```java
+n = 0
+temp = Head
+while(temp != null){
+ n++
+ temp = temp.next
+}
+```
+2. **Go to the middle element**
+// If n = 10(even), we'll reverse from 6th node.
+// If n = 9(odd), then also we'll reverse from 6th node.(**5th node will be middle one that need not be compared with any node**)
+
+So, regardless of even/odd, we can skip (n + 1) / 2 nodes.
+```java
+temp Head
+(for i --> 1 to (n + 1) / 2){
+ temp =temp.next
+}
+//temp middle
+```
+3. Now reverse the linked list from $((n+1)/2 + 1)th$ node.
+4. Compare both the linked list
+
+#### T.C & S.C
+
+Total time complexity for checking palindrome is O(N) and space complexity is O(N).
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Linked List 2 Sorting and Detecting Loop.md b/Academy DSA Typed Notes/Advanced/DSA Linked List 2 Sorting and Detecting Loop.md
new file mode 100644
index 0000000..13691b3
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Linked List 2 Sorting and Detecting Loop.md
@@ -0,0 +1,503 @@
+# Linked List 2: Sorting and Detecting Loop
+
+---
+### Question
+What is the time complexity needed to delete a node from a linked list?
+
+**Choices**
+- [ ] O(1)
+- [ ] O(log(N))
+- [x] O(N)
+- [ ] O(N^2)
+
+#### Explanation
+
+To delete a node from the linked list we need to traverse till that node. In the worst case, the time-complexity would be O(N).
+
+---
+
+### Question
+What is the time complexity needed to insert a node as the head of a linked list?
+
+
+**Choices**
+- [x] O(1)
+- [ ] O(log(N))
+- [ ] O(N)
+- [ ] O(N$^2$)
+
+
+**Explanation**
+
+No traversal is needed to reach the head node. Therefore the time complexity needed is constant i.e. O(1).
+
+---
+### Question
+
+What is the time complexity needed to delete the last node from a linked list?
+
+**Choices**
+- [ ] O(1)
+- [ ] O(log(N))
+- [x] O(N)
+- [ ] O(N$^2$)
+
+**Explanation:**
+
+To delete the last node from the linked list we need to traverse till that node. In that case, the time-complexity would be O(N).
+
+---
+### Question
+
+Can we do Binary Search in a sorted Linked List?
+
+**Choices**
+- [ ] Yes
+- [x] No
+
+
+**Explanation:**
+
+Binary search relies on random access to elements, which is not possible in a linked list.
+
+
+
+---
+### Problem 1 Find the middle element.
+
+Given a Linked List, Find the middle element.
+
+**Examples**
+
+Following 0 based indexing: The middle node is the node having the index (n / 2), where n is the number of nodes.
+
+```cpp
+Input: [1 -> 2 -> 3 -> 4 -> 5]
+Output: [3]
+
+Here 3 is the middle element
+
+```
+
+```cpp
+Input: [1 -> 2 -> 3 -> 4]
+Output: [2]
+
+There are two middle elements here: 2 and 3 respectively.
+
+```
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+### Find the middle element Solution
+#### Solution
+
+* First, We will find the length of the linked-list.
+* Now we will traverse half the length to find the middle node
+
+
+
+#### Pseudocode
+```cpp
+function findMiddle(head)
+ if head is null
+ return null
+
+ count = 0
+ current = head
+ while current is not null
+ count = count + 1
+ current = current.next
+
+ middleIndex = count / 2
+ current = head
+ for i = 0 to middleIndex - 1
+ current = current.next
+
+ return current
+}
+```
+
+#### Complexity
+**Time Complexity:** O(n * 2) = O(n)
+**Space Complexity:** O(1)
+
+#### Optimized Solution
+We can optimize the solution using the **Two Pointers** technique.
+* Take two pointers initially pointing at the head of the Linked List and name them slowPointer and fastPointer respectively.
+* The fastPointer will travel two nodes at a time, whereas the slowPointer will traverse a single node at a time
+* When the fastPointer reaches the end node, the slowPointer must necessarily be pointing at the middle node
+
+ +
+#### Pseudocode
+```java
+function findMiddleTwoPointers(head)
+ if head is null
+ return null
+
+ slowPointer = head
+ fastPointer = head
+
+ while fastPointer is not null and fastPointer.next is not null
+ slowPointer = slowPointer.next
+ fastPointer = fastPointer.next.next
+
+ return slowPointer
+```
+
+#### Complexity
+**Time Complexity:** O(n / 2) = O(n)
+**Space Complexity:** O(1)
+
+
+
+---
+### Problem 2 Merge two sorted Linked Lists
+
+Given two sorted Linked Lists, Merge them into a single sorted linked list.
+
+**Example 1 :**
+
+```cpp
+Input: [1 -> 2 -> 8 -> 10], [3 -> 5 -> 9 -> 11]
+
+Output: [1 -> 2 -> 3 -> 8 -> 9 -> 10 -> 11]
+```
+
+**Example 2 :**
+
+```cpp
+Input: [1 -> 7 -> 8 -> 9], [2 -> 5 -> 10 -> 11]
+
+Output: [1 -> 2 -> 5 -> 7 -> 8 -> 9 -> 11]
+```
+
+---
+### Question
+Given two sorted Linked Lists, Merge them into a single sorted linked list.
+
+`Input: [2 -> 10 -> 11] [1 -> 5 -> 12 -> 15]`
+
+**Choices**
+- [x] [1 -> 2 -> 5 -> 10 -> 11 -> 12 -> 15]
+- [ ] [2 -> 10 -> 11 -> 1 -> 5 -> 12 -> 15]
+- [ ] [1 -> 5 -> 12 -> 15 -> 2 -> 10 -> 11]
+- [ ] [1 -> 2 -> 10 -> 5 -> 12 -> 11 -> 15]
+
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+### Merge two sorted Linked Lists Solution
+#### Solution
+ * Base Cases Handling: First of all, we need to take care of the Base cases: if either list is empty,we return the other list
+ * Determine Merged List's Head: The algorithm compares the first nodes of the two lists. The smaller node becomes the head of the merged list.
+ * Merge the Remaining Nodes:Merge the remaining nodes in such a way that whichever linked lists node is the smallest, we add it to the current list
+ * We continue doing this till the end of one of the linked lists is reached
+ * Finally we attach any remaining nodes from list1 or list2
+* Returning the Result: We return the linked list
+
+#### Pseudocode
+
+```cpp
+function mergeSortedLists(list1, list2)
+ if list1 is null
+ return list2
+ if list2 is null
+ return list1
+
+ mergedList = null
+
+ if list1.data <= list2.data
+ mergedList = list1
+ list1 = list1.next
+ else
+ mergedList = list2
+ list2 = list2.next
+
+ current = mergedList
+
+ while list1 is not null and list2 is not null
+ if list1.data <= list2.data
+ current.next = list1
+ list1 = list1.next
+ else
+ current.next = list2
+ list2 = list2.next
+ current = current.next
+
+ if list1 is not null
+ current.next = list1
+ if list2 is not null
+ current.next = list2
+
+ return mergedList
+
+}
+```
+
+#### Complexity
+**Time Complexity:** O(n + m)
+**Space Complexity:** O(1)
+
+---
+### Problem 3 Sort a Linked List
+
+A Linked List is given, Sort the Linked list using merge sort.
+
+**Example**
+```cpp
+Input: [1 -> 2 -> 5 -> 4 -> 3]
+Output: [1 -> 2 -> 3 -> 4 -> 5]
+
+```
+
+```cpp
+Input: [1 -> 4 -> 3 -> 2]
+Output: [1 -> 2 -> 3 -> 4]
+
+```
+
+
+#### Solution
+
+**Base Case:**
+
+#### Pseudocode
+```java
+function findMiddleTwoPointers(head)
+ if head is null
+ return null
+
+ slowPointer = head
+ fastPointer = head
+
+ while fastPointer is not null and fastPointer.next is not null
+ slowPointer = slowPointer.next
+ fastPointer = fastPointer.next.next
+
+ return slowPointer
+```
+
+#### Complexity
+**Time Complexity:** O(n / 2) = O(n)
+**Space Complexity:** O(1)
+
+
+
+---
+### Problem 2 Merge two sorted Linked Lists
+
+Given two sorted Linked Lists, Merge them into a single sorted linked list.
+
+**Example 1 :**
+
+```cpp
+Input: [1 -> 2 -> 8 -> 10], [3 -> 5 -> 9 -> 11]
+
+Output: [1 -> 2 -> 3 -> 8 -> 9 -> 10 -> 11]
+```
+
+**Example 2 :**
+
+```cpp
+Input: [1 -> 7 -> 8 -> 9], [2 -> 5 -> 10 -> 11]
+
+Output: [1 -> 2 -> 5 -> 7 -> 8 -> 9 -> 11]
+```
+
+---
+### Question
+Given two sorted Linked Lists, Merge them into a single sorted linked list.
+
+`Input: [2 -> 10 -> 11] [1 -> 5 -> 12 -> 15]`
+
+**Choices**
+- [x] [1 -> 2 -> 5 -> 10 -> 11 -> 12 -> 15]
+- [ ] [2 -> 10 -> 11 -> 1 -> 5 -> 12 -> 15]
+- [ ] [1 -> 5 -> 12 -> 15 -> 2 -> 10 -> 11]
+- [ ] [1 -> 2 -> 10 -> 5 -> 12 -> 11 -> 15]
+
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+### Merge two sorted Linked Lists Solution
+#### Solution
+ * Base Cases Handling: First of all, we need to take care of the Base cases: if either list is empty,we return the other list
+ * Determine Merged List's Head: The algorithm compares the first nodes of the two lists. The smaller node becomes the head of the merged list.
+ * Merge the Remaining Nodes:Merge the remaining nodes in such a way that whichever linked lists node is the smallest, we add it to the current list
+ * We continue doing this till the end of one of the linked lists is reached
+ * Finally we attach any remaining nodes from list1 or list2
+* Returning the Result: We return the linked list
+
+#### Pseudocode
+
+```cpp
+function mergeSortedLists(list1, list2)
+ if list1 is null
+ return list2
+ if list2 is null
+ return list1
+
+ mergedList = null
+
+ if list1.data <= list2.data
+ mergedList = list1
+ list1 = list1.next
+ else
+ mergedList = list2
+ list2 = list2.next
+
+ current = mergedList
+
+ while list1 is not null and list2 is not null
+ if list1.data <= list2.data
+ current.next = list1
+ list1 = list1.next
+ else
+ current.next = list2
+ list2 = list2.next
+ current = current.next
+
+ if list1 is not null
+ current.next = list1
+ if list2 is not null
+ current.next = list2
+
+ return mergedList
+
+}
+```
+
+#### Complexity
+**Time Complexity:** O(n + m)
+**Space Complexity:** O(1)
+
+---
+### Problem 3 Sort a Linked List
+
+A Linked List is given, Sort the Linked list using merge sort.
+
+**Example**
+```cpp
+Input: [1 -> 2 -> 5 -> 4 -> 3]
+Output: [1 -> 2 -> 3 -> 4 -> 5]
+
+```
+
+```cpp
+Input: [1 -> 4 -> 3 -> 2]
+Output: [1 -> 2 -> 3 -> 4]
+
+```
+
+
+#### Solution
+
+**Base Case:**The function starts by checking if the head of the linked list is null or if it has only one element (i.e., head.next is null). These are the base cases for the recursion. If either of these conditions is met, it means that the list is already sorted (either empty or has only one element), so the function simply returns the head itself. + +**Find the Middle Node:**
If the base case is not met, the function proceeds to sort the list. First, it calls the findMiddle function to find the middle node of the current list. This step is essential for dividing the list into two halves for sorting. + +**Split the List:**
After finding the middle node (middle), the function creates a new pointer nextToMiddle to store the next node after the middle node. Then, it severs the connection between the middle node and the next node by setting middle.next to null. This effectively splits the list into two separate sublists: left, which starts from head and ends at middle, and right, which starts from nextToMiddle. + +**Recursively Sort Both Halves:**
The function now recursively calls itself on both left and right sublists. This recursive step continues until each sublist reaches the base case (empty or one element). Each recursive call sorts its respective sublist. + +**Merge the Sorted Halves:**
Once the recursive calls return and both left and right sublists are sorted, the function uses the mergeSortedLists function to merge these two sorted sublists into a single sorted list. This merging process combines the elements from left and right in ascending order. + +**Return the Sorted List:**
Finally, the function returns the sortedList, which is the fully sorted linked list obtained by merging the sorted left and right sublists + +#### Pseudocode +```cpp +// Function to merge two sorted linked lists + +function mergeSortedLists(list1, list2) + if list1 is null + return list2 + if list2 is null + return list1 + + mergedList = null + + if list1.data <= list2.data + mergedList = list1 + mergedList.next = mergeSortedLists(list1.next, list2) + else + mergedList = list2 + mergedList.next = mergeSortedLists(list1, list2.next) + + return mergedList + +function findMiddle(head) + if head is null or head.next is null + return head + + slow = head + fast = head.next + + while fast is not null and fast.next is not null + slow = slow.next + fast = fast.next.next + + return slow + +function mergeSort(head) + if head is null or head.next is null + return head + + // Find the middle node + middle = findMiddle(head) + nextToMiddle = middle.next + middle.next = null + + // Recursively sort both halves + left = mergeSort(head) + right = mergeSort(nextToMiddle) + + // Merge the sorted halves + sortedList = mergeSortedLists(left, right) + + return sortedList +``` + +#### Complexity +**Time Complexity:** O(Nlog(N)) +**Space Complexity:** O(log(N)) + +--- +### Problem 4 Detect Cycle in a Linked List. + +Given a Linked List, Find whether it contains a cycle. + +**Example 1** + +**Input:** + +
 +
+**Output:**
+```plaintext
+Yes
+```
+
+**Example 2**
+
+**Input:**
+Input: [1 -> 4 -> 3 -> 2 -> 11 -> 45 -> 99]
+
+
+**Output:**
+```plaintext
+No
+```
+
+---
+### Detect Cycle in a Linked List Solution
+#### Solution
+
+
+* **Initialization:**
+
+**Output:**
+```plaintext
+Yes
+```
+
+**Example 2**
+
+**Input:**
+Input: [1 -> 4 -> 3 -> 2 -> 11 -> 45 -> 99]
+
+
+**Output:**
+```plaintext
+No
+```
+
+---
+### Detect Cycle in a Linked List Solution
+#### Solution
+
+
+* **Initialization:**Start with two pointers, slow and fast, both pointing to the head of the linked list. + +* **Traversal:**
In each iteration, the slow pointer advances by one step, while the fast pointer advances by two steps. This mimics the tortoise and hare analogy. If there is a cycle, these two pointers will eventually meet at some point within the cycle. + +* **Cycle Detection:**
While traversing, if the slow pointer becomes equal to the fast pointer, this indicates that the linked list contains a cycle. This is because the fast pointer "catches up" to the slow pointer within the cycle. + +* **No Cycle Check:**
If the fast pointer reaches the end of the linked list and becomes null or if the fast pointer's next becomes nullp, this means there is no cycle in the linked list. + +* **Cycle Detected:**
If the slow and fast pointers meet, it implies that the linked list contains a cycle. The function returns true. + + +#### Pseudo Code +```cpp +function hasCycle(head) + if head is null or head.next is null + return false // No cycle in an empty or single-node list + + slow = head + fast = head.next + + while fast is not null and fast.next is not null + if slow is the same as fast + return true // Cycle detected + slow = slow.next + fast = fast.next.next + + return false // No cycle detected + + +``` + +#### Complexity +**Time Complexity:** O(N) +**Space Complexity:** O(1) + + +--- +### Problem 5 Find the starting point + +Given a Linked List which contains a cycle , Find the start point of the cycle. + +**Example** + +**Input:** + +
 +
+
+**Output:**
+```plaintext
+5
+```
+
+
+---
+### Find the starting point Solution
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+#### Solution
+* **Initialization:**
+
+
+**Output:**
+```plaintext
+5
+```
+
+
+---
+### Find the starting point Solution
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+#### Solution
+* **Initialization:**Similar to cycle detection, start with two pointers, slow and fast, both pointing to the head of the linked list. + +* **Cycle Detection:**
In each iteration, move the slow pointer by one step and the fast pointer by two steps. If a cycle exists, they will eventually meet within the cycle. + +* **Meeting Point:**
If a cycle is detected (slow meets fast), set a flag hasCycle to true. + +* **Start Point Identification:**
Reset the slow pointer to the head of the list while keeping the fast pointer at the meeting point. Advance both pointers by one step in each iteration. They will eventually meet at the start point of the cycle. + +* **Returning the Result:**
Once the slow and fast pointers meet again, it implies that the linked list has a cycle, and the meeting point is the start of the cycle. Return this pointer. + + + +Assume that the length from the head to the first node of cycle is x and the distance from the first node of cycle to the meeting point is y. Also the length from the meeting point to the first node is z. + +Now, speed of the fast pointer is twice the slow pointer + +```cpp +2(x + y) = x + y + z + y + +x = z + +``` + +
 +
+
+* **No Cycle Check:** If the fast pointer reaches the end of the linked list (i.e., becomes nullptr) or if the fast pointer's next becomes nullptr, there is no cycle. In such cases, return nullptr.
+
+This approach ensures that you can find the start point of the cycle using the Floyd's Tortoise and Hare algorithm with a slightly modified process.
+
+
+#### Pseudo Code
+```cpp
+function detectCycleStart(head)
+ if head is null or head.next is null
+ return null // No cycle in an empty or single-node list
+
+ slow = head
+ fast = head
+ hasCycle = false
+
+ while fast is not null and fast.next is not null
+ slow = slow.next
+ fast = fast.next.next
+
+ if slow is the same as fast
+ hasCycle = true
+ break
+
+ if not hasCycle
+ return null // No cycle detected
+
+ slow = head
+ while slow is not the same as fast
+ slow = slow.next
+ fast = fast.next
+
+ return slow // Return the start point of the cycle
+
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(1)
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Linked List 3 Problems & Doubly Linked List.md b/Academy DSA Typed Notes/Advanced/DSA Linked List 3 Problems & Doubly Linked List.md
new file mode 100644
index 0000000..15b7700
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Linked List 3 Problems & Doubly Linked List.md
@@ -0,0 +1,340 @@
+# Linked List 3: Problems & Doubly Linked List
+
+---
+## What is doubly linked list
+
+A doubly linked list is a type of data structure used in computer science and programming to store and organize a collection of elements, such as nodes. It is similar to a singly linked list but with an additional feature: each node in a doubly linked list contains pointers or references to both the next and the previous nodes in the list.
+
+**Example**
+
+
+
+
+* **No Cycle Check:** If the fast pointer reaches the end of the linked list (i.e., becomes nullptr) or if the fast pointer's next becomes nullptr, there is no cycle. In such cases, return nullptr.
+
+This approach ensures that you can find the start point of the cycle using the Floyd's Tortoise and Hare algorithm with a slightly modified process.
+
+
+#### Pseudo Code
+```cpp
+function detectCycleStart(head)
+ if head is null or head.next is null
+ return null // No cycle in an empty or single-node list
+
+ slow = head
+ fast = head
+ hasCycle = false
+
+ while fast is not null and fast.next is not null
+ slow = slow.next
+ fast = fast.next.next
+
+ if slow is the same as fast
+ hasCycle = true
+ break
+
+ if not hasCycle
+ return null // No cycle detected
+
+ slow = head
+ while slow is not the same as fast
+ slow = slow.next
+ fast = fast.next
+
+ return slow // Return the start point of the cycle
+
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(1)
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Linked List 3 Problems & Doubly Linked List.md b/Academy DSA Typed Notes/Advanced/DSA Linked List 3 Problems & Doubly Linked List.md
new file mode 100644
index 0000000..15b7700
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Linked List 3 Problems & Doubly Linked List.md
@@ -0,0 +1,340 @@
+# Linked List 3: Problems & Doubly Linked List
+
+---
+## What is doubly linked list
+
+A doubly linked list is a type of data structure used in computer science and programming to store and organize a collection of elements, such as nodes. It is similar to a singly linked list but with an additional feature: each node in a doubly linked list contains pointers or references to both the next and the previous nodes in the list.
+
+**Example**
+
+ +
+### Correlation with Singly Linked List
+
+The main difference between singly linked lists and doubly linked lists lies in the bidirectional traversal capability of the latter, which comes at the cost of increased memory usage. The choice between them depends on the specific requirements of the problem we're solving and the operations we need to perform on the list
+
+> **Note-1**: Sometimes the `previous` pointer is called the `left` pointer and the `next` pointer is called the `right` pointer.
+> **Note-2**: The `previous` pointer of the first node always points to `null` and the `next` pointer of the last node also points to `null` in the doubly linked list.
+
+---
+### Question
+`prev` Pointer of Head of Doubly LinkedLIst points to:
+
+**Choices**
+- [ ] Next to Head Node
+- [x] Null pointer
+- [ ] Tail
+- [ ] Depends
+
+
+---
+### Problem 1 Insert node in a doubly linked list
+
+A doubly linked list is given. A node is to be inserted with data ``X`` at position ``K``. The range of ``K`` is between 0 and ``N`` where ``N`` is the length of the doubly Linked list.
+
+**Example**
+
+
+
+### Correlation with Singly Linked List
+
+The main difference between singly linked lists and doubly linked lists lies in the bidirectional traversal capability of the latter, which comes at the cost of increased memory usage. The choice between them depends on the specific requirements of the problem we're solving and the operations we need to perform on the list
+
+> **Note-1**: Sometimes the `previous` pointer is called the `left` pointer and the `next` pointer is called the `right` pointer.
+> **Note-2**: The `previous` pointer of the first node always points to `null` and the `next` pointer of the last node also points to `null` in the doubly linked list.
+
+---
+### Question
+`prev` Pointer of Head of Doubly LinkedLIst points to:
+
+**Choices**
+- [ ] Next to Head Node
+- [x] Null pointer
+- [ ] Tail
+- [ ] Depends
+
+
+---
+### Problem 1 Insert node in a doubly linked list
+
+A doubly linked list is given. A node is to be inserted with data ``X`` at position ``K``. The range of ``K`` is between 0 and ``N`` where ``N`` is the length of the doubly Linked list.
+
+**Example**
+
+ +
+---
+
+### Question
+In a doubly linked list, the number of pointers affected for an insertion operation between two nodes will be?
+
+**Choices**
+- [ ] 1
+- [ ] 2
+- [ ] 3
+- [x] 4
+- [ ] Depends
+
+
+For insertions in the middle of the list **four** pointer assignments take place.
+
+---
+### Insert node in a doubly linked list Solution
+#### Solution
+A naive approach to insert a node with data `X` at position `K` in a doubly linked list of length `N` would involve traversing the list from the beginning until position `K` is reached, and then updating the pointers of the adjacent nodes to include the new node. This approach takes `O(K)` time complexity in the worst case.
+
+#### Our Approach
+Let us now move on to the below approach:
+
+Suppose given data are `X = 8` and `K = 3` and the provided linked list contains the nodes 1, 2, 3, 4, 5. Now, describe the overall approach in a step-wise manner.
+
+1. The very first thing that can be done is to create a node with data `X` whose previous and next pointers are pointing toward `null` currently.
+2. Next, we need to check if our linked list is empty or not. In the case of an empty linked list head pointer points towards `null`. So, if the head pointer is pointing towards `null`, we can simply return a new node with data `X`.
+3. The next thing that we need to take care of is if the value of `K` is zero. In this case, we need to add a new node with data `X` pointed by the head pointer. we also need to update the head pointer and the next pointer of the newly created node.
+4. Now that we have covered the two base cases, we can simply add the node by making `K - 1` jumps from the head pointer. For this, we can create a temporary node that is currently pointing toward the head, and we will traverse the `K - 1` nodes to reach the position where we want to add the new node.
+5. The last and most important thing that we need to do here is to update the next and previous pointers of `K - 1` and `K + 1` nodes.
+
+Let us now see the pseudo code of our approach.
+
+#### Pseudocode
+```cpp
+xn = new Node(x) // xn.next = xn.pre = null
+
+// Empty List
+if (head == null)
+ return xn
+
+// Update head
+if (k == 0) {
+ xn.next = head
+ head.pre = xn
+ head = xn
+ return head
+}
+
+temp = head
+for i = 1 to(k - 1)
+temp = temp.next
+
+xn.next = temp.next
+xn.pre = temp
+if (temp.next != null)
+ temp.next.pre = xn
+temp.next = xn
+return head
+```
+
+>**Note**: we should also check if our current position of insertion is the last node or not. In the case of the last node, the next pointer is pointing toward the `null`. So, we have to make it point to the current node.
+
+#### Time and Space Complexity
+- **Time Complexity**: **O(N)**, since we traverse the linked list only once.
+- **Space Complexity**: **O(1)** as we are not using any extra list.
+
+---
+### Problem 2 Delete the first occurrence of a node from the doubly linked list
+
+We have been given a doubly linked list of length `N`, we have to delete the first occurrence of data `X` from the given doubly linked list. If element `X` is not present, don't do anything.
+
+**Example**
+
+
+
+---
+
+### Question
+In a doubly linked list, the number of pointers affected for an insertion operation between two nodes will be?
+
+**Choices**
+- [ ] 1
+- [ ] 2
+- [ ] 3
+- [x] 4
+- [ ] Depends
+
+
+For insertions in the middle of the list **four** pointer assignments take place.
+
+---
+### Insert node in a doubly linked list Solution
+#### Solution
+A naive approach to insert a node with data `X` at position `K` in a doubly linked list of length `N` would involve traversing the list from the beginning until position `K` is reached, and then updating the pointers of the adjacent nodes to include the new node. This approach takes `O(K)` time complexity in the worst case.
+
+#### Our Approach
+Let us now move on to the below approach:
+
+Suppose given data are `X = 8` and `K = 3` and the provided linked list contains the nodes 1, 2, 3, 4, 5. Now, describe the overall approach in a step-wise manner.
+
+1. The very first thing that can be done is to create a node with data `X` whose previous and next pointers are pointing toward `null` currently.
+2. Next, we need to check if our linked list is empty or not. In the case of an empty linked list head pointer points towards `null`. So, if the head pointer is pointing towards `null`, we can simply return a new node with data `X`.
+3. The next thing that we need to take care of is if the value of `K` is zero. In this case, we need to add a new node with data `X` pointed by the head pointer. we also need to update the head pointer and the next pointer of the newly created node.
+4. Now that we have covered the two base cases, we can simply add the node by making `K - 1` jumps from the head pointer. For this, we can create a temporary node that is currently pointing toward the head, and we will traverse the `K - 1` nodes to reach the position where we want to add the new node.
+5. The last and most important thing that we need to do here is to update the next and previous pointers of `K - 1` and `K + 1` nodes.
+
+Let us now see the pseudo code of our approach.
+
+#### Pseudocode
+```cpp
+xn = new Node(x) // xn.next = xn.pre = null
+
+// Empty List
+if (head == null)
+ return xn
+
+// Update head
+if (k == 0) {
+ xn.next = head
+ head.pre = xn
+ head = xn
+ return head
+}
+
+temp = head
+for i = 1 to(k - 1)
+temp = temp.next
+
+xn.next = temp.next
+xn.pre = temp
+if (temp.next != null)
+ temp.next.pre = xn
+temp.next = xn
+return head
+```
+
+>**Note**: we should also check if our current position of insertion is the last node or not. In the case of the last node, the next pointer is pointing toward the `null`. So, we have to make it point to the current node.
+
+#### Time and Space Complexity
+- **Time Complexity**: **O(N)**, since we traverse the linked list only once.
+- **Space Complexity**: **O(1)** as we are not using any extra list.
+
+---
+### Problem 2 Delete the first occurrence of a node from the doubly linked list
+
+We have been given a doubly linked list of length `N`, we have to delete the first occurrence of data `X` from the given doubly linked list. If element `X` is not present, don't do anything.
+
+**Example**
+
+ +
+
+---
+### Delete the first occurrence Solution
+
+#### Solution
+A naive approach to solving this problem would be to start from the beginning of the doubly linked list and traverse it node by node. If the data of a node matches the given element, X, then remove that node by updating the next and previous pointers of the adjacent nodes to bypass the node to be deleted.
+
+#### Our Approach
+Suppose we have a DLL having nodes 9, 7, 3, 7, and 3, and we have to delete node 7. Let's break it into smaller steps:
+1. The simple thing that we need to do in this problem is to grab the previous node and the next node of node `X`.
+2. Then make the next pointer of the previous node point to the next node and make the previous pointer of the next node point to the previous node.
+3. Now, move on to corner cases. The first corner case is when the head pointer is pointing to `null`. In this case, we simply need to return null as we cannot delete anything.
+4. Now let's move on to the normal case and search for our next node. For searching we just need to create a temporary nod that is pointing to the head.
+5. Now, we will traverse the entire list using temporary nodes and check if the current node's value is the same as the `X`'s value.
+6. If the value is found, we just need to stop searching and delete the node.
+
+After traversal, we can have three situations:
+1. If the temp pointer is pointing to null, this means that we have not found our node. So, we can simply return the head pointer.
+2. If the previous pointer of the temporary node is pointing to null, then this means that our desired node is the first node. So, we need to delete the head pointer and simply return null. This will work the same if the next pointer of temp is null.
+3. If both the above corner cases are not encountered, then we can simply delete the current node that is pointed by temp.
+
+Let us now see the pseudo code of our approach.
+
+#### Pseudocode
+```cpp
+temp = head
+
+// Searching
+while (temp != null) {
+ if (temp.data == X)
+ break
+ temp = temp.next
+}
+
+// No update
+if (temp == null) {
+ return head
+}
+
+// Single node
+if (temp.pre == null and temp.next == null) {
+ return null
+} else if (temp.pre == null) // delete head
+{
+ temp.next.pre = null
+ head = temp.next
+} else if (temp.next == null) {
+ temp.pre.next = null
+} else {
+ temp.pre.next = temp.next
+ temp.next.pre = temp.pre
+}
+
+return head
+```
+
+
+#### Time and Space Complexity
+- **Time Complexity**: **O(N)**, since we traverse the linked list only once.
+- **Space Complexity**: **O(1)** as we are not using any extra list.
+
+---
+### Problem 3 LRU
+
+We have been given a running stream of integers and the fixed memory size of `M`, we have to maintain the most recent `M` elements. In case the current memory is full, we have to delete the least recent element and insert the current data into the memory (as the most recent item).
+
+**Example**
+This question is closely related to the concept of an LRU (Least Recently Used) cache memory. An LRU cache is a data structure that maintains a fixed-size memory and stores the most recently accessed items. When the cache is full and a new item needs to be inserted, the least recently used item is evicted to make space for the new item.
+
+
+
+
+---
+### Delete the first occurrence Solution
+
+#### Solution
+A naive approach to solving this problem would be to start from the beginning of the doubly linked list and traverse it node by node. If the data of a node matches the given element, X, then remove that node by updating the next and previous pointers of the adjacent nodes to bypass the node to be deleted.
+
+#### Our Approach
+Suppose we have a DLL having nodes 9, 7, 3, 7, and 3, and we have to delete node 7. Let's break it into smaller steps:
+1. The simple thing that we need to do in this problem is to grab the previous node and the next node of node `X`.
+2. Then make the next pointer of the previous node point to the next node and make the previous pointer of the next node point to the previous node.
+3. Now, move on to corner cases. The first corner case is when the head pointer is pointing to `null`. In this case, we simply need to return null as we cannot delete anything.
+4. Now let's move on to the normal case and search for our next node. For searching we just need to create a temporary nod that is pointing to the head.
+5. Now, we will traverse the entire list using temporary nodes and check if the current node's value is the same as the `X`'s value.
+6. If the value is found, we just need to stop searching and delete the node.
+
+After traversal, we can have three situations:
+1. If the temp pointer is pointing to null, this means that we have not found our node. So, we can simply return the head pointer.
+2. If the previous pointer of the temporary node is pointing to null, then this means that our desired node is the first node. So, we need to delete the head pointer and simply return null. This will work the same if the next pointer of temp is null.
+3. If both the above corner cases are not encountered, then we can simply delete the current node that is pointed by temp.
+
+Let us now see the pseudo code of our approach.
+
+#### Pseudocode
+```cpp
+temp = head
+
+// Searching
+while (temp != null) {
+ if (temp.data == X)
+ break
+ temp = temp.next
+}
+
+// No update
+if (temp == null) {
+ return head
+}
+
+// Single node
+if (temp.pre == null and temp.next == null) {
+ return null
+} else if (temp.pre == null) // delete head
+{
+ temp.next.pre = null
+ head = temp.next
+} else if (temp.next == null) {
+ temp.pre.next = null
+} else {
+ temp.pre.next = temp.next
+ temp.next.pre = temp.pre
+}
+
+return head
+```
+
+
+#### Time and Space Complexity
+- **Time Complexity**: **O(N)**, since we traverse the linked list only once.
+- **Space Complexity**: **O(1)** as we are not using any extra list.
+
+---
+### Problem 3 LRU
+
+We have been given a running stream of integers and the fixed memory size of `M`, we have to maintain the most recent `M` elements. In case the current memory is full, we have to delete the least recent element and insert the current data into the memory (as the most recent item).
+
+**Example**
+This question is closely related to the concept of an LRU (Least Recently Used) cache memory. An LRU cache is a data structure that maintains a fixed-size memory and stores the most recently accessed items. When the cache is full and a new item needs to be inserted, the least recently used item is evicted to make space for the new item.
+
+ +
+---
+### Question
+What is the behavior of an LRU cache memory when a new item is inserted and the cache is already full?
+
+**Choices**
+
+- [x] The new item is added to the cache, and the least recently used item is removed from the cache.
+- [ ] The new item is not added to the cache, and the least recently used item is not removed from the cache.
+- [ ] The new item is added to the cache, and the least recently used item is updated to be the most recently used item.
+- [ ] The new item is not added to the cache, and the most recently used item is removed from the cache.
+
+
+
+In an LRU cache, the least recently used item is always the one that is removed when the cache is full and a new item needs to be inserted. This ensures that the most recently accessed items are always prioritized and kept in the cache.
+
+---
+### LRU Solution
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Solution
+Suppose we have several data to be inserted and the memory size is `M = 5`. So, we will take data one by one and insert it into the memory. As soon as the memory gets full, we have to delete the oldest data. In case a number comes and the same number is present in the memory pool, it will not be deleted but it will be considered as the most recent element.
+
+A decision tree or flow chart can also be created for the problem.
+
+
+
+---
+### Question
+What is the behavior of an LRU cache memory when a new item is inserted and the cache is already full?
+
+**Choices**
+
+- [x] The new item is added to the cache, and the least recently used item is removed from the cache.
+- [ ] The new item is not added to the cache, and the least recently used item is not removed from the cache.
+- [ ] The new item is added to the cache, and the least recently used item is updated to be the most recently used item.
+- [ ] The new item is not added to the cache, and the most recently used item is removed from the cache.
+
+
+
+In an LRU cache, the least recently used item is always the one that is removed when the cache is full and a new item needs to be inserted. This ensures that the most recently accessed items are always prioritized and kept in the cache.
+
+---
+### LRU Solution
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Solution
+Suppose we have several data to be inserted and the memory size is `M = 5`. So, we will take data one by one and insert it into the memory. As soon as the memory gets full, we have to delete the oldest data. In case a number comes and the same number is present in the memory pool, it will not be deleted but it will be considered as the most recent element.
+
+A decision tree or flow chart can also be created for the problem.
+
+ +
+There can be two cases when a new number is to be inserted.
+1. If the current number is not present in the memory pool. In this case, we can simply delete the oldest number (i.e. deleting the head node).
+2. If the current number is present in the memory pool. In this case, we have to maintain the number `X`, as well as its position. So we can use a data structure called HashMap.
+
+Let us now see the pseudo code of our approach.
+
+#### Our Approach
+So, the conclusion is that we have to use a Doubly Linked List or a hashmap for the solution to this problem. Let now move on to the Coding / Solution part:
+1. Create a HashMap. Storing the value `X`, and the node of `X`.
+2. Check if the HashMap contains `X` and the size of memory is not full, then we can simply put a new number at the last position. In this case, we also need to tackle the corner cases of the problem - Deletion of a new node from the doubly linked list.
+3. The last case is when the number `X` is not present in the memory pool. Here, if the memory is full, we have to delete the oldest number i.e. the head node of the DLL( that we covered in the previous question). If the memory is not full we need to insert a new node into DLL at last.
+
+#### Important Concept
+There is an important concept in the Doubly linked list that is shallow copying and deep copying.
+
+In a doubly linked list, the concept related to shallow copying and deep copying is about how references (pointers) to nodes are managed during copying: "Shallow copying" involves copying the structure of the list, including the references, while "deep copying" involves creating new nodes and copying their content to have an independent copy of the original list.
+
+
+
+There can be two cases when a new number is to be inserted.
+1. If the current number is not present in the memory pool. In this case, we can simply delete the oldest number (i.e. deleting the head node).
+2. If the current number is present in the memory pool. In this case, we have to maintain the number `X`, as well as its position. So we can use a data structure called HashMap.
+
+Let us now see the pseudo code of our approach.
+
+#### Our Approach
+So, the conclusion is that we have to use a Doubly Linked List or a hashmap for the solution to this problem. Let now move on to the Coding / Solution part:
+1. Create a HashMap. Storing the value `X`, and the node of `X`.
+2. Check if the HashMap contains `X` and the size of memory is not full, then we can simply put a new number at the last position. In this case, we also need to tackle the corner cases of the problem - Deletion of a new node from the doubly linked list.
+3. The last case is when the number `X` is not present in the memory pool. Here, if the memory is full, we have to delete the oldest number i.e. the head node of the DLL( that we covered in the previous question). If the memory is not full we need to insert a new node into DLL at last.
+
+#### Important Concept
+There is an important concept in the Doubly linked list that is shallow copying and deep copying.
+
+In a doubly linked list, the concept related to shallow copying and deep copying is about how references (pointers) to nodes are managed during copying: "Shallow copying" involves copying the structure of the list, including the references, while "deep copying" involves creating new nodes and copying their content to have an independent copy of the original list.
+
+ +
+#### Pseudocode
+```cpp
+// Take a hashmap (hm)
+HashMap < x, node of x > hm;
+
+if (h.containsKey(X)) {
+ // Delete x from its position
+ xn = hm.get(x)
+ head = deleteNode(xn, head)
+ // insert as as node
+ tail.next = xn
+ xn.pre = tail
+ tail = xn
+} else // Not present
+{
+ // full memory
+ if (hm.size() == M) {
+ hm.remove(head.data)
+ deleteNode(head)
+ }
+ xn = new Node(x)
+ hm.put(x, xn)
+ if (hm.size() > 1) {
+ // Insert as last node
+ tail.next = xn
+ xn.pre = tail
+ tail = xn
+ } else {
+ head = tail = xn
+ }
+}
+```
+
+#### Time and Space Complexity
+- **Time Complexity**: **O(N)**, since we traverse the linked list only once.
+- **Space Complexity**: **O(1)** since we are not using any additional list.
+
+---
+### Problem 4 Deep copy of a doubly linked list
+
+we have to create a deep copy of the Doubly Linked list with random pointers. Here there is no certain next and previous pointer, a node can point to some other node.
+
+**Example**
+
+
+
+#### Pseudocode
+```cpp
+// Take a hashmap (hm)
+HashMap < x, node of x > hm;
+
+if (h.containsKey(X)) {
+ // Delete x from its position
+ xn = hm.get(x)
+ head = deleteNode(xn, head)
+ // insert as as node
+ tail.next = xn
+ xn.pre = tail
+ tail = xn
+} else // Not present
+{
+ // full memory
+ if (hm.size() == M) {
+ hm.remove(head.data)
+ deleteNode(head)
+ }
+ xn = new Node(x)
+ hm.put(x, xn)
+ if (hm.size() > 1) {
+ // Insert as last node
+ tail.next = xn
+ xn.pre = tail
+ tail = xn
+ } else {
+ head = tail = xn
+ }
+}
+```
+
+#### Time and Space Complexity
+- **Time Complexity**: **O(N)**, since we traverse the linked list only once.
+- **Space Complexity**: **O(1)** since we are not using any additional list.
+
+---
+### Problem 4 Deep copy of a doubly linked list
+
+we have to create a deep copy of the Doubly Linked list with random pointers. Here there is no certain next and previous pointer, a node can point to some other node.
+
+**Example**
+
+ +
+
+---
+### Deep Copy Solution
+
+#### Solution
+A naive approach to creating a deep copy of a doubly linked list with random pointers could involve iteratively traversing the original list, creating new nodes with the same data and random pointers, and then using additional passes to update the random pointers to point to the corresponding new nodes in the copied list.
+
+#### Our Approach
+1. In a node, we have two pointers. The first one is the next pointer and the second one is a random pointer.
+2. Our goal is to populate the Doubly Linked list using the next and random pointer. For this, we will be using the concept of deep copying in this.
+3. Now, since we don't have the previous and next pointer as of the Doubly Linked list, we can use a HashMap to map the original nodes.
+4. So, we will be creating the HashMap containing two things one is an old node and another is a new node but there is a small problem in this approach, we are using extra space here. As we only want the original mapping, we can solve this with constant space.
+
+A systematic approach can be:
+1. we will create a copy of each node calling it ``node_1`` and making it pointed by the first node.
+2. After this, we will make it point to the second node. So we are pushing a node between two nodes.
+ >**Note**: Here, we can teach that this problem can be summarized as pushing a copy of a node between two nodes and then changing the random pointer.
+3. Now, the problem becomes sorted as we only must copy a node and insert it in the middle of its previous and next node.
+4. Finally, we will be shuffling the random pointer. For this, we will be using an extra node ``X``, and ``X`` will be traversing until the last node of the list.
+
+#### Pseudocode
+```cpp
+// Populate random pointers
+x = head
+while (x != null) {
+ y = x.next
+ y.random = x.random.next
+ x = x.next.next
+}
+
+// Separate two
+h = head.next
+x = head
+while (x != null) {
+ y = x.next
+ x.next = x.next.next
+ if (y.next != null) {
+ y.next = y.next.next
+ }
+ x = x.next
+}
+
+return h
+```
+
+#### Time and Space Complexity
+- **Time Complexity**: **O(N)**, as we are creating a deep copy of the doubly linked list with random pointers.
+- **Space Complexity**:**O(N)**. In the case of deleting the first node, the time complexity remains **O(1)** as long as the deletion operation itself is **O(1)**.
+
+
+---
+
+
+### Question
+What is the time complexity of creating a deep copy of a Doubly Linked List consists of N nodes with random pointers using extra space?
+
+**Choices**
+- [x] O(N)
+- [ ] O(N * N)
+- [ ] O(1)
+- [ ] O(log(N))
\ No newline at end of file
diff --git a/Academy DSA Typed Notes/Advanced/DSA Maths 1 Modular Arithmetic & GCD.md b/Academy DSA Typed Notes/Advanced/DSA Maths 1 Modular Arithmetic & GCD.md
new file mode 100644
index 0000000..abaea6e
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Maths 1 Modular Arithmetic & GCD.md
@@ -0,0 +1,438 @@
+# Maths 1: Modular Arithmetic & GCD
+
+---
+## Modular Arithmetic Introduction
+
+A % B = Remainder when A is divided by B
+
+Range of A % B will be within **[0, B - 1]**
+
+### Why do we need Modular Arithmetic(%) ?
+
+The most useful need of `%` is to limit the range of data. We don't have unlimited range in **Integer** OR **Long**, hence after a certain limit, we cannot store data. In such cases, we can apply mod to limit the range.
+
+### Rules for applying mod on Arithmetic Operations
+
+**1.** `(a + b) % m = (a % m + b % m) % m`
+
+
+**Example:**
+
+
+
+---
+### Deep Copy Solution
+
+#### Solution
+A naive approach to creating a deep copy of a doubly linked list with random pointers could involve iteratively traversing the original list, creating new nodes with the same data and random pointers, and then using additional passes to update the random pointers to point to the corresponding new nodes in the copied list.
+
+#### Our Approach
+1. In a node, we have two pointers. The first one is the next pointer and the second one is a random pointer.
+2. Our goal is to populate the Doubly Linked list using the next and random pointer. For this, we will be using the concept of deep copying in this.
+3. Now, since we don't have the previous and next pointer as of the Doubly Linked list, we can use a HashMap to map the original nodes.
+4. So, we will be creating the HashMap containing two things one is an old node and another is a new node but there is a small problem in this approach, we are using extra space here. As we only want the original mapping, we can solve this with constant space.
+
+A systematic approach can be:
+1. we will create a copy of each node calling it ``node_1`` and making it pointed by the first node.
+2. After this, we will make it point to the second node. So we are pushing a node between two nodes.
+ >**Note**: Here, we can teach that this problem can be summarized as pushing a copy of a node between two nodes and then changing the random pointer.
+3. Now, the problem becomes sorted as we only must copy a node and insert it in the middle of its previous and next node.
+4. Finally, we will be shuffling the random pointer. For this, we will be using an extra node ``X``, and ``X`` will be traversing until the last node of the list.
+
+#### Pseudocode
+```cpp
+// Populate random pointers
+x = head
+while (x != null) {
+ y = x.next
+ y.random = x.random.next
+ x = x.next.next
+}
+
+// Separate two
+h = head.next
+x = head
+while (x != null) {
+ y = x.next
+ x.next = x.next.next
+ if (y.next != null) {
+ y.next = y.next.next
+ }
+ x = x.next
+}
+
+return h
+```
+
+#### Time and Space Complexity
+- **Time Complexity**: **O(N)**, as we are creating a deep copy of the doubly linked list with random pointers.
+- **Space Complexity**:**O(N)**. In the case of deleting the first node, the time complexity remains **O(1)** as long as the deletion operation itself is **O(1)**.
+
+
+---
+
+
+### Question
+What is the time complexity of creating a deep copy of a Doubly Linked List consists of N nodes with random pointers using extra space?
+
+**Choices**
+- [x] O(N)
+- [ ] O(N * N)
+- [ ] O(1)
+- [ ] O(log(N))
\ No newline at end of file
diff --git a/Academy DSA Typed Notes/Advanced/DSA Maths 1 Modular Arithmetic & GCD.md b/Academy DSA Typed Notes/Advanced/DSA Maths 1 Modular Arithmetic & GCD.md
new file mode 100644
index 0000000..abaea6e
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Maths 1 Modular Arithmetic & GCD.md
@@ -0,0 +1,438 @@
+# Maths 1: Modular Arithmetic & GCD
+
+---
+## Modular Arithmetic Introduction
+
+A % B = Remainder when A is divided by B
+
+Range of A % B will be within **[0, B - 1]**
+
+### Why do we need Modular Arithmetic(%) ?
+
+The most useful need of `%` is to limit the range of data. We don't have unlimited range in **Integer** OR **Long**, hence after a certain limit, we cannot store data. In such cases, we can apply mod to limit the range.
+
+### Rules for applying mod on Arithmetic Operations
+
+**1.** `(a + b) % m = (a % m + b % m) % m`
+
+
+**Example:**
+ +
+---
+**2.** `(a * b) % m = (a % m * b % m) % m`
+
+
+**3.** `(a + m) % m = (a % m + m % m) % m = (a % m) % m = a % m`
+
+---
+**4.** `(a - b) % m = (a % m - b % m + m) % m`
+
+This extra **m** term is added to ensure that the result remains within the range of **0 to m-1** even if the intermediate result of **(a % m - b % m) is negative**. This guarantees that the final remainder is a non-negative value.
+
+Example:
+Let's take **a = 7**, **b = 10**, and **m = 5**.
+
+$(a - b)~ \%~ m ~=~ (7 - 10) ~\%~ 5 ~=~ -3 ~\%~ 5 = -3$ (which is not in the range 0 to 4)
+
+Now we can simly do
+(-3 + 5) % 5 = 2 (now value is in the range 0 to 4)
+
+---
+**5.** `(a ^ b) % m = ( (a % m) ^ b ) % m`
+(a raise to power b)
+
+---
+### Question
+
+Evaluate :
+
+$(37^{103} - 1) \% 12$
+
+**Choices**
+
+- [ ] 1
+- [x] 0
+- [ ] No Idea
+- [ ] 10
+
+**Explanation**:
+
+
+$(37^{103}-1)\%12$
+
+$=>~ ((37^{103}~\%12)-(1\%12)+12)\%12$
+
+$=>~ (((37\%12){103}~\%12)-1+12)~\%12$
+
+$=>~ (1-1+12)\%12 = 12\%12 =0$
+
+---
+### Question
+
+What is the result of the following modular arithmetic operation?
+(25+13)%7
+
+**Choices**
+
+- [ ] 1
+- [ ] 2
+- [x] 6
+- [ ] 4
+
+**Explanation**
+
+(25+13)%7=38%7=3⋅7+3=3
+Therefore, the correct choice is 6.
+
+---
+### Question 1 Count pairs whose sum is a multiple of m
+
+Given N array elements, find count of pairs (i, j) such that $(arr[i] + arr[j]) ~\%~ m = 0$
+
+**Note:** $i~!=~j$ and pair(i, j) is same as pair(j, i)
+
+**Example**
+`A[ ] = {4, 3, 6, 3, 8, 12}`
+`m = 6`
+
+Pairs that satisfy **$(arr[i] + arr[j]) ~\%~ 6 = 0$** are:
+`(4 + 8) % 6 = 0`
+`(3 + 3) % 6 = 0`
+`(6 + 12) % 6 = 0`
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Brute Force Approach
+
+* For each pair of distinct indices `i` and `j` (where `i != j`), the sum $arr[i] ~+~ arr[j]$ is calculated, and then the remainder of this sum when divided by `m` is checked.
+* If the remainder is 0, then the pair `(i, j)` satisfies the condition, and the count is incremented. This approach has a time complexity of $O(N^2)$, where N is the number of elements in the array, as it involves checking all possible pairs.
+
+#### Optimal Approach
+
+**Hint:**
+We can utilise the property: $(a + b) \% m = (a \% m + b \% m) \% m$
+Instead of directly checking for $(a+b)\%m$, we can check for $(a ~\%~ m ~+~ b \% m) \% m$
+
+**Idea:**
+* Iterate through the array and calculate `A[i] % m` for all values.
+* Now, the sum of `A[i] % m` for two values should be divisible by m.
+
+
+**Example**:
+```java
+A[ ] = {2, 3, 4, 8, 6, 15, 5, 12, 17, 7, 18}
+m = 6
+```
+After doing mod with 6, we'll get
+```java
+{2, 3, 4, 2, 0, 3, 5, 0, 5, 1, 0}
+Note: The range of A[i] % 6 is from 0 to 5
+```
+* Summing 1 with 5 will give sum divisible by 6.
+* Likewise, 2 with 4, 3 with 3, and lastly 0 with 0.
+
+#### Algorithm
+
+* Iterate given array and calculate $A[i]\%m$.
+* Create a frequency array of size **m** to store the frequency of remainders obtained from the elements.
+* For each element, find the complement remainder needed for the sum to be divisible by `m`. Count frequency of complement remainder. Add these counts to get the total count of pairs satisfying the condition.
+* **Note:** Mod 0 will form a pair with 0, i.e if m = 6, and say 12 & 18 are present in given array, doing 12 % 6 and 18 % 6 will result in 0.
+
+#### Dry Run
+```java
+A[ ] = {2, 3, 4, 8, 6, 15, 5, 12, 17, 7, 18}
+m = 6
+```
+After doing mod with 6, we'll get
+```java
+{2, 3, 4, 2, 0, 3, 5, 0, 5, 1, 0}
+```
+
+* We'll keep inserting frequency of elements in frequency array while iterating over remainder values -
+
+| Remainder | Pair for it | Frequency | Count | Freq array |
+|:---------:|:-------------------:|:----------------------------------------------------------------------:|:-----:| --- |
+| 2 | $6-2 = 4$ | 4 is not yet present, but insert 2 for future use. | 0 | 2:1 |
+| 3 | $6-3 = 3$ | 3 is not yet present, but insert 3 for future use. | 0 | 2:1 3:1 |
+| 4 | $6-4 = 2$ | 2 is present with freq 1, count += 1 i.e, **1**; insert 4 for future use | 1 | 2:1 3:1 4:1 |
+| 2 | $6-2 = 4$ | 4 is present with freq 1, count += 1 i.e, **2**; update frequency of 2. | 2 | 2:2 3:1 4:1 |
+| 0 | 0 forms pair with 0 | 0 is not yet present, but insert 0 for future use. | 2 | 2:2 3:1 4:1 0:1 |
+| 3 | $6-3 = 3$ | 3 is present with freq 1, count += 1 i.e, **3**; update frequency of 3. | 3 | 2:2 3:2 4:1 0:1 |
+| 5 | $6-5 = 1$ | 1 is not yet present, but insert 5 for future use. | 3 | 2:2 3:2 4:1 0:1 5:1 |
+| 0 | 0 forms pair with 0 | 0 is present with freq 1, count += 1 i.e, **4**; update frequency of 0. | 4 | 2:2 3:2 4:1 0:2 5:1 |
+| 5 | $6-5 = 1$ | 1 is not yet present, but update frequency of 5 | 4 | 2:2 3:2 4:1 0:2 5:2 |
+| 1 | $6-1 = 5$ | 5 is present with freq 2, count += 2 i.e, **6**; update frequency of 1. | 6 | 2:2 3:2 4:1 0:2 5:2 1:1 |
+| 0 | 0 forms pair with 0 | 0 is present with freq 2, count += 2 i.e, **8**; update frequency of 0. | 8 | 2:2 3:2 4:1 0:3 5:2 1:1 |
+
+
+
+
+
+#### Pseudocode
+
+```cpp
+int pairSumDivisibleByM(A, m) {
+ N = A.length;
+ freq[N] = {
+ 0
+ };
+ count = 0;
+
+ for (int i = 0; i < N; i++) {
+ val = A[i] % m;
+
+ if (val == 0) {
+ pair = 0;
+ } else {
+ pair = m - val;
+ }
+ ans += freq[pair];
+ freq[val]++;
+ }
+
+ return count;
+}
+```
+
+**Time Complexity** - `O(N)`
+
+
+---
+### Question
+
+**Space Complexity**: Pair Sum Divisible by M
+
+**Choices**
+
+- [ ] O(N)
+- [x] O(M)
+- [ ] O(N+M)
+
+**Explanation**
+
+Space Complexity (SC) is `O(M)`, where M is the modulus value. This is because the frequency array of size M is required to store frequency of elements from 0 to M-1.
+
+---
+## GCD Basics
+
+### Explanation
+
+* GCD - Greatest Common Division
+* HCF - Highest Common Factor
+* GCD(A, B) - Greatest factor that divides both a and b
+
+If we have `GCD(A, B) = x`
+
+This implies:-
+
+* A % x = 0
+* B % x = 0
+
+and hence `x` is the highest factor of both A and B
+
+**Example - 1**
+
+GCD(15, 25) = 5
+
+
+
+---
+**2.** `(a * b) % m = (a % m * b % m) % m`
+
+
+**3.** `(a + m) % m = (a % m + m % m) % m = (a % m) % m = a % m`
+
+---
+**4.** `(a - b) % m = (a % m - b % m + m) % m`
+
+This extra **m** term is added to ensure that the result remains within the range of **0 to m-1** even if the intermediate result of **(a % m - b % m) is negative**. This guarantees that the final remainder is a non-negative value.
+
+Example:
+Let's take **a = 7**, **b = 10**, and **m = 5**.
+
+$(a - b)~ \%~ m ~=~ (7 - 10) ~\%~ 5 ~=~ -3 ~\%~ 5 = -3$ (which is not in the range 0 to 4)
+
+Now we can simly do
+(-3 + 5) % 5 = 2 (now value is in the range 0 to 4)
+
+---
+**5.** `(a ^ b) % m = ( (a % m) ^ b ) % m`
+(a raise to power b)
+
+---
+### Question
+
+Evaluate :
+
+$(37^{103} - 1) \% 12$
+
+**Choices**
+
+- [ ] 1
+- [x] 0
+- [ ] No Idea
+- [ ] 10
+
+**Explanation**:
+
+
+$(37^{103}-1)\%12$
+
+$=>~ ((37^{103}~\%12)-(1\%12)+12)\%12$
+
+$=>~ (((37\%12){103}~\%12)-1+12)~\%12$
+
+$=>~ (1-1+12)\%12 = 12\%12 =0$
+
+---
+### Question
+
+What is the result of the following modular arithmetic operation?
+(25+13)%7
+
+**Choices**
+
+- [ ] 1
+- [ ] 2
+- [x] 6
+- [ ] 4
+
+**Explanation**
+
+(25+13)%7=38%7=3⋅7+3=3
+Therefore, the correct choice is 6.
+
+---
+### Question 1 Count pairs whose sum is a multiple of m
+
+Given N array elements, find count of pairs (i, j) such that $(arr[i] + arr[j]) ~\%~ m = 0$
+
+**Note:** $i~!=~j$ and pair(i, j) is same as pair(j, i)
+
+**Example**
+`A[ ] = {4, 3, 6, 3, 8, 12}`
+`m = 6`
+
+Pairs that satisfy **$(arr[i] + arr[j]) ~\%~ 6 = 0$** are:
+`(4 + 8) % 6 = 0`
+`(3 + 3) % 6 = 0`
+`(6 + 12) % 6 = 0`
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Brute Force Approach
+
+* For each pair of distinct indices `i` and `j` (where `i != j`), the sum $arr[i] ~+~ arr[j]$ is calculated, and then the remainder of this sum when divided by `m` is checked.
+* If the remainder is 0, then the pair `(i, j)` satisfies the condition, and the count is incremented. This approach has a time complexity of $O(N^2)$, where N is the number of elements in the array, as it involves checking all possible pairs.
+
+#### Optimal Approach
+
+**Hint:**
+We can utilise the property: $(a + b) \% m = (a \% m + b \% m) \% m$
+Instead of directly checking for $(a+b)\%m$, we can check for $(a ~\%~ m ~+~ b \% m) \% m$
+
+**Idea:**
+* Iterate through the array and calculate `A[i] % m` for all values.
+* Now, the sum of `A[i] % m` for two values should be divisible by m.
+
+
+**Example**:
+```java
+A[ ] = {2, 3, 4, 8, 6, 15, 5, 12, 17, 7, 18}
+m = 6
+```
+After doing mod with 6, we'll get
+```java
+{2, 3, 4, 2, 0, 3, 5, 0, 5, 1, 0}
+Note: The range of A[i] % 6 is from 0 to 5
+```
+* Summing 1 with 5 will give sum divisible by 6.
+* Likewise, 2 with 4, 3 with 3, and lastly 0 with 0.
+
+#### Algorithm
+
+* Iterate given array and calculate $A[i]\%m$.
+* Create a frequency array of size **m** to store the frequency of remainders obtained from the elements.
+* For each element, find the complement remainder needed for the sum to be divisible by `m`. Count frequency of complement remainder. Add these counts to get the total count of pairs satisfying the condition.
+* **Note:** Mod 0 will form a pair with 0, i.e if m = 6, and say 12 & 18 are present in given array, doing 12 % 6 and 18 % 6 will result in 0.
+
+#### Dry Run
+```java
+A[ ] = {2, 3, 4, 8, 6, 15, 5, 12, 17, 7, 18}
+m = 6
+```
+After doing mod with 6, we'll get
+```java
+{2, 3, 4, 2, 0, 3, 5, 0, 5, 1, 0}
+```
+
+* We'll keep inserting frequency of elements in frequency array while iterating over remainder values -
+
+| Remainder | Pair for it | Frequency | Count | Freq array |
+|:---------:|:-------------------:|:----------------------------------------------------------------------:|:-----:| --- |
+| 2 | $6-2 = 4$ | 4 is not yet present, but insert 2 for future use. | 0 | 2:1 |
+| 3 | $6-3 = 3$ | 3 is not yet present, but insert 3 for future use. | 0 | 2:1 3:1 |
+| 4 | $6-4 = 2$ | 2 is present with freq 1, count += 1 i.e, **1**; insert 4 for future use | 1 | 2:1 3:1 4:1 |
+| 2 | $6-2 = 4$ | 4 is present with freq 1, count += 1 i.e, **2**; update frequency of 2. | 2 | 2:2 3:1 4:1 |
+| 0 | 0 forms pair with 0 | 0 is not yet present, but insert 0 for future use. | 2 | 2:2 3:1 4:1 0:1 |
+| 3 | $6-3 = 3$ | 3 is present with freq 1, count += 1 i.e, **3**; update frequency of 3. | 3 | 2:2 3:2 4:1 0:1 |
+| 5 | $6-5 = 1$ | 1 is not yet present, but insert 5 for future use. | 3 | 2:2 3:2 4:1 0:1 5:1 |
+| 0 | 0 forms pair with 0 | 0 is present with freq 1, count += 1 i.e, **4**; update frequency of 0. | 4 | 2:2 3:2 4:1 0:2 5:1 |
+| 5 | $6-5 = 1$ | 1 is not yet present, but update frequency of 5 | 4 | 2:2 3:2 4:1 0:2 5:2 |
+| 1 | $6-1 = 5$ | 5 is present with freq 2, count += 2 i.e, **6**; update frequency of 1. | 6 | 2:2 3:2 4:1 0:2 5:2 1:1 |
+| 0 | 0 forms pair with 0 | 0 is present with freq 2, count += 2 i.e, **8**; update frequency of 0. | 8 | 2:2 3:2 4:1 0:3 5:2 1:1 |
+
+
+
+
+
+#### Pseudocode
+
+```cpp
+int pairSumDivisibleByM(A, m) {
+ N = A.length;
+ freq[N] = {
+ 0
+ };
+ count = 0;
+
+ for (int i = 0; i < N; i++) {
+ val = A[i] % m;
+
+ if (val == 0) {
+ pair = 0;
+ } else {
+ pair = m - val;
+ }
+ ans += freq[pair];
+ freq[val]++;
+ }
+
+ return count;
+}
+```
+
+**Time Complexity** - `O(N)`
+
+
+---
+### Question
+
+**Space Complexity**: Pair Sum Divisible by M
+
+**Choices**
+
+- [ ] O(N)
+- [x] O(M)
+- [ ] O(N+M)
+
+**Explanation**
+
+Space Complexity (SC) is `O(M)`, where M is the modulus value. This is because the frequency array of size M is required to store frequency of elements from 0 to M-1.
+
+---
+## GCD Basics
+
+### Explanation
+
+* GCD - Greatest Common Division
+* HCF - Highest Common Factor
+* GCD(A, B) - Greatest factor that divides both a and b
+
+If we have `GCD(A, B) = x`
+
+This implies:-
+
+* A % x = 0
+* B % x = 0
+
+and hence `x` is the highest factor of both A and B
+
+**Example - 1**
+
+GCD(15, 25) = 5
+
+ +
+
+**Example - 2**
+
+GCD(12, 30) = 6
+
+
+
+
+**Example - 2**
+
+GCD(12, 30) = 6
+
+ +
+**Example - 3**
+
+GCD(0, 4) = 4
+
+
+
+**Example - 3**
+
+GCD(0, 4) = 4
+
+ +
+
+
+**Example - 4**
+
+GCD(0, 0) = Infinity
+
+
+
+
+
+**Example - 4**
+
+GCD(0, 0) = Infinity
+
+ +
+
+---
+## Properties of GCD
+
+### Property - 1
+
+GCD(A, B) = GCD(B, A)
+
+### Property - 2
+
+GCD(0, A) = A
+
+### Property - 3
+
+GCD(A, B, C) = GCD(A, GCD(B, C)) = GCD(B, GCD(C, A)) = GCD(C, GCD(A, B))
+
+
+
+
+---
+## Properties of GCD
+
+### Property - 1
+
+GCD(A, B) = GCD(B, A)
+
+### Property - 2
+
+GCD(0, A) = A
+
+### Property - 3
+
+GCD(A, B, C) = GCD(A, GCD(B, C)) = GCD(B, GCD(C, A)) = GCD(C, GCD(A, B))
+
+ +
+### Property - 4
+
+Given `A >= B > 0`,
+**GCD(A, B) = GCD(A - B, B)**
+
+
+**Example:**
+
+
+
+### Property - 4
+
+Given `A >= B > 0`,
+**GCD(A, B) = GCD(A - B, B)**
+
+
+**Example:**
+
+ +
+### Property - 5
+
+GCD(A, B) = GCD(A % B, B)
+
+---
+### Question
+gcd(0,8) = ?
+Chose the correct answer
+
+**Choices**
+- [ ] 1
+- [x] 8
+- [ ] 0
+- [ ] not defined
+
+
+---
+### Question
+TC of gcd(a1,a2,a3,....,an) is:
+Chose the correct answer
+
+**Choices**
+- [ ] O(log(max number))
+- [ ] O(N)
+- [x] O(N*log(max number)
+- [ ] O(N^2)
+
+---
+### Question
+Given an array A = [15, 21, 33, 45], find the GCD of all elements in the array.
+
+**Choices**
+- [ ] 4
+- [x] 3
+- [ ] 6
+- [ ] 9
+
+---
+## Function of GCD
+
+### Write a function to find GCD(A, B)
+
+
+
+### Property - 5
+
+GCD(A, B) = GCD(A % B, B)
+
+---
+### Question
+gcd(0,8) = ?
+Chose the correct answer
+
+**Choices**
+- [ ] 1
+- [x] 8
+- [ ] 0
+- [ ] not defined
+
+
+---
+### Question
+TC of gcd(a1,a2,a3,....,an) is:
+Chose the correct answer
+
+**Choices**
+- [ ] O(log(max number))
+- [ ] O(N)
+- [x] O(N*log(max number)
+- [ ] O(N^2)
+
+---
+### Question
+Given an array A = [15, 21, 33, 45], find the GCD of all elements in the array.
+
+**Choices**
+- [ ] 4
+- [x] 3
+- [ ] 6
+- [ ] 9
+
+---
+## Function of GCD
+
+### Write a function to find GCD(A, B)
+
+ +
+
+Suppose we have two positive numbers a, b then:
+
+```java
+int gcd(a, b) {
+ if (b == 0) {
+ return a;
+ }
+ return gcd(b, a % b);
+}
+```
+
+**Time Complexity(TC):** O(log(max(a, b)))
+
+### Given an array, calculate GCD of the entire array
+
+**Example:**
+
+
+
+
+Suppose we have two positive numbers a, b then:
+
+```java
+int gcd(a, b) {
+ if (b == 0) {
+ return a;
+ }
+ return gcd(b, a % b);
+}
+```
+
+**Time Complexity(TC):** O(log(max(a, b)))
+
+### Given an array, calculate GCD of the entire array
+
+**Example:**
+
+ +
+```java
+int gcdArr(int[] arr) {
+ int ans = arr[0];
+ int n = arr.length();
+ for (int i = 0; i < n; i++) {
+ ans = gcd(ans, arr[i])
+ }
+ return ans;
+}
+```
+---
+### Problem 2 Delete One
+
+**Question**
+
+Given arr[N] elements , we have to delete one element such that GCD of the remaining elements becomes maximum.
+
+**Example:**
+
+
+
+```java
+int gcdArr(int[] arr) {
+ int ans = arr[0];
+ int n = arr.length();
+ for (int i = 0; i < n; i++) {
+ ans = gcd(ans, arr[i])
+ }
+ return ans;
+}
+```
+---
+### Problem 2 Delete One
+
+**Question**
+
+Given arr[N] elements , we have to delete one element such that GCD of the remaining elements becomes maximum.
+
+**Example:**
+
+ +
+#### Brute Force Approach
+
+The brute approach for this problem will be to delete arr[i], and then calculate the GCD for all the remaining elements. This will be repeated for all the elements.
+
+
+
+#### Brute Force Approach
+
+The brute approach for this problem will be to delete arr[i], and then calculate the GCD for all the remaining elements. This will be repeated for all the elements.
+
+ +
+:::warning
+Please take some time to think about the optimised approach on your own before reading further.....
+:::
+
+#### Optimal Approach: Prefix Array
+
+
+**Approach:**
+
+* Idea is to find the GCD value of all the sub-sequences of length (N – 1) and removing the element which is not present in the sub-sequence with that GCD. The maximum GCD found would be the answer.
+* To find the GCD of the sub-sequences optimally, maintain a `prefixGCD[]` and a `suffixGCD[]` array using single state dynamic programming.
+* The maximum value of GCD(`prefixGCD[i – 1]`, `suffixGCD[i + 1]`) is the required answer.
+
+The implementation is given below:
+
+```java
+ // Recursive function to return gcd of a and b
+ static int gcd(int a, int b) {
+ if (b == 0)
+ return a;
+ return gcd(b, a % b);
+ }
+
+ static int MaxGCD(int a[], int n) {
+
+ // Prefix and Suffix arrays
+ int Prefix[] = new int[n + 2];
+ int Suffix[] = new int[n + 2] ;
+
+ Prefix[1] = a[0];
+ for (int i = 2; i <= n; i += 1) {
+ Prefix[i] = gcd(Prefix[i - 1], a[i - 1]);
+ }
+
+ Suffix[n] = a[n - 1];
+ for (int i = n - 1; i >= 1; i -= 1) {
+ Suffix[i] = gcd(Suffix[i + 1], a[i - 1]);
+ }
+
+ // If first or last element of the array has to be removed
+ int ans = Math.max(Suffix[2], Prefix[n - 1]);
+
+ // If any other element is replaced
+ for (int i = 2; i < n; i += 1) {
+ ans = Math.max(ans, gcd(Prefix[i - 1], Suffix[i + 1]));
+ }
+ return ans;
+ }
+```
+
+
+
+:::warning
+Please take some time to think about the optimised approach on your own before reading further.....
+:::
+
+#### Optimal Approach: Prefix Array
+
+
+**Approach:**
+
+* Idea is to find the GCD value of all the sub-sequences of length (N – 1) and removing the element which is not present in the sub-sequence with that GCD. The maximum GCD found would be the answer.
+* To find the GCD of the sub-sequences optimally, maintain a `prefixGCD[]` and a `suffixGCD[]` array using single state dynamic programming.
+* The maximum value of GCD(`prefixGCD[i – 1]`, `suffixGCD[i + 1]`) is the required answer.
+
+The implementation is given below:
+
+```java
+ // Recursive function to return gcd of a and b
+ static int gcd(int a, int b) {
+ if (b == 0)
+ return a;
+ return gcd(b, a % b);
+ }
+
+ static int MaxGCD(int a[], int n) {
+
+ // Prefix and Suffix arrays
+ int Prefix[] = new int[n + 2];
+ int Suffix[] = new int[n + 2] ;
+
+ Prefix[1] = a[0];
+ for (int i = 2; i <= n; i += 1) {
+ Prefix[i] = gcd(Prefix[i - 1], a[i - 1]);
+ }
+
+ Suffix[n] = a[n - 1];
+ for (int i = n - 1; i >= 1; i -= 1) {
+ Suffix[i] = gcd(Suffix[i + 1], a[i - 1]);
+ }
+
+ // If first or last element of the array has to be removed
+ int ans = Math.max(Suffix[2], Prefix[n - 1]);
+
+ // If any other element is replaced
+ for (int i = 2; i < n; i += 1) {
+ ans = Math.max(ans, gcd(Prefix[i - 1], Suffix[i + 1]));
+ }
+ return ans;
+ }
+```
+
+ +
+---
+### Proof of gcd(a, b) = gcd(a-b, b)
+
+
+
+
+---
+### Proof of gcd(a, b) = gcd(a-b, b)
+
+
+ \ No newline at end of file
diff --git a/Academy DSA Typed Notes/Advanced/DSA Maths 2 Combinatorics Basics.md b/Academy DSA Typed Notes/Advanced/DSA Maths 2 Combinatorics Basics.md
new file mode 100644
index 0000000..49d8d2e
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Maths 2 Combinatorics Basics.md
@@ -0,0 +1,339 @@
+# Maths 2: Combinatorics Basic
+
+
+---
+## Addition and Multiplication Rule Example 1
+
+### Example - 1
+
+Given 10 girls and 7 boys, How many different pairs can be formed?
+
+**Note: pair = 1 boy + 1 girl**
+
+
\ No newline at end of file
diff --git a/Academy DSA Typed Notes/Advanced/DSA Maths 2 Combinatorics Basics.md b/Academy DSA Typed Notes/Advanced/DSA Maths 2 Combinatorics Basics.md
new file mode 100644
index 0000000..49d8d2e
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Maths 2 Combinatorics Basics.md
@@ -0,0 +1,339 @@
+# Maths 2: Combinatorics Basic
+
+
+---
+## Addition and Multiplication Rule Example 1
+
+### Example - 1
+
+Given 10 girls and 7 boys, How many different pairs can be formed?
+
+**Note: pair = 1 boy + 1 girl**
+
+ +
+Since each pair consists of one boy and one girl, you can pair each of the 7 boys with any of the 10 girls. This results in a total of 7 boys × 10 girls = 70 different pairs that can be formed.
+
+---
+### Addition and Multiplication Rule Example 2
+
+### Example - 2
+
+
+
+Since each pair consists of one boy and one girl, you can pair each of the 7 boys with any of the 10 girls. This results in a total of 7 boys × 10 girls = 70 different pairs that can be formed.
+
+---
+### Addition and Multiplication Rule Example 2
+
+### Example - 2
+
+ +
+
+**Approach:**
+
+
+
+
+**Approach:**
+
+ +
+To reach Agra via Delhi from Pune, you can combine the ways to get from Pune to Delhi (3 ways) with the ways to get from Delhi to Agra (2 ways).
+
+So, the total number of ways to reach Agra via Delhi from Pune is:
+
+3 ways (Pune to Delhi) * 2 ways (Delhi to Agra) = 6 ways.
+
+---
+
+
+# Question
+
+No. of ways of reaching Agra from Pune ?
+
+
+To reach Agra via Delhi from Pune, you can combine the ways to get from Pune to Delhi (3 ways) with the ways to get from Delhi to Agra (2 ways).
+
+So, the total number of ways to reach Agra via Delhi from Pune is:
+
+3 ways (Pune to Delhi) * 2 ways (Delhi to Agra) = 6 ways.
+
+---
+
+
+# Question
+
+No. of ways of reaching Agra from Pune ?
+ +
+# Choices
+
+- [ ] 72
+- [ ] 12
+- [x] 18
+- [ ] 20
+
+To go to Pune to delhi , there are 3 ways. And do go from delhi to agra there are 4 ways. From pune to Mumbai there are 2 ways, from Mumbai to agra there are 3 ways.
+
+
+
+# Choices
+
+- [ ] 72
+- [ ] 12
+- [x] 18
+- [ ] 20
+
+To go to Pune to delhi , there are 3 ways. And do go from delhi to agra there are 4 ways. From pune to Mumbai there are 2 ways, from Mumbai to agra there are 3 ways.
+
+ +
+To calculate the number of ways to reach Agra from Pune through different routes, you need to consider the combination of routes from Pune to Delhi and from Delhi to Agra, as well as the routes from Pune to Mumbai and from Mumbai to Agra. Then, you can add these possibilities together.
+
+From Pune to Delhi, there are 3 ways.
+From Delhi to Agra, there are 4 ways.
+
+From Pune to Mumbai, there are 2 ways.
+From Mumbai to Agra, there are 3 ways.
+
+So, to find the total number of ways to reach Agra from Pune via these routes, you add the possibilities:
+
+(3 ways from Pune to Delhi * 4 ways from Delhi to Agra) + (2 ways from Pune to Mumbai * 3 ways from Mumbai to Agra) = $(3 * 4) + (2 * 3) = 12 + 6 = 18$ ways.
+
+There are 18 different ways to reach Agra from Pune through these routes.
+
+* (Multiplication) = AND: Used when counting possibilities that occur together in sequence.
+* (Addition) = OR: Used when counting possibilities that occur in separate ways.
+
+
+
+To calculate the number of ways to reach Agra from Pune through different routes, you need to consider the combination of routes from Pune to Delhi and from Delhi to Agra, as well as the routes from Pune to Mumbai and from Mumbai to Agra. Then, you can add these possibilities together.
+
+From Pune to Delhi, there are 3 ways.
+From Delhi to Agra, there are 4 ways.
+
+From Pune to Mumbai, there are 2 ways.
+From Mumbai to Agra, there are 3 ways.
+
+So, to find the total number of ways to reach Agra from Pune via these routes, you add the possibilities:
+
+(3 ways from Pune to Delhi * 4 ways from Delhi to Agra) + (2 ways from Pune to Mumbai * 3 ways from Mumbai to Agra) = $(3 * 4) + (2 * 3) = 12 + 6 = 18$ ways.
+
+There are 18 different ways to reach Agra from Pune through these routes.
+
+* (Multiplication) = AND: Used when counting possibilities that occur together in sequence.
+* (Addition) = OR: Used when counting possibilities that occur in separate ways.
+
+ +
+---
+## Permutation
+
+
+### Explanation
+
+Permutation is defined as the arrangements of objects. In permutation, **order matters**. To simplify `(i, j) != (j, i)`
+
+### Example - 1
+
+Given 3 distinct characters, in how many ways can we arrange them?
+
+**Approach:**
+
+
+
+---
+## Permutation
+
+
+### Explanation
+
+Permutation is defined as the arrangements of objects. In permutation, **order matters**. To simplify `(i, j) != (j, i)`
+
+### Example - 1
+
+Given 3 distinct characters, in how many ways can we arrange them?
+
+**Approach:**
+
+ +
+---
+
+### Question
+
+In how many ways n distinct characters can be arranged?
+
+**Choices**
+
+- [ ] N * (N + 1) / 2
+- [x] N! (N Factorial)
+- [ ] N ^ 2
+- [ ] N
+
+
+### Explanation:
+
+N distinct characters can be arranged in n! (n factorial) ways. This means that for each distinct character you have, you can multiply the total number of arrangements by the count of characters. Here's the formula:
+
+
+
+---
+
+### Question
+
+In how many ways n distinct characters can be arranged?
+
+**Choices**
+
+- [ ] N * (N + 1) / 2
+- [x] N! (N Factorial)
+- [ ] N ^ 2
+- [ ] N
+
+
+### Explanation:
+
+N distinct characters can be arranged in n! (n factorial) ways. This means that for each distinct character you have, you can multiply the total number of arrangements by the count of characters. Here's the formula:
+
+ +
+---
+## nPr Formulae
+
+### Example - 2
+
+Given N distinct characters, in how many ways you can arrange R out of N distinct chracters?
+
+
+
+---
+## nPr Formulae
+
+### Example - 2
+
+Given N distinct characters, in how many ways you can arrange R out of N distinct chracters?
+
+ +
+**Approach:**
+
+When arranging 2 distinct characters from a set of 4, and order matters (e.g., AB and BA are considered different arrangements), the number of ways is indeed $4 * 3 = 12$ ways.
+
+When arranging **R** characters out of **N** distinct characters:
+
+* For the first position, you have **N** choices
+* For the second position, since you've used one character, you have **N-1** choices.
+* For the third position, you have **N-2** choices, and so on.
+
+This continues until the **R-th** position, for which you have $N-(R-1)$ choices.
+
+Thus, the total number of ways to arrange **R** characters out of **N** distinct characters is `N ∗ (N − 1) ∗ (N − 2) ∗ ... ∗ (N − (R − 1))`.
+
+
+
+
+
+**Approach:**
+
+When arranging 2 distinct characters from a set of 4, and order matters (e.g., AB and BA are considered different arrangements), the number of ways is indeed $4 * 3 = 12$ ways.
+
+When arranging **R** characters out of **N** distinct characters:
+
+* For the first position, you have **N** choices
+* For the second position, since you've used one character, you have **N-1** choices.
+* For the third position, you have **N-2** choices, and so on.
+
+This continues until the **R-th** position, for which you have $N-(R-1)$ choices.
+
+Thus, the total number of ways to arrange **R** characters out of **N** distinct characters is `N ∗ (N − 1) ∗ (N − 2) ∗ ... ∗ (N − (R − 1))`.
+
+
+
+ +
+
+
+
+Here:
+
+* **n** is the total number of distinct characters.
+* **r** is the number of characters you want to arrange.
+* **nPr** represents the permutations of **n** items taken **r** at a time.
+
+---
+## Combination
+
+### Explanation
+
+Combination is defined as the number of ways to select something.
+
+**Note:** In combination, **order of selection does not matter**. To simplify `(i, j) = (j, i)`
+
+
+### Example - 1
+
+Given 4 players, count the number of ways of selecting 3 players.
+
+
+
+
+
+
+Here:
+
+* **n** is the total number of distinct characters.
+* **r** is the number of characters you want to arrange.
+* **nPr** represents the permutations of **n** items taken **r** at a time.
+
+---
+## Combination
+
+### Explanation
+
+Combination is defined as the number of ways to select something.
+
+**Note:** In combination, **order of selection does not matter**. To simplify `(i, j) = (j, i)`
+
+
+### Example - 1
+
+Given 4 players, count the number of ways of selecting 3 players.
+
+ +
+### Example - 2
+
+Given 4 players, write the number of ways to arrange players in 3 slots
+
+
+
+### Example - 2
+
+Given 4 players, write the number of ways to arrange players in 3 slots
+
+ +
+* **Number of Selections (x):** You are selecting 3 players out of 4, which is represented as **4C3**, and it equals 4.
+* **Number of Arrangements in Each Selection (6):** There are 3! (3 factorial) ways to arrange 3 players within 3 slots, which is 6.
+* **Total Number of Arrangements:** Multiply the number of selections by the number of arrangements in each selection:
+
+Number of Selections * Number of Arrangements in Each Selection = $4 * 6 = 24$
+
+
+
+* **Number of Selections (x):** You are selecting 3 players out of 4, which is represented as **4C3**, and it equals 4.
+* **Number of Arrangements in Each Selection (6):** There are 3! (3 factorial) ways to arrange 3 players within 3 slots, which is 6.
+* **Total Number of Arrangements:** Multiply the number of selections by the number of arrangements in each selection:
+
+Number of Selections * Number of Arrangements in Each Selection = $4 * 6 = 24$
+
+ +
+
+---
+## nCr Formulae
+
+### Example - 3
+
+Given **n** distinct elements, in how many ways we can select **r** elements s.t `0 <= r <= n`
+
+
+
+
+---
+## nCr Formulae
+
+### Example - 3
+
+Given **n** distinct elements, in how many ways we can select **r** elements s.t `0 <= r <= n`
+
+ +
+
+
+ +
+
+
+ +
+
+
+
+
+ +
+---
+## Properties of Combination
+
+### Property - 1
+
+ The number of ways of selecting **0** items from **N** items, i.e. number of ways to **not select anything**, will always be **1**.
+
+
+
+---
+## Properties of Combination
+
+### Property - 1
+
+ The number of ways of selecting **0** items from **N** items, i.e. number of ways to **not select anything**, will always be **1**.
+
+ +
+### Property - 2
+
+The number of ways of selecting **n** items from **n**, i.e. number of ways to **select everything** will also be **1**.
+
+
+
+### Property - 2
+
+The number of ways of selecting **n** items from **n**, i.e. number of ways to **select everything** will also be **1**.
+
+ +
+
+### Property - 3
+
+Number of ways of selecting **(n-r)** items from **n**:
+
+
+
+
+### Property - 3
+
+Number of ways of selecting **(n-r)** items from **n**:
+
+ +
+---
+## Special Property
+
+
+### Property - 4
+
+Given **n** distinct elements, select **r** items:
+
+For each elements, we have 2 options, either to select or not select:
+
+
+
+---
+## Special Property
+
+
+### Property - 4
+
+Given **n** distinct elements, select **r** items:
+
+For each elements, we have 2 options, either to select or not select:
+
+ +
+**Select Case:**
+When you choose to "select" an element from the available n distinct elements, it means that you are including that specific element as one of the r items you want to pick. In this case:
+
+* You decrease the number of items you need to select by 1, so it becomes r - 1.
+* You decrease the total number of available elements by 1, as you've already chosen one element, so it becomes n - 1.
+* You continue the selection process, considering the reduced values of r and n.
+
+**Reject Case:**
+When you choose to "reject" an element, it means that you are not including that particular element as part of your selection. In this case:
+
+* You keep the number of items you need to select the same, which remains as r.
+* You decrease the total number of available elements by 1, as you've decided not to choose one element, so it becomes n - 1.
+* You continue the selection process with the same value of r and the reduced value of n.
+
+---
+## Problem 1 Pascal Triangle
+
+Generate Pascal's triangle for given value of `n`.
+
+**Example**
+
+Pascal Triangle for `n = 4` is given below
+
+
+
+**Select Case:**
+When you choose to "select" an element from the available n distinct elements, it means that you are including that specific element as one of the r items you want to pick. In this case:
+
+* You decrease the number of items you need to select by 1, so it becomes r - 1.
+* You decrease the total number of available elements by 1, as you've already chosen one element, so it becomes n - 1.
+* You continue the selection process, considering the reduced values of r and n.
+
+**Reject Case:**
+When you choose to "reject" an element, it means that you are not including that particular element as part of your selection. In this case:
+
+* You keep the number of items you need to select the same, which remains as r.
+* You decrease the total number of available elements by 1, as you've decided not to choose one element, so it becomes n - 1.
+* You continue the selection process with the same value of r and the reduced value of n.
+
+---
+## Problem 1 Pascal Triangle
+
+Generate Pascal's triangle for given value of `n`.
+
+**Example**
+
+Pascal Triangle for `n = 4` is given below
+
+ +
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+**Brute Force:** For each and every value, calculate the factorial and print it.
+
+`c[i][j]` represents the element in the i-th and j-th column. Each element is the sum of the two numbers directly above it from the previous row. In combinatorial terms, `c[i][j]` indicates the number of ways to choose j items from a set of i items without repetition and without order.
+
+But as we know that, factorial grows very fast as the number increases, hence this approach won't work properly.
+
+### Optimized Approach
+
+* Pascal's Triangle elements are calculated using `c[i][j] = c[i - 1][j] + c[i - 1][j - 1]`, summing elements from the row above.
+* Start with `c[0][0] = 1`, forming the foundation of the triangle.
+* Calculate rows iteratively using the relation, reusing previous row values to minimize redundant calculations.
+* Utilize only two rows (previous and current) to calculate and update elements, saving memory.
+* Print each row's elements to see Pascal's Triangle emerge from the calculated values.
+
+
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+**Brute Force:** For each and every value, calculate the factorial and print it.
+
+`c[i][j]` represents the element in the i-th and j-th column. Each element is the sum of the two numbers directly above it from the previous row. In combinatorial terms, `c[i][j]` indicates the number of ways to choose j items from a set of i items without repetition and without order.
+
+But as we know that, factorial grows very fast as the number increases, hence this approach won't work properly.
+
+### Optimized Approach
+
+* Pascal's Triangle elements are calculated using `c[i][j] = c[i - 1][j] + c[i - 1][j - 1]`, summing elements from the row above.
+* Start with `c[0][0] = 1`, forming the foundation of the triangle.
+* Calculate rows iteratively using the relation, reusing previous row values to minimize redundant calculations.
+* Utilize only two rows (previous and current) to calculate and update elements, saving memory.
+* Print each row's elements to see Pascal's Triangle emerge from the calculated values.
+
+ +
+### Pseudo Code
+
+```java
+void pascalsTriangle(int n) {
+ nCr[n][n] = {0};
+ for (int i = 0; i < n; i++) {
+ nCr[i][0] = 1;
+ nCr[i][i] = 1;
+ for (int j = 1; j < i; j++) {
+ nCr[i][j] = nCr[i-1][j] + nCr[i-1][j-1];
+ // If mentioned in the question to take % M then:
+ // nCr[i][j] = (nCr[i-1][j] + nCr[i-1][j-1]) % M;
+ }
+ return nCr;
+ }
+}
+```
+
+### Complexity
+**Time Complexity:** $O(N^2)$
+**Space Complexity:** $O(N^2)$
+
+---
+### Problem 2 Finding N-th column title
+
+Find the n-th column title, the columns are titled as A, B, C... and after Z, it is AA, AB, AC... and so on. Given the column number, find the title of the column.
+
+
+
+
+### Pseudo Code
+
+```java
+void pascalsTriangle(int n) {
+ nCr[n][n] = {0};
+ for (int i = 0; i < n; i++) {
+ nCr[i][0] = 1;
+ nCr[i][i] = 1;
+ for (int j = 1; j < i; j++) {
+ nCr[i][j] = nCr[i-1][j] + nCr[i-1][j-1];
+ // If mentioned in the question to take % M then:
+ // nCr[i][j] = (nCr[i-1][j] + nCr[i-1][j-1]) % M;
+ }
+ return nCr;
+ }
+}
+```
+
+### Complexity
+**Time Complexity:** $O(N^2)$
+**Space Complexity:** $O(N^2)$
+
+---
+### Problem 2 Finding N-th column title
+
+Find the n-th column title, the columns are titled as A, B, C... and after Z, it is AA, AB, AC... and so on. Given the column number, find the title of the column.
+
+
+ +
+Base for mapping A-Z will be 26
+
+#### Example
+
+
+
+Base for mapping A-Z will be 26
+
+#### Example
+
+ +
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Approach
+
+* Start with the given number **n**.
+* For each digit of the column title (from right to left):
+ * Find the remainder when **n** is divided by 26.
+ * Map the remainder to the corresponding letter ('A' to 'Y' for 1-25, 'Z' for 0).
+ * Append the letter to the Excel column title.
+ * Divide **n** by **26** (integer division) to process the next digit.
+* Repeat step 2 until n becomes zero.
+* The resulting string is the Excel column title for the original number n.
+
+
+#### Code
+```java
+void columnTitle(int n) {
+ ans = "";
+ while(n > 0) {
+ ans = (char) ((n - 1) % 26 + 'A') + ans; // char + string
+ n = (n - 1) / 26
+ }
+ return ans
+}
+```
+
+#### Complexity
+**Time Complexity:** O(log(N)) [base 26]
+**Space Complexity:** O(1)
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Maths 3 Prime Numbers.md b/Academy DSA Typed Notes/Advanced/DSA Maths 3 Prime Numbers.md
new file mode 100644
index 0000000..b9fc846
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Maths 3 Prime Numbers.md
@@ -0,0 +1,300 @@
+# Maths 3: Prime Numbers
+
+---
+## Introduction to Prime Numbers
+
+
+### What are Prime Numbers?
+
+Numbers having only 2 factors i.e, 1 and the number itself are known as Prime Numbers
+
+**Example:** 2, 5, 7, 11
+
+---
+### Problem 1 Check if a number is prime or not
+
+Given a number, we need to check wheather its a prime number or not
+
+**Example**
+**Input:**
+```
+n = 3
+
+n = 4
+```
+
+**Output:**
+```
+true
+
+false
+```
+
+---
+### Question
+Check whether 11 is a prime number or not!
+
+**Choices**
+- [x] true, 11 is a prime number
+- [ ] false, 11 is not a prime number
+
+
+
+### Approach
+
+* We need to count the number of factors:
+ * if factors = 2, then it is prime
+ * otherwise if factors >2, then it is non prime
+
+
+### Code snippet
+
+```java
+boolean checkPrime(int n) {
+ count = 0;
+ for (int i = 1; i * i <= n; i++) {
+ if (n % i == 0) {
+ if (i == n / i) {
+ count++;
+ } else {
+ count += 2;
+ }
+ }
+ }
+ if (count == 2) {
+ print("prime");
+ } else {
+ print("Not Prime");
+ }
+}
+```
+
+---
+## Problem 2 Print all prime numbers from 1 to N
+
+Given a number N, we need to print all the prime no. from 1 to N
+
+**Example**
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Approach
+
+* Start with the given number **n**.
+* For each digit of the column title (from right to left):
+ * Find the remainder when **n** is divided by 26.
+ * Map the remainder to the corresponding letter ('A' to 'Y' for 1-25, 'Z' for 0).
+ * Append the letter to the Excel column title.
+ * Divide **n** by **26** (integer division) to process the next digit.
+* Repeat step 2 until n becomes zero.
+* The resulting string is the Excel column title for the original number n.
+
+
+#### Code
+```java
+void columnTitle(int n) {
+ ans = "";
+ while(n > 0) {
+ ans = (char) ((n - 1) % 26 + 'A') + ans; // char + string
+ n = (n - 1) / 26
+ }
+ return ans
+}
+```
+
+#### Complexity
+**Time Complexity:** O(log(N)) [base 26]
+**Space Complexity:** O(1)
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Maths 3 Prime Numbers.md b/Academy DSA Typed Notes/Advanced/DSA Maths 3 Prime Numbers.md
new file mode 100644
index 0000000..b9fc846
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Maths 3 Prime Numbers.md
@@ -0,0 +1,300 @@
+# Maths 3: Prime Numbers
+
+---
+## Introduction to Prime Numbers
+
+
+### What are Prime Numbers?
+
+Numbers having only 2 factors i.e, 1 and the number itself are known as Prime Numbers
+
+**Example:** 2, 5, 7, 11
+
+---
+### Problem 1 Check if a number is prime or not
+
+Given a number, we need to check wheather its a prime number or not
+
+**Example**
+**Input:**
+```
+n = 3
+
+n = 4
+```
+
+**Output:**
+```
+true
+
+false
+```
+
+---
+### Question
+Check whether 11 is a prime number or not!
+
+**Choices**
+- [x] true, 11 is a prime number
+- [ ] false, 11 is not a prime number
+
+
+
+### Approach
+
+* We need to count the number of factors:
+ * if factors = 2, then it is prime
+ * otherwise if factors >2, then it is non prime
+
+
+### Code snippet
+
+```java
+boolean checkPrime(int n) {
+ count = 0;
+ for (int i = 1; i * i <= n; i++) {
+ if (n % i == 0) {
+ if (i == n / i) {
+ count++;
+ } else {
+ count += 2;
+ }
+ }
+ }
+ if (count == 2) {
+ print("prime");
+ } else {
+ print("Not Prime");
+ }
+}
+```
+
+---
+## Problem 2 Print all prime numbers from 1 to N
+
+Given a number N, we need to print all the prime no. from 1 to N
+
+**Example**
+ +
+### Question
+Find all the prime numbers from 1 to N
+
+**Choices**
+- [ ] 1, 2, 3, 5, 7
+- [ ] 2, 3, 5, 7, 8
+- [x] 2, 3, 5, 7
+- [ ] 2, 5 ,7
+
+### Solution
+**Brute Force:** Iterate from 1 to N, and check if a number is prime or not.
+
+```java
+void printAllPrime(int n) {
+ for (int i = 2; i <= n; ++i) {
+ boolean isPrime = true;
+ for (int j = 2; j * j <= i; ++j) {
+ if (i % j == 0) {
+ isPrime = false;
+ break;
+ }
+ }
+ }
+```
+
+* **Time Complexity (TC):** The time complexity of the given function is $O(n√n)$, as it iterates through numbers from 2 to N and for each number, it checks divisibility up to the square root of that number.
+* **Space Complexity (SC):** The space complexity is O(1), as the function uses a constant amount of extra space regardless of the input size.
+
+---
+## Sieve of Eratosthenes
+
+### Optimized approach for counting number of primes between 1 to N
+
+**Approach**
+
+* **Assumption:** Begin by assuming that all numbers from 2 to N are prime numbers.
+* **Marking Non-Primes:** Start with the first prime number, which is 2. Since 2 is a prime number, mark all its multiples as non-prime. These multiples are 4, 6, 8, and so on.
+* **Move to Next Unmarked Number:** Move to the next unmarked number, which is 3. Since 3 is a prime number, mark all its multiples as non-prime. These multiples are 6, 9, 12, and so on. Notice that we skip numbers that have already been marked as non-prime in previous steps. Unmarked numbers are prime as they do not have any number less then themselves a factor of the number except 1. Which means they are prime
+* **Repeat for Remaining Unmarked Numbers:** Continue this process for the remaining unmarked numbers, each time marking all their multiples as non-prime.
+* **Completion:** After going through all numbers up to the square root of N, the remaining unmarked numbers are prime numbers. This is because their multiples have been marked as non-prime in previous steps.
+
+
+
+### Question
+Find all the prime numbers from 1 to N
+
+**Choices**
+- [ ] 1, 2, 3, 5, 7
+- [ ] 2, 3, 5, 7, 8
+- [x] 2, 3, 5, 7
+- [ ] 2, 5 ,7
+
+### Solution
+**Brute Force:** Iterate from 1 to N, and check if a number is prime or not.
+
+```java
+void printAllPrime(int n) {
+ for (int i = 2; i <= n; ++i) {
+ boolean isPrime = true;
+ for (int j = 2; j * j <= i; ++j) {
+ if (i % j == 0) {
+ isPrime = false;
+ break;
+ }
+ }
+ }
+```
+
+* **Time Complexity (TC):** The time complexity of the given function is $O(n√n)$, as it iterates through numbers from 2 to N and for each number, it checks divisibility up to the square root of that number.
+* **Space Complexity (SC):** The space complexity is O(1), as the function uses a constant amount of extra space regardless of the input size.
+
+---
+## Sieve of Eratosthenes
+
+### Optimized approach for counting number of primes between 1 to N
+
+**Approach**
+
+* **Assumption:** Begin by assuming that all numbers from 2 to N are prime numbers.
+* **Marking Non-Primes:** Start with the first prime number, which is 2. Since 2 is a prime number, mark all its multiples as non-prime. These multiples are 4, 6, 8, and so on.
+* **Move to Next Unmarked Number:** Move to the next unmarked number, which is 3. Since 3 is a prime number, mark all its multiples as non-prime. These multiples are 6, 9, 12, and so on. Notice that we skip numbers that have already been marked as non-prime in previous steps. Unmarked numbers are prime as they do not have any number less then themselves a factor of the number except 1. Which means they are prime
+* **Repeat for Remaining Unmarked Numbers:** Continue this process for the remaining unmarked numbers, each time marking all their multiples as non-prime.
+* **Completion:** After going through all numbers up to the square root of N, the remaining unmarked numbers are prime numbers. This is because their multiples have been marked as non-prime in previous steps.
+
+ +
+### Code Snippet
+
+```java
+void printAllPrime(int n) {
+ boolean[] isPrime = new boolean[n + 1]; // Initialize a boolean array to track prime numbers
+ Arrays.fill(isPrime, 2, n + 1, true); // Assume all numbers from 2 to n are prime
+
+ for (int i = 2; i * i <= n; ++i) {
+ if (isPrime[i]) {
+ for (int j = i * i; j <= n; j += i) {
+ isPrime[j] = false; // Mark multiples of the current prime as non-prime
+ }
+ }
+ }
+}
+```
+
+### Optimization in Sieve of Eratosthenes
+
+
+
+### Code Snippet
+
+```java
+void printAllPrime(int n) {
+ boolean[] isPrime = new boolean[n + 1]; // Initialize a boolean array to track prime numbers
+ Arrays.fill(isPrime, 2, n + 1, true); // Assume all numbers from 2 to n are prime
+
+ for (int i = 2; i * i <= n; ++i) {
+ if (isPrime[i]) {
+ for (int j = i * i; j <= n; j += i) {
+ isPrime[j] = false; // Mark multiples of the current prime as non-prime
+ }
+ }
+ }
+}
+```
+
+### Optimization in Sieve of Eratosthenes
+
+) +
+Starting from the square of each prime number, mark all its multiples as non-prime in the sieve. This is efficient because smaller multiples of the prime would have already been marked by smaller primes. By avoiding redundant marking, we optimize the Sieve of Eratosthenes algorithm.
+
+
+
+Starting from the square of each prime number, mark all its multiples as non-prime in the sieve. This is efficient because smaller multiples of the prime would have already been marked by smaller primes. By avoiding redundant marking, we optimize the Sieve of Eratosthenes algorithm.
+
+ +
+
+
+ +
+* **Time Complexity (TC):** The optimized Sieve of Eratosthenes has a time complexity of O(n log log n), which means it grows very slowly. This is because the algorithm only visits and marks numbers up to the square root of N, and the number of non-prime numbers marked is logarithmic with respect to N.
+* **Space Complexity (SC):** The space complexity is O(n), which is used to store the boolean array indicating whether each number is prime or not. The space used is directly proportional to the input size N.
+
+---
+### Problem 3 Smallest Prime Factor
+
+Given N, return the smallest prime factors for all numbers from 2 to N
+
+**Example:**
+
+
+
+* **Time Complexity (TC):** The optimized Sieve of Eratosthenes has a time complexity of O(n log log n), which means it grows very slowly. This is because the algorithm only visits and marks numbers up to the square root of N, and the number of non-prime numbers marked is logarithmic with respect to N.
+* **Space Complexity (SC):** The space complexity is O(n), which is used to store the boolean array indicating whether each number is prime or not. The space used is directly proportional to the input size N.
+
+---
+### Problem 3 Smallest Prime Factor
+
+Given N, return the smallest prime factors for all numbers from 2 to N
+
+**Example:**
+
+ +
+### Question
+What is the smallest prime factor of 25
+
+**Choices**
+- [ ] 1
+- [x] 5
+- [ ] 10
+- [ ] 25
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Smallest Prime Factor Approach
+
+* **Initialization:** Create an integer array to store the smallest prime factors for each number from 2 to N. Initialize each element of the array to its own value, indicating that it's not yet known if the number is prime or not.
+* **Smallest Prime Factor Determination:** Starting from the first prime number (2), for each prime number:
+ * If the smallest prime factor for a number is still its own value (indicating it's not determined yet), mark it as the smallest prime factor for all its multiples.
+* **Iterate Over All Numbers:** Go through each number from 2 to N, and for each number, if its smallest prime factor is still itself, mark it as prime and set its smallest prime factor to itself.
+* **Smallest Prime Factors:** The array will now hold the smallest prime factors for all numbers from 2 to N.
+
+
+
+### Question
+What is the smallest prime factor of 25
+
+**Choices**
+- [ ] 1
+- [x] 5
+- [ ] 10
+- [ ] 25
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Smallest Prime Factor Approach
+
+* **Initialization:** Create an integer array to store the smallest prime factors for each number from 2 to N. Initialize each element of the array to its own value, indicating that it's not yet known if the number is prime or not.
+* **Smallest Prime Factor Determination:** Starting from the first prime number (2), for each prime number:
+ * If the smallest prime factor for a number is still its own value (indicating it's not determined yet), mark it as the smallest prime factor for all its multiples.
+* **Iterate Over All Numbers:** Go through each number from 2 to N, and for each number, if its smallest prime factor is still itself, mark it as prime and set its smallest prime factor to itself.
+* **Smallest Prime Factors:** The array will now hold the smallest prime factors for all numbers from 2 to N.
+
+ +
+```java
+public int[] smallestPrimeFactors(int n) {
+ int[] spf = new int[n + 1];
+
+ for (int i = 2; i <= n; ++i) {
+ spf[i] = i; // Initialize smallest prime factor with its own value
+
+ if (spf[i] == i) { // i is prime
+ for (int j = i * i; j <= n; j += i) {
+ if (spf[j] == j) {
+ spf[j] = i; // Mark smallest prime factor for multiples
+ }
+ }
+ }
+ }
+
+ return spf;
+}
+```
+
+---
+## Prime Factorization
+
+Prime factorization is the process of finding the prime numbers, which are multiplied together to get the original number. For example, the prime factors of 16 are $2 × 2 × 2 × 2$.
+
+
+
+
+
+```java
+public int[] smallestPrimeFactors(int n) {
+ int[] spf = new int[n + 1];
+
+ for (int i = 2; i <= n; ++i) {
+ spf[i] = i; // Initialize smallest prime factor with its own value
+
+ if (spf[i] == i) { // i is prime
+ for (int j = i * i; j <= n; j += i) {
+ if (spf[j] == j) {
+ spf[j] = i; // Mark smallest prime factor for multiples
+ }
+ }
+ }
+ }
+
+ return spf;
+}
+```
+
+---
+## Prime Factorization
+
+Prime factorization is the process of finding the prime numbers, which are multiplied together to get the original number. For example, the prime factors of 16 are $2 × 2 × 2 × 2$.
+
+
+
+ +
+
+
+
+
+ +
+---
+### Problem 4 Total Number of Factors
+
+Given a number n, assume its prime factorization
+
+$n=i^{a1}*j^{a2}*k^{a3}...z^{ax}$
+
+the number of choices we have for the power of every prime is [0, a1], [0,a2], [0, a3].............[0, ax]
+
+the number of divisor/factors will be given by the formula:
+
+(a1 + 1)*(a2 + 1)*(a3 + 1)*.....(ax + 1)
+
+
+Example
+
+**Example 1**
+$25 = 5^2$
+
+Number of divisors = $(2+1) = 3$
+
+
+**Example 2**
+
+
+
+---
+### Problem 4 Total Number of Factors
+
+Given a number n, assume its prime factorization
+
+$n=i^{a1}*j^{a2}*k^{a3}...z^{ax}$
+
+the number of choices we have for the power of every prime is [0, a1], [0,a2], [0, a3].............[0, ax]
+
+the number of divisor/factors will be given by the formula:
+
+(a1 + 1)*(a2 + 1)*(a3 + 1)*.....(ax + 1)
+
+
+Example
+
+**Example 1**
+$25 = 5^2$
+
+Number of divisors = $(2+1) = 3$
+
+
+**Example 2**
+
+ +
+### Question
+Find the total number of factors of 20
+
+**Choices**
+- [x] 5
+- [ ] 1
+- [ ] 3
+- [ ] 4
+
+
+**Explanation:**
+
+20 = 2^2^ * 5^1^
+ = (2 + 1) * (1 + 1)
+ = 5
+
+
+The factors are 1, 2, 5, 10, 20.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+---
+### Total Number of Factors Approach
+
+#### Approach
+
+* **Prime Factorization:** For each number from 1 to N, find its prime factorization. Determine the prime factors of the number and their respective powers.
+* **Counting Factors:** The number of factors for a given number is calculated by adding 1 to each power of its prime factors and then multiplying those incremented powers together.
+* **Iterate through Numbers:** Iterate through the numbers from 1 to N. For each number:
+ * Calculate its prime factorization.
+ * Count the factors using the prime factors' powers.
+* **Store or Output Results:** Store or output the number of factors/divisors for each number.
+
+The number of factors for a given number is calculated by adding 1 to each power of its prime factors and then multiplying those incremented powers together.
+
+* **For 1:** $(1+1) = 2$ factors (1 and itself).
+* **For 2:** $(1+1) = 2$ factors (1 and 2).
+* **For 3:** $(1+1) = 2$ factors (1 and 3).
+* **For 4:** $(2+1) = 3$ factors (1, 2, and 4).
+* **For 5:** $(1+1) = 2$ factors (1 and 5).
+* **For 6:** $(1+1) * (1+1) = 4$ factors (1, 2, 3, and 6).
+* **For 7:** $(1+1) = 2$ factors (1 and 7).
+* **For 8:** $(3+1) = 4$ factors (1, 2, 4, and 8).
+* **For 9:** $(2+1) = 3$ factors (1, 3, and 9).
+* **For 10:** $(1+1) * (1+1) = 4$ factors (1, 2, 5, and 10).
+
+
+
+### Question
+Find the total number of factors of 20
+
+**Choices**
+- [x] 5
+- [ ] 1
+- [ ] 3
+- [ ] 4
+
+
+**Explanation:**
+
+20 = 2^2^ * 5^1^
+ = (2 + 1) * (1 + 1)
+ = 5
+
+
+The factors are 1, 2, 5, 10, 20.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+---
+### Total Number of Factors Approach
+
+#### Approach
+
+* **Prime Factorization:** For each number from 1 to N, find its prime factorization. Determine the prime factors of the number and their respective powers.
+* **Counting Factors:** The number of factors for a given number is calculated by adding 1 to each power of its prime factors and then multiplying those incremented powers together.
+* **Iterate through Numbers:** Iterate through the numbers from 1 to N. For each number:
+ * Calculate its prime factorization.
+ * Count the factors using the prime factors' powers.
+* **Store or Output Results:** Store or output the number of factors/divisors for each number.
+
+The number of factors for a given number is calculated by adding 1 to each power of its prime factors and then multiplying those incremented powers together.
+
+* **For 1:** $(1+1) = 2$ factors (1 and itself).
+* **For 2:** $(1+1) = 2$ factors (1 and 2).
+* **For 3:** $(1+1) = 2$ factors (1 and 3).
+* **For 4:** $(2+1) = 3$ factors (1, 2, and 4).
+* **For 5:** $(1+1) = 2$ factors (1 and 5).
+* **For 6:** $(1+1) * (1+1) = 4$ factors (1, 2, 3, and 6).
+* **For 7:** $(1+1) = 2$ factors (1 and 7).
+* **For 8:** $(3+1) = 4$ factors (1, 2, 4, and 8).
+* **For 9:** $(2+1) = 3$ factors (1, 3, and 9).
+* **For 10:** $(1+1) * (1+1) = 4$ factors (1, 2, 5, and 10).
+
+ +
+#### Code
+
+
+
+#### Code
+
+ +
+* **Time Complexity (TC):** The time complexity of this code is O(N * log N), mainly due to the prime factorization process for each number from 1 to N.
+* **Space Complexity (SC):** The space complexity is O(N), where the primary space usage comes from the arrays for storing the smallest prime factors and the hashmap for storing the factors count for each number.
diff --git a/Academy DSA Typed Notes/Advanced/DSA OOPS 1 Introduction.md b/Academy DSA Typed Notes/Advanced/DSA OOPS 1 Introduction.md
new file mode 100644
index 0000000..091d661
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA OOPS 1 Introduction.md
@@ -0,0 +1,488 @@
+# OOPS 1
+
+
+### Programming Paradigms
+
+Types:
+* **Imperative Programming** - It tells the computer how to do the task by giving a set of instructions in a particular order i.e. line by line.
+```cpp
+// For eg:
+int a = 10;
+int b = 20;
+int sum = a + b;
+print(sum);
+int dif = a - b;
+print(dif);
+```
+* **Procedural Programming** - It splits the entire program into small procedures or functions (section of code that perform a specific task) which are reusable code blocks.
+```cpp
+// For eg:
+int a = 10;
+int b = 20;
+addTwoNumbers(a, b);
+subtractTwoNumbers(a, b);
+
+void addTwoNumbers(a, b) {
+ int sum = a + b;
+ print(sum);
+}
+
+void subtractTwoNumbers(a, b) {
+ int dif = a - b;
+ print(dif);
+}
+```
+
+* **Object Oriented Programming** - It builds the entire program using classes and objects. [will discuss this in detail today!]
+
+* **Declarative Programming** - In this paradigm, you specify "what" you want the program to do without specifying "how" it should be done.
+```SQL
+-- For eg: (SQL Queries)
+select * from Customer;
+```
+* **Functional Programming**, **Logic Programming**, etc.
+
+Most of the people start their coding journey with procedural programming and hence let's start with the first type of paradigm i.e. procedural programming.
+
+---
+## Procedural Programming
+It splits the entire program into small procedures or functions (section of code that perform a specific task) which are reusable code blocks. Eg - C, C++, etc.
+
+Procedure is an oldage name of function/method.
+
+```cpp
+// For eg:
+void addTwoNumbers(a, b) {
+ int sum = a + b;
+ print(sum);
+}
+
+void addThreeNumbers(a, b, c) {
+ int sum = a + b;
+ addTwoNumbers(sum, c);
+}
+
+void main() {
+ addThreeNumbers(10, 20, 30);
+}
+```
+---
+### Problems with Procedural Programming
+
+**Cons of Procedural programming:**
+* Difficult to make sense
+* Difficult to debug and understand
+* Spaghetti code i.e. unstructured and needs to be tracked form multiple locations.
+
+So this is all about procedural programming, now lets move to OOPs as we are preparing for the base of OOPs.
+
+---
+## Object Oriented Programming Introduction
+
+### OOPS
+
+OOPs came from the need of thinking of software systems in terms of how we humans think about real world.
+* Entities are core in OOPs
+* Every entity has some attribute and behaviour
+
+In object oriented programming we build the entire program using classes and objects (entity).
+
+**Class:** Blueprint of an idea.
+
+Example - Floor plan of an apartment.
+So, while designing new house, we make something called blue print.
+
+
+* **Time Complexity (TC):** The time complexity of this code is O(N * log N), mainly due to the prime factorization process for each number from 1 to N.
+* **Space Complexity (SC):** The space complexity is O(N), where the primary space usage comes from the arrays for storing the smallest prime factors and the hashmap for storing the factors count for each number.
diff --git a/Academy DSA Typed Notes/Advanced/DSA OOPS 1 Introduction.md b/Academy DSA Typed Notes/Advanced/DSA OOPS 1 Introduction.md
new file mode 100644
index 0000000..091d661
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA OOPS 1 Introduction.md
@@ -0,0 +1,488 @@
+# OOPS 1
+
+
+### Programming Paradigms
+
+Types:
+* **Imperative Programming** - It tells the computer how to do the task by giving a set of instructions in a particular order i.e. line by line.
+```cpp
+// For eg:
+int a = 10;
+int b = 20;
+int sum = a + b;
+print(sum);
+int dif = a - b;
+print(dif);
+```
+* **Procedural Programming** - It splits the entire program into small procedures or functions (section of code that perform a specific task) which are reusable code blocks.
+```cpp
+// For eg:
+int a = 10;
+int b = 20;
+addTwoNumbers(a, b);
+subtractTwoNumbers(a, b);
+
+void addTwoNumbers(a, b) {
+ int sum = a + b;
+ print(sum);
+}
+
+void subtractTwoNumbers(a, b) {
+ int dif = a - b;
+ print(dif);
+}
+```
+
+* **Object Oriented Programming** - It builds the entire program using classes and objects. [will discuss this in detail today!]
+
+* **Declarative Programming** - In this paradigm, you specify "what" you want the program to do without specifying "how" it should be done.
+```SQL
+-- For eg: (SQL Queries)
+select * from Customer;
+```
+* **Functional Programming**, **Logic Programming**, etc.
+
+Most of the people start their coding journey with procedural programming and hence let's start with the first type of paradigm i.e. procedural programming.
+
+---
+## Procedural Programming
+It splits the entire program into small procedures or functions (section of code that perform a specific task) which are reusable code blocks. Eg - C, C++, etc.
+
+Procedure is an oldage name of function/method.
+
+```cpp
+// For eg:
+void addTwoNumbers(a, b) {
+ int sum = a + b;
+ print(sum);
+}
+
+void addThreeNumbers(a, b, c) {
+ int sum = a + b;
+ addTwoNumbers(sum, c);
+}
+
+void main() {
+ addThreeNumbers(10, 20, 30);
+}
+```
+---
+### Problems with Procedural Programming
+
+**Cons of Procedural programming:**
+* Difficult to make sense
+* Difficult to debug and understand
+* Spaghetti code i.e. unstructured and needs to be tracked form multiple locations.
+
+So this is all about procedural programming, now lets move to OOPs as we are preparing for the base of OOPs.
+
+---
+## Object Oriented Programming Introduction
+
+### OOPS
+
+OOPs came from the need of thinking of software systems in terms of how we humans think about real world.
+* Entities are core in OOPs
+* Every entity has some attribute and behaviour
+
+In object oriented programming we build the entire program using classes and objects (entity).
+
+**Class:** Blueprint of an idea.
+
+Example - Floor plan of an apartment.
+So, while designing new house, we make something called blue print.
+ +
+Now this will have exact dimensions as per need. Is the house built? No not yet, but whenever it will get built, the design will be look like this.
+
+**Class represent the strucutre of the idea.**
+Class has attributes to define data and methods to define functionalities/behaviour.
+
+Lets build a `Student` class with some attributes and methods.
+
+Its the basic structure, its not a real thing, it just show what data every student holds upto. Also, You can create multiple instances of this class.
+
+
+Now this will have exact dimensions as per need. Is the house built? No not yet, but whenever it will get built, the design will be look like this.
+
+**Class represent the strucutre of the idea.**
+Class has attributes to define data and methods to define functionalities/behaviour.
+
+Lets build a `Student` class with some attributes and methods.
+
+Its the basic structure, its not a real thing, it just show what data every student holds upto. Also, You can create multiple instances of this class.
+ +
+**Object:** They are real instances of the class.
+
+### Question
+
+Will the object of a class occupy memory?
+
+**Choices**
+
+- [ ] No
+- [ ] In some cases only
+- [x] Yes
+
+
+Yes they will occupy memory because they are real instance of the class / blueprint.
+
+---
+### Classes & Objects Example
+
+Now lets create a class and object and see how this thing works on machine.
+
+1. We will create a class named Student
+
+
+
+**Object:** They are real instances of the class.
+
+### Question
+
+Will the object of a class occupy memory?
+
+**Choices**
+
+- [ ] No
+- [ ] In some cases only
+- [x] Yes
+
+
+Yes they will occupy memory because they are real instance of the class / blueprint.
+
+---
+### Classes & Objects Example
+
+Now lets create a class and object and see how this thing works on machine.
+
+1. We will create a class named Student
+
+ +```java
+}
+```
+
+2. Then, we will create the main class
+
+
+```java
+}
+```
+
+2. Then, we will create the main class
+
+ +
+3. And we can see that both naman and dinesh have their own identity
+
+
+3. And we can see that both naman and dinesh have their own identity
+ +
+---
+### Pillars of Object Oriented Programming
+
+Now what is principle and pillar?
+* **Principle** - Fundamental foundation / concept.
+* **Pillar** - Support to hold things together
+
+
+**So what does the principle of OOP says?**
+
+Idea of OOP is based on **abstraction** and the whole software system is build around abstraction.
+
+But how would we implement the abstraction? ---> Using the 3 pillars of OOPs i.e.
+* **Inheritance**
+* **Polymorphism**
+* **Encapsulation**
+
+
+**For example:**
+
+Your **principal** can be:
+- I will be a good person.
+
+But how you would be a good person? Here comes your **pillars**:
+- I will be truthfull,
+- I will do hardwork,
+- I respect everyone, etc.
+
+So we got to know that abstraction is not the pillar of OOPs, it is the main principle on which whole concept of OOP is based.
+
+
+---
+### OOPs Abstraction
+
+Abstraction means ---> **Representing in terms of ideas**.
+
+Now what does ideas mean? ---> Anything in software system that has attrubute and associated behaviour.
+
+So if you are building scaler, you don't have to think about storing individuals like, Naman, Anshuman, Indarjeet. You can use Students, Mentors, TAs, Classes, etc. with their attributes.
+
+**Do they have a behaviour?**
+
+Yes they all have some behaviour. Student can send messages, pause courses these are all behaviours.
+So abstraction is an idea of representing complex software system interms of ideas, because ideas are easy to understand.
+So, its an concept of making something abstract.
+
+### What is the purpose of abstraction?
+
+The main purpose is that others dont need to know the details of the idea.
+
+Suppose you are driving a car, and you want it to turn left and speed up, and you steer the steering to left and press the acceleration pedal. It works right? Do you need to know how does this happen? What combustion is happening, how much fuel is used, How steering wheel turned the car?
+No right? This is what we call as abstraction.
+
+Abstraction is way to represent complex software system, in terms of ideas.
+
+What needed to be represented in terms of ideas?
+* Data
+* Anything that has behaviours
+
+No one else need to know the details about the ideas.
+
+Now let's move to encapsulation.
+
+---
+## OOPs Encapsulation
+
+
+So what are the purpose for making capsules, and not normal medicine?
+
+If the capsule breaks away, what will happen?
+- It will flow away. So first purpose is to hold the medicine powder together.
+- Then there are multiple powders are present in the capsule, it helps them to avoid mixing with each other.
+- Third purpose is it protects the medicine from the outside environment.
+
+This is exactly the purpose of Encapsulation in OOP.
+
+Encapsulation allows us to store attribute and Behaviours together.
+
+### Question
+
+Where do we store attribute and behavious together? What is the technical term for that?
+
+**Choices**
+
+- [x] Class
+- [ ] Object
+- [ ] Project
+
+
+
+Yes, a **class**, and it protects attributes & methods from outer environment i.e. other classes can't have access to it if we restrict.
+
+
+
+---
+### Pillars of Object Oriented Programming
+
+Now what is principle and pillar?
+* **Principle** - Fundamental foundation / concept.
+* **Pillar** - Support to hold things together
+
+
+**So what does the principle of OOP says?**
+
+Idea of OOP is based on **abstraction** and the whole software system is build around abstraction.
+
+But how would we implement the abstraction? ---> Using the 3 pillars of OOPs i.e.
+* **Inheritance**
+* **Polymorphism**
+* **Encapsulation**
+
+
+**For example:**
+
+Your **principal** can be:
+- I will be a good person.
+
+But how you would be a good person? Here comes your **pillars**:
+- I will be truthfull,
+- I will do hardwork,
+- I respect everyone, etc.
+
+So we got to know that abstraction is not the pillar of OOPs, it is the main principle on which whole concept of OOP is based.
+
+
+---
+### OOPs Abstraction
+
+Abstraction means ---> **Representing in terms of ideas**.
+
+Now what does ideas mean? ---> Anything in software system that has attrubute and associated behaviour.
+
+So if you are building scaler, you don't have to think about storing individuals like, Naman, Anshuman, Indarjeet. You can use Students, Mentors, TAs, Classes, etc. with their attributes.
+
+**Do they have a behaviour?**
+
+Yes they all have some behaviour. Student can send messages, pause courses these are all behaviours.
+So abstraction is an idea of representing complex software system interms of ideas, because ideas are easy to understand.
+So, its an concept of making something abstract.
+
+### What is the purpose of abstraction?
+
+The main purpose is that others dont need to know the details of the idea.
+
+Suppose you are driving a car, and you want it to turn left and speed up, and you steer the steering to left and press the acceleration pedal. It works right? Do you need to know how does this happen? What combustion is happening, how much fuel is used, How steering wheel turned the car?
+No right? This is what we call as abstraction.
+
+Abstraction is way to represent complex software system, in terms of ideas.
+
+What needed to be represented in terms of ideas?
+* Data
+* Anything that has behaviours
+
+No one else need to know the details about the ideas.
+
+Now let's move to encapsulation.
+
+---
+## OOPs Encapsulation
+
+
+So what are the purpose for making capsules, and not normal medicine?
+
+If the capsule breaks away, what will happen?
+- It will flow away. So first purpose is to hold the medicine powder together.
+- Then there are multiple powders are present in the capsule, it helps them to avoid mixing with each other.
+- Third purpose is it protects the medicine from the outside environment.
+
+This is exactly the purpose of Encapsulation in OOP.
+
+Encapsulation allows us to store attribute and Behaviours together.
+
+### Question
+
+Where do we store attribute and behavious together? What is the technical term for that?
+
+**Choices**
+
+- [x] Class
+- [ ] Object
+- [ ] Project
+
+
+
+Yes, a **class**, and it protects attributes & methods from outer environment i.e. other classes can't have access to it if we restrict.
+
+ +
+Here no one can access the age of student other than the class student.
+
+---
+## Access Modifiers
+
+We got to know that Encapsulation has two advantages,
+* ONE is it holds data and attributes together and
+* SECOND is it protect members from illegitimate access. You can't access the data from class unless the class allows you to.
+
+Now, The first thing gets sorted by class, i.e. we create a class, and it holds the behaviors and attributes together.
+
+But, **How the SECOND one is implemented?**
+i.e., How in code illegitimate access is prevented?
+How the encapsulation prevents access to class data?
+
+That is something called **access modifiers**.
+
+---
+### Question
+
+Which one of these is **not** an access modifier?
+
+**Choices**
+
+- [ ] Public
+- [x] Open
+- [ ] Private
+- [ ] Protected
+
+---
+### Types of Access Modifiers
+
+There are four access modifiers in most of the programming languages, they are:
+* **Public**
+* **Private**
+* **Protected**
+* **Default** (if we don't use any of the above three, then its the default one)
+
+So what are these access modifiers? Let's quickly look at them.
+
+**Public access modifier** - A public attribute or method can be accessed by everyone.
+
+**Private access modifiers** - A private attribute or method can be accessed by no one, not even the child class.
+**Explanation** - It can be accessed by the **same** class. No one outside the class has access to private methods.
+
+**Protected access modifier** - A protected attribute or method can be accessed only from the classes of the same package.
+
+Let me show you a diagram that will be helpful in understanding and will clear most of your doubts.
+
+where:
+
+Here no one can access the age of student other than the class student.
+
+---
+## Access Modifiers
+
+We got to know that Encapsulation has two advantages,
+* ONE is it holds data and attributes together and
+* SECOND is it protect members from illegitimate access. You can't access the data from class unless the class allows you to.
+
+Now, The first thing gets sorted by class, i.e. we create a class, and it holds the behaviors and attributes together.
+
+But, **How the SECOND one is implemented?**
+i.e., How in code illegitimate access is prevented?
+How the encapsulation prevents access to class data?
+
+That is something called **access modifiers**.
+
+---
+### Question
+
+Which one of these is **not** an access modifier?
+
+**Choices**
+
+- [ ] Public
+- [x] Open
+- [ ] Private
+- [ ] Protected
+
+---
+### Types of Access Modifiers
+
+There are four access modifiers in most of the programming languages, they are:
+* **Public**
+* **Private**
+* **Protected**
+* **Default** (if we don't use any of the above three, then its the default one)
+
+So what are these access modifiers? Let's quickly look at them.
+
+**Public access modifier** - A public attribute or method can be accessed by everyone.
+
+**Private access modifiers** - A private attribute or method can be accessed by no one, not even the child class.
+**Explanation** - It can be accessed by the **same** class. No one outside the class has access to private methods.
+
+**Protected access modifier** - A protected attribute or method can be accessed only from the classes of the same package.
+
+Let me show you a diagram that will be helpful in understanding and will clear most of your doubts.
+
+where: +
+---
+### Question
+
+Which is the **most restricted** access modifier?
+
+**Choices**
+
+- [ ] Public
+- [ ] Default
+- [x] Private
+- [ ] Protected
+
+---
+### Question
+
+Which is the **most open** access modifier?
+
+**Choices**
+
+- [x] Public
+- [ ] Default
+- [ ] Private
+- [ ] Protected
+
+---
+### `this` Keyword
+
+Before we see the example of access modifier, let's understand **"this" keyword**:
+* In programming, "this" is a keyword used to refer to the **current instance of a class or object**.
+* It's typically used to distinguish between instance variables and local variables or method parameters with the same names, and to access or modify instance members within methods.
+* This enhances code clarity and prevents naming conflicts in object-oriented languages like Java and C++.
+
+Here is an example:
+```Java
+public class Person {
+ private String name;
+
+ public Person(String name) {
+ this.name = name; // "this" refers to the current instance of the class
+ }
+
+ public void introduceYourself() {
+ System.out.println("Hello, I am " + this.name); // Using "this" to access the instance variable
+ }
+
+ public static void main(String[] args) {
+ Person person1 = new Person("Alice");
+ Person person2 = new Person("Bob");
+
+ person1.introduceYourself(); // Output: Hello, I am Alice
+ person2.introduceYourself(); // Output: Hello, I am Bob
+ }
+}
+```
+In this example, the "this" keyword is used to differentiate between the instance variable name and the constructor parameter name, ensuring that the correct value is assigned and accessed within the class methods.
+
+---
+### Example of Access Modifiers
+
+```Java
+package mypackage;
+
+public class AccessModifierExample {
+ public int publicVariable = 10; // Public access
+
+ private int privateVariable = 20; // Private access
+
+ protected int protectedVariable = 30; // Protected access
+
+ int defaultVariable = 40; // Default (package-private) access
+
+ public void publicMethod() {
+ System.out.println("This is a public method.");
+ }
+
+ private void privateMethod() {
+ System.out.println("This is a private method.");
+ }
+
+ public static void main(String[] args) {
+ AccessModifierExample example = new AccessModifierExample();
+
+ System.out.println("Public variable: " + example.publicVariable);
+ System.out.println("Private variable: " + example.privateVariable);
+ System.out.println("Protected variable: " + example.protectedVariable);
+ System.out.println("Default variable: " + example.defaultVariable);
+ }
+}
+```
+```Java
+package otherpackage;
+
+import mypackage.AccessModifierExample; // Import the class from a different package
+
+public class AnotherClass {
+ public static void main(String[] args) {
+ AccessModifierExample example = new AccessModifierExample();
+
+ System.out.println(example.publicVariable); // Accessing publicVariable is valid
+ System.out.println(example.defaultVariable); // Error: Cannot access defaultVariable from a different package
+
+ example.publicMethod();
+ example.privateMethod(); // Error: Private method is not accessible outside the class
+ }
+}
+```
+In this example:
+
+The class **AccessModifierExample** has variables and methods with different access modifiers: public, private, protected, and default.
+Access modifiers control the visibility and accessibility of members (variables and methods) outside the class.
+Public members are accessible from anywhere, private members are only accessible within the class, protected members are accessible within the class and its subclasses, and default members are accessible within the same package.
+
+Now, you can try all these on your machine just by creating classes and accessing them.
+
+---
+
+### `static` Keyword
+
+The **static** keyword in programming languages like Java and C++ is used to declare **class-level members or methods**, which are associated with the class itself rather than with instances (objects) of the class.
+
+1. **Static Variables (Class Variables):** When you declare a variable as "static" within a class, it becomes a class variable. These variables are shared among all instances of the class. They are initialized only once when the class is loaded, and their values are common to all objects of the class.
+
+2. **Static Methods (Class Methods):** When you declare a method as "static," it becomes a class method. These methods are invoked on the class itself, not on instances of the class. They can access static variables and perform operations that don't require access to instance-specific data.
+
+The **static** keyword is often used for utility methods and constants that are relevant at the class level rather than the instance level. It allows you to access these members without creating an object of the class.
+
+Static variable is created when we load a class.
+
+Here is an example:
+```Java
+public class MyClass {
+ // Static variable
+ static int staticVar = 0;
+
+ // Instance variable
+ int instanceVar;
+
+ public MyClass(int value) {
+ this.instanceVar = value;
+ staticVar++;
+ }
+
+ public static void main(String[] args) {
+ MyClass obj1 = new MyClass(10);
+ MyClass obj2 = new MyClass(20);
+
+ System.out.println("Static Variable: " + staticVar); // Output: Static Variable: 2
+ System.out.println("Instance Variable (obj1): " + obj1.instanceVar); // Output: Instance Variable (obj1): 10
+ System.out.println("Instance Variable (obj2): " + obj2.instanceVar); // Output: Instance Variable (obj2): 20
+ }
+}
+```
+In this example, we have a static variable **staticVar** and an instance variable **instanceVar**. The staticVar is incremented every time an object is created, and we access both static and instance variables directly within the main method.
+
+---
+
+### Scope of a variable
+
+Now let's talk about scope of a variable within a program!
+
+In Java, scope refers to the region or context within your code where a specific variable or identifier is accessible and can be used. The scope of a variable is determined by where it is declared, and it influences its visibility and lifetime within the program.
+**There are primarily four types of variable scope in Java:**
+
+1. **Class/Static Scope:** Variables declared as `static` within a class have class-level scope. These variables are associated with the class itself rather than with instances (objects) of the class. They can be accessed using the class name and are shared among all instances of the class.
+
+2. **Instance Scope:** Variables declared within a class but outside any method or constructor have instance scope. These are often referred to as instance variables, and they are associated with specific instances (objects) of the class. Each object has its own copy of these variables.
+
+3. **Method/Local Scope:** Variables declared within a method or a block of code have method or local scope. These variables are only accessible within the specific method or block where they are defined. They go out of scope when the method or block's execution is complete.
+
+4. **Block Scope:** Variables declared within a pair of curly braces `{}` have scope limited to that block. These variables are only accessible within the block in which they are defined.
+
+The scope of a variable is essential for ensuring that the right variables are accessed at the right time and for avoiding naming conflicts. Properly managing variable scope contributes to the clarity and reliability of your code.
+
+Here's a brief example to illustrate variable scope in Java:
+
+```java
+public class ScopeExample {
+ // Class-level variable (static scope)
+ static int classVar = 10;
+
+ // Instance variable (instance scope)
+ int instanceVar = 20;
+
+ public void exampleMethod() {
+ // Method-level variable (method scope)
+ int methodVar = 30;
+
+ if (true) {
+ // Block-level variable (block scope)
+ int blockVar = 40;
+ System.out.println(classVar + instanceVar + methodVar + blockVar);
+ }
+ // The 'blockVar' is out of scope here.
+ }
+
+ public static void main(String[] args) {
+ ScopeExample obj = new ScopeExample();
+ obj.exampleMethod();
+ // The 'methodVar' and 'blockVar' are out of scope here.
+ }
+}
+```
+
+In this example, you can see how variables with different scopes are defined and accessed within a Java class.
diff --git a/Academy DSA Typed Notes/Advanced/DSA OOPS 2 Constuctors, Inheritance & Polymorphism.md b/Academy DSA Typed Notes/Advanced/DSA OOPS 2 Constuctors, Inheritance & Polymorphism.md
new file mode 100644
index 0000000..6b50d85
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA OOPS 2 Constuctors, Inheritance & Polymorphism.md
@@ -0,0 +1,660 @@
+# OOPs 2
+### Constructors
+
+If you remember, we have studied **classes and objects** in the previous lecture, so what is a class and object? Let's have a quick recap of it.
+
+
+**Class:** Blueprint of an entity.
+**Object:** Instance of class
+
+Now let's look at how a class comes into reality.
+
+Let's define a class named Student.
+```java
+Student {
+ String name;
+ int age;
+ doubly psp;
+}
+```
+Now, let's make an object of the Student class.
+```java
+Student st = new Student();
+```
+Now, from the basics of programming, we all know that to declare a variable, we write:
+```java
+int a = 12;
+```
+Let's compare this with object creation:
+```java
+int a = 12;
+Student st = new Student();
+```
+We can see that **Student** is the Data type here and **st** is a variable name, but
+
+
+This thing => **Student();** is called a **constructor**, which creates the object of the class.
+
+This thing, when you don't create a constructor, is called a **default constructor**. Let's discuss it in detail.
+
+---
+
+### Default Constructor
+If we don't create our own constructor in a class, a **default constructor** is created.
+
+**Default constructor** creates a new object of the class and sets the value of each attribute as the default value of that type.
+
+Examples of default values of datatype:
+* **0** for integer,
+* **null** for String,
+* **0.0** for float, etc.
+
+> **Note:** A default constructor will assign default values only if we haven't assigned values to class attributes while declaring the variable.
+
+So if we are not creating any constructor, then our class is going to make its own constructor.
+
+A default constructor can be assumed to be present like this:
+```java
+class Student {
+ String name;
+ int age;
+ double psp;
+ String univName;
+
+ Student() {
+ name = null;
+ age = 0;
+ psp = 0.0;
+ univName = null;
+ }
+}
+```
+
+
+
+---
+### Question
+
+Which is the **most restricted** access modifier?
+
+**Choices**
+
+- [ ] Public
+- [ ] Default
+- [x] Private
+- [ ] Protected
+
+---
+### Question
+
+Which is the **most open** access modifier?
+
+**Choices**
+
+- [x] Public
+- [ ] Default
+- [ ] Private
+- [ ] Protected
+
+---
+### `this` Keyword
+
+Before we see the example of access modifier, let's understand **"this" keyword**:
+* In programming, "this" is a keyword used to refer to the **current instance of a class or object**.
+* It's typically used to distinguish between instance variables and local variables or method parameters with the same names, and to access or modify instance members within methods.
+* This enhances code clarity and prevents naming conflicts in object-oriented languages like Java and C++.
+
+Here is an example:
+```Java
+public class Person {
+ private String name;
+
+ public Person(String name) {
+ this.name = name; // "this" refers to the current instance of the class
+ }
+
+ public void introduceYourself() {
+ System.out.println("Hello, I am " + this.name); // Using "this" to access the instance variable
+ }
+
+ public static void main(String[] args) {
+ Person person1 = new Person("Alice");
+ Person person2 = new Person("Bob");
+
+ person1.introduceYourself(); // Output: Hello, I am Alice
+ person2.introduceYourself(); // Output: Hello, I am Bob
+ }
+}
+```
+In this example, the "this" keyword is used to differentiate between the instance variable name and the constructor parameter name, ensuring that the correct value is assigned and accessed within the class methods.
+
+---
+### Example of Access Modifiers
+
+```Java
+package mypackage;
+
+public class AccessModifierExample {
+ public int publicVariable = 10; // Public access
+
+ private int privateVariable = 20; // Private access
+
+ protected int protectedVariable = 30; // Protected access
+
+ int defaultVariable = 40; // Default (package-private) access
+
+ public void publicMethod() {
+ System.out.println("This is a public method.");
+ }
+
+ private void privateMethod() {
+ System.out.println("This is a private method.");
+ }
+
+ public static void main(String[] args) {
+ AccessModifierExample example = new AccessModifierExample();
+
+ System.out.println("Public variable: " + example.publicVariable);
+ System.out.println("Private variable: " + example.privateVariable);
+ System.out.println("Protected variable: " + example.protectedVariable);
+ System.out.println("Default variable: " + example.defaultVariable);
+ }
+}
+```
+```Java
+package otherpackage;
+
+import mypackage.AccessModifierExample; // Import the class from a different package
+
+public class AnotherClass {
+ public static void main(String[] args) {
+ AccessModifierExample example = new AccessModifierExample();
+
+ System.out.println(example.publicVariable); // Accessing publicVariable is valid
+ System.out.println(example.defaultVariable); // Error: Cannot access defaultVariable from a different package
+
+ example.publicMethod();
+ example.privateMethod(); // Error: Private method is not accessible outside the class
+ }
+}
+```
+In this example:
+
+The class **AccessModifierExample** has variables and methods with different access modifiers: public, private, protected, and default.
+Access modifiers control the visibility and accessibility of members (variables and methods) outside the class.
+Public members are accessible from anywhere, private members are only accessible within the class, protected members are accessible within the class and its subclasses, and default members are accessible within the same package.
+
+Now, you can try all these on your machine just by creating classes and accessing them.
+
+---
+
+### `static` Keyword
+
+The **static** keyword in programming languages like Java and C++ is used to declare **class-level members or methods**, which are associated with the class itself rather than with instances (objects) of the class.
+
+1. **Static Variables (Class Variables):** When you declare a variable as "static" within a class, it becomes a class variable. These variables are shared among all instances of the class. They are initialized only once when the class is loaded, and their values are common to all objects of the class.
+
+2. **Static Methods (Class Methods):** When you declare a method as "static," it becomes a class method. These methods are invoked on the class itself, not on instances of the class. They can access static variables and perform operations that don't require access to instance-specific data.
+
+The **static** keyword is often used for utility methods and constants that are relevant at the class level rather than the instance level. It allows you to access these members without creating an object of the class.
+
+Static variable is created when we load a class.
+
+Here is an example:
+```Java
+public class MyClass {
+ // Static variable
+ static int staticVar = 0;
+
+ // Instance variable
+ int instanceVar;
+
+ public MyClass(int value) {
+ this.instanceVar = value;
+ staticVar++;
+ }
+
+ public static void main(String[] args) {
+ MyClass obj1 = new MyClass(10);
+ MyClass obj2 = new MyClass(20);
+
+ System.out.println("Static Variable: " + staticVar); // Output: Static Variable: 2
+ System.out.println("Instance Variable (obj1): " + obj1.instanceVar); // Output: Instance Variable (obj1): 10
+ System.out.println("Instance Variable (obj2): " + obj2.instanceVar); // Output: Instance Variable (obj2): 20
+ }
+}
+```
+In this example, we have a static variable **staticVar** and an instance variable **instanceVar**. The staticVar is incremented every time an object is created, and we access both static and instance variables directly within the main method.
+
+---
+
+### Scope of a variable
+
+Now let's talk about scope of a variable within a program!
+
+In Java, scope refers to the region or context within your code where a specific variable or identifier is accessible and can be used. The scope of a variable is determined by where it is declared, and it influences its visibility and lifetime within the program.
+**There are primarily four types of variable scope in Java:**
+
+1. **Class/Static Scope:** Variables declared as `static` within a class have class-level scope. These variables are associated with the class itself rather than with instances (objects) of the class. They can be accessed using the class name and are shared among all instances of the class.
+
+2. **Instance Scope:** Variables declared within a class but outside any method or constructor have instance scope. These are often referred to as instance variables, and they are associated with specific instances (objects) of the class. Each object has its own copy of these variables.
+
+3. **Method/Local Scope:** Variables declared within a method or a block of code have method or local scope. These variables are only accessible within the specific method or block where they are defined. They go out of scope when the method or block's execution is complete.
+
+4. **Block Scope:** Variables declared within a pair of curly braces `{}` have scope limited to that block. These variables are only accessible within the block in which they are defined.
+
+The scope of a variable is essential for ensuring that the right variables are accessed at the right time and for avoiding naming conflicts. Properly managing variable scope contributes to the clarity and reliability of your code.
+
+Here's a brief example to illustrate variable scope in Java:
+
+```java
+public class ScopeExample {
+ // Class-level variable (static scope)
+ static int classVar = 10;
+
+ // Instance variable (instance scope)
+ int instanceVar = 20;
+
+ public void exampleMethod() {
+ // Method-level variable (method scope)
+ int methodVar = 30;
+
+ if (true) {
+ // Block-level variable (block scope)
+ int blockVar = 40;
+ System.out.println(classVar + instanceVar + methodVar + blockVar);
+ }
+ // The 'blockVar' is out of scope here.
+ }
+
+ public static void main(String[] args) {
+ ScopeExample obj = new ScopeExample();
+ obj.exampleMethod();
+ // The 'methodVar' and 'blockVar' are out of scope here.
+ }
+}
+```
+
+In this example, you can see how variables with different scopes are defined and accessed within a Java class.
diff --git a/Academy DSA Typed Notes/Advanced/DSA OOPS 2 Constuctors, Inheritance & Polymorphism.md b/Academy DSA Typed Notes/Advanced/DSA OOPS 2 Constuctors, Inheritance & Polymorphism.md
new file mode 100644
index 0000000..6b50d85
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA OOPS 2 Constuctors, Inheritance & Polymorphism.md
@@ -0,0 +1,660 @@
+# OOPs 2
+### Constructors
+
+If you remember, we have studied **classes and objects** in the previous lecture, so what is a class and object? Let's have a quick recap of it.
+
+
+**Class:** Blueprint of an entity.
+**Object:** Instance of class
+
+Now let's look at how a class comes into reality.
+
+Let's define a class named Student.
+```java
+Student {
+ String name;
+ int age;
+ doubly psp;
+}
+```
+Now, let's make an object of the Student class.
+```java
+Student st = new Student();
+```
+Now, from the basics of programming, we all know that to declare a variable, we write:
+```java
+int a = 12;
+```
+Let's compare this with object creation:
+```java
+int a = 12;
+Student st = new Student();
+```
+We can see that **Student** is the Data type here and **st** is a variable name, but
+
+
+This thing => **Student();** is called a **constructor**, which creates the object of the class.
+
+This thing, when you don't create a constructor, is called a **default constructor**. Let's discuss it in detail.
+
+---
+
+### Default Constructor
+If we don't create our own constructor in a class, a **default constructor** is created.
+
+**Default constructor** creates a new object of the class and sets the value of each attribute as the default value of that type.
+
+Examples of default values of datatype:
+* **0** for integer,
+* **null** for String,
+* **0.0** for float, etc.
+
+> **Note:** A default constructor will assign default values only if we haven't assigned values to class attributes while declaring the variable.
+
+So if we are not creating any constructor, then our class is going to make its own constructor.
+
+A default constructor can be assumed to be present like this:
+```java
+class Student {
+ String name;
+ int age;
+ double psp;
+ String univName;
+
+ Student() {
+ name = null;
+ age = 0;
+ psp = 0.0;
+ univName = null;
+ }
+}
+```
+
+ +
+But,
+* By the definition of the default constructor, we know that, **if we create our own constructor** then a default constructor is not created.
+
+So, by looking at Student(), we can say that no parameters are passed here, right?
+So, **the default constructors take no parameters**.
+
+**Summarising** the default constructor:
+1. Takes no parameter.
+2. Sets every attribute of class to it's default value (unless defined).
+3. Created only if we don't write our own constructor.
+4. It's public i.e. can be access from anywhere.
+
+---
+
+### Manual Constructor
+Now, let's create our own constructor using the same `Student` class
+
+```java
+public class Student {
+ String name;
+ private int age = 21;
+ String univName;
+ double psp;
+
+ public Student (String studentName, String universityName) {
+ name = studentName;
+ univName = universityName;
+ }
+}
+```
+Let's create a client class.
+```java
+public class Client {
+ public static void main(String[] args) {
+ Student st = new Student(); //ERROR
+}
+```
+But here, why its throwing error?
+* Because now there is no default constructor, since we have our own constructor, and it has parameters. So we have to pass the parameters here.
+
+So, let's do like this,
+```java
+public class Client {
+public static void main(String[] args) {
+ Student st = new Student("Utkarsh", "JIIT");
+}
+```
+
+
+But,
+* By the definition of the default constructor, we know that, **if we create our own constructor** then a default constructor is not created.
+
+So, by looking at Student(), we can say that no parameters are passed here, right?
+So, **the default constructors take no parameters**.
+
+**Summarising** the default constructor:
+1. Takes no parameter.
+2. Sets every attribute of class to it's default value (unless defined).
+3. Created only if we don't write our own constructor.
+4. It's public i.e. can be access from anywhere.
+
+---
+
+### Manual Constructor
+Now, let's create our own constructor using the same `Student` class
+
+```java
+public class Student {
+ String name;
+ private int age = 21;
+ String univName;
+ double psp;
+
+ public Student (String studentName, String universityName) {
+ name = studentName;
+ univName = universityName;
+ }
+}
+```
+Let's create a client class.
+```java
+public class Client {
+ public static void main(String[] args) {
+ Student st = new Student(); //ERROR
+}
+```
+But here, why its throwing error?
+* Because now there is no default constructor, since we have our own constructor, and it has parameters. So we have to pass the parameters here.
+
+So, let's do like this,
+```java
+public class Client {
+public static void main(String[] args) {
+ Student st = new Student("Utkarsh", "JIIT");
+}
+```
+ +
+Now, let's move to the copy constructor and learn more about it.
+
+---
+### Copy Constructor
+
+Now, **What is a copy constructor?**
+Let's say we already have an object of student class, and then we want to create a new object of student that has the exact same values of attributes as older objects.
+
+**For example:**
+
+
+Now, let's move to the copy constructor and learn more about it.
+
+---
+### Copy Constructor
+
+Now, **What is a copy constructor?**
+Let's say we already have an object of student class, and then we want to create a new object of student that has the exact same values of attributes as older objects.
+
+**For example:**
+ +
+If `st1` as an object and we need to create one more object `st2`, with the same attribute values, we can do it with the copy constructor.
+
+```java
+class Student {
+ String name;
+ int age;
+
+ Student() {
+ name = null;
+ age = 0;
+ }
+ Student(Student st) {
+ name = st.name;
+ age = st.age;
+ }
+}
+```
+
+So basically, to make a copy, we need to pass it as a parameter to the copy constructor, as the data type is Student.
+```java
+Student st1 = new Student();
+st1.name = "Utkarsh";
+st1.age = 27;
+
+Student st2 = new Student(st1); // Copy Constructor
+```
+
+So now we understand how to write a copy constructor, but what is the use case of the copy constructor?
+
+* The copy constructor comes in use when we have an object, and a newly created object needs the same values, so we don't assign it ourselves. We use the copy constructor the get the work done.
+* Some of the attributes may be private and cannot be accessed by the user, but a copy constructor can access it and make the copy itself.
+
+### Question
+
+Is copy constructor same as doing `Student st2 = st1;`?
+
+**Choices**
+
+- [ ] Yes
+- [ ] In some cases only
+- [x] No
+
+
+Let's see how do things work internally?
+
+
+If `st1` as an object and we need to create one more object `st2`, with the same attribute values, we can do it with the copy constructor.
+
+```java
+class Student {
+ String name;
+ int age;
+
+ Student() {
+ name = null;
+ age = 0;
+ }
+ Student(Student st) {
+ name = st.name;
+ age = st.age;
+ }
+}
+```
+
+So basically, to make a copy, we need to pass it as a parameter to the copy constructor, as the data type is Student.
+```java
+Student st1 = new Student();
+st1.name = "Utkarsh";
+st1.age = 27;
+
+Student st2 = new Student(st1); // Copy Constructor
+```
+
+So now we understand how to write a copy constructor, but what is the use case of the copy constructor?
+
+* The copy constructor comes in use when we have an object, and a newly created object needs the same values, so we don't assign it ourselves. We use the copy constructor the get the work done.
+* Some of the attributes may be private and cannot be accessed by the user, but a copy constructor can access it and make the copy itself.
+
+### Question
+
+Is copy constructor same as doing `Student st2 = st1;`?
+
+**Choices**
+
+- [ ] Yes
+- [ ] In some cases only
+- [x] No
+
+
+Let's see how do things work internally?
+ +
+* So we have a memory, and st1 is present in the memory with all the data, as shown in the above diagram.
+* When we write student `st2 = st1`, we just make st2 to point as s1, i.e., **a new object is not created**.
+* Now the problem here is if we do changes in st2, i.e. `st2.name = 'xyz'`, it will change the value of st1.
+
+
+Now if we create the object using copy constructor then it has a different address. So it's not pointing in the memory, as we have seen in the example above.
+
+---
+### Deep and Shallow copy
+
+### Shallow copy
+
+* When we have created a new object, but behind the scenes, the new object still refer to attributes of the old object. i.e., the new object still refers to the same data as the old copy.
+
+```python
+original_books = ["Book A", "Book B"]
+shallow_copy_books = original_books
+
+shallow_copy_books.append("Book C")
+
+print(original_books) # Output: ["Book A", "Book B", "Book C"]
+```
+
+### Deep copy
+
+* When we have created a new object behind the scenes, the new object do not refer to attributes of the old object. i.e., the new object has no shared data.
+
+```python
+import copy
+
+original_books = ["Book A", "Book B"]
+deep_copy_books = copy.deepcopy(original_books)
+
+deep_copy_books.append("Book C")
+
+print(original_books) # Output: ["Book A", "Book B"]
+```
+
+---
+### Inheritance
+
+
+
+**How is inheritance represented?**
+**Ans** - Inheritance is represented as parent-child relations between different classes.
+
+Now, let's talk about the scaler's hierarchy of representation.
+
+
+
+* So we have a memory, and st1 is present in the memory with all the data, as shown in the above diagram.
+* When we write student `st2 = st1`, we just make st2 to point as s1, i.e., **a new object is not created**.
+* Now the problem here is if we do changes in st2, i.e. `st2.name = 'xyz'`, it will change the value of st1.
+
+
+Now if we create the object using copy constructor then it has a different address. So it's not pointing in the memory, as we have seen in the example above.
+
+---
+### Deep and Shallow copy
+
+### Shallow copy
+
+* When we have created a new object, but behind the scenes, the new object still refer to attributes of the old object. i.e., the new object still refers to the same data as the old copy.
+
+```python
+original_books = ["Book A", "Book B"]
+shallow_copy_books = original_books
+
+shallow_copy_books.append("Book C")
+
+print(original_books) # Output: ["Book A", "Book B", "Book C"]
+```
+
+### Deep copy
+
+* When we have created a new object behind the scenes, the new object do not refer to attributes of the old object. i.e., the new object has no shared data.
+
+```python
+import copy
+
+original_books = ["Book A", "Book B"]
+deep_copy_books = copy.deepcopy(original_books)
+
+deep_copy_books.append("Book C")
+
+print(original_books) # Output: ["Book A", "Book B"]
+```
+
+---
+### Inheritance
+
+
+
+**How is inheritance represented?**
+**Ans** - Inheritance is represented as parent-child relations between different classes.
+
+Now, let's talk about the scaler's hierarchy of representation.
+
+ +
+Now, Let's say User has the following attributes:
+* Username
+* Login
+
+
+So, We can say that:
+* Instructor
+* Mentor
+* TA
+* Student
+
+They all are **specific types** of users i.e. they will share all the members / attributes / methods of **User** and may have some more of their own.
+
+A **child class / subclass** can have specific attributes / behaviors which may not be present in the **parent class / superclass**.
+
+>Consider the below diagram for explaining child / subclass & parent / superclass terms more clearly.
+
+
+Now, Let's say User has the following attributes:
+* Username
+* Login
+
+
+So, We can say that:
+* Instructor
+* Mentor
+* TA
+* Student
+
+They all are **specific types** of users i.e. they will share all the members / attributes / methods of **User** and may have some more of their own.
+
+A **child class / subclass** can have specific attributes / behaviors which may not be present in the **parent class / superclass**.
+
+>Consider the below diagram for explaining child / subclass & parent / superclass terms more clearly.
+ +
+So we can **conclude**: A child class inherits all the members of the parent class and may or may not add their own members.
+
+---
+
+### Parent-Child Relationship in Code
+
+How can we represent a parent-child relationship in code? Let's say we need to make a relationship between the User and the Instructor.
+
+
+To build this, Let's say we have a **Parent class called User**, as shown below:
+```java
+class User {
+ String userName;
+
+ void login() {
+ ...
+ }
+}
+```
+**Instructor** is a child/subclass of User, so how can we do that?
+```java
+Class Instructor extends User.
+```
+So here `extends` is the **keyword in Java** that is used to create a child class.
+
+The `extend` keyword is specific to Java and is used to create a subclass that inherits properties and behaviors from a superclass.
+
+While the keyword itself may vary in other programming languages, the concept is similar. Here are a few examples from different languages:
+
+- **In Python:** The inheritance is indicated using **parentheses**.
+For example: `class Subclass(SuperClass):`
+
+- **In C++:** The inheritance is specified using a **colon**.
+For example: `class Subclass : public SuperClass { };`
+
+- **In C#:** The inheritance is specified using a **colon**.
+For example: `class Subclass : BaseClass { }`
+
+So, while the specific syntax and keywords may differ, the concept of class extension or inheritance is present in various object-oriented programming languages.
+
+The instructor class has the following methods:
+```java
+class Instructor extends User {
+ String batchName;
+ double avgRating;
+
+ void scheduleClass() {
+ ...
+ }
+}
+```
+
+* Does the Instructor class needs a username property?
+ * Yes
+* Do we need to code it?
+ * No
+* So, how can we use it?
+ * We are extending it from the User class.
+
+Extends means, **keeping the original things and adding more things to it**.
+
+---
+### Constructor Chaining
+
+
+How do we create an object of any class?
+```java
+Instructor i = new Instructor();
+```
+* Did we ever created `Instructor()` constructor?
+ * No, Right?
+
+* So, how it came into the picture?
+ * Yes, It is a Default Constructor.
+This constructor initializes to default values of all the attributes, so can we do like:
+```java
+i.username = "Utkarsh";
+i.login();
+```
+Yes, because it's coming from the `User` class.
+
+Can we also do:
+```java
+i.avgRating = 4
+```
+Yes, because it's part of the Instructor's class.
+
+**Note:** In Inheritance, a parent class is nothing but generalization, and every child is a specification.
+
+Now, assume we are given this relation:
+
+
+So we can **conclude**: A child class inherits all the members of the parent class and may or may not add their own members.
+
+---
+
+### Parent-Child Relationship in Code
+
+How can we represent a parent-child relationship in code? Let's say we need to make a relationship between the User and the Instructor.
+
+
+To build this, Let's say we have a **Parent class called User**, as shown below:
+```java
+class User {
+ String userName;
+
+ void login() {
+ ...
+ }
+}
+```
+**Instructor** is a child/subclass of User, so how can we do that?
+```java
+Class Instructor extends User.
+```
+So here `extends` is the **keyword in Java** that is used to create a child class.
+
+The `extend` keyword is specific to Java and is used to create a subclass that inherits properties and behaviors from a superclass.
+
+While the keyword itself may vary in other programming languages, the concept is similar. Here are a few examples from different languages:
+
+- **In Python:** The inheritance is indicated using **parentheses**.
+For example: `class Subclass(SuperClass):`
+
+- **In C++:** The inheritance is specified using a **colon**.
+For example: `class Subclass : public SuperClass { };`
+
+- **In C#:** The inheritance is specified using a **colon**.
+For example: `class Subclass : BaseClass { }`
+
+So, while the specific syntax and keywords may differ, the concept of class extension or inheritance is present in various object-oriented programming languages.
+
+The instructor class has the following methods:
+```java
+class Instructor extends User {
+ String batchName;
+ double avgRating;
+
+ void scheduleClass() {
+ ...
+ }
+}
+```
+
+* Does the Instructor class needs a username property?
+ * Yes
+* Do we need to code it?
+ * No
+* So, how can we use it?
+ * We are extending it from the User class.
+
+Extends means, **keeping the original things and adding more things to it**.
+
+---
+### Constructor Chaining
+
+
+How do we create an object of any class?
+```java
+Instructor i = new Instructor();
+```
+* Did we ever created `Instructor()` constructor?
+ * No, Right?
+
+* So, how it came into the picture?
+ * Yes, It is a Default Constructor.
+This constructor initializes to default values of all the attributes, so can we do like:
+```java
+i.username = "Utkarsh";
+i.login();
+```
+Yes, because it's coming from the `User` class.
+
+Can we also do:
+```java
+i.avgRating = 4
+```
+Yes, because it's part of the Instructor's class.
+
+**Note:** In Inheritance, a parent class is nothing but generalization, and every child is a specification.
+
+Now, assume we are given this relation:
+ +
+---
+### Question
+
+Which of these classes has the highest level of abstraction?
+
+**Choices**
+
+- [x] A
+- [ ] B
+- [ ] C
+- [ ] D
+
+
+First of all, what is abstraction?
+- It's an idea.
+
+So, what does the highest level of abstraction mean?
+- A bigger idea that means a more general idea.
+
+So out of them, **A** is the most generic class, right?
+That's why **A has the highest level of abstraction.**
+
+---
+### Question
+
+Do the child class contains all the attributes of parent class?
+
+**Choices**
+
+- [x] Yes
+- [ ] No
+- [ ] Can't say
+
+
+Definitely, **Yes**.
+Example is Animal :arrow_right: Dog
+
+So now the question is, how are they initialized? Who initializes them?
+
+Let's see what happens behind the scenes:
+
+* Let's say we have a User class as shown below:
+
+
+---
+### Question
+
+Which of these classes has the highest level of abstraction?
+
+**Choices**
+
+- [x] A
+- [ ] B
+- [ ] C
+- [ ] D
+
+
+First of all, what is abstraction?
+- It's an idea.
+
+So, what does the highest level of abstraction mean?
+- A bigger idea that means a more general idea.
+
+So out of them, **A** is the most generic class, right?
+That's why **A has the highest level of abstraction.**
+
+---
+### Question
+
+Do the child class contains all the attributes of parent class?
+
+**Choices**
+
+- [x] Yes
+- [ ] No
+- [ ] Can't say
+
+
+Definitely, **Yes**.
+Example is Animal :arrow_right: Dog
+
+So now the question is, how are they initialized? Who initializes them?
+
+Let's see what happens behind the scenes:
+
+* Let's say we have a User class as shown below:
+  +And we create a `User` object:
+ **`User user = new User();`**
+
+So,
+How will the attributes get initialized?
+**Ans** - Since we haven't created our constructor, our attributes get assigned to null values by default constructor, as shown below.
+ *
+And we create a `User` object:
+ **`User user = new User();`**
+
+So,
+How will the attributes get initialized?
+**Ans** - Since we haven't created our constructor, our attributes get assigned to null values by default constructor, as shown below.
+ *  +
+* Or we may create our own constructor:
+
+
+* Or we may create our own constructor:
+ +
+
+Now, If we create a child class / sub-class named instructor:
+
+
+
+Now, If we create a child class / sub-class named instructor:
+ +
+**Now the question is:** When we create an instructor, someone has to initialize the attribute that came from the parent.
+
+There are scenarios now:
+1. We know how to initialize, and we understand how to change, so **we will initialize** the values to those attributes, like this:
+
+
+**Now the question is:** When we create an instructor, someone has to initialize the attribute that came from the parent.
+
+There are scenarios now:
+1. We know how to initialize, and we understand how to change, so **we will initialize** the values to those attributes, like this:
+ +
+But DO YOU THINK we will always Know how to initialize the attributes?
+Ans - **No!** But there is someone who'll always know how and what to initialize.
+
+2. A **constructor of the parent** definitely knows how and what to initialize the attributes. Let's understand How it's done!
+
+---
+### Steps to Create an Object of Child
+
+**(Assuiming no constructor is created, its only default constructors are present)**
+
+Suppose we have a class named **A**.
+
+
+But DO YOU THINK we will always Know how to initialize the attributes?
+Ans - **No!** But there is someone who'll always know how and what to initialize.
+
+2. A **constructor of the parent** definitely knows how and what to initialize the attributes. Let's understand How it's done!
+
+---
+### Steps to Create an Object of Child
+
+**(Assuiming no constructor is created, its only default constructors are present)**
+
+Suppose we have a class named **A**.
+ +
+Now `B` is a child of `A`,
+`C` is a child of `B`, and
+`D` is a child of `C.`
+
+Suppose we create an object of **D**:
+```java
+D d = new D();
+```
+
+So, **What really happens when we call `D()`?**
+1. Constructor of D will be called.
+2. Since D is also a child of someone, so before its execution, it will call the constructor of C.
+3. Similarly, C will call the constructor of B first.
+4. And B will call the constructor of A before it's execution.
+
+So, **Who's constructor will be finished first?**
+- **A**'s constructor will be finished first, then **B** will be finished, then **C** will be finished, then **D** will be finished.
+
+Because,
+* **Can a child be born before its parents are born?**
+**No**, right?
+ * That's why the parent class constructor will be called first. We haven't specifically called the parents constructor but by default, the parent constructor is called.
+
+**Note:**
+
+
+Now `B` is a child of `A`,
+`C` is a child of `B`, and
+`D` is a child of `C.`
+
+Suppose we create an object of **D**:
+```java
+D d = new D();
+```
+
+So, **What really happens when we call `D()`?**
+1. Constructor of D will be called.
+2. Since D is also a child of someone, so before its execution, it will call the constructor of C.
+3. Similarly, C will call the constructor of B first.
+4. And B will call the constructor of A before it's execution.
+
+So, **Who's constructor will be finished first?**
+- **A**'s constructor will be finished first, then **B** will be finished, then **C** will be finished, then **D** will be finished.
+
+Because,
+* **Can a child be born before its parents are born?**
+**No**, right?
+ * That's why the parent class constructor will be called first. We haven't specifically called the parents constructor but by default, the parent constructor is called.
+
+**Note:**
+ +
+What will happen if we add a parameterized constructor in class **C** as shown below:
+```java
+public class C extends B {
+ C() {
+ System.out.println("Constructor of C");
+ }
+ C(String a) {
+ System.out.println("Constructor of C with params");
+ }
+}
+```
+What will be the output if we run the code now?
+The output will still be the same right, i.e., `Default Constructor of C` will be printed with all other constructors from A, B & D.
+
+But, What if we want to **print the manual constructor** of class C?
+
+To make this happen, we need to make changes in our **D** class.
+We have to add the **super** function in the first line of our constructor.
+
+```java
+public class D extends C {
+ D() {
+ super ("Hello"); // This must be the first line
+ System.out.println("Constructor of D");
+ }
+}
+```
+The **super("Hello");** will make the parametrized constructor from Class C become active.
+
+**Note:** This super() line in the code must be written in the **first line inside a constructor**. Otherwise, it throws an error.
+
+---
+## Polymorphism
+
+What really is polymorphism?
+
+There's a very famous explanation of Polymorphism i.e. **Poly means Many** and **Morphism means Form**.
+
+Which means, someone who has multiple forms.
+
+So, till now, in today's class, have you learned about something which had multiple forms?
+**Ans** - Yes, a user could have multiple forms. Because a user can be a student, instructor, TA, etc.
+
+So this can be an example of multiple forms.
+
+**Another example** - Suppose we have a list of Animals. Animals have Mammals, Reptiles, Aquatic, etc. classifications.
+
+**Can we write:**
+`Animal a = new Dog();`
+Yes, because this is an **object of type Dog**, which is a Mammal and which is an Animal. So we can write it!
+
+**But, Can we write:**
+`Dog d = new Animal();`
+No, this is **not allowed** since every Dog is an Animal, but every Animal must not be a Dog.
+
+**That means: We can put an object of the child class in a variable that takes parent data type.**
+
+**Suppose we have three classes, A, B, and C.** as shown below:
+
+
+What will happen if we add a parameterized constructor in class **C** as shown below:
+```java
+public class C extends B {
+ C() {
+ System.out.println("Constructor of C");
+ }
+ C(String a) {
+ System.out.println("Constructor of C with params");
+ }
+}
+```
+What will be the output if we run the code now?
+The output will still be the same right, i.e., `Default Constructor of C` will be printed with all other constructors from A, B & D.
+
+But, What if we want to **print the manual constructor** of class C?
+
+To make this happen, we need to make changes in our **D** class.
+We have to add the **super** function in the first line of our constructor.
+
+```java
+public class D extends C {
+ D() {
+ super ("Hello"); // This must be the first line
+ System.out.println("Constructor of D");
+ }
+}
+```
+The **super("Hello");** will make the parametrized constructor from Class C become active.
+
+**Note:** This super() line in the code must be written in the **first line inside a constructor**. Otherwise, it throws an error.
+
+---
+## Polymorphism
+
+What really is polymorphism?
+
+There's a very famous explanation of Polymorphism i.e. **Poly means Many** and **Morphism means Form**.
+
+Which means, someone who has multiple forms.
+
+So, till now, in today's class, have you learned about something which had multiple forms?
+**Ans** - Yes, a user could have multiple forms. Because a user can be a student, instructor, TA, etc.
+
+So this can be an example of multiple forms.
+
+**Another example** - Suppose we have a list of Animals. Animals have Mammals, Reptiles, Aquatic, etc. classifications.
+
+**Can we write:**
+`Animal a = new Dog();`
+Yes, because this is an **object of type Dog**, which is a Mammal and which is an Animal. So we can write it!
+
+**But, Can we write:**
+`Dog d = new Animal();`
+No, this is **not allowed** since every Dog is an Animal, but every Animal must not be a Dog.
+
+**That means: We can put an object of the child class in a variable that takes parent data type.**
+
+**Suppose we have three classes, A, B, and C.** as shown below:
+ +
+Now if we write:
+```java
+A a = new C();
+a.company = "ABC";
+```
+This will **throw an error** because **a** has a datatype of **A**, but A doesn't have any variable named company.
+
+* Compiler only allows you access to members of the data type of the variable.
+
+Now, suppose you have a method called:
+**changePassword()**
+
+* Is this change password method need a Student / TA / Instructor, OR just a user?
+ * Just a User, right?
+Because it doesn't matter which type of user is asking for a changepassword.
+
+=> **The more generic your code is, the better the reusability will be.**
+This is one of the use cases of Polymorphism.
+
+There are **two types of polymorphism**:
+1. Compile Time Polyphormism
+2. RunTime Polymorphism
+
+Now we have seen that one way of having many forms is **Inheritance**. The other is called **Method overloading**.
+
+---
+
+### Method Overloading
+
+
+Now if we write:
+```java
+A a = new C();
+a.company = "ABC";
+```
+This will **throw an error** because **a** has a datatype of **A**, but A doesn't have any variable named company.
+
+* Compiler only allows you access to members of the data type of the variable.
+
+Now, suppose you have a method called:
+**changePassword()**
+
+* Is this change password method need a Student / TA / Instructor, OR just a user?
+ * Just a User, right?
+Because it doesn't matter which type of user is asking for a changepassword.
+
+=> **The more generic your code is, the better the reusability will be.**
+This is one of the use cases of Polymorphism.
+
+There are **two types of polymorphism**:
+1. Compile Time Polyphormism
+2. RunTime Polymorphism
+
+Now we have seen that one way of having many forms is **Inheritance**. The other is called **Method overloading**.
+
+---
+
+### Method Overloading
+ +
+Suppose we have a class **A**, and it has a method named `hello()`.
+
+* Can a class have another method with the same name but having different parameters?
+ * Yes, this second method `hello(String Name)` is having same name.
+
+Now, this is called **Method overloading**.
+
+Here also, can you identify **Polymorphism**?
+**Ans** - The same method name has many forms.
+
+So, If we write:
+```java
+hello();
+hello(name);
+```
+Does the compiler knows which method to call? In each of the statements?
+* Yes, It knows. So it will be the respective parameters which matches the method definition.
+
+:arrow_right: As here, the final form that will execute is known to the *Compiler*. That's why it is known as **Compile time Polymorphism**.
+
+Which of the following is a method overloading, and which of them is not?
+*
+
+Suppose we have a class **A**, and it has a method named `hello()`.
+
+* Can a class have another method with the same name but having different parameters?
+ * Yes, this second method `hello(String Name)` is having same name.
+
+Now, this is called **Method overloading**.
+
+Here also, can you identify **Polymorphism**?
+**Ans** - The same method name has many forms.
+
+So, If we write:
+```java
+hello();
+hello(name);
+```
+Does the compiler knows which method to call? In each of the statements?
+* Yes, It knows. So it will be the respective parameters which matches the method definition.
+
+:arrow_right: As here, the final form that will execute is known to the *Compiler*. That's why it is known as **Compile time Polymorphism**.
+
+Which of the following is a method overloading, and which of them is not?
+*  +Yes, the first 2 are method overloading, but the last one is not method overloading.
+
+
+:arrow_right: So there is something called a **Method Signature**.
+A method signature is: **`Name of method (Data type of Params)`**
+
+Example: If we have a method:
+`void printHello(String Name, int age)`
+
+* Method signature for this method will be:
+ `printHello(String, int)`
+
+**Methods are known to be overloaded when they have the same name but different signatures.**
+
+---
+### Question
+
+Is this allowed in the same class?
+```
+void printHello(String s) {...}
+
+String printHello(String s) {...}
+```
+
+**Choices**
+
+- [ ] Yes
+- [x] No
+- [ ] Can't say
+
+
+Since the method signature of both the functions is same, the compiler will not be able to distinguish between the functions and hence will give **compile time error**.
+
+---
+### Method overriding
+
+Suppose we have a class **A**,
+```java
+Class A {
+ void doSomething(String a) {
+ ...
+ }
+}
+```
+And we have another class **B** which inherits from **A**, and this class also had a method named `doSometihng`,
+```java
+Class B extends A {
+ String doSomething(String c) {
+ ...
+ }
+}
+```
+So, Is this allowed?
+**Ans** - No,
+Since all the methods of the parent class are present in the child class, like:
+```java
+Class B extends A {
+ String doSomething(String c) {
+ ...
+ }
+ // Parent method inherited
+ void doSomething(String a) {
+ ...
+ }
+}
+```
+And, in the child class, we are having 2 methods with the same signature which it's not allowed. It's going to give us a **Compile time error**.
+
+
+Now let's see another scenario of the same classes. But here, the **return type of both methods is going to be the same**.
+
+Suppose we have a class **A**,
+```java
+Class A {
+ void doSomething(String a) {
+ ...
+ }
+}
+```
+And we have another class **B** which inherits from **A**, and this class also had a method named `doSometihng`, like:
+```java
+Class B extends A {
+ void doSomething(String c) {
+ ...
+ }
+}
+```
+
+If parent and child classes have the same method with the same name and same return type, and the same signature, this is called **Method overriding.**
+In Method overriding, the Parent class methods get hidden.
+
+Let's say we have two classes, as shown below:
+
+Yes, the first 2 are method overloading, but the last one is not method overloading.
+
+
+:arrow_right: So there is something called a **Method Signature**.
+A method signature is: **`Name of method (Data type of Params)`**
+
+Example: If we have a method:
+`void printHello(String Name, int age)`
+
+* Method signature for this method will be:
+ `printHello(String, int)`
+
+**Methods are known to be overloaded when they have the same name but different signatures.**
+
+---
+### Question
+
+Is this allowed in the same class?
+```
+void printHello(String s) {...}
+
+String printHello(String s) {...}
+```
+
+**Choices**
+
+- [ ] Yes
+- [x] No
+- [ ] Can't say
+
+
+Since the method signature of both the functions is same, the compiler will not be able to distinguish between the functions and hence will give **compile time error**.
+
+---
+### Method overriding
+
+Suppose we have a class **A**,
+```java
+Class A {
+ void doSomething(String a) {
+ ...
+ }
+}
+```
+And we have another class **B** which inherits from **A**, and this class also had a method named `doSometihng`,
+```java
+Class B extends A {
+ String doSomething(String c) {
+ ...
+ }
+}
+```
+So, Is this allowed?
+**Ans** - No,
+Since all the methods of the parent class are present in the child class, like:
+```java
+Class B extends A {
+ String doSomething(String c) {
+ ...
+ }
+ // Parent method inherited
+ void doSomething(String a) {
+ ...
+ }
+}
+```
+And, in the child class, we are having 2 methods with the same signature which it's not allowed. It's going to give us a **Compile time error**.
+
+
+Now let's see another scenario of the same classes. But here, the **return type of both methods is going to be the same**.
+
+Suppose we have a class **A**,
+```java
+Class A {
+ void doSomething(String a) {
+ ...
+ }
+}
+```
+And we have another class **B** which inherits from **A**, and this class also had a method named `doSometihng`, like:
+```java
+Class B extends A {
+ void doSomething(String c) {
+ ...
+ }
+}
+```
+
+If parent and child classes have the same method with the same name and same return type, and the same signature, this is called **Method overriding.**
+In Method overriding, the Parent class methods get hidden.
+
+Let's say we have two classes, as shown below:
+ +
+And in the **Main()** method we run the following:
+
+
+And in the **Main()** method we run the following:
+ +So we can see that at first, we have `Hello` as output, and in the last statement, we get `Bye` as output.
+
+Now there are some points that you have to understand:
+
+* The method that is executed is of the data type that is **actually** present at the time of code and **not the type of variable**.
+* Do we know the exact code that is about to run in compile time?
+ * No, and that's why it's called **RunTime polymorphism**
+
+=> ***Compiler relies on the data type of variable, whereas runtime relies on the actual object.***
diff --git a/Academy DSA Typed Notes/Advanced/DSA Queues Implementation & Problems.md b/Academy DSA Typed Notes/Advanced/DSA Queues Implementation & Problems.md
new file mode 100644
index 0000000..c88a699
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Queues Implementation & Problems.md
@@ -0,0 +1,500 @@
+# Queues: Implementation & Problems
+
+---
+## Queue
+
+A queue represents a linear data structure where items are added at one end and removed from the other end. It follows the "First-In-First-Out" (FIFO) principle, meaning that the item that has been inserted first in queue will be the first one to be removed. To illustrate this concept, let's use a ticket counter as an example.
+
+**Example: Ticket Counter Queue**
+
+Imagine you're at a ticket counter for a popular event, and there are several people waiting in line to purchase tickets. This line of people forms a queue, and the first person who has come in this line will get the ticket first.
+
+
+So we can see that at first, we have `Hello` as output, and in the last statement, we get `Bye` as output.
+
+Now there are some points that you have to understand:
+
+* The method that is executed is of the data type that is **actually** present at the time of code and **not the type of variable**.
+* Do we know the exact code that is about to run in compile time?
+ * No, and that's why it's called **RunTime polymorphism**
+
+=> ***Compiler relies on the data type of variable, whereas runtime relies on the actual object.***
diff --git a/Academy DSA Typed Notes/Advanced/DSA Queues Implementation & Problems.md b/Academy DSA Typed Notes/Advanced/DSA Queues Implementation & Problems.md
new file mode 100644
index 0000000..c88a699
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Queues Implementation & Problems.md
@@ -0,0 +1,500 @@
+# Queues: Implementation & Problems
+
+---
+## Queue
+
+A queue represents a linear data structure where items are added at one end and removed from the other end. It follows the "First-In-First-Out" (FIFO) principle, meaning that the item that has been inserted first in queue will be the first one to be removed. To illustrate this concept, let's use a ticket counter as an example.
+
+**Example: Ticket Counter Queue**
+
+Imagine you're at a ticket counter for a popular event, and there are several people waiting in line to purchase tickets. This line of people forms a queue, and the first person who has come in this line will get the ticket first.
+
+ +
+
+Common operations in a queue include:
+
+1. **Enqueue**:
+
+
+Common operations in a queue include:
+
+1. **Enqueue**:This operation adds an element to the back (or rear) of the queue. It is also called "push" in some contexts. +2. **Dequeue**:
This operation removes and returns the element from the front of the queue. It is also called "pop" in some contexts. +3. **Peek or Front**:
This operation allows you to look at the element at the front of the queue without removing it. It is useful for inspecting the next item to be processed. +4. **IsEmpty**:
This operation checks if the queue is empty. If it's empty, it means there are no elements in the queue. +5. **Size or Length**:
This operation returns the number of elements currently in the queue. It provides the count of items in the queue. + +**Q. Can a stack or queue have a limit of elements it can have, and then we can use isFull()?** + +**Sol.** Yes, both stacks and queues can have a limit on the number of elements they can hold, and you can use an "isFull()" method to check if they have reached their capacity. This concept is commonly referred to as a "bounded" stack or queue. + + +--- + Implementaion of queue +description: Discussion about the various concepts related to implementaion of queue in detail. +duration: 2100 +card_type: cue_card +--- + +### Implementaion of Queue +Here's how you can implement a queue using a dynamic array along with pseudocode for the `enqueue`, `dequeue`, and `isEmpty` operations: + +```sql +Queue using Dynamic Array: +- Initialize an empty dynamic array (e.g., ArrayList or Python list) to store the elements. +- Initialize two pointers: 'front' and 'rear'. Initially, both are set to -1. + +Pseudocode for Enqueue (Add an element to the rear of the queue): +enqueue(element): + if rear is -1: + # Empty queue, set both front and rear to 0 + set front and rear to 0 + else if rear is at the end of the array: + # Check if there is space for expansion + if front > 0: + # Move elements to the beginning of the array + for i from front to rear: + array[i - front] = array[i] + set rear to (rear - front) + set front to 0 + else: + # If no space, resize the array by creating a new larger array + new_size = current_array_size * 2 # You can choose your resizing strategy + create a new array of size new_size + copy elements from the current array to the new array + set array to new_array + set rear to (rear - front) + set front to 0 + + + array[rear] = element + increment rear by 1 + +Pseudocode for Dequeue (Remove an element from the front of the queue): +dequeue(): + if front is -1: + # Empty queue, nothing to dequeue + return "Queue is empty" + else: + element = array[front] + increment front by 1 + if front > rear: + # Reset front and rear to -1 if the queue is empty + set front and rear to -1 + return element + +Pseudocode for isEmpty (Check if the queue is empty): +isEmpty(): + if front is -1: + return true + else: + return false +``` + +This pseudocode provides a basic implementation of a queue using a dynamic array. It handles the enqueue and dequeue operations efficiently by resizing the array when necessary to accommodate more elements. The `isEmpty` function checks if the queue is empty by examining the state of the `front` pointer. + +### Implementation of Queues using linkedlist + +1. **Insert at Head (prepend):** + - **Time Complexity:** O(1) + - **Explanation:** Inserting a node at the head of a singly linked list involves creating a new node, setting its `next` pointer to the current head, and updating the head pointer to the new node. This operation takes constant time because it doesn't depend on the size of the list. + +2. **Insert at Tail (append):** + - **Time Complexity:** O(n) + - **Explanation:** To insert a node at the tail of a singly linked list, you typically need to traverse the entire list to find the current tail node. This operation takes linear time since you have to visit each node in the list to reach the end. + +3. **Delete at Head:** + - **Time Complexity:** O(1) + - **Explanation:** Deleting a node at the head of a singly linked list is a constant-time operation. You simply update the head pointer to point to the next node in the list. + +4. **Delete at Tail:** + - **Time Complexity:** O(n) + - **Explanation:** Deleting a node at the tail of a singly linked list also requires traversing the entire list to find the current tail node. This operation takes linear time since you have to reach the end of the list to perform the deletion. + + +Queue functionality can be achieved by using two of the methods mentioned: + +1. **Insertion at Head and Deletion at tail:**
This approach can be used to provide the functionality of queue.Elements are inserted at the head (enqueue operation)with TC O(1) and removed from the tail with TC O(n)(dequeue operation). This ensures that the first element added to the queue is the first one to be removed. + +2. **Insertion at Tail and Deletion at Head:**
This approach can also be used to create a queue using LinkedList.Elements are inserted at tail with TC O(n) and removed from the head with TC O(1). We can optimise the TC of insertion at tail to O(1) by maintaining a tail pointer and this is why we generally used this approach for queue creation through LinkedList. + + + +--- +### Question +What will be the state of the queue after these operations + +enqueue(3), enqueue(7), enqueue(12), dqueue(), dqueue(), enqueue(8), enqueue(3) + +**Choices** +- [x] 12, 8, 3 +- [ ] 3, 7, 12, 8 +- [ ] 3, 8, 3 +- [ ] 7, 12, 3 + + +**Explanation** + +Let's break down the sequence of queue operations: + +enqueue(3) : Queue becomes [3] +enqueue(7) : Queue becomes [3, 7] +enqueue(12) : Queue becomes [3, 7, 12] +dequeue() : Removes the element from the front, and the queue becomes [7, 12] +dequeue() : Removes the element from the front, and the queue becomes [12] +enqueue(8) : Queue becomes [12, 8] +enqueue(3) : Queue becomes [12, 8, 3] + +So, after these operations, the final state of the queue is [12, 8, 3] + + +--- +### Question +What will be the state of the queue after these operations + +enqueue(4), dqueue(), enqueue(9), enqueue(3), enqueue(7), enqueue(11), enqueue(20), dqueue() + + +**Choices** +- [ ] 4, 9, 3, 7 +- [x] 3, 7, 11, 20 +- [ ] 9, 3, 7, 11 +- [ ] 3, 7, 20 + + + +**Explanation** +Let's go through the sequence of queue operations: + +enqueue(4): Queue becomes [4] +dequeue(): Removes the element from the front, and the queue becomes empty. +enqueue(9): Queue becomes [9] +enqueue(3): Queue becomes [9, 3] +enqueue(7): Queue becomes [9, 3, 7] +enqueue(11): Queue becomes [9, 3, 7, 11] +enqueue(20): Queue becomes [9, 3, 7, 11, 20] +dequeue(): Removes the element from the front, and the queue becomes [3, 7, 11, 20] + +So, after these operations, the final state of the queue is [3, 7, 11, 20] + + + +--- +### Implementaion of queue using Stack + + +The explaination for implementing a queue using two stacks step by step: + +```cpp +class QueueUsingTwoStacks { +private: + std::stack
 +
+**Question Explanation**
+
+
+
+**Question Explanation**
+
+ +
+
+
+ +
+* As we can see in above example, we have to insert 1 and 2 in the queue.
+* The next numbers can be made using the previous digits by appending the combination of 1 and 2.
+* Like to get 11 we append 1 after 1, to get 12 we append 2 after 1.
+* Similarly, we can generate numbers 21 by appending 1 after 2, and to get the 22, we can append 2 to 2 and so on.
+* As we have to append and remove digits frequently so queue can help us here.
+
+
+---
+### Question
+What is the **5th** perfect number formed by the only digits 1 and 2.
+
+**Choices**
+- [ ] 11111
+- [ ] 22222
+- [x] 21
+- [ ] 12
+
+
+
+**Explanation:**
+
+
+
+* As we can see in above example, we have to insert 1 and 2 in the queue.
+* The next numbers can be made using the previous digits by appending the combination of 1 and 2.
+* Like to get 11 we append 1 after 1, to get 12 we append 2 after 1.
+* Similarly, we can generate numbers 21 by appending 1 after 2, and to get the 22, we can append 2 to 2 and so on.
+* As we have to append and remove digits frequently so queue can help us here.
+
+
+---
+### Question
+What is the **5th** perfect number formed by the only digits 1 and 2.
+
+**Choices**
+- [ ] 11111
+- [ ] 22222
+- [x] 21
+- [ ] 12
+
+
+
+**Explanation:**
+
+ +
+From the image, the 5th Perfect Number is **21**.
+
+---
+### Nth perfect number Solution
+
+#### Solution
+
+```javascript
+int solve(N) {
+ if (N <= 2) return N
+ // Queue ->q
+ q.enqueue(1) q.enqueue(2)
+ i = 3
+ while (i <= N) {
+ x = q.dequeue()
+ a = x * 10 + 1
+ b = x * 10 + 2 //a + 1
+ if (i == N) return a
+ if (i + 1 == N) return b
+ q.enqueue(a)
+ q.enqueue(b)
+ i = i + 2
+ }
+}
+```
+
+#### Dry Run
+
+To dry run the provided code for N = 10, we'll create a table to keep track of the values of `q` (the queue) and `i` at each step.
+
+```plaintext
+| N | q | i | |
+|:---:|:----:| --- |:-----------------:|
+| 10 | 1, 2 | 3 | // Initial values |
+
+// Loop starts
+| N | q | i |
+|-------|----------------|-----|
+| 10 | 2, 11, 12 | 3 |// Dequeue 1, enqueue 11 and 12
+| 10 | 11, 12,21,22 | 5 |// Dequeue 2, enqueue 21 and 22
+| 10 |12,21,22,111,112| 7 |// Dequeue 11, enqueue 111 and 112
+| 10 |21,22,111,112,121,122| 9 |// Dequeue 12, enqueue 121 and 122
+
+// Now Loop ends at N == 10 , and ans = 122
+
+```
+
+The function dequeues and enqueues values in the queue until `i` reaches `N`. When `i` equals `N`, it returns the current value of `a`. In this case, for `N = 10`, the function returns 112.
+
+
+#### Complexity
+**Time Complexity:** O(n)
+**Space Complexity:** O(n)
+
+---
+### Doubly Ended Queue
+
+
+A double-ended queue (deque) is a data structure that allows elements to be added or removed from both ends, making it versatile for various operations. A double-linked list is a common choice for implementing a deque because it provides efficient operations for adding and removing elements from both ends.
+
+Here are some basic operations that are possible with a doubly-ended queue implemented using a double-linked list:
+
+1. **Insertion at Front (push_front)**: Add an element to the front (head) of the deque.
+2. **Insertion at Back (push_back)**: Add an element to the back (tail) of the deque.
+3. **Removal from Front (pop_front)**: Remove and return the element from the front of the deque.
+4. **Removal from Back (pop_back)**: Remove and return the element from the back of the deque.
+5. **Front Element Access (front)**: Get the element at the front of the deque without removing it.
+6. **Back Element Access (back)**: Get the element at the back of the deque without removing it.
+
+A **double-linked list** is well-suited for implementing a **deque** because it allows for efficient insertions and removals at both ends. Each node in the linked list has pointers to the next and previous nodes, making it easy to manipulate the list in both directions.
+
+
+---
+### Problem 2 Sliding Window Maximum
+#### Problem Statement
+
+Given an integer array `A` and an window of size k find the max element.
+
+**Input**
+
+- An integer array `A` and integer `k` .
+
+**Output**
+
+- An integer representing the maximum length of a subarray of `A` in which the average of all elements is greater than or equal to `k`. If no such subarray exists, return 0.
+
+**Example**
+
+
+
+From the image, the 5th Perfect Number is **21**.
+
+---
+### Nth perfect number Solution
+
+#### Solution
+
+```javascript
+int solve(N) {
+ if (N <= 2) return N
+ // Queue ->q
+ q.enqueue(1) q.enqueue(2)
+ i = 3
+ while (i <= N) {
+ x = q.dequeue()
+ a = x * 10 + 1
+ b = x * 10 + 2 //a + 1
+ if (i == N) return a
+ if (i + 1 == N) return b
+ q.enqueue(a)
+ q.enqueue(b)
+ i = i + 2
+ }
+}
+```
+
+#### Dry Run
+
+To dry run the provided code for N = 10, we'll create a table to keep track of the values of `q` (the queue) and `i` at each step.
+
+```plaintext
+| N | q | i | |
+|:---:|:----:| --- |:-----------------:|
+| 10 | 1, 2 | 3 | // Initial values |
+
+// Loop starts
+| N | q | i |
+|-------|----------------|-----|
+| 10 | 2, 11, 12 | 3 |// Dequeue 1, enqueue 11 and 12
+| 10 | 11, 12,21,22 | 5 |// Dequeue 2, enqueue 21 and 22
+| 10 |12,21,22,111,112| 7 |// Dequeue 11, enqueue 111 and 112
+| 10 |21,22,111,112,121,122| 9 |// Dequeue 12, enqueue 121 and 122
+
+// Now Loop ends at N == 10 , and ans = 122
+
+```
+
+The function dequeues and enqueues values in the queue until `i` reaches `N`. When `i` equals `N`, it returns the current value of `a`. In this case, for `N = 10`, the function returns 112.
+
+
+#### Complexity
+**Time Complexity:** O(n)
+**Space Complexity:** O(n)
+
+---
+### Doubly Ended Queue
+
+
+A double-ended queue (deque) is a data structure that allows elements to be added or removed from both ends, making it versatile for various operations. A double-linked list is a common choice for implementing a deque because it provides efficient operations for adding and removing elements from both ends.
+
+Here are some basic operations that are possible with a doubly-ended queue implemented using a double-linked list:
+
+1. **Insertion at Front (push_front)**: Add an element to the front (head) of the deque.
+2. **Insertion at Back (push_back)**: Add an element to the back (tail) of the deque.
+3. **Removal from Front (pop_front)**: Remove and return the element from the front of the deque.
+4. **Removal from Back (pop_back)**: Remove and return the element from the back of the deque.
+5. **Front Element Access (front)**: Get the element at the front of the deque without removing it.
+6. **Back Element Access (back)**: Get the element at the back of the deque without removing it.
+
+A **double-linked list** is well-suited for implementing a **deque** because it allows for efficient insertions and removals at both ends. Each node in the linked list has pointers to the next and previous nodes, making it easy to manipulate the list in both directions.
+
+
+---
+### Problem 2 Sliding Window Maximum
+#### Problem Statement
+
+Given an integer array `A` and an window of size k find the max element.
+
+**Input**
+
+- An integer array `A` and integer `k` .
+
+**Output**
+
+- An integer representing the maximum length of a subarray of `A` in which the average of all elements is greater than or equal to `k`. If no such subarray exists, return 0.
+
+**Example**
+
+ +
+#### Question Explanation
+Find max elements in 4-element sliding windows of array A:
+- `[1, 8, 5, 6]` -> max: 8
+- `[8, 5, 6, 7]` -> max: 8
+- `[5, 6, 7, 4]` -> max: 7
+- `[6, 7, 4, 2]` -> max: 7
+- `[7, 4, 2, 0]` -> max: 7
+- `[4, 2, 0, 3]` -> max: 4
+Result: `[8, 8, 7, 7, 7, 4]`.
+
+1. Initialize an empty list `max_elements`.
+2. Iterate from index 0 to 3 (inclusive) to create windows of size 4.
+3. Find the maximum element in each window and append it to `max_elements`.
+4. Result: `[8, 8, 7, 7, 7, 4]`, representing max elements in each 4-element window in `A`.
+
+---
+### Question
+Given an integer array `A` and an window of size k find the max element.
+
+A = [1, 4, 3, 2, 5]
+k = 3
+
+**Choices**
+- [x] [4, 4, 5]
+- [ ] [5, 5, 5]
+- [ ] [1, 4, 3]
+- [ ] [5, 4, 3]
+
+
+**Explanation:**
+
+Maximum of [1, 4, 3] is 4
+Maximum of [4, 3, 2] is 4
+Maximum of [3, 2, 5] is 5
+
+So, `[4, 4, 5]` is the answer.
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Sliding Window Maximum Approaches
+
+#### Brute Force Approach
+
+Brute-force approach to find max element in a window of size `k` in array `A` involves iterating through windows, finding max within each, and storing results. Time complexity: **O(n * k)** and space complexity: **O(1)**.
+
+#### Dry Run using the Sliding Window Approach
+
+Array `A = [1, 8, 5, 6, 7, 4, 2, 0, 3]` and `k = 4`.
+
+
+
+#### Question Explanation
+Find max elements in 4-element sliding windows of array A:
+- `[1, 8, 5, 6]` -> max: 8
+- `[8, 5, 6, 7]` -> max: 8
+- `[5, 6, 7, 4]` -> max: 7
+- `[6, 7, 4, 2]` -> max: 7
+- `[7, 4, 2, 0]` -> max: 7
+- `[4, 2, 0, 3]` -> max: 4
+Result: `[8, 8, 7, 7, 7, 4]`.
+
+1. Initialize an empty list `max_elements`.
+2. Iterate from index 0 to 3 (inclusive) to create windows of size 4.
+3. Find the maximum element in each window and append it to `max_elements`.
+4. Result: `[8, 8, 7, 7, 7, 4]`, representing max elements in each 4-element window in `A`.
+
+---
+### Question
+Given an integer array `A` and an window of size k find the max element.
+
+A = [1, 4, 3, 2, 5]
+k = 3
+
+**Choices**
+- [x] [4, 4, 5]
+- [ ] [5, 5, 5]
+- [ ] [1, 4, 3]
+- [ ] [5, 4, 3]
+
+
+**Explanation:**
+
+Maximum of [1, 4, 3] is 4
+Maximum of [4, 3, 2] is 4
+Maximum of [3, 2, 5] is 5
+
+So, `[4, 4, 5]` is the answer.
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Sliding Window Maximum Approaches
+
+#### Brute Force Approach
+
+Brute-force approach to find max element in a window of size `k` in array `A` involves iterating through windows, finding max within each, and storing results. Time complexity: **O(n * k)** and space complexity: **O(1)**.
+
+#### Dry Run using the Sliding Window Approach
+
+Array `A = [1, 8, 5, 6, 7, 4, 2, 0, 3]` and `k = 4`.
+
+ +
+Let's dry run the code with the given example:
+
+Array `A = [1, 8, 5, 6, 7, 4, 2, 0, 3]` and `k = 4`.
+
+1. Initialize an empty queue `q`.
+2. Start iterating through the array elements.
+ - **For i = 0, A[i] = 1:**
+ - Queue `q` is empty, so nothing happens.
+ - Enqueue `i` at the rear of the queue. `q = [0]`.
+ - **For i = 1, A[i] = 8:**
+ - The front element of the queue is at index `0`, which is smaller than the current element and thus can't be the maximum for any window.
+ - Deque the element and Enqueue `i` at the rear of the queue. `q = [1]`.
+
+ - **For i = 2, A[i] = 5:**
+ - `q` is not empty, and `A[r]` (element at index `1`) is greater than `A[i]`, so we don't do anything.
+ - Enqueue `i` at the rear of the queue. `q = [2]`.
+
+ - **For i = 3, A[i] = 6:**
+ - `q` is not empty, and `A[r]` (element at index `2`) is smaller than `A[i]`, so we deque it, now 8 is greater than 6 so don't do anything.
+ - Enqueue `i` at the rear of the queue. `q = [3]`.
+
+ **After the first K insertions, the q = [8,6];
+Now the maximum of this window is present in the front so print it and slide the window.
+To slide the window, check if A[i - k] is present in front, if yes then dequeue it. Add the next element to slide the window**
+
+ - Continue this process for the remaining elements.
+
+3. The final output will be the maximum elements in each group of size `k`:
+
+ - For `k = 4`, the maximum elements are `[8, 8, 7, 7, 4, 2, 3]`.
+
+So, the dry run demonstrates how the code finds and prints the maximum elements in groups of size `k` as it iterates through the array.
+
+#### Pseudocode (Using Dequeue)
+
+```javascript
+function findMaximumInGroups(A, k):
+ Initialize an empty queue q
+ n = length(A) // Total number of elements in the array A
+
+ for i from 0 to k - 1:
+ while (!q.isEmpty() and A[i] >= A[q.rear()]):
+ q.dequeueRear() // Remove elements that are smaller than A[i]
+ q.enqueueRear(i) // Add the current element to the queue
+
+ print A[q.front()] // Print the maximum element in the current group
+
+ // Slide for next windows
+
+ for i from k to n - 1:
+ if (!q.isEmpty() and q.front() == i - k):
+ q.dequeueFront() // Remove elements that are outside the current window
+
+ while (!q.isEmpty() and A[i] >= A[q.rear()]):
+ q.dequeueRear() // Remove elements that are smaller than A[i]
+ q.enqueueRear(i) // Add the current element to the queue
+
+ print A[q.front()] // Print the maximum element in the last group
+
+# Example usage:
+A = [1, 8, 5, 6, 7, 4, 2, 0, 3]
+k = 4
+findMaximumInGroups(A, k)
+
+```
+
+#### Complexity
+**Time Complexity:** O(n)
+**Space Complexity:** O(n)
diff --git a/Academy DSA Typed Notes/Advanced/DSA Recursion 1.md b/Academy DSA Typed Notes/Advanced/DSA Recursion 1.md
new file mode 100644
index 0000000..ab20916
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Recursion 1.md
@@ -0,0 +1,374 @@
+# Recursion 1
+
+---
+## Introduction to Recursion
+
+### Definition
+1. See this video - [LINK](https://www.youtube.com/watch?v=-xMYvVr9fd4)
+2. Function calling itself.
+3. A problem is broke into smaller problem(subproblem) and the solution is generated using the subproblems.
+
+
+**Example**
+Here's an example of how recursion can be used to calculate the sum of the first **N** natural numbers:
+```cpp
+sum(N) = 1 + 2 + 3 + 4 + ..... + N-1 + N
+sum(N) = sum(N-1) + N
+```
+Here, **sum(N-1)** is smaller instance of same problem that is **sum(N)**.
+sum(N-1) is known as a subproblem.
+
+### How to write a recursive code?
+We can solve any recursive problem using below magic steps:
+
+1. **Assumptions:** Decide what the function does for the given problem.
+2. **Main logic:** Break the problem down into smaller subproblems to solve the assumption.
+3. **Base case:** Identify the inputs for which we need to stop the recursion.
+
+---
+## Function Call Tracing
+
+* Function call tracing involves tracing the sequence of function calls that are made when a program is executed.
+* It involves keeping track of the function calls, their arguments, and the return values in order to understand the flow of the program and how the functions are interacting with each other.
+
+### Example:
+We have the following code:
+```cpp
+int add(int x, int y) {
+ return x + y;
+}
+
+int mul(int x, int y, int z) {
+ return x * y * z;
+}
+
+int sub(int x, int y) {
+ return x - y;
+}
+
+void(int x) {
+ cout << x << endl;
+}
+
+int main() {
+ int x = 10;
+ int y = 20;
+ print(sub(mul(add(x, y), 30), 75));
+ return 0;
+}
+```
+Here are the steps involved in function call tracing of the above code:
+
+
+
+Let's dry run the code with the given example:
+
+Array `A = [1, 8, 5, 6, 7, 4, 2, 0, 3]` and `k = 4`.
+
+1. Initialize an empty queue `q`.
+2. Start iterating through the array elements.
+ - **For i = 0, A[i] = 1:**
+ - Queue `q` is empty, so nothing happens.
+ - Enqueue `i` at the rear of the queue. `q = [0]`.
+ - **For i = 1, A[i] = 8:**
+ - The front element of the queue is at index `0`, which is smaller than the current element and thus can't be the maximum for any window.
+ - Deque the element and Enqueue `i` at the rear of the queue. `q = [1]`.
+
+ - **For i = 2, A[i] = 5:**
+ - `q` is not empty, and `A[r]` (element at index `1`) is greater than `A[i]`, so we don't do anything.
+ - Enqueue `i` at the rear of the queue. `q = [2]`.
+
+ - **For i = 3, A[i] = 6:**
+ - `q` is not empty, and `A[r]` (element at index `2`) is smaller than `A[i]`, so we deque it, now 8 is greater than 6 so don't do anything.
+ - Enqueue `i` at the rear of the queue. `q = [3]`.
+
+ **After the first K insertions, the q = [8,6];
+Now the maximum of this window is present in the front so print it and slide the window.
+To slide the window, check if A[i - k] is present in front, if yes then dequeue it. Add the next element to slide the window**
+
+ - Continue this process for the remaining elements.
+
+3. The final output will be the maximum elements in each group of size `k`:
+
+ - For `k = 4`, the maximum elements are `[8, 8, 7, 7, 4, 2, 3]`.
+
+So, the dry run demonstrates how the code finds and prints the maximum elements in groups of size `k` as it iterates through the array.
+
+#### Pseudocode (Using Dequeue)
+
+```javascript
+function findMaximumInGroups(A, k):
+ Initialize an empty queue q
+ n = length(A) // Total number of elements in the array A
+
+ for i from 0 to k - 1:
+ while (!q.isEmpty() and A[i] >= A[q.rear()]):
+ q.dequeueRear() // Remove elements that are smaller than A[i]
+ q.enqueueRear(i) // Add the current element to the queue
+
+ print A[q.front()] // Print the maximum element in the current group
+
+ // Slide for next windows
+
+ for i from k to n - 1:
+ if (!q.isEmpty() and q.front() == i - k):
+ q.dequeueFront() // Remove elements that are outside the current window
+
+ while (!q.isEmpty() and A[i] >= A[q.rear()]):
+ q.dequeueRear() // Remove elements that are smaller than A[i]
+ q.enqueueRear(i) // Add the current element to the queue
+
+ print A[q.front()] // Print the maximum element in the last group
+
+# Example usage:
+A = [1, 8, 5, 6, 7, 4, 2, 0, 3]
+k = 4
+findMaximumInGroups(A, k)
+
+```
+
+#### Complexity
+**Time Complexity:** O(n)
+**Space Complexity:** O(n)
diff --git a/Academy DSA Typed Notes/Advanced/DSA Recursion 1.md b/Academy DSA Typed Notes/Advanced/DSA Recursion 1.md
new file mode 100644
index 0000000..ab20916
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Recursion 1.md
@@ -0,0 +1,374 @@
+# Recursion 1
+
+---
+## Introduction to Recursion
+
+### Definition
+1. See this video - [LINK](https://www.youtube.com/watch?v=-xMYvVr9fd4)
+2. Function calling itself.
+3. A problem is broke into smaller problem(subproblem) and the solution is generated using the subproblems.
+
+
+**Example**
+Here's an example of how recursion can be used to calculate the sum of the first **N** natural numbers:
+```cpp
+sum(N) = 1 + 2 + 3 + 4 + ..... + N-1 + N
+sum(N) = sum(N-1) + N
+```
+Here, **sum(N-1)** is smaller instance of same problem that is **sum(N)**.
+sum(N-1) is known as a subproblem.
+
+### How to write a recursive code?
+We can solve any recursive problem using below magic steps:
+
+1. **Assumptions:** Decide what the function does for the given problem.
+2. **Main logic:** Break the problem down into smaller subproblems to solve the assumption.
+3. **Base case:** Identify the inputs for which we need to stop the recursion.
+
+---
+## Function Call Tracing
+
+* Function call tracing involves tracing the sequence of function calls that are made when a program is executed.
+* It involves keeping track of the function calls, their arguments, and the return values in order to understand the flow of the program and how the functions are interacting with each other.
+
+### Example:
+We have the following code:
+```cpp
+int add(int x, int y) {
+ return x + y;
+}
+
+int mul(int x, int y, int z) {
+ return x * y * z;
+}
+
+int sub(int x, int y) {
+ return x - y;
+}
+
+void(int x) {
+ cout << x << endl;
+}
+
+int main() {
+ int x = 10;
+ int y = 20;
+ print(sub(mul(add(x, y), 30), 75));
+ return 0;
+}
+```
+Here are the steps involved in function call tracing of the above code:
+
+ +
+* We start with the call to **sub(mul(add(10, 20), 30), 75)**.
+* That called: **mul(add(10, 20), 30)**.
+* That called: **add(10, 20)**.
+* add will return **10+20 = 30** to **mul** function.
+* mul will return **30*30 = 900** to **sub** function.
+* sub will return **900-75 = 825** to print function.
+
+### Data structure involved in function calls
+* We need to store calling function so that we can come back to it once answer of the called function has been evaluated.
+* **Stack Data Structure** is used to store function calls, their arguments, and return values.
+* In recursion, stack is called "call stack" and is used by the program to keep track of function calls in progress.
+
+
+* We start with the call to **sub(mul(add(10, 20), 30), 75)**.
+* That called: **mul(add(10, 20), 30)**.
+* That called: **add(10, 20)**.
+* add will return **10+20 = 30** to **mul** function.
+* mul will return **30*30 = 900** to **sub** function.
+* sub will return **900-75 = 825** to print function.
+
+### Data structure involved in function calls
+* We need to store calling function so that we can come back to it once answer of the called function has been evaluated.
+* **Stack Data Structure** is used to store function calls, their arguments, and return values.
+* In recursion, stack is called "call stack" and is used by the program to keep track of function calls in progress.
+ +
+---
+### Problem 1 : Factorial of N
+Given a positive integer N, find the factorial of N.
+
+### Question
+If N = 5, find the factorial of N.
+
+**Choices**
+- [ ] 100
+- [x] 120
+- [ ] 150
+- [ ] 125
+
+**Solution**
+
+**Assumptions:** Create a function which -
+* takes an integer value `N` as parameter.
+* calculates and returns N!.
+* return type should be integer.
+
+**Main logic:**
+* The factorial of N is equal to N times the factorial of (N-1)
+* We made assumption that sum(N) calculates and return factorial of N natural number. Similarly, sum(N-1) shall calculate and return the factorial of N-1 natural number.
+`factorial(N) = N * factorial(N-1)`
+
+**Base case:** The base case is when N equals 0, i.e., `0! = 1`
+
+For example,
+When we perform, `factorial(N) = N * factorial(N-1)`, value of N keeps on decreasing by 1.
+`N -> (N-1) -> (N-2) ........ 2 -> 1`
+for N = 1 as well as 0, the factorial is 1.
+So, we can write base case for N = 0 which will also cover for N = 1.
+
+#### Pseudocode
+```cpp
+int factorial(int N) {
+ // base case
+ if (N == 0) {
+ return 1;
+ }
+ // recursive case
+ return N * factorial(N - 1);
+}
+```
+
+### Dry Run
+
+
+
+---
+### Problem 1 : Factorial of N
+Given a positive integer N, find the factorial of N.
+
+### Question
+If N = 5, find the factorial of N.
+
+**Choices**
+- [ ] 100
+- [x] 120
+- [ ] 150
+- [ ] 125
+
+**Solution**
+
+**Assumptions:** Create a function which -
+* takes an integer value `N` as parameter.
+* calculates and returns N!.
+* return type should be integer.
+
+**Main logic:**
+* The factorial of N is equal to N times the factorial of (N-1)
+* We made assumption that sum(N) calculates and return factorial of N natural number. Similarly, sum(N-1) shall calculate and return the factorial of N-1 natural number.
+`factorial(N) = N * factorial(N-1)`
+
+**Base case:** The base case is when N equals 0, i.e., `0! = 1`
+
+For example,
+When we perform, `factorial(N) = N * factorial(N-1)`, value of N keeps on decreasing by 1.
+`N -> (N-1) -> (N-2) ........ 2 -> 1`
+for N = 1 as well as 0, the factorial is 1.
+So, we can write base case for N = 0 which will also cover for N = 1.
+
+#### Pseudocode
+```cpp
+int factorial(int N) {
+ // base case
+ if (N == 0) {
+ return 1;
+ }
+ // recursive case
+ return N * factorial(N - 1);
+}
+```
+
+### Dry Run
+
+ +
+
+---
+### Problem 2 : Nth number in the Fibonacci Series
+
+The Fibonacci sequence is a series of numbers in which each number is the sum of the two preceding numbers.
+
+
+The sequence goes like this:
+| N | 0 | 1 | 2 | 3 | 4 | 5 |....|
+|---|---|---|---|---|---|---|---|
+| Fibonacci(N) | 0 | 1 | 1 | 2 | 3 | 5 |....|
+
+
+Given a positive integer N, write a function to compute the Nth number in the Fibonacci sequence using recursion.
+
+**Example**
+```cpp
+Input = 6
+Output = 8
+```
+**Explanation:**
+| N | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
+|---|---|---|---|---|---|---|---|
+| Fibonacci(N) | 0 | 1 | 1 | 2 | 3 | 5 | 8 |
+
+Fibonacci(6) = Fibonacci(5) + Fibonacci(4) = 3 + 5 = 8.
+
+---
+### Question
+If N = 7, find the Nth number in the fibonacci sequence.
+
+**Choices**
+- [ ] 8
+- [ ] 5
+- [x] 13
+- [ ] 10
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Nth number in the Fibonacci sequence Solution
+#### Solution
+**Assumptions:** Create a function which -
+* takes an integer value `N` as parameter.
+* calculates and returns Nth number in the fibonacci sequence.
+* return type should be integer.
+
+**Main logic:** Recursively compute the (N-1)th and (N-2)th numbers in the sequence and add them together to get the nth number.
+`fibonacci(N) = fibonacci(N - 1) + fibonacci(N - 2)`
+
+**Base case:** If N is 0 or 1, return the corresponding value in the Fibonacci sequence.
+
+* Since, according to the definition of fibonacci sequence, the smallest two possible values of N are `N = 1` & `N = 2`, therefore, stop recursion as soon as N becomes 0 or 1.
+
+#### Pseudocode
+```cpp
+int fibonacci(int N) {
+ // base case
+ if (N == 0 || N == 1) {
+ return N;
+ }
+
+ // recursive case
+ return fibonacci(N - 1) + fibonacci(N - 2);
+}
+
+```
+#### Function Call Tracing
+
+
+
+---
+### Problem 2 : Nth number in the Fibonacci Series
+
+The Fibonacci sequence is a series of numbers in which each number is the sum of the two preceding numbers.
+
+
+The sequence goes like this:
+| N | 0 | 1 | 2 | 3 | 4 | 5 |....|
+|---|---|---|---|---|---|---|---|
+| Fibonacci(N) | 0 | 1 | 1 | 2 | 3 | 5 |....|
+
+
+Given a positive integer N, write a function to compute the Nth number in the Fibonacci sequence using recursion.
+
+**Example**
+```cpp
+Input = 6
+Output = 8
+```
+**Explanation:**
+| N | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
+|---|---|---|---|---|---|---|---|
+| Fibonacci(N) | 0 | 1 | 1 | 2 | 3 | 5 | 8 |
+
+Fibonacci(6) = Fibonacci(5) + Fibonacci(4) = 3 + 5 = 8.
+
+---
+### Question
+If N = 7, find the Nth number in the fibonacci sequence.
+
+**Choices**
+- [ ] 8
+- [ ] 5
+- [x] 13
+- [ ] 10
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Nth number in the Fibonacci sequence Solution
+#### Solution
+**Assumptions:** Create a function which -
+* takes an integer value `N` as parameter.
+* calculates and returns Nth number in the fibonacci sequence.
+* return type should be integer.
+
+**Main logic:** Recursively compute the (N-1)th and (N-2)th numbers in the sequence and add them together to get the nth number.
+`fibonacci(N) = fibonacci(N - 1) + fibonacci(N - 2)`
+
+**Base case:** If N is 0 or 1, return the corresponding value in the Fibonacci sequence.
+
+* Since, according to the definition of fibonacci sequence, the smallest two possible values of N are `N = 1` & `N = 2`, therefore, stop recursion as soon as N becomes 0 or 1.
+
+#### Pseudocode
+```cpp
+int fibonacci(int N) {
+ // base case
+ if (N == 0 || N == 1) {
+ return N;
+ }
+
+ // recursive case
+ return fibonacci(N - 1) + fibonacci(N - 2);
+}
+
+```
+#### Function Call Tracing
+ +
+
+
+---
+### Time Complexity of Recursion - using Recurrence Relation
+
+**Factorial(N)**
+#### Pseudocode
+```cpp
+int factorial(int N) {
+ // base case
+ if (N == 0) {
+ return 1;
+ }
+ // recursive case
+ return N * factorial(N - 1);
+}
+```
+
+* Let's assume that time taken to calculate **factorial(n)** = **T(n)**.
+* **factorial(n)** depends on the time taken by **factorial(n-1)** and other than that, constant work is being performed.
+* Time taken by **factorial(n-1) = T(n-1) + O(1)**.
+* Therefore, for the sum of digits, the recursive relation will be defined as follows:
+
+#### Equation 1
+```
+T(n) = T(n-1) + 1
+```
+**1** is added because other than function calls, a constant amount of work is being done.
+
+Substituting the value of ```T(n-1) = T(n-2) + 1```
+
+#### Equation 2
+```
+T(n) = T(n-2) + 2
+```
+Substituting the value of ```T(n-2) = T(n-3) + 1```
+
+#### Equation 3
+```
+T(n) = T(n-3) + 3
+```
+Substituting the value of ```T(n-3) = T(n-4) + 1```
+#### Equation 4
+```
+T(n) = T(n-4) + 4
+```
+
+After say **k** iterations, we shall reach to the base step.
+The equation will be:
+#### Equation 5
+```
+T(n) = T(n-k) + k
+```
+
+The base case shall take constant time:
+
+```
+T(0) = O(1)
+```
+
+We shall substitute the value of **n - k = 0**
+
+```
+=> n - k = 0
+=> n = k
+```
+Put the above value in a generalized equation, we get
+```
+T(n) = T(0) + n
+T(n) = 1 + n
+T(n) = O(n)
+```
+Hence we can say that.
+```
+T(n) = O(n)
+```
+---
+### Time Complexity of Fibonacci
+
+#### Pseudocode
+```cpp
+Function fibonacci(int n) {
+ if (n == 0 || n == 1) return n;
+ return fibonacci(n - 1) + fibonacci(n - 2);
+}
+```
+Recurrence Relation is:
+```
+ T(n) = T(n-1) + T(n-2)
+```
+For easy calculation, we can write the recurrence relation as follows:
+```
+ T(n) = 2 * T(n-1)
+```
+It will evaluate to **O(2N)**
+>Note to Instructor: Please evaluate above recurrence relation in class.
+
+
+### Another definition of Time Complexity
+
+Time Complexity can also be defined as
+
+**Time taken in a single function call * Number of function calls**
+
+---
+### Question
+How many recursive calls in the factorial(6)?
+
+Choose the correct answer
+**Choices**
+- [ ] 0
+- [ ] 2
+- [x] 6
+- [ ] 10
+
+---
+### Space Complexity of Recursive Code
+
+
+The space complexity of recursion refers to the amount of memory required by a recursive algorithm as it executes. It is determined by the maximum amount of memory needed on the call stack at any given point during the recursion.
+
+### Space Complexity of factorial(N)
+Total N call will be stored in the stack.
+```
+factorial(1)
+factorial(2)
+---------------
+---------------
+---------------
+factorial(N-1)
+factorial(N)
+```
+
+Maximum stack space used is N, hence space is O(N)
+
+Hence, total O(N) space is required to execute all the recursive calls.
+
+### Space complexity of fibonacci(n)
+If the time complexity of our recursive Fibonacci is O(2^n), what’s the space complexity?
+
+***Tempted to say the same?***
+> NOTE to Instructor: Show it using a stack
+
+**SPACE COMPLEXITY** can also be calculated using **RECURSIVE TREE**
+
+
+
+
+
+
+---
+### Time Complexity of Recursion - using Recurrence Relation
+
+**Factorial(N)**
+#### Pseudocode
+```cpp
+int factorial(int N) {
+ // base case
+ if (N == 0) {
+ return 1;
+ }
+ // recursive case
+ return N * factorial(N - 1);
+}
+```
+
+* Let's assume that time taken to calculate **factorial(n)** = **T(n)**.
+* **factorial(n)** depends on the time taken by **factorial(n-1)** and other than that, constant work is being performed.
+* Time taken by **factorial(n-1) = T(n-1) + O(1)**.
+* Therefore, for the sum of digits, the recursive relation will be defined as follows:
+
+#### Equation 1
+```
+T(n) = T(n-1) + 1
+```
+**1** is added because other than function calls, a constant amount of work is being done.
+
+Substituting the value of ```T(n-1) = T(n-2) + 1```
+
+#### Equation 2
+```
+T(n) = T(n-2) + 2
+```
+Substituting the value of ```T(n-2) = T(n-3) + 1```
+
+#### Equation 3
+```
+T(n) = T(n-3) + 3
+```
+Substituting the value of ```T(n-3) = T(n-4) + 1```
+#### Equation 4
+```
+T(n) = T(n-4) + 4
+```
+
+After say **k** iterations, we shall reach to the base step.
+The equation will be:
+#### Equation 5
+```
+T(n) = T(n-k) + k
+```
+
+The base case shall take constant time:
+
+```
+T(0) = O(1)
+```
+
+We shall substitute the value of **n - k = 0**
+
+```
+=> n - k = 0
+=> n = k
+```
+Put the above value in a generalized equation, we get
+```
+T(n) = T(0) + n
+T(n) = 1 + n
+T(n) = O(n)
+```
+Hence we can say that.
+```
+T(n) = O(n)
+```
+---
+### Time Complexity of Fibonacci
+
+#### Pseudocode
+```cpp
+Function fibonacci(int n) {
+ if (n == 0 || n == 1) return n;
+ return fibonacci(n - 1) + fibonacci(n - 2);
+}
+```
+Recurrence Relation is:
+```
+ T(n) = T(n-1) + T(n-2)
+```
+For easy calculation, we can write the recurrence relation as follows:
+```
+ T(n) = 2 * T(n-1)
+```
+It will evaluate to **O(2N)**
+>Note to Instructor: Please evaluate above recurrence relation in class.
+
+
+### Another definition of Time Complexity
+
+Time Complexity can also be defined as
+
+**Time taken in a single function call * Number of function calls**
+
+---
+### Question
+How many recursive calls in the factorial(6)?
+
+Choose the correct answer
+**Choices**
+- [ ] 0
+- [ ] 2
+- [x] 6
+- [ ] 10
+
+---
+### Space Complexity of Recursive Code
+
+
+The space complexity of recursion refers to the amount of memory required by a recursive algorithm as it executes. It is determined by the maximum amount of memory needed on the call stack at any given point during the recursion.
+
+### Space Complexity of factorial(N)
+Total N call will be stored in the stack.
+```
+factorial(1)
+factorial(2)
+---------------
+---------------
+---------------
+factorial(N-1)
+factorial(N)
+```
+
+Maximum stack space used is N, hence space is O(N)
+
+Hence, total O(N) space is required to execute all the recursive calls.
+
+### Space complexity of fibonacci(n)
+If the time complexity of our recursive Fibonacci is O(2^n), what’s the space complexity?
+
+***Tempted to say the same?***
+> NOTE to Instructor: Show it using a stack
+
+**SPACE COMPLEXITY** can also be calculated using **RECURSIVE TREE**
+
+
+ +>Please Note: This tree is known as Recursive Tree.
+
+Space complexity is the amount of memory used by the algorithm.
+
+When a function is called, it is added to the stack.
+
+When a function returns, it is popped off the stack.
+
+We’re not adding all of the function calls to the stack at once.
+
+We only make n calls at any given time as we move up and down branches.
+
+We proceed branch by branch, making our function calls until our base case is met, then we return and make our calls down to the next branch.
+
+
+>Please Note: This tree is known as Recursive Tree.
+
+Space complexity is the amount of memory used by the algorithm.
+
+When a function is called, it is added to the stack.
+
+When a function returns, it is popped off the stack.
+
+We’re not adding all of the function calls to the stack at once.
+
+We only make n calls at any given time as we move up and down branches.
+
+We proceed branch by branch, making our function calls until our base case is met, then we return and make our calls down to the next branch.
+
+ +
+We can also define **Space Complexity** as **height of the Recursive Tree**.
+
+---
+### Question
+What is the height of tree for fibonacci(6) ?
+Choose the correct answer
+
+**Choices**
+- [ ] 0
+- [ ] 7
+- [x] 6
+- [ ] 8
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Recursion 2.md b/Academy DSA Typed Notes/Advanced/DSA Recursion 2.md
new file mode 100644
index 0000000..4bf0555
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Recursion 2.md
@@ -0,0 +1,547 @@
+# Recursion 2
+
+## Question
+What is the output of the following code for N = 3?
+```cpp
+void solve(int N){
+ if(N == 0)
+ return;
+ solve(N-1);
+ print(N);
+}
+```
+
+**Choices**
+
+- [x] 1 2 3
+- [ ] 0 1 2
+- [ ] 2 1 0
+- [ ] 3 2 1
+
+
+
+
+```cpp
+void solve(int N) {
+ if (N == 0)
+ return;
+ solve(N - 1);
+ print(N);
+}
+```
+N=3
+
+1. So first of all, solve(3) is called,
+1. Then solve(3) will first call for solve(2) as n!=0,
+1. Similarly, solve(2) calls for solve(1), and then solve(1) calls for solve(0).
+
+
+
+We can also define **Space Complexity** as **height of the Recursive Tree**.
+
+---
+### Question
+What is the height of tree for fibonacci(6) ?
+Choose the correct answer
+
+**Choices**
+- [ ] 0
+- [ ] 7
+- [x] 6
+- [ ] 8
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Recursion 2.md b/Academy DSA Typed Notes/Advanced/DSA Recursion 2.md
new file mode 100644
index 0000000..4bf0555
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Recursion 2.md
@@ -0,0 +1,547 @@
+# Recursion 2
+
+## Question
+What is the output of the following code for N = 3?
+```cpp
+void solve(int N){
+ if(N == 0)
+ return;
+ solve(N-1);
+ print(N);
+}
+```
+
+**Choices**
+
+- [x] 1 2 3
+- [ ] 0 1 2
+- [ ] 2 1 0
+- [ ] 3 2 1
+
+
+
+
+```cpp
+void solve(int N) {
+ if (N == 0)
+ return;
+ solve(N - 1);
+ print(N);
+}
+```
+N=3
+
+1. So first of all, solve(3) is called,
+1. Then solve(3) will first call for solve(2) as n!=0,
+1. Similarly, solve(2) calls for solve(1), and then solve(1) calls for solve(0).
+
+ +
+
+Now n==0 so return.
+
+Then solve(1) will print 1, then it will return, and after that solve(2) will print 2, in this way 1, 2, 3 will be printed as an output.
+
+
+
+
+---
+### Question
+What is the output of the following code for N = 3?
+```cpp
+void solve(int N){
+ if(N == 0)
+ return;
+ print(N);
+ solve(N-1);
+}
+```
+
+**Choices**
+
+- [ ] 1 2 3
+
+- [ ] 0 1 2
+
+- [ ] 2 1 0
+
+- [x] 3 2 1
+
+
+
+```cpp
+void solve(int N){
+ if(N == 0)
+ return;
+ print(N);
+ solve(N-1);
+}
+```
+N=3
+
+1. So first of all, solve(3) is called,
+1. Then solve(3) will first **print 3**, then call for solve(2) as n!=0,
+1. In this way solve(2) first **print 2**, then call for solve(1), and then solve(1) will **print 1**, then call for solve(0).
+
+
+
+
+Now n==0 so return.
+
+Then solve(1) will print 1, then it will return, and after that solve(2) will print 2, in this way 1, 2, 3 will be printed as an output.
+
+
+
+
+---
+### Question
+What is the output of the following code for N = 3?
+```cpp
+void solve(int N){
+ if(N == 0)
+ return;
+ print(N);
+ solve(N-1);
+}
+```
+
+**Choices**
+
+- [ ] 1 2 3
+
+- [ ] 0 1 2
+
+- [ ] 2 1 0
+
+- [x] 3 2 1
+
+
+
+```cpp
+void solve(int N){
+ if(N == 0)
+ return;
+ print(N);
+ solve(N-1);
+}
+```
+N=3
+
+1. So first of all, solve(3) is called,
+1. Then solve(3) will first **print 3**, then call for solve(2) as n!=0,
+1. In this way solve(2) first **print 2**, then call for solve(1), and then solve(1) will **print 1**, then call for solve(0).
+
+ +
+
+Now n==0 so return.
+
+Then solve(1) will return, after that solve(2) will return.
+In this way 3, 2, 1 will be printed as an output.
+
+
+
+
+---
+### Question
+What is the output of the following code for N = -3?
+```cpp
+void solve(int N){
+ if(N == 0)
+ return;
+ print(N);
+ solve(N-1);
+}
+```
+
+**Choices**
+
+- [ ] -3 -2 -1
+
+- [ ] 3 2 1
+
+- [x] Error; Stack Overflow
+
+- [ ] 1 2 3
+
+
+
+```cpp
+void solve(int N){
+ if(N == 0)
+ return;
+ print(N);
+ solve(N-1);
+}
+```
+`N = -3`
+
+
+In this question we will never reach 0, that's why we are getting stack overflow.
+At first solve(-3) is called, then it will print -3
+call for solve(-4), then it will print -4
+call for solve(-5), in this way, it will keep making calls infinitely, as we will not reach zero, hence stack overflow error occurs.
+
+---
+## Problem 1 Power Function
+**Problem Statement**
+
+Given two integers **a** and **n**, find **an** using recursion.
+
+**Input**
+```
+a = 2
+n = 3
+```
+**Output**
+```
+8
+```
+**Explanation**
+23 i.e, 2 * 2 * 2 = 8.
+
+:::warning
+Please take some time to think about the recursive approach on your own before reading further.....
+:::
+
+#### Brute Force Approach
+The above problem can be redefined as:
+```
+a ^ n = a * a * a......* a (n times).
+```
+The problem can be broken into subproblem as:
+```
+a ^ n = a ^ (n-1) * a
+```
+So we can say that pow(a,n) is equivalent to
+```
+pow(a,n) = pow(a,n-1) * a
+```
+Here, pow(a,n) is the defined as `a^n`.
+We have seen how the problem is broken into subproblems. Hence, it can be solved using recursion.
+Below is the algorithm:
+* Assumption step:
+ * Define a recursive function pow(a,n).
+* Main Logic:
+ * Define a recursive case: if **n** > 0, then calculate the pow(a,n-1).
+ * Return a * pow(a,n-1).
+* Base Case:
+ * Base condition: if **n** = 0, then return 1.
+
+#### Pseudocode
+```cpp
+function pow(int a, int n) {
+ if (n == 0) return 1;
+ return a * pow(a, n - 1);
+}
+```
+
+#### Complexity
+We shall calculate Time Complexity at the end.
+
+---
+### Power Function Optimized Approach 1
+We can also divide pow(a, n) as follows:
+if **n** is even:
+```
+pow(a,n) = pow(a,n/2) * pow(a,n/2)
+```
+if **n** is odd:
+```
+pow(a,n) = pow(a,n/2) * pow(a,n/2) * a
+```
+#### Recursion Steps:
+* Assumption Step:
+ * Define a recursive function pow(a,n).
+* Main Logic:
+ * if n is odd, then return pow(a,n/2) * pow(a,n/2) * a.
+ * else return pow(a,n/2) * p(a,n/2).
+* Base Condition:
+ * if **n** is equal to 0, then return 1.
+
+#### Pseudocode
+```cpp
+Function pow(int a, int n) {
+ if (n == 0) return 1;
+
+ if (n % 2 == 0) {
+ return pow(a, n / 2) * pow(a, n / 2);
+ } else {
+ return pow(a, n / 2) * pow(a, n / 2) * a;
+ }
+}
+```
+The above function will have more time complexity due to calling the same function twice. We will see it while calculating Time Compleixity.
+
+---
+### Time Complexity of Power Function
+
+#### Pseudocode
+```cpp
+Function pow(int a, int n) {
+ if (n == 0) return 1;
+
+ if (n % 2 == 0) {
+ return pow(a, n / 2) * pow(a, n / 2);
+ } else {
+ return pow(a, n / 2) * pow(a, n / 2) * a;
+ }
+}
+```
+
+Let Time taken to calculate pow(a,n) = f(n).
+```
+T(n) = 2 * T(n/2) + 1
+```
+
+Substituting the value of T(n/2) = 2 * T(n/4) + 1
+```
+T(n) = 2 * [2 * T(n/4) + 1] + 1
+ = 4 * T(n/4) + 3
+ = 2^2 * T(n/2^2) + (2^2 - 1)
+```
+
+Substituting the value of T(n/4) = 2 * T(n/8) + 1
+```
+T(n) = 4 * [2 * T(n/8) + 1] + 3
+ = 8 * T(n/8) + 7
+ = 2^3 * T(n/2^3) + (2^3 - 1)
+```
+Substituting the value of T(n/8) = 2 * T(n/16) + 1
+```
+T(n) = 8 * [ 2 * T(n/16) + 1] + 7
+ = 16 * T(n/16) + 15
+ = 2^4 * T(n/2^4) + (2^4 - 1)
+```
+After, say, **k** iterations, we shall reach the base step.
+The equation will be:
+```
+T(n) = 2^k * T(n/2^k) + (2^k - 1)
+```
+The base case shall take contant time:
+
+```
+T(0) = O(1) or T(1) will also be constant
+```
+
+```
+n/(2 ^ k) = 1
+n = 2^k
+k = log2(n)
+```
+Hence we can say that
+```
+T(n) = n * T(1) + (n - 1)
+ = O(n)
+```
+
+Let's see time complexity of the optimised pow function.
+
+
+---
+### Power Function Optimized Approach - Fast Power
+
+In above approach, we are calling function **pow(a, n/2)** twice. Rather, we can just call it once and use the result twice.
+Below is the algorithm:
+* Assumption Step:
+ * Define a recursive function **pow(a,n)**.
+* Main Logic:
+ * Calculate **pow(a,n/2)** and store it in a variable **p**.
+ * if n is odd, then return **p * p * a**.
+ * else return **p * p**.
+* Base Condition:
+ * if **n = 0**, then return **1**.
+
+#### Pseudocode
+```cpp
+Function pow(int a, int n) {
+ if (n == 0) return 1;
+
+ int p = pow(a, n / 2);
+
+ if (n % 2 == 0) {
+ return p * p;
+ } else {
+ return p * p * a;
+ }
+}
+```
+> Note: The above function is known as Fast Power or Fast Exponentiation.
+
+---
+### Time Complexity of Fast Power
+
+#### Pseudocode
+```cpp
+Function pow(int a, int n) {
+ if (n == 0) return 1;
+
+ long p = pow(a, n / 2);
+
+ if (n % 2 == 0) {
+ return p * p;
+ } else {
+ return p * p * a;
+ }
+}
+```
+Let time taken to calculate pow(a,n) = f(n).
+Recurrence Relation is:
+```
+T(n) = T(n/2) + 1
+```
+
+Substituting the value of T(n/2) = T(n/4) + 1
+```
+T(n) = [T(n/4) + 1] + 1
+ = T(n/4) + 2
+```
+
+Substituting the value of T(n/4) = T(n/8) + 1
+```
+T(n) = [T(n/8) + 1] + 2
+ = T(n/8) + 3
+```
+Substituting the value of T(n/8) = T(n/16) + 1
+```
+T(n) = [T(n/16) + 1] + 3
+ = T(n/16) + 4
+```
+After say **k** iterations, we shall reach to the base step.
+The equation will be:
+```
+T(n) = T(n/2^k) + k
+```
+Base case shall take constant time:
+
+```
+T(0) = O(1) or T(1) will also be constant
+```
+
+```
+n/(2 ^ k) = 1
+n = 2^k
+k = log2(n)
+```
+Hence we can say that
+```
+T(n) = T(1) + log2(n)
+ = O(log2(n))
+```
+
+---
+### Question
+How many recursive call in the FAST pow(2,5)?
+
+Choose the correct answer
+
+**Choices**
+- [ ] 0
+- [ ] 2
+- [x] 4
+- [ ] 5
+
+
+
+This is ~ log N calls.
+Therefore, time complexity of sum of digits = O(log N) * 1 = O(log N)
+
+
+---
+### Space Complexity of pow(a,n)
+
+There are total **log2(N)** recursive calls as shown below:
+```
+pow(a,0)
+pow(a,1)
+pow(a,2)
+pow(a,4)
+---------------
+---------------
+---------------
+sumofdigits(a,N/2)
+sumofdigits(a,N)
+```
+Hence, the total O(log2(N)) space required to execute all the recursive calls.
+
+---
+### Problem 2 Tower of Hanoi
+There are n disks placed on tower A of different sizes.
+
+**Goal**
+Move all disks from tower A to C using tower B if needed.
+
+**Constraint**
+- Only 1 disk can be moved at a time.
+- Larger disk can not be placed on a small disk at any step.
+
+Print the movement of disks from A to C in minimum steps.
+
+**Example 1**
+
+**Input:** N = 1
+
+
+
+
+Now n==0 so return.
+
+Then solve(1) will return, after that solve(2) will return.
+In this way 3, 2, 1 will be printed as an output.
+
+
+
+
+---
+### Question
+What is the output of the following code for N = -3?
+```cpp
+void solve(int N){
+ if(N == 0)
+ return;
+ print(N);
+ solve(N-1);
+}
+```
+
+**Choices**
+
+- [ ] -3 -2 -1
+
+- [ ] 3 2 1
+
+- [x] Error; Stack Overflow
+
+- [ ] 1 2 3
+
+
+
+```cpp
+void solve(int N){
+ if(N == 0)
+ return;
+ print(N);
+ solve(N-1);
+}
+```
+`N = -3`
+
+
+In this question we will never reach 0, that's why we are getting stack overflow.
+At first solve(-3) is called, then it will print -3
+call for solve(-4), then it will print -4
+call for solve(-5), in this way, it will keep making calls infinitely, as we will not reach zero, hence stack overflow error occurs.
+
+---
+## Problem 1 Power Function
+**Problem Statement**
+
+Given two integers **a** and **n**, find **an** using recursion.
+
+**Input**
+```
+a = 2
+n = 3
+```
+**Output**
+```
+8
+```
+**Explanation**
+23 i.e, 2 * 2 * 2 = 8.
+
+:::warning
+Please take some time to think about the recursive approach on your own before reading further.....
+:::
+
+#### Brute Force Approach
+The above problem can be redefined as:
+```
+a ^ n = a * a * a......* a (n times).
+```
+The problem can be broken into subproblem as:
+```
+a ^ n = a ^ (n-1) * a
+```
+So we can say that pow(a,n) is equivalent to
+```
+pow(a,n) = pow(a,n-1) * a
+```
+Here, pow(a,n) is the defined as `a^n`.
+We have seen how the problem is broken into subproblems. Hence, it can be solved using recursion.
+Below is the algorithm:
+* Assumption step:
+ * Define a recursive function pow(a,n).
+* Main Logic:
+ * Define a recursive case: if **n** > 0, then calculate the pow(a,n-1).
+ * Return a * pow(a,n-1).
+* Base Case:
+ * Base condition: if **n** = 0, then return 1.
+
+#### Pseudocode
+```cpp
+function pow(int a, int n) {
+ if (n == 0) return 1;
+ return a * pow(a, n - 1);
+}
+```
+
+#### Complexity
+We shall calculate Time Complexity at the end.
+
+---
+### Power Function Optimized Approach 1
+We can also divide pow(a, n) as follows:
+if **n** is even:
+```
+pow(a,n) = pow(a,n/2) * pow(a,n/2)
+```
+if **n** is odd:
+```
+pow(a,n) = pow(a,n/2) * pow(a,n/2) * a
+```
+#### Recursion Steps:
+* Assumption Step:
+ * Define a recursive function pow(a,n).
+* Main Logic:
+ * if n is odd, then return pow(a,n/2) * pow(a,n/2) * a.
+ * else return pow(a,n/2) * p(a,n/2).
+* Base Condition:
+ * if **n** is equal to 0, then return 1.
+
+#### Pseudocode
+```cpp
+Function pow(int a, int n) {
+ if (n == 0) return 1;
+
+ if (n % 2 == 0) {
+ return pow(a, n / 2) * pow(a, n / 2);
+ } else {
+ return pow(a, n / 2) * pow(a, n / 2) * a;
+ }
+}
+```
+The above function will have more time complexity due to calling the same function twice. We will see it while calculating Time Compleixity.
+
+---
+### Time Complexity of Power Function
+
+#### Pseudocode
+```cpp
+Function pow(int a, int n) {
+ if (n == 0) return 1;
+
+ if (n % 2 == 0) {
+ return pow(a, n / 2) * pow(a, n / 2);
+ } else {
+ return pow(a, n / 2) * pow(a, n / 2) * a;
+ }
+}
+```
+
+Let Time taken to calculate pow(a,n) = f(n).
+```
+T(n) = 2 * T(n/2) + 1
+```
+
+Substituting the value of T(n/2) = 2 * T(n/4) + 1
+```
+T(n) = 2 * [2 * T(n/4) + 1] + 1
+ = 4 * T(n/4) + 3
+ = 2^2 * T(n/2^2) + (2^2 - 1)
+```
+
+Substituting the value of T(n/4) = 2 * T(n/8) + 1
+```
+T(n) = 4 * [2 * T(n/8) + 1] + 3
+ = 8 * T(n/8) + 7
+ = 2^3 * T(n/2^3) + (2^3 - 1)
+```
+Substituting the value of T(n/8) = 2 * T(n/16) + 1
+```
+T(n) = 8 * [ 2 * T(n/16) + 1] + 7
+ = 16 * T(n/16) + 15
+ = 2^4 * T(n/2^4) + (2^4 - 1)
+```
+After, say, **k** iterations, we shall reach the base step.
+The equation will be:
+```
+T(n) = 2^k * T(n/2^k) + (2^k - 1)
+```
+The base case shall take contant time:
+
+```
+T(0) = O(1) or T(1) will also be constant
+```
+
+```
+n/(2 ^ k) = 1
+n = 2^k
+k = log2(n)
+```
+Hence we can say that
+```
+T(n) = n * T(1) + (n - 1)
+ = O(n)
+```
+
+Let's see time complexity of the optimised pow function.
+
+
+---
+### Power Function Optimized Approach - Fast Power
+
+In above approach, we are calling function **pow(a, n/2)** twice. Rather, we can just call it once and use the result twice.
+Below is the algorithm:
+* Assumption Step:
+ * Define a recursive function **pow(a,n)**.
+* Main Logic:
+ * Calculate **pow(a,n/2)** and store it in a variable **p**.
+ * if n is odd, then return **p * p * a**.
+ * else return **p * p**.
+* Base Condition:
+ * if **n = 0**, then return **1**.
+
+#### Pseudocode
+```cpp
+Function pow(int a, int n) {
+ if (n == 0) return 1;
+
+ int p = pow(a, n / 2);
+
+ if (n % 2 == 0) {
+ return p * p;
+ } else {
+ return p * p * a;
+ }
+}
+```
+> Note: The above function is known as Fast Power or Fast Exponentiation.
+
+---
+### Time Complexity of Fast Power
+
+#### Pseudocode
+```cpp
+Function pow(int a, int n) {
+ if (n == 0) return 1;
+
+ long p = pow(a, n / 2);
+
+ if (n % 2 == 0) {
+ return p * p;
+ } else {
+ return p * p * a;
+ }
+}
+```
+Let time taken to calculate pow(a,n) = f(n).
+Recurrence Relation is:
+```
+T(n) = T(n/2) + 1
+```
+
+Substituting the value of T(n/2) = T(n/4) + 1
+```
+T(n) = [T(n/4) + 1] + 1
+ = T(n/4) + 2
+```
+
+Substituting the value of T(n/4) = T(n/8) + 1
+```
+T(n) = [T(n/8) + 1] + 2
+ = T(n/8) + 3
+```
+Substituting the value of T(n/8) = T(n/16) + 1
+```
+T(n) = [T(n/16) + 1] + 3
+ = T(n/16) + 4
+```
+After say **k** iterations, we shall reach to the base step.
+The equation will be:
+```
+T(n) = T(n/2^k) + k
+```
+Base case shall take constant time:
+
+```
+T(0) = O(1) or T(1) will also be constant
+```
+
+```
+n/(2 ^ k) = 1
+n = 2^k
+k = log2(n)
+```
+Hence we can say that
+```
+T(n) = T(1) + log2(n)
+ = O(log2(n))
+```
+
+---
+### Question
+How many recursive call in the FAST pow(2,5)?
+
+Choose the correct answer
+
+**Choices**
+- [ ] 0
+- [ ] 2
+- [x] 4
+- [ ] 5
+
+
+
+This is ~ log N calls.
+Therefore, time complexity of sum of digits = O(log N) * 1 = O(log N)
+
+
+---
+### Space Complexity of pow(a,n)
+
+There are total **log2(N)** recursive calls as shown below:
+```
+pow(a,0)
+pow(a,1)
+pow(a,2)
+pow(a,4)
+---------------
+---------------
+---------------
+sumofdigits(a,N/2)
+sumofdigits(a,N)
+```
+Hence, the total O(log2(N)) space required to execute all the recursive calls.
+
+---
+### Problem 2 Tower of Hanoi
+There are n disks placed on tower A of different sizes.
+
+**Goal**
+Move all disks from tower A to C using tower B if needed.
+
+**Constraint**
+- Only 1 disk can be moved at a time.
+- Larger disk can not be placed on a small disk at any step.
+
+Print the movement of disks from A to C in minimum steps.
+
+**Example 1**
+
+**Input:** N = 1
+
+ +
+
+**Explanation:**
+
+
+
+**Explanation:**
+ +
+**Output:**
+1: A -> C
+
+
+**Example 2**
+**Input:** N = 2
+
+
+**Output:**
+1: A -> C
+
+
+**Example 2**
+**Input:** N = 2
+ +
+**Explanation:**
+1: A -> B
+
+
+**Explanation:**
+1: A -> B
+ +
+2: A -> C
+
+
+2: A -> C
+ +
+
+1: B -> C
+
+
+
+1: B -> C
+ +
+**Output:**
+1: A -> B
+2: A -> C
+1: B -> C
+
+**Example 3**
+**Input:** N = 3
+
+
+**Output:**
+1: A -> B
+2: A -> C
+1: B -> C
+
+**Example 3**
+**Input:** N = 3
+ +
+**Explanation:**
+1: A -> C
+2: A -> B
+1: C -> B
+
+
+
+**Explanation:**
+1: A -> C
+2: A -> B
+1: C -> B
+
+ +
+3: A -> C
+
+
+3: A -> C
+ +
+1: B -> A
+2: B -> C
+1: A -> C
+
+
+
+1: B -> A
+2: B -> C
+1: A -> C
+
+ +
+**Output:**
+1: A -> C
+2: A -> B
+1: C -> B
+3: A -> C
+1: B -> A
+2: B -> C
+1: A -> C
+
+#### n disks
+
+
+
+**Output:**
+1: A -> C
+2: A -> B
+1: C -> B
+3: A -> C
+1: B -> A
+2: B -> C
+1: A -> C
+
+#### n disks
+
+ +
+**Step 1:**
+Move (n-1) disks from A to B
+
+
+**Step 1:**
+Move (n-1) disks from A to B
+ +
+**Step 2:**
+Move n disk to C
+
+
+**Step 2:**
+Move n disk to C
+ +
+**Step 3:**
+Move (n-1) disks from B to C
+
+
+
+**Step 3:**
+Move (n-1) disks from B to C
+
+ +
+#### Pseudocode
+```cpp
+ src temp dest
+void TOH(int n, A, B, C){
+ 1. if(n == 0)
+ return;
+ 2. TOH(n - 1, A, C, B); // move n-1 disks A->B
+ 3. print(n : A -> C); // moving n disk A->C
+ 4. TOH(n - 1, B, A, C); // move n-1 disks B->C
+}
+```
+
+#### Dry Run
+**n = 3**
+
+
+#### Pseudocode
+```cpp
+ src temp dest
+void TOH(int n, A, B, C){
+ 1. if(n == 0)
+ return;
+ 2. TOH(n - 1, A, C, B); // move n-1 disks A->B
+ 3. print(n : A -> C); // moving n disk A->C
+ 4. TOH(n - 1, B, A, C); // move n-1 disks B->C
+}
+```
+
+#### Dry Run
+**n = 3**
+ +
+
+
+ +
+**Output:**
+1: A -> C
+2: A -> B
+1: C -> B
+3: A -> C
+1: B -> A
+2: B -> C
+1: A -> C
+
+#### Time Complexity
+It can be observed in terms of number of steps taken for N
+
+
+**Output:**
+1: A -> C
+2: A -> B
+1: C -> B
+3: A -> C
+1: B -> A
+2: B -> C
+1: A -> C
+
+#### Time Complexity
+It can be observed in terms of number of steps taken for N
+ +
+
+#### Space Complexity
+
+
+
+#### Space Complexity
+ +
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Searching 1 Binary Search on Array.md b/Academy DSA Typed Notes/Advanced/DSA Searching 1 Binary Search on Array.md
new file mode 100644
index 0000000..e3887c9
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Searching 1 Binary Search on Array.md
@@ -0,0 +1,488 @@
+# Searching 1: Binary Search on Array
+
+---
+
+
+### Introduction to Searching - Story
+
+* Let us say you lost something
+* When you go to the police, you tell them what to search for—the target—and where to search—the search space.
+* It is easy to look for a word in the dictionary as compared to searching for a word in a book or newspaper. This is because along with the target element, we also have defined search space(alphabetical order).
+* In the Phone book as well, we have names sorted in the contacts list, so it's easier to find a person's number.
+* **Search space** - The area where we know the result exists and we search there only
+* **Target** - The item we are looking for
+* **Condition** - Some condition to discard some part of the search space repeatedly to make it smaller and finally reach the result.
+* **Binary Search** - divide the search space into two parts and repeatedly keep on neglecting one-half of the search space.
+
+---
+### Question
+
+In binary search, at each step, the search range is typically:
+
+**Choices**
+- [x] Halved
+- [ ] Tripled
+- [ ] Doubled
+- [ ] Reduced by one
+
+---
+## Binary Search
+
+
+### Binary Search Question
+Given a sorted array with distinct elements, search the index of an element **k**, if k is not present return -1.
+arr[] =
+
+| 3 | 6 | 9 | 12 | 14 | 19 | 20 | 23 | 25 | 27 |
+| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
+#### Brute Force Approach - Linear Search
+* We can traverse the array and compare each element with the target element. This is done until we find the target element or all the elements of the array are compared. This method is called linear search and the time complexity in the worst case is **O(N)** where **N** is the number of elements in the array.
+* We can perform the same operation with less number of comparisons and with better time complexity using Binary Search as the array is sorted.
+#### Binary Search Approach
+* Binary search has three elements,
+ * **Search space -** array
+ * **target -** we are given a target element to be found from the array
+ * **condition ->**
+ * array is sorted, say I am at some random position, if I compare the current element with the target element.
+ * If `current_element > target_element`, I can discard all the element appearing before current element and the target_element as they will always be smaller than current element.
+ * Similarly, if the `current_element < target_element`, the target element and the elements appearing after it can be discareded.
+ * We have all the three elements and thus, binary search can be easily applied to it.
+* Let us take the middle index.
+* if `arr[mid] == k`, i.e. we found the target, we return the index of the target.
+* if `arr[mid] < k` i.e. the target exists on the right side of the array so the left half is of no use and we can move to the right.
+* Similarly, if `arr[mid] > k` i.e. the target exists on the left, and the right half can be discarded.
+
+
+
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Searching 1 Binary Search on Array.md b/Academy DSA Typed Notes/Advanced/DSA Searching 1 Binary Search on Array.md
new file mode 100644
index 0000000..e3887c9
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Searching 1 Binary Search on Array.md
@@ -0,0 +1,488 @@
+# Searching 1: Binary Search on Array
+
+---
+
+
+### Introduction to Searching - Story
+
+* Let us say you lost something
+* When you go to the police, you tell them what to search for—the target—and where to search—the search space.
+* It is easy to look for a word in the dictionary as compared to searching for a word in a book or newspaper. This is because along with the target element, we also have defined search space(alphabetical order).
+* In the Phone book as well, we have names sorted in the contacts list, so it's easier to find a person's number.
+* **Search space** - The area where we know the result exists and we search there only
+* **Target** - The item we are looking for
+* **Condition** - Some condition to discard some part of the search space repeatedly to make it smaller and finally reach the result.
+* **Binary Search** - divide the search space into two parts and repeatedly keep on neglecting one-half of the search space.
+
+---
+### Question
+
+In binary search, at each step, the search range is typically:
+
+**Choices**
+- [x] Halved
+- [ ] Tripled
+- [ ] Doubled
+- [ ] Reduced by one
+
+---
+## Binary Search
+
+
+### Binary Search Question
+Given a sorted array with distinct elements, search the index of an element **k**, if k is not present return -1.
+arr[] =
+
+| 3 | 6 | 9 | 12 | 14 | 19 | 20 | 23 | 25 | 27 |
+| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
+#### Brute Force Approach - Linear Search
+* We can traverse the array and compare each element with the target element. This is done until we find the target element or all the elements of the array are compared. This method is called linear search and the time complexity in the worst case is **O(N)** where **N** is the number of elements in the array.
+* We can perform the same operation with less number of comparisons and with better time complexity using Binary Search as the array is sorted.
+#### Binary Search Approach
+* Binary search has three elements,
+ * **Search space -** array
+ * **target -** we are given a target element to be found from the array
+ * **condition ->**
+ * array is sorted, say I am at some random position, if I compare the current element with the target element.
+ * If `current_element > target_element`, I can discard all the element appearing before current element and the target_element as they will always be smaller than current element.
+ * Similarly, if the `current_element < target_element`, the target element and the elements appearing after it can be discareded.
+ * We have all the three elements and thus, binary search can be easily applied to it.
+* Let us take the middle index.
+* if `arr[mid] == k`, i.e. we found the target, we return the index of the target.
+* if `arr[mid] < k` i.e. the target exists on the right side of the array so the left half is of no use and we can move to the right.
+* Similarly, if `arr[mid] > k` i.e. the target exists on the left, and the right half can be discarded.
+
+ +
+#### Dry Run
+
+Let us dry run binary search for the array:
+
+| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |8 | 9 |
+| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
+| 3 | 6 | 9 | 12 | 14 | 19 | 20 | 23 | 25 | 27 |
+
+**First Iteration:**
+* low = 0, high = 9
+*
+
+#### Dry Run
+
+Let us dry run binary search for the array:
+
+| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |8 | 9 |
+| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
+| 3 | 6 | 9 | 12 | 14 | 19 | 20 | 23 | 25 | 27 |
+
+**First Iteration:**
+* low = 0, high = 9
+*  +* arr[4] (14) > target (12) (Since 14 already is larger and array is sorted, so all the elements to the right of mid will be even larger, hence, we should move left.)
+* go left -> high = mid - 1 = 3
+
+**Second Iteration:**
+* low = 0, high = 3
+* the mid =
+* arr[4] (14) > target (12) (Since 14 already is larger and array is sorted, so all the elements to the right of mid will be even larger, hence, we should move left.)
+* go left -> high = mid - 1 = 3
+
+**Second Iteration:**
+* low = 0, high = 3
+* the mid =  +* arr[1] (6) < target (12)
+* go right -> left = mid + 1 = 2
+
+**Third Iteration:**
+* low = 2, high = 3
+* the mid =
+* arr[1] (6) < target (12)
+* go right -> left = mid + 1 = 2
+
+**Third Iteration:**
+* low = 2, high = 3
+* the mid =  +* arr[2] (9) < target (12)
+* go right -> left = mid + 1 = 3
+
+**Fourth Iteration:**
+* low = high = 3 = mid
+* arr[3] (12) == target (12)
+* break;
+
+
+* arr[2] (9) < target (12)
+* go right -> left = mid + 1 = 3
+
+**Fourth Iteration:**
+* low = high = 3 = mid
+* arr[3] (12) == target (12)
+* break;
+
+ +
+* Dry run for target element not present, let's say **11**.
+
+
+
+#### Binary Search Pseudo Code
+```javascript
+int search(int arr[], int N, int k) {
+ lo = 0, hi = N - 1;
+ while (lo <= hi) {
+ mid = lo + (hi + lo) / 2;
+ if (arr[mid] == k) {
+ return mid;
+ } else if (arr[mid] < k) {
+ lo = mid + 1;
+ } else {
+ hi = mid - 1;
+ }
+ }
+ return -1;
+}
+```
+
+#### Complexity
+**Time Complexity:** O(log N)
+**Space Complexity:** O(1)
+
+
+---
+### Question
+
+If the element 'k' is found in a sorted array, what will be the time complexity of binary search?
+
+**Choices**
+- [ ] O(1)
+- [x] O(log n)
+- [ ] O(n)
+- [ ] O(n^2)
+
+---
+### Best Practices - Binary Search
+
+
+* Some write the formula of mid calculation as
+
+* Dry run for target element not present, let's say **11**.
+
+
+
+#### Binary Search Pseudo Code
+```javascript
+int search(int arr[], int N, int k) {
+ lo = 0, hi = N - 1;
+ while (lo <= hi) {
+ mid = lo + (hi + lo) / 2;
+ if (arr[mid] == k) {
+ return mid;
+ } else if (arr[mid] < k) {
+ lo = mid + 1;
+ } else {
+ hi = mid - 1;
+ }
+ }
+ return -1;
+}
+```
+
+#### Complexity
+**Time Complexity:** O(log N)
+**Space Complexity:** O(1)
+
+
+---
+### Question
+
+If the element 'k' is found in a sorted array, what will be the time complexity of binary search?
+
+**Choices**
+- [ ] O(1)
+- [x] O(log n)
+- [ ] O(n)
+- [ ] O(n^2)
+
+---
+### Best Practices - Binary Search
+
+
+* Some write the formula of mid calculation as  but it is incorrect, as in some cases it may lead to overflow.
+* e.g, Let us assume that maximum number stored by a particular data type is `100` (It's Integer.Max_Int but just to make maths easy, assuming its 100), and the number of elements in the array is `100` for which last index will be `99` for zero indexing and thus, is in the limit.
+* There is the posibility that the target element is at the position `98` and value of `low = 98` and `high = 99`. When we calculate `mid` for this scenario, the `high` and the `low` are in limits but while calculating the mid
but it is incorrect, as in some cases it may lead to overflow.
+* e.g, Let us assume that maximum number stored by a particular data type is `100` (It's Integer.Max_Int but just to make maths easy, assuming its 100), and the number of elements in the array is `100` for which last index will be `99` for zero indexing and thus, is in the limit.
+* There is the posibility that the target element is at the position `98` and value of `low = 98` and `high = 99`. When we calculate `mid` for this scenario, the `high` and the `low` are in limits but while calculating the mid  first the sum `197` will be calculated and stored. This will cause the overflow as the limit of the variable is `100` only(assumption).
+* This may result in incorrect or negative value.
+* Whereas, when we write
first the sum `197` will be calculated and stored. This will cause the overflow as the limit of the variable is `100` only(assumption).
+* This may result in incorrect or negative value.
+* Whereas, when we write  we will get
we will get  which even in the worst case be `99` and will not overflow.
+
+
+
which even in the worst case be `99` and will not overflow.
+
+
+ +
+---
+### Identify 2024's First Email
+
+
+All emails in your mailbox are sorted chronologically. Can you find the first mail that you received in 2024?
+
+---
+### Binary Search Problems - Find first occurrence
+
+Given a sorted array of N elements, find the first occurrence of the target element.
+arr[] =
+| -5 | -5 | -3 | 0 | 0 | 1 | 1 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 8 | 10 | 10 | 15 | 15 |
+| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
+
+For `5` first occurence is at index `7` so we have to return `7`.
+* Brute force approach is linear search.
+* Now the array is sorted so using binary search we can find at least one of the occurences of the given target element.
+* The challenge is to **find the first occurence**. What we know about the first occurence is that it is always going to be the current position or in the left.
+* Now in left, we can do linear search but in worst it will take about O(N) time complexity.
+* What we have got is the potential answer, it can or cannot be final anser.
+* We can store the current position in a variable, in case it is the first occurence. Next, we can apply binary search in the left side of the array.
+* The only change we are required to make is to not stop if we find the target element instead keep looking in the left side of the array until `low > high`.
+* If the `mid == target` store mid, go left.
+* else if `mid > target` go right.
+* else go left.
+
+
+
+
+
+---
+### Identify 2024's First Email
+
+
+All emails in your mailbox are sorted chronologically. Can you find the first mail that you received in 2024?
+
+---
+### Binary Search Problems - Find first occurrence
+
+Given a sorted array of N elements, find the first occurrence of the target element.
+arr[] =
+| -5 | -5 | -3 | 0 | 0 | 1 | 1 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 8 | 10 | 10 | 15 | 15 |
+| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
+
+For `5` first occurence is at index `7` so we have to return `7`.
+* Brute force approach is linear search.
+* Now the array is sorted so using binary search we can find at least one of the occurences of the given target element.
+* The challenge is to **find the first occurence**. What we know about the first occurence is that it is always going to be the current position or in the left.
+* Now in left, we can do linear search but in worst it will take about O(N) time complexity.
+* What we have got is the potential answer, it can or cannot be final anser.
+* We can store the current position in a variable, in case it is the first occurence. Next, we can apply binary search in the left side of the array.
+* The only change we are required to make is to not stop if we find the target element instead keep looking in the left side of the array until `low > high`.
+* If the `mid == target` store mid, go left.
+* else if `mid > target` go right.
+* else go left.
+
+
+
+ +
+
+#### Dry run for the example
+
+
+
+
+
+#### Dry run for the example
+
+
+ +
+
+
+| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
+| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
+| -5 | -5 | -3 | 0 | 0 | 1 | 1 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 8 | 10 | 10 | 15 | 15 |
+
+**First Iteration:**
+* low = 0, high = 18
+* the mid =
+
+
+
+| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
+| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
+| -5 | -5 | -3 | 0 | 0 | 1 | 1 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 8 | 10 | 10 | 15 | 15 |
+
+**First Iteration:**
+* low = 0, high = 18
+* the mid =  +* arr[9] (5) == target (5)
+* ans = 9
+* go left -> high = mid - 1 = 8
+
+**Second Iteration:**
+* low = 0, high = 8
+* the mid =
+* arr[9] (5) == target (5)
+* ans = 9
+* go left -> high = mid - 1 = 8
+
+**Second Iteration:**
+* low = 0, high = 8
+* the mid =  +* arr[4] (0) < target (5)
+* go right -> left = mid + 1 = 5
+
+**Third Iteration:**
+* low = 5, high = 8
+* the mid =
+* arr[4] (0) < target (5)
+* go right -> left = mid + 1 = 5
+
+**Third Iteration:**
+* low = 5, high = 8
+* the mid =  +* arr[6] (1) < target (5)
+* go right -> left = mid + 1 = 7
+
+**Fourth Iteration:**
+* low = 7, high = 8
+* the mid =
+* arr[6] (1) < target (5)
+* go right -> left = mid + 1 = 7
+
+**Fourth Iteration:**
+* low = 7, high = 8
+* the mid =  +* arr[7] (5) == target (5)
+* go left -> high = mid - 1 = 6
+* break;
+
+---
+### Question
+
+When searching for the first occurrence of an element in a sorted array, what should you do if the current element matches the target 'k'?
+
+**Choices**
+- [ ] Return the current index
+- [ ] Continue searching in the right subarray
+- [x] Continue searching in the left subarray
+- [ ] Stop searching immediately
+
+
+---
+### Question
+
+What is the time complexity of finding the first occurrence of an element in a sorted array using binary search?
+
+**Choices**
+- [x] O(log n)
+- [ ] O(n)
+- [ ] O(1)
+- [ ] O(n^2)
+
+
+---
+#### Complexity
+**Time Complexity:** O(logn) (Everytime you are discarding the search space by half).
+**Space Complexity:** O(1)
+
+#### Follow up question
+* Try for the last occurence
+
+
+
+---
+### Find the unique element
+
+**Question**
+Every element occurs twice except for 1, find the unique element.
+**Note:** Duplicate elements are adjacent to each other but the array is not sorted.
+
+**Example:**
+
+* arr[7] (5) == target (5)
+* go left -> high = mid - 1 = 6
+* break;
+
+---
+### Question
+
+When searching for the first occurrence of an element in a sorted array, what should you do if the current element matches the target 'k'?
+
+**Choices**
+- [ ] Return the current index
+- [ ] Continue searching in the right subarray
+- [x] Continue searching in the left subarray
+- [ ] Stop searching immediately
+
+
+---
+### Question
+
+What is the time complexity of finding the first occurrence of an element in a sorted array using binary search?
+
+**Choices**
+- [x] O(log n)
+- [ ] O(n)
+- [ ] O(1)
+- [ ] O(n^2)
+
+
+---
+#### Complexity
+**Time Complexity:** O(logn) (Everytime you are discarding the search space by half).
+**Space Complexity:** O(1)
+
+#### Follow up question
+* Try for the last occurence
+
+
+
+---
+### Find the unique element
+
+**Question**
+Every element occurs twice except for 1, find the unique element.
+**Note:** Duplicate elements are adjacent to each other but the array is not sorted.
+
+**Example:**
+ +
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Brute Force Approach
+* The brute force approach can be comparing A[i] with A[i+1]. If `(A[i]!=A[i+1])`, then `A[i]` is the unique element.
+
+#### Optimal Approach
+* Can we apply Binary Search ?
+ * Say we land at mid, how to know current element is the answer? => We can check element at its right and at its left. If both are different, then `mid` is the ans.
+ * If `A[mid]` is not the answer, then how to decide in which direction shall we move?
+ * For that, let's make some observation.
+ * We are given that only one element is unique, there are two occurences of remaining elements.
+ * **`Can you make some observation w.r.t first occurrences of elements before and after unique element ?`**
+ * Before unique element, first occurrences are at even index. After unique element, all first appear at odd indices.
+
+**Let us say the array is as follows:**
+
+| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10
+| -------- | -------- | -------- | -------- | -------- | -------- | ------- | -------- | -------- | -------- | -------- |
+7|7|6|6|3|8|8|1|1|9|9|
+
+* 3 is unique.
+* First occurrence of 7 and 6 is at index even and after 3, first occurrences of elements, 8, 1, 9 is at odd index.
+
+#### Steps for applying Binary Search
+* Land at mid, if `A[mid] != A[mid-1] && A[mid] != A[mid+1]`, then `A[mid]` is the answer.
+* NOTE: To avoid accessing invalid indices, above conditions shall be modified as follows-
+ * `mid == 0 || A[mid] != A[mid-1]`
+ * `mid == N-1 || A[mid] != A[mid+1]`
+* Else, we will check index of first occurrence of the element we landed on.
+ * If index is even, then unique element must be present on right.
+ * Else, on left.
+
+#### Dry Run for An Example
+
+| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
+| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
+| Elements | 3 | 3 | 1 | 1 | 8 | 8 | 10 | 10 | 19 | 6 | 6 | 2 | 2 | 4 | 4 |
+
+For the above array,
+**1st Iteration:**
+* `low = 0, high = 14`,
+* $mid = 0 + (14-0)/2 = 7$
+* It's not unique.
+* `arr[mid] == arr[mid - 1]` -> `mid - 1` is the first occurence.
+* `mid - 1 = 6` which is even -> go to right
+* `low = mid + 1`
+
+**2nd iteration:**
+* `low = 8, high = 14`
+* $mid = 8 + (14-8)/2 = 11$
+* It's not unique.
+* `mid - 1 = 10`
+* `arr[mid] != arr[mid - 1]`
+* `mid + 1 = 12`
+* `arr[mid] == arr[mid + 1]` -> mid is the first occurence.
+* `mid % 2 != 0` i.e. mid is odd and thus, left subarray has the unique element. We will move high to `mid - 1 = 10`.
+
+**3rd iteration:**
+* `low = 8, high = 10`
+* $mid = 8 + (10-8)/2 = 9$
+* Its not unique.
+* `mid - 1 = 8`
+* `arr[mid] != arr[mid - 1]`
+* `mid + 1 = 10`
+* `arr[mid] == arr[mid + 1]` -> mid is the first occurence.
+* `mid % 2 != 0` i.e. mid is odd and thus, left subarray has the unique element. We will move high to `mid - 1 = 8`.
+
+**4th iteration:**
+* `low = 8, high = 8`
+* `mid = (8 + (8 - 8) / 2) = 8`
+* `mid - 1 = 7`
+* `arr[mid] != arr[mid - 1]`
+* `mid + 1 = 9`
+* `arr[mid] != arr[mid + 1]` -> mid is the **unique element.** We will terminate the loop.
+
+
+#### Pseudo Code
+```cpp
+int findUnique(int arr[], int N) {
+
+ lo = 0, hi = N - 1;
+
+ // binary search
+ while (lo <= hi) {
+ mid = lo + (hi - lo) / 2;
+
+ if ((mid == 0 || arr[mid] != arr[mid - 1]) && (mid == N - 1 || arr[mid] != arr[mid + 1])) { //checking mid is unique
+ return A[mid];
+ } else if (mid == 0 || arr[mid] == arr[mid - 1]) { //at first occurrence
+ if (mid % 2 == 0) lo = mid + 2;
+ else hi = mid - 1;
+ } else { //at second occurrence
+ if (mid % 2 == 0) hi = mid - 2;
+ else lo = mid + 1;
+ }
+ }
+}
+```
+
+#### Complexities
+
+**Time Complexity:** O(log(N)
+**Space Complexity:** O(1)
+
+---
+### Increasing Decreasing Array
+
+Given an increasing decreasing array with distinct elements. Find max element.
+
+**Examples**
+
+arr[] = {1, 3, 5, 2}
+In the above array `5` is the max value.
+arr[] = {1, 3, 5, 10, 15, 12, 6}
+In the given example max element is `15`
+
+The increasing decreasing array will look something like this:
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Brute Force Approach
+* The brute force approach can be comparing A[i] with A[i+1]. If `(A[i]!=A[i+1])`, then `A[i]` is the unique element.
+
+#### Optimal Approach
+* Can we apply Binary Search ?
+ * Say we land at mid, how to know current element is the answer? => We can check element at its right and at its left. If both are different, then `mid` is the ans.
+ * If `A[mid]` is not the answer, then how to decide in which direction shall we move?
+ * For that, let's make some observation.
+ * We are given that only one element is unique, there are two occurences of remaining elements.
+ * **`Can you make some observation w.r.t first occurrences of elements before and after unique element ?`**
+ * Before unique element, first occurrences are at even index. After unique element, all first appear at odd indices.
+
+**Let us say the array is as follows:**
+
+| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10
+| -------- | -------- | -------- | -------- | -------- | -------- | ------- | -------- | -------- | -------- | -------- |
+7|7|6|6|3|8|8|1|1|9|9|
+
+* 3 is unique.
+* First occurrence of 7 and 6 is at index even and after 3, first occurrences of elements, 8, 1, 9 is at odd index.
+
+#### Steps for applying Binary Search
+* Land at mid, if `A[mid] != A[mid-1] && A[mid] != A[mid+1]`, then `A[mid]` is the answer.
+* NOTE: To avoid accessing invalid indices, above conditions shall be modified as follows-
+ * `mid == 0 || A[mid] != A[mid-1]`
+ * `mid == N-1 || A[mid] != A[mid+1]`
+* Else, we will check index of first occurrence of the element we landed on.
+ * If index is even, then unique element must be present on right.
+ * Else, on left.
+
+#### Dry Run for An Example
+
+| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
+| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
+| Elements | 3 | 3 | 1 | 1 | 8 | 8 | 10 | 10 | 19 | 6 | 6 | 2 | 2 | 4 | 4 |
+
+For the above array,
+**1st Iteration:**
+* `low = 0, high = 14`,
+* $mid = 0 + (14-0)/2 = 7$
+* It's not unique.
+* `arr[mid] == arr[mid - 1]` -> `mid - 1` is the first occurence.
+* `mid - 1 = 6` which is even -> go to right
+* `low = mid + 1`
+
+**2nd iteration:**
+* `low = 8, high = 14`
+* $mid = 8 + (14-8)/2 = 11$
+* It's not unique.
+* `mid - 1 = 10`
+* `arr[mid] != arr[mid - 1]`
+* `mid + 1 = 12`
+* `arr[mid] == arr[mid + 1]` -> mid is the first occurence.
+* `mid % 2 != 0` i.e. mid is odd and thus, left subarray has the unique element. We will move high to `mid - 1 = 10`.
+
+**3rd iteration:**
+* `low = 8, high = 10`
+* $mid = 8 + (10-8)/2 = 9$
+* Its not unique.
+* `mid - 1 = 8`
+* `arr[mid] != arr[mid - 1]`
+* `mid + 1 = 10`
+* `arr[mid] == arr[mid + 1]` -> mid is the first occurence.
+* `mid % 2 != 0` i.e. mid is odd and thus, left subarray has the unique element. We will move high to `mid - 1 = 8`.
+
+**4th iteration:**
+* `low = 8, high = 8`
+* `mid = (8 + (8 - 8) / 2) = 8`
+* `mid - 1 = 7`
+* `arr[mid] != arr[mid - 1]`
+* `mid + 1 = 9`
+* `arr[mid] != arr[mid + 1]` -> mid is the **unique element.** We will terminate the loop.
+
+
+#### Pseudo Code
+```cpp
+int findUnique(int arr[], int N) {
+
+ lo = 0, hi = N - 1;
+
+ // binary search
+ while (lo <= hi) {
+ mid = lo + (hi - lo) / 2;
+
+ if ((mid == 0 || arr[mid] != arr[mid - 1]) && (mid == N - 1 || arr[mid] != arr[mid + 1])) { //checking mid is unique
+ return A[mid];
+ } else if (mid == 0 || arr[mid] == arr[mid - 1]) { //at first occurrence
+ if (mid % 2 == 0) lo = mid + 2;
+ else hi = mid - 1;
+ } else { //at second occurrence
+ if (mid % 2 == 0) hi = mid - 2;
+ else lo = mid + 1;
+ }
+ }
+}
+```
+
+#### Complexities
+
+**Time Complexity:** O(log(N)
+**Space Complexity:** O(1)
+
+---
+### Increasing Decreasing Array
+
+Given an increasing decreasing array with distinct elements. Find max element.
+
+**Examples**
+
+arr[] = {1, 3, 5, 2}
+In the above array `5` is the max value.
+arr[] = {1, 3, 5, 10, 15, 12, 6}
+In the given example max element is `15`
+
+The increasing decreasing array will look something like this:
+ +
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Solution
+* Increasing decreasing arrays are the array that increases first and after reaching its peek it starts decreasing. We are supposed to find the peek or the max element of the array. The increasing side is sorted in ascending order and the decreasing side is sorted in descending order.
+* Brute force approach is a linear search with O(N) time complexity.
+* But as we see the elements are sorted in increasing and then decreasing order, so can we do better than O(N) time complexity?
+* Can we apply **Binary Search**? What do we need ?
+ * **Search space** -> array
+ * **target** -> peak element
+ * **Condition:** ->
+ * **Case 1**: if`(arr[mid] > arr[mid - 1] && arr[mid] < arr[mid + 1])` return mid;
+ * If immediate left and right are less than current element than we are at peek element.
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Solution
+* Increasing decreasing arrays are the array that increases first and after reaching its peek it starts decreasing. We are supposed to find the peek or the max element of the array. The increasing side is sorted in ascending order and the decreasing side is sorted in descending order.
+* Brute force approach is a linear search with O(N) time complexity.
+* But as we see the elements are sorted in increasing and then decreasing order, so can we do better than O(N) time complexity?
+* Can we apply **Binary Search**? What do we need ?
+ * **Search space** -> array
+ * **target** -> peak element
+ * **Condition:** ->
+ * **Case 1**: if`(arr[mid] > arr[mid - 1] && arr[mid] < arr[mid + 1])` return mid;
+ * If immediate left and right are less than current element than we are at peek element.
+ + * **Case 2**: if`(arr[mid] > arr[mid - 1] and arr[mid] < arr[mid + 1])` go right;
+ * Implies our mid is at the part of the array where it is still increasing. So the peek will be at the right side of the array.
+
+ * **Case 2**: if`(arr[mid] > arr[mid - 1] and arr[mid] < arr[mid + 1])` go right;
+ * Implies our mid is at the part of the array where it is still increasing. So the peek will be at the right side of the array.
+ + * **Case 3**: go left
+ * This infers that mid is at the decreasing side of the array and peek must be at left.
+
+ * **Case 3**: go left
+ * This infers that mid is at the decreasing side of the array and peek must be at left.
+ +
+#### Pseudocode
+
+
+#### Pseudocode
+ +
+ +
+
+---
+### Local Minima in an Array
+
+Given an array of N distinct elements, find any local minima in the array
+
+**Local Minima** - a no. which is smaller than its adjacent neighbors.
+
+**Examples**
+
+
+
+
+---
+### Local Minima in an Array
+
+Given an array of N distinct elements, find any local minima in the array
+
+**Local Minima** - a no. which is smaller than its adjacent neighbors.
+
+**Examples**
+
+ +
+
+
+* A = {**3**,6,1,**0**,9,15,**8**}
+ * Here, we have 3 local minima, `3`, `0`, and `8`.
+ * `3 < 6`, `0 < 1 && 0 < 9`, and `8 < 15`. All these are smaller than their left and right neighbours.
+
+* B = {21,20,19,17,15,9,**7**}
+ * All the numbers are in decreasing order, so we only have one local minima `7`.
+* C = {**5**,9,15,16,20,21}
+ * Similarly, all the numbers are strictly increasing so `5` is the only local minima in this example.
+* D = {**5**,8,12,**3**}
+ * Here, the series first increases and then decreases. So we have two local minima `5` and `3`. `5 < 8` and `3 < 12`.
+* This can have multiple local minima
+* We have to return any local minima
+
+#### Solution
+* **Case 1:** Current element is smaller than the next and the previous element returns the current element, since this is local minima.
+* **Case 2:** If the current element is greater than the previous element and less than the next element.
+
+
+
+
+
+* A = {**3**,6,1,**0**,9,15,**8**}
+ * Here, we have 3 local minima, `3`, `0`, and `8`.
+ * `3 < 6`, `0 < 1 && 0 < 9`, and `8 < 15`. All these are smaller than their left and right neighbours.
+
+* B = {21,20,19,17,15,9,**7**}
+ * All the numbers are in decreasing order, so we only have one local minima `7`.
+* C = {**5**,9,15,16,20,21}
+ * Similarly, all the numbers are strictly increasing so `5` is the only local minima in this example.
+* D = {**5**,8,12,**3**}
+ * Here, the series first increases and then decreases. So we have two local minima `5` and `3`. `5 < 8` and `3 < 12`.
+* This can have multiple local minima
+* We have to return any local minima
+
+#### Solution
+* **Case 1:** Current element is smaller than the next and the previous element returns the current element, since this is local minima.
+* **Case 2:** If the current element is greater than the previous element and less than the next element.
+
+ +
+* Here we are not looking for global minimia, we are looking for local minima. If `arr[mid - 1] < arr[mid] < arr[m + 1]` there are two posiblities, either `arr[m - 1]` is one of the local minima or we will definitely find a local minima in left direction as elements to the left are in decreasing order.
+* **Case 3:** If the current element is greater than the next element and is smaller than the previous element go to the right. As Left may or may not have local minima but the right will definitely have local minima.
+* **Case 4:** The current element is greater than the previous as well next element. Then we can go to either the left or to the right, because both will contain atleast one local minima.
+
+
+* Here we are not looking for global minimia, we are looking for local minima. If `arr[mid - 1] < arr[mid] < arr[m + 1]` there are two posiblities, either `arr[m - 1]` is one of the local minima or we will definitely find a local minima in left direction as elements to the left are in decreasing order.
+* **Case 3:** If the current element is greater than the next element and is smaller than the previous element go to the right. As Left may or may not have local minima but the right will definitely have local minima.
+* **Case 4:** The current element is greater than the previous as well next element. Then we can go to either the left or to the right, because both will contain atleast one local minima.
+ +
+#### Pseudo Code
+```javascript
+int localMinima(int[] A) {
+ l = 0, h = n - 1;
+ while (l <= h) {
+ mid = l + (h - l) / 2;
+ if ((mid == 0 || arr[mid] < arr[mid - 1]) && (mid == N - 1 || arr[mid] < arr[mid + 1])) {
+ return mid;
+ } else if (mid == 0 || arr[mid] < arr[mid - 1]) {
+ l = mid + 1;
+ } else {
+ h = mid - 1;
+ }
+ }
+}
+```
+
+#### Dry run
+
+
+
+#### Pseudo Code
+```javascript
+int localMinima(int[] A) {
+ l = 0, h = n - 1;
+ while (l <= h) {
+ mid = l + (h - l) / 2;
+ if ((mid == 0 || arr[mid] < arr[mid - 1]) && (mid == N - 1 || arr[mid] < arr[mid + 1])) {
+ return mid;
+ } else if (mid == 0 || arr[mid] < arr[mid - 1]) {
+ l = mid + 1;
+ } else {
+ h = mid - 1;
+ }
+ }
+}
+```
+
+#### Dry run
+
+ +
+
+
+| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
+| ------- | ---- | --- | --- | --- | --- | --- | --- | ---- |
+| Element | 9 | 8 | 2 |7 |6 |4 |1 | 5 |
+
+**1st Iteration**
+* `low = 0, high = 7`
+* `mid = 3`
+* The element to the left of mid -> `2 < 7` Thus, `7` cannot be local minima.
+* The array is increasing and thus, one of the local minima must be in the left of the array, so we will change `high = mid - 1 = 2`.
+
+**2nd iteration**
+* `low = 0, high = 2`
+* `mid = 1`
+* Element to the left of mid -> `9 > 8`
+* Element to the right of mid -> `2 < 8`
+* `8` cannot be local minima. As `2` is smaller than `8`, we are at decreasing array and thus, the local minima must exist in the right.
+* `low = mid + 1`
+
+**3rd iteration**
+* `low = 2, high = 2`
+* `mid = 2`
+* Element to the left of mid -> `2 < 8`
+* Element to the right of mid -> `2 < 7`
+* **2 is our local minima.**
+
+#### Complexities
+* **Time Complexity: O(log(N))**
+* **Space Complexity: O(1)**
\ No newline at end of file
diff --git a/Academy DSA Typed Notes/Advanced/DSA Searching 2 Binary Search Problems.md b/Academy DSA Typed Notes/Advanced/DSA Searching 2 Binary Search Problems.md
new file mode 100644
index 0000000..71b3183
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Searching 2 Binary Search Problems.md
@@ -0,0 +1,569 @@
+# Searching 2: Binary Search Problems
+
+---
+## Understanding Binary Search
+
+### Introduction:
+We will continue with our second lecture on Binary Search. In our previous session, we explored the fundamental concepts of this efficient searching algorithm. Today, we will dive even deeper into the world of binary search, uncovering advanced techniques and applications that expand its capabilities.
+
+In this lecture, we will build upon the foundation laid in the first session. We'll delve into topics such as binary search on rotated arrays, finding square root using binary search etc and addressing various edge cases and challenges that may arise during binary search implementation.
+
+### Pseudocode
+```java
+function binarySearch(array, target):
+ left = 0
+ right = length(array) - 1
+
+ while left <= right:
+ mid = left + (right - left) / 2
+
+ if array[mid] == target:
+ return mid
+ else if array[mid] < target:
+ left = mid + 1
+ else:
+ right = mid - 1
+
+ return NOT_FOUND
+```
+
+### Use Cases:
+Binary search has numerous applications, including:
+* Searching in databases.
+* Finding an element in a sorted array.
+* Finding an insertion point for a new element in a sorted array.
+* Implementing features like autocomplete in search engines.
+
+---
+### Question
+In what scenario does Binary Search become ineffective?
+
+**Choices**
+- [x] When the dataset is unsorted.
+- [ ] When the dataset is extremely large.
+- [ ] When the dataset is sorted in descending order.
+- [ ] When the dataset contains only unique elements.
+
+
+---
+### Problem 1 Searching in Rotated Sorted Arrays
+
+### Introduction:
+We'll explore the fascinating problem of searching in rotated sorted arrays using the Binary Search algorithm. This scenario arises when a previously sorted array has been rotated at an unknown pivot point. We'll discuss how to adapt the Binary Search technique to efficiently find a target element in such arrays.
+
+### Scenario:
+Imagine you have an array that was sorted initially, but someone rotated it at an unknown index. The resulting array is a rotated sorted array. The challenge is to find a specific element in this rotated array without reverting to linear search.
+
+### Example: Finding an Element in a Rotated Array
+
+Suppose we have the following rotated sorted array:
+```javascript
+Original Sorted Rotated Array: [4, 5, 6, 7, 8, 9, 1, 2, 3]
+```
+Let's say we want to find the element 7 within this rotated array using a brute-force approach (Linear Search).
+
+### Brute-Force Approach:
+
+* Initialize a variable target with the value we want to find (e.g., 7).
+* Loop through each element in the array one by one, starting from the first element.
+* Compare the current element with the target:
+* If the current element matches the target, we have found our element, and we can return its index.
+* If the current element does not match the target, continue to the next element.
+* Repeat step 3 until we either find the target or reach the end of the array without finding it.
+
+### Adapting Binary Search:
+While the array is rotated, we can still leverage the divide-and-conquer nature of Binary Search. However, we need to make a few adjustments to handle the rotation.
+
+**Intution:**
+* In a rotated sorted array, elements were initially sorted in ascending order but have been rotated at some point.
+* Let's asusme array contain distinct elements only.
+* The goal is to find a specific target element within this rotated array.
+* The key to binary search in a rotated array is to determine the pivot point, which is where the array rotation occurred.
+* The pivot point is essentially the maximum element in the array.
+* Once you've identified the pivot point, you have split the array into two subarrays, each of which is sorted.
+* Then you can apply individual binary search in both the parts, and find the target element.
+* **Another Idea of Doing it in one Binary Search we'll discuss below**
+* **Partitioning of Rotated Sorted Array:**
+ * A rotated sorted array can be visualized as being split into two parts: part 1 and part 2.
+ * Crucially, both part 1 and part 2 are sorted individually, but every element in part 1 is greater than those in part 2 due to the rotation.
+
+
+
+
+| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
+| ------- | ---- | --- | --- | --- | --- | --- | --- | ---- |
+| Element | 9 | 8 | 2 |7 |6 |4 |1 | 5 |
+
+**1st Iteration**
+* `low = 0, high = 7`
+* `mid = 3`
+* The element to the left of mid -> `2 < 7` Thus, `7` cannot be local minima.
+* The array is increasing and thus, one of the local minima must be in the left of the array, so we will change `high = mid - 1 = 2`.
+
+**2nd iteration**
+* `low = 0, high = 2`
+* `mid = 1`
+* Element to the left of mid -> `9 > 8`
+* Element to the right of mid -> `2 < 8`
+* `8` cannot be local minima. As `2` is smaller than `8`, we are at decreasing array and thus, the local minima must exist in the right.
+* `low = mid + 1`
+
+**3rd iteration**
+* `low = 2, high = 2`
+* `mid = 2`
+* Element to the left of mid -> `2 < 8`
+* Element to the right of mid -> `2 < 7`
+* **2 is our local minima.**
+
+#### Complexities
+* **Time Complexity: O(log(N))**
+* **Space Complexity: O(1)**
\ No newline at end of file
diff --git a/Academy DSA Typed Notes/Advanced/DSA Searching 2 Binary Search Problems.md b/Academy DSA Typed Notes/Advanced/DSA Searching 2 Binary Search Problems.md
new file mode 100644
index 0000000..71b3183
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Searching 2 Binary Search Problems.md
@@ -0,0 +1,569 @@
+# Searching 2: Binary Search Problems
+
+---
+## Understanding Binary Search
+
+### Introduction:
+We will continue with our second lecture on Binary Search. In our previous session, we explored the fundamental concepts of this efficient searching algorithm. Today, we will dive even deeper into the world of binary search, uncovering advanced techniques and applications that expand its capabilities.
+
+In this lecture, we will build upon the foundation laid in the first session. We'll delve into topics such as binary search on rotated arrays, finding square root using binary search etc and addressing various edge cases and challenges that may arise during binary search implementation.
+
+### Pseudocode
+```java
+function binarySearch(array, target):
+ left = 0
+ right = length(array) - 1
+
+ while left <= right:
+ mid = left + (right - left) / 2
+
+ if array[mid] == target:
+ return mid
+ else if array[mid] < target:
+ left = mid + 1
+ else:
+ right = mid - 1
+
+ return NOT_FOUND
+```
+
+### Use Cases:
+Binary search has numerous applications, including:
+* Searching in databases.
+* Finding an element in a sorted array.
+* Finding an insertion point for a new element in a sorted array.
+* Implementing features like autocomplete in search engines.
+
+---
+### Question
+In what scenario does Binary Search become ineffective?
+
+**Choices**
+- [x] When the dataset is unsorted.
+- [ ] When the dataset is extremely large.
+- [ ] When the dataset is sorted in descending order.
+- [ ] When the dataset contains only unique elements.
+
+
+---
+### Problem 1 Searching in Rotated Sorted Arrays
+
+### Introduction:
+We'll explore the fascinating problem of searching in rotated sorted arrays using the Binary Search algorithm. This scenario arises when a previously sorted array has been rotated at an unknown pivot point. We'll discuss how to adapt the Binary Search technique to efficiently find a target element in such arrays.
+
+### Scenario:
+Imagine you have an array that was sorted initially, but someone rotated it at an unknown index. The resulting array is a rotated sorted array. The challenge is to find a specific element in this rotated array without reverting to linear search.
+
+### Example: Finding an Element in a Rotated Array
+
+Suppose we have the following rotated sorted array:
+```javascript
+Original Sorted Rotated Array: [4, 5, 6, 7, 8, 9, 1, 2, 3]
+```
+Let's say we want to find the element 7 within this rotated array using a brute-force approach (Linear Search).
+
+### Brute-Force Approach:
+
+* Initialize a variable target with the value we want to find (e.g., 7).
+* Loop through each element in the array one by one, starting from the first element.
+* Compare the current element with the target:
+* If the current element matches the target, we have found our element, and we can return its index.
+* If the current element does not match the target, continue to the next element.
+* Repeat step 3 until we either find the target or reach the end of the array without finding it.
+
+### Adapting Binary Search:
+While the array is rotated, we can still leverage the divide-and-conquer nature of Binary Search. However, we need to make a few adjustments to handle the rotation.
+
+**Intution:**
+* In a rotated sorted array, elements were initially sorted in ascending order but have been rotated at some point.
+* Let's asusme array contain distinct elements only.
+* The goal is to find a specific target element within this rotated array.
+* The key to binary search in a rotated array is to determine the pivot point, which is where the array rotation occurred.
+* The pivot point is essentially the maximum element in the array.
+* Once you've identified the pivot point, you have split the array into two subarrays, each of which is sorted.
+* Then you can apply individual binary search in both the parts, and find the target element.
+* **Another Idea of Doing it in one Binary Search we'll discuss below**
+* **Partitioning of Rotated Sorted Array:**
+ * A rotated sorted array can be visualized as being split into two parts: part 1 and part 2.
+ * Crucially, both part 1 and part 2 are sorted individually, but every element in part 1 is greater than those in part 2 due to the rotation.
+ +
+* **Identifying Target's Part**
+ * To determine which part the Target belongs to (part 1 or 2), compare it with the 0th element.
+ * If the midpoint is greater than (also equals to) the 0th element, then it belongs to part 1. Otherwise, it's in part 2.
+
+
+* **Identifying Target's Part**
+ * To determine which part the Target belongs to (part 1 or 2), compare it with the 0th element.
+ * If the midpoint is greater than (also equals to) the 0th element, then it belongs to part 1. Otherwise, it's in part 2.
+  +
+
+* **Identifying Midpoint's Part:**
+
+ * To determine which part the midpoint belongs to (part 1 or 2), compare it with the 0th element.
+ * If the midpoint is greater than (also equals to) the 0th element, then it belongs to part 1. Otherwise, it's in part 2.
+* **Midpoint vs Target:**
+ * If the midpoint is the equals to the target, you've found it.
+ * If not, then check if the target lies in the same part as the midpoint. If yes, both target and midpoint is within the same sorted part, perform a binary search in that part to move your midpoint towards the target.
+
+
+
+* **Identifying Midpoint's Part:**
+
+ * To determine which part the midpoint belongs to (part 1 or 2), compare it with the 0th element.
+ * If the midpoint is greater than (also equals to) the 0th element, then it belongs to part 1. Otherwise, it's in part 2.
+* **Midpoint vs Target:**
+ * If the midpoint is the equals to the target, you've found it.
+ * If not, then check if the target lies in the same part as the midpoint. If yes, both target and midpoint is within the same sorted part, perform a binary search in that part to move your midpoint towards the target.
+  +
+ * If no, move your search towards the other part, effectively approaching the midpoint towards target.
+
+
+ * If no, move your search towards the other part, effectively approaching the midpoint towards target.
+  +
+* **Iterative Process:**
+ * Continue adjusting your boundaries based on the decisions made in the previous step until you either find the target or exhaust your search space.
+* **Result:**
+ * Return the index of the target if found, or -1 if not.
+
+**Algorithm:**
+* Initialize left to 0 and right to len(nums) - 1.
+* While left is less than or equal to right, do the following:
+* Calculate the middle index mid as left + (right - left)/2.
+* If nums[mid] is equal to the target, return mid as the index of the target.
+* Check if the target is less than nums[0] (indicating it's on part 2):
+* If target < nums[0], check if nums[mid] is greater than or equal to nums[0]:
+* If true, update left to mid + 1 to search the right half.
+* If false, update right to mid - 1 based on target's relation to nums[mid].
+* If the target is greater than or equal to nums[0] (indicating it's on the left side of the pivot):
+* If target >= nums[0], check if nums[mid] is less than nums[0]:
+* If true, update right to mid - 1 to search the left half.
+* If false, update left to mid + 1 based on target's relation to nums[mid].
+* Repeat steps 2-6 until left is less than or equal to right.
+* If the loop exits without finding the target, return -1 to indicate the target is not in the array.
+
+### Example:
+
+**Scenario:**
+Consider the rotated sorted array **[4, 5, 6, 7, 0, 1, 2]** and our target is 0.
+
+**Solution:**
+* Using the provided algorithm:
+* Initialize left to 0 and right to 6.
+* Calculate mid as (left + right) // 2, which is 3.
+* Check if nums[mid] (element at index 3) is equal to the target (0). It's not equal.
+* Check if target (0) is less than nums[0] (4). It's not.
+* Check if nums[mid] (7) is greater than or equal to nums[0] (4). It's true.
+* Update left to mid + 1, making left equal to 4.
+* Calculate mid as (left + right) // 2, which is 5.
+* Check if nums[mid] (element at index 5) is equal to the target (0). It is equal.
+* Return mid, which is 5.
+
+ **We found the target 0 at index 5.**
+
+---
+### Searching in Rotated Sorted Arrays Pseudocode
+
+#### Pseudocode:
+
+```cpp
+function searchRotatedArray(nums, target):
+ left = 0
+ right = length(nums) - 1
+
+ while left <= right:
+ mid = left + (right - left) / 2
+
+ if nums[mid] == target:
+ return mid
+
+ if target < nums[0]:
+ if nums[mid] >= nums[0]:
+ left = mid + 1
+ else:
+ if nums[mid] < target:
+ left = mid + 1
+ else:
+ right = mid - 1
+ else:
+ if nums[mid] < nums[0]:
+ right = mid - 1
+ else:
+ if nums[mid] < target:
+ left = mid + 1
+ else:
+ right = mid - 1
+
+ return -1
+```
+
+#### Complexity Analysis:
+The time complexity of this modified Binary Search algorithm is still O(log n), making it efficient even in rotated sorted arrays.
+**Reason**:
+* **Divide and Conquer:**
+
+* **Iterative Process:**
+ * Continue adjusting your boundaries based on the decisions made in the previous step until you either find the target or exhaust your search space.
+* **Result:**
+ * Return the index of the target if found, or -1 if not.
+
+**Algorithm:**
+* Initialize left to 0 and right to len(nums) - 1.
+* While left is less than or equal to right, do the following:
+* Calculate the middle index mid as left + (right - left)/2.
+* If nums[mid] is equal to the target, return mid as the index of the target.
+* Check if the target is less than nums[0] (indicating it's on part 2):
+* If target < nums[0], check if nums[mid] is greater than or equal to nums[0]:
+* If true, update left to mid + 1 to search the right half.
+* If false, update right to mid - 1 based on target's relation to nums[mid].
+* If the target is greater than or equal to nums[0] (indicating it's on the left side of the pivot):
+* If target >= nums[0], check if nums[mid] is less than nums[0]:
+* If true, update right to mid - 1 to search the left half.
+* If false, update left to mid + 1 based on target's relation to nums[mid].
+* Repeat steps 2-6 until left is less than or equal to right.
+* If the loop exits without finding the target, return -1 to indicate the target is not in the array.
+
+### Example:
+
+**Scenario:**
+Consider the rotated sorted array **[4, 5, 6, 7, 0, 1, 2]** and our target is 0.
+
+**Solution:**
+* Using the provided algorithm:
+* Initialize left to 0 and right to 6.
+* Calculate mid as (left + right) // 2, which is 3.
+* Check if nums[mid] (element at index 3) is equal to the target (0). It's not equal.
+* Check if target (0) is less than nums[0] (4). It's not.
+* Check if nums[mid] (7) is greater than or equal to nums[0] (4). It's true.
+* Update left to mid + 1, making left equal to 4.
+* Calculate mid as (left + right) // 2, which is 5.
+* Check if nums[mid] (element at index 5) is equal to the target (0). It is equal.
+* Return mid, which is 5.
+
+ **We found the target 0 at index 5.**
+
+---
+### Searching in Rotated Sorted Arrays Pseudocode
+
+#### Pseudocode:
+
+```cpp
+function searchRotatedArray(nums, target):
+ left = 0
+ right = length(nums) - 1
+
+ while left <= right:
+ mid = left + (right - left) / 2
+
+ if nums[mid] == target:
+ return mid
+
+ if target < nums[0]:
+ if nums[mid] >= nums[0]:
+ left = mid + 1
+ else:
+ if nums[mid] < target:
+ left = mid + 1
+ else:
+ right = mid - 1
+ else:
+ if nums[mid] < nums[0]:
+ right = mid - 1
+ else:
+ if nums[mid] < target:
+ left = mid + 1
+ else:
+ right = mid - 1
+
+ return -1
+```
+
+#### Complexity Analysis:
+The time complexity of this modified Binary Search algorithm is still O(log n), making it efficient even in rotated sorted arrays.
+**Reason**:
+* **Divide and Conquer:**The algorithm works by repeatedly dividing the search space in half. In each step, it either eliminates half of the remaining elements or finds the target element. This is a characteristic of binary search, which has a time complexity of O(log N). +* **Comparison Operations:**
The main operations within each iteration are comparisons of the target element with the middle element. Since we're dividing the array in half with each comparison, we need at most O(log N) comparisons to find the element or determine that it's not present. +* **No Need to Examine All Elements:**
Unlike linear search, which would require examining all N elements in the worst case, binary search significantly reduces the number of elements that need to be considered, leading to a logarithmic time complexity. + +--- +### Question +In the problem of searching for a target element in a rotated sorted array, what advantage does Binary Search offer over Linear Search? + + +**Choices** +- [ ] Binary Search doesn't require any comparisons. +- [ ] Binary Search works faster on unsorted arrays. +- [x] Binary Search divides the search space in half with each step. +- [ ] Binary Search is always faster than Linear Search. + + + +**Explanation:** +Binary Search offers a significant advantage over Linear Search when searching in a rotated sorted array. With each step, Binary Search efficiently narrows down the search interval by dividing it in half, greatly reducing the number of elements under consideration. This characteristic leads to a time complexity of O(log n), making Binary Search much faster compared to Linear Search's O(n) time complexity, especially for larger arrays. + + +--- +### Problem 2 Finding the square root of a number + + +### Introduction: +Now, we'll explore a fascinating application of Binary Search: finding the square root of a number. The square root operation is a fundamental mathematical operation, and we'll see how Binary Search helps us approximate this value with great efficiency. + +### Motivation: +Imagine you're working on a mathematical problem or a scientific simulation that requires the square root of a number. Calculating square roots manually can be time-consuming, and a reliable and fast method is needed. Binary Search provides an elegant way to approximate square roots efficiently. + +### Brute-Force Algorithm to Find the Square Root: + +* **Input Validation:** If it's negative, return "Undefined" because the square root of a negative number is undefined. +* **Special Cases:** If x is 0 or 1, return x because the square root of 0 or 1 is the number itself. +* **Initialize Guess:** Start with an initial guess of 1. +* Check if the square of the current guess is less than or equal to x. If it is, continue to the next step. If not, exit the loop. +* **Increment Guess:** Increment the guess by 1. +* **Exit Loop:** When the loop exits, it means guess * guess exceeds x. The square root is approximated as guess - 1 because guess at this point is the smallest integer greater than or equal to the square root of x. +* Return Result: Return guess - 1 as the square root of x. + +```cpp +function sqrt_with_floor(x): + if x < 0: + return "Undefined" // Square root of a negative number is undefined + + if x == 0 or x == 1: + return x // Square root of 0 or 1 is the number itself + + // Start from 1 and increment until the square is greater than x + guess = 1 + while guess * guess <= x: + guess = guess + 1 + + // Since the loop ends when guess^2 > x, the floor(sqrt(x)) is guess - 1 + return guess - 1 +``` + +:::warning +Please take some time to think about the Binary Search approach on your own before reading further..... +::: + +### Binary Search Principle for Square Root: +The Binary Search algorithm can be adapted to find the square root of a number by treating the square root as a search problem. The key idea is to search for a number within a certain range that, when squared, is closest to the target value. We'll repeatedly narrow down this range until we achieve a satisfactory approximation. +Establish a search range: The square root of a non-negative number is always within the range of 0 to the number itself. So, you set up an initial search range as [0, x], where 'x' is the number for which you want to find the square root. + +**Intution**: +* **Binary search:** You then start a binary search within this range. The midpoint of the range is calculated, and you compute the square of this midpoint. +* **Comparison:** You compare the square of the midpoint to the original number (x). Three cases can arise: + * **Exact Match:** If the square of the midpoint is exactly equal to x, you've found a value very close to the square root. + * **Square Less Than x:** If the squared midpoint is less than x, it suggests that midpoint can be the answer but we can get the more closer value towards right only(if present). So, adjust the search range to be [midpoint+1, right end of current range]. + * **Square Greater Than x:** If the squared midpoint is greater than x, it indicates the square root lies to the left of the midpoint. Consequently, adjust the search range to be [left end of current range, midpoint-1]. +* **Convergence:** You repeat the binary search by calculating new midpoints and comparing the squares until you converge on an approximation that is sufficiently close to the actual square root. + +For example: +
 +
+
+### Example: Finding Square Root using Binary Search
+
+**Scenario:**
+We want to find the square root of the number 9 using Binary Search.
+
+**Solution:**
+* Initialize left = 1 and right = 9 (since the square root of 9 won't be greater than 9).
+* Calculate mid = (left + right) / 2 = 5.
+* Compare 5 * 5 with 9.
+* Since 25 is greater than 9, narrow the search to the left half.
+* Update right = 4.
+* Calculate mid = (left + right) / 2 = 2.
+* Compare 2 * 2 with 9.
+* Since 4 is less than 9, adjust the range to the right half.
+* Update left = 3.
+* Calculate mid = (left + right) / 2 = 3.
+* Compare 3 * 3 with 9.
+* We found an exact match! The square root of 9 is 3.
+
+---
+### Finding the square root of a number Pseudocode
+#### Pseudocode:
+Here's a simple pseudocode representation of finding the square root using Binary Search:
+
+```cpp
+function findSquareRoot(target):
+ if target == 0 or target == 1:
+ return target
+
+ left = 1
+ right = target
+ result = 0
+
+ while left <= right:
+ mid = left + (right - left) / 2
+
+ if mid * mid == target:
+ return mid
+ else if mid * mid < target:
+ left = mid + 1
+ result = mid
+ else:
+ right = mid - 1
+
+ return result
+```
+
+
+### Analysis and Complexity:
+
+In each step of the Binary Search, we compare the square of the middle element with the target value. Depending on the result of this comparison, we adjust the search range. Since Binary Search divides the range in half with each step, the time complexity of this algorithm is O(log n), where n is the value of the target number.
+
+### Use Cases:
+Finding the square root using Binary Search has applications in various fields, such as mathematics, engineering, physics, and computer graphics. It's often used when precise square root calculations are required, especially in scenarios where hardware or library-based square root functions are not available.
+
+---
+### Question
+
+What advantage does using Binary Search for finding the square root of a number offer over directly calculating the square root?
+
+
+**Choices**
+- [ ] Binary Search has a lower time complexity.
+- [x] Binary Search provides a more precise result.
+- [ ] Binary Search doesn't require any comparisons.
+- [ ] Binary Search can find the square root of any number.
+
+
+---
+### Problem 3 Finding the Ath magical number
+In this problem, we are tasked with finding the a-th magical number that satisfies a specific condition. A magical number, in the context of this problem, is defined as a positive integer that is divisible by either b or c (or both).
+* Magical Number Definition: A magical number is a positive integer that is divisible by either b or c or both. In other words, if a number x is a magical number, it means that x % b == 0 or x % c == 0, or both conditions hold.
+* Task: Our task is to find and return the a-th magical number based on the conditions mentioned above.
+
+#### Example
+
+
+
+### Example: Finding Square Root using Binary Search
+
+**Scenario:**
+We want to find the square root of the number 9 using Binary Search.
+
+**Solution:**
+* Initialize left = 1 and right = 9 (since the square root of 9 won't be greater than 9).
+* Calculate mid = (left + right) / 2 = 5.
+* Compare 5 * 5 with 9.
+* Since 25 is greater than 9, narrow the search to the left half.
+* Update right = 4.
+* Calculate mid = (left + right) / 2 = 2.
+* Compare 2 * 2 with 9.
+* Since 4 is less than 9, adjust the range to the right half.
+* Update left = 3.
+* Calculate mid = (left + right) / 2 = 3.
+* Compare 3 * 3 with 9.
+* We found an exact match! The square root of 9 is 3.
+
+---
+### Finding the square root of a number Pseudocode
+#### Pseudocode:
+Here's a simple pseudocode representation of finding the square root using Binary Search:
+
+```cpp
+function findSquareRoot(target):
+ if target == 0 or target == 1:
+ return target
+
+ left = 1
+ right = target
+ result = 0
+
+ while left <= right:
+ mid = left + (right - left) / 2
+
+ if mid * mid == target:
+ return mid
+ else if mid * mid < target:
+ left = mid + 1
+ result = mid
+ else:
+ right = mid - 1
+
+ return result
+```
+
+
+### Analysis and Complexity:
+
+In each step of the Binary Search, we compare the square of the middle element with the target value. Depending on the result of this comparison, we adjust the search range. Since Binary Search divides the range in half with each step, the time complexity of this algorithm is O(log n), where n is the value of the target number.
+
+### Use Cases:
+Finding the square root using Binary Search has applications in various fields, such as mathematics, engineering, physics, and computer graphics. It's often used when precise square root calculations are required, especially in scenarios where hardware or library-based square root functions are not available.
+
+---
+### Question
+
+What advantage does using Binary Search for finding the square root of a number offer over directly calculating the square root?
+
+
+**Choices**
+- [ ] Binary Search has a lower time complexity.
+- [x] Binary Search provides a more precise result.
+- [ ] Binary Search doesn't require any comparisons.
+- [ ] Binary Search can find the square root of any number.
+
+
+---
+### Problem 3 Finding the Ath magical number
+In this problem, we are tasked with finding the a-th magical number that satisfies a specific condition. A magical number, in the context of this problem, is defined as a positive integer that is divisible by either b or c (or both).
+* Magical Number Definition: A magical number is a positive integer that is divisible by either b or c or both. In other words, if a number x is a magical number, it means that x % b == 0 or x % c == 0, or both conditions hold.
+* Task: Our task is to find and return the a-th magical number based on the conditions mentioned above.
+
+#### Example
+ +
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Brute force
+```cpp
+Function findAMagicalNumberBruteForce(a, b, c):
+ number = 1 // Start with the first positive integer
+ count = 0 // Initialize the count of magical numbers found
+
+ while count < a:
+ if number is divisible by b or c:
+ count = count + 1 // Increment the count if it's divisible by either b or c
+ number = number + 1
+
+ return number - 1 // Subtract 1 because we increased 'number' after finding the a-th magical number
+```
+
+#### Observation
+
+Answer has to be a multiple of either B or C. So, we know we will get answer till A * B or A * C depending on which is smaller. Therefore, our answer range will be between`[1 to A * min(B,C)]`
+
+Example:
+A = 8
+B = 2
+C = 3
+
+A * B = 16
+A * C = 24
+So, our answer will be within range [1 to 16]
+
+**Que: How many multiples of B, C will be within range [1 to x]?** => x/B + x/C - x/LCM(B,C)$
+
+`The LCM of 'b' and 'c' represents the smallest common multiple of 'b' and 'c' such that any number that is divisible by both 'b' and 'c' will be a multiple of their LCM and we will have to subtract it`
+
+Example:
+A = 5
+B = 3
+C = 4
+Range => [1 to 15]
+Multiples
+=> 15/3 + 15/4 - 15/LCM(3,4)
+=> 5 + 3 + 1 = 7 `[3, 4, 6, 8, 9, 12, 15]`
+
+**Que: How to calculate LCM(B,C) ?**
+LCM(B,C) = (B * C) / GCD(B,C) [We know how to calculate GCD!]
+
+
+### Can we apply Binary Search ?
+
+**Search Space** => `[1 to A * min(B,C)]`
+**Target** => Ath Magical Number
+**Condition** =>
+* Say we land at mid.
+* To check mid is magical, we need to know how many magical numbers are there in the range [1, mid].
+* Compare with A: If the count is more than A, it means we need to search in the lower range [low, mid-1].
+* Otherwise, if count is < A, we need to search in higher range
+* If count == A, then we store mid as answer, and go left.
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Brute force
+```cpp
+Function findAMagicalNumberBruteForce(a, b, c):
+ number = 1 // Start with the first positive integer
+ count = 0 // Initialize the count of magical numbers found
+
+ while count < a:
+ if number is divisible by b or c:
+ count = count + 1 // Increment the count if it's divisible by either b or c
+ number = number + 1
+
+ return number - 1 // Subtract 1 because we increased 'number' after finding the a-th magical number
+```
+
+#### Observation
+
+Answer has to be a multiple of either B or C. So, we know we will get answer till A * B or A * C depending on which is smaller. Therefore, our answer range will be between`[1 to A * min(B,C)]`
+
+Example:
+A = 8
+B = 2
+C = 3
+
+A * B = 16
+A * C = 24
+So, our answer will be within range [1 to 16]
+
+**Que: How many multiples of B, C will be within range [1 to x]?** => x/B + x/C - x/LCM(B,C)$
+
+`The LCM of 'b' and 'c' represents the smallest common multiple of 'b' and 'c' such that any number that is divisible by both 'b' and 'c' will be a multiple of their LCM and we will have to subtract it`
+
+Example:
+A = 5
+B = 3
+C = 4
+Range => [1 to 15]
+Multiples
+=> 15/3 + 15/4 - 15/LCM(3,4)
+=> 5 + 3 + 1 = 7 `[3, 4, 6, 8, 9, 12, 15]`
+
+**Que: How to calculate LCM(B,C) ?**
+LCM(B,C) = (B * C) / GCD(B,C) [We know how to calculate GCD!]
+
+
+### Can we apply Binary Search ?
+
+**Search Space** => `[1 to A * min(B,C)]`
+**Target** => Ath Magical Number
+**Condition** =>
+* Say we land at mid.
+* To check mid is magical, we need to know how many magical numbers are there in the range [1, mid].
+* Compare with A: If the count is more than A, it means we need to search in the lower range [low, mid-1].
+* Otherwise, if count is < A, we need to search in higher range
+* If count == A, then we store mid as answer, and go left.
+ +
+
+#### Pseudocode:
+```cpp
+int count(x, B, C) {
+ return x/B + x/C - x/LCM(B,C);
+}
+
+int magical(A, B, C) {
+ l = 1, h = A * min(B,C)
+ while(l <= h) {
+ m = l + (h-l)/2;
+ if(count(m,B,C) > A) {
+ h = m-1;
+ }
+ else if(count(m,B,C) < A) {
+ l = m+1;
+ }
+ else {
+ ans = m;
+ h = m-1;
+ }
+ }
+ return ans;
+}
+```
+
+---
+### Question
+What is the time complexity of the binary search approach for finding the a-th magical number in terms of A, B, and C?
+
+**Choices**
+
+- [ ] O(A)
+- [x] O(log A)
+- [ ] O(A * B * C)
+- [ ] O(log(A * B * C))
+
+---
+### Problem 4 Finding median of array
+
+**What is Median?**
+The median of an array is the middle element of the array when it is sorted. For arrays with an odd number of elements, the median is the value at the exact center. For arrays with an even number of elements, the median is typically defined as the average of the two middle elements. It's a measure of central tendency and divides the data into two equal halves when sorted.
+
+### Brute-Force Algorithm to Find the Median of an Array:
+
+* Sort the given array in ascending order. You can use any sorting algorithm (e.g., bubble sort, insertion sort, quicksort, or mergesort).
+* Calculate the length of the sorted array, denoted as n.
+* If n is odd, return the middle element of the sorted array as the median (e.g., sorted_array[n // 2]).
+* If n is even, calculate the average of the two middle elements and return it as the median (e.g., (sorted_array[n // 2 - 1] + sorted_array[n // 2]) / 2).
+
+```cpp
+def find_median_brute_force(arr):
+ # Step 1: Sort the array
+ sorted_array = sorted(arr)
+
+ # Step 2: Calculate the length of the sorted array
+ n = len(sorted_array)
+
+ # Step 3: Find the median
+ if n % 2 == 1:
+ median = sorted_array[n // 2]
+ else:
+ median = (sorted_array[n // 2 - 1] + sorted_array[n // 2]) / 2.0
+
+ return median
+```
+
+:::warning
+Please take some time to think about the Binary Search approach on your own before reading further.....
+:::
+
+### Binary Search Approach:
+The Binary Search technique can be harnessed to find the median of two sorted arrays by partitioning the arrays in such a way that the elements on the left side are less than or equal to the elements on the right side. The median will be either the middle element in a combined array (for an odd number of total elements) or the average of two middle elements (for an even number of elements).
+
+### Example: Finding Median of Two Sorted Arrays
+
+**Scenario**:
+Consider the two sorted arrays: nums1 = [1, 3, 5] and nums2 = [2, 4, 6]. We want to find the median of the combined array.
+
+**Intuition:**
+
+* **Combined Sorted Array:** To find the median of two sorted arrays, you can think of combining them into a single sorted array. The median of this combined array will be our solution.
+* **Partitioning:** The key idea is to partition both arrays into two parts such that:
+ * The elements on the left side are smaller than or equal to the elements on the right side.
+ * The partitioning should be done in such a way that we can calculate the median easily.
+
+
+
+
+#### Pseudocode:
+```cpp
+int count(x, B, C) {
+ return x/B + x/C - x/LCM(B,C);
+}
+
+int magical(A, B, C) {
+ l = 1, h = A * min(B,C)
+ while(l <= h) {
+ m = l + (h-l)/2;
+ if(count(m,B,C) > A) {
+ h = m-1;
+ }
+ else if(count(m,B,C) < A) {
+ l = m+1;
+ }
+ else {
+ ans = m;
+ h = m-1;
+ }
+ }
+ return ans;
+}
+```
+
+---
+### Question
+What is the time complexity of the binary search approach for finding the a-th magical number in terms of A, B, and C?
+
+**Choices**
+
+- [ ] O(A)
+- [x] O(log A)
+- [ ] O(A * B * C)
+- [ ] O(log(A * B * C))
+
+---
+### Problem 4 Finding median of array
+
+**What is Median?**
+The median of an array is the middle element of the array when it is sorted. For arrays with an odd number of elements, the median is the value at the exact center. For arrays with an even number of elements, the median is typically defined as the average of the two middle elements. It's a measure of central tendency and divides the data into two equal halves when sorted.
+
+### Brute-Force Algorithm to Find the Median of an Array:
+
+* Sort the given array in ascending order. You can use any sorting algorithm (e.g., bubble sort, insertion sort, quicksort, or mergesort).
+* Calculate the length of the sorted array, denoted as n.
+* If n is odd, return the middle element of the sorted array as the median (e.g., sorted_array[n // 2]).
+* If n is even, calculate the average of the two middle elements and return it as the median (e.g., (sorted_array[n // 2 - 1] + sorted_array[n // 2]) / 2).
+
+```cpp
+def find_median_brute_force(arr):
+ # Step 1: Sort the array
+ sorted_array = sorted(arr)
+
+ # Step 2: Calculate the length of the sorted array
+ n = len(sorted_array)
+
+ # Step 3: Find the median
+ if n % 2 == 1:
+ median = sorted_array[n // 2]
+ else:
+ median = (sorted_array[n // 2 - 1] + sorted_array[n // 2]) / 2.0
+
+ return median
+```
+
+:::warning
+Please take some time to think about the Binary Search approach on your own before reading further.....
+:::
+
+### Binary Search Approach:
+The Binary Search technique can be harnessed to find the median of two sorted arrays by partitioning the arrays in such a way that the elements on the left side are less than or equal to the elements on the right side. The median will be either the middle element in a combined array (for an odd number of total elements) or the average of two middle elements (for an even number of elements).
+
+### Example: Finding Median of Two Sorted Arrays
+
+**Scenario**:
+Consider the two sorted arrays: nums1 = [1, 3, 5] and nums2 = [2, 4, 6]. We want to find the median of the combined array.
+
+**Intuition:**
+
+* **Combined Sorted Array:** To find the median of two sorted arrays, you can think of combining them into a single sorted array. The median of this combined array will be our solution.
+* **Partitioning:** The key idea is to partition both arrays into two parts such that:
+ * The elements on the left side are smaller than or equal to the elements on the right side.
+ * The partitioning should be done in such a way that we can calculate the median easily.
+
+ +
+* **Binary Search:** To achieve this, we can perform a binary search on the smaller array (in this case, nums1). We calculate a partition point in nums1, and then we can calculate the corresponding partition point in nums2.
+
+
+
+* **Binary Search:** To achieve this, we can perform a binary search on the smaller array (in this case, nums1). We calculate a partition point in nums1, and then we can calculate the corresponding partition point in nums2.
+
+ +
+* **Median Calculation:** Once we have the partitions, we can calculate the maximum element on the left side (max_left) and the minimum element on the right side (min_right) in both arrays. The median will be the average of max_left and min_right.
+
+
+* **Median Calculation:** Once we have the partitions, we can calculate the maximum element on the left side (max_left) and the minimum element on the right side (min_right) in both arrays. The median will be the average of max_left and min_right.
+ +
+* **Handling Even and Odd Lengths:** Depending on whether the total length of the combined array is even or odd, the median calculation varies. If it's even, we average the two values; if it's odd, we take the middle value.
+
+**Solution**:
+* We start by calculating the total length of the combined arrays to determine if the median will be even or odd.
+* Then, we use binary search on the smaller array (nums1) to find a partition point that satisfies the conditions mentioned earlier. This ensures that elements on the left are smaller or equal to elements on the right.
+* We calculate max_left and min_right for both arrays based on the partitions.
+* Finally, we calculate the median as the average of max_left and min_right.
+
+**Binary Search:**
+
+* Initialize left = 0 and right = len(nums1) = 3.
+* Iteration 1:
+* Calculate partition_nums1 = $(0 + 3) / 2 = 1$.
+* Calculate partition_nums2 = $(6 + 1) / 2 - 1 = 2$.
+* Calculate max_left_nums1 = 1 and max_left_nums2 = 2.
+* Calculate min_right_nums1 = 3 and min_right_nums2 = 4.
+* Since 1 <= 4 and 2 <= 3, we have found the correct partition.
+* Since the total length is even (6), the median is the average of the maximum of left elements and the minimum of right elements, which is $(2 + 3) / 2 = 2.5$.
+
+---
+
+#### Pseudocode:
+Here's a simplified pseudocode representation of finding the median of two sorted arrays using Binary Search:
+
+
+```cpp
+function findMedianSortedArrays(nums1, nums2):
+ if len(nums1) > len(nums2):
+ nums1, nums2 = nums2, nums1
+
+ total_length = len(nums1) + len(nums2)
+ left = 0
+ right = len(nums1)
+
+ while left <= right:
+ partition_nums1 = (left + right) / 2
+ partition_nums2 = (total_length + 1) / 2 - partition_nums1
+
+ max_left_nums1 = float('-inf') if partition_nums1 == 0 else nums1[partition_nums1 - 1]
+ max_left_nums2 = float('-inf') if partition_nums2 == 0 else nums2[partition_nums2 - 1]
+
+ min_right_nums1 = float('inf') if partition_nums1 == len(nums1) else nums1[partition_nums1]
+ min_right_nums2 = float('inf') if partition_nums2 == len(nums2) else nums2[partition_nums2]
+
+ if max_left_nums1 <= min_right_nums2 and max_left_nums2 <= min_right_nums1:
+ if total_length % 2 == 0:
+ return (max(max_left_nums1, max_left_nums2) + min(min_right_nums1, min_right_nums2)) / 2
+ else:
+ return max(max_left_nums1, max_left_nums2)
+ elif max_left_nums1 > min_right_nums2:
+ right = partition_nums1 - 1
+ else:
+ left = partition_nums1 + 1
+```
+#### Analysis:
+In each iteration, the algorithm adjusts the partition positions based on the comparison of maximum elements on the left side with minimum elements on the right side of the partitions. The Binary Search nature of this algorithm leads to a time complexity of O(log(min(m, n))), where m and n are the lengths of the two input arrays.
+
+#### Use Cases:
+The concept of finding the median of two sorted arrays is crucial in various fields, including data analysis, algorithms, and statistics.
+
+
+---
+### Observations
+
+* **Sorted Arrays:** Binary Search excels in sorted arrays, capitalizing on their inherent order to quickly locate elements.
+* **Search Space:** Identify the range within which the solution exists, which guides setting up the initial search range.
+* **Midpoint Element:** The middle element provides insights into the properties of elements in different subranges, aiding decisions in adjusting the search range.
+* **Stopping Condition:** Define conditions under which the search should stop, whether an element is found or the search range becomes empty.
+* **Divide and Conquer:** Binary Search employs a "divide and conquer" strategy, progressively reducing the problem size.
+* **Boundary Handling:** Pay special attention to handling boundary conditions, avoiding index out-of-bounds errors.
+* **Precision & Approximations:** Binary Search can yield approximate solutions by adjusting the search criteria.
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Searching 3 Binary Search on Answer.md b/Academy DSA Typed Notes/Advanced/DSA Searching 3 Binary Search on Answer.md
new file mode 100644
index 0000000..fa33107
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Searching 3 Binary Search on Answer.md
@@ -0,0 +1,441 @@
+# Searching 3: Binary Search on Answer
+
+---
+## Problem 1 Painter's Partition
+
+We have to paint all N boards of length [C0, C1, C2, C3 … CN - 1]. There are K painters available and each of them takes 1 units of time to paint 1 unit of the board.
+
+Calculate and return the minimum time required to get the job done.
+> NOTE:
+> 1. Two painters cannot share a board to paint. That is to say, a board cannot be painted partially by one painter, and partially by another.
+> 2. A painter will only paint contiguous boards. This means a painter paints a continous subarray of boards
+
+**Example 1**
+Below are some of the possible configurations:
+
+
+* **Handling Even and Odd Lengths:** Depending on whether the total length of the combined array is even or odd, the median calculation varies. If it's even, we average the two values; if it's odd, we take the middle value.
+
+**Solution**:
+* We start by calculating the total length of the combined arrays to determine if the median will be even or odd.
+* Then, we use binary search on the smaller array (nums1) to find a partition point that satisfies the conditions mentioned earlier. This ensures that elements on the left are smaller or equal to elements on the right.
+* We calculate max_left and min_right for both arrays based on the partitions.
+* Finally, we calculate the median as the average of max_left and min_right.
+
+**Binary Search:**
+
+* Initialize left = 0 and right = len(nums1) = 3.
+* Iteration 1:
+* Calculate partition_nums1 = $(0 + 3) / 2 = 1$.
+* Calculate partition_nums2 = $(6 + 1) / 2 - 1 = 2$.
+* Calculate max_left_nums1 = 1 and max_left_nums2 = 2.
+* Calculate min_right_nums1 = 3 and min_right_nums2 = 4.
+* Since 1 <= 4 and 2 <= 3, we have found the correct partition.
+* Since the total length is even (6), the median is the average of the maximum of left elements and the minimum of right elements, which is $(2 + 3) / 2 = 2.5$.
+
+---
+
+#### Pseudocode:
+Here's a simplified pseudocode representation of finding the median of two sorted arrays using Binary Search:
+
+
+```cpp
+function findMedianSortedArrays(nums1, nums2):
+ if len(nums1) > len(nums2):
+ nums1, nums2 = nums2, nums1
+
+ total_length = len(nums1) + len(nums2)
+ left = 0
+ right = len(nums1)
+
+ while left <= right:
+ partition_nums1 = (left + right) / 2
+ partition_nums2 = (total_length + 1) / 2 - partition_nums1
+
+ max_left_nums1 = float('-inf') if partition_nums1 == 0 else nums1[partition_nums1 - 1]
+ max_left_nums2 = float('-inf') if partition_nums2 == 0 else nums2[partition_nums2 - 1]
+
+ min_right_nums1 = float('inf') if partition_nums1 == len(nums1) else nums1[partition_nums1]
+ min_right_nums2 = float('inf') if partition_nums2 == len(nums2) else nums2[partition_nums2]
+
+ if max_left_nums1 <= min_right_nums2 and max_left_nums2 <= min_right_nums1:
+ if total_length % 2 == 0:
+ return (max(max_left_nums1, max_left_nums2) + min(min_right_nums1, min_right_nums2)) / 2
+ else:
+ return max(max_left_nums1, max_left_nums2)
+ elif max_left_nums1 > min_right_nums2:
+ right = partition_nums1 - 1
+ else:
+ left = partition_nums1 + 1
+```
+#### Analysis:
+In each iteration, the algorithm adjusts the partition positions based on the comparison of maximum elements on the left side with minimum elements on the right side of the partitions. The Binary Search nature of this algorithm leads to a time complexity of O(log(min(m, n))), where m and n are the lengths of the two input arrays.
+
+#### Use Cases:
+The concept of finding the median of two sorted arrays is crucial in various fields, including data analysis, algorithms, and statistics.
+
+
+---
+### Observations
+
+* **Sorted Arrays:** Binary Search excels in sorted arrays, capitalizing on their inherent order to quickly locate elements.
+* **Search Space:** Identify the range within which the solution exists, which guides setting up the initial search range.
+* **Midpoint Element:** The middle element provides insights into the properties of elements in different subranges, aiding decisions in adjusting the search range.
+* **Stopping Condition:** Define conditions under which the search should stop, whether an element is found or the search range becomes empty.
+* **Divide and Conquer:** Binary Search employs a "divide and conquer" strategy, progressively reducing the problem size.
+* **Boundary Handling:** Pay special attention to handling boundary conditions, avoiding index out-of-bounds errors.
+* **Precision & Approximations:** Binary Search can yield approximate solutions by adjusting the search criteria.
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Searching 3 Binary Search on Answer.md b/Academy DSA Typed Notes/Advanced/DSA Searching 3 Binary Search on Answer.md
new file mode 100644
index 0000000..fa33107
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Searching 3 Binary Search on Answer.md
@@ -0,0 +1,441 @@
+# Searching 3: Binary Search on Answer
+
+---
+## Problem 1 Painter's Partition
+
+We have to paint all N boards of length [C0, C1, C2, C3 … CN - 1]. There are K painters available and each of them takes 1 units of time to paint 1 unit of the board.
+
+Calculate and return the minimum time required to get the job done.
+> NOTE:
+> 1. Two painters cannot share a board to paint. That is to say, a board cannot be painted partially by one painter, and partially by another.
+> 2. A painter will only paint contiguous boards. This means a painter paints a continous subarray of boards
+
+**Example 1**
+Below are some of the possible configurations:
+ +
+Configuration 1: Max is 31
+Configuration 2: Max is 26
+Configuration 3: Max is 25
+
+**Out of above least is 25**, hence configuration 3 is better. We want to minimize the maximum value.
+
+There can be more configurations, but you'll find the 3rd to be the best, hence **`25`** is the answer.
+
+**Example 2**
+```cpp
+A = [10,20,30,40]
+K = 2
+```
+P1 => red
+P2 => green
+
+
+Configuration 1: Max is 31
+Configuration 2: Max is 26
+Configuration 3: Max is 25
+
+**Out of above least is 25**, hence configuration 3 is better. We want to minimize the maximum value.
+
+There can be more configurations, but you'll find the 3rd to be the best, hence **`25`** is the answer.
+
+**Example 2**
+```cpp
+A = [10,20,30,40]
+K = 2
+```
+P1 => red
+P2 => green
+ +Max = 70
+
+
+Max = 70
+
+ +
+Max = 60
+
+**Output**
+60
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Painter's Partition Greedy Approach
+
+* Greedy Approach:- We can just divide the total time by total number of painters.
+* One might think it as by dividing the boards among the painters would result in least time per painter
+* But is this idea valid ?
+
+### Flaw:
+```cpp
+A = [1,2,3,4,100] K = 2
+```
+According to Idea 1 :- $110/2 = 55$
+
+But we see that it is impossible, because we can't divide the boards among two painters with 55 length each.
+
+---
+### Question
+What is the minimum time to get the job done?
+
+A = [1,2,3,4,100] K = 2
+
+**Choices**
+- [ ] 55
+- [x] 100
+- [ ] 1
+- [ ] 110
+
+
+**Explanation:**
+The minimum time required to Finish the job is 100.
+
+The configuration of the boards is as follows
+
+* painter1 = [1, 2, 3, 4] = 10
+* painter2 = [100] = 100
+
+Thus the maximum of (10, 100) is the minimum time taken to complete the job.
+
+Among all possible configuration **100** is the minimum time achieved.
+
+
+---
+### Painter's Partition Binary Search
+
+
+Lets's look at example below :-
+
+`[3, 5, 1, 7, 8, 2, 5, 3, 10, 1, 4, 7, 5, 4, 6]` ans `K = 4`
+
+Color code for each painter:
+> P1 -> Red
+> P2 -> Green
+> P3 -> Blue
+> P4 -> Orange
+
+---
+#### Search Space
+**Best Case**
+Say we have as many painters as the number of boards, in which case each painter can paint one board. The maximum value will be the answer.
+**Example:**
+`A[ ] = {2, 5, 3, 8}, K = 4`
+`Then 8 is the answer.`
+
+**Worst Case**
+There is ony 1 painter. In this case, sum(array) is the answer.
+
+So, our Search Space will be within range: **[max(array) to sum(array)]**
+
+---
+#### Target
+The max time to complete the task
+
+---
+#### Condition
+
+* Say we land at mid. How can we decide whether mid is the answer?
+* We can check if we can complete the task within mid amount of time at max.
+ * If yes, then we should save it as the answer and move left to try for a lesser time.
+ * Else, move right(it means we will need more time to complete the task )
+
+---
+### Painter's Partition Dry Run and Pseudocode
+
+
+`[3, 5, 1, 7, 8, 2, 5, 3, 10, 1, 4, 7, 5, 4, 6]` ans `K = 4`
+
+* Intially the **Lo = 10** and **Hi = 71** (By using above defined criteria for search space) therefore using the above algorithm Mid = $10 + (71 - 10)/2 = 40$ then we check if it is possible to paint all boards in atleast 40 units below is the configuration that satisfy the condition :-
+ * Painter P1 takes = $3 + 5 + 1 + 7 + 8 + 2 + 5 + 3 = 34$
+ * Painter P2 takes = $10 + 1 + 4 + 7 + 5 + 4 + 6 = 37$
+ *
+
+Max = 60
+
+**Output**
+60
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Painter's Partition Greedy Approach
+
+* Greedy Approach:- We can just divide the total time by total number of painters.
+* One might think it as by dividing the boards among the painters would result in least time per painter
+* But is this idea valid ?
+
+### Flaw:
+```cpp
+A = [1,2,3,4,100] K = 2
+```
+According to Idea 1 :- $110/2 = 55$
+
+But we see that it is impossible, because we can't divide the boards among two painters with 55 length each.
+
+---
+### Question
+What is the minimum time to get the job done?
+
+A = [1,2,3,4,100] K = 2
+
+**Choices**
+- [ ] 55
+- [x] 100
+- [ ] 1
+- [ ] 110
+
+
+**Explanation:**
+The minimum time required to Finish the job is 100.
+
+The configuration of the boards is as follows
+
+* painter1 = [1, 2, 3, 4] = 10
+* painter2 = [100] = 100
+
+Thus the maximum of (10, 100) is the minimum time taken to complete the job.
+
+Among all possible configuration **100** is the minimum time achieved.
+
+
+---
+### Painter's Partition Binary Search
+
+
+Lets's look at example below :-
+
+`[3, 5, 1, 7, 8, 2, 5, 3, 10, 1, 4, 7, 5, 4, 6]` ans `K = 4`
+
+Color code for each painter:
+> P1 -> Red
+> P2 -> Green
+> P3 -> Blue
+> P4 -> Orange
+
+---
+#### Search Space
+**Best Case**
+Say we have as many painters as the number of boards, in which case each painter can paint one board. The maximum value will be the answer.
+**Example:**
+`A[ ] = {2, 5, 3, 8}, K = 4`
+`Then 8 is the answer.`
+
+**Worst Case**
+There is ony 1 painter. In this case, sum(array) is the answer.
+
+So, our Search Space will be within range: **[max(array) to sum(array)]**
+
+---
+#### Target
+The max time to complete the task
+
+---
+#### Condition
+
+* Say we land at mid. How can we decide whether mid is the answer?
+* We can check if we can complete the task within mid amount of time at max.
+ * If yes, then we should save it as the answer and move left to try for a lesser time.
+ * Else, move right(it means we will need more time to complete the task )
+
+---
+### Painter's Partition Dry Run and Pseudocode
+
+
+`[3, 5, 1, 7, 8, 2, 5, 3, 10, 1, 4, 7, 5, 4, 6]` ans `K = 4`
+
+* Intially the **Lo = 10** and **Hi = 71** (By using above defined criteria for search space) therefore using the above algorithm Mid = $10 + (71 - 10)/2 = 40$ then we check if it is possible to paint all boards in atleast 40 units below is the configuration that satisfy the condition :-
+ * Painter P1 takes = $3 + 5 + 1 + 7 + 8 + 2 + 5 + 3 = 34$
+ * Painter P2 takes = $10 + 1 + 4 + 7 + 5 + 4 + 6 = 37$
+ *  + * Since the condition is satisfied let's go to left i.e. $Hi = mid -1 = 40 - 1 = 39$
+
+* Now **Hi = 39** and **Lo = 10**; Mid = $10 + (39 - 10)/2 = 24$
+ * Painter P1 takes = $3 + 5 + 1 + 7 + 8 = 24$
+ * Painter P2 takes = $2 + 5 + 3 + 10 + 1 = 21$
+ * Painter P3 takes = $4 + 7 + 5 + 4 = 20$
+ * Painter P4 takes = 6
+ *
+ * Since the condition is satisfied let's go to left i.e. $Hi = mid -1 = 40 - 1 = 39$
+
+* Now **Hi = 39** and **Lo = 10**; Mid = $10 + (39 - 10)/2 = 24$
+ * Painter P1 takes = $3 + 5 + 1 + 7 + 8 = 24$
+ * Painter P2 takes = $2 + 5 + 3 + 10 + 1 = 21$
+ * Painter P3 takes = $4 + 7 + 5 + 4 = 20$
+ * Painter P4 takes = 6
+ *  + * Since the condition is satisfied let's go to left i.e. $Hi = mid -1 = 24 - 1 = 23$
+
+* Now Hi = 23 and Lo = 10 therefore using the above algorithm Mid = $10 + (23 - 10)/2 = 16$ then we check if it is possible to paint all boards in atleast 10 units We find that there is no configuration that satisfy the condition therefore we go to right.
+
+* Similarly we follow the algorithm to arrive at the solution.
+
+ * Since the condition is satisfied let's go to left i.e. $Hi = mid -1 = 24 - 1 = 23$
+
+* Now Hi = 23 and Lo = 10 therefore using the above algorithm Mid = $10 + (23 - 10)/2 = 16$ then we check if it is possible to paint all boards in atleast 10 units We find that there is no configuration that satisfy the condition therefore we go to right.
+
+* Similarly we follow the algorithm to arrive at the solution.
+ +
+
+#### Pseudocode
+```cpp
+
+// Find minimum painters required for given maximum length (Length that painter can paint)
+paintersNumber(arr[], N, mid, K) {
+ res = 0, numPainters = 1;
+
+ for (i = 0; i < N; i++) {
+ res += arr[i];
+
+ if (res > mid) {
+ res = arr[i];
+ numPainters++;
+ }
+ }
+ //if we have used less than or equal to given number of painters,
+ //then the configurations works
+ if (numPainters <= K) return true;
+ else return false;
+}
+
+partition(arr[], N, K) {
+ Lo = maxEle(arr, N);
+ Hi = sumArr(arr, N);
+
+ while (Lo <= Hi) {
+ mid = Lo + (Hi - Lo) / 2;
+
+ if (paintersNumber(arr, N, mid, K))
+ ans = mid
+ Hi = mid - 1;
+ else
+ Lo = mid + 1;
+ }
+ return ans;
+}
+```
+
+#### Complexities
+
+**Time Complexity:** O(log (sum - max) * N )
+**Space Complexity:** O(1)
+
+
+---
+### Question
+What is the time complexity of the Painters Partition Problem?
+
+**Choices**
+- [x] O( log(k) * (sum(boards) - max(boards)))
+- [ ] O(k * log(sum(boards) - max(boards)))
+- [ ] O(N * log(sum(boards) - max(boards)))
+- [ ] O(k * log N)
+
+
+
+---
+### Problem 2 Aggresive Cows
+
+Given N cows & M stalls ,all M stalls are located at the different locations at x-axis, place all the cows such that minimum distance between any two cows is maximized.
+> Note :
+> 1. There can be only one cow in a stall at a time
+> 2. We need to place all cows
+
+**Testcase 1**
+```cpp
+stalls = [1, 2, 4, 8, 9]
+cows = 3
+stall = 5
+```
+**Solution**
+
+```cpp
+T = 3
+```
+**Explaination TestCase 1**
+
+
+
+| 1 | 2 | 4 | 8 | 9 | Min distance |
+|:---:|:---:|:---:|:---:|:---:|:------------:|
+| c1 | c2 | c3 | | | 1 |
+| c1 | | c2 | | c3 | 3 |
+| c1 | | | c2 | c3 | 1 |
+
+
+* If we put cows according to the first configuration then min distance = 1 because of c1 and c2 (shortest distance between any two cows is 1).
+* If we put cows according to the Second configuration then min distance = 3 because of c1 and c2 (shortest distance between any two cows is 3)
+* If we put cows according to the third configuration then min distance = 1 because of c2 and c3 (shortest distance between any two cows is 1).
+* Therefore answer = max(1,3,1) = 3
+
+**Testcase 2**
+```cpp
+stalls = [2, 6, 11, 14, 19, 25, 30, 39, 43]
+cows = 4
+stall = 9
+```
+**Solution**
+
+```cpp
+T = 12
+```
+**Explaination TestCase 2**
+
+| 2 | 6 | 11 | 14 | 19 | 25 | 30 | 39 | 43 | Min distance |
+|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:------------:|
+| c1 | c2 | c3 | c4 | | | | | | 3 |
+| c1 | | c2 | | c3 | | c4 | | | 8 |
+| c1 | | | c2 | | | c3 | | c4 | 12 |
+
+* If we put cows according to the first configuration then min distance = 3
+* If we put cows according to the Second configuration then min distance = 8
+* If we put cows according to the third configuration then min distance = 12
+* Therefore answer = max(3,8,12) = 12
+
+
+---
+### Question
+What is the objective of the problem described?
+
+**Choices**
+- [ ] Place cows in stalls randomly.
+- [ ] Place cows in stalls such that the distance between any two cows is minimized.
+- [x] Place cows in stalls such that the minimum distance between any two cows is maximized.
+- [ ] Place cows in stalls such that the total distance is minimized.
+
+---
+### Question
+What will be the maximum value of the distance between the closest cows in this case?
+A: 0, 3, 4, 7, 9, 10
+K = 4
+
+
+**Choices**
+- [ ] 10
+- [ ] 4
+- [x] 3
+- [ ] 2
+
+
+
+**Explanation:**
+
+The 4 cows are placed in stalls at 0, 3, 7, 10. This is the optimal configuration.
+
+The value between the closest cows can be found by
+= min(3 - 0, 7 - 3, 10 - 7)
+= min(3, 4, 3)
+= 3
+
+Thus the maximum result is 3 over all possible configurations.
+
+
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+### Aggresive Cows Binary Search Approach
+
+
+Let's use testcase 2 to get the intuition of the question.
+
+This question is similar to Painter's Partition problem. Instead of minimising the maximum answer, we have to maximise the minimum distance.
+
+#### Search Space
+
+* **Worst Case:**
+If say there are same cows as the number of stalls, then we place each cow at 1 stall. Then we can find difference between adjacent stalls. The minimum out of them is the answer.
+**Example:**
+`A[ ] = {4, 7, 14, 20}`
+`7 - 4 = 3`
+`14 - 7 = 7`
+`20 - 14 = 6`
+`min(3, 7, 6) = 3(answer)`
+Though, we can take 1 as the minimum value.
+
+* **Best Case:**
+There are two cows. Then, we can place them at the corner stalls. The distance between first and last stall will be the answer.
+
+**Search Space:** [1 A[N-1]-A[0]]
+
+#### Condition
+Say we land at mid, now we can check if it is possible to keep cows at a minimum distance of mid.
+* If yes, save it and check for farther distance, i.e, move right.
+* Else, if keeping at a distance of mid is not possible, then we should try reducing the distance; hence, move left.
+
+**Example 1:**
+*Let's check if we can put 4 cows at minimum distance of 20.*
+
+ | 2 | 6 | 11 | 14 | 19 | 25 | 30 | 39 | 43 | Min distance |
+ |:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:------------:|
+ | c1 | | | | | c2 | | | | 20 |
+
+In above configuration minimum distance is 20 but we are unable to accommodate all cows(no place for c3 and c4). This means that we have to reduce the distance to accomodate all cows.
+
+**Example 2:**
+*Let's check if we can put cows at minimum distance of atleast 5 below is a configuration that satisfy the condition.*
+
+| 2 | 6 | 11 | 14 | 19 | 25 | 30 | 39 | 43 | Min distance |
+|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:------------:|
+| c1 | | c2 | | c3 | c4 | | | | 5 |
+
+Since we are able to place all cows at a minimum distance of 5, we should save it as answer and try to maximise this distance.
+
+
+---
+### Aggresive Cows Dry Run and Pseudocode
+
+
+Below is the trace of algorithm on above Example :-
+
+* Intially the Hi = 41 and Lo = 3 (By using above defined criteria for search space) therefore using the above algorithm Mid = $3 + (41 - 3)/2 = 22$ then we check if it is possible to accommodate 4 cows completely in the shelters with min distance being 22 units We could not find any such configuration that satisfy the condition (got to left) below one failed configuration :-
+
+ | 2 | 6 | 11 | 14 | 19 | 25 | 30 | 39 | 43 | Min distance |
+ |:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:-----------------------------------:|
+ | c1 | | | c2 | | | | c3 | | N/A since all cows not accommodated |
+
+* Now the Hi = 21 and Lo = 3 therefore using the above algorithm Mid = $3 + (21 - 3)/2 = 12$ then we check if it is possible to accommodate 4 cows completely in the shelters with min distance being 12 units below is configuration that satisfies the condition (we go to right) :-
+
+| 2 | 6 | 11 | 14 | 19 | 25 | 30 | 39 | 43 | Min distance |
+|:---:|:---:|:---:|:---:| --- | --- |:---:| --- | --- |:------------:|
+| c1 | | | c2 | | | c3 | | c4 | 12 |
+
+* Now the Hi = 21 and Lo = 13 therefore using the above algorithm Mid = $13 + (21 - 13)/2 = 17$ then we check if it is possible to accommodate 4 cows completely in the shelters with min distance being 17 units We could not find any such configuration that satisfy the condition (got to left) below one failed configuration :-
+
+ | 2 | 6 | 11 | 14 | 19 | 25 | 30 | 39 | 43 | Min distance |
+|:---:|:---:|:---:|:---:| --- | --- |:---:| --- | --- |:------------:|
+| c1 | | | | c2 | | | c3 | | N/A since all cows not accommodated |
+
+
+
+
+
+#### Pseudocode
+```cpp
+
+// Find minimum painters required for given maximum length (Length that painter can paint)
+paintersNumber(arr[], N, mid, K) {
+ res = 0, numPainters = 1;
+
+ for (i = 0; i < N; i++) {
+ res += arr[i];
+
+ if (res > mid) {
+ res = arr[i];
+ numPainters++;
+ }
+ }
+ //if we have used less than or equal to given number of painters,
+ //then the configurations works
+ if (numPainters <= K) return true;
+ else return false;
+}
+
+partition(arr[], N, K) {
+ Lo = maxEle(arr, N);
+ Hi = sumArr(arr, N);
+
+ while (Lo <= Hi) {
+ mid = Lo + (Hi - Lo) / 2;
+
+ if (paintersNumber(arr, N, mid, K))
+ ans = mid
+ Hi = mid - 1;
+ else
+ Lo = mid + 1;
+ }
+ return ans;
+}
+```
+
+#### Complexities
+
+**Time Complexity:** O(log (sum - max) * N )
+**Space Complexity:** O(1)
+
+
+---
+### Question
+What is the time complexity of the Painters Partition Problem?
+
+**Choices**
+- [x] O( log(k) * (sum(boards) - max(boards)))
+- [ ] O(k * log(sum(boards) - max(boards)))
+- [ ] O(N * log(sum(boards) - max(boards)))
+- [ ] O(k * log N)
+
+
+
+---
+### Problem 2 Aggresive Cows
+
+Given N cows & M stalls ,all M stalls are located at the different locations at x-axis, place all the cows such that minimum distance between any two cows is maximized.
+> Note :
+> 1. There can be only one cow in a stall at a time
+> 2. We need to place all cows
+
+**Testcase 1**
+```cpp
+stalls = [1, 2, 4, 8, 9]
+cows = 3
+stall = 5
+```
+**Solution**
+
+```cpp
+T = 3
+```
+**Explaination TestCase 1**
+
+
+
+| 1 | 2 | 4 | 8 | 9 | Min distance |
+|:---:|:---:|:---:|:---:|:---:|:------------:|
+| c1 | c2 | c3 | | | 1 |
+| c1 | | c2 | | c3 | 3 |
+| c1 | | | c2 | c3 | 1 |
+
+
+* If we put cows according to the first configuration then min distance = 1 because of c1 and c2 (shortest distance between any two cows is 1).
+* If we put cows according to the Second configuration then min distance = 3 because of c1 and c2 (shortest distance between any two cows is 3)
+* If we put cows according to the third configuration then min distance = 1 because of c2 and c3 (shortest distance between any two cows is 1).
+* Therefore answer = max(1,3,1) = 3
+
+**Testcase 2**
+```cpp
+stalls = [2, 6, 11, 14, 19, 25, 30, 39, 43]
+cows = 4
+stall = 9
+```
+**Solution**
+
+```cpp
+T = 12
+```
+**Explaination TestCase 2**
+
+| 2 | 6 | 11 | 14 | 19 | 25 | 30 | 39 | 43 | Min distance |
+|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:------------:|
+| c1 | c2 | c3 | c4 | | | | | | 3 |
+| c1 | | c2 | | c3 | | c4 | | | 8 |
+| c1 | | | c2 | | | c3 | | c4 | 12 |
+
+* If we put cows according to the first configuration then min distance = 3
+* If we put cows according to the Second configuration then min distance = 8
+* If we put cows according to the third configuration then min distance = 12
+* Therefore answer = max(3,8,12) = 12
+
+
+---
+### Question
+What is the objective of the problem described?
+
+**Choices**
+- [ ] Place cows in stalls randomly.
+- [ ] Place cows in stalls such that the distance between any two cows is minimized.
+- [x] Place cows in stalls such that the minimum distance between any two cows is maximized.
+- [ ] Place cows in stalls such that the total distance is minimized.
+
+---
+### Question
+What will be the maximum value of the distance between the closest cows in this case?
+A: 0, 3, 4, 7, 9, 10
+K = 4
+
+
+**Choices**
+- [ ] 10
+- [ ] 4
+- [x] 3
+- [ ] 2
+
+
+
+**Explanation:**
+
+The 4 cows are placed in stalls at 0, 3, 7, 10. This is the optimal configuration.
+
+The value between the closest cows can be found by
+= min(3 - 0, 7 - 3, 10 - 7)
+= min(3, 4, 3)
+= 3
+
+Thus the maximum result is 3 over all possible configurations.
+
+
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+### Aggresive Cows Binary Search Approach
+
+
+Let's use testcase 2 to get the intuition of the question.
+
+This question is similar to Painter's Partition problem. Instead of minimising the maximum answer, we have to maximise the minimum distance.
+
+#### Search Space
+
+* **Worst Case:**
+If say there are same cows as the number of stalls, then we place each cow at 1 stall. Then we can find difference between adjacent stalls. The minimum out of them is the answer.
+**Example:**
+`A[ ] = {4, 7, 14, 20}`
+`7 - 4 = 3`
+`14 - 7 = 7`
+`20 - 14 = 6`
+`min(3, 7, 6) = 3(answer)`
+Though, we can take 1 as the minimum value.
+
+* **Best Case:**
+There are two cows. Then, we can place them at the corner stalls. The distance between first and last stall will be the answer.
+
+**Search Space:** [1 A[N-1]-A[0]]
+
+#### Condition
+Say we land at mid, now we can check if it is possible to keep cows at a minimum distance of mid.
+* If yes, save it and check for farther distance, i.e, move right.
+* Else, if keeping at a distance of mid is not possible, then we should try reducing the distance; hence, move left.
+
+**Example 1:**
+*Let's check if we can put 4 cows at minimum distance of 20.*
+
+ | 2 | 6 | 11 | 14 | 19 | 25 | 30 | 39 | 43 | Min distance |
+ |:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:------------:|
+ | c1 | | | | | c2 | | | | 20 |
+
+In above configuration minimum distance is 20 but we are unable to accommodate all cows(no place for c3 and c4). This means that we have to reduce the distance to accomodate all cows.
+
+**Example 2:**
+*Let's check if we can put cows at minimum distance of atleast 5 below is a configuration that satisfy the condition.*
+
+| 2 | 6 | 11 | 14 | 19 | 25 | 30 | 39 | 43 | Min distance |
+|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:------------:|
+| c1 | | c2 | | c3 | c4 | | | | 5 |
+
+Since we are able to place all cows at a minimum distance of 5, we should save it as answer and try to maximise this distance.
+
+
+---
+### Aggresive Cows Dry Run and Pseudocode
+
+
+Below is the trace of algorithm on above Example :-
+
+* Intially the Hi = 41 and Lo = 3 (By using above defined criteria for search space) therefore using the above algorithm Mid = $3 + (41 - 3)/2 = 22$ then we check if it is possible to accommodate 4 cows completely in the shelters with min distance being 22 units We could not find any such configuration that satisfy the condition (got to left) below one failed configuration :-
+
+ | 2 | 6 | 11 | 14 | 19 | 25 | 30 | 39 | 43 | Min distance |
+ |:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:-----------------------------------:|
+ | c1 | | | c2 | | | | c3 | | N/A since all cows not accommodated |
+
+* Now the Hi = 21 and Lo = 3 therefore using the above algorithm Mid = $3 + (21 - 3)/2 = 12$ then we check if it is possible to accommodate 4 cows completely in the shelters with min distance being 12 units below is configuration that satisfies the condition (we go to right) :-
+
+| 2 | 6 | 11 | 14 | 19 | 25 | 30 | 39 | 43 | Min distance |
+|:---:|:---:|:---:|:---:| --- | --- |:---:| --- | --- |:------------:|
+| c1 | | | c2 | | | c3 | | c4 | 12 |
+
+* Now the Hi = 21 and Lo = 13 therefore using the above algorithm Mid = $13 + (21 - 13)/2 = 17$ then we check if it is possible to accommodate 4 cows completely in the shelters with min distance being 17 units We could not find any such configuration that satisfy the condition (got to left) below one failed configuration :-
+
+ | 2 | 6 | 11 | 14 | 19 | 25 | 30 | 39 | 43 | Min distance |
+|:---:|:---:|:---:|:---:| --- | --- |:---:| --- | --- |:------------:|
+| c1 | | | | c2 | | | c3 | | N/A since all cows not accommodated |
+
+
+ +
+#### Pseudocode
+```cpp
+
+bool check(v[], int x, int c) {
+ n = v.size();
+ count = 1;
+ last = 0;
+ for (i = 0; i < n; i++) {
+ if (v[i] - v[last] >= x) {
+ last = i; //cow placed
+ count++;
+ }
+ if (count >= c) {
+ return true;
+ }
+ }
+ return false;
+}
+
+// Function to find the maximum possible
+// minimum distance between the cows
+aggressive_cows(v[], size, cows) {
+ int lo = 0;
+ for (i = 1; i < n; i++) {
+ lo = min(lo, v[i] - v[i - 1]);
+ }
+ hi = v[n - 1] - v[0];
+ ans = -1;
+
+ // Applying Binary search
+ while (lo <= hi) {
+ mid = lo + (hi - lo) / 2;
+ if (check(v, mid, cows)) {
+ ans = mid;
+ lo = mid + 1;
+ } else {
+ hi = mid - 1;
+ }
+ }
+
+ return ans;
+}
+```
+
+---
+### Binary Search Problems Identification
+
+* These type of problems generally has following characteristics :-
+ * There are two or three parameter & constraints
+ * Requirement is to maximize or minimize the given parameter
+* One tricky point is to find search space which is generally the parameter asked to maximize or minimize.
+* The problem should be **Monotonic** in nature i.e after one point it is not feasible to solve or vice versa.
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Sorting 1 Count Sort & Merge Sort.md b/Academy DSA Typed Notes/Advanced/DSA Sorting 1 Count Sort & Merge Sort.md
new file mode 100644
index 0000000..3c9b5fa
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Sorting 1 Count Sort & Merge Sort.md
@@ -0,0 +1,556 @@
+# Count Sort & Merge Sort
+
+---
+## Count Sort
+
+Find the smallest number that can be formed by rearranging the digits of the given number in an array. Return the smallest number in the form an array.
+
+**Example:**
+A[ ] = `{6, 3, 4, 2, 7, 2, 1}`
+Answer: `{1, 2, 2, 3, 4, 6, 7}`
+
+A[ ] = `{4, 2, 7, 3, 9, 0}`
+Answer: `{0, 2, 3, 4, 7, 9}`
+
+#### Observation/Hint
+we can to construct a number using digits. The digits in a number can only `range from 0 to 9`, thus instead of sorting the number which takes `O(N log N)` time, one can leverage this fixed range to derive a faster solution.
+
+#### Approach
+
+* **Frequency Count:** Create an `array of size 10` to count the frequency of each digit in the given number.
+* Using the frequency array, reconstruct the original array in ascending order.
+* This method of sorting based on frequency counting is often called "**`Count Sort`**".
+
+#### Pseudocode
+
+```cpp
+Frequency Array of size 10
+F = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
+
+for i -> 0 to(N - 1) {
+ F[A[i]]++
+}
+
+k = 0
+
+for d -> 0 to 9 { // For each digit
+ for i -> 1 to F[d] {
+ A[k] = d
+ k++
+ }
+}
+
+return A
+```
+
+#### Dry Run
+
+* A = `[1, 3, 8, 2, 3, 5, 3, 8, 5, 2, 2, 3]` (Given Array)
+* F = `[0, 1, 3, 4, 0, 2, 0, 0, 2, 0]` (Frequency Array)
+* Reconstructing A using F:
+1 (once), 2 (three times), 3 (four times), 5 (two times), 8 (two times)
+* Resulting A = `[1, 2, 2, 2, 3, 3, 3, 3, 5, 5, 8, 8]`
+
+#### TC and SC
+* **Time Complexity:** O(N)
+* **Space Complexity:** O(1) (Since the size of the frequency array is constant, regardless of the size of N).
+
+---
+### Count Sort on large values
+
+### Will Count Sort work if the range of A[i] is more than $10^9$?
+
+* Count Sort isn't suitable for a range of $10^9$ because a frequency array of this size would demand too much memory.
+* Count Sort works well when the range of A[i] is ~ $10^6$.
+
+Each integer typically occupies `4 Bytes`.
+
+Storing $10^9$ integers requires 4GB, which is often impractical. An array up to $10^6$ in length is more manageable, needing 4MB.
+
+---
+### Count Sort on Negative Numbers
+
+Implement Count Sort for an array containing negative numbers.
+
+#### Observation/Hint
+Unlike conventional **Count Sort**, which operates on non-negative integers, this variation needs to account for negative numbers. The method involves adjusting indices in the frequency array based on the smallest element in the original array.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Approach
+
+* **Find Range:** Determine the smallest and largest elements in the array to ascertain the range.
+* **Adjust for Negative Numbers:** By adjusting indices in the frequency array based on the smallest element, negative numbers can be accounted for.
+
+**Example**
+
+* Given A = [-2, 3, 8, 3, -2, 3]
+* Smallest = -2, Largest = 8
+* Range = 11 (8 - (-2) + 1)
+* Frequency array F = [2, 0, 0, 3, 0, 0, 0, 0, 1]
+* 0th index frequency is mapped with -2, 1st index with -1, and so on.
+* Reconstructed A using F: -2, -2, 3, 3, 3, 8
+
+#### Pseudocode
+
+```cpp
+//Find smallest and largest elements in A
+//Create a frequency array F of size (largest - smallest + 1)
+
+for i -> 0 to(N - 1) {
+ F[A[i] - smallest_element]++
+}
+
+//Reconstruct array A using F
+
+for each index i in F {
+ while F[i] > 0 {
+ Append(i + smallest_element) to A
+ F[i]--
+ }
+}
+```
+
+#### TC and SC
+* **Time Complexity (TC):** O(N)
+* **Space Complexity (SC):** O(N + Range)
+
+---
+### Merge two sorted arrays
+
+Giver an integer array where all odd elements are sorted and all even elements are sorted. Sort the entire array.
+
+A[] = {`2, 5, 4, 8, 11, 13, 10, 15, 21`}
+
+#### Approach
+We can take two separate arrays to keep even(EVEN[]) and odd(ODD[]) elements. Then we can merge them in the original array.
+
+We will keep three pointers here: `a(for original array)`, `e(for even array)` and `o(for odd array)`, all starting at index 0.
+
+If A[a] is odd, ODD[o]=A[a], o++, a++
+If A[a] is even, EVEN[e]=A[a], e++, a++
+
+---
+#### Pseudocode
+
+```java
+void merge(A[]) {
+ int N = A.length();
+ //n1: count of even elements
+ //n2: count of odd elements
+ int EVEN[n1], ODD[n2];
+ int a = 0, e = 0, o = 0;
+
+ for (int i = 0; i < N; i++) {
+ if (A[a] % 2 == 0) {
+ EVEN[e] = A[a];
+ e++;
+ } else {
+ ODD[o] = A[a];
+ o++;
+ }
+ a++;
+ }
+
+ a = 0; // moves over A
+ e = 0; // moves over EVEN
+ o = 0; // moves over ODD
+
+ while (e < n1 && o < n2) {
+ if (EVEN[e] < ODD[o]) {
+ A[a] = EVEN[e];
+ e++;
+ } else {
+ A[a] = ODD[o];
+ o++;
+ }
+ a++;
+ }
+
+ while (e < n1) {
+ A[a] = EVEN[e];
+ e++;
+ a++;
+ }
+
+ while (o < n2) {
+ A[a] = ODD[o];
+ a++;
+ o++;
+ }
+}
+```
+
+---
+### Question
+Iteration of merging 2 Arrays?
+
+**Choices**
+- [ ] N ^ 3
+- [ ] N ^ 2
+- [x] 2 * N
+- [ ] Constant
+
+
+---
+### Merge Sort
+
+### Example: Sorting Examination Sheets
+>A teacher collected the examination sheets of students randomly. Now, she needs to sort those sheets as per roll number of students. As she is smart, instead of sorting it by herself, she divided the sheets into two halves and gave each half to Kishore and Suraj for sorting.
+
+>Once she has the sorted halves, she just need to merge two sorted halves, which is significantly easier.
+
+>Kishore and Suraj also decided to repeat this and divided the sheets in two halves and gave them to their friends for sorting.
+
+
+
+#### Pseudocode
+```cpp
+
+bool check(v[], int x, int c) {
+ n = v.size();
+ count = 1;
+ last = 0;
+ for (i = 0; i < n; i++) {
+ if (v[i] - v[last] >= x) {
+ last = i; //cow placed
+ count++;
+ }
+ if (count >= c) {
+ return true;
+ }
+ }
+ return false;
+}
+
+// Function to find the maximum possible
+// minimum distance between the cows
+aggressive_cows(v[], size, cows) {
+ int lo = 0;
+ for (i = 1; i < n; i++) {
+ lo = min(lo, v[i] - v[i - 1]);
+ }
+ hi = v[n - 1] - v[0];
+ ans = -1;
+
+ // Applying Binary search
+ while (lo <= hi) {
+ mid = lo + (hi - lo) / 2;
+ if (check(v, mid, cows)) {
+ ans = mid;
+ lo = mid + 1;
+ } else {
+ hi = mid - 1;
+ }
+ }
+
+ return ans;
+}
+```
+
+---
+### Binary Search Problems Identification
+
+* These type of problems generally has following characteristics :-
+ * There are two or three parameter & constraints
+ * Requirement is to maximize or minimize the given parameter
+* One tricky point is to find search space which is generally the parameter asked to maximize or minimize.
+* The problem should be **Monotonic** in nature i.e after one point it is not feasible to solve or vice versa.
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Sorting 1 Count Sort & Merge Sort.md b/Academy DSA Typed Notes/Advanced/DSA Sorting 1 Count Sort & Merge Sort.md
new file mode 100644
index 0000000..3c9b5fa
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Sorting 1 Count Sort & Merge Sort.md
@@ -0,0 +1,556 @@
+# Count Sort & Merge Sort
+
+---
+## Count Sort
+
+Find the smallest number that can be formed by rearranging the digits of the given number in an array. Return the smallest number in the form an array.
+
+**Example:**
+A[ ] = `{6, 3, 4, 2, 7, 2, 1}`
+Answer: `{1, 2, 2, 3, 4, 6, 7}`
+
+A[ ] = `{4, 2, 7, 3, 9, 0}`
+Answer: `{0, 2, 3, 4, 7, 9}`
+
+#### Observation/Hint
+we can to construct a number using digits. The digits in a number can only `range from 0 to 9`, thus instead of sorting the number which takes `O(N log N)` time, one can leverage this fixed range to derive a faster solution.
+
+#### Approach
+
+* **Frequency Count:** Create an `array of size 10` to count the frequency of each digit in the given number.
+* Using the frequency array, reconstruct the original array in ascending order.
+* This method of sorting based on frequency counting is often called "**`Count Sort`**".
+
+#### Pseudocode
+
+```cpp
+Frequency Array of size 10
+F = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
+
+for i -> 0 to(N - 1) {
+ F[A[i]]++
+}
+
+k = 0
+
+for d -> 0 to 9 { // For each digit
+ for i -> 1 to F[d] {
+ A[k] = d
+ k++
+ }
+}
+
+return A
+```
+
+#### Dry Run
+
+* A = `[1, 3, 8, 2, 3, 5, 3, 8, 5, 2, 2, 3]` (Given Array)
+* F = `[0, 1, 3, 4, 0, 2, 0, 0, 2, 0]` (Frequency Array)
+* Reconstructing A using F:
+1 (once), 2 (three times), 3 (four times), 5 (two times), 8 (two times)
+* Resulting A = `[1, 2, 2, 2, 3, 3, 3, 3, 5, 5, 8, 8]`
+
+#### TC and SC
+* **Time Complexity:** O(N)
+* **Space Complexity:** O(1) (Since the size of the frequency array is constant, regardless of the size of N).
+
+---
+### Count Sort on large values
+
+### Will Count Sort work if the range of A[i] is more than $10^9$?
+
+* Count Sort isn't suitable for a range of $10^9$ because a frequency array of this size would demand too much memory.
+* Count Sort works well when the range of A[i] is ~ $10^6$.
+
+Each integer typically occupies `4 Bytes`.
+
+Storing $10^9$ integers requires 4GB, which is often impractical. An array up to $10^6$ in length is more manageable, needing 4MB.
+
+---
+### Count Sort on Negative Numbers
+
+Implement Count Sort for an array containing negative numbers.
+
+#### Observation/Hint
+Unlike conventional **Count Sort**, which operates on non-negative integers, this variation needs to account for negative numbers. The method involves adjusting indices in the frequency array based on the smallest element in the original array.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Approach
+
+* **Find Range:** Determine the smallest and largest elements in the array to ascertain the range.
+* **Adjust for Negative Numbers:** By adjusting indices in the frequency array based on the smallest element, negative numbers can be accounted for.
+
+**Example**
+
+* Given A = [-2, 3, 8, 3, -2, 3]
+* Smallest = -2, Largest = 8
+* Range = 11 (8 - (-2) + 1)
+* Frequency array F = [2, 0, 0, 3, 0, 0, 0, 0, 1]
+* 0th index frequency is mapped with -2, 1st index with -1, and so on.
+* Reconstructed A using F: -2, -2, 3, 3, 3, 8
+
+#### Pseudocode
+
+```cpp
+//Find smallest and largest elements in A
+//Create a frequency array F of size (largest - smallest + 1)
+
+for i -> 0 to(N - 1) {
+ F[A[i] - smallest_element]++
+}
+
+//Reconstruct array A using F
+
+for each index i in F {
+ while F[i] > 0 {
+ Append(i + smallest_element) to A
+ F[i]--
+ }
+}
+```
+
+#### TC and SC
+* **Time Complexity (TC):** O(N)
+* **Space Complexity (SC):** O(N + Range)
+
+---
+### Merge two sorted arrays
+
+Giver an integer array where all odd elements are sorted and all even elements are sorted. Sort the entire array.
+
+A[] = {`2, 5, 4, 8, 11, 13, 10, 15, 21`}
+
+#### Approach
+We can take two separate arrays to keep even(EVEN[]) and odd(ODD[]) elements. Then we can merge them in the original array.
+
+We will keep three pointers here: `a(for original array)`, `e(for even array)` and `o(for odd array)`, all starting at index 0.
+
+If A[a] is odd, ODD[o]=A[a], o++, a++
+If A[a] is even, EVEN[e]=A[a], e++, a++
+
+---
+#### Pseudocode
+
+```java
+void merge(A[]) {
+ int N = A.length();
+ //n1: count of even elements
+ //n2: count of odd elements
+ int EVEN[n1], ODD[n2];
+ int a = 0, e = 0, o = 0;
+
+ for (int i = 0; i < N; i++) {
+ if (A[a] % 2 == 0) {
+ EVEN[e] = A[a];
+ e++;
+ } else {
+ ODD[o] = A[a];
+ o++;
+ }
+ a++;
+ }
+
+ a = 0; // moves over A
+ e = 0; // moves over EVEN
+ o = 0; // moves over ODD
+
+ while (e < n1 && o < n2) {
+ if (EVEN[e] < ODD[o]) {
+ A[a] = EVEN[e];
+ e++;
+ } else {
+ A[a] = ODD[o];
+ o++;
+ }
+ a++;
+ }
+
+ while (e < n1) {
+ A[a] = EVEN[e];
+ e++;
+ a++;
+ }
+
+ while (o < n2) {
+ A[a] = ODD[o];
+ a++;
+ o++;
+ }
+}
+```
+
+---
+### Question
+Iteration of merging 2 Arrays?
+
+**Choices**
+- [ ] N ^ 3
+- [ ] N ^ 2
+- [x] 2 * N
+- [ ] Constant
+
+
+---
+### Merge Sort
+
+### Example: Sorting Examination Sheets
+>A teacher collected the examination sheets of students randomly. Now, she needs to sort those sheets as per roll number of students. As she is smart, instead of sorting it by herself, she divided the sheets into two halves and gave each half to Kishore and Suraj for sorting.
+
+>Once she has the sorted halves, she just need to merge two sorted halves, which is significantly easier.
+
+>Kishore and Suraj also decided to repeat this and divided the sheets in two halves and gave them to their friends for sorting.
+
+ +
+>In this way, the last students will have one sheet only. They can directly gave that sheet to the students before them whose job will be to arrange those two sheets and pass it above.
+
+
+
+>In this way, the last students will have one sheet only. They can directly gave that sheet to the students before them whose job will be to arrange those two sheets and pass it above.
+
+ +
+
+>In this way, the sheets are finally sorted.
+
+**Example: Sorting Numbers**
+Sort the array, A = {3, 10, 6, 8, 15, 2, 12, 18, 17}
+
+#### Divide
+
+* The idea is to divide the numbers in two halves and then start merging the sorted arrays from bottom and pass above.
+
+
+
+>In this way, the sheets are finally sorted.
+
+**Example: Sorting Numbers**
+Sort the array, A = {3, 10, 6, 8, 15, 2, 12, 18, 17}
+
+#### Divide
+
+* The idea is to divide the numbers in two halves and then start merging the sorted arrays from bottom and pass above.
+ +
+
+#### Merge
+- Merging [3] and [10] as [3, 10]
+
+
+
+#### Merge
+- Merging [3] and [10] as [3, 10]
+ +
+- Merging [3, 10] and [6] as [3, 6, 10]
+
+
+- Merging [3, 10] and [6] as [3, 6, 10]
+ +
+- Merging [8] and [15] as [8, 15]
+
+
+- Merging [8] and [15] as [8, 15]
+ +
+- Merging [3, 6, 10] and [8, 15] as [3, 6, 8, 10, 15]
+
+
+- Merging [3, 6, 10] and [8, 15] as [3, 6, 8, 10, 15]
+ +
+- Merging [2] and [12] as [2, 12]
+
+
+- Merging [2] and [12] as [2, 12]
+ +
+- Merging [18] and [17] as [17, 18]
+
+
+- Merging [18] and [17] as [17, 18]
+ +
+- Merging [2, 12] and [17, 18] as [2, 12, 17, 18]
+
+
+- Merging [2, 12] and [17, 18] as [2, 12, 17, 18]
+ +
+- Merging [3, 6, 8, 10, 15] and [2, 12, 17, 18] as [2, 3, 6, 8, 10, 12, 15, 17, 18]
+
+
+- Merging [3, 6, 8, 10, 15] and [2, 12, 17, 18] as [2, 3, 6, 8, 10, 12, 15, 17, 18]
+ +
+In this way, we have finally sorted the array.
+
+***This algorithm of dividing the array into multiple subproblems and merging them one by one is called Merge Sort.***
+
+*Since we are breaking down the array into multiple subproblems and applying the same idea to merge them, we are using the technique of Recursion.*
+
+
+#### Psuedocode
+```java
+void merge(A[], l, mid, r) {
+ int N = A.length();
+ int n1 = mid - l + 1;
+ int n2 = r - mid;
+
+ int B[n1], C[n2];
+
+ int idx = 0;
+ for (int i = l; i <= mid; i++) {
+ B[idx] = A[i];
+ idx++;
+ }
+
+ idx = 0;
+ for (int i = mid + 1; i <= r; i++) {
+ C[idx] = A[i];
+ idx++;
+ }
+
+ idx = l;
+ i = 0; // moves over A
+ j = 0; // moves over B
+
+ while (i < n1 && j < n2) {
+ if (B[i] <= C[j]) {
+ A[idx] = B[i];
+ i++;
+ } else {
+ A[idx] = C[j];
+ j++;
+ }
+ idx++;
+ }
+
+ while (i < n1) {
+ A[idx] = B[i];
+ idx++;
+ i++;
+ }
+
+ while (j < n2) {
+ A[idx] = C[j];
+ idx++;
+ j++;
+ }
+}
+
+void mergeSort(int A[], l, r) {
+ if (l == r) return; // base case
+
+ int mid = (l + r) / 2;
+ mergeSort(A, l, mid);
+ mergeSort(A, mid + 1, r);
+ merge(A, l, mid, r);
+}
+```
+
+#### Complexity Analysis:
+If we divide the arrays in two halves, we will have a tree structure as:
+
+
+
+In this way, we have finally sorted the array.
+
+***This algorithm of dividing the array into multiple subproblems and merging them one by one is called Merge Sort.***
+
+*Since we are breaking down the array into multiple subproblems and applying the same idea to merge them, we are using the technique of Recursion.*
+
+
+#### Psuedocode
+```java
+void merge(A[], l, mid, r) {
+ int N = A.length();
+ int n1 = mid - l + 1;
+ int n2 = r - mid;
+
+ int B[n1], C[n2];
+
+ int idx = 0;
+ for (int i = l; i <= mid; i++) {
+ B[idx] = A[i];
+ idx++;
+ }
+
+ idx = 0;
+ for (int i = mid + 1; i <= r; i++) {
+ C[idx] = A[i];
+ idx++;
+ }
+
+ idx = l;
+ i = 0; // moves over A
+ j = 0; // moves over B
+
+ while (i < n1 && j < n2) {
+ if (B[i] <= C[j]) {
+ A[idx] = B[i];
+ i++;
+ } else {
+ A[idx] = C[j];
+ j++;
+ }
+ idx++;
+ }
+
+ while (i < n1) {
+ A[idx] = B[i];
+ idx++;
+ i++;
+ }
+
+ while (j < n2) {
+ A[idx] = C[j];
+ idx++;
+ j++;
+ }
+}
+
+void mergeSort(int A[], l, r) {
+ if (l == r) return; // base case
+
+ int mid = (l + r) / 2;
+ mergeSort(A, l, mid);
+ mergeSort(A, mid + 1, r);
+ merge(A, l, mid, r);
+}
+```
+
+#### Complexity Analysis:
+If we divide the arrays in two halves, we will have a tree structure as:
+
+ +
++The time taken at every level is the time taken by merging the arrays which will be O(N). + +Height of Tree / Number of Levels - O(log N) + +Thus, +***Time Complexity:* O(N * log(N))** + + +**Space Complexity:** O(N) + +For recursive stack, we require O(logN) space. And at every level, we are using O(N) space for merging but since we are freeing that as well. We are utilizing O(N) in total merging. +Thus, space complexity is O(logN) + O(N) = O(N) + +> Merge sort is stable as arrangement of elements is taking place at merge step which is essentially maintaining the relative order of elements. + +--- +### Calculate no of pairs such that A[i] > B[j] +Given two array, A[n] and B[m]; Calculate number of pairs i,j such that A[i] > B[j]. + +**Example** +A[3] = `{7, 3, 5}` +B[3] = `{2, 0, 6}` + +**Explanation** +`(7,2) (7,0) (7,6) (3,2) (3,0) (5,2) (5,0)` (7 pairs) + +:::warning +Please take some time to think about the bruteforce approach on your own before reading further..... +::: + +#### Brute Force Approach +Take 2 loops and compare the values + +#### TC & SC +* Time complexity is O(n * m) +* Space complexity is O(1) + +#### Appoach 2 with Dry Run + +1. Sort both the arrays +2. Create one array, C[6] for merging both the arrays +3. Assign pointer P1, P2, P3 to A[0], B[0], C[0] respectively +4. A[3] = {3, 5, 7} `<-- P1` +5. B[3] = {0, 2, 6} `<-- P2` +6. `B[0] < A[0]` means 0 is smaller than every element in A from index 0 onwards; **`count of pairs = 3 (3,0)(5,0)(7,0)`**; C[] ={0}; `P2=1` +7. `B[1] < A[0]` means 2 is smaller than every element in A from index 0 onwards; **`count of pairs = 6 (3,0)(5,0)(7,0)(3,2)(5,2)(7,2)`**; C[] ={0, 2}; `P2=2` +8. `B[2] > A[0]` means 6 can't form a pair with 3. We are done with 3, because if 6 can't make a pair, no other element after 6 can make a pair with 3; C[]={0, 2, 3}; `P1=1` +9. `B[2] > A[1]` means 6 can't form a pair with 5. We are done with 5, because if 6 can't make a pair, no other element after 6 can make a pair with 5; C[]={0, 2, 3, 5}; `P1=2` +10. `B[2] < A[2]` means 6 is smaller than every element in A from index 2 onwards; **`count of pairs = 7(3,0)(5,0)(7,0)(3,2)(5,2)(7,2)(7,6)`**; C[] ={0, 2, 3, 5, 6}; `P2=3` +11. B is empty, we can push all elements remaining in A to C; C[] ={0, 2, 3, 5, 6, 7}; + + +#### Time Complexity +O(nlogn + mlogm + m + n) + +Here nlogn is the time complexity of sorting A array, mlogm is the time complexity for B array and m+n is the time complexity for merging both the arrays + +--- +### Inversion Count + +Given an a[n], calculate no of pairs [i,j] such that i
 +
+
+### Example:
+>
+
+
+### Example:
+>  +
+
+
+
+
++ +**The State of the array after Partitioning will be:** + +>
 +
+
+---
+### Question
+Given an integer array, consider first element as pivot **p**, rearrange the elements such that for all **`i`**:
+
+if **`A[i] < p`** then it should be present on left side
+if **`A[i] > p`** then it should be present on right side
+
+`A = [10, 13, 7, 8, 25, 20, 23, 5]`
+
+
+**Choices**
+- [ ] left side = [10, 7, 5, 8] right side = [10, 13, 25, 20, 23]
+- [ ] left side = [10, 13, 7, 8] right side = [25, 20, 23, 5]
+- [ ] left side = [13, 25, 20, 23] right side = [7, 8, 5]
+- [x] left side = [7, 8, 5] right side = [13, 25, 20, 23]
+
+
+
+**Explanation**:
+
+The pivot value is `10`
+
+The elements lesser than the pivot are `[7, 8, 5]`
+The elements greater than the pivot are `[13, 25, 20, 23]`
+
+Thus, `left side = [7, 8, 5] right side = [13, 25, 20, 23]`
+
+
+
+
+---
+### Partition the array Approach
+
+
+* Partitioning begins by locating two position markers—let’s call them **`leftmark`** and **`rightmark`**—at the beginning and end of the remaining items in the list.
+* The goal of the partition process is to move items that are on the wrong side with respect to the pivot value while also converging on the split point.
+
+#### Process
+
+* We begin by incrementing leftmark until we locate a value that is greater than the pivot value.
+* We then decrement rightmark until we find a value that is less than the pivot value.
+* At this point we have discovered two items that are out of place with respect to the eventual split point. **For our example, this occurs at 93 and 20. Now we can exchange these two items and then repeat the process again.**
+>
+
+
+---
+### Question
+Given an integer array, consider first element as pivot **p**, rearrange the elements such that for all **`i`**:
+
+if **`A[i] < p`** then it should be present on left side
+if **`A[i] > p`** then it should be present on right side
+
+`A = [10, 13, 7, 8, 25, 20, 23, 5]`
+
+
+**Choices**
+- [ ] left side = [10, 7, 5, 8] right side = [10, 13, 25, 20, 23]
+- [ ] left side = [10, 13, 7, 8] right side = [25, 20, 23, 5]
+- [ ] left side = [13, 25, 20, 23] right side = [7, 8, 5]
+- [x] left side = [7, 8, 5] right side = [13, 25, 20, 23]
+
+
+
+**Explanation**:
+
+The pivot value is `10`
+
+The elements lesser than the pivot are `[7, 8, 5]`
+The elements greater than the pivot are `[13, 25, 20, 23]`
+
+Thus, `left side = [7, 8, 5] right side = [13, 25, 20, 23]`
+
+
+
+
+---
+### Partition the array Approach
+
+
+* Partitioning begins by locating two position markers—let’s call them **`leftmark`** and **`rightmark`**—at the beginning and end of the remaining items in the list.
+* The goal of the partition process is to move items that are on the wrong side with respect to the pivot value while also converging on the split point.
+
+#### Process
+
+* We begin by incrementing leftmark until we locate a value that is greater than the pivot value.
+* We then decrement rightmark until we find a value that is less than the pivot value.
+* At this point we have discovered two items that are out of place with respect to the eventual split point. **For our example, this occurs at 93 and 20. Now we can exchange these two items and then repeat the process again.**
+>  +
+**Continue:**
+
+>
+
+**Continue:**
+
+>  +
+* **At the point where rightmark becomes less than leftmark, we stop**. The position of rightmark is now the split point. The pivot value can be exchanged with the contents of the split point and the pivot value is now in place
+>
+
+* **At the point where rightmark becomes less than leftmark, we stop**. The position of rightmark is now the split point. The pivot value can be exchanged with the contents of the split point and the pivot value is now in place
+> +
+* **Now, we can exchange the 54(Pivot) with 31**
+>
+
+* **Now, we can exchange the 54(Pivot) with 31**
+>  +
+
+#### Pseudocode
+```cpp
+partition(A,first,last):
+ pivotvalue = A[first]
+
+ leftmark = first+1
+ rightmark = last
+
+ while leftmark <= rightmark:
+
+ if A[leftmark] <= pivotvalue:
+ leftmark = leftmark + 1
+
+ else if A[rightmark] > pivotvalue:
+ rightmark = rightmark -1
+
+ else:
+ temp = A[leftmark]
+ A[leftmark] = A[rightmark]
+ A[rightmark] = temp
+
+ // swap pivot element with element present at rightmark
+ temp = A[first]
+ A[first] = A[rightmark]
+ A[rightmark] = temp
+```
+
+---
+## Quick Sort
+
+
+*Sorting is the process of organizing elements in a structured manner.*
+
+**Quicksort** is one of the most popular sorting algorithms that uses **nlogn** comparisons to sort an array of n elements in a typical situation. Quicksort is based on the **divide-and-conquer strategy**. We’ll take a look at the Quicksort algorithm in this session and see how it works.
+
+* A quick sort first selects a value, which is called the **pivot value**.
+* Although there are many different ways to choose the pivot value, we will simply use the first item in the list.
+* The role of the pivot value is to assist with splitting the list.
+* The actual position where the pivot value belongs in the final sorted list, commonly called the **split point**, will be used to divide the list for subsequent calls to the quick sort.
+
+As per the previous example,
+>
+
+
+#### Pseudocode
+```cpp
+partition(A,first,last):
+ pivotvalue = A[first]
+
+ leftmark = first+1
+ rightmark = last
+
+ while leftmark <= rightmark:
+
+ if A[leftmark] <= pivotvalue:
+ leftmark = leftmark + 1
+
+ else if A[rightmark] > pivotvalue:
+ rightmark = rightmark -1
+
+ else:
+ temp = A[leftmark]
+ A[leftmark] = A[rightmark]
+ A[rightmark] = temp
+
+ // swap pivot element with element present at rightmark
+ temp = A[first]
+ A[first] = A[rightmark]
+ A[rightmark] = temp
+```
+
+---
+## Quick Sort
+
+
+*Sorting is the process of organizing elements in a structured manner.*
+
+**Quicksort** is one of the most popular sorting algorithms that uses **nlogn** comparisons to sort an array of n elements in a typical situation. Quicksort is based on the **divide-and-conquer strategy**. We’ll take a look at the Quicksort algorithm in this session and see how it works.
+
+* A quick sort first selects a value, which is called the **pivot value**.
+* Although there are many different ways to choose the pivot value, we will simply use the first item in the list.
+* The role of the pivot value is to assist with splitting the list.
+* The actual position where the pivot value belongs in the final sorted list, commonly called the **split point**, will be used to divide the list for subsequent calls to the quick sort.
+
+As per the previous example,
+>  +
+Now that there are two separate subarrays, we can apply partitioning on both separately and recursively. With each call, pivot element will be placed at its correct possition and eventually all elements will come at their correct place.
+
+### Steps to execute Quick Sort
+1. **Pick**: Select an element.
+2. **Divide**: Split the problem set, move smaller parts to the left of the pivot and larger items to the right.
+3. **Repeat and combine**: Repeat the steps on smaller subarrays and combine the arrays that have previously been sorted.
+
+#### Dry Run
+
+
+
+Now that there are two separate subarrays, we can apply partitioning on both separately and recursively. With each call, pivot element will be placed at its correct possition and eventually all elements will come at their correct place.
+
+### Steps to execute Quick Sort
+1. **Pick**: Select an element.
+2. **Divide**: Split the problem set, move smaller parts to the left of the pivot and larger items to the right.
+3. **Repeat and combine**: Repeat the steps on smaller subarrays and combine the arrays that have previously been sorted.
+
+#### Dry Run
+
+ +
+#### Pseudocode
+
+Below is the code for QuickSort
+
+```java
+void quicksort(int[] A, int start, int end) {
+ if (start < end) {
+ int pivotIndex = partition(A, start, end);
+ quicksort(A, start, pivotIndex - 1);
+ quicksort(A, pivotIndex + 1, end);
+ }
+}
+```
+
+---
+### Quick Sort Time Complexity and Space Complexity
+
+#### Best-Case Time Complexity:
+
+The best-case scenario for QuickSort occurs when the pivot chosen at each step divides the input into approximately equal-sized subarrays.
+
+
+>
+
+#### Pseudocode
+
+Below is the code for QuickSort
+
+```java
+void quicksort(int[] A, int start, int end) {
+ if (start < end) {
+ int pivotIndex = partition(A, start, end);
+ quicksort(A, start, pivotIndex - 1);
+ quicksort(A, pivotIndex + 1, end);
+ }
+}
+```
+
+---
+### Quick Sort Time Complexity and Space Complexity
+
+#### Best-Case Time Complexity:
+
+The best-case scenario for QuickSort occurs when the pivot chosen at each step divides the input into approximately equal-sized subarrays.
+
+
+>  +
+#### Worst-Case Time Complexity:
+
+The worst-case scenario for QuickSort occurs when the pivot chosen at each step is either the smallest or largest element in the remaining unsorted portion of the array. This leads to imbalanced partitions, and the algorithm performs poorly. The worst-case time complexity is $O(N^2)$, which occurs when the input is already sorted in ascending or descending order.
+>
+
+#### Worst-Case Time Complexity:
+
+The worst-case scenario for QuickSort occurs when the pivot chosen at each step is either the smallest or largest element in the remaining unsorted portion of the array. This leads to imbalanced partitions, and the algorithm performs poorly. The worst-case time complexity is $O(N^2)$, which occurs when the input is already sorted in ascending or descending order.
+>  +
+
+#### Average-Case Time Complexity
+
+There are many ways to avoid the worst case of quicksort, like choosing the element from the middle of the array as pivot, randomly generating a pivot for each subarray, selecting the median of the first, last, and middle element as pivot, etc. By using these methods, we can ensure equal partitioning, on average. Thus, quick sort's average case time complexity is O(NlogN)
+
+
+#### Space Complexity
+The Space Complexity in quick sort will be because of recursion space. Partition function doesn't take any extra space.
+
+So, space in Quick Sort is only because of Recursion Stack whereas in Merge Sort, the extra space is also taken by Merge Fucntion.
+
+**In Quick Sort**,
+In worst case, Space is **O(N)** since in recursive tree we have N levels.
+
+In best case, Space is **O(log N)** since there are log N levels.
+
+---
+### Randomised QuickSort
+
+The randomised quicksort is a technique where we randomly pick the pivot element, not necessarily the first and last.
+
+There is a random function available in all the languages, to which we can pass Array and get random index. Now, we can swap random index element with first element and execute our algorithm as it is.
+
+#### Why picking random element helps?
+
+Randomised quicksort help us to get away with the worst case time complexity.
+
+The odds of always choosing the minimum element or maximum element is very low.
+
+**Example:**
+Given N elements, probablity that a random element is minimum - 1/N
+Probability that again next time the random element is munimum - 1/N-1
+Then,.. 1/N-2
+Then,.. 1/N-3...
+
+1/N * 1/N-1 * 1/N-2 * .....
+1/N!
+
+This value is very small!!
+
+Hence, using randomised quick sort, we can achieve average case of O(N logN) most of the time.
+
+---
+## Comparator
+
+
+* In programming, a **comparator** is a function that compares two values and returns a result indicating whether the values are equal, less than, or greater than each other.
+* The **comparator** is typically used in sorting algorithms to compare elements in a data structure and arrange them in a specified order.
+
+**Comparator** is a function that takes **two arguments**.
+
+
+For languages - **Java, Python, JS, C#, Ruby**, the following logic is followed.
+
+```
+1. In sorted form, if first argument should come before second, -ve value is returned.
+2. In sorted form, if second argument should come before first, +ve value is returned.
+3. If both are same, 0 is returned.
+```
+For **C++**, following logic is followed.
+```
+1. In sorted form, if first argument should come before second, true is returned.
+2. Otherwise, false is returned.
+```
+
+---
+### Problem 2 Sorting based on factors
+
+
+Given an array of size n, sort the data in ascending order of count of factors, if count of factors are equal then sort the elements on the basis of their magnitude.
+
+**Example 1**
+
+```plaintext
+A[ ] = { 9, 3, 10, 6, 4 }
+Ans = { 3, 4, 9, 6, 10 }
+```
+**Explanation:**
+
+Total number of factors of 3, 4, 9, 6, 10 are 2, 3, 3, 4, 4.
+
+---
+### Question
+Given an array A of size n, sort the data in ascending order of count of factors, if count of factors are equal then sort the elements on the basis of their magnitude.
+
+`A = [10, 4, 5, 13, 1]`
+
+**Choices**
+- [ ] [1, 4, 5, 10, 13]
+- [x] [1, 5, 13, 4, 10]
+- [ ] [13, 10, 4, 5, 1]
+- [ ] [1, 4, 5, 13, 10]
+
+**Explanation:**
+
+Total number of factors of 1, 5, 13, 4, 10 are 1, 2, 2, 3, 4.
+
+
+---
+
+
+### Sorting based on factors Solutions
+
+#### C++
+```cpp
+int factors(int n) {
+ int count = 0;
+ int sq = sqrt(n);
+
+ // if the number is a perfect square
+ if (sq * sq == n)
+ count++;
+
+ // count all other factors
+ for (int i = 1; i < sqrt(n); i++) {
+ // if i is a factor then n/i will be
+ // another factor. So increment by 2
+ if (n % i == 0)
+ count += 2;
+ }
+ return count;
+}
+
+bool compare(int val1, int val2) {
+ int cnt_x = count_factors(x);
+ int cnt_y = count_factors(y);
+
+ if (factors(val1) == factors(val2)) {
+ if (val1 < val2) {
+ return true;
+ }
+ return false;
+ } else if (factors(val1) < factors(val2)) {
+ return true;
+ }
+ return false;
+}
+
+vector < int > solve(vector < int > A) {
+ sort(A.begin(), A.end(), compare);
+ return A;
+}
+```
+
+
+#### Python
+```cpp
+import functools
+
+//please write the code for finding factors by yourself
+
+def compare(v1, v2):
+ if (factors(v1) == factors(v2)):
+ if (v1 < v2):
+ return -1;
+if (v2 < v1):
+ return 1;
+else
+ return 0;
+elif(factors(v1) < factors(v2)):
+ return -1;
+else
+ return 1;
+
+class Solution:
+ def solve(self, A):
+ A = sorted(A, key = functools.cmp_to_key(compare))
+return A
+```
+#### Java
+```cpp
+//please write the code for finding factors by yourself
+
+public ArrayList < Integer > solve(ArrayList < Integer > A) {
+ Collections.sort(A, new Comparator < Integer > () {
+ @Override
+ public int comp(Integer v1, Integer v2) {
+ if (factors(v1) == factors(v2)) {
+ if (v1 < v2) return -1;
+ else if (v2 < v1) return 1;
+ return 0;
+ } else if (factors(v1) < factors(v2)) {
+ return -1;
+ }
+ return 1;
+ }
+ });
+ return A;
+}
+```
+
+---
+### Problem 3 B Closest Points to Origin
+
+
+Given an array of points where points[i] = [xi, yi] represents a point on the X-Y plane and an integer k, return the B closest points to the origin (0, 0).
+
+The distance between two points on the X-Y plane is the Euclidean distance (i.e., $√(x1 - x2)^2 + (y1 - y2)^2$).
+
+You may return the answer in any order.
+
+**Example 1:**
+>
+
+
+#### Average-Case Time Complexity
+
+There are many ways to avoid the worst case of quicksort, like choosing the element from the middle of the array as pivot, randomly generating a pivot for each subarray, selecting the median of the first, last, and middle element as pivot, etc. By using these methods, we can ensure equal partitioning, on average. Thus, quick sort's average case time complexity is O(NlogN)
+
+
+#### Space Complexity
+The Space Complexity in quick sort will be because of recursion space. Partition function doesn't take any extra space.
+
+So, space in Quick Sort is only because of Recursion Stack whereas in Merge Sort, the extra space is also taken by Merge Fucntion.
+
+**In Quick Sort**,
+In worst case, Space is **O(N)** since in recursive tree we have N levels.
+
+In best case, Space is **O(log N)** since there are log N levels.
+
+---
+### Randomised QuickSort
+
+The randomised quicksort is a technique where we randomly pick the pivot element, not necessarily the first and last.
+
+There is a random function available in all the languages, to which we can pass Array and get random index. Now, we can swap random index element with first element and execute our algorithm as it is.
+
+#### Why picking random element helps?
+
+Randomised quicksort help us to get away with the worst case time complexity.
+
+The odds of always choosing the minimum element or maximum element is very low.
+
+**Example:**
+Given N elements, probablity that a random element is minimum - 1/N
+Probability that again next time the random element is munimum - 1/N-1
+Then,.. 1/N-2
+Then,.. 1/N-3...
+
+1/N * 1/N-1 * 1/N-2 * .....
+1/N!
+
+This value is very small!!
+
+Hence, using randomised quick sort, we can achieve average case of O(N logN) most of the time.
+
+---
+## Comparator
+
+
+* In programming, a **comparator** is a function that compares two values and returns a result indicating whether the values are equal, less than, or greater than each other.
+* The **comparator** is typically used in sorting algorithms to compare elements in a data structure and arrange them in a specified order.
+
+**Comparator** is a function that takes **two arguments**.
+
+
+For languages - **Java, Python, JS, C#, Ruby**, the following logic is followed.
+
+```
+1. In sorted form, if first argument should come before second, -ve value is returned.
+2. In sorted form, if second argument should come before first, +ve value is returned.
+3. If both are same, 0 is returned.
+```
+For **C++**, following logic is followed.
+```
+1. In sorted form, if first argument should come before second, true is returned.
+2. Otherwise, false is returned.
+```
+
+---
+### Problem 2 Sorting based on factors
+
+
+Given an array of size n, sort the data in ascending order of count of factors, if count of factors are equal then sort the elements on the basis of their magnitude.
+
+**Example 1**
+
+```plaintext
+A[ ] = { 9, 3, 10, 6, 4 }
+Ans = { 3, 4, 9, 6, 10 }
+```
+**Explanation:**
+
+Total number of factors of 3, 4, 9, 6, 10 are 2, 3, 3, 4, 4.
+
+---
+### Question
+Given an array A of size n, sort the data in ascending order of count of factors, if count of factors are equal then sort the elements on the basis of their magnitude.
+
+`A = [10, 4, 5, 13, 1]`
+
+**Choices**
+- [ ] [1, 4, 5, 10, 13]
+- [x] [1, 5, 13, 4, 10]
+- [ ] [13, 10, 4, 5, 1]
+- [ ] [1, 4, 5, 13, 10]
+
+**Explanation:**
+
+Total number of factors of 1, 5, 13, 4, 10 are 1, 2, 2, 3, 4.
+
+
+---
+
+
+### Sorting based on factors Solutions
+
+#### C++
+```cpp
+int factors(int n) {
+ int count = 0;
+ int sq = sqrt(n);
+
+ // if the number is a perfect square
+ if (sq * sq == n)
+ count++;
+
+ // count all other factors
+ for (int i = 1; i < sqrt(n); i++) {
+ // if i is a factor then n/i will be
+ // another factor. So increment by 2
+ if (n % i == 0)
+ count += 2;
+ }
+ return count;
+}
+
+bool compare(int val1, int val2) {
+ int cnt_x = count_factors(x);
+ int cnt_y = count_factors(y);
+
+ if (factors(val1) == factors(val2)) {
+ if (val1 < val2) {
+ return true;
+ }
+ return false;
+ } else if (factors(val1) < factors(val2)) {
+ return true;
+ }
+ return false;
+}
+
+vector < int > solve(vector < int > A) {
+ sort(A.begin(), A.end(), compare);
+ return A;
+}
+```
+
+
+#### Python
+```cpp
+import functools
+
+//please write the code for finding factors by yourself
+
+def compare(v1, v2):
+ if (factors(v1) == factors(v2)):
+ if (v1 < v2):
+ return -1;
+if (v2 < v1):
+ return 1;
+else
+ return 0;
+elif(factors(v1) < factors(v2)):
+ return -1;
+else
+ return 1;
+
+class Solution:
+ def solve(self, A):
+ A = sorted(A, key = functools.cmp_to_key(compare))
+return A
+```
+#### Java
+```cpp
+//please write the code for finding factors by yourself
+
+public ArrayList < Integer > solve(ArrayList < Integer > A) {
+ Collections.sort(A, new Comparator < Integer > () {
+ @Override
+ public int comp(Integer v1, Integer v2) {
+ if (factors(v1) == factors(v2)) {
+ if (v1 < v2) return -1;
+ else if (v2 < v1) return 1;
+ return 0;
+ } else if (factors(v1) < factors(v2)) {
+ return -1;
+ }
+ return 1;
+ }
+ });
+ return A;
+}
+```
+
+---
+### Problem 3 B Closest Points to Origin
+
+
+Given an array of points where points[i] = [xi, yi] represents a point on the X-Y plane and an integer k, return the B closest points to the origin (0, 0).
+
+The distance between two points on the X-Y plane is the Euclidean distance (i.e., $√(x1 - x2)^2 + (y1 - y2)^2$).
+
+You may return the answer in any order.
+
+**Example 1:**
+> +
+>**Input:** points = [[1,3],[-2,2]], B = 1
+**Output:** [[-2,2]]
+**Explanation:**
+The distance between (1, 3) and the origin is sqrt(10).
+The distance between (-2, 2) and the origin is sqrt(8).
+Since sqrt(8) < sqrt(10), (-2, 2) is closer to the origin.
+We only want the closest B = 1 points from the origin, so the answer is just [[-2,2]].
+
+
+**Example 2:**
+
+>**Input:** points = [[3,3],[5,-1],[-2,4]], B = 2
+**Output:** [[3,3],[-2,4]]
+**Explanation:** The answer [[-2,4],[3,3]] would also be accepted.
+
+---
+**B Closest Points to Origin Approach**
+
+
+We find the B-th distance by creating an array of distances and then sorting them using custom sorting based on distances from origin or points.
+
+After, we select all the points with distance less than or equal to this K-th distance.
+
+**Logic for Custom Sorting**
+
+Say there are two points, (x1, y1) and (x2, y2),
+The distance of (x1, y1) from origin will be ${sqrt((x1-0)^2 + (y1-0)^2)}$
+The distance of (x2, y2) from origin will be ${sqrt((x2-0)^2 + (y2-0)^2)}$
+
+We can leave root part and just compare $(x1^2 + y1^2) and (x2^2 + y2^2)$
+
+**Below logic works for languages like - Java, Python, JS, ...**
+```cpp
+// Need to arrange in ascending order based on distance
+
+// If first argument needs to be placed before, negative gets returned
+if((x1*x1 + y1*y1) < (x2*x2 + y2*y2))
+ return -1;
+// If second argument needs to be placed before, positive gets returned
+else if ((x1*x1 + y1*y1) > (x2*x2 + y2*y2))
+ return 1;
+// If both are same, 0 is returned
+else return 0
+---------------------------------------------
+// Instead of writing like above, we could have also written
+
+return ((x1*x1 + y1*y1) - (x2*x2 + y2*y2))
+```
+
+#### Below logic works for C++
+```cpp
+// If first argument needs to be placed before, true gets returned
+if ((x1 * x1 + y1 * y1) < (x2 * x2 + y2 * y2))
+ return true;
+//Else false is returned
+else return false
+```
+
+---
+### Problem 4 Largest Number
+
+Given a list of non-negative integers nums, arrange them such that they form the largest number and return it.
+
+Since the result may be very large, so you need to return a string instead of an integer.
+
+Example 1:
+
+>Input: nums = [10,2]
+Output: "210"
+
+Example 2:
+
+>Input: nums = [3,30,34,5,9]
+Output: "9534330"
+
+#### Idea:
+
+Should we sort the numbers in descending order and append them ?
+
+While it might be tempting to simply sort the numbers in descending order,
+but this doesn't work.
+
+**For example,** sorting the problem example in descending order would produce the number **9534303**, while the correct answer is achieved by putting **3** before **30**.
+
+---
+### Question
+Given a list of non-negative integers **nums**, arrange them such that they form the largest number and return it.
+
+nums = [10, 5, 2, 8, 200]
+
+**Choices**
+- [ ] 20010825
+- [x] 85220010
+- [ ] 88888888
+- [ ] 85200210
+
+
+**Explanation:**
+
+After rearrangeing the nums, [8, 5, 2, 200, 10] will form the largest number as **"85220010"**.
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+---
+### Larget Number Approach
+
+We shall use **custom sorting**.
+Say we pick two numbers **X** and **Y**. Now, we can check if **`X (appends) Y`** > **`Y (appends) X`**, then it means that **Y** should come before **X**.
+
+For example, let X and Y be 542 and 60. To compare X and Y, we compare 54260 and 60542. Since 60542 is greater than 54260, we put Y first.
+
+Once the array is sorted, the most "signficant" number will be at the front.
+
+**Edge Case**
+There is a minor edge case that comes up when the array consists of only
+zeroes, so if the most significant number is 0, we can simply return 0. Otherwise, we build a string out of the sorted array and return it.
+
+**Example**
+Upon sorting this array - **`[3,30,34,5,9]`**,
+we shall get - **`[9, 5, 34, 3, 30]`**
+
+Now, we can simply append the numbers to get - **`9534330`**
+
+#### Complexity
+**Time complexity :** O(n log n)
+Although we are doing extra work in our comparator, it is only by a constant factor. Therefore, the overall runtime is dominated by the complexity of sort, which is O(n log n).
+
+**Space complexity :** O(n)
+Space depends on the type of algorithm used by the sort function internally.
+
+---
+### Larget Number Codes in different langauges
+#### C++
+```cpp
+bool compare(int a, int b) {
+ return to_string(a) + to_string(b) > to_string(b) + to_string(a);
+}
+
+string largestNumber(vector < int > & A) {
+ sort(A.begin(), A.end(), compare);
+ string ans = "";
+ for (auto & x: A)
+ ans += to_string(x);
+ if (ans[0] == '0') return "0";
+ return ans;
+}
+```
+
+#### Java
+
+```cpp
+public class Solution {
+ public String largestNumber(ArrayList < Integer > A) {
+ Collections.sort(A, new Comparator < Integer > () {
+ public int compare(Integer a, Integer b) {
+ String XY = String.valueOf(a) + String.valueOf(b);
+ String YX = String.valueOf(b) + String.valueOf(a);
+ return XY.compareTo(YX) > 0 ? -1 : 1;
+ }
+ });
+ StringBuilder ans = new StringBuilder();
+ for (int x: A) {
+ ans.append(String.valueOf(x));
+ }
+ if (ans.charAt(0) == '0')
+ return "0";
+ return ans.toString();
+ }
+}
+```
+
+#### Python
+```cpp
+from functools import cmp_to_key
+
+class Solution:
+ # @param A : list of integers
+ # @return a strings
+ def largestNumber(self, A):
+ def cmp_func(x, y):
+ if x + y > y + x:
+ return -1
+ elif x == y:
+ return 0
+ else:
+ return 1
+
+ nums = [str(num) for num in A]
+ nums.sort(key = cmp_to_key(cmp_func))
+ if nums[0] == '0':
+ return '0'
+ return ''.join(nums)
+```
+
+---
+### Question
+Best case TC of quick sort?
+
+**Choices**
+- [ ] N
+- [ ] N^2
+- [x] N log N
+- [ ] Constant
+
+### Question
+Worst case TC of quick sort?
+
+**Choices**
+- [ ] N
+- [x] N^2
+- [ ] N log N
+- [ ] Constant
+
+---
+### Question
+Worst case SC of quick sort?
+
+**Choices**
+- [x] N
+- [ ] N^2
+- [ ] N log N
+- [ ] Constant
+
+---
+### Question
+Best case SC of quick sort?
+
+**Choices**
+- [ ] N
+- [ ] N^2
+- [ ] N log N
+- [x] log N
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Stacks 1 Implementation & Basic Problems.md b/Academy DSA Typed Notes/Advanced/DSA Stacks 1 Implementation & Basic Problems.md
new file mode 100644
index 0000000..416ca3a
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Stacks 1 Implementation & Basic Problems.md
@@ -0,0 +1,507 @@
+# Stacks 1: Implementation & Basic Problems
+
+---
+## Introduction to Stacks with Example
+
+### Definition
+* A stack is a linear data structure that stores information in a sequence, from **bottom to top**.
+* The data items can only be accessed from the top and new elements can only be added to the top, i.e it follows **LIFO (Last In First Out)** principle.
+
+**Examples**
+Before proceeding to more technical examples, let's start from the real life basic examples.
+1. **Pile of Plates**:
+
+>**Input:** points = [[1,3],[-2,2]], B = 1
+**Output:** [[-2,2]]
+**Explanation:**
+The distance between (1, 3) and the origin is sqrt(10).
+The distance between (-2, 2) and the origin is sqrt(8).
+Since sqrt(8) < sqrt(10), (-2, 2) is closer to the origin.
+We only want the closest B = 1 points from the origin, so the answer is just [[-2,2]].
+
+
+**Example 2:**
+
+>**Input:** points = [[3,3],[5,-1],[-2,4]], B = 2
+**Output:** [[3,3],[-2,4]]
+**Explanation:** The answer [[-2,4],[3,3]] would also be accepted.
+
+---
+**B Closest Points to Origin Approach**
+
+
+We find the B-th distance by creating an array of distances and then sorting them using custom sorting based on distances from origin or points.
+
+After, we select all the points with distance less than or equal to this K-th distance.
+
+**Logic for Custom Sorting**
+
+Say there are two points, (x1, y1) and (x2, y2),
+The distance of (x1, y1) from origin will be ${sqrt((x1-0)^2 + (y1-0)^2)}$
+The distance of (x2, y2) from origin will be ${sqrt((x2-0)^2 + (y2-0)^2)}$
+
+We can leave root part and just compare $(x1^2 + y1^2) and (x2^2 + y2^2)$
+
+**Below logic works for languages like - Java, Python, JS, ...**
+```cpp
+// Need to arrange in ascending order based on distance
+
+// If first argument needs to be placed before, negative gets returned
+if((x1*x1 + y1*y1) < (x2*x2 + y2*y2))
+ return -1;
+// If second argument needs to be placed before, positive gets returned
+else if ((x1*x1 + y1*y1) > (x2*x2 + y2*y2))
+ return 1;
+// If both are same, 0 is returned
+else return 0
+---------------------------------------------
+// Instead of writing like above, we could have also written
+
+return ((x1*x1 + y1*y1) - (x2*x2 + y2*y2))
+```
+
+#### Below logic works for C++
+```cpp
+// If first argument needs to be placed before, true gets returned
+if ((x1 * x1 + y1 * y1) < (x2 * x2 + y2 * y2))
+ return true;
+//Else false is returned
+else return false
+```
+
+---
+### Problem 4 Largest Number
+
+Given a list of non-negative integers nums, arrange them such that they form the largest number and return it.
+
+Since the result may be very large, so you need to return a string instead of an integer.
+
+Example 1:
+
+>Input: nums = [10,2]
+Output: "210"
+
+Example 2:
+
+>Input: nums = [3,30,34,5,9]
+Output: "9534330"
+
+#### Idea:
+
+Should we sort the numbers in descending order and append them ?
+
+While it might be tempting to simply sort the numbers in descending order,
+but this doesn't work.
+
+**For example,** sorting the problem example in descending order would produce the number **9534303**, while the correct answer is achieved by putting **3** before **30**.
+
+---
+### Question
+Given a list of non-negative integers **nums**, arrange them such that they form the largest number and return it.
+
+nums = [10, 5, 2, 8, 200]
+
+**Choices**
+- [ ] 20010825
+- [x] 85220010
+- [ ] 88888888
+- [ ] 85200210
+
+
+**Explanation:**
+
+After rearrangeing the nums, [8, 5, 2, 200, 10] will form the largest number as **"85220010"**.
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+---
+### Larget Number Approach
+
+We shall use **custom sorting**.
+Say we pick two numbers **X** and **Y**. Now, we can check if **`X (appends) Y`** > **`Y (appends) X`**, then it means that **Y** should come before **X**.
+
+For example, let X and Y be 542 and 60. To compare X and Y, we compare 54260 and 60542. Since 60542 is greater than 54260, we put Y first.
+
+Once the array is sorted, the most "signficant" number will be at the front.
+
+**Edge Case**
+There is a minor edge case that comes up when the array consists of only
+zeroes, so if the most significant number is 0, we can simply return 0. Otherwise, we build a string out of the sorted array and return it.
+
+**Example**
+Upon sorting this array - **`[3,30,34,5,9]`**,
+we shall get - **`[9, 5, 34, 3, 30]`**
+
+Now, we can simply append the numbers to get - **`9534330`**
+
+#### Complexity
+**Time complexity :** O(n log n)
+Although we are doing extra work in our comparator, it is only by a constant factor. Therefore, the overall runtime is dominated by the complexity of sort, which is O(n log n).
+
+**Space complexity :** O(n)
+Space depends on the type of algorithm used by the sort function internally.
+
+---
+### Larget Number Codes in different langauges
+#### C++
+```cpp
+bool compare(int a, int b) {
+ return to_string(a) + to_string(b) > to_string(b) + to_string(a);
+}
+
+string largestNumber(vector < int > & A) {
+ sort(A.begin(), A.end(), compare);
+ string ans = "";
+ for (auto & x: A)
+ ans += to_string(x);
+ if (ans[0] == '0') return "0";
+ return ans;
+}
+```
+
+#### Java
+
+```cpp
+public class Solution {
+ public String largestNumber(ArrayList < Integer > A) {
+ Collections.sort(A, new Comparator < Integer > () {
+ public int compare(Integer a, Integer b) {
+ String XY = String.valueOf(a) + String.valueOf(b);
+ String YX = String.valueOf(b) + String.valueOf(a);
+ return XY.compareTo(YX) > 0 ? -1 : 1;
+ }
+ });
+ StringBuilder ans = new StringBuilder();
+ for (int x: A) {
+ ans.append(String.valueOf(x));
+ }
+ if (ans.charAt(0) == '0')
+ return "0";
+ return ans.toString();
+ }
+}
+```
+
+#### Python
+```cpp
+from functools import cmp_to_key
+
+class Solution:
+ # @param A : list of integers
+ # @return a strings
+ def largestNumber(self, A):
+ def cmp_func(x, y):
+ if x + y > y + x:
+ return -1
+ elif x == y:
+ return 0
+ else:
+ return 1
+
+ nums = [str(num) for num in A]
+ nums.sort(key = cmp_to_key(cmp_func))
+ if nums[0] == '0':
+ return '0'
+ return ''.join(nums)
+```
+
+---
+### Question
+Best case TC of quick sort?
+
+**Choices**
+- [ ] N
+- [ ] N^2
+- [x] N log N
+- [ ] Constant
+
+### Question
+Worst case TC of quick sort?
+
+**Choices**
+- [ ] N
+- [x] N^2
+- [ ] N log N
+- [ ] Constant
+
+---
+### Question
+Worst case SC of quick sort?
+
+**Choices**
+- [x] N
+- [ ] N^2
+- [ ] N log N
+- [ ] Constant
+
+---
+### Question
+Best case SC of quick sort?
+
+**Choices**
+- [ ] N
+- [ ] N^2
+- [ ] N log N
+- [x] log N
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Stacks 1 Implementation & Basic Problems.md b/Academy DSA Typed Notes/Advanced/DSA Stacks 1 Implementation & Basic Problems.md
new file mode 100644
index 0000000..416ca3a
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Stacks 1 Implementation & Basic Problems.md
@@ -0,0 +1,507 @@
+# Stacks 1: Implementation & Basic Problems
+
+---
+## Introduction to Stacks with Example
+
+### Definition
+* A stack is a linear data structure that stores information in a sequence, from **bottom to top**.
+* The data items can only be accessed from the top and new elements can only be added to the top, i.e it follows **LIFO (Last In First Out)** principle.
+
+**Examples**
+Before proceeding to more technical examples, let's start from the real life basic examples.
+1. **Pile of Plates**:Imagine a scenario where you have a pile of plates, you can only put a plate on the pile from top also only pick a plate from top. You can't really see the plates underneath the top one without first removing the top plate, which means only the first plate is accessible to you. + +
 +
+2. **Stack of Chairs**:
+
+2. **Stack of Chairs**:We usually place identical chairs on the top of on another, which makes them look like a stack. Similar to the previous example you can only position or choose a chair from top, and you won't be able to take or see the chair in middle without picking out all chairs on top of that one. + +
 +
+
+### Algorithmic Examples
+1. **Recursion**:
+
+
+### Algorithmic Examples
+1. **Recursion**:Recursion happens when a function calls itself. Each call is stacked on top of the previous one. When call execution finishes, control goes back to the second-to-last function call. This all happens with a stack data structure. +2. **Undo / Redo Operations**:
In software programs, stacks are commonly used to store the state during Undo and Redo operations. Consider the given example we have performed several calculations here, our first stack stores the current state. As soon as user performs UNDO operation the state is moved to REDO stack so that later it can be restored from there. +
 +
+
+
+---
+### Question
+What is the most common application of a stack?
+
+**Choices**
+- [ ] Evaluating arithmetic expressions
+- [ ] Implementing undo/redo functionality
+- [ ] Representing parenthesis in expressions
+- [x] All of the above
+
+
+Answer: All of the above
+
+Explanation: Stacks are versatile data structures that find applications in various domains. They are commonly used in expression evaluation, undo/redo functionality, and representing parenthesis in expressions.
+
+
+---
+### Operations on Stack
+
+These operations are generally used on the stack. The time complexity for all of these operations is constant **O(1)**.
+
+#### 1. Push
+Push operation is to insert a new element into the top of stack.
+```cpp
+push(data)
+```
+
+#### 2. Pop
+Pop operation is to remove an element from the top of stack.
+```cpp
+pop()
+```
+
+#### 3. Peek
+Peek means to access the top element of the stack, this operation is also called as **top**.
+```cpp
+data = peek()
+// or
+data = top()
+```
+
+#### 4. isEmpty
+This operation is used to check whether stack is empty or not. It is an important operation because it allows program to run efficiently by checking conditions of overflow and underflow.
+```cpp
+isEmpty()
+```
+
+### Question
+What is the time complexity of the push and pop operations in a stack?
+
+**Choices**
+- [x] O(1) for both push and pop
+- [ ] O(n) for push and O(1) for pop
+- [ ] O(1) for push and O(n) for pop
+- [ ] O(n) for both push and pop
+
+
+Answer: O(1) for both push and pop
+
+Explanation: The push and pop operations in a stack operate on the top element, making them constant time operations. This is because the top element is always accessible regardless of the stack's size.
+
+---
+
+
+### Implement Stack using Arrays
+* Just try to think what a data structure is, a data structure is nothing but a way to store some data in memory along with some rules to insert/access/modify that data.
+* So, stacks is also a way to store data with LIFO principle. The conclusion of this is we can implement stacks by using arrays.
+* You might know that array is filled from left to right so the **rightmost part of the array can act as top of stack**, for each pop operation we can remove the rightmost element from array.
+* We can keep track of the top element index in array because we can always know how many elements we have inserted so directly access that index from array to know about top element.
+* To store an element we can just add 1 to top index and assign the element.
+
+
+
+
+
+---
+### Question
+What is the most common application of a stack?
+
+**Choices**
+- [ ] Evaluating arithmetic expressions
+- [ ] Implementing undo/redo functionality
+- [ ] Representing parenthesis in expressions
+- [x] All of the above
+
+
+Answer: All of the above
+
+Explanation: Stacks are versatile data structures that find applications in various domains. They are commonly used in expression evaluation, undo/redo functionality, and representing parenthesis in expressions.
+
+
+---
+### Operations on Stack
+
+These operations are generally used on the stack. The time complexity for all of these operations is constant **O(1)**.
+
+#### 1. Push
+Push operation is to insert a new element into the top of stack.
+```cpp
+push(data)
+```
+
+#### 2. Pop
+Pop operation is to remove an element from the top of stack.
+```cpp
+pop()
+```
+
+#### 3. Peek
+Peek means to access the top element of the stack, this operation is also called as **top**.
+```cpp
+data = peek()
+// or
+data = top()
+```
+
+#### 4. isEmpty
+This operation is used to check whether stack is empty or not. It is an important operation because it allows program to run efficiently by checking conditions of overflow and underflow.
+```cpp
+isEmpty()
+```
+
+### Question
+What is the time complexity of the push and pop operations in a stack?
+
+**Choices**
+- [x] O(1) for both push and pop
+- [ ] O(n) for push and O(1) for pop
+- [ ] O(1) for push and O(n) for pop
+- [ ] O(n) for both push and pop
+
+
+Answer: O(1) for both push and pop
+
+Explanation: The push and pop operations in a stack operate on the top element, making them constant time operations. This is because the top element is always accessible regardless of the stack's size.
+
+---
+
+
+### Implement Stack using Arrays
+* Just try to think what a data structure is, a data structure is nothing but a way to store some data in memory along with some rules to insert/access/modify that data.
+* So, stacks is also a way to store data with LIFO principle. The conclusion of this is we can implement stacks by using arrays.
+* You might know that array is filled from left to right so the **rightmost part of the array can act as top of stack**, for each pop operation we can remove the rightmost element from array.
+* We can keep track of the top element index in array because we can always know how many elements we have inserted so directly access that index from array to know about top element.
+* To store an element we can just add 1 to top index and assign the element.
+
+ +
+
+#### Pseudocode
+```cpp
+// Consider an array `A`.
+int A[];
+
+// Consider a counter to keep track of stack size and currently used index
+int t = -1;
+```
+
+1. For push operation we can keep pushing data from left to right.
+```cpp
+void push(data){
+ t++;
+ A[t] = data;
+}
+```
+
+2. And as we are maintaining a counter we can always access the top element in O(1) by just index access of array.
+```cpp
+int top(){
+ return A[t];
+}
+```
+
+3. To remove element we can simply decrement our counter. Also we can place some value at that index to denote that it is not part of our data.
+```cpp
+void pop(){
+ t--;
+}
+```
+
+4. We are maintaining our counter in such a way that it indicates the size of stack. We can simply perform an equality check on counter to know whether stack is empty.
+```cpp
+bool isEmpty(){
+ return t == -1;
+}
+```
+
+
+---
+### Overflow and Underflow in stack and it's solution
+* Overflow occurs when we try to store new data even when there is no empty space in array. For this we have to introduce a overflow condition before push operation.
+
+```cpp
+void push(x){
+ // Whenever our counter reaches to the size of the array
+ // It means stack is already full
+ if(t >= A.size())
+ return;
+ t++;
+ A[t] = x;
+}
+```
+
+* Underflow means when we try to perform pop operation or try to access the element of stack but there are none. Again we have to introduce conditions during pop and top operation.
+
+```cpp
+void pop(){
+ if(!isEmpty()) return;
+ t--;
+}
+```
+
+
+```cpp
+int top(){
+ if(!isEmpty()) return -1;
+ return A[t];
+}
+```
+
+### Problem with implementation using Arrays
+We have to predefine the size of stack to create array. To overcome this problem we can create a dynamic array which can grow or shrink at runtime according to need.
+
+---
+### Question
+What happens when you try to pop an element from an empty Stack?
+
+**Choices**
+- [ ] It returns null
+- [ ] It returns the top element
+- [x] It causes an underflow
+- [ ] It causes an overflow
+
+Attempting to pop an element from an empty stack will cause an underflow.
+
+
+---
+
+### Implement Stack using Linked List
+* We can also implement stack using linked list, similar to the array it also has constant `O(1)` time complexity for all operations.
+* We choose head as our top element because push and pop operations can be executed in `O(1)` in that case.
+* Unlike array linkedlist can grow or shrink at runtime, because all operations are performed at head.
+
+
+
+
+#### Pseudocode
+```cpp
+// Consider an array `A`.
+int A[];
+
+// Consider a counter to keep track of stack size and currently used index
+int t = -1;
+```
+
+1. For push operation we can keep pushing data from left to right.
+```cpp
+void push(data){
+ t++;
+ A[t] = data;
+}
+```
+
+2. And as we are maintaining a counter we can always access the top element in O(1) by just index access of array.
+```cpp
+int top(){
+ return A[t];
+}
+```
+
+3. To remove element we can simply decrement our counter. Also we can place some value at that index to denote that it is not part of our data.
+```cpp
+void pop(){
+ t--;
+}
+```
+
+4. We are maintaining our counter in such a way that it indicates the size of stack. We can simply perform an equality check on counter to know whether stack is empty.
+```cpp
+bool isEmpty(){
+ return t == -1;
+}
+```
+
+
+---
+### Overflow and Underflow in stack and it's solution
+* Overflow occurs when we try to store new data even when there is no empty space in array. For this we have to introduce a overflow condition before push operation.
+
+```cpp
+void push(x){
+ // Whenever our counter reaches to the size of the array
+ // It means stack is already full
+ if(t >= A.size())
+ return;
+ t++;
+ A[t] = x;
+}
+```
+
+* Underflow means when we try to perform pop operation or try to access the element of stack but there are none. Again we have to introduce conditions during pop and top operation.
+
+```cpp
+void pop(){
+ if(!isEmpty()) return;
+ t--;
+}
+```
+
+
+```cpp
+int top(){
+ if(!isEmpty()) return -1;
+ return A[t];
+}
+```
+
+### Problem with implementation using Arrays
+We have to predefine the size of stack to create array. To overcome this problem we can create a dynamic array which can grow or shrink at runtime according to need.
+
+---
+### Question
+What happens when you try to pop an element from an empty Stack?
+
+**Choices**
+- [ ] It returns null
+- [ ] It returns the top element
+- [x] It causes an underflow
+- [ ] It causes an overflow
+
+Attempting to pop an element from an empty stack will cause an underflow.
+
+
+---
+
+### Implement Stack using Linked List
+* We can also implement stack using linked list, similar to the array it also has constant `O(1)` time complexity for all operations.
+* We choose head as our top element because push and pop operations can be executed in `O(1)` in that case.
+* Unlike array linkedlist can grow or shrink at runtime, because all operations are performed at head.
+
+ +
+
+#### Pseudocode
+
+1. To push data into stack, just create a node and attach before head.
+```cpp
+void push(data) {
+ new_node = Create a new Node with 'data'
+ new_node.next = head
+ head = new_node
+ // Increment size
+ t++
+}
+```
+
+2. To pop data just remove one node from the beginning of linked list.
+```cpp
+void pop() {
+ if (!isEmpty()) return;
+ head = head.next
+ // Decrement size
+ t--
+}
+```
+
+3. To find the data on top just access the head node.
+```cpp
+int top() {
+ if (!isEmpty()) return -1;
+ return head.data;
+}
+```
+
+> Note: While accessing top value in function, We can use another concept to indicate that stack is empty if we are using -1 as value to store in stack.
+
+---
+### Problem 3 Balanced Paranthesis Concept with Implementation
+
+Check whether the given sequence of parenthesis is valid ?
+
+#### Explanation of Problem
+Imagine you have a bunch of different types of brackets, like `{` and `}` (curly brackets), `[` and `]` (square brackets), and `(` and `)` (round brackets).
+
+A valid sequence of these brackets means that for every opening bracket, there is a matching closing bracket. It's like having pairs of shoes; you need a left shoe and a right shoe for each pair. In a valid sequence, you have the same number of left and right brackets, and they are correctly matched.
+
+For example, `(({}))` is a valid sequence because for each opening bracket `(` or `{`, there is a corresponding closing bracket `)` or `}`.
+
+On the other hand, `{{})` is not valid because the second curly bracket `}` doesn't have a matching opening bracket, so it's like having an extra right shoe without a left shoe to match with.
+
+In summary, a valid sequence of brackets is like having balanced pairs of brackets, where each opening bracket has a matching closing bracket.
+
+**Technical Application -**
+Imagine you are writing a small compiler for your college project and one of the tasks (or say sub-tasks) for the compiler would be to detect if the parenthesis are in place or not.
+
+---
+### Question
+Which of the following expressions is balanced with respect to parentheses?
+
+**Choices**
+- [x] `(a + b) * c`
+- [ ] `(a + b)) * c`
+- [ ] `(a + b)(c`
+- [ ] `(a + b)c`
+
+---
+### Balanced Parenthesis Implementation
+#### Idea
+An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
+
+
+
+
+#### Pseudocode
+
+1. To push data into stack, just create a node and attach before head.
+```cpp
+void push(data) {
+ new_node = Create a new Node with 'data'
+ new_node.next = head
+ head = new_node
+ // Increment size
+ t++
+}
+```
+
+2. To pop data just remove one node from the beginning of linked list.
+```cpp
+void pop() {
+ if (!isEmpty()) return;
+ head = head.next
+ // Decrement size
+ t--
+}
+```
+
+3. To find the data on top just access the head node.
+```cpp
+int top() {
+ if (!isEmpty()) return -1;
+ return head.data;
+}
+```
+
+> Note: While accessing top value in function, We can use another concept to indicate that stack is empty if we are using -1 as value to store in stack.
+
+---
+### Problem 3 Balanced Paranthesis Concept with Implementation
+
+Check whether the given sequence of parenthesis is valid ?
+
+#### Explanation of Problem
+Imagine you have a bunch of different types of brackets, like `{` and `}` (curly brackets), `[` and `]` (square brackets), and `(` and `)` (round brackets).
+
+A valid sequence of these brackets means that for every opening bracket, there is a matching closing bracket. It's like having pairs of shoes; you need a left shoe and a right shoe for each pair. In a valid sequence, you have the same number of left and right brackets, and they are correctly matched.
+
+For example, `(({}))` is a valid sequence because for each opening bracket `(` or `{`, there is a corresponding closing bracket `)` or `}`.
+
+On the other hand, `{{})` is not valid because the second curly bracket `}` doesn't have a matching opening bracket, so it's like having an extra right shoe without a left shoe to match with.
+
+In summary, a valid sequence of brackets is like having balanced pairs of brackets, where each opening bracket has a matching closing bracket.
+
+**Technical Application -**
+Imagine you are writing a small compiler for your college project and one of the tasks (or say sub-tasks) for the compiler would be to detect if the parenthesis are in place or not.
+
+---
+### Question
+Which of the following expressions is balanced with respect to parentheses?
+
+**Choices**
+- [x] `(a + b) * c`
+- [ ] `(a + b)) * c`
+- [ ] `(a + b)(c`
+- [ ] `(a + b)c`
+
+---
+### Balanced Parenthesis Implementation
+#### Idea
+An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
+
+ +
+#### Hint
+What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression?
+
+The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Approach
+* Iterate through the sequence, and whenever you encounter an opening parenthesis, you push it onto the stack.
+* When you encounter a closing parenthesis, you pop the top element from the stack and compare it to the current closing parenthesis. If they are of the same type (matching), you continue; otherwise, the sequence is invalid.
+
+Additionally, if you finish iterating through the sequence and the stack is not empty, the sequence is also invalid.
+
+
+#### Pseudocode
+```cpp
+bool is_valid_parentheses(sequence):
+ // Initialize an empty stack
+
+ For each character 'char' in sequence:
+ If 'char' is an opening parenthesis ('(', '{', '['):
+ Push 'char' onto the stack
+ Else if 'char' is a closing parenthesis (')', '}', ']'):
+ If the stack is empty:
+ Return false
+ Pop the top element from the stack into 'top'
+ If 'top' is not of the corresponding opening type for 'char':
+ Return false
+
+ If the stack is not empty:
+ Return false
+ Else:
+ Return true
+```
+
+#### Dry Run
+**Example:** `{()[]}`
+
+
+
+#### Hint
+What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression?
+
+The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Approach
+* Iterate through the sequence, and whenever you encounter an opening parenthesis, you push it onto the stack.
+* When you encounter a closing parenthesis, you pop the top element from the stack and compare it to the current closing parenthesis. If they are of the same type (matching), you continue; otherwise, the sequence is invalid.
+
+Additionally, if you finish iterating through the sequence and the stack is not empty, the sequence is also invalid.
+
+
+#### Pseudocode
+```cpp
+bool is_valid_parentheses(sequence):
+ // Initialize an empty stack
+
+ For each character 'char' in sequence:
+ If 'char' is an opening parenthesis ('(', '{', '['):
+ Push 'char' onto the stack
+ Else if 'char' is a closing parenthesis (')', '}', ']'):
+ If the stack is empty:
+ Return false
+ Pop the top element from the stack into 'top'
+ If 'top' is not of the corresponding opening type for 'char':
+ Return false
+
+ If the stack is not empty:
+ Return false
+ Else:
+ Return true
+```
+
+#### Dry Run
+**Example:** `{()[]}`
+
+ +
+1. Iterate on the example string.
+2. First of all we will encounter `{`. We will push it onto the stack.
+3. Next we have `(` again push onto the stack.
+4. Now when we encountered `)`, It means there is a match so pop the top element and continue the iteration.
+5. In next iteration we will encounter `[`. Similarly we will find the closing bracket in next iteration `]`. Pop that from stack.
+6. In the end stack will only contain `{`. Now when we will encounter `}`, we will again pop the topmost bracket.
+7. Finally there is nothing to iterate on as well as the stack is now empty. Which means the paranthesis sequence was valid.
+
+
+
+---
+### Problem 4 Remove equal pair of consecutive elements till possible
+
+
+
+Given a string, remove equal pair of consecutive elements till possible
+
+**Example**
+Let's say we have a string like `abcddc`, The idea here is to check if there are any consecutive pairs of characters that are the same. In this case, we see `dd` is such a pair. When you find such a pair, you simply remove it from the string, and it becomes `abcc` Then, you repeat the process with the new string, searching for and removing consecutive matching pairs of letters. This cycle continues until there are no more matching pairs left to remove.
+In the end the final string would be the solution.
+
+
+**Approach**
+This problem can be solved very efficiently by using the concept of stack. The stack will help you keep track of the elements that haven't been canceled out by a matching element.
+```cpp
+string remove_equal_pairs(s):
+ Initialize an empty stack
+
+ For each character 'char' in s:
+ If the stack is not empty and 'char' matches the character at the top of the stack:
+ Pop the element from the stack
+ Else:
+ Push 'char' onto the stack
+
+ Initialize an empty string 'result'
+
+ While the stack is not empty:
+ Pop an element from the stack and prepend it to 'result'
+
+ Return 'result'
+```
+
+#### Complexity
+**Time Complexity:** O(n)
+**Space Complexity:** O(n)
+
+---
+### Question
+If we remove equal pair of consecutive characters in this string multiple times then what will be the final string: `abbcbbcacx`
+
+**Choices**
+- [ ] empty string
+- [ ] ax
+- [x] cx
+- [ ] x
+
+
+
+**Explanation:**
+
+Let's go through the step-by-step process for the given example: `abbcbbcacx`.
+
+1. Begin by pushing `a` onto the stack: **Stack - [a]**
+2. Next, push `b` onto the stack: **Stack - [a, b]**
+3. During the next iteration, we will encounter `b` which matches the top element `b` of the stack. Continue iterating with a pop operation. **Stack - [a]**
+4. Proceed to push `c` during the next iteration, followed by `b`. **Stack - [a, c, b]**
+5. During the subsequent iteration, encountering `b` matches the top element of the stack. Since a consecutive pair is found, perform a pop operation to remove the topmost character, which is `b`. **Stack - [a, c]**
+6. As we encounter `c` again, and another `c` is already at the top of stack, pop `c` and continue iterating. **Stack - [a]**
+7. The stack now contains only `a`. In the next iteration, encountering `a` leads to a pop operation for the existing `a`. **Stack - []**
+8. Towards the end, push `c` and `x` onto the stack. Since there's no more to continue, the final stack **[c, x]**, represents the answer.
+
+
+
+---
+### Problem 5 Evaluate Postfix Expression
+
+Given a postfix expression, evaluate it.
+
+**Postfix Expression** contains operator after the operands.
+Below is an example of postfix expression:
+
+```cpp
+2 + 3 => Postfix => 2 3 +
+```
+
+#### Idea
+An operator is present after the operands on which we need to apply that operator, hence stack is perfect data structure for this problem.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+We'll process the expression as follows-
+
+**Example 1**
+```cpp
+[2, 3, +]
+```
+1. First we push 2 on stack.
+2. Then we push 3.
+3. Then we found '`+`', so we will pop top two operands, i.e 3 & 2 in this case
+4. Final result is 2 + 3 = 5
+
+**Example 2**
+```cpp
+[4, 3, 3, *, +, 2, -]
+```
+1. First we push 4 on stack.
+2. Then we push 3 and again 3.
+3. Then we found ' `*` ', so we will pop top two operands, i.e 3 & 3 in this case and push 3 * 3 to the stack. So push 9.
+4. Again we found '`+`', so pop the top two operands 9 and 4. Apply '`+`' operator 9 + 4 = 13 and push into the stack. Push 13.
+5. Push 2.
+6. Now we have an operator again '`-`', hence pop top two operands and push the result on the stack. 13-2 = 11. Push 11.
+7. In the end the single operand on the stack will be our final answer which is 11.
+
+
+---
+### Question
+What is the final answer obtained using the stack-based evaluation algorithm for the expression `[5, 2, *, 3, -]`?
+
+**Choices**
+- [ ] 8
+- [ ] 13
+- [x] 7
+- [ ] 15
+
+
+**Explanation:**
+
+1. Push 5 onto the stack.
+ `Stack: [5]`
+2. Push 2 onto the stack.
+ `Stack: [5, 2]`
+3. Encountering '*' - Pop the top two operands (2 and 5), and push the result (2 * 5 = 10) onto the stack.
+ `Stack: [10]`
+4. Push 3 onto the stack.
+ `Stack: [10, 3]`
+5. Encountering '-' - Pop the top two operands (3 and 10), and push the result (10 - 3 = 7) onto the stack.
+ `Stack: [7]`
+6. Therefore, the final answer obtained using the stack-based evaluation algorithm for the expression `[5, 2, *, 3, -]`is 7.
+
+
+---
+### Question
+
+Evaluate the given postfix expression:
+```cpp
+3 5 + 2 - 2 5 * -
+```
+
+**Choices**
+- [ ] 0
+- [ ] 4
+- [x] -4
+- [ ] 8
+
+
+**Explanation:**
+
+Let's evaluate the given postfix expression step by step: `3 5 + 2 - 2 5 * -`
+
+1. Push 3 onto the stack: **Stack - [3]**
+2. Push 5 onto the stack: **Stack - [3, 5]**
+3. Encounter '`+`', pop 5 and 3, perform 3 + 5 = 8, push 8 onto the stack: **Stack - [8]**
+4. Push 2 onto the stack: **Stack - [8, 2]**
+5. Encounter '`-`', pop 2 and 8, perform 8 - 2 = 6, push 6 onto the stack: **Stack - [6]**
+6. Push 2 onto the stack: **Stack - [6, 2]**
+7. Push 5 onto the stack: **Stack - [6, 2, 5]**
+8. Encounter '` * `', pop 5 and 2, perform 2 * 5 = 10, push 10 onto the stack: **Stack - [6, 10]**
+9. Encounter '`-`', pop 10 and 6, perform 6 - 10 = -4, push -4 onto the stack: **Stack - [-4]**
+10. End of the expression, the stack contains the final result: -4
+11. So, the result of the expression `3 5 + 2 - 2 5 * -` is `-4`.
+
+
+
+---
+### Evaluate Postfix Expression Pseudocode
+#### Pseudocode
+```cpp
+int evaluate_postfix(expression):
+ Initialize an empty stack
+
+ For each element 'element' in expression:
+ If 'element' is an operand:
+ Push 'element' onto the stack
+ Else if 'element' is an operator:
+ Pop 'operand2' from the stack
+ Pop 'operand1' from the stack
+ Perform the operation 'element' on 'operand1' and 'operand2'
+ Push the result back onto the stack
+
+ The final result is at the top of the stack
+ Pop and return the result
+```
+
+#### Complexity
+**Time Complexity:** O(n)
+**Space Complexity:** O(n)
diff --git a/Academy DSA Typed Notes/Advanced/DSA Stacks 2 Nearest Smaller or Greater Element.md b/Academy DSA Typed Notes/Advanced/DSA Stacks 2 Nearest Smaller or Greater Element.md
new file mode 100644
index 0000000..2e23962
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Stacks 2 Nearest Smaller or Greater Element.md
@@ -0,0 +1,506 @@
+# Stacks 2: Nearest Smaller/Greater Element
+
+---
+## Problem 1 Nearest smallest element on left
+
+Given an integer array A, find the index of nearest smallest element on left for all i index in A[].
+Formally , for all i find j such that `A[j] < A[i]`, `j < i` and j is maximum.
+
+**Example:**
+
+A[] = [8, 2, 4, 9, 7, 5, 3, 10]
+Answer = [-1, -1, 1, 2, 2, 2, 1, 6]
+
+For each element in the input array, the output indicates the index of the nearest smaller element on the left side of that element. If there's no smaller element on the left, it's represented by -1.
+
+| Element | Nearest Smaller Element | Index of Nearest Smaller Element |
+|:-------:|:-----------------------:|:--------------------------------:|
+| 8 | NA | -1 |
+| 2 | NA | -1 |
+| 4 | 2 | 1 |
+| 9 | 4 | 2 |
+| 7 | 4 | 2 |
+| 5 | 4 | 2 |
+| 3 | 2 | 1 |
+| 10 | 3 | 6 |
+
+---
+### Question
+
+Given N array elements, find the nearest smaller element on the left side for all the elements. If there is NO smaller element on left side, return -1. (Assume all elements are positive).
+
+A = [4, 6, 10, 11, 7, 8, 3, 5]
+
+**Choices**
+
+- [ ] [-1, 4, 6, 10, 4, 7, -1, 3]
+- [ ] [-1, 4, 6, 10, 6, 6, -1, 3]
+- [x] [-1, 4, 6, 10, 6, 7, -1, 3]
+
+
+---
+### Question
+
+Given N array elements, find the nearest smaller element on the left side for all the elements. If there is NO smaller element on left side, return -1. (Assume all elements are positive).
+
+A = [4, 5, 2, 10, 8, 2]
+
+**Choices**
+
+- [ ] [4, 4, -1, 2, 2, -1]
+- [x] [-1, 4, -1, 2, 2, -1]
+- [ ] [-1, 4, 4, 2, 2, -1]
+- [ ] [-1, 4, 2, 2, 2, 2]
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Nearest smallest element on left Brute Force
+
+For each element in the array, iterate through all the elements to its left.
+
+#### Pseudocode
+```java
+result[n];
+for (int i = 0; i < n; i++) {
+ int nearestSmaller = -1;
+
+ for (int j = i - 1; j >= 0; j--) {
+ if (arr[j] < arr[i]) {
+ nearestSmaller = j;
+ break;
+ }
+ }
+
+ result[i] = nearestSmaller;
+}
+return result;
+```
+
+#### Time Complexity
+
+This approach has a time complexity of $O(n^2)$ because for each element, it requires checking all elements to its left. It is inefficient for large input arrays.
+
+---
+### Question
+
+If A = [8, x, x, x, x, 5, x, x, x, x...]
+For any element > 5 can the element 8 become nearest smaller element on left?
+
+**Choices**
+
+- [ ] Yes
+- [x] No
+
+
+#### Explanation
+
+Not really since 5 will be the answer for them.
+
+---
+### Nearest Smallest Element Optimized Approach
+#### Observation/Intuition:
+
+When iterating through the array from left to right, we want to find the nearest smaller element on the left for each element efficiently.
+* Using a stack helps us keep track of potential candidates for the nearest smaller element as we move from left to right. The stack stores the indices of elements that have not yet found their nearest smaller element.
+* When we encounter a new element, we check if it is smaller than the element at the top of the stack (the most recent candidate for the nearest smaller element). If it is, we know that the element at the top of the stack cannot be the nearest smaller element for any future elements because the new element is closer and smaller. Therefore, we pop elements from the stack until we find an element that is smaller than the current element or until the stack becomes empty.
+* The popped elements from the stack are assigned as the nearest smaller elements on the left for the corresponding indices.
+* By doing this, we efficiently find the nearest smaller element for each element in the array without the need for nested loops or extensive comparisons, resulting in a linear time complexity of O(n).
+
+
+#### Optimized Approach:
+
+* Create an empty stack to store the indices of elements.
+* Initialize an empty result array with -1 values.
+* Iterate through the input array from left to right.
+* For each element, while the stack is not empty and the element at the current index is less than or equal to the element at the index stored at the top of the stack, pop elements from the stack and update the result array for those popped elements.
+* After the loop, the stack will contain indices of elements that haven't found their nearest smaller element. These elements have no smaller element on the left side.
+* The result array will contain the index of the nearest smaller element for all other elements.
+* Return the result array.
+
+---
+### Nearest Smallest Element Optimized Approach Dry Run
+
+
+* Initialize an empty stack and an empty result array of the same length as A filled with -1s.
+* Start iterating through the array from left to right:
+
+| i | Element | Pop index | Stack | Nearest Smaller Element | Push index |
+|:---:|:-------:|:---------:|:-----:|:-----------------------:|:----------:|
+| 0 | 8 | NIL | EMPTY | NA | 0 |
+| 1 | 2 | 0 | EMPTY | NA | 1 |
+| 2 | 4 | NIL | 1 | 2 | 2 |
+| 3 | 9 | NIL | 1, 2 | 4 | 3 |
+| 4 | 7 | 3 | 1, 2 | 4 | 4 |
+| 5 | 5 | 4 | 1, 2 | 4 | 5 |
+| 6 | 3 | 5, 2 | 1 | 2 | 6 |
+| 7 | 10 | NIL | 1, 6 | 3 | 7 |
+
+
+**Code:**
+
+```java
+for (int i = 0; i < n; i++) {
+ // While the stack is not empty and the element at the current index is less than or
+ // equal to the element at the index stored at the top of the stack, pop elements from
+ // the stack and update the result array.
+ while (!stack.isEmpty() && arr[i] <= arr[stack.peek()]) {
+ stack.pop();
+ }
+
+ // If the stack is not empty, the top element's index is the nearest smaller element on the left.
+ if (!stack.isEmpty()) {
+ result[i] = stack.peek();
+ }
+
+ // Push the current index onto the stack.
+ stack.push(i);
+}
+
+return result;
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(N)
+
+---
+### Nearest Smallest Element related questions
+
+### Question-2
+
+For all `i`, find nearest smaller or equal element on left
+
+**ANS:** For this question, we need to change the sign from `<=` to `<` in the above code of the approach in line number 5.
+
+### Question-3
+
+For all `i`, find nearest greater element on left
+
+**ANS:** For this question, we need to change the sign from `<=` to `>=` in the above code of the approach.
+
+### Question-4
+
+For all `i`, find nearest greater or equal element on left.
+
+**ANS:** For this question, we need to change the sign from `<=` to `>` in the above code of the approach.
+
+### Question-5
+
+For all `i`, find nearest smaller element on right.
+
+**ANS:** For this question, the for loop iterates through the input array arr in reverse order (from right to left), and it finds the nearest smaller element on the right for each element using a stack.
+
+```java
+for (int i = n - 1; i >= 0; i--) {
+ // While the stack is not empty and the element at the current index is less than or
+ // equal to the element at the index stored at the top of the stack, pop elements from
+ // the stack and update the result array.
+ while (!stack.isEmpty() && arr[i] <= arr[stack.peek()]) {
+ stack.pop();
+ }
+
+ // If the stack is not empty, the top element's index is the nearest smaller element on the right.
+ if (!stack.isEmpty()) {
+ result[i] = stack.peek();
+ }
+
+ // Push the current index onto the stack.
+ stack.push(i);
+}
+
+return result;
+```
+
+### Question-6
+For all `i`, find nearest smaller or equal element on right.
+
+**ANS:** For this question, we need to change the sign from `<=` to `>` in the above code of the approach.
+
+### Question - 7
+
+For all `i`, find nearest greater element on right.
+
+**ANS:** For this question, we need to change the sign from `<=` to `>=` in the above code of the approach.
+
+### Question-8
+
+For all `i`, find the nearest greater or equal element on right.
+
+**ANS:** For this question, we need to change the sign from `<=` to `>` in the above code of the approach.
+
+
+
+
+---
+### Problem 2 Largest Rectangle in histogram
+
+
+Given an integer array A, where
+A[i] = height of i-th bar.
+Width of each bar is = 1.
+
+Find the area of the largest rectangle formed by continious bars.
+
+
+**Given Array (heights):** [8, 6, 2, 5, 6, 5, 7, 4]
+
+The goal is to find the largest rectangle that can be formed using continuous bars from this array. In this example, the largest rectangle is formed by bars with heights 5, 6, 5, and 7. The width of each bar is 1, so the area of this rectangle is 5 (height) * 4 (width) = 20.
+
+
+
+1. Iterate on the example string.
+2. First of all we will encounter `{`. We will push it onto the stack.
+3. Next we have `(` again push onto the stack.
+4. Now when we encountered `)`, It means there is a match so pop the top element and continue the iteration.
+5. In next iteration we will encounter `[`. Similarly we will find the closing bracket in next iteration `]`. Pop that from stack.
+6. In the end stack will only contain `{`. Now when we will encounter `}`, we will again pop the topmost bracket.
+7. Finally there is nothing to iterate on as well as the stack is now empty. Which means the paranthesis sequence was valid.
+
+
+
+---
+### Problem 4 Remove equal pair of consecutive elements till possible
+
+
+
+Given a string, remove equal pair of consecutive elements till possible
+
+**Example**
+Let's say we have a string like `abcddc`, The idea here is to check if there are any consecutive pairs of characters that are the same. In this case, we see `dd` is such a pair. When you find such a pair, you simply remove it from the string, and it becomes `abcc` Then, you repeat the process with the new string, searching for and removing consecutive matching pairs of letters. This cycle continues until there are no more matching pairs left to remove.
+In the end the final string would be the solution.
+
+
+**Approach**
+This problem can be solved very efficiently by using the concept of stack. The stack will help you keep track of the elements that haven't been canceled out by a matching element.
+```cpp
+string remove_equal_pairs(s):
+ Initialize an empty stack
+
+ For each character 'char' in s:
+ If the stack is not empty and 'char' matches the character at the top of the stack:
+ Pop the element from the stack
+ Else:
+ Push 'char' onto the stack
+
+ Initialize an empty string 'result'
+
+ While the stack is not empty:
+ Pop an element from the stack and prepend it to 'result'
+
+ Return 'result'
+```
+
+#### Complexity
+**Time Complexity:** O(n)
+**Space Complexity:** O(n)
+
+---
+### Question
+If we remove equal pair of consecutive characters in this string multiple times then what will be the final string: `abbcbbcacx`
+
+**Choices**
+- [ ] empty string
+- [ ] ax
+- [x] cx
+- [ ] x
+
+
+
+**Explanation:**
+
+Let's go through the step-by-step process for the given example: `abbcbbcacx`.
+
+1. Begin by pushing `a` onto the stack: **Stack - [a]**
+2. Next, push `b` onto the stack: **Stack - [a, b]**
+3. During the next iteration, we will encounter `b` which matches the top element `b` of the stack. Continue iterating with a pop operation. **Stack - [a]**
+4. Proceed to push `c` during the next iteration, followed by `b`. **Stack - [a, c, b]**
+5. During the subsequent iteration, encountering `b` matches the top element of the stack. Since a consecutive pair is found, perform a pop operation to remove the topmost character, which is `b`. **Stack - [a, c]**
+6. As we encounter `c` again, and another `c` is already at the top of stack, pop `c` and continue iterating. **Stack - [a]**
+7. The stack now contains only `a`. In the next iteration, encountering `a` leads to a pop operation for the existing `a`. **Stack - []**
+8. Towards the end, push `c` and `x` onto the stack. Since there's no more to continue, the final stack **[c, x]**, represents the answer.
+
+
+
+---
+### Problem 5 Evaluate Postfix Expression
+
+Given a postfix expression, evaluate it.
+
+**Postfix Expression** contains operator after the operands.
+Below is an example of postfix expression:
+
+```cpp
+2 + 3 => Postfix => 2 3 +
+```
+
+#### Idea
+An operator is present after the operands on which we need to apply that operator, hence stack is perfect data structure for this problem.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+We'll process the expression as follows-
+
+**Example 1**
+```cpp
+[2, 3, +]
+```
+1. First we push 2 on stack.
+2. Then we push 3.
+3. Then we found '`+`', so we will pop top two operands, i.e 3 & 2 in this case
+4. Final result is 2 + 3 = 5
+
+**Example 2**
+```cpp
+[4, 3, 3, *, +, 2, -]
+```
+1. First we push 4 on stack.
+2. Then we push 3 and again 3.
+3. Then we found ' `*` ', so we will pop top two operands, i.e 3 & 3 in this case and push 3 * 3 to the stack. So push 9.
+4. Again we found '`+`', so pop the top two operands 9 and 4. Apply '`+`' operator 9 + 4 = 13 and push into the stack. Push 13.
+5. Push 2.
+6. Now we have an operator again '`-`', hence pop top two operands and push the result on the stack. 13-2 = 11. Push 11.
+7. In the end the single operand on the stack will be our final answer which is 11.
+
+
+---
+### Question
+What is the final answer obtained using the stack-based evaluation algorithm for the expression `[5, 2, *, 3, -]`?
+
+**Choices**
+- [ ] 8
+- [ ] 13
+- [x] 7
+- [ ] 15
+
+
+**Explanation:**
+
+1. Push 5 onto the stack.
+ `Stack: [5]`
+2. Push 2 onto the stack.
+ `Stack: [5, 2]`
+3. Encountering '*' - Pop the top two operands (2 and 5), and push the result (2 * 5 = 10) onto the stack.
+ `Stack: [10]`
+4. Push 3 onto the stack.
+ `Stack: [10, 3]`
+5. Encountering '-' - Pop the top two operands (3 and 10), and push the result (10 - 3 = 7) onto the stack.
+ `Stack: [7]`
+6. Therefore, the final answer obtained using the stack-based evaluation algorithm for the expression `[5, 2, *, 3, -]`is 7.
+
+
+---
+### Question
+
+Evaluate the given postfix expression:
+```cpp
+3 5 + 2 - 2 5 * -
+```
+
+**Choices**
+- [ ] 0
+- [ ] 4
+- [x] -4
+- [ ] 8
+
+
+**Explanation:**
+
+Let's evaluate the given postfix expression step by step: `3 5 + 2 - 2 5 * -`
+
+1. Push 3 onto the stack: **Stack - [3]**
+2. Push 5 onto the stack: **Stack - [3, 5]**
+3. Encounter '`+`', pop 5 and 3, perform 3 + 5 = 8, push 8 onto the stack: **Stack - [8]**
+4. Push 2 onto the stack: **Stack - [8, 2]**
+5. Encounter '`-`', pop 2 and 8, perform 8 - 2 = 6, push 6 onto the stack: **Stack - [6]**
+6. Push 2 onto the stack: **Stack - [6, 2]**
+7. Push 5 onto the stack: **Stack - [6, 2, 5]**
+8. Encounter '` * `', pop 5 and 2, perform 2 * 5 = 10, push 10 onto the stack: **Stack - [6, 10]**
+9. Encounter '`-`', pop 10 and 6, perform 6 - 10 = -4, push -4 onto the stack: **Stack - [-4]**
+10. End of the expression, the stack contains the final result: -4
+11. So, the result of the expression `3 5 + 2 - 2 5 * -` is `-4`.
+
+
+
+---
+### Evaluate Postfix Expression Pseudocode
+#### Pseudocode
+```cpp
+int evaluate_postfix(expression):
+ Initialize an empty stack
+
+ For each element 'element' in expression:
+ If 'element' is an operand:
+ Push 'element' onto the stack
+ Else if 'element' is an operator:
+ Pop 'operand2' from the stack
+ Pop 'operand1' from the stack
+ Perform the operation 'element' on 'operand1' and 'operand2'
+ Push the result back onto the stack
+
+ The final result is at the top of the stack
+ Pop and return the result
+```
+
+#### Complexity
+**Time Complexity:** O(n)
+**Space Complexity:** O(n)
diff --git a/Academy DSA Typed Notes/Advanced/DSA Stacks 2 Nearest Smaller or Greater Element.md b/Academy DSA Typed Notes/Advanced/DSA Stacks 2 Nearest Smaller or Greater Element.md
new file mode 100644
index 0000000..2e23962
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Stacks 2 Nearest Smaller or Greater Element.md
@@ -0,0 +1,506 @@
+# Stacks 2: Nearest Smaller/Greater Element
+
+---
+## Problem 1 Nearest smallest element on left
+
+Given an integer array A, find the index of nearest smallest element on left for all i index in A[].
+Formally , for all i find j such that `A[j] < A[i]`, `j < i` and j is maximum.
+
+**Example:**
+
+A[] = [8, 2, 4, 9, 7, 5, 3, 10]
+Answer = [-1, -1, 1, 2, 2, 2, 1, 6]
+
+For each element in the input array, the output indicates the index of the nearest smaller element on the left side of that element. If there's no smaller element on the left, it's represented by -1.
+
+| Element | Nearest Smaller Element | Index of Nearest Smaller Element |
+|:-------:|:-----------------------:|:--------------------------------:|
+| 8 | NA | -1 |
+| 2 | NA | -1 |
+| 4 | 2 | 1 |
+| 9 | 4 | 2 |
+| 7 | 4 | 2 |
+| 5 | 4 | 2 |
+| 3 | 2 | 1 |
+| 10 | 3 | 6 |
+
+---
+### Question
+
+Given N array elements, find the nearest smaller element on the left side for all the elements. If there is NO smaller element on left side, return -1. (Assume all elements are positive).
+
+A = [4, 6, 10, 11, 7, 8, 3, 5]
+
+**Choices**
+
+- [ ] [-1, 4, 6, 10, 4, 7, -1, 3]
+- [ ] [-1, 4, 6, 10, 6, 6, -1, 3]
+- [x] [-1, 4, 6, 10, 6, 7, -1, 3]
+
+
+---
+### Question
+
+Given N array elements, find the nearest smaller element on the left side for all the elements. If there is NO smaller element on left side, return -1. (Assume all elements are positive).
+
+A = [4, 5, 2, 10, 8, 2]
+
+**Choices**
+
+- [ ] [4, 4, -1, 2, 2, -1]
+- [x] [-1, 4, -1, 2, 2, -1]
+- [ ] [-1, 4, 4, 2, 2, -1]
+- [ ] [-1, 4, 2, 2, 2, 2]
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Nearest smallest element on left Brute Force
+
+For each element in the array, iterate through all the elements to its left.
+
+#### Pseudocode
+```java
+result[n];
+for (int i = 0; i < n; i++) {
+ int nearestSmaller = -1;
+
+ for (int j = i - 1; j >= 0; j--) {
+ if (arr[j] < arr[i]) {
+ nearestSmaller = j;
+ break;
+ }
+ }
+
+ result[i] = nearestSmaller;
+}
+return result;
+```
+
+#### Time Complexity
+
+This approach has a time complexity of $O(n^2)$ because for each element, it requires checking all elements to its left. It is inefficient for large input arrays.
+
+---
+### Question
+
+If A = [8, x, x, x, x, 5, x, x, x, x...]
+For any element > 5 can the element 8 become nearest smaller element on left?
+
+**Choices**
+
+- [ ] Yes
+- [x] No
+
+
+#### Explanation
+
+Not really since 5 will be the answer for them.
+
+---
+### Nearest Smallest Element Optimized Approach
+#### Observation/Intuition:
+
+When iterating through the array from left to right, we want to find the nearest smaller element on the left for each element efficiently.
+* Using a stack helps us keep track of potential candidates for the nearest smaller element as we move from left to right. The stack stores the indices of elements that have not yet found their nearest smaller element.
+* When we encounter a new element, we check if it is smaller than the element at the top of the stack (the most recent candidate for the nearest smaller element). If it is, we know that the element at the top of the stack cannot be the nearest smaller element for any future elements because the new element is closer and smaller. Therefore, we pop elements from the stack until we find an element that is smaller than the current element or until the stack becomes empty.
+* The popped elements from the stack are assigned as the nearest smaller elements on the left for the corresponding indices.
+* By doing this, we efficiently find the nearest smaller element for each element in the array without the need for nested loops or extensive comparisons, resulting in a linear time complexity of O(n).
+
+
+#### Optimized Approach:
+
+* Create an empty stack to store the indices of elements.
+* Initialize an empty result array with -1 values.
+* Iterate through the input array from left to right.
+* For each element, while the stack is not empty and the element at the current index is less than or equal to the element at the index stored at the top of the stack, pop elements from the stack and update the result array for those popped elements.
+* After the loop, the stack will contain indices of elements that haven't found their nearest smaller element. These elements have no smaller element on the left side.
+* The result array will contain the index of the nearest smaller element for all other elements.
+* Return the result array.
+
+---
+### Nearest Smallest Element Optimized Approach Dry Run
+
+
+* Initialize an empty stack and an empty result array of the same length as A filled with -1s.
+* Start iterating through the array from left to right:
+
+| i | Element | Pop index | Stack | Nearest Smaller Element | Push index |
+|:---:|:-------:|:---------:|:-----:|:-----------------------:|:----------:|
+| 0 | 8 | NIL | EMPTY | NA | 0 |
+| 1 | 2 | 0 | EMPTY | NA | 1 |
+| 2 | 4 | NIL | 1 | 2 | 2 |
+| 3 | 9 | NIL | 1, 2 | 4 | 3 |
+| 4 | 7 | 3 | 1, 2 | 4 | 4 |
+| 5 | 5 | 4 | 1, 2 | 4 | 5 |
+| 6 | 3 | 5, 2 | 1 | 2 | 6 |
+| 7 | 10 | NIL | 1, 6 | 3 | 7 |
+
+
+**Code:**
+
+```java
+for (int i = 0; i < n; i++) {
+ // While the stack is not empty and the element at the current index is less than or
+ // equal to the element at the index stored at the top of the stack, pop elements from
+ // the stack and update the result array.
+ while (!stack.isEmpty() && arr[i] <= arr[stack.peek()]) {
+ stack.pop();
+ }
+
+ // If the stack is not empty, the top element's index is the nearest smaller element on the left.
+ if (!stack.isEmpty()) {
+ result[i] = stack.peek();
+ }
+
+ // Push the current index onto the stack.
+ stack.push(i);
+}
+
+return result;
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(N)
+
+---
+### Nearest Smallest Element related questions
+
+### Question-2
+
+For all `i`, find nearest smaller or equal element on left
+
+**ANS:** For this question, we need to change the sign from `<=` to `<` in the above code of the approach in line number 5.
+
+### Question-3
+
+For all `i`, find nearest greater element on left
+
+**ANS:** For this question, we need to change the sign from `<=` to `>=` in the above code of the approach.
+
+### Question-4
+
+For all `i`, find nearest greater or equal element on left.
+
+**ANS:** For this question, we need to change the sign from `<=` to `>` in the above code of the approach.
+
+### Question-5
+
+For all `i`, find nearest smaller element on right.
+
+**ANS:** For this question, the for loop iterates through the input array arr in reverse order (from right to left), and it finds the nearest smaller element on the right for each element using a stack.
+
+```java
+for (int i = n - 1; i >= 0; i--) {
+ // While the stack is not empty and the element at the current index is less than or
+ // equal to the element at the index stored at the top of the stack, pop elements from
+ // the stack and update the result array.
+ while (!stack.isEmpty() && arr[i] <= arr[stack.peek()]) {
+ stack.pop();
+ }
+
+ // If the stack is not empty, the top element's index is the nearest smaller element on the right.
+ if (!stack.isEmpty()) {
+ result[i] = stack.peek();
+ }
+
+ // Push the current index onto the stack.
+ stack.push(i);
+}
+
+return result;
+```
+
+### Question-6
+For all `i`, find nearest smaller or equal element on right.
+
+**ANS:** For this question, we need to change the sign from `<=` to `>` in the above code of the approach.
+
+### Question - 7
+
+For all `i`, find nearest greater element on right.
+
+**ANS:** For this question, we need to change the sign from `<=` to `>=` in the above code of the approach.
+
+### Question-8
+
+For all `i`, find the nearest greater or equal element on right.
+
+**ANS:** For this question, we need to change the sign from `<=` to `>` in the above code of the approach.
+
+
+
+
+---
+### Problem 2 Largest Rectangle in histogram
+
+
+Given an integer array A, where
+A[i] = height of i-th bar.
+Width of each bar is = 1.
+
+Find the area of the largest rectangle formed by continious bars.
+
+
+**Given Array (heights):** [8, 6, 2, 5, 6, 5, 7, 4]
+
+The goal is to find the largest rectangle that can be formed using continuous bars from this array. In this example, the largest rectangle is formed by bars with heights 5, 6, 5, and 7. The width of each bar is 1, so the area of this rectangle is 5 (height) * 4 (width) = 20.
+
+ +
+
+Sure, here is a brief MCQ based on finding the largest rectangle formed by continuous bars in an integer array representing bar heights:
+
+---
+### Question
+Find the area of the largest rectangle formed by continious bars.
+
+bars = [1, 2, 3, 2, 1]
+
+**Choices**
+- [ ] 5
+- [ ] 9
+- [ ] 7
+- [x] 6
+- [ ] 3
+
+**Explanation:**
+
+The largest rectangle is formed from [2, 3, 2] whose contribution is [2, 2, 2] thus the area of the largest rectangle is 6.
+
+
+#### Largest Rectangle Brute Force
+
+**Brute - Force Approach Pseudo Code:**
+
+```cpp
+function findMaxRectangleArea(hist):
+ maxArea = 0
+
+ for i from 0 to len(hist) - 1:
+ // Consider each bar as a potential starting point
+ minHeight = hist[i]
+
+ for j from i to len(hist) - 1:
+ // Iterate through bars to the right
+ minHeight = min(minHeight, hist[j])
+ width = j - i + 1
+ area = minHeight * width
+ maxArea = max(maxArea, area)
+
+ return maxArea
+```
+
+The brute-force approach involves nested loops and has a time complexity of O(n^2) because it considers all possible combinations of starting and ending points for rectangles.
+
+:::warning
+Please take some time to think about the optimised approach on your own before reading further.....
+:::
+
+#### Optimized Approch
+
+**Mathematical Representation:**
+
+* Let a[i] represent the height of the bar at index i.
+* We use j to represent the index of the nearest smaller bar to the left of i.
+* Similarly, we use k to represent the index of the nearest smaller bar to the right of i.
+* The area of the rectangle that can be formed with the bar at index i as its base is given by `a[i] * (k - j - 1)`.
+
+**Observation/Intuition:**
+
+* The key insight here is that for each potential base (represented by indices in the stack), we can efficiently calculate the area of the rectangle by finding the width between the current index and the index at the top of the stack.
+* By using a stack, we maintain a list of potential bases and calculate the area of rectangles as we encounter new heights, ensuring we consider all possible rectangles efficiently.
+
+**Optimized Approach Pseudo Code:**
+
+```cpp
+function findMaxRectangleArea(hist):
+ stack = [] // Initialize an empty stack to store indices of bars.
+ maxArea = 0
+
+ for i from 0 to len(hist) - 1:
+ while (stack is not empty and hist[i] < hist[stack.top()]):
+ // Pop elements from the stack and calculate areas
+ // with their heights as the potential bases.
+ height = hist[stack.pop()]
+ width = (i - stack.top() - 1) if stack is not empty else i
+ area = height * width
+ maxArea = max(maxArea, area)
+
+ stack.push(i) // Push the current index onto the stack.
+
+ while (stack is not empty):
+ // Process the remaining elements in the stack.
+ height = hist[stack.pop()]
+ width = (len(hist) - stack.top() - 1) if stack is not empty else len(hist)
+ area = height * width
+ maxArea = max(maxArea, area)
+
+ return maxArea
+```
+
+
+**Mathematical Representation of the Answer:**
+
+* The answer (maximum area) is given by the formula:
+* $ans ~=~ max(a[i] * (nearest~smaller~right[i] * nearest~smaller~left[i] - 1))$
+* Where a[i] is the height of the bar at index i.
+* `nearest_smaller_right[i]` is the index of the nearest smaller bar to the right of i.
+* `nearest_smaller_left[i]` is the index of the nearest smaller bar to the left of i.
+* We subtract 1 from the product of `nearest_smaller_right[i]` and `nearest_smaller_left[i]` to account for the width of the rectangle.
+
+---
+### Problem 3 Sum of (Max-Min) of all subarrays
+
+
+Giver an integer array with distinct integers, for all subarrays find (max-min) and return its sum as the answer.
+
+**Example:**
+
+Given Array: [2, 5, 3]
+
+The goal is to find the sum of the differences between the maximum and minimum elements for all possible subarrays.
+
+* Subarray [2]: Max = 2, Min = 2, Difference = 0
+* Subarray [5]: Max = 5, Min = 5, Difference = 0
+* Subarray [3]: Max = 3, Min = 3, Difference = 0
+* Subarrays of length 2:
+ * [2, 5]: Max = 5, Min = 2, Difference = 3
+ * [5, 3]: Max = 5, Min = 3, Difference = 2
+* Subarray [2, 5, 3]: Max = 5, Min = 2, Difference = 3
+
+
+The sum of all differences is 0 + 0 + 0 + 3 + 2 + 3 = 8.
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Sum of (Max-Min) of all subarrays Brute force approach
+**Brute-Force Approach Pseudo Code:**
+
+```cpp
+function sumOfDifferences(arr):
+ result = 0
+
+ for start from 0 to len(arr) - 1:
+ for end from start to len(arr) - 1:
+ // Find the maximum and minimum elements within the subarray
+ maxElement = arr[start]
+ minElement = arr[start]
+
+ for i from start to end:
+ maxElement = max(maxElement, arr[i])
+ minElement = min(minElement, arr[i])
+
+ // Calculate the difference between the maximum and minimum elements
+ difference = maxElement - minElement
+
+ // Add this difference to the result
+ result += difference
+
+ return result
+```
+
+#### Complexity
+**Time Complexity:** O(N * N)
+**Space Complexity:** O(1)
+
+---
+### Question
+Giver an integer array, A with distinct integers, for all subarrays find (max-min) and return its sum as the answer.
+
+A = [1, 2, 3]
+
+**Choices**
+- [x] 4
+- [ ] 6
+- [ ] 5
+- [ ] 0
+
+
+#### Explanation:
+
+The goal is to find the sum of the differences between the maximum and minimum elements for all possible subarrays.
+
+Subarrays of length 1:
+* [1]: Max = 1, Min = 1, Difference = 0
+* [2]: Max = 2, Min = 2, Difference = 0
+* [3]: Max = 3, Min = 3, Difference = 0
+
+Subarrays of length 2:
+* [1, 2]: Max = 2, Min = 1, Difference = 1
+* [2, 3]: Max = 3, Min = 1, Difference = 1
+
+Subarrays of length 3:
+* [1, 2, 3]: Max = 3, Min = 1, Difference = 2
+
+The sum of all differences is 0 + 0 + 0 + 1 + 1 + 2 = 4.
+
+
+---
+### Sum of (Max-Min) of all subarrays Optimized approach
+
+#### Optimized Approach
+
+**Intuition:**
+
+* The contribution technique eliminates redundant calculations by efficiently counting the number of subarrays in which each element can be the maximum or minimum element.
+* By tracking the elements that are greater or smaller than the current element in both directions, we can calculate their contributions to the sum of (max - min) differences without repeatedly considering the same subarrays.
+
+**Optimized Approach Pseudo code:**
+
+```cpp
+function sumOfDifferences(arr):
+ n = length of arr
+ left = new array of size n
+ right = new array of size n
+ max_stack = empty stack
+ min_stack = empty stack
+ result = 0
+
+ // Initialize left and right arrays
+ for i from 0 to n - 1:
+ left[i] = (i + 1) * (n - i)
+ right[i] = (i + 1) * (i + 1)
+
+ // Calculate left contributions
+ for i from 0 to n - 1:
+ while (not max_stack.isEmpty() and arr[i] > arr[max_stack.top()]):
+ max_stack.pop()
+
+ if (max_stack.isEmpty()):
+ left[i] = (i + 1) * (i + 1)
+ else:
+ left[i] = (i - max_stack.top()) * (i + 1)
+
+ max_stack.push(i)
+
+ // Calculate right contributions
+ for i from n - 1 to 0:
+ while (not min_stack.isEmpty() and arr[i] < arr[min_stack.top()]):
+ min_stack.pop()
+
+ if (min_stack.isEmpty()):
+ right[i] = (n - i) * (n - i)
+ else:
+ right[i] = (min_stack.top() - i) * (n - i)
+
+ min_stack.push(i)
+
+ // Calculate the sum of (max - min) differences
+ for i from 0 to n - 1:
+ contribution = (right[i] * left[i]) * arr[i]
+ result += contribution
+
+ return result
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(N)
diff --git a/Academy DSA Typed Notes/Advanced/DSA Trees 1 Structure & Traversal.md b/Academy DSA Typed Notes/Advanced/DSA Trees 1 Structure & Traversal.md
new file mode 100644
index 0000000..2e1c599
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Trees 1 Structure & Traversal.md
@@ -0,0 +1,521 @@
+# Trees 1: Structure & Traversal
+
+---
+## What is a tree
+
+Till now, we have seen data structures such as Arrays, Linked Lists, Stacks, Queues... They are **Linear Data Structure** which means we can access them in sequencial order.
+
+The other category is **Non Linear Data Structure**
+
+At a lot of places, you must have seen hierarchy - Family, Office, Computer File System, etc. Therefore, there arise a need to be able to store such type of data and process it.
+
+**Tree is an example of a non/linear or hierarchical data structure.**
+
+
+### Example
+Let us see the **hierachy of people in an organization**:
+```sql
+CEO (Chief Executive Officer)
+├── CTO (Chief Technology Officer)
+│ ├── Engineering Manager
+│ │ ├── Software Development Team Lead
+│ │ │ ├── Software Engineer
+│ │ │ └── Software Engineer
+│ │ └── QA Team Lead
+│ │ ├── QA Engineer
+│ │ └── QA Engineer
+│ └── IT Manager
+│ ├── IT Specialist
+│ └── IT Specialist
+├── CFO (Chief Financial Officer)
+│ ├── Finance Manager
+│ │ ├── Accountant
+│ │ └── Accountant
+│ └── Procurement Manager
+│ ├── Procurement Officer
+│ └── Procurement Officer
+└── CMO (Chief Marketing Officer)
+ ├── Marketing Manager
+ │ ├── Marketing Specialist
+ │ └── Marketing Specialist
+ └── Sales Manager
+ ├── Sales Representative
+ └── Sales Representative
+```
+
+As we know that every tree has roots which are below the leaves but in the computer science the case is different the roots are at the top and leaves below it.
+
+---
+## Tree naming
+
+Example
+```sql
+ 1
+ / \
+ 2 3
+ / \ / \
+ 4 5 6 7
+ /
+ 8
+```
+* **Node**: An element in a tree that contains data and may have child nodes connected to it. 1, 2, 3, 4, 5, 6, 7, 8.
+
+
+
+
+Sure, here is a brief MCQ based on finding the largest rectangle formed by continuous bars in an integer array representing bar heights:
+
+---
+### Question
+Find the area of the largest rectangle formed by continious bars.
+
+bars = [1, 2, 3, 2, 1]
+
+**Choices**
+- [ ] 5
+- [ ] 9
+- [ ] 7
+- [x] 6
+- [ ] 3
+
+**Explanation:**
+
+The largest rectangle is formed from [2, 3, 2] whose contribution is [2, 2, 2] thus the area of the largest rectangle is 6.
+
+
+#### Largest Rectangle Brute Force
+
+**Brute - Force Approach Pseudo Code:**
+
+```cpp
+function findMaxRectangleArea(hist):
+ maxArea = 0
+
+ for i from 0 to len(hist) - 1:
+ // Consider each bar as a potential starting point
+ minHeight = hist[i]
+
+ for j from i to len(hist) - 1:
+ // Iterate through bars to the right
+ minHeight = min(minHeight, hist[j])
+ width = j - i + 1
+ area = minHeight * width
+ maxArea = max(maxArea, area)
+
+ return maxArea
+```
+
+The brute-force approach involves nested loops and has a time complexity of O(n^2) because it considers all possible combinations of starting and ending points for rectangles.
+
+:::warning
+Please take some time to think about the optimised approach on your own before reading further.....
+:::
+
+#### Optimized Approch
+
+**Mathematical Representation:**
+
+* Let a[i] represent the height of the bar at index i.
+* We use j to represent the index of the nearest smaller bar to the left of i.
+* Similarly, we use k to represent the index of the nearest smaller bar to the right of i.
+* The area of the rectangle that can be formed with the bar at index i as its base is given by `a[i] * (k - j - 1)`.
+
+**Observation/Intuition:**
+
+* The key insight here is that for each potential base (represented by indices in the stack), we can efficiently calculate the area of the rectangle by finding the width between the current index and the index at the top of the stack.
+* By using a stack, we maintain a list of potential bases and calculate the area of rectangles as we encounter new heights, ensuring we consider all possible rectangles efficiently.
+
+**Optimized Approach Pseudo Code:**
+
+```cpp
+function findMaxRectangleArea(hist):
+ stack = [] // Initialize an empty stack to store indices of bars.
+ maxArea = 0
+
+ for i from 0 to len(hist) - 1:
+ while (stack is not empty and hist[i] < hist[stack.top()]):
+ // Pop elements from the stack and calculate areas
+ // with their heights as the potential bases.
+ height = hist[stack.pop()]
+ width = (i - stack.top() - 1) if stack is not empty else i
+ area = height * width
+ maxArea = max(maxArea, area)
+
+ stack.push(i) // Push the current index onto the stack.
+
+ while (stack is not empty):
+ // Process the remaining elements in the stack.
+ height = hist[stack.pop()]
+ width = (len(hist) - stack.top() - 1) if stack is not empty else len(hist)
+ area = height * width
+ maxArea = max(maxArea, area)
+
+ return maxArea
+```
+
+
+**Mathematical Representation of the Answer:**
+
+* The answer (maximum area) is given by the formula:
+* $ans ~=~ max(a[i] * (nearest~smaller~right[i] * nearest~smaller~left[i] - 1))$
+* Where a[i] is the height of the bar at index i.
+* `nearest_smaller_right[i]` is the index of the nearest smaller bar to the right of i.
+* `nearest_smaller_left[i]` is the index of the nearest smaller bar to the left of i.
+* We subtract 1 from the product of `nearest_smaller_right[i]` and `nearest_smaller_left[i]` to account for the width of the rectangle.
+
+---
+### Problem 3 Sum of (Max-Min) of all subarrays
+
+
+Giver an integer array with distinct integers, for all subarrays find (max-min) and return its sum as the answer.
+
+**Example:**
+
+Given Array: [2, 5, 3]
+
+The goal is to find the sum of the differences between the maximum and minimum elements for all possible subarrays.
+
+* Subarray [2]: Max = 2, Min = 2, Difference = 0
+* Subarray [5]: Max = 5, Min = 5, Difference = 0
+* Subarray [3]: Max = 3, Min = 3, Difference = 0
+* Subarrays of length 2:
+ * [2, 5]: Max = 5, Min = 2, Difference = 3
+ * [5, 3]: Max = 5, Min = 3, Difference = 2
+* Subarray [2, 5, 3]: Max = 5, Min = 2, Difference = 3
+
+
+The sum of all differences is 0 + 0 + 0 + 3 + 2 + 3 = 8.
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Sum of (Max-Min) of all subarrays Brute force approach
+**Brute-Force Approach Pseudo Code:**
+
+```cpp
+function sumOfDifferences(arr):
+ result = 0
+
+ for start from 0 to len(arr) - 1:
+ for end from start to len(arr) - 1:
+ // Find the maximum and minimum elements within the subarray
+ maxElement = arr[start]
+ minElement = arr[start]
+
+ for i from start to end:
+ maxElement = max(maxElement, arr[i])
+ minElement = min(minElement, arr[i])
+
+ // Calculate the difference between the maximum and minimum elements
+ difference = maxElement - minElement
+
+ // Add this difference to the result
+ result += difference
+
+ return result
+```
+
+#### Complexity
+**Time Complexity:** O(N * N)
+**Space Complexity:** O(1)
+
+---
+### Question
+Giver an integer array, A with distinct integers, for all subarrays find (max-min) and return its sum as the answer.
+
+A = [1, 2, 3]
+
+**Choices**
+- [x] 4
+- [ ] 6
+- [ ] 5
+- [ ] 0
+
+
+#### Explanation:
+
+The goal is to find the sum of the differences between the maximum and minimum elements for all possible subarrays.
+
+Subarrays of length 1:
+* [1]: Max = 1, Min = 1, Difference = 0
+* [2]: Max = 2, Min = 2, Difference = 0
+* [3]: Max = 3, Min = 3, Difference = 0
+
+Subarrays of length 2:
+* [1, 2]: Max = 2, Min = 1, Difference = 1
+* [2, 3]: Max = 3, Min = 1, Difference = 1
+
+Subarrays of length 3:
+* [1, 2, 3]: Max = 3, Min = 1, Difference = 2
+
+The sum of all differences is 0 + 0 + 0 + 1 + 1 + 2 = 4.
+
+
+---
+### Sum of (Max-Min) of all subarrays Optimized approach
+
+#### Optimized Approach
+
+**Intuition:**
+
+* The contribution technique eliminates redundant calculations by efficiently counting the number of subarrays in which each element can be the maximum or minimum element.
+* By tracking the elements that are greater or smaller than the current element in both directions, we can calculate their contributions to the sum of (max - min) differences without repeatedly considering the same subarrays.
+
+**Optimized Approach Pseudo code:**
+
+```cpp
+function sumOfDifferences(arr):
+ n = length of arr
+ left = new array of size n
+ right = new array of size n
+ max_stack = empty stack
+ min_stack = empty stack
+ result = 0
+
+ // Initialize left and right arrays
+ for i from 0 to n - 1:
+ left[i] = (i + 1) * (n - i)
+ right[i] = (i + 1) * (i + 1)
+
+ // Calculate left contributions
+ for i from 0 to n - 1:
+ while (not max_stack.isEmpty() and arr[i] > arr[max_stack.top()]):
+ max_stack.pop()
+
+ if (max_stack.isEmpty()):
+ left[i] = (i + 1) * (i + 1)
+ else:
+ left[i] = (i - max_stack.top()) * (i + 1)
+
+ max_stack.push(i)
+
+ // Calculate right contributions
+ for i from n - 1 to 0:
+ while (not min_stack.isEmpty() and arr[i] < arr[min_stack.top()]):
+ min_stack.pop()
+
+ if (min_stack.isEmpty()):
+ right[i] = (n - i) * (n - i)
+ else:
+ right[i] = (min_stack.top() - i) * (n - i)
+
+ min_stack.push(i)
+
+ // Calculate the sum of (max - min) differences
+ for i from 0 to n - 1:
+ contribution = (right[i] * left[i]) * arr[i]
+ result += contribution
+
+ return result
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(N)
diff --git a/Academy DSA Typed Notes/Advanced/DSA Trees 1 Structure & Traversal.md b/Academy DSA Typed Notes/Advanced/DSA Trees 1 Structure & Traversal.md
new file mode 100644
index 0000000..2e1c599
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Trees 1 Structure & Traversal.md
@@ -0,0 +1,521 @@
+# Trees 1: Structure & Traversal
+
+---
+## What is a tree
+
+Till now, we have seen data structures such as Arrays, Linked Lists, Stacks, Queues... They are **Linear Data Structure** which means we can access them in sequencial order.
+
+The other category is **Non Linear Data Structure**
+
+At a lot of places, you must have seen hierarchy - Family, Office, Computer File System, etc. Therefore, there arise a need to be able to store such type of data and process it.
+
+**Tree is an example of a non/linear or hierarchical data structure.**
+
+
+### Example
+Let us see the **hierachy of people in an organization**:
+```sql
+CEO (Chief Executive Officer)
+├── CTO (Chief Technology Officer)
+│ ├── Engineering Manager
+│ │ ├── Software Development Team Lead
+│ │ │ ├── Software Engineer
+│ │ │ └── Software Engineer
+│ │ └── QA Team Lead
+│ │ ├── QA Engineer
+│ │ └── QA Engineer
+│ └── IT Manager
+│ ├── IT Specialist
+│ └── IT Specialist
+├── CFO (Chief Financial Officer)
+│ ├── Finance Manager
+│ │ ├── Accountant
+│ │ └── Accountant
+│ └── Procurement Manager
+│ ├── Procurement Officer
+│ └── Procurement Officer
+└── CMO (Chief Marketing Officer)
+ ├── Marketing Manager
+ │ ├── Marketing Specialist
+ │ └── Marketing Specialist
+ └── Sales Manager
+ ├── Sales Representative
+ └── Sales Representative
+```
+
+As we know that every tree has roots which are below the leaves but in the computer science the case is different the roots are at the top and leaves below it.
+
+---
+## Tree naming
+
+Example
+```sql
+ 1
+ / \
+ 2 3
+ / \ / \
+ 4 5 6 7
+ /
+ 8
+```
+* **Node**: An element in a tree that contains data and may have child nodes connected to it. 1, 2, 3, 4, 5, 6, 7, 8.
+
+ +
+
+* **Root**:
+
+
+* **Root**:The topmost node in a tree from which all other nodes descend. It has no parent. Node 1 is the root. +* **Parent**:
A node that has child nodes connected to it. Nodes 1, 2, 3 and 7.. +* **Child**:
A node that has a parent node connected to it. Nodes 2, 3, 4, 5, 6, and 7 are children. +* **Leaf**:
A node that has no child nodes. It's a terminal node. Nodes 4, 5, 6, and 8 are leaves. +* **Depth:**
The level at which a node resides in the tree. The root is at depth 0. Depth of node 1 is 0, 2 and 3 are at depth 1, 4, 5, 6, and 7 are at depth 2, and 8 is at depth 3. +* **Height:**
The length of the longest path from a node to a leaf. The height of the tree is the height of the root node. Height of the tree is 3, which is the number of edges from the root to a farthest leaf (8). +* **Subtree**:
A tree structure that is part of a larger tree. Subtree rooted at node 2 consists of nodes 2, 4, and 5. +* **Siblings**:
Nodes that share the same parent node. Nodes 2 and 3 are siblings. +* **Ancestor:**
All nodes from parent to the root node upwards are the ancestors of a node. Nodes 1, 3, 7 are ancestors of node 8. +* **Descendant**:
All nodes from child to the leaf node along that path. Nodes 4 and 5 are descendants of node 2. + + +--- +### Question +Can a leaf node also be a subtree? + +**Choices** +- [x] YES +- [ ] NO +- [ ] Can't say + + + +**Explanation:** + +Yes, a leaf node can also be considered a subtree. A subtree is a portion of a tree structure that is itself a tree. + +--- +### Question +Do all nodes have a parent node? + +**Choices** +- [ ] YES +- [x] NO +- [ ] Can't say + + +**Explanation:** + +In a tree data structure, all nodes except for the root node have a parent node. + +--- +### Levels of a tree + + +```sql + 1 Level 0 + / \ + 2 3 Level 1 + / \ +4 5 Level 2 +``` +In this example: + +* **Level 0:** Node 1 is at level 0 (root level). +* **Level 1:** Nodes 2 and 3 are at level 1. +* **Level 2:** Nodes 4 and 5 are at level 2. + +--- +### Question +What is the height of the leaf node in any tree? + + +**Choices** +- [x] 0 +- [ ] 1 +- [ ] 2 +- [ ] 3 + + +**Explanation** + +The height of a leaf node in any tree, including a binary tree, is 0. This is because the height of a node is defined as the length of the longest path from that node to a leaf node, and a leaf node is a node that doesn't have any children. Since there are no edges to traverse from a leaf node to a leaf node, the length of the path is 0. + +--- + +### Binary Tree + +A type of tree in which each node can have at most two children i.e, either 0, 1 or 2, referred to as the left child and the right child. + +**Example of a binary tree:** +```sql + 10 + / \ + 5 15 + / \ / \ + 3 8 12 18 +``` + +--- +### Traversals in a Tree + + +### How can we traverse a Tree ? + +There are many ways to traverse the tree. + +**L:** Left Subtree, **R:** Right Subtree, **N:** Root Node + +| L N R | L R N | R N L | +|:---------:|:---------:|:---------:| +| **R L N** | **N L R** | **N R L** | + +Having so many traversals can be confusing and are unnecessary. Threfore, a standard has been set where first we'll always consider the Left Subtree and then the Right Subtree. +Therefore, we boil down to 3 traverals. + + + +| L N R | **Named as Inorder** | +|:---------:|:----------------------:| +| **N L R** | **Named as Preorder** | +| **L R N** | **Named as Postorder** | + +Names are given w.r.t the position of the root node. + +> There are more techniques for traversing a tree that'll be covered in next set of sessions. + +#### Pre-order +Pre-order traversal is a depth-first traversal technique used to visit all nodes of a binary tree in a specific order. In pre-order traversal, you start from the root node and follow these steps for each node: +1. Visit the current node. +2. Traverse the left subtree (recursively). +3. Traverse the right subtree (recursively). + +**This traversal order ensures that the root node is visited before its children and the left subtree is explored before the right subtree.** + +**Example:** +```sql + 10 + / \ + 5 15 + / \ / \ + 3 8 12 18 +``` +Pre-order traversal sequence: 10, 5, 3, 8, 15, 12, 18 + +#### Pseudocode +```cpp +void preorder(root) { + if (root == null) + return; + + print(root.data); //node + preorder(root.left); //left + preorder(root.right) //right +} +``` +#### In-order traversal +In-order traversal is another depth-first traversal technique used to visit all nodes of a binary tree, but in a specific order. In in-order traversal, you follow these steps for each node: + +1. Traverse the left subtree (recursively). +2. Visit the current node. +3. Traverse the right subtree (recursively). + +**This traversal order ensures that nodes are visited in ascending order if the binary tree represents a search tree.** + +Here's an example of in-order traversal on a binary tree: +```cpp + 10 + / \ + 5 15 + / \ / \ + 3 8 12 18 +``` +In-order traversal sequence: 3, 5, 8, 10, 12, 15, 18 + +#### Pseudocode +```cpp +void inorder(root) { + if (root == null) + return; + + inorder(root.left); //left + print(root.data); //node + inorder(root.right) //right +} +``` +#### Post-order Traversal +Post-order traversal is another depth-first traversal technique used to visit all nodes of a binary tree, but in a specific order. In post-order traversal, you follow these steps for each node: + +1. Traverse the left subtree (recursively). +2. Traverse the right subtree (recursively). +3. Visit the current node. + +**This traversal order ensures that nodes are visited from the bottom up, starting from the leaf nodes and moving towards the root node.** + +**Example** +```cpp + 10 + / \ + 5 15 + / \ / \ + 3 8 12 18 +``` +Post-order traversal sequence: 3, 8, 5, 12, 18, 15, 10 + +#### Pseudocode: +```cpp +void postorder(root) { + if (root = null) return; + postorder(root.left) left + postorder(root.right) right + print(root.data) Node +} +``` + +--- +### Question +What is the inorder traversal sequence of the below tree? +```cpp + 1 + / \ + 2 4 + / / \ + 3 5 6 +``` +**Choices** +- [ ] [1, 2, 3, 4, 5, 6] +- [x] [3, 2, 1, 5, 4, 6] +- [ ] [3, 2, 1, 4, 5, 6] +- [ ] [4, 5, 6, 1, 2, 3] + + + +**Explanation** + +The inorder traversal sequence is [3, 2, 1, 5, 4, 6]. + + +--- +### Iterative Inorder traversal + + +### Approach: +* Iterative Inorder traversal is a method to visit all the nodes in a binary tree in a specific order without using recursion. +* In the case of Inorder traversal, you visit the nodes in the following order: left subtree, current node, right subtree. +* Here's how you can perform an iterative Inorder traversal using a stack data structure, along with an example: + +Let's say we have the following binary tree as an example: +```cpp + 1 + / \ + 2 3 + / \ + 4 5 +``` +#### Dry-Run: +* Start at the root node (1). +* Push 1 onto the stack and move left to node 2. +* Push 2 onto the stack and move left to node 4. +* Push 4 onto the stack and move left; there are no left children, so pop 4, visit it, and move right (which is null). +* Pop 2, visit it, and move to its right child, node 5. +* Push 5 onto the stack and move left; there are no left children, so pop 5, visit it, and move right (which is null). +* Pop 1, visit it, and move to its right child, node 3. +* Push 3 onto the stack and move left; there are no left children, so pop 3, visit it, and move right (which is null). +* The stack is empty, and all nodes have been visited. +* So, the iterative Inorder traversal of the tree is 4, 2, 5, 1, 3. + +#### Need of recursion/stack: +In inorder traversal of a binary tree, you need a data structure like a stack or recursion because you need to keep track of the order in which you visit the nodes of the tree. The reason for using these techniques is to handle the backtracking that's inherent in traversing a binary tree in inorder fashion. In a binary tree's inorder traversal, you visit nodes in a specific order: left, current, right. You use a stack or recursion to remember where you left off in the tree when moving between nodes, ensuring you visit nodes in the correct order and navigate through the tree efficiently. This backtracking is essential for proper traversal. + +#### Pseudocode: +```cpp +cur = root; +while (cur != null || st.isempty()) { + if (cur != null) { + st.push(curr) + cur = cur.left; + } else { + cur = st.pop(); + print(cur.data) + cur = cur.right + } +} +``` + +#### Complexity +**Time Complexity:** O(N) +**Space Complexity:** O(N) + +--- + +### Construct binary tree from inorder and post order + +Constructing a binary tree from its inorder and postorder traversals involves a recursive process. Here's a brief explanation with an example: + + + +#### Brute-Force Approach + + +* Generate all possible permutations of the given inorder traversal. +* For each permutation, check if it forms a valid binary tree when combined with the given postorder traversal. +* Return the first valid binary tree found. + +**Example:** +Inorder: [4, 2, 7, 5, 1, 3, 6] +Postorder: [4, 7, 5, 2, 6, 3, 1] + +#### Dry-Run: +* Identify the root: In the postorder traversal, the last element is 1, which is the root of the binary tree. +* Split into left and right subtrees: In the inorder traversal, find the position of the root element (1). Elements to the left of this position represent the left subtree, and elements to the right represent the right subtree. +* Recurse on left subtree: For the left subtree, the root is 2 (found in postorder traversal). Split the left subtree's inorder and postorder traversals, and repeat the process. +* Recurse on right subtree: For the right subtree, the root is 3 (found in postorder traversal). Split the right subtree's inorder and postorder traversals, and repeat the process. +* Continue the recursion: Repeat steps 3 and 4 for each subtree until the entire binary tree is constructed. + + +#### Pseudocode: +```cpp +function buildTreeBruteForce(inorder, postorder): + for each permutation of inorder: + if formsValidBinaryTree(permutation, postorder): + return constructBinaryTree(permutation, postorder) + return null +``` + +#### Complexity +**Time Complexity:** O(N! * N) +**Space Complexity:** O(N) + +--- + +:::warning +Please take some time to think about the optimised approach on your own before reading further..... +::: + +### Most-Optimised Approach: + +* The last element in the postorder traversal is the root of the binary tree. +* Find the root element in the inorder traversal to determine the left and right subtrees. +* Recursively repeat the process for the left and right subtrees. + +
 +
+Now as we can see in the above image let us understand this with the help of a dry/run:
+
+#### Dry-Run/Example:
+inorder={4,2,7,5,1,3,6} and postorder={4,7,5,2,6,3,1}
+
+1. The last element in the postorder traversal is 1, which is the root of the binary tree.
+
+Binary Tree:
+```plaintext
+1
+```
+2. Find 1 in the inorder traversal to split it into left and right subtrees. The elements to the left are the left subtree, and the elements to the right are the right subtree.
+
+```cpp
+Inorder: [4,2,7,5,1,3,6]
+Postorder: [4,7,5,2,6,3,1]
+```
+
+Left Subtree (Inorder: [4,2,7,5], Postorder: [4,7,5,2]):
+
+```cpp
+ 1
+ /
+2
+ \
+ 5
+ / \
+4 7
+```
+Right Subtree (Inorder: [3,6], Postorder: [6,3]):
+
+```cpp
+6
+ \
+ 3
+```
+3. Repeat the process for the left and right subtrees:
+
+For the left subtree:
+* The last element in the postorder traversal is 2, which is the root of the left subtree.
+* Find 2 in the inorder traversal to split it into left and right subtrees.
+* Left Subtree (Inorder: [4], Postorder: [4]):
+```cpp
+ 2
+ /
+4
+```
+Right Subtree (Inorder: [7,5], Postorder: [7,5]):
+```cpp
+ 5
+ /
+7
+```
+For the right subtree:
+
+* The last element in the postorder traversal is 3, which is the root of the right subtree.
+* Find 3 in the inorder traversal to split it into left and right subtrees.
+* Left Subtree (Inorder: [6], Postorder: [6]):
+```cpp
+ 3
+ \
+ 6
+```
+
+The final binary tree would look like this:
+```cpp
+ 1
+ / \
+ 2 3
+ / \ \
+ 4 5 6
+ /
+ 7
+```
+
+---
+### Question
+The inorder traversal sequence `[4, 2, 5, 1, 6, 3]` and the postorder traversal sequence `[4, 5, 2, 6, 3, 1]`. What is the root of the binary tree?
+
+**Choices**
+- [x] 1
+- [ ] 2
+- [ ] 3
+- [ ] 4
+
+
+**Explanation:**
+
+In postorder traversal, the last element is always the root of the tree, so here, 1 is the root.
+
+
+---
+### Construct binary tree Pseudocode
+#### Pseudocode:
+* rootIndex is the index of the root value in the inorder array.
+* rootIndex + 1 represents the start of the right subtree in the arrays.
+* end represents the end of the right subtree in the arrays.
+* start represents the start of the left subtree in the arrays.
+* rootIndex - 1 represents the end of the left subtree in the arrays.
+```cpp
+function buildTree(inorder, postorder):
+ if postorder is empty:
+ return null
+
+ // The last element in postorder is the root of the current subtree
+ rootValue = postorder.last
+ root = new TreeNode(rootValue)
+
+ // Find the index of the rootValue in inorder to split it into left and right subtrees
+ rootIndex = indexOf(inorder, rootValue)
+
+ // Recursive call for right subtree
+ root.right = buildTree(subarray(inorder, rootIndex + 1, end), subarray(postorder, rootIndex, end - 1))
+
+ // Recursive call for left subtree
+ root.left = buildTree(subarray(inorder, start, rootIndex - 1), subarray(postorder, start, rootIndex - 1))
+
+ return root
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(N)
diff --git a/Academy DSA Typed Notes/Advanced/DSA Trees 2 Views & Types.md b/Academy DSA Typed Notes/Advanced/DSA Trees 2 Views & Types.md
new file mode 100644
index 0000000..2a5f69e
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Trees 2 Views & Types.md
@@ -0,0 +1,601 @@
+# Advanced DSA : Trees 2: Views & Types
+
+---
+## Level Order Traversal
+Input: 1, 2, 3, 5, 8, 10, 13, 6, 9, 7, 4, 12, 11.
+
+The diagram for the following nodes will be:
+
+
+
+Now as we can see in the above image let us understand this with the help of a dry/run:
+
+#### Dry-Run/Example:
+inorder={4,2,7,5,1,3,6} and postorder={4,7,5,2,6,3,1}
+
+1. The last element in the postorder traversal is 1, which is the root of the binary tree.
+
+Binary Tree:
+```plaintext
+1
+```
+2. Find 1 in the inorder traversal to split it into left and right subtrees. The elements to the left are the left subtree, and the elements to the right are the right subtree.
+
+```cpp
+Inorder: [4,2,7,5,1,3,6]
+Postorder: [4,7,5,2,6,3,1]
+```
+
+Left Subtree (Inorder: [4,2,7,5], Postorder: [4,7,5,2]):
+
+```cpp
+ 1
+ /
+2
+ \
+ 5
+ / \
+4 7
+```
+Right Subtree (Inorder: [3,6], Postorder: [6,3]):
+
+```cpp
+6
+ \
+ 3
+```
+3. Repeat the process for the left and right subtrees:
+
+For the left subtree:
+* The last element in the postorder traversal is 2, which is the root of the left subtree.
+* Find 2 in the inorder traversal to split it into left and right subtrees.
+* Left Subtree (Inorder: [4], Postorder: [4]):
+```cpp
+ 2
+ /
+4
+```
+Right Subtree (Inorder: [7,5], Postorder: [7,5]):
+```cpp
+ 5
+ /
+7
+```
+For the right subtree:
+
+* The last element in the postorder traversal is 3, which is the root of the right subtree.
+* Find 3 in the inorder traversal to split it into left and right subtrees.
+* Left Subtree (Inorder: [6], Postorder: [6]):
+```cpp
+ 3
+ \
+ 6
+```
+
+The final binary tree would look like this:
+```cpp
+ 1
+ / \
+ 2 3
+ / \ \
+ 4 5 6
+ /
+ 7
+```
+
+---
+### Question
+The inorder traversal sequence `[4, 2, 5, 1, 6, 3]` and the postorder traversal sequence `[4, 5, 2, 6, 3, 1]`. What is the root of the binary tree?
+
+**Choices**
+- [x] 1
+- [ ] 2
+- [ ] 3
+- [ ] 4
+
+
+**Explanation:**
+
+In postorder traversal, the last element is always the root of the tree, so here, 1 is the root.
+
+
+---
+### Construct binary tree Pseudocode
+#### Pseudocode:
+* rootIndex is the index of the root value in the inorder array.
+* rootIndex + 1 represents the start of the right subtree in the arrays.
+* end represents the end of the right subtree in the arrays.
+* start represents the start of the left subtree in the arrays.
+* rootIndex - 1 represents the end of the left subtree in the arrays.
+```cpp
+function buildTree(inorder, postorder):
+ if postorder is empty:
+ return null
+
+ // The last element in postorder is the root of the current subtree
+ rootValue = postorder.last
+ root = new TreeNode(rootValue)
+
+ // Find the index of the rootValue in inorder to split it into left and right subtrees
+ rootIndex = indexOf(inorder, rootValue)
+
+ // Recursive call for right subtree
+ root.right = buildTree(subarray(inorder, rootIndex + 1, end), subarray(postorder, rootIndex, end - 1))
+
+ // Recursive call for left subtree
+ root.left = buildTree(subarray(inorder, start, rootIndex - 1), subarray(postorder, start, rootIndex - 1))
+
+ return root
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(N)
diff --git a/Academy DSA Typed Notes/Advanced/DSA Trees 2 Views & Types.md b/Academy DSA Typed Notes/Advanced/DSA Trees 2 Views & Types.md
new file mode 100644
index 0000000..2a5f69e
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Trees 2 Views & Types.md
@@ -0,0 +1,601 @@
+# Advanced DSA : Trees 2: Views & Types
+
+---
+## Level Order Traversal
+Input: 1, 2, 3, 5, 8, 10, 13, 6, 9, 7, 4, 12, 11.
+
+The diagram for the following nodes will be:
+
+ +
+
+```cpp
+1
+2 3
+5 8 10 13
+6 9 7 4
+12 11
+```
+
+
+---
+### Question
+Will the last level node always be a leaf node?
+
+**Choices**
+- [x] YES
+- [ ] NO
+- [ ] Cant say
+
+
+
+**Explanation**
+
+Yes, in the context of a binary tree's right view, the last level node will always be a leaf node. This is because the right view of a binary tree focuses on the rightmost nodes at each level as seen from a top-down view.
+
+
+---
+### Question
+Which traversal is best to print the nodes from top to bottom?
+
+**Choices**
+- [x] Level order traversal
+- [ ] Pre order
+- [ ] post order
+
+
+
+**Explanation:**
+
+When you want to print nodes from top to bottom, the level-order traversal, also known as Breadth-First Search (BFS), is the best choice. Level-order traversal ensures that nodes at the same level are processed before moving to the next level. This results in a top-to-bottom exploration of the tree.
+
+---
+### Level order traversal Observations
+
+
+#### Observations:
+* Level order traversal visits nodes level by level, starting from the root.
+* It uses a queue to keep track of the nodes to be processed.
+* Nodes at the same level are processed before moving on to the next level.
+* This traversal ensures that nodes at higher levels are visited before nodes at lower levels.
+
+Since this will be done level by level hence we will be requiring a queue data structure to solve this problem:
+
+
+
+
+```cpp
+1
+2 3
+5 8 10 13
+6 9 7 4
+12 11
+```
+
+
+---
+### Question
+Will the last level node always be a leaf node?
+
+**Choices**
+- [x] YES
+- [ ] NO
+- [ ] Cant say
+
+
+
+**Explanation**
+
+Yes, in the context of a binary tree's right view, the last level node will always be a leaf node. This is because the right view of a binary tree focuses on the rightmost nodes at each level as seen from a top-down view.
+
+
+---
+### Question
+Which traversal is best to print the nodes from top to bottom?
+
+**Choices**
+- [x] Level order traversal
+- [ ] Pre order
+- [ ] post order
+
+
+
+**Explanation:**
+
+When you want to print nodes from top to bottom, the level-order traversal, also known as Breadth-First Search (BFS), is the best choice. Level-order traversal ensures that nodes at the same level are processed before moving to the next level. This results in a top-to-bottom exploration of the tree.
+
+---
+### Level order traversal Observations
+
+
+#### Observations:
+* Level order traversal visits nodes level by level, starting from the root.
+* It uses a queue to keep track of the nodes to be processed.
+* Nodes at the same level are processed before moving on to the next level.
+* This traversal ensures that nodes at higher levels are visited before nodes at lower levels.
+
+Since this will be done level by level hence we will be requiring a queue data structure to solve this problem:
+
+ +
+After the whole process the queue data strucutre will look somewhat like this:
+
+
+
+After the whole process the queue data strucutre will look somewhat like this:
+
+ +
+Like this(in theabove example) it will be done for all of the nodes.
+Let us see the pseudocde to solve the problem in printing in one line only:
+
+#### Pseudocode:
+
+```cpp
+q.enqueue(root) {
+ while (!q.eempty()) {
+ x = q.dequeue()
+ print(x.data)
+ if (x.left != null) q.enqueue(x.left)
+ if (x.right != null) q.enqueue(x.right)
+ }
+}
+```
+Each level will be printed in seperate line:
+```cpp
+1
+2 3
+5 8 10 13
+6 9 7 4
+12 11
+```
+
+
+#### Observations:
+
+* Level order traversal prints nodes at the same depth before moving to the next level, ensuring that nodes on the same level are printed on separate lines.
+
+#### Approach:
+1. Start with the root node and enqueue it.
+2. Initialize last as the root.
+3. While the queue is not empty:
+ * Dequeue a node, print its data.
+ * Enqueue its children (if any).
+ * If the dequeued node is the same as last, print a newline and update last.
+
+#### Dry-Run:
+```cpp
+ 1
+ / \
+ 2 3
+ / \
+ 4 5
+```
+* Enqueue root node 1 and initialize last as 1.
+* Dequeue 1 and print it. Enqueue its children 2 and 3.
+* Dequeue 2 and print it. Enqueue its children 4 and 5.
+* Dequeue 3 and print it. Since 3 is the last node in the current level, print a newline.
+* Dequeue 4 and print it. There are no children to enqueue for 4.
+* Dequeue 5 and print it. There are no children to enqueue for 5.
+
+**Final Output:**
+```plaintext
+1
+2
+3
+4
+5
+```
+
+
+
+Let us see the pseudocode to solve the problem in printing in **seperate** line only:
+
+#### Pseudocode:
+
+```cpp
+q.enqueue(root) {
+ last = root;
+ while (!q.empty()) {
+ x.dequeue()
+ print(x.data)
+ if (x.left != null) q.enqueue(x.left)
+ if (x.right != null) q.enqueue(x.right)
+ if (x == last && !q.empty()) {
+ print("\n");
+ last = q.rear();
+ }
+ }
+}
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(N)
+
+---
+### Problem 2 Right and left view
+
+
+### Example:
+Let us see an example below:
+```cpp
+ 1
+ / \
+ 2 3
+ / \ \
+ 4 5 6
+ \
+ 7
+```
+The right view of this tree would be [1, 3, 6, 7] when viewed from the right side.
+
+To solve this we need to print last node of every level.
+
+
+---
+### Question
+Print right view of the given binary tree,
+
+```cpp
+ 1
+ / \
+ 2 3
+ \ \
+ 5 6
+ / \
+ 8 7
+ / \
+ 9 10
+```
+
+**Choices**
+- [ ] [1, 3, 6, 7]
+- [ ] [1, 3, 6, 8, 9]
+- [ ] [1, 3, 6, 7, 8, 9, 10]
+- [x] [1, 3, 6, 7, 10]
+- [ ] [1, 2, 5]
+
+
+---
+### Right view Observations
+
+#### Observations/Idea
+
+* The idea behind obtaining the right view of a binary tree is to perform a level-order traversal, and for each level, identify and print the rightmost node. This process ensures that we capture the rightmost nodes at each level, giving us the right view of the binary tree. We can obtain the right-view of the tree using a breadth-first level-order traversal with a queue and a loop.
+
+
+#### Approach:
+1. Initialize an empty queue for level order traversal and enqueue the root node.
+2. While the queue is not empty, do the following:
+ * Get the number of nodes at the current level (levelSize) by checking the queue's size.
+ * Iterate through the nodes at the current level.
+ * If the current node is the rightmost node at the current level, print its value.
+ * Enqueue the left and right children of the current node if they exist.
+ * Repeat this process until the queue is empty.
+
+Let us see the pseudocode to solve the problem:
+
+#### Pseudocode:
+```cpp
+q.enqueue(root)
+last = root;
+while (!q.empty(1)) {
+ x = q.dequeue()
+ if (x.left != null) q.enqueue(x.left)
+ if (x.right != null) q.enqueue(x.right)
+ if (x == last) {
+ print(x.data)
+ if (!q.empty()) {
+ print("\n");
+ last = q.rear();
+ }
+
+ }
+}
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(M)
+
+---
+### Vertical Order traversal
+
+**Examples:**
+Consider the following binary tree:
+```cpp
+ 1
+ / \
+ 2 3
+ / \ / \
+ 4 5 6 7
+ / \
+ 8 9
+```
+Vertical order traversal of this tree would yield the following output:
+```cpp
+Vertical Line 1: 4
+Vertical Line 2: 2, 8
+Vertical Line 3: 1, 5, 6
+Vertical Line 4: 3, 9
+Vertical Line 5: 7
+```
+
+We need to print the vertical lines from top to bottom.
+
+
+---
+### Question
+Consider the following binary tree:
+```cpp
+ 1
+ / \
+ 2 3
+ \ \
+ 5 6
+ / \
+ 8 7
+ / \
+ 9 10
+```
+
+Pick the vertical order traversal of the given Binary Tree.
+
+**Choices**
+- [x] [2, 1, 5, 9, 3, 8, 6, 10, 7]
+- [ ] [1, 2, 5, 3, 6, 8 ,9, 10, 7]
+- [ ] [1, 2, 3, 5, 6, 8, 7, 9, 10]
+- [ ] [1, 5, 2, 3, 6, 10, 8, 7, 9]
+
+**Explanation:**
+
+Vertical order traversal of this tree would yield the following output:
+```cpp
+Vertical Line 1: 2
+Vertical Line 2: 1, 5, 9
+Vertical Line 3: 3, 8
+Vertical Line 4: 6, 10
+Vertical Line 5: 7
+```
+
+
+---
+### Vertical Order traversal Observations
+#### Observation:
+* Vertical order traversal of a binary tree prints nodes column by column, with nodes in the same column printed together.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+These are the steps to Print vertical order traversal:
+#### Approach:
+* Assign horizontal distances to nodes (root gets distance 0, left decreases by 1, right increases by 1).
+* Create a map/hash table where keys are distances and values are lists of node values.
+* Update the map while traversing: append node values to corresponding distance lists.
+* After traversal, print the values from the map in ascending order of distances.
+
+
+---
+### Vertical Order traversal Pseudocode
+#### Pseudocode
+
+Let us see the pseudocode to solve this:
+```cpp
+procedure levelOrderTraversal(root)
+ if root is null
+ return
+
+ Create a queue
+ Enqueue root
+
+ while queue is not empty
+ currentNode = dequeue a node from the queue
+ print currentNode's value
+
+ if currentNode has left child
+ enqueue left child
+ end if
+
+ if currentNode has right child
+ enqueue right child
+ end if
+ end while
+end procedure
+```
+
+---
+### Problem 4 Top View
+
+**Example:**
+Consider the following binary tree:
+```cpp
+ 1
+ / \
+ 2 3
+ / \ / \
+ 4 5 6 7
+```
+The top view of this tree would be [4, 2, 1, 3, 7].
+
+
+---
+### Question
+Consider the following binary tree:
+```cpp
+ 1
+ / \
+ 2 3
+ \ \
+ 5 6
+ / \
+ 8 9
+```
+
+What is the top view of the given binary tree.
+
+**Choices**
+- [ ] [5, 2, 1, 3, 6, 9]
+- [ ] [8, 5, 2, 1, 3, 6, 9]
+- [ ] [2, 1, 5, 3, 8, 6, 9]
+- [x] [2, 1, 3, 6, 9]
+
+
+**Explanation:**
+
+The Top view of the Given Binary tree is [2, 1, 3, 6, 9].
+
+
+---
+### Top View Observations
+
+#### Observations:
+* Assign Horizontal Distances: Nodes are assigned horizontal distances, with the root at distance 0, left children decreasing by 1, and right children increasing by 1. This helps identify the nodes in the top view efficiently.
+
+#### Approach:
+For this we need to follow these steps:
+* Traverse the binary tree.
+* Maintain a map of horizontal distances and corresponding nodes.
+* Only store the first node encountered at each unique distance.
+* Print the stored nodes in ascending order of distances to get the top view.
+
+#### Pseudocode:
+```cpp
+procedure topView(root)
+ if root is null
+ return
+
+ Create an empty map
+
+ Queue: enqueue (root, horizontal distance 0)
+
+ while queue is not empty
+ (currentNode, currentDistance) = dequeue a node
+
+ if currentDistance is not in the map
+ add currentDistance and currentNode's value to map
+
+ enqueue (currentNode's left child, currentDistance - 1) if left child exists
+ enqueue (currentNode's right child, currentDistance + 1) if right child exists
+
+ Print values in map sorted by keys
+end procedure
+
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(W)
+
+---
+### Types of binary tree
+
+
+
+1. **Proper Binary Tree (Strict Binary Tree):**
+Every node has either 0 or 2 children (never 1 child).
+Diagram:
+```cpp
+ A
+ / \
+ B C
+/ \ / \
+```
+2. **Complete Binary Tree:**
+All levels are filled except possibly the last level, which is filled left to right.
+Diagram:
+```cpp
+ A
+ / \
+ B C
+/ \ /
+```
+3. **Perfect Binary Tree:**
+All internal nodes have exactly two children, and all leaf nodes are at the same level.
+Diagram:
+```cpp
+ A
+ / \
+ B C
+/ \ / \
+```
+
+
+---
+### Question
+Perfect Binary Trees are also:
+
+**Choices**
+- [ ] Proper binary tree
+- [ ] Complete binary tree
+- [x] both
+- [ ] none
+
+
+**Explanation:**
+
+A perfect binary tree is a specialized case of both a proper binary tree and a complete binary tree, where all internal nodes have two children, all leaf nodes are at the same level, and all levels are completely filled.
+
+---
+### Problem 5 : Check height balanced tree
+
+### Definition
+For all nodes if(`height_ofleftchild-height_ofrightchild`) <= 1
+
+**Example:**
+```cpp
+ 1
+ / \
+ 2 3
+ / \
+ 4 5
+ /
+ 6
+```
+This tree is not height-balanced because the left subtree of node 2 has a height of 3, while the right subtree of node 2 has a height of 0, and the difference is greater than 1.
+
+:::warning
+Please take some time to think about the brute force approach on your own before reading further.....
+:::
+
+### Brute Force
+#### Approach
+* For each node in the binary tree, calculate the height of its left and right subtrees.
+* Check if the absolute difference between the heights of the left and right subtrees for each node is less than or equal to 1.
+* If step 2 is true for all nodes in the tree, the tree is height-balanced.
+
+
+#### Pseudocode:
+```cpp
+// Helper function to calculate the height of a tree
+function calculateHeight(root):
+ if root is null:
+ return -1
+ return 1 + max(calculateHeight(root.left), calculateHeight(root.right))
+
+function isHeightBalanced(node):
+ if node is null:
+ return true // An empty tree is height-balanced
+
+ // Check if the current node's subtrees are height-balanced
+ leftHeight = calculateHeight(node.left)
+ rightHeight = calculateHeight(node.right)
+
+ // Check if the current node is height-balanced
+ if abs(leftHeight - rightHeight) > 1:
+ return false
+
+ // Recursively check the left and right subtrees
+ return isHeightBalanced(node.left) && isHeightBalanced(node.right)
+
+// Example usage:
+root = buildTree() // Build your binary tree
+result = isHeightBalanced(root)
+```
+
+> NOTE: For a null node: **height = -1**
+
+
+#### Complexity
+**Time Complexity:** $O(N^2)$
+**Space Complexity:** O(N)
+
+---
+### Question
+Which traversal is best to use when finding the height of the tree?
+
+**Choices**
+- [ ] Level order
+- [ ] Inorder
+- [x] postorder
+- [ ] preorder
+
+
+**Explanation:**
+
+Postorder traversal works best for calculating the height of a tree because it considers the height of subtrees before calculating the height of parent nodes, which mirrors the hierarchical nature of tree height calculation.
+
+---
+### Check height balanced tree Optimised Approach
+
+#### Observation/Idea:
+* To solve the problem of determining whether a binary tree is height-balanced we can consider using a recursive approach where you calculate the height of left and right subtrees and check their balance condition at each step. Keep track of a boolean flag to indicate whether the tree is still balanced.
+
+#### Approach:
+* We use a helper function height(root) to calculate the height of each subtree starting from the root.
+* In the height function:
+* If the root is null (i.e., an empty subtree), we return -1 to indicate a height of -1.
+* We recursively calculate the heights of the left and right subtrees using the height function.
+* We check if the absolute difference between the left and right subtree heights is greater than 1. If it is, we set the ishb flag to false, indicating that the tree is not height-balanced.
+* We return the maximum of the left and right subtree heights plus 1, which represents the height of the current subtree.
+* The ishb flag is initially set to true, and we start the height calculation from the root of the tree.
+* If, at any point, the ishb flag becomes false, we know that the tree is not height-balanced, and we can stop further calculations.
+* After the traversal is complete, if the ishb flag is still true, the tree is height-balanced.
+
+#### Example:
+```cpp
+ 1
+ / \
+ 2 3
+ / \
+ 4 5
+```
+This tree is height-balanced because the height of the left and right subtrees of every node differs by at most 1.
+
+#### Pseudocode
+```cpp
+int height(root, ishb) {
+ if (root == null) return -1;
+ l = height(root.left)
+ r = height(root.right)
+ if (abs(l - r) > 1) ishb = false;
+ return max(l, r) + 1
+}
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(log N)
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Trees 3 BST.md b/Academy DSA Typed Notes/Advanced/DSA Trees 3 BST.md
new file mode 100644
index 0000000..543a0ca
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Trees 3 BST.md
@@ -0,0 +1,484 @@
+# Advanced DSA : Trees 3: BST
+
+---
+## Binary Search Tree
+
+Binary search tree is searching data in an organized dataset using divide and conquer.
+
+For a node X in a binary search tree everything on the left has data less than x and on the right greater than x.
+
+
+
+Like this(in theabove example) it will be done for all of the nodes.
+Let us see the pseudocde to solve the problem in printing in one line only:
+
+#### Pseudocode:
+
+```cpp
+q.enqueue(root) {
+ while (!q.eempty()) {
+ x = q.dequeue()
+ print(x.data)
+ if (x.left != null) q.enqueue(x.left)
+ if (x.right != null) q.enqueue(x.right)
+ }
+}
+```
+Each level will be printed in seperate line:
+```cpp
+1
+2 3
+5 8 10 13
+6 9 7 4
+12 11
+```
+
+
+#### Observations:
+
+* Level order traversal prints nodes at the same depth before moving to the next level, ensuring that nodes on the same level are printed on separate lines.
+
+#### Approach:
+1. Start with the root node and enqueue it.
+2. Initialize last as the root.
+3. While the queue is not empty:
+ * Dequeue a node, print its data.
+ * Enqueue its children (if any).
+ * If the dequeued node is the same as last, print a newline and update last.
+
+#### Dry-Run:
+```cpp
+ 1
+ / \
+ 2 3
+ / \
+ 4 5
+```
+* Enqueue root node 1 and initialize last as 1.
+* Dequeue 1 and print it. Enqueue its children 2 and 3.
+* Dequeue 2 and print it. Enqueue its children 4 and 5.
+* Dequeue 3 and print it. Since 3 is the last node in the current level, print a newline.
+* Dequeue 4 and print it. There are no children to enqueue for 4.
+* Dequeue 5 and print it. There are no children to enqueue for 5.
+
+**Final Output:**
+```plaintext
+1
+2
+3
+4
+5
+```
+
+
+
+Let us see the pseudocode to solve the problem in printing in **seperate** line only:
+
+#### Pseudocode:
+
+```cpp
+q.enqueue(root) {
+ last = root;
+ while (!q.empty()) {
+ x.dequeue()
+ print(x.data)
+ if (x.left != null) q.enqueue(x.left)
+ if (x.right != null) q.enqueue(x.right)
+ if (x == last && !q.empty()) {
+ print("\n");
+ last = q.rear();
+ }
+ }
+}
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(N)
+
+---
+### Problem 2 Right and left view
+
+
+### Example:
+Let us see an example below:
+```cpp
+ 1
+ / \
+ 2 3
+ / \ \
+ 4 5 6
+ \
+ 7
+```
+The right view of this tree would be [1, 3, 6, 7] when viewed from the right side.
+
+To solve this we need to print last node of every level.
+
+
+---
+### Question
+Print right view of the given binary tree,
+
+```cpp
+ 1
+ / \
+ 2 3
+ \ \
+ 5 6
+ / \
+ 8 7
+ / \
+ 9 10
+```
+
+**Choices**
+- [ ] [1, 3, 6, 7]
+- [ ] [1, 3, 6, 8, 9]
+- [ ] [1, 3, 6, 7, 8, 9, 10]
+- [x] [1, 3, 6, 7, 10]
+- [ ] [1, 2, 5]
+
+
+---
+### Right view Observations
+
+#### Observations/Idea
+
+* The idea behind obtaining the right view of a binary tree is to perform a level-order traversal, and for each level, identify and print the rightmost node. This process ensures that we capture the rightmost nodes at each level, giving us the right view of the binary tree. We can obtain the right-view of the tree using a breadth-first level-order traversal with a queue and a loop.
+
+
+#### Approach:
+1. Initialize an empty queue for level order traversal and enqueue the root node.
+2. While the queue is not empty, do the following:
+ * Get the number of nodes at the current level (levelSize) by checking the queue's size.
+ * Iterate through the nodes at the current level.
+ * If the current node is the rightmost node at the current level, print its value.
+ * Enqueue the left and right children of the current node if they exist.
+ * Repeat this process until the queue is empty.
+
+Let us see the pseudocode to solve the problem:
+
+#### Pseudocode:
+```cpp
+q.enqueue(root)
+last = root;
+while (!q.empty(1)) {
+ x = q.dequeue()
+ if (x.left != null) q.enqueue(x.left)
+ if (x.right != null) q.enqueue(x.right)
+ if (x == last) {
+ print(x.data)
+ if (!q.empty()) {
+ print("\n");
+ last = q.rear();
+ }
+
+ }
+}
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(M)
+
+---
+### Vertical Order traversal
+
+**Examples:**
+Consider the following binary tree:
+```cpp
+ 1
+ / \
+ 2 3
+ / \ / \
+ 4 5 6 7
+ / \
+ 8 9
+```
+Vertical order traversal of this tree would yield the following output:
+```cpp
+Vertical Line 1: 4
+Vertical Line 2: 2, 8
+Vertical Line 3: 1, 5, 6
+Vertical Line 4: 3, 9
+Vertical Line 5: 7
+```
+
+We need to print the vertical lines from top to bottom.
+
+
+---
+### Question
+Consider the following binary tree:
+```cpp
+ 1
+ / \
+ 2 3
+ \ \
+ 5 6
+ / \
+ 8 7
+ / \
+ 9 10
+```
+
+Pick the vertical order traversal of the given Binary Tree.
+
+**Choices**
+- [x] [2, 1, 5, 9, 3, 8, 6, 10, 7]
+- [ ] [1, 2, 5, 3, 6, 8 ,9, 10, 7]
+- [ ] [1, 2, 3, 5, 6, 8, 7, 9, 10]
+- [ ] [1, 5, 2, 3, 6, 10, 8, 7, 9]
+
+**Explanation:**
+
+Vertical order traversal of this tree would yield the following output:
+```cpp
+Vertical Line 1: 2
+Vertical Line 2: 1, 5, 9
+Vertical Line 3: 3, 8
+Vertical Line 4: 6, 10
+Vertical Line 5: 7
+```
+
+
+---
+### Vertical Order traversal Observations
+#### Observation:
+* Vertical order traversal of a binary tree prints nodes column by column, with nodes in the same column printed together.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+These are the steps to Print vertical order traversal:
+#### Approach:
+* Assign horizontal distances to nodes (root gets distance 0, left decreases by 1, right increases by 1).
+* Create a map/hash table where keys are distances and values are lists of node values.
+* Update the map while traversing: append node values to corresponding distance lists.
+* After traversal, print the values from the map in ascending order of distances.
+
+
+---
+### Vertical Order traversal Pseudocode
+#### Pseudocode
+
+Let us see the pseudocode to solve this:
+```cpp
+procedure levelOrderTraversal(root)
+ if root is null
+ return
+
+ Create a queue
+ Enqueue root
+
+ while queue is not empty
+ currentNode = dequeue a node from the queue
+ print currentNode's value
+
+ if currentNode has left child
+ enqueue left child
+ end if
+
+ if currentNode has right child
+ enqueue right child
+ end if
+ end while
+end procedure
+```
+
+---
+### Problem 4 Top View
+
+**Example:**
+Consider the following binary tree:
+```cpp
+ 1
+ / \
+ 2 3
+ / \ / \
+ 4 5 6 7
+```
+The top view of this tree would be [4, 2, 1, 3, 7].
+
+
+---
+### Question
+Consider the following binary tree:
+```cpp
+ 1
+ / \
+ 2 3
+ \ \
+ 5 6
+ / \
+ 8 9
+```
+
+What is the top view of the given binary tree.
+
+**Choices**
+- [ ] [5, 2, 1, 3, 6, 9]
+- [ ] [8, 5, 2, 1, 3, 6, 9]
+- [ ] [2, 1, 5, 3, 8, 6, 9]
+- [x] [2, 1, 3, 6, 9]
+
+
+**Explanation:**
+
+The Top view of the Given Binary tree is [2, 1, 3, 6, 9].
+
+
+---
+### Top View Observations
+
+#### Observations:
+* Assign Horizontal Distances: Nodes are assigned horizontal distances, with the root at distance 0, left children decreasing by 1, and right children increasing by 1. This helps identify the nodes in the top view efficiently.
+
+#### Approach:
+For this we need to follow these steps:
+* Traverse the binary tree.
+* Maintain a map of horizontal distances and corresponding nodes.
+* Only store the first node encountered at each unique distance.
+* Print the stored nodes in ascending order of distances to get the top view.
+
+#### Pseudocode:
+```cpp
+procedure topView(root)
+ if root is null
+ return
+
+ Create an empty map
+
+ Queue: enqueue (root, horizontal distance 0)
+
+ while queue is not empty
+ (currentNode, currentDistance) = dequeue a node
+
+ if currentDistance is not in the map
+ add currentDistance and currentNode's value to map
+
+ enqueue (currentNode's left child, currentDistance - 1) if left child exists
+ enqueue (currentNode's right child, currentDistance + 1) if right child exists
+
+ Print values in map sorted by keys
+end procedure
+
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(W)
+
+---
+### Types of binary tree
+
+
+
+1. **Proper Binary Tree (Strict Binary Tree):**
+Every node has either 0 or 2 children (never 1 child).
+Diagram:
+```cpp
+ A
+ / \
+ B C
+/ \ / \
+```
+2. **Complete Binary Tree:**
+All levels are filled except possibly the last level, which is filled left to right.
+Diagram:
+```cpp
+ A
+ / \
+ B C
+/ \ /
+```
+3. **Perfect Binary Tree:**
+All internal nodes have exactly two children, and all leaf nodes are at the same level.
+Diagram:
+```cpp
+ A
+ / \
+ B C
+/ \ / \
+```
+
+
+---
+### Question
+Perfect Binary Trees are also:
+
+**Choices**
+- [ ] Proper binary tree
+- [ ] Complete binary tree
+- [x] both
+- [ ] none
+
+
+**Explanation:**
+
+A perfect binary tree is a specialized case of both a proper binary tree and a complete binary tree, where all internal nodes have two children, all leaf nodes are at the same level, and all levels are completely filled.
+
+---
+### Problem 5 : Check height balanced tree
+
+### Definition
+For all nodes if(`height_ofleftchild-height_ofrightchild`) <= 1
+
+**Example:**
+```cpp
+ 1
+ / \
+ 2 3
+ / \
+ 4 5
+ /
+ 6
+```
+This tree is not height-balanced because the left subtree of node 2 has a height of 3, while the right subtree of node 2 has a height of 0, and the difference is greater than 1.
+
+:::warning
+Please take some time to think about the brute force approach on your own before reading further.....
+:::
+
+### Brute Force
+#### Approach
+* For each node in the binary tree, calculate the height of its left and right subtrees.
+* Check if the absolute difference between the heights of the left and right subtrees for each node is less than or equal to 1.
+* If step 2 is true for all nodes in the tree, the tree is height-balanced.
+
+
+#### Pseudocode:
+```cpp
+// Helper function to calculate the height of a tree
+function calculateHeight(root):
+ if root is null:
+ return -1
+ return 1 + max(calculateHeight(root.left), calculateHeight(root.right))
+
+function isHeightBalanced(node):
+ if node is null:
+ return true // An empty tree is height-balanced
+
+ // Check if the current node's subtrees are height-balanced
+ leftHeight = calculateHeight(node.left)
+ rightHeight = calculateHeight(node.right)
+
+ // Check if the current node is height-balanced
+ if abs(leftHeight - rightHeight) > 1:
+ return false
+
+ // Recursively check the left and right subtrees
+ return isHeightBalanced(node.left) && isHeightBalanced(node.right)
+
+// Example usage:
+root = buildTree() // Build your binary tree
+result = isHeightBalanced(root)
+```
+
+> NOTE: For a null node: **height = -1**
+
+
+#### Complexity
+**Time Complexity:** $O(N^2)$
+**Space Complexity:** O(N)
+
+---
+### Question
+Which traversal is best to use when finding the height of the tree?
+
+**Choices**
+- [ ] Level order
+- [ ] Inorder
+- [x] postorder
+- [ ] preorder
+
+
+**Explanation:**
+
+Postorder traversal works best for calculating the height of a tree because it considers the height of subtrees before calculating the height of parent nodes, which mirrors the hierarchical nature of tree height calculation.
+
+---
+### Check height balanced tree Optimised Approach
+
+#### Observation/Idea:
+* To solve the problem of determining whether a binary tree is height-balanced we can consider using a recursive approach where you calculate the height of left and right subtrees and check their balance condition at each step. Keep track of a boolean flag to indicate whether the tree is still balanced.
+
+#### Approach:
+* We use a helper function height(root) to calculate the height of each subtree starting from the root.
+* In the height function:
+* If the root is null (i.e., an empty subtree), we return -1 to indicate a height of -1.
+* We recursively calculate the heights of the left and right subtrees using the height function.
+* We check if the absolute difference between the left and right subtree heights is greater than 1. If it is, we set the ishb flag to false, indicating that the tree is not height-balanced.
+* We return the maximum of the left and right subtree heights plus 1, which represents the height of the current subtree.
+* The ishb flag is initially set to true, and we start the height calculation from the root of the tree.
+* If, at any point, the ishb flag becomes false, we know that the tree is not height-balanced, and we can stop further calculations.
+* After the traversal is complete, if the ishb flag is still true, the tree is height-balanced.
+
+#### Example:
+```cpp
+ 1
+ / \
+ 2 3
+ / \
+ 4 5
+```
+This tree is height-balanced because the height of the left and right subtrees of every node differs by at most 1.
+
+#### Pseudocode
+```cpp
+int height(root, ishb) {
+ if (root == null) return -1;
+ l = height(root.left)
+ r = height(root.right)
+ if (abs(l - r) > 1) ishb = false;
+ return max(l, r) + 1
+}
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(log N)
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Trees 3 BST.md b/Academy DSA Typed Notes/Advanced/DSA Trees 3 BST.md
new file mode 100644
index 0000000..543a0ca
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Trees 3 BST.md
@@ -0,0 +1,484 @@
+# Advanced DSA : Trees 3: BST
+
+---
+## Binary Search Tree
+
+Binary search tree is searching data in an organized dataset using divide and conquer.
+
+For a node X in a binary search tree everything on the left has data less than x and on the right greater than x.
+
+ +
+Example of a binary search tree:
+
+```cpp
+ 5
+ / \
+ 3 8
+ /\ /\
+ 1 4 6 9
+```
+
+---
+### Question
+What is a Binary Search Tree (BST)?
+
+
+**Choices**
+- [ ] A tree with only two nodes
+- [ ] A tree where the left child of a node has a value <= the node, and the right child has a value > the node
+- [x] A tree where for a node x, everything on the left has data <= x and on the right > x.
+- [ ] A tree that has height log N.
+
+
+
+---
+### Problem 1 Searching in Binary Search Tree
+
+Searching in a Binary Search Tree (BST) involves utilizing the property that values in the left subtree are smaller and values in the right subtree are larger than the current node's value. This property allows for efficient search operations.
+Here's an example using the BST diagram from earlier:
+```cpp
+ 5
+ / \
+ 3 8
+ /\ /\
+ 1 4 6 9
+```
+**Suppose you're searching for the value 6:**
+
+* Start at the root (value 5).
+* Compare 6 with 5. Since 6 is greater, move to the right child (value 8).
+* Compare 6 with 8. Since 6 is smaller, move to the left child (value 6).
+* The value 6 matches the current node's value, so the search is successful.
+
+---
+### Question
+What is the number of nodes you need to visit to find the number `1` in the following BST?
+
+```cpp
+ 5
+ / \
+ 3 8
+ /\ /\
+ 1 4 6 9
+```
+
+**Choices**
+- [ ] 2
+- [x] 3
+- [ ] 4
+- [ ] 1
+
+
+**Explanation**
+First node: 5. From 5 you move left.
+Second node: 3. From 3 you move left, again.
+Third node: 1. You finally get 1.
+
+---
+### Searching in Binary Search Tree Pseudo Code
+
+#### Pseudo Code
+```cpp
+function search(root, target):
+ if root is None:
+ return None
+
+ if root.value == target:
+ return root
+
+ if target < root.value:
+ return search(root.left, target)
+
+ if target > root.value:
+ return search(root.right, target)
+```
+
+
+---
+### Problem 2 Insertion in Binary Search Tree
+
+
+### Insertion in BST:
+Inserting a new value into a Binary Search Tree (BST) involves maintaining the property that values in the left subtree are smaller and values in the right subtree are larger than the current node's value.
+
+Here's an example using the BST diagram from earlier:
+```cpp
+ 5
+ / \
+ 3 8
+ /\ /\
+ 1 4 6 9
+```
+**Suppose you want to insert the value 7:**
+
+* Start at the root (value 5).
+* Compare 7 with 5. Since 7 is greater, move to the right child (value 8).
+* Compare 7 with 8. Since 7 is smaller, move to the left child (value 6).
+* Compare 7 with 6. Since 7 is greater, move to the right child (null).
+* Insert the value 7 as the right child of the node with value 6.
+
+The updated tree after insertion:
+```cpp
+ 5
+ / \
+ 3 8
+ /\ /\
+ 1 4 6 9
+ \
+ 7
+```
+
+#### Pseudocode:
+```cpp
+function insert(root, value):
+ if root is null:
+ return createNode(value)
+
+ if value < root.value:
+ root.left = insert(root.left, value)
+ else:
+ root.right = insert(root.right, value)
+
+ return root
+```
+
+---
+### Question
+Where does the node with the smallest value resides in a BST?
+
+**Choices**
+- [x] We keep on going left and we get the smallest one.
+- [ ] Depends on the tree.
+- [ ] We keep on going right and we get the smallest one.
+- [ ] The root node.
+
+
+
+For every node, we need to go to its left, that's the only way we can reach the smallest one.
+
+---
+### Problem 3 Find smallest in Binary Search Tree
+
+Find smallest in Binary Search Tree
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+**Approach**
+
+The left most node in the tree, will be the smallest.
+
+**Example:**
+Suppose we have the following BST:
+```cpp
+ 5
+ / \
+ 3 8
+ / \ \
+ 2 4 9
+```
+To find the smallest element:
+
+* Start at the root node (5).
+* Move to the left child (3).
+* Continue moving to the left child until you reach a node with no left child.
+* The node with no left child is the smallest element in the BST. In this case, it's the node with the value 2.
+* So, in this example, the smallest element in the BST is 2.
+
+#### Pseudocode
+
+```cpp
+temp = root // not null
+while (temp.left != null) {
+ temp = temp.left
+}
+return temp.data;
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(1)
+
+---
+### Problem 4 Find largest in Binary Search Tree
+#### Approach
+
+The right most node in the tree, will be the largest.
+
+**Example:**
+Suppose we have the following BST:
+```cpp
+ 5
+ / \
+ 3 8
+ / \ \
+ 2 4 9
+```
+* To find the largest element:
+* Start at the root node (5).
+* Move to the right child (8).
+* Continue moving to the right child until you reach a node with no right child.
+* The node with no right child is the largest element in the BST. In this case, it's the node with the value 9.
+* So, in this example, the largest element in the BST is 9.
+
+#### Pseudocode
+
+```cpp
+temp = root // not null
+while (temp.right != null) {
+ temp = temp.right
+}
+return temp.data;
+```
+
+---
+### Problem 5 Deletion in Binary Search Tree
+
+Deleting a node from a Binary Search Tree (BST) involves maintaining the BST property while handling various cases depending on the node's structure. Here's how the deletion process works:
+
+* Find the Node to Delete: Start at the root and traverse the tree to find the node you want to delete. Remember to keep track of the parent node as well.
+
+#### Case 1: Node with No Children (Leaf Node)
+In this case, we have a node with no children (a leaf node). Deleting it is straightforward; we simply remove it from the tree.
+
+**Example:**
+Suppose we have the following BST, and we want to delete the node with the value 7.
+```cpp
+ 10
+ / \
+ 5 15
+ / \ / \
+ 3 7 12 18
+```
+After deleting the node with the value 7, the tree becomes:
+```cpp
+ 10
+ / \
+ 5 15
+ / / \
+ 3 12 18
+```
+#### Case 2: Node with One Child
+In this case, the node to be deleted has only one child. To delete it, we replace the node with its child.
+
+**Example:**
+Suppose we have the following BST, and we want to delete the node with the value 5.
+```cpp
+ 10
+ / \
+ 5 15
+ / / \
+ 3 12 18
+```
+After deleting the node with the value 5, we replace it with its child (3):
+```cpp
+ 10
+ / \
+ 3 15
+ / \
+ 12 18
+```
+
+
+#### Case 3: Node with Two Children
+In this case, the node to be deleted has two children. To delete it, we find either the in-order predecessor or successor and replace the node's value with the value of the predecessor or successor. Then, we recursively delete the predecessor or successor.
+
+**Example:**
+Suppose we have the following BST, and we want to delete the node with the value 10 (which has two children).
+```cpp
+ 10
+ / \
+ 5 15
+ / \ / \
+ 3 9 12 18
+```
+To delete the node with value 10, we can either choose its in-order predecessor (9) or in-order successor (12). Let's choose the in-order predecessor (9):
+
+* Find the in-order predecessor (the largest value in the left subtree). In this case, it's 9.
+* Replace the value of the node to be deleted (10) with the value of the in-order predecessor (9).
+* Recursively delete the in-order predecessor (9), which falls into either Case 1 (no children) or Case 2 (one child).
+* After deleting the node with the value 10, the tree becomes:
+```cpp
+ 9
+ / \
+ 5 15
+ / / \
+ 3 12 18
+```
+These are the three main cases for deleting a node in a Binary Search Tree (BST).
+
+#### Pseudo Code
+Here's the pseudo code with each of the cases mentioned.
+
+
+Example of a binary search tree:
+
+```cpp
+ 5
+ / \
+ 3 8
+ /\ /\
+ 1 4 6 9
+```
+
+---
+### Question
+What is a Binary Search Tree (BST)?
+
+
+**Choices**
+- [ ] A tree with only two nodes
+- [ ] A tree where the left child of a node has a value <= the node, and the right child has a value > the node
+- [x] A tree where for a node x, everything on the left has data <= x and on the right > x.
+- [ ] A tree that has height log N.
+
+
+
+---
+### Problem 1 Searching in Binary Search Tree
+
+Searching in a Binary Search Tree (BST) involves utilizing the property that values in the left subtree are smaller and values in the right subtree are larger than the current node's value. This property allows for efficient search operations.
+Here's an example using the BST diagram from earlier:
+```cpp
+ 5
+ / \
+ 3 8
+ /\ /\
+ 1 4 6 9
+```
+**Suppose you're searching for the value 6:**
+
+* Start at the root (value 5).
+* Compare 6 with 5. Since 6 is greater, move to the right child (value 8).
+* Compare 6 with 8. Since 6 is smaller, move to the left child (value 6).
+* The value 6 matches the current node's value, so the search is successful.
+
+---
+### Question
+What is the number of nodes you need to visit to find the number `1` in the following BST?
+
+```cpp
+ 5
+ / \
+ 3 8
+ /\ /\
+ 1 4 6 9
+```
+
+**Choices**
+- [ ] 2
+- [x] 3
+- [ ] 4
+- [ ] 1
+
+
+**Explanation**
+First node: 5. From 5 you move left.
+Second node: 3. From 3 you move left, again.
+Third node: 1. You finally get 1.
+
+---
+### Searching in Binary Search Tree Pseudo Code
+
+#### Pseudo Code
+```cpp
+function search(root, target):
+ if root is None:
+ return None
+
+ if root.value == target:
+ return root
+
+ if target < root.value:
+ return search(root.left, target)
+
+ if target > root.value:
+ return search(root.right, target)
+```
+
+
+---
+### Problem 2 Insertion in Binary Search Tree
+
+
+### Insertion in BST:
+Inserting a new value into a Binary Search Tree (BST) involves maintaining the property that values in the left subtree are smaller and values in the right subtree are larger than the current node's value.
+
+Here's an example using the BST diagram from earlier:
+```cpp
+ 5
+ / \
+ 3 8
+ /\ /\
+ 1 4 6 9
+```
+**Suppose you want to insert the value 7:**
+
+* Start at the root (value 5).
+* Compare 7 with 5. Since 7 is greater, move to the right child (value 8).
+* Compare 7 with 8. Since 7 is smaller, move to the left child (value 6).
+* Compare 7 with 6. Since 7 is greater, move to the right child (null).
+* Insert the value 7 as the right child of the node with value 6.
+
+The updated tree after insertion:
+```cpp
+ 5
+ / \
+ 3 8
+ /\ /\
+ 1 4 6 9
+ \
+ 7
+```
+
+#### Pseudocode:
+```cpp
+function insert(root, value):
+ if root is null:
+ return createNode(value)
+
+ if value < root.value:
+ root.left = insert(root.left, value)
+ else:
+ root.right = insert(root.right, value)
+
+ return root
+```
+
+---
+### Question
+Where does the node with the smallest value resides in a BST?
+
+**Choices**
+- [x] We keep on going left and we get the smallest one.
+- [ ] Depends on the tree.
+- [ ] We keep on going right and we get the smallest one.
+- [ ] The root node.
+
+
+
+For every node, we need to go to its left, that's the only way we can reach the smallest one.
+
+---
+### Problem 3 Find smallest in Binary Search Tree
+
+Find smallest in Binary Search Tree
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+**Approach**
+
+The left most node in the tree, will be the smallest.
+
+**Example:**
+Suppose we have the following BST:
+```cpp
+ 5
+ / \
+ 3 8
+ / \ \
+ 2 4 9
+```
+To find the smallest element:
+
+* Start at the root node (5).
+* Move to the left child (3).
+* Continue moving to the left child until you reach a node with no left child.
+* The node with no left child is the smallest element in the BST. In this case, it's the node with the value 2.
+* So, in this example, the smallest element in the BST is 2.
+
+#### Pseudocode
+
+```cpp
+temp = root // not null
+while (temp.left != null) {
+ temp = temp.left
+}
+return temp.data;
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(1)
+
+---
+### Problem 4 Find largest in Binary Search Tree
+#### Approach
+
+The right most node in the tree, will be the largest.
+
+**Example:**
+Suppose we have the following BST:
+```cpp
+ 5
+ / \
+ 3 8
+ / \ \
+ 2 4 9
+```
+* To find the largest element:
+* Start at the root node (5).
+* Move to the right child (8).
+* Continue moving to the right child until you reach a node with no right child.
+* The node with no right child is the largest element in the BST. In this case, it's the node with the value 9.
+* So, in this example, the largest element in the BST is 9.
+
+#### Pseudocode
+
+```cpp
+temp = root // not null
+while (temp.right != null) {
+ temp = temp.right
+}
+return temp.data;
+```
+
+---
+### Problem 5 Deletion in Binary Search Tree
+
+Deleting a node from a Binary Search Tree (BST) involves maintaining the BST property while handling various cases depending on the node's structure. Here's how the deletion process works:
+
+* Find the Node to Delete: Start at the root and traverse the tree to find the node you want to delete. Remember to keep track of the parent node as well.
+
+#### Case 1: Node with No Children (Leaf Node)
+In this case, we have a node with no children (a leaf node). Deleting it is straightforward; we simply remove it from the tree.
+
+**Example:**
+Suppose we have the following BST, and we want to delete the node with the value 7.
+```cpp
+ 10
+ / \
+ 5 15
+ / \ / \
+ 3 7 12 18
+```
+After deleting the node with the value 7, the tree becomes:
+```cpp
+ 10
+ / \
+ 5 15
+ / / \
+ 3 12 18
+```
+#### Case 2: Node with One Child
+In this case, the node to be deleted has only one child. To delete it, we replace the node with its child.
+
+**Example:**
+Suppose we have the following BST, and we want to delete the node with the value 5.
+```cpp
+ 10
+ / \
+ 5 15
+ / / \
+ 3 12 18
+```
+After deleting the node with the value 5, we replace it with its child (3):
+```cpp
+ 10
+ / \
+ 3 15
+ / \
+ 12 18
+```
+
+
+#### Case 3: Node with Two Children
+In this case, the node to be deleted has two children. To delete it, we find either the in-order predecessor or successor and replace the node's value with the value of the predecessor or successor. Then, we recursively delete the predecessor or successor.
+
+**Example:**
+Suppose we have the following BST, and we want to delete the node with the value 10 (which has two children).
+```cpp
+ 10
+ / \
+ 5 15
+ / \ / \
+ 3 9 12 18
+```
+To delete the node with value 10, we can either choose its in-order predecessor (9) or in-order successor (12). Let's choose the in-order predecessor (9):
+
+* Find the in-order predecessor (the largest value in the left subtree). In this case, it's 9.
+* Replace the value of the node to be deleted (10) with the value of the in-order predecessor (9).
+* Recursively delete the in-order predecessor (9), which falls into either Case 1 (no children) or Case 2 (one child).
+* After deleting the node with the value 10, the tree becomes:
+```cpp
+ 9
+ / \
+ 5 15
+ / / \
+ 3 12 18
+```
+These are the three main cases for deleting a node in a Binary Search Tree (BST).
+
+#### Pseudo Code
+Here's the pseudo code with each of the cases mentioned.
+ +
+### Question
+What is the purpose of balancing a Binary Search Tree?
+
+**Choices**
+- [ ] To make it visually appealing
+- [ ] To ensure all nodes have the same value
+- [x] To maintain efficient search, insert, and delete operations
+- [ ] Balancing is not necessary in a Binary Search Tree
+
+
+---
+### Problem 6 Construct a binary search tree
+
+
+#### Approach:
+* Find the middle element of the sorted array.
+* Create a new node with this middle element as the root of the tree.
+* Recursively repeat steps 1 and 2 for the left and right halves of the array, making the middle element of each subarray the root of its respective subtree.
+* Continue this process until all elements are processed.
+* The final tree will be a valid BST with the given sorted array as its inorder traversal.
+* Here's an example construction of a BST using the values 8, 3, 10, 1, 6, 14, 4, 7, and 13:
+
+#### Example:
+* Sorted Array - 1, 3, 4, 6, 7, 8, 10, 13, 14
+* Create the root node with value 8.
+* Insert 3: Move to the left child of the root (value 3).
+* Insert 10: Move to the right child of the root (value 10).
+* Insert 1: Move to the left child of the node with value 3 (value 1).
+* Insert 6: Move to the right child of the node with value 3 (value 6).
+* Insert 14: Move to the right child of the root (value 14).
+* Insert 4: Move to the left child of the node with value 6 (value 4).
+* Insert 7: Move to the right child of the node with value 6 (value 7).
+* Insert 13: Move to the left child of the node with value 14 (value 13).
+The constructed BST:
+```cpp
+ 8
+ / \
+ 3 10
+ / \ \
+ 1 6 14
+ / \ /
+ 4 7 13
+```
+
+
+#### Pseudocode:
+
+```cpp
+function insert(root, value):
+ if root is null:
+ return [value, null, null]
+
+ if value < root[0]:
+ root[1] = insert(root[1], value)
+ else:
+ root[2] = insert(root[2], value)
+
+ return root
+
+// Construct a BST by inserting values
+root = null
+values = [8, 3, 10, 1, 6, 14, 4, 7, 13]
+for each value in values:
+ root = insert(root, value)
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(logn)
+
+---
+### Problem 7 Check if a binary tree is a binary search tree
+
+To check if a binary tree is a binary search tree (BST), you can perform an inorder traversal of the tree and ensure that the values encountered during the traversal are in ascending order. Here's how you can do it:
+
+**Conditions are:**
+
+
+
+### Question
+What is the purpose of balancing a Binary Search Tree?
+
+**Choices**
+- [ ] To make it visually appealing
+- [ ] To ensure all nodes have the same value
+- [x] To maintain efficient search, insert, and delete operations
+- [ ] Balancing is not necessary in a Binary Search Tree
+
+
+---
+### Problem 6 Construct a binary search tree
+
+
+#### Approach:
+* Find the middle element of the sorted array.
+* Create a new node with this middle element as the root of the tree.
+* Recursively repeat steps 1 and 2 for the left and right halves of the array, making the middle element of each subarray the root of its respective subtree.
+* Continue this process until all elements are processed.
+* The final tree will be a valid BST with the given sorted array as its inorder traversal.
+* Here's an example construction of a BST using the values 8, 3, 10, 1, 6, 14, 4, 7, and 13:
+
+#### Example:
+* Sorted Array - 1, 3, 4, 6, 7, 8, 10, 13, 14
+* Create the root node with value 8.
+* Insert 3: Move to the left child of the root (value 3).
+* Insert 10: Move to the right child of the root (value 10).
+* Insert 1: Move to the left child of the node with value 3 (value 1).
+* Insert 6: Move to the right child of the node with value 3 (value 6).
+* Insert 14: Move to the right child of the root (value 14).
+* Insert 4: Move to the left child of the node with value 6 (value 4).
+* Insert 7: Move to the right child of the node with value 6 (value 7).
+* Insert 13: Move to the left child of the node with value 14 (value 13).
+The constructed BST:
+```cpp
+ 8
+ / \
+ 3 10
+ / \ \
+ 1 6 14
+ / \ /
+ 4 7 13
+```
+
+
+#### Pseudocode:
+
+```cpp
+function insert(root, value):
+ if root is null:
+ return [value, null, null]
+
+ if value < root[0]:
+ root[1] = insert(root[1], value)
+ else:
+ root[2] = insert(root[2], value)
+
+ return root
+
+// Construct a BST by inserting values
+root = null
+values = [8, 3, 10, 1, 6, 14, 4, 7, 13]
+for each value in values:
+ root = insert(root, value)
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(logn)
+
+---
+### Problem 7 Check if a binary tree is a binary search tree
+
+To check if a binary tree is a binary search tree (BST), you can perform an inorder traversal of the tree and ensure that the values encountered during the traversal are in ascending order. Here's how you can do it:
+
+**Conditions are:**
+
+ +
+
+#### Approach:
+* Perform an inorder traversal of the binary tree.
+* During the traversal, keep track of the previously visited node's value.
+* At each step, compare the current node's value with the previously visited node's value.
+* If the current node's value is less than or equal to the previously visited node's value, the tree is not a BST.
+* If you complete the entire traversal without encountering any violations of the BST property, the tree is a BST.
+
+
+
+**Example:**
+Suppose we have the following binary tree:
+```cpp
+ 4
+ / \
+ 2 6
+ / \ / \
+ 1 3 5 7
+```
+* Initialize prevValue as -∞ (negative infinity).
+* Begin the inorder traversal:
+* Start at the root node (4).
+* Recursively traverse the left subtree (node 2).
+* Check 2 > -∞, so it's okay.
+* Update prevValue to 2.
+* Recursively traverse the left subtree (node 1).
+* Check 1 > 2. This is a violation.
+* Since there's a violation, the tree is not a BST.
+
+---
+### Question
+Check where the given binary tree is a Binary Search Tree.
+
+```cpp
+ 5
+ / \
+ 2 6
+ / \ / \
+ 1 3 4 7
+```
+
+**Choices**
+- [ ] Yes, It is a Binary Search Tree
+- [x] No, It is not a Binary Search Tree
+- [ ] May be
+- [ ] Not sure
+
+
+**Explanation:**
+
+No, It is not a Binary Search Tree.
+
+The node with the value 4 should not be on the right sub of the root node, since the root is 5, the node has to be placed on left subtree.
+
+---
+
+
+### Pseudocode:
+```cpp
+function isBST(root):
+ // Initialize a variable to keep track of the previously visited node's value
+ prevValue = -infinity // A small negative value
+
+ // Helper function for the inorder traversal
+ function inorderTraversal(node):
+ if node is null:
+ return true // Reached the end of the subtree, no violations
+
+ // Recursively traverse the left subtree
+ if not inorderTraversal(node.left):
+ return false
+
+ // Check if the current node's value violates the BST property
+ if node.value <= prevValue:
+ return false
+
+ // Update the previously visited node's value
+ prevValue = node.value
+
+ // Recursively traverse the right subtree
+ return inorderTraversal(node.right)
+
+ // Start the inorder traversal from the root
+ return inorderTraversal(root)
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(N)
\ No newline at end of file
diff --git a/Academy DSA Typed Notes/Advanced/DSA Trees 4 LCA + Morris Inorder Traversal.md b/Academy DSA Typed Notes/Advanced/DSA Trees 4 LCA + Morris Inorder Traversal.md
new file mode 100644
index 0000000..5ff3a70
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Trees 4 LCA + Morris Inorder Traversal.md
@@ -0,0 +1,726 @@
+# Advanced DSA : Trees 4: LCA
+
+---
+## Understanding Binary Trees and Binary Search Trees
+
+### Binary Trees
+
+A Binary Tree is a hierarchical data structure composed of nodes, where each node has at most two children: a left child and a right child. The top node is called the root, and nodes without children are called leaves.
+
+### Binary Search Trees (BSTs)
+
+A Binary Search Tree is a type of binary tree with an additional property: for each node, all nodes in its left subtree have values smaller than the node's value, and all nodes in its right subtree have values greater than the node's value.
+
+---
+### Problem 1 Finding the kth Smallest Element in a Binary Search Tree
+
+
+Given a Binary Search Tree and a positive integer k, the problem is to find the kth smallest element in the BST.
+
+:::warning
+Please take some time to think about the brute force approach on your own before reading further.....
+:::
+
+### In-Order Traversal storing elements in array(Brute Force):
+
+#### Algorithm
+1. Initialize a binary search tree (BST) as root.
+2. Iterate through the elements of the array and insert each element into the BST.
+3. Perform an in-order traversal of the BST to collect the elements in sorted order.
+4. Access the Kth element from the sorted elements list.
+5. Return the Kth element as the Kth smallest element.
+
+#### Pseudocode:
+```java
+// Define a TreeNode structure
+Struct TreeNode:
+ val
+ left
+ right
+
+// Function to find the Kth smallest element in a BST
+Function findKthSmallestElement(arr, k):
+ If arr is empty:
+ Return None // Array is empty, no elements to find
+
+ Root = null // Initialize the root of the binary search tree
+
+ // Step 1: Create a binary search tree (BST) from the array
+ For each element in arr:
+ Root = insert(Root, element)
+
+ SortedElements = [] // Initialize an empty list to store sorted elements
+
+ // Step 2: Perform an in-order traversal of the BST
+ InorderTraversal(Root, SortedElements)
+
+ // Step 3: Return the Kth element from the sorted elements list
+ If 1 <= k <= length(SortedElements):
+ Return SortedElements[k - 1] // Subtract 1 because indices are 0-based
+ Else:
+ Return None // Handle the case when k is out of bounds
+
+// Function to insert a value into a BST
+Function insert(root, value):
+ If root is null:
+ Return TreeNode(value) // Create a new node with the given value
+
+ If value < root.val:
+ root.left = insert(root.left, value) // Insert into the left subtree
+ Else:
+ root.right = insert(root.right, value) // Insert into the right subtree
+
+ Return root
+
+// Function to perform an in-order traversal of the BST
+Function InorderTraversal(root, result):
+ If root is null:
+ Return
+
+ // Step 4: Perform an in-order traversal recursively
+ InorderTraversal(root.left, result)
+ Append root.val to result
+ InorderTraversal(root.right, result)
+
+// Example usage:
+Elements = [12, 3, 7, 15, 9, 20]
+K = 3 // Find the 3rd smallest element
+
+Result = findKthSmallestElement(Elements, K)
+
+If Result is not null:
+ Output "The Kth smallest element is: " + Result
+Else:
+ Output "Invalid value of K: " + K
+
+```
+
+#### In-Order Traversal Approach(Count Method):
+The in-order traversal of a BST visits the nodes in ascending order. Therefore, by performing an in-order traversal and keeping track of the count of visited nodes, we can identify the kth smallest element when the count matches k.
+
+#### Example: Finding the 3rd Smallest Element in a BST
+
+**BST:**
+
+```java
+ 4
+ / \
+ 2 6
+ / \ / \
+1 3 5 7
+```
+
+**Scenario:**
+We want to find the 3rd smallest element in the given BST.
+
+**Solution:**
+
+* Perform an in-order traversal of the BST:
+* In-order traversal: 1, 2, 3, 4, 5, 6, 7
+* The 3rd smallest element is 3.
+
+#### Pseudocode:
+Here's a simplified pseudocode representation of finding the kth smallest element using in-order traversal:
+```java
+function findKthSmallest(root, k):
+ count = 0
+ stack = []
+
+ while stack or root:
+ while root:
+ stack.append(root)
+ root = root.left
+
+ root = stack.pop()
+ count += 1
+
+ if count == k:
+ return root.val
+
+ root = root.right
+```
+
+
+#### Analysis:
+
+The in-order traversal visits every node once, making the time complexity of this algorithm $O(n)$, where n is the number of nodes in the BST. The space complexity is $O(h)$, where h is the height of the BST, due to the stack used for traversal.
+
+
+---
+### Problem 2 Morris Traversal
+
+#### Morris Traversal Approach:
+Morris Traversal takes advantage of unused null pointers in the tree structure to link nodes temporarily, effectively threading the tree. By doing so, it enables us to traverse the tree in a specific order without requiring a stack or recursion.
+
+#### In-Order Morris Traversal:
+
+* Start at the root.
+* Initialize the current node as the root.
+* While the current node is not null:
+ * If the current node's left child is null, print the current node's value and move to the right child.
+ * If the current node's left child is not null:
+ * Find the rightmost node in the left subtree.
+ * Make the current node the right child of the rightmost node.
+ * Move to the left child of the current node.
+* Repeat the process until the current node becomes null.
+
+#### Pre-Order Morris Traversal:
+
+* Start at the root.
+* Initialize the current node as the root.
+* While the current node is not null:
+ * Print the current node's value.
+ * If the current node's left child is null, move to the right child.
+ * If the current node's left child is not null:
+ * Find the rightmost node in the left subtree.
+ * Make the current node the right child of the rightmost node.
+ * Move to the left child of the current node.
+* Repeat the process until the current node becomes null.
+
+
+**Example:**
+```java
+ 1
+ / \
+ 2 3
+ / \
+ 4 5
+```
+We will carefully go through each step:
+
+- **Step 1: Start at the root node, which is 1.**
+ 1. Initialize current pointer as current = 1.
+
+- **Step 2: At node 1:**
+ 1. Check if the left subtree of the current node is null.
+ 2. Since the left subtree of 1 is not null, find the rightmost node in the left subtree. This is node 5.
+ 3. Create a thread (temporary link) from 5 to the current node (1): 5 -> 1.
+ 4. Update the current node to its left child: current = 2.
+
+- **Step 3: At node 2:**
+ 1. Check if the left subtree of the current node is null.
+ 2. The left subtree of 2 is not null, so find the rightmost node in the left subtree of 2, which is 5.
+ 3. Remove the thread from 5 to 1 (undoing the link created earlier).
+ 4. Print the current node's value, which is 2.
+ 5. Move to the right child of the current node: current = 3
+
+
+- **Step 4: At node 3:**
+ 1. Check if the left subtree of the current node is null.
+ 2. The left subtree of 3 is null, so print the current node's value, which is 3.
+ 3. Move to the right child of the current node (null): current = None.
+
+- **Step 5:** Since the current node is now None, we've reached the end of the traversal.
+ 1. The Morris Inorder Traversal of the binary tree 1 -> 2 -> 4 -> 5 -> 3 allows us to visit all the nodes in ascending order without using additional data structures or modifying the tree's structure. It's an efficient way to perform an inorder traversal.
+
+
+#### Pseudocode Example (In-Order):
+
+```java
+function morrisInOrderTraversal(root):
+ current = root
+ while current is not null:
+ if current.left is null:
+ print current.value
+ current = current.right
+ else:
+ pre = current.left
+ while pre.right is not null and pre.right != current:
+ pre = pre.right
+ if pre.right is null:
+ pre.right = current
+ current = current.left
+ else:
+ pre.right = null
+ print current.value
+ current = current.right
+```
+
+
+#### Analysis:
+Morris Traversal eliminates the need for an explicit stack, leading to a constant space complexity of $O(1)$. The time complexity for traversing the entire tree remains $O(n)$, where n is the number of nodes.
+
+---
+### Question
+What is the primary advantage of Morris Traversal for binary trees?
+
+**Choices**
+- [ ] It uses an auxiliary stack to save memory.
+- [ ] It guarantees the fastest traversal among all traversal methods.
+- [ ] It allows for traversal in reverse order (right-to-left).
+- [x] It achieves memory-efficient traversal without using additional data structures.
+
+
+
+
+---
+### Problem 3 Finding an element
+
+
+#### Approach:
+Finding an element in a binary tree involves traversing the tree in a systematic way to search for the desired value. We'll focus on a common approach known as depth-first search (DFS), which includes pre-order, in-order, and post-order traversal methods.
+
+#### Algorithm:
+1. Start at the root node of the binary tree.
+2. If the root node is null (indicating an empty tree), return False (element not found).
+3. Check if the value of the current node matches the target value:
+4. If they are equal, return True (element found).
+5. Recursively search for the target element in the left subtree by calling the function with the left child node.
+6. Recursively search for the target element in the right subtree by calling the function with the right child node.
+7. If the element is found in either the left or right subtree (or both), return True.
+8. If the element is not found in either subtree, return False.
+
+#### Example:
+```java
+ 1
+ / \
+ 2 3
+ / \
+ 4 5
+```
+**Dry Run:**
+1. Start at the root (1).
+2. Check if it matches the target (3) - No.
+3. Move to the left child (2).
+4. Check if it matches the target (3) - No.
+5. Move to the left child (4).
+6. Check if it matches the target (3) - No.
+7. Move to the right child (null).
+8. Move back to 4's parent (2).
+9. Move to the right child (5).
+10. Check if it matches the target (3) - No.
+11. Move to the left child (null).
+12. Move back to 5's parent (2).
+13. Move back to 2's parent (1).
+14. Check if it matches the target (3) - Yes, found!
+15. Finish the search.
+
+#### Pseudocode Example:
+
+```java
+function findElement(root, target)
+ if root is null
+ return False // Element not found in an empty tree
+
+ if root.value is equal to target
+ return True // Element found at the current node
+
+ // Recursively search in the left subtree
+ found_in_left = findElement(root.left, target)
+
+ // Recursively search in the right subtree
+ found_in_right = findElement(root.right, target)
+
+ // Return True if found in either left or right subtree
+ return found_in_left OR found_in_right
+```
+
+
+#### Analysis:
+The time complexity of finding an element in a binary tree using DFS depends on the height of the tree. In the worst case, it's O(n), where n is the number of nodes in the tree. The space complexity is determined by the depth of the recursion stack.
+
+
+---
+### Problem 4 Path from root to node in Binary Tree
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Approach:
+To find the path from the root to a specific node, we'll leverage depth-first search (DFS), a versatile traversal method that includes pre-order, in-order, and post-order traversal techniques.
+
+#### DFS Pre-Order Traversal for Finding Path:
+
+1. Initialize an empty list path to store the path.
+2. Define a recursive function findPath(root, target, path):
+3. If root is null, return False.
+4. If root matches the target, append it to path and return True.
+5. Recursively call findPath on the left subtree and right subtree.
+6. If either subtree returns True, append root to path and return True.
+7. Start the search from the root node by calling findPath(root, target, path).
+8. If the search returns True, reverse the path list to get the path from root to target.
+9. Return the reversed path.
+
+#### Pseudocode Example (DFS Pre-Order):
+
+```java
+function findPath(root, target):
+ if root is null:
+ return false // Element not found in an empty tree
+
+ if root.value == target:
+ list.add(root) // Add the current node to the list (path found)
+ return true; // Element found
+
+ res = findPath(root -> left, target) OR findPath(root -> right, target)
+
+ if res == true:
+ list.add(root) // Add the current node to the list (part of the path)
+
+ return res;
+
+// Reverse the list to get the answer (the path from root to target)
+
+```
+#### Analysis:
+The time complexity of finding the path from the root to a node using DFS depends on the height of the tree. In the worst case, it's O(n), where n is the number of nodes in the tree. The space complexity is determined by the depth of the recursion stack and the length of the path.
+
+---
+### Question
+What is the primary benefit of using depth-first search (DFS) for finding the path from the root to a specific node in a Binary Tree?
+
+**Choices**
+- [ ] DFS guarantees the shortest path between the root and the target node.
+- [ ] DFS ensures that the tree remains balanced during traversal.
+- [ ] DFS enables efficient path finding with a time complexity of O(log n).
+- [x] DFS allows us to explore the structure of the tree while tracking visited nodes.
+
+---
+### Problem 5 finding the Lowest Common Ancestor (LCA) of two nodes
+
+#### Approach:
+To find the LCA of two nodes in a binary tree, we'll utilize a recursive approach that capitalizes on the tree's structure. The LCA is the deepest node that has one of the nodes in its left subtree and the other node in its right subtree.
+
+#### Recursive Algorithm for LCA:
+
+* Start at the root of the binary tree.
+* If the root is null or matches either of the target nodes, return the root as the LCA.
+* Recursively search for the target nodes in the left and right subtrees of the current root.
+* If both target nodes are found in different subtrees, the current root is the LCA.
+* If only one target node is found, return that node as the LCA.
+* If both target nodes are found in the same subtree, continue the search in that subtree.
+
+
+**Example**:
+```java
+ 1
+ / \
+ 2 3
+ / \
+ 4 5
+ / \
+ 6 7
+ ```
+**LCA of nodes 6 and 3 is node 1.**
+1. Start at the root (1).
+2. Check for nodes 6 and 3 in the subtree rooted at 1.
+3. Recursively search the left subtree (2).
+4. Continue searching left (4).
+5. Continue searching left (6).
+6. Found node 6, but not node 3 in the left subtree.
+7. Go back to node 4 and check the right subtree (null).
+8. Go back to node 2 and check the right subtree (5).
+9. Continue searching right (5).
+10. Not found node 6 in the right subtree.
+11. Go back to node 2 and check for nodes 6 and 3.
+12. Found node 6 in the left subtree.
+13. Return node 2 as the Lowest Common Ancestor (LCA).
+
+
+#### Pseudocode Example:
+
+```java
+function findLCA(root, node1, node2):
+ # Base case: if root is null or matches either of the nodes, return root
+ if root is null or root == node1 or root == node2:
+ return root
+
+ # Recursively search for the target nodes in the left and right subtrees
+ left_lca = findLCA(root.left, node1, node2)
+ right_lca = findLCA(root.right, node1, node2)
+
+ # Determine the LCA based on the search results
+ if left_lca and right_lca:
+ return root # Current root is the LCA
+ if left_lca:
+ return left_lca # LCA found in the left subtree
+ return right_lca # LCA found in the right subtree
+```
+
+#### Analysis:
+The time complexity of finding the LCA in a binary tree using this recursive approach is O(n), where n is the number of nodes in the tree. The space complexity is determined by the depth of the recursion stack.
+
+---
+### Problem 6 Lowest Common Ancestor (LCA) in a Binary Search Tree (BST)
+
+#### Approach:
+To find the LCA of two nodes in a Binary Search Tree, we'll utilize the properties of BSTs that make traversal and comparison more efficient.
+
+#### Algorithm for Finding LCA in a BST:
+
+* Start at the root of the BST.
+* Compare the values of the root node, node1, and node2.
+* If both nodes are smaller than the root's value, move to the left subtree.
+* If both nodes are larger than the root's value, move to the right subtree.
+* If one node is smaller and the other is larger than the root's value, or if either node matches the root's value, the root is the LCA.
+* Repeat steps 2-5 in the chosen subtree until the LCA is found.
+
+#### Example: Finding LCA in a Binary Search Tree
+
+**BST:**
+```java
+ 8
+ / \
+ 3 10
+ / \ \
+ 1 6 14
+ / \ /
+ 4 7 13
+```
+Let's find the LCA of nodes 4 and 7 in this BST:
+
+- **Step 1:**
+ 1. Start at the root, which is node 8.
+ 2. Compare node 4 and node 7 with the current node's value (8).
+ 3. Both are smaller, so move to the left subtree (node 3).
+
+- **Step 2:**
+ 1. Move to node 3.
+ 2. Compare node 4 and node 7 with the current node's value (3).
+ 3. Both are larger, so move to the right subtree (node 6).
+
+- **Step 3:**
+ 1. Move to node 6.
+ 2. Compare node 4 and node 7 with the current node's value (6).
+ 3. Node 4 is smaller, and node 7 is larger.
+ 4. The current node (6) is the LCA of nodes 4 and 7.
+ 5. So, in this example, the LCA of nodes 4 and 7 in the BST is node 6.
+
+#### Pseudocode Example:
+
+```java
+function findLCA(root, node1, node2):
+ if root is null:
+ return null // If the tree is empty, there's no LCA
+
+ while root is not null:
+ // If both nodes are smaller than the current node, go left
+ if node1.value < root.value and node2.value < root.value:
+ root = root.left
+ // If both nodes are larger than the current node, go right
+ else if node1.value > root.value and node2.value > root.value:
+ root = root.right
+ // If one node is smaller and the other is larger, or if one matches, this is the LCA
+ else:
+ return root
+
+ return null // If no LCA is found (unlikely in a valid BST)
+
+```
+#### Analysis:
+The time complexity of finding the LCA in a BST is O(h), where h is the height of the BST. In a balanced BST, the height is log(n), making the LCA operation highly efficient. The space complexity is determined by the depth of the recursion stack.
+
+
+---
+### Problem 7 In-time and Out-time of Binary Tree
+
+
+#### Approach:
+The Interval Assignment technique involves three main steps: DFS traversal, interval assignment, and construction of the rooted tree.
+
+:::warning
+Please take some time to think about the further solution approach on your own before reading further.....
+:::
+
+#### DFS Traversal and Interval Assignment:
+
+* Start a DFS traversal of the tree from any chosen starting node.
+* As nodes are visited, assign start times when a node is entered and finish times when the traversal returns from that node. These times define intervals for each node.
+#### Constructing the Rooted Tree:
+
+1. From the DFS traversal, we have a collection of intervals (start and finish times) for each node.
+2. Choose the node with the smallest start time as the root of the rooted tree.
+3. For each remaining node:
+ 1. Find the node with the largest start time that is still smaller than the current node's finish time. This node becomes the parent of the current node in the rooted tree.
+ 2. Repeat this process for all nodes.
+
+---
+### Question
+What is the significance of in-time and out-time values in DFS traversal?
+
+**Choices**
+- [ ] They indicate the number of times each node is visited during the traversal.
+- [ ] They represent the depth of each node in the tree.
+- [x] They help create hierarchical visualizations of trees.
+- [ ] They are used to determine the balance of the tree.
+
+
+
+**Example:**
+```java
+ 1
+ / \
+ 2 3
+ / \
+ 4 5
+```
+1. We initialize the global time variable to 1.
+2. We traverse the tree using Depth-First Search (DFS):
+3. Starting at Node 1:
+4. In-Time for Node 1 is recorded as 1.
+5. We recursively visit the left child, Node 2.
+6. At Node 2:
+7. In-Time for Node 2 is recorded as 2.
+8. We recursively visit the left child, Node 4.
+9. At Node 4:
+10. In-Time for Node 4 is recorded as 3.
+11. Since Node 4 has no further children, we record its Out-Time as 5.
+12. Now, we return to Node 2:
+13. We recursively visit the right child, Node 5.
+14. At Node 5:
+15. In-Time for Node 5 is recorded as 8.
+16. Since Node 5 has no further children, we record its Out-Time as 10
+17. We return to Node 2 and record its Out-Time as 11.
+18. We return to Node 1 and recursively visit its right child, Node 3.
+19. At Node 3:
+20. In-Time for Node 3 is recorded as 12.
+21. We recursively visit its right child, but it's null.
+22. We record the Out-Time for Node 3 as 14.
+23. Finally, we return to Node 1 and record its Out-Time as 15.
+
+**The in-time and out-time values are now calculated:**
+* Node 1 - In-Time: 1, Out-Time: 15
+* Node 2 - In-Time: 2, Out-Time: 11
+* Node 3 - In-Time: 12, Out-Time: 14
+* Node 4 - In-Time: 3, Out-Time: 5
+* Node 5 - In-Time: 8, Out-Time: 10
+
+#### Pseudocode
+```java
+function calculateInTimeOutTime(root):
+ global time // A global variable to keep track of time
+
+ // Initialize arrays to store in-time and out-time for each node
+ inTime = [0] * (2 * n) // Assuming 'n' is the number of nodes in the tree
+ outTime = [0] * (2 * n)
+
+ // Helper function for DFS traversal
+ function dfs(node):
+ nonlocal time
+
+ // Record the in-time for the current node and increment time
+ inTime[node] = time
+ time = time + 1
+
+ // Recursively visit left child (if exists)
+ if node.left is not null:
+ dfs(node.left)
+
+ // Recursively visit right child (if exists)
+ if node.right is not null:
+ dfs(node.right)
+
+ // Record the out-time for the current node and increment time
+ outTime[node] = time
+ time = time + 1
+
+ // Start DFS traversal from the root
+ dfs(root)
+
+```
+
+
+---
+### Problem 8 For multiple queries find LCA(x,y)
+
+#### Algorithm:
+1. Calculate In-Time and Out-Time for Each Node:
+2. First, calculate the in-time and out-time for each node in the binary tree as explained in a previous response.
+3. Answer LCA Queries:
+4. To find the LCA of multiple pairs of nodes (x, y):
+5. For each LCA query (x, y):
+6. Check if inTime[x] is less than or equal to inTime[y] and outTime[x] is greater than or equal to outTime[y]. If true, it means that node x is an ancestor of node y.
+7. Check if inTime[y] is less than or equal to inTime[x] and outTime[y] is greater than or equal to outTime[x]. If true, it means that node y is an ancestor of node x.
+8. If neither of the above conditions is met, it means that x and y have different ancestors.
+9. In such cases, move up the tree from the deeper node until you find a node that is at the same level as the shallower node. This node will be their LCA.
+
+#### Example
+```java
+ 1
+ / \
+ 2 3
+ / \
+ 4 5
+```
+And we'll find the Lowest Common Ancestor (LCA) for a few pairs of nodes (x, y) using the in-time and out-time approach.
+
+* **Step 1: Calculate In-Time and Out-Time**
+
+
+#### Approach:
+* Perform an inorder traversal of the binary tree.
+* During the traversal, keep track of the previously visited node's value.
+* At each step, compare the current node's value with the previously visited node's value.
+* If the current node's value is less than or equal to the previously visited node's value, the tree is not a BST.
+* If you complete the entire traversal without encountering any violations of the BST property, the tree is a BST.
+
+
+
+**Example:**
+Suppose we have the following binary tree:
+```cpp
+ 4
+ / \
+ 2 6
+ / \ / \
+ 1 3 5 7
+```
+* Initialize prevValue as -∞ (negative infinity).
+* Begin the inorder traversal:
+* Start at the root node (4).
+* Recursively traverse the left subtree (node 2).
+* Check 2 > -∞, so it's okay.
+* Update prevValue to 2.
+* Recursively traverse the left subtree (node 1).
+* Check 1 > 2. This is a violation.
+* Since there's a violation, the tree is not a BST.
+
+---
+### Question
+Check where the given binary tree is a Binary Search Tree.
+
+```cpp
+ 5
+ / \
+ 2 6
+ / \ / \
+ 1 3 4 7
+```
+
+**Choices**
+- [ ] Yes, It is a Binary Search Tree
+- [x] No, It is not a Binary Search Tree
+- [ ] May be
+- [ ] Not sure
+
+
+**Explanation:**
+
+No, It is not a Binary Search Tree.
+
+The node with the value 4 should not be on the right sub of the root node, since the root is 5, the node has to be placed on left subtree.
+
+---
+
+
+### Pseudocode:
+```cpp
+function isBST(root):
+ // Initialize a variable to keep track of the previously visited node's value
+ prevValue = -infinity // A small negative value
+
+ // Helper function for the inorder traversal
+ function inorderTraversal(node):
+ if node is null:
+ return true // Reached the end of the subtree, no violations
+
+ // Recursively traverse the left subtree
+ if not inorderTraversal(node.left):
+ return false
+
+ // Check if the current node's value violates the BST property
+ if node.value <= prevValue:
+ return false
+
+ // Update the previously visited node's value
+ prevValue = node.value
+
+ // Recursively traverse the right subtree
+ return inorderTraversal(node.right)
+
+ // Start the inorder traversal from the root
+ return inorderTraversal(root)
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(N)
\ No newline at end of file
diff --git a/Academy DSA Typed Notes/Advanced/DSA Trees 4 LCA + Morris Inorder Traversal.md b/Academy DSA Typed Notes/Advanced/DSA Trees 4 LCA + Morris Inorder Traversal.md
new file mode 100644
index 0000000..5ff3a70
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Trees 4 LCA + Morris Inorder Traversal.md
@@ -0,0 +1,726 @@
+# Advanced DSA : Trees 4: LCA
+
+---
+## Understanding Binary Trees and Binary Search Trees
+
+### Binary Trees
+
+A Binary Tree is a hierarchical data structure composed of nodes, where each node has at most two children: a left child and a right child. The top node is called the root, and nodes without children are called leaves.
+
+### Binary Search Trees (BSTs)
+
+A Binary Search Tree is a type of binary tree with an additional property: for each node, all nodes in its left subtree have values smaller than the node's value, and all nodes in its right subtree have values greater than the node's value.
+
+---
+### Problem 1 Finding the kth Smallest Element in a Binary Search Tree
+
+
+Given a Binary Search Tree and a positive integer k, the problem is to find the kth smallest element in the BST.
+
+:::warning
+Please take some time to think about the brute force approach on your own before reading further.....
+:::
+
+### In-Order Traversal storing elements in array(Brute Force):
+
+#### Algorithm
+1. Initialize a binary search tree (BST) as root.
+2. Iterate through the elements of the array and insert each element into the BST.
+3. Perform an in-order traversal of the BST to collect the elements in sorted order.
+4. Access the Kth element from the sorted elements list.
+5. Return the Kth element as the Kth smallest element.
+
+#### Pseudocode:
+```java
+// Define a TreeNode structure
+Struct TreeNode:
+ val
+ left
+ right
+
+// Function to find the Kth smallest element in a BST
+Function findKthSmallestElement(arr, k):
+ If arr is empty:
+ Return None // Array is empty, no elements to find
+
+ Root = null // Initialize the root of the binary search tree
+
+ // Step 1: Create a binary search tree (BST) from the array
+ For each element in arr:
+ Root = insert(Root, element)
+
+ SortedElements = [] // Initialize an empty list to store sorted elements
+
+ // Step 2: Perform an in-order traversal of the BST
+ InorderTraversal(Root, SortedElements)
+
+ // Step 3: Return the Kth element from the sorted elements list
+ If 1 <= k <= length(SortedElements):
+ Return SortedElements[k - 1] // Subtract 1 because indices are 0-based
+ Else:
+ Return None // Handle the case when k is out of bounds
+
+// Function to insert a value into a BST
+Function insert(root, value):
+ If root is null:
+ Return TreeNode(value) // Create a new node with the given value
+
+ If value < root.val:
+ root.left = insert(root.left, value) // Insert into the left subtree
+ Else:
+ root.right = insert(root.right, value) // Insert into the right subtree
+
+ Return root
+
+// Function to perform an in-order traversal of the BST
+Function InorderTraversal(root, result):
+ If root is null:
+ Return
+
+ // Step 4: Perform an in-order traversal recursively
+ InorderTraversal(root.left, result)
+ Append root.val to result
+ InorderTraversal(root.right, result)
+
+// Example usage:
+Elements = [12, 3, 7, 15, 9, 20]
+K = 3 // Find the 3rd smallest element
+
+Result = findKthSmallestElement(Elements, K)
+
+If Result is not null:
+ Output "The Kth smallest element is: " + Result
+Else:
+ Output "Invalid value of K: " + K
+
+```
+
+#### In-Order Traversal Approach(Count Method):
+The in-order traversal of a BST visits the nodes in ascending order. Therefore, by performing an in-order traversal and keeping track of the count of visited nodes, we can identify the kth smallest element when the count matches k.
+
+#### Example: Finding the 3rd Smallest Element in a BST
+
+**BST:**
+
+```java
+ 4
+ / \
+ 2 6
+ / \ / \
+1 3 5 7
+```
+
+**Scenario:**
+We want to find the 3rd smallest element in the given BST.
+
+**Solution:**
+
+* Perform an in-order traversal of the BST:
+* In-order traversal: 1, 2, 3, 4, 5, 6, 7
+* The 3rd smallest element is 3.
+
+#### Pseudocode:
+Here's a simplified pseudocode representation of finding the kth smallest element using in-order traversal:
+```java
+function findKthSmallest(root, k):
+ count = 0
+ stack = []
+
+ while stack or root:
+ while root:
+ stack.append(root)
+ root = root.left
+
+ root = stack.pop()
+ count += 1
+
+ if count == k:
+ return root.val
+
+ root = root.right
+```
+
+
+#### Analysis:
+
+The in-order traversal visits every node once, making the time complexity of this algorithm $O(n)$, where n is the number of nodes in the BST. The space complexity is $O(h)$, where h is the height of the BST, due to the stack used for traversal.
+
+
+---
+### Problem 2 Morris Traversal
+
+#### Morris Traversal Approach:
+Morris Traversal takes advantage of unused null pointers in the tree structure to link nodes temporarily, effectively threading the tree. By doing so, it enables us to traverse the tree in a specific order without requiring a stack or recursion.
+
+#### In-Order Morris Traversal:
+
+* Start at the root.
+* Initialize the current node as the root.
+* While the current node is not null:
+ * If the current node's left child is null, print the current node's value and move to the right child.
+ * If the current node's left child is not null:
+ * Find the rightmost node in the left subtree.
+ * Make the current node the right child of the rightmost node.
+ * Move to the left child of the current node.
+* Repeat the process until the current node becomes null.
+
+#### Pre-Order Morris Traversal:
+
+* Start at the root.
+* Initialize the current node as the root.
+* While the current node is not null:
+ * Print the current node's value.
+ * If the current node's left child is null, move to the right child.
+ * If the current node's left child is not null:
+ * Find the rightmost node in the left subtree.
+ * Make the current node the right child of the rightmost node.
+ * Move to the left child of the current node.
+* Repeat the process until the current node becomes null.
+
+
+**Example:**
+```java
+ 1
+ / \
+ 2 3
+ / \
+ 4 5
+```
+We will carefully go through each step:
+
+- **Step 1: Start at the root node, which is 1.**
+ 1. Initialize current pointer as current = 1.
+
+- **Step 2: At node 1:**
+ 1. Check if the left subtree of the current node is null.
+ 2. Since the left subtree of 1 is not null, find the rightmost node in the left subtree. This is node 5.
+ 3. Create a thread (temporary link) from 5 to the current node (1): 5 -> 1.
+ 4. Update the current node to its left child: current = 2.
+
+- **Step 3: At node 2:**
+ 1. Check if the left subtree of the current node is null.
+ 2. The left subtree of 2 is not null, so find the rightmost node in the left subtree of 2, which is 5.
+ 3. Remove the thread from 5 to 1 (undoing the link created earlier).
+ 4. Print the current node's value, which is 2.
+ 5. Move to the right child of the current node: current = 3
+
+
+- **Step 4: At node 3:**
+ 1. Check if the left subtree of the current node is null.
+ 2. The left subtree of 3 is null, so print the current node's value, which is 3.
+ 3. Move to the right child of the current node (null): current = None.
+
+- **Step 5:** Since the current node is now None, we've reached the end of the traversal.
+ 1. The Morris Inorder Traversal of the binary tree 1 -> 2 -> 4 -> 5 -> 3 allows us to visit all the nodes in ascending order without using additional data structures or modifying the tree's structure. It's an efficient way to perform an inorder traversal.
+
+
+#### Pseudocode Example (In-Order):
+
+```java
+function morrisInOrderTraversal(root):
+ current = root
+ while current is not null:
+ if current.left is null:
+ print current.value
+ current = current.right
+ else:
+ pre = current.left
+ while pre.right is not null and pre.right != current:
+ pre = pre.right
+ if pre.right is null:
+ pre.right = current
+ current = current.left
+ else:
+ pre.right = null
+ print current.value
+ current = current.right
+```
+
+
+#### Analysis:
+Morris Traversal eliminates the need for an explicit stack, leading to a constant space complexity of $O(1)$. The time complexity for traversing the entire tree remains $O(n)$, where n is the number of nodes.
+
+---
+### Question
+What is the primary advantage of Morris Traversal for binary trees?
+
+**Choices**
+- [ ] It uses an auxiliary stack to save memory.
+- [ ] It guarantees the fastest traversal among all traversal methods.
+- [ ] It allows for traversal in reverse order (right-to-left).
+- [x] It achieves memory-efficient traversal without using additional data structures.
+
+
+
+
+---
+### Problem 3 Finding an element
+
+
+#### Approach:
+Finding an element in a binary tree involves traversing the tree in a systematic way to search for the desired value. We'll focus on a common approach known as depth-first search (DFS), which includes pre-order, in-order, and post-order traversal methods.
+
+#### Algorithm:
+1. Start at the root node of the binary tree.
+2. If the root node is null (indicating an empty tree), return False (element not found).
+3. Check if the value of the current node matches the target value:
+4. If they are equal, return True (element found).
+5. Recursively search for the target element in the left subtree by calling the function with the left child node.
+6. Recursively search for the target element in the right subtree by calling the function with the right child node.
+7. If the element is found in either the left or right subtree (or both), return True.
+8. If the element is not found in either subtree, return False.
+
+#### Example:
+```java
+ 1
+ / \
+ 2 3
+ / \
+ 4 5
+```
+**Dry Run:**
+1. Start at the root (1).
+2. Check if it matches the target (3) - No.
+3. Move to the left child (2).
+4. Check if it matches the target (3) - No.
+5. Move to the left child (4).
+6. Check if it matches the target (3) - No.
+7. Move to the right child (null).
+8. Move back to 4's parent (2).
+9. Move to the right child (5).
+10. Check if it matches the target (3) - No.
+11. Move to the left child (null).
+12. Move back to 5's parent (2).
+13. Move back to 2's parent (1).
+14. Check if it matches the target (3) - Yes, found!
+15. Finish the search.
+
+#### Pseudocode Example:
+
+```java
+function findElement(root, target)
+ if root is null
+ return False // Element not found in an empty tree
+
+ if root.value is equal to target
+ return True // Element found at the current node
+
+ // Recursively search in the left subtree
+ found_in_left = findElement(root.left, target)
+
+ // Recursively search in the right subtree
+ found_in_right = findElement(root.right, target)
+
+ // Return True if found in either left or right subtree
+ return found_in_left OR found_in_right
+```
+
+
+#### Analysis:
+The time complexity of finding an element in a binary tree using DFS depends on the height of the tree. In the worst case, it's O(n), where n is the number of nodes in the tree. The space complexity is determined by the depth of the recursion stack.
+
+
+---
+### Problem 4 Path from root to node in Binary Tree
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Approach:
+To find the path from the root to a specific node, we'll leverage depth-first search (DFS), a versatile traversal method that includes pre-order, in-order, and post-order traversal techniques.
+
+#### DFS Pre-Order Traversal for Finding Path:
+
+1. Initialize an empty list path to store the path.
+2. Define a recursive function findPath(root, target, path):
+3. If root is null, return False.
+4. If root matches the target, append it to path and return True.
+5. Recursively call findPath on the left subtree and right subtree.
+6. If either subtree returns True, append root to path and return True.
+7. Start the search from the root node by calling findPath(root, target, path).
+8. If the search returns True, reverse the path list to get the path from root to target.
+9. Return the reversed path.
+
+#### Pseudocode Example (DFS Pre-Order):
+
+```java
+function findPath(root, target):
+ if root is null:
+ return false // Element not found in an empty tree
+
+ if root.value == target:
+ list.add(root) // Add the current node to the list (path found)
+ return true; // Element found
+
+ res = findPath(root -> left, target) OR findPath(root -> right, target)
+
+ if res == true:
+ list.add(root) // Add the current node to the list (part of the path)
+
+ return res;
+
+// Reverse the list to get the answer (the path from root to target)
+
+```
+#### Analysis:
+The time complexity of finding the path from the root to a node using DFS depends on the height of the tree. In the worst case, it's O(n), where n is the number of nodes in the tree. The space complexity is determined by the depth of the recursion stack and the length of the path.
+
+---
+### Question
+What is the primary benefit of using depth-first search (DFS) for finding the path from the root to a specific node in a Binary Tree?
+
+**Choices**
+- [ ] DFS guarantees the shortest path between the root and the target node.
+- [ ] DFS ensures that the tree remains balanced during traversal.
+- [ ] DFS enables efficient path finding with a time complexity of O(log n).
+- [x] DFS allows us to explore the structure of the tree while tracking visited nodes.
+
+---
+### Problem 5 finding the Lowest Common Ancestor (LCA) of two nodes
+
+#### Approach:
+To find the LCA of two nodes in a binary tree, we'll utilize a recursive approach that capitalizes on the tree's structure. The LCA is the deepest node that has one of the nodes in its left subtree and the other node in its right subtree.
+
+#### Recursive Algorithm for LCA:
+
+* Start at the root of the binary tree.
+* If the root is null or matches either of the target nodes, return the root as the LCA.
+* Recursively search for the target nodes in the left and right subtrees of the current root.
+* If both target nodes are found in different subtrees, the current root is the LCA.
+* If only one target node is found, return that node as the LCA.
+* If both target nodes are found in the same subtree, continue the search in that subtree.
+
+
+**Example**:
+```java
+ 1
+ / \
+ 2 3
+ / \
+ 4 5
+ / \
+ 6 7
+ ```
+**LCA of nodes 6 and 3 is node 1.**
+1. Start at the root (1).
+2. Check for nodes 6 and 3 in the subtree rooted at 1.
+3. Recursively search the left subtree (2).
+4. Continue searching left (4).
+5. Continue searching left (6).
+6. Found node 6, but not node 3 in the left subtree.
+7. Go back to node 4 and check the right subtree (null).
+8. Go back to node 2 and check the right subtree (5).
+9. Continue searching right (5).
+10. Not found node 6 in the right subtree.
+11. Go back to node 2 and check for nodes 6 and 3.
+12. Found node 6 in the left subtree.
+13. Return node 2 as the Lowest Common Ancestor (LCA).
+
+
+#### Pseudocode Example:
+
+```java
+function findLCA(root, node1, node2):
+ # Base case: if root is null or matches either of the nodes, return root
+ if root is null or root == node1 or root == node2:
+ return root
+
+ # Recursively search for the target nodes in the left and right subtrees
+ left_lca = findLCA(root.left, node1, node2)
+ right_lca = findLCA(root.right, node1, node2)
+
+ # Determine the LCA based on the search results
+ if left_lca and right_lca:
+ return root # Current root is the LCA
+ if left_lca:
+ return left_lca # LCA found in the left subtree
+ return right_lca # LCA found in the right subtree
+```
+
+#### Analysis:
+The time complexity of finding the LCA in a binary tree using this recursive approach is O(n), where n is the number of nodes in the tree. The space complexity is determined by the depth of the recursion stack.
+
+---
+### Problem 6 Lowest Common Ancestor (LCA) in a Binary Search Tree (BST)
+
+#### Approach:
+To find the LCA of two nodes in a Binary Search Tree, we'll utilize the properties of BSTs that make traversal and comparison more efficient.
+
+#### Algorithm for Finding LCA in a BST:
+
+* Start at the root of the BST.
+* Compare the values of the root node, node1, and node2.
+* If both nodes are smaller than the root's value, move to the left subtree.
+* If both nodes are larger than the root's value, move to the right subtree.
+* If one node is smaller and the other is larger than the root's value, or if either node matches the root's value, the root is the LCA.
+* Repeat steps 2-5 in the chosen subtree until the LCA is found.
+
+#### Example: Finding LCA in a Binary Search Tree
+
+**BST:**
+```java
+ 8
+ / \
+ 3 10
+ / \ \
+ 1 6 14
+ / \ /
+ 4 7 13
+```
+Let's find the LCA of nodes 4 and 7 in this BST:
+
+- **Step 1:**
+ 1. Start at the root, which is node 8.
+ 2. Compare node 4 and node 7 with the current node's value (8).
+ 3. Both are smaller, so move to the left subtree (node 3).
+
+- **Step 2:**
+ 1. Move to node 3.
+ 2. Compare node 4 and node 7 with the current node's value (3).
+ 3. Both are larger, so move to the right subtree (node 6).
+
+- **Step 3:**
+ 1. Move to node 6.
+ 2. Compare node 4 and node 7 with the current node's value (6).
+ 3. Node 4 is smaller, and node 7 is larger.
+ 4. The current node (6) is the LCA of nodes 4 and 7.
+ 5. So, in this example, the LCA of nodes 4 and 7 in the BST is node 6.
+
+#### Pseudocode Example:
+
+```java
+function findLCA(root, node1, node2):
+ if root is null:
+ return null // If the tree is empty, there's no LCA
+
+ while root is not null:
+ // If both nodes are smaller than the current node, go left
+ if node1.value < root.value and node2.value < root.value:
+ root = root.left
+ // If both nodes are larger than the current node, go right
+ else if node1.value > root.value and node2.value > root.value:
+ root = root.right
+ // If one node is smaller and the other is larger, or if one matches, this is the LCA
+ else:
+ return root
+
+ return null // If no LCA is found (unlikely in a valid BST)
+
+```
+#### Analysis:
+The time complexity of finding the LCA in a BST is O(h), where h is the height of the BST. In a balanced BST, the height is log(n), making the LCA operation highly efficient. The space complexity is determined by the depth of the recursion stack.
+
+
+---
+### Problem 7 In-time and Out-time of Binary Tree
+
+
+#### Approach:
+The Interval Assignment technique involves three main steps: DFS traversal, interval assignment, and construction of the rooted tree.
+
+:::warning
+Please take some time to think about the further solution approach on your own before reading further.....
+:::
+
+#### DFS Traversal and Interval Assignment:
+
+* Start a DFS traversal of the tree from any chosen starting node.
+* As nodes are visited, assign start times when a node is entered and finish times when the traversal returns from that node. These times define intervals for each node.
+#### Constructing the Rooted Tree:
+
+1. From the DFS traversal, we have a collection of intervals (start and finish times) for each node.
+2. Choose the node with the smallest start time as the root of the rooted tree.
+3. For each remaining node:
+ 1. Find the node with the largest start time that is still smaller than the current node's finish time. This node becomes the parent of the current node in the rooted tree.
+ 2. Repeat this process for all nodes.
+
+---
+### Question
+What is the significance of in-time and out-time values in DFS traversal?
+
+**Choices**
+- [ ] They indicate the number of times each node is visited during the traversal.
+- [ ] They represent the depth of each node in the tree.
+- [x] They help create hierarchical visualizations of trees.
+- [ ] They are used to determine the balance of the tree.
+
+
+
+**Example:**
+```java
+ 1
+ / \
+ 2 3
+ / \
+ 4 5
+```
+1. We initialize the global time variable to 1.
+2. We traverse the tree using Depth-First Search (DFS):
+3. Starting at Node 1:
+4. In-Time for Node 1 is recorded as 1.
+5. We recursively visit the left child, Node 2.
+6. At Node 2:
+7. In-Time for Node 2 is recorded as 2.
+8. We recursively visit the left child, Node 4.
+9. At Node 4:
+10. In-Time for Node 4 is recorded as 3.
+11. Since Node 4 has no further children, we record its Out-Time as 5.
+12. Now, we return to Node 2:
+13. We recursively visit the right child, Node 5.
+14. At Node 5:
+15. In-Time for Node 5 is recorded as 8.
+16. Since Node 5 has no further children, we record its Out-Time as 10
+17. We return to Node 2 and record its Out-Time as 11.
+18. We return to Node 1 and recursively visit its right child, Node 3.
+19. At Node 3:
+20. In-Time for Node 3 is recorded as 12.
+21. We recursively visit its right child, but it's null.
+22. We record the Out-Time for Node 3 as 14.
+23. Finally, we return to Node 1 and record its Out-Time as 15.
+
+**The in-time and out-time values are now calculated:**
+* Node 1 - In-Time: 1, Out-Time: 15
+* Node 2 - In-Time: 2, Out-Time: 11
+* Node 3 - In-Time: 12, Out-Time: 14
+* Node 4 - In-Time: 3, Out-Time: 5
+* Node 5 - In-Time: 8, Out-Time: 10
+
+#### Pseudocode
+```java
+function calculateInTimeOutTime(root):
+ global time // A global variable to keep track of time
+
+ // Initialize arrays to store in-time and out-time for each node
+ inTime = [0] * (2 * n) // Assuming 'n' is the number of nodes in the tree
+ outTime = [0] * (2 * n)
+
+ // Helper function for DFS traversal
+ function dfs(node):
+ nonlocal time
+
+ // Record the in-time for the current node and increment time
+ inTime[node] = time
+ time = time + 1
+
+ // Recursively visit left child (if exists)
+ if node.left is not null:
+ dfs(node.left)
+
+ // Recursively visit right child (if exists)
+ if node.right is not null:
+ dfs(node.right)
+
+ // Record the out-time for the current node and increment time
+ outTime[node] = time
+ time = time + 1
+
+ // Start DFS traversal from the root
+ dfs(root)
+
+```
+
+
+---
+### Problem 8 For multiple queries find LCA(x,y)
+
+#### Algorithm:
+1. Calculate In-Time and Out-Time for Each Node:
+2. First, calculate the in-time and out-time for each node in the binary tree as explained in a previous response.
+3. Answer LCA Queries:
+4. To find the LCA of multiple pairs of nodes (x, y):
+5. For each LCA query (x, y):
+6. Check if inTime[x] is less than or equal to inTime[y] and outTime[x] is greater than or equal to outTime[y]. If true, it means that node x is an ancestor of node y.
+7. Check if inTime[y] is less than or equal to inTime[x] and outTime[y] is greater than or equal to outTime[x]. If true, it means that node y is an ancestor of node x.
+8. If neither of the above conditions is met, it means that x and y have different ancestors.
+9. In such cases, move up the tree from the deeper node until you find a node that is at the same level as the shallower node. This node will be their LCA.
+
+#### Example
+```java
+ 1
+ / \
+ 2 3
+ / \
+ 4 5
+```
+And we'll find the Lowest Common Ancestor (LCA) for a few pairs of nodes (x, y) using the in-time and out-time approach.
+
+* **Step 1: Calculate In-Time and Out-Time** We've already calculated the in-time and out-time values for this tree as follows: + 1. Node 1 - In-Time: 1, Out-Time: 10 + 2. Node 2 - In-Time: 2, Out-Time: 7 + 3. Node 3 - In-Time: 8, Out-Time: 9 + 4. Node 4 - In-Time: 3, Out-Time: 4 + 5. Node 5 - In-Time: 5, Out-Time: 6 + +* **Step 2: Find LCA for Pairs** + * Find LCA(4, 5): + * Check in-time and out-time: + * In-Time(4) <= In-Time(5) and Out-Time(4) >= Out-Time(5) is true. + * So, LCA(4, 5) is 4. + * Find LCA(2, 3): + * Check in-time and out-time: + * In-Time(2) <= In-Time(3) and Out-Time(2) >= Out-Time(3) is false. + * Now, bring both nodes to the same depth: + * Move 2 up once: 2 is now at the same depth as 3. + * Continue moving both nodes up: + * LCA(2, 3) is 1. + * Find LCA(4, 3): + * Check in-time and out-time: + * In-Time(4) <= In-Time(3) and Out-Time(4) >= Out-Time(3) is false. + * Now, bring both nodes to the same depth: + * Move 4 up once: 4 is now at the same depth as 3. + * Continue moving both nodes up: + * LCA(4, 3) is 1. + * Find LCA(5, 2): + * Check in-time and out-time: + * In-Time(5) <= In-Time(2) and Out-Time(5) >= Out-Time(2) is false. + * Now, bring both nodes to the same depth: + * Move 5 up once: 5 is now at the same depth as 2. + * Continue moving both nodes up: + * LCA(5, 2) is 1. + +#### Pseudocode: +```java +function findLCA(x, y): + if inTime[x] <= inTime[y] and outTime[x] >= outTime[y]: + return x # x is an ancestor of y + + if inTime[y] <= inTime[x] and outTime[y] >= outTime[x]: + return y # y is an ancestor of x + + # Move x and y up the tree to the same depth + while depth[x] > depth[y]: + x = parent[x] + + while depth[y] > depth[x]: + y = parent[y] + + # Move x and y up simultaneously until they meet at the LCA + while x != y: + x = parent[x] + y = parent[y] + + return x # LCA found +``` + +--- +### Question +What is the primary purpose of constructing a rooted tree using the start and finish times obtained during the DFS traversal? + +**Choices** +- [ ] To optimize the tree structure for faster traversal. +- [ ] To visualize the tree with nodes arranged in increasing order. +- [x] To efficiently represent the hierarchy and relationships within the tree. +- [ ] To eliminate the need for recursion in tree traversal. + +--- +### Observations + +* **In-Order Traversal:**
It visits Binary Search Tree (BST) nodes in ascending order, enabling efficient kth smallest element retrieval. +* **Morris Traversal:**
An efficient memory-saving tree traversal method with O(1) space complexity. +* **Path from Root:**
DFS traversal is used to find the path from the root to a node, with space complexity tied to recursion depth. +* **Lowest Common Ancestor (LCA) in Tree:**
LCA is found through recursion with O(n) time complexity and stack space. +* **In-Time & Out-Time:**
These values in DFS help create hierarchical visualizations of trees. +* **Interval Assignment Visualization:**
Provides a visual hierarchy for analyzing complex structures in various fields. +* **Finding LCA for Multiple Queries:**
LCA retrieval for multiple pairs involves adjusting node depths until they meet. + diff --git a/Academy DSA Typed Notes/Advanced/DSA Trees 5 Problems on Trees.md b/Academy DSA Typed Notes/Advanced/DSA Trees 5 Problems on Trees.md new file mode 100644 index 0000000..b942262 --- /dev/null +++ b/Academy DSA Typed Notes/Advanced/DSA Trees 5 Problems on Trees.md @@ -0,0 +1,587 @@ +# Advanced DSA : Trees 5: Problems on Trees + +--- +## Problem 1 Invert Binary Tree + +Given the root node of a binary tree, write a function to invert the tree. + +**Example** +Original Binary Tree : +```plaintext + 1 + / \ + 2 3 + / \ + 4 5 +``` +After Inverting the Binary Tree : +```plaintext + 1 + / \ + 3 2 + / \ + 5 4 +``` +--- +### Question +Select the correct inverted binary tree for this given tree: + +``` + 4 + / \ + 2 7 + / \ \ +1 3 9 +``` +**Choices** + +- [ ] **Option 1:** + +``` + 4 + / \ + 7 2 + / \ / +9 3 1 +``` + +- [ ] **Option 2:** + +``` + 4 + / \ + 7 2 + \ / \ + 3 1 9 +``` + +- [ ] **Option 3:** + +``` + 4 + / \ + 2 7 + \ / \ + 1 9 3 +``` + +- [x] **Option 4:** + +``` + 4 + / \ + 7 2 + / \ / +9 1 3 +``` + +:::warning +Please take some time to think about the solution approach on your own before reading further..... +::: + +**Solution** +To solve this problem,we can recursively invert the binary tree by swapping the left and right subtrees for each node. + +```cpp +void invertTree(TreeNode * root) { + if (root == nullptr) { + return; // Return if the root is null + } + + // Use a temporary variable to swap left and right subtrees + TreeNode * temp = root -> left; + root -> left = root -> right; + root -> right = temp; + + // Recursively invert the left and right subtrees + invertTree(root -> left); + invertTree(root -> right); +} + +``` + +#### Complexity +**Time Complexity:** O(N) +**Space Complexity:** O(H) + +--- +### Problem 2 Equal Tree Partition + +Given the root of a binary tree, return ***true*** if the tree can be split into two non-empty subtrees with equal sums, or ***false*** otherwise. + +**Example 1** +```cpp +Input: + 5 + / \ + 10 10 + / \ + 2 3 + +Output: True +``` + +**Explanation:** + +```cpp + 5 + / + 10 + +Sum: 15 +``` + +```cpp + 10 + / \ + 2 3 + +Sum: 15 +``` +**Example 2** +```cpp +Input: + 1 + / \ + 2 10 + / \ + 2 15 +Output: false + +``` +**Explanation:** +There is no way to split the tree into two subtrees with equal sums. + + +--- +### Question +Check whether the given tree can be split into two non-empty subtrees with equal sums or not. + +```cpp + 5 + / \ + 10 10 + / \ + 20 3 + / + 8 +``` + +**Choices** +- [x] Yes, It is possible. +- [ ] It is impossible. + + +**Explanation:** + +Yes It is possible to split the tree into two non-empty subtrees with sum 28. + +Sub-Tree 1: +```cpp + 5 + / \ + 10 10 + \ + 3 + +``` + +Sub-Tree 2: +```cpp + 20 + / + 8 +``` + +:::warning +Please take some time to think about the solution approach on your own before reading further..... +::: + +**Solution** + +1. **Total Sum Check**: +If the total sum of all nodes in the binary tree is odd, it is impossible to divide the tree into two subtrees with equal sums. This is because the sum of two equal values is always even, and if the total sum is odd, it cannot be divided equally into two parts. +2. **Subtree Sum Check**: +If we can find a subtree in the binary tree with a sum equal to half of the total sum, we can split the tree into two equal partitions by removing the edge leading to the root of that subtree. This means that we don't necessarily need to compare sums of all possible subtrees, but we can look for a single subtree that meets the subtree sum check condition. + +#### Pseudocode +```cpp +int sum(TreeNode * root) { + if (!root) { + return 0; + } + return sum(root -> left) + sum(root -> right) + root -> val; +} + +bool hasSubtreeWithHalfSum(TreeNode * root, int totalSum) { + if (!root) { + return false; + } + + int leftSum = sum(root -> left); + int rightSum = sum(root -> right); + + if ((leftSum == totalSum / 2 || rightSum == totalSum / 2) || hasSubtreeWithHalfSum(root -> left, totalSum) || hasSubtreeWithHalfSum(root -> right, totalSum)) { + return true; + } + + return false; +} + +bool isEqualTreePartition(TreeNode * root) { + if (!root) { + return false; // An empty tree cannot be partitioned + } + + int totalSum = sum(root); + + if (totalSum % 2 == 1) { + return false; // If the total sum is odd, partition is not possible + } + + return hasSubtreeWithHalfSum(root, totalSum); +} +``` + +#### Complexity +**Time Complexity:** O(N) +**Space Complexity:** O(H) + +--- +### Problem 3 Next Pointer in Binary Tree + +Given a perfect binary tree initially with all next pointers set to nullptr, modify the tree in-place to connect each node's next pointer to the next node in the same level from left to right, following an in-order traversal. + + +**Example** +```cpp +Input: + 1 + / \ + 2 3 + / \ / \ + 4 5 6 7 + +Output : + 1 -> nullptr + / \ + 2 -> 3 -> nullptr + / \ / \ + 4 -> 5 -> 6 -> 7 -> nullptr + +``` + +:::warning +Please take some time to think about the bruteforce approach on your own before reading further..... +::: + +#### Brute force solution +**Level order Traversal** : +1. We check if the binary tree is empty; if so, we return the root since there's nothing to connect. +2. A queue is created for level order traversal, initialized with the root node. +3. In the main loop, we process nodes at the current level. +4. At the start of each level, we determine the number of nodes at the current level (levelSize). +5. In the inner loop, we process each node at the current level: + * We dequeue the current node from the front of the queue. + * If the current node is not the last node in the level (i.e., i < levelSize - 1), we update its next pointer to point to the front of the queue, which connects nodes from left to right within the same level. + * We enqueue the left and right children of the current node (if they exist) into the queue for the next level. +6. The loop continues until all levels are processed. +7. Finally, the function returns the modified root of the binary tree, which now has next pointers connecting nodes at the same level, except for the last node in each level, whose next pointer remains nullptr. + + +#### Pseudocode : +```cpp +Node * connect(Node * root) { + // Check if the tree is empty + if (root is null) { + return null; + } + + // Create a queue and enqueue the root + queue < Node * > q; + q.push(root); + + // Traverse the tree level by level + while (!q.empty()) { + int levelSize = q.size(); + + // Process nodes at the current level + for (int i = 0; i < levelSize; ++i) { + Node * node = q.front(); + q.pop(); + + // Connect the current node to the next node in the same level + if (i < levelSize - 1) { + node -> next = q.front(); + } + + // Enqueue the left and right children (if they exist) for the next level + if (node has a left child) { + q.push(node 's left child); + } + if (node has a right child) { + q.push(node 's right child); + } + } + } + + // Return the modified root + return root; + } +``` + +#### Complexity +**Time Complexity:** O(N) +**Space Complexity:** O(N) + +#### Optimized Solution: +1. We create a dummy node and a temp pointer initially pointing to it. +2. We traverse the tree level by level from left to right. +3. For each node: +* If it has a left child, we connect the temp node's next pointer to the left child and update temp. +* If it has a right child, we connect the temp node's next pointer to the right child and update temp. +4. Level Completion: +5. When the current level is done, we move to the next level by updating root to the dummy node's next. We reset dummy's next and reset temp to the dummy node. +6. We repeat these steps until all levels are traversed. +7. The loop ends when there are no more levels to traverse. + + +#### Pseudocode +```cpp +void populateNextPointers(Node * root) { + if (!root) { + return; + } + + Node * dummy = new Node(-1); + Node * temp = dummy; + + while (root != nullptr) { + if (root -> left != nullptr) { + temp -> next = root -> left; + temp = temp -> next; + } + if (root -> right != nullptr) { + temp -> next = root -> right; + temp = temp -> next; + } + root = root -> next; + if (root == nullptr) { + root = dummy -> next; + dummy -> next = nullptr; + temp = dummy; + } + } +``` + +#### Complexity +**Time Complexity:** O(N) +**Space Complexity:** O(1) + +--- +### Problem 4 Check if Root to Leaf Path Sum Equals to K + +Given a binary tree and an integer k, determine if there exists a root-to-leaf path in the tree such that adding up all the node values along the path equals k. + +Example: +```cpp + +Input: + Binary Tree: + 5 + / \ + 4 8 + / / \ + 11 13 4 + / \ \ + 7 2 1 + + k = 22 + +Output: true +``` +**Explanation**: + +In the given binary tree, there exists a root-to-leaf path 5 -> 4 -> 11 -> 2 with a sum of 5 + 4 + 11 + 2 = 22, which equals k. Therefore, the function should return true. + +--- +### Question +Tell if there exists a root to leaf path with sum value `k = 19` +```cpp + 5 + / \ + 3 7 + / \ + 10 2 + / \ \ + 19 1 5 + + k = 20 + +``` +**Choices** +- [x] true +- [ ] false + + +:::warning +Please take some time to think about the solution approach on your own before reading further..... +::: + +**Solution:** +* To solve this problem,we first check if the current node is a leaf node (having no left and right children) and if the current value equals k. If both conditions are met, it returns true, indicating that a valid path is found. +* If not, it recursively checks the left and right subtrees with a reduced sum (k - root->val). +* It returns true if there's a path in either the left or right subtree, indicating that a valid path is found. + + +#### Pseudocode +```cpp +bool hasPathSum(TreeNode * root, int k) { + if (!root) { + return false; // No path if the tree is empty + } + + if (!root -> left && !root -> right) { + return (k == root -> val); + } + + return hasPathSum(root -> left, k - root -> val) || hasPathSum(root -> right, k - root -> val); +} + +``` + +#### Complexity +**Time Complexity:** O(N) +**Space Complexity:** O(H) + +--- +### Problem 5 Diameter of Binary Tree + + +Given a binary tree, find the length of the longest path between any two nodes in the tree. This path may or may not pass through the root. + +**Definition of Diameter**: The diameter of a binary tree is defined as the number of nodes along the longest path between any two leaf nodes in the tree. This path may or may not pass through the root. + +--- +### Question +How would you find the diameter of a binary tree? + +**Choices** +- [ ] Add the height of the left and right subtrees. +- [ ] Count the number of nodes in the tree. +- [x] The maximum of the following three: Diameter of the left subtree, Diameter of the right subtree, Sum of the heights of the left and right subtrees plus one +- [ ] Divide the height of the tree by 2. + + + +**Example**: +Example that illustrates that the diameter of the tree can pass through a root node. +```cpp +Input: + + 1 + / \ + 2 3 + / \ + 4 5 +Output: 4 +``` +**Explanation**: +The diameter of the binary tree shown above is the path 4 -> 2 -> 1 -> 3, which contains four nodes. + + +**Example:** +Example that illustrates that the diameter of the tree can pass through a non-root node: +```cpp +Input: + 1 + / + 2 + / \ + 4 5 + / \ \ + 6 7 3 + +Output: 5 +``` +**Explanation:** +The diameter of the binary tree shown above is the path 6 - 4 - 2 - 5 - 3, which includes 5 nodes. + + +--- +### Question +What is the diameter of the Given Binary Tree. + +```cpp + 1 + / + 2 + / \ + 4 5 + / \ + 6 7 + \ + 8 + \ + 10 +``` + + +**Choices** +- [x] 6 +- [ ] 5 +- [ ] 7 +- [ ] 4 + + +**Explanation:** + +The path 1 -> 2 -> 4 -> 7 -> 8 -> 10 has 6 nodes, which is the diameter of the given tree. + + +:::warning +Please take some time to think about the solution approach on your own before reading further..... +::: + +**Solution:** +1. To solve this problem,we initialize a diameter variable to 0 to track the maximum diameter. +2. Define a helper function that recursively computes both the height of the tree and the diameter +3. In the helper function: + * If the node is null, we return -1 to signify no height. + * We recursively find left and right subtree heights. + * We update diameter with the maximum diameter found, including the current node and connecting path (2 units). + * The height of the current node is the max of left and right subtree heights, plus 1. + * Call the helper function with the root of the binary tree from the main function or method. +4. Retrieve and use the maximum diameter found during traversal as the result. + +#### Pseudocode: +```cpp +int diameterOfBinaryTree(TreeNode * root) { + int diameter = 0; + + // Helper function to calculate height and update diameter + std:: function < int(TreeNode * ) > calculateHeight = [ & ](TreeNode * node) { + if (!node) { + return -1; // Height of a null node is -1 + } + + int leftHeight = calculateHeight(node -> left); + int rightHeight = calculateHeight(node -> right); + + // Update diameter with the current node's diameter + diameter = std::max(diameter, leftHeight + rightHeight + 2); + + // Return the height of the current node + return std::max(leftHeight, rightHeight) + 1; + }; + + calculateHeight(root); // Start the recursive calculation + + return diameter; +} + +``` + +#### Complexity +**Time Complexity:** O(N) +**Space Complexity:** O(H) diff --git a/Academy DSA Typed Notes/Advanced/DSA Two Pointers.md b/Academy DSA Typed Notes/Advanced/DSA Two Pointers.md new file mode 100644 index 0000000..a40a9fd --- /dev/null +++ b/Academy DSA Typed Notes/Advanced/DSA Two Pointers.md @@ -0,0 +1,645 @@ +# Two Pointers + +--- +## Problem 1 Pairs with given sum 2 + +*Given an integer sorted array `A` and an integer `k`, find any pair (i, j) such that `A[i] + A[j] = k`, `i != j`.* + + +**Example**: +A = [-5, -2, 1, 8, 10, 12, 15] +k = 11 + +Ans: (2, 4) as A[2] + A[4] = 1 + 10 = 11 = k + + + +--- +### Question +Check if there exists a pair with sum k +`A [ ] = { -3, 0, 1, 3, 6, 8, 11, 14, 18, 25 }` +`k = 12` + +**Choices** +- [x] Yes +- [ ] No + +**Explanation:** + +Yes. Because there are 2 pairs with sum as 11, They are +- (1, 11) +- (3, 8) +--- + +:::warning +Please take some time to think about the solution approach on your own before reading further..... +::: +### Pairs with given sum 2 Approaches + + +#### Brute Force Apporach: +*Run two for loops and for every indices: i, j, check if sum is k.* + +- **Time Complexity:** +
 , as we need to use two for loops.
+- **Space Complexity:**
+O(1), as no additional space is required.
+
+#### Binary Search Apporach
+**Observation**:
+- We need to find two elements whose sum is `k`, i.e., `A[i] + A[j] == k`.
+- So, `A[j] = k - A[i]`. Essentially, for an element, `A[i]`, we need to find an element `k - A[i]`.
+- Since, array `A` is sorted, we can use binary search to find the element `k - A[i]`. (make sure, we are not choosing the same index again)
+
+**Approach**: *For all `i`, binary search and find `k - A[i]`.*
+
+- **Time Complexity:**
+O(N * log(N)), as we need to apply binary search for every element in the worst case.
+- **Space Complexity:**
+O(1), as no additional space is required.
+
+
+
+---
+### Pairs with given sum 2 Two Pointers Approach
+
+Let's keep two pointers, `i` and `j` and we put them at 0 and 1st idx.
+
+We have, A = {-5, -2, 1, 8, 10, 12, 15} and k = 11
+
+If A[0] = A[i] = -5 and A[1] = A[j] = -2
+A[i] + A[j] = -5 + (-2) = -7
+So, **A[i] + A[j] < k**
+
+To achieve the sum as `k`, we have to either increase i or j as the array is sorted.
+
+Now, if A[5] = A[i] = 12 and A[6] = A[j] = 15
+A[i] + A[j] = 12 + 15 = 27
+So, **A[i] + A[j] > k**
+
+In this case, to achieve `k`, we have to either decrease i or j. *Why?*
+
+> Essentially, we want to decrease the sum. The sum can be decreased by decreasing A[i] or A[j]. Since array is sorted, decrease the pointers will decrease the value as well.
+
+*Where should we place the pointers initially?*
+
+Initially, the pointers should be place at the beginning and end of the array as this way, we will have only one pointer in option to move in order to increase / decrease the sum.
+
+**Step 1:**
+So, if we take A[i] = A[0] and A[j] = A[6] then,
+A[i] + A[j] = A[0] + A[6] = -5 + 15 = 10 < k. So, we need to increase the sum. Which pointer should we move?
+
+Observations:
+- This implies `-5 + largest element` is less than `k`. Therefore, `-5 + any element of A` will always be less than `k`. So, we do not need to check `-5` with any other number as the array is sorted.
+- Hence, we should increase the `i` pointer to increase the sum.
+
+> **Note:** Our motive here is to eliminate the elements one by one till we reach towards the elements who can build the required sum. Since, `-5 + largset element < k`, we can safely eliminate `-5`.
+
+**Step 2:**
+Now, taking A[i] = A[1] = -2 and A[j] = A[6] = 15
+A[i] + A[j] = -2 + 15 = 13
+Here, **A[i] + A[j] > k**
+Following the same approach, we should decrease the index of j to decrease the sum. As decreasing the `i` would take us to the Step 1.
+
+**Step 3:**
+Now, taking A[i] = A[1] = -2 and A[j] = A[5] = 12
+A[i] + A[j] = -2 + 12 = 10
+Here **A[i] + A[j] < k**
+Following the same approach, we should increase the index of i to increase the sum.
+
+**Step 4:**
+Similary, taking A[i] = A[2] = 1 and A[j] = A[5] = 10
+A[i] + A[j] = 1 + 10
+Here, **A[i] + A[j] = k**.
+
+#### Pseudocode:
+
+```java
+while (i < j) {
+ if (A[i] + A[j] == k) {
+ return (i, j);
+ } else if (A[i] + A[j] < k) {
+ i++;
+ } else {
+ j--;
+ }
+}
+```
+
+- **Time Complexity:**
+O(N), as we need to traverse the complete array once in the worst case.
+- **Space Complexity:**
+O(1), as no additional space is required.
+
+---
+### Problem 2 Count Pair Sum K
+
+
+Find all the pairs in a sorted array whose sum is k.
+
+**Example:**
+A = {1, 2, 3, 4, 5, 6, 8}
+k = 10
+
+**Ans:** (2, 8), (4, 6)
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Two Pointer Approach:
+**`Case 1: When elements are distinct`**
+- Use two pointer approach to find the first pair whose sum is 10.
+- For array `A`, it will be (2, 8).
+- As the elements are distinct, neither 2 nor 8 can make pair with any other pair whose sum is 10. So, increase the pointer `i` and decrease the pointer `j` and continue finding the pair whose sum is 10.
+- The next pair with this approach would be (4, 6). Similary, move the pointers in required direction to find another pairs.
+- Since, there aren't any more pairs. The final result would be: (2, 8) and (4, 6).
+
+**`Pseudocode:`**
+```java
+count = 0;
+while (i < j) {
+ if (A[i] + A[j] == k) {
+ count++;
+ i++, j--;
+ } else if (A[i] + A[j] < k) {
+ i++;
+ } else {
+ j--;
+ }
+}
+return count;
+```
+
+**`Case 2: When elements are repeating (duplicates)`**
+- **Using Frequency Array:**
+ - Consider the array, ( A = {2, 3, 3, 10, 10, 10, 15} ) with a target sum ( k = 13 ).
+ - Let's create the frequency map for the above. It would be - map ={[2 => 1], [3 => 2], [10 => 3], [15 => 1]}
+ - Now, create an array (A' = {2, 3, 10, 15}) by taking only the unique elements from array (A).
+ - Find the pair that contributes to the sum (13) in array (A'). The pair in this case would be (3, 10).
+ - The frequency of (3) is (2) and the frequency of (10) is (3) in the original array. So, the total number of such pairs in the original array would be ( 2 * 3 = 6).
+ - The key idea here is to transform the array with duplicate elements into an array of unique elements, find all the unique pairs that sum up to the target sum, and then use the frequencies of the elements in the original array to determine the count of all such pairs.
+
+- **Without using frequency array:**
+ - Consider array, A = {2, 3, 3, 5, 5, 7, 7, 10, 10, 10, 15} and k = 13
+ - Find the pair whose sum is equal to k. In this case, (3, 10).
+ - Now, count the number of 3s and 10s and multiply them to find the effective number of pairs, i.e., 2 * 3 = 6.
+ - Change the position of i and j to next of last occurred 3 and 10, and continue the process.
+ - Final result would be 6.
+
+**`Pseudocode:`**
+```javascript
+count = 0;
+while (i < j) {
+ if (A[i] + A[j] == k) {
+ counti = 1, countj = 1;
+ while (i < j && A[i] == A[i + 1]) {
+ counti++;
+ i++;
+ }
+
+ while (i < j && A[j] == A[j - 1]) {
+ countj++;
+ j--;
+ }
+
+ count = counti * countj;
+ i++, j--;
+ } else if (A[i] + A[j] < k) {
+ i++;
+ } else {
+ j--;
+ }
+}
+print(count)
+```
+
+---
+### Problem 3 Pair Difference K
+
+Given a sorted integer array A and an integer k. Find any pair (i, j) such that A[j] - A[i] = k, i != j and k > 0.
+
+Note: 0-based indexing
+**Example:**
+A[] =
+
+| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
+|-------|---|---|---|---|---|---|---|
+| Value | -5 | -2 | 1 | 8 | 10 | 12 | 15 |
+
+k = 11
+
+Ans: (2, 5) as A[5] - A[2] = 12 - 1 = 11 = k.
+
+
+#### Brute Force Apporach:
+*Run two for loops and for every indices: i, j, check if difference is k.*
+
+- **Time Complexity:**
+
, as we need to use two for loops.
+- **Space Complexity:**
+O(1), as no additional space is required.
+
+#### Binary Search Apporach
+**Observation**:
+- We need to find two elements whose sum is `k`, i.e., `A[i] + A[j] == k`.
+- So, `A[j] = k - A[i]`. Essentially, for an element, `A[i]`, we need to find an element `k - A[i]`.
+- Since, array `A` is sorted, we can use binary search to find the element `k - A[i]`. (make sure, we are not choosing the same index again)
+
+**Approach**: *For all `i`, binary search and find `k - A[i]`.*
+
+- **Time Complexity:**
+O(N * log(N)), as we need to apply binary search for every element in the worst case.
+- **Space Complexity:**
+O(1), as no additional space is required.
+
+
+
+---
+### Pairs with given sum 2 Two Pointers Approach
+
+Let's keep two pointers, `i` and `j` and we put them at 0 and 1st idx.
+
+We have, A = {-5, -2, 1, 8, 10, 12, 15} and k = 11
+
+If A[0] = A[i] = -5 and A[1] = A[j] = -2
+A[i] + A[j] = -5 + (-2) = -7
+So, **A[i] + A[j] < k**
+
+To achieve the sum as `k`, we have to either increase i or j as the array is sorted.
+
+Now, if A[5] = A[i] = 12 and A[6] = A[j] = 15
+A[i] + A[j] = 12 + 15 = 27
+So, **A[i] + A[j] > k**
+
+In this case, to achieve `k`, we have to either decrease i or j. *Why?*
+
+> Essentially, we want to decrease the sum. The sum can be decreased by decreasing A[i] or A[j]. Since array is sorted, decrease the pointers will decrease the value as well.
+
+*Where should we place the pointers initially?*
+
+Initially, the pointers should be place at the beginning and end of the array as this way, we will have only one pointer in option to move in order to increase / decrease the sum.
+
+**Step 1:**
+So, if we take A[i] = A[0] and A[j] = A[6] then,
+A[i] + A[j] = A[0] + A[6] = -5 + 15 = 10 < k. So, we need to increase the sum. Which pointer should we move?
+
+Observations:
+- This implies `-5 + largest element` is less than `k`. Therefore, `-5 + any element of A` will always be less than `k`. So, we do not need to check `-5` with any other number as the array is sorted.
+- Hence, we should increase the `i` pointer to increase the sum.
+
+> **Note:** Our motive here is to eliminate the elements one by one till we reach towards the elements who can build the required sum. Since, `-5 + largset element < k`, we can safely eliminate `-5`.
+
+**Step 2:**
+Now, taking A[i] = A[1] = -2 and A[j] = A[6] = 15
+A[i] + A[j] = -2 + 15 = 13
+Here, **A[i] + A[j] > k**
+Following the same approach, we should decrease the index of j to decrease the sum. As decreasing the `i` would take us to the Step 1.
+
+**Step 3:**
+Now, taking A[i] = A[1] = -2 and A[j] = A[5] = 12
+A[i] + A[j] = -2 + 12 = 10
+Here **A[i] + A[j] < k**
+Following the same approach, we should increase the index of i to increase the sum.
+
+**Step 4:**
+Similary, taking A[i] = A[2] = 1 and A[j] = A[5] = 10
+A[i] + A[j] = 1 + 10
+Here, **A[i] + A[j] = k**.
+
+#### Pseudocode:
+
+```java
+while (i < j) {
+ if (A[i] + A[j] == k) {
+ return (i, j);
+ } else if (A[i] + A[j] < k) {
+ i++;
+ } else {
+ j--;
+ }
+}
+```
+
+- **Time Complexity:**
+O(N), as we need to traverse the complete array once in the worst case.
+- **Space Complexity:**
+O(1), as no additional space is required.
+
+---
+### Problem 2 Count Pair Sum K
+
+
+Find all the pairs in a sorted array whose sum is k.
+
+**Example:**
+A = {1, 2, 3, 4, 5, 6, 8}
+k = 10
+
+**Ans:** (2, 8), (4, 6)
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Two Pointer Approach:
+**`Case 1: When elements are distinct`**
+- Use two pointer approach to find the first pair whose sum is 10.
+- For array `A`, it will be (2, 8).
+- As the elements are distinct, neither 2 nor 8 can make pair with any other pair whose sum is 10. So, increase the pointer `i` and decrease the pointer `j` and continue finding the pair whose sum is 10.
+- The next pair with this approach would be (4, 6). Similary, move the pointers in required direction to find another pairs.
+- Since, there aren't any more pairs. The final result would be: (2, 8) and (4, 6).
+
+**`Pseudocode:`**
+```java
+count = 0;
+while (i < j) {
+ if (A[i] + A[j] == k) {
+ count++;
+ i++, j--;
+ } else if (A[i] + A[j] < k) {
+ i++;
+ } else {
+ j--;
+ }
+}
+return count;
+```
+
+**`Case 2: When elements are repeating (duplicates)`**
+- **Using Frequency Array:**
+ - Consider the array, ( A = {2, 3, 3, 10, 10, 10, 15} ) with a target sum ( k = 13 ).
+ - Let's create the frequency map for the above. It would be - map ={[2 => 1], [3 => 2], [10 => 3], [15 => 1]}
+ - Now, create an array (A' = {2, 3, 10, 15}) by taking only the unique elements from array (A).
+ - Find the pair that contributes to the sum (13) in array (A'). The pair in this case would be (3, 10).
+ - The frequency of (3) is (2) and the frequency of (10) is (3) in the original array. So, the total number of such pairs in the original array would be ( 2 * 3 = 6).
+ - The key idea here is to transform the array with duplicate elements into an array of unique elements, find all the unique pairs that sum up to the target sum, and then use the frequencies of the elements in the original array to determine the count of all such pairs.
+
+- **Without using frequency array:**
+ - Consider array, A = {2, 3, 3, 5, 5, 7, 7, 10, 10, 10, 15} and k = 13
+ - Find the pair whose sum is equal to k. In this case, (3, 10).
+ - Now, count the number of 3s and 10s and multiply them to find the effective number of pairs, i.e., 2 * 3 = 6.
+ - Change the position of i and j to next of last occurred 3 and 10, and continue the process.
+ - Final result would be 6.
+
+**`Pseudocode:`**
+```javascript
+count = 0;
+while (i < j) {
+ if (A[i] + A[j] == k) {
+ counti = 1, countj = 1;
+ while (i < j && A[i] == A[i + 1]) {
+ counti++;
+ i++;
+ }
+
+ while (i < j && A[j] == A[j - 1]) {
+ countj++;
+ j--;
+ }
+
+ count = counti * countj;
+ i++, j--;
+ } else if (A[i] + A[j] < k) {
+ i++;
+ } else {
+ j--;
+ }
+}
+print(count)
+```
+
+---
+### Problem 3 Pair Difference K
+
+Given a sorted integer array A and an integer k. Find any pair (i, j) such that A[j] - A[i] = k, i != j and k > 0.
+
+Note: 0-based indexing
+**Example:**
+A[] =
+
+| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
+|-------|---|---|---|---|---|---|---|
+| Value | -5 | -2 | 1 | 8 | 10 | 12 | 15 |
+
+k = 11
+
+Ans: (2, 5) as A[5] - A[2] = 12 - 1 = 11 = k.
+
+
+#### Brute Force Apporach:
+*Run two for loops and for every indices: i, j, check if difference is k.*
+
+- **Time Complexity:**
+ , as we need to use two for loops.
+- **Space Complexity:**
+O(1), as no additional space is required.
+
+#### Binary Search Apporach
+*For all `i`, binary search and find `k + A[i]`.*
+
+- **Time Complexity:**
+O(N * log(N)), as we need to apply binary search for every element in the worst case.
+- **Space Complexity:**
+O(1), as no additional space is required.
+
+
+
+---
+
+### Question
+Given an array A is **[5, 4, 2, 12, 1, 6]** and K is 10.
+
+Find any pair `(i, j)` such that
+* A[j] - A[i] = k
+* i != j
+
+Note: 0-based indexing
+**Choices**
+- [x] (2, 3)
+- [ ] (5, 5)
+- [ ] (0, 0)
+- [ ] (3, 2)
+
+**Explanation:**
+
+The answer is (2, 3).
+
+Since (2, 3) satisfies both the condition:
+* A[3] - A[2] = 10
+* 3 != 2
+
+
+---
+### Pair Difference K Two Pointers Apporach
+
+We have, A[] =
+| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
+|-------|---|---|---|---|---|---|---|
+| Value | -5 | -2 | 1 | 8 | 10 | 12 | 15 |
+
+and k = 11
+
+*Where should we keep the pointers?*
+
+**Option 1:**
+Let's start with keeping the pointers, `i` and `j` at the beginning and end of the array respectively, i.e., `i` = 0 and `j` = `N - 1` = 6.
+
+Observations:
+- A[j] - A[i] = 15 - (-5) = 20 > k(11). So, to decrease the difference we need to either decrease A[j] or increase A[i].
+- We know that, either we can increase pointer `i` or decrease pointer `j`. Increasing pointer `i` will increase the `A[i]` and similarly, decreasing pointer `j` will decrease the `A[j]`.
+- Since we do not have a single direction to move, we cannot eliminate any element. Therefore, placing the pointers at the beginning and the end isn't helpful.
+
+
+**Option 2:**
+Let's now place the pointers at (N - 2) and (N - 1) indices, i.e., i = N - 2 = 5 and j = N - 1 = 6.
+
+Observations:
+- A[i] = A[5] = 12 and A[j] = A[6] = 15. A[j] - A[i] = A[6] - A[5] = 15 - 12 = 3. Therefore, **A[j] - A[i] < k**
+- Here, we either need to increase A[j] or decrease A[i]. To increase A[j], j should be increased but it isn't possible as j is already pointing to the last element. So, we can decrease i.
+- Doing so will eliminate the 12 to be possible second value of the pair. This is true because from here, we can conclude that the `largest element - A[i] < k`. So, `any element - A[i] < k` because the array is sorted.
+- Thus, N - 2 and N - 1 are the correct possible initial values of pointers.
+
+
+Similary result can be obtained by starting with index 0 and 1.
+So, let's place the pointers at 0 and 1 indices, i.e., i = 0 and j = 1.
+
+**Step 1: i = 0, j = 1**
+- A[i] = A[0] = -5 and A[j] = A[1] = -2. A[j] - A[i] = A[1] - A[0] = -2 - (-5) = 3. Therefore, **A[j] - A[i] < k**
+- Here, we either need to increase A[j] or decrease A[i]. To decrease A[i], i should be decreased but it isn't possible as i is already pointing to the first element. So, we can increase j.
+
+**Step 2: i = 0, j = 2**
+- A[i] = A[0] = -5 and A[j] = A[2] = 1. A[j] - A[i] = A[2] - A[0] = 1 - (-5) = 6. Therefore, **A[j] - A[i] < k**
+- Similarly, increasing j.
+
+**Step 3: i = 0, j = 3**
+- A[i] = A[0] = -5 and A[j] = A[3] = 8. A[j] - A[i] = A[3] - A[0] = 8 - (-5) = 13. Therefore, **A[j] - A[i] > k**.
+- Since difference is greater than k, we need to decrease A[j] or increase A[i]. Hence, increasing i to increase A[i].
+
+**Step 4: i = 1, j = 3**
+- A[i] = A[1] = -2 and A[j] = A[3] = 8. A[j] - A[i] = A[3] - A[0] = 8 - (-2) = 10. Therefore, **A[j] - A[i] < k**.
+- Since difference is less than k, we need to increase A[j] or decrease A[i]. Hence, increasing j to increase A[j].
+
+**Step 5: i = 1, j = 4**
+- A[i] = A[1] = -2 and A[j] = A[4] = 10. A[j] - A[i] = A[4] - A[0] = 10 - (-2) = 12. Therefore, **A[j] - A[i] > k**.
+- Since difference is greater than k, we need to decrease A[j] or increase A[i]. Hence, increasing i to increase A[i].
+
+**Step 6: i = 2, j = 4**
+- A[i] = A[2] = 1 and A[j] = A[4] = 10. A[j] - A[i] = A[4] - A[0] = 10 - 1 = 9. Therefore, **A[j] - A[i] < k**.
+- Since difference is less than k, we need to increase A[j] or decrease A[i]. Hence, increasing j to increase A[j].
+
+**Step 7: i = 2, j = 5**
+- A[i] = A[2] = 1 and A[j] = A[5] = 12. A[j] - A[i] = A[5] - A[0] = 12 - 1 = 11. Finally, **A[j] - A[i] = k**.
+- Required pair: (i, j) = (2, 5).
+
+#### Pseudocode:
+```java
+i = 0, j = 1
+while (j < n) {
+ diff = A[j] - A[i];
+ if (diff == k) {
+ return (i, j);
+ } else if (diff < k) {
+ j++;
+ } else {
+ i--;
+ }
+}
+```
+
+*Why the `while` loop condition should be `j < n` and not `i < n`?*
+
+It is based on assumption that `i` will always be <= `j`.
+Proof:
+Suppose we start with `i = 0`, `j = 1` and after some steps `j` reaches `x`.
+To `i` cross `j`, `i` should first reach `j`. When `i` reaches `j`, then `diff = 0`. It is given that `k > 0`, so in order to achieve this, `j` should be increased, and hence `i` can never exceed `j`.
+
+
+- **Time Complexity:**
+O(N), as we need to traverse the complete array once in the worst case.
+- **Space Complexity:**
+O(1), as no additional space is required.
+
+---
+### Problem 4 Check subarray with sum k
+
+Given an integer array `A` and an integer `k`. Check if there exists a subarray with sum `k`
+
+**Example:**
+A = {1, 3, 15, 10, 20, 3, 23}; k = 33
+
+**Ans:** True, because {10, 20, 3} sums upto 33.
+
+A = {1, 3, 15, 10, 20, 3, 23}; k = 43
+
+**Ans:** False, because no subarray exists that sums upto 43
+
+> Number of subarrays in an array of length n is `n * (n + 1) / 2`.
+
+
+#### Brute Force Apporach:
+*Check every subarray sum (with carry forward approach)*
+
+- **Time Complexity:**
+
, as we need to use two for loops.
+- **Space Complexity:**
+O(1), as no additional space is required.
+
+#### Binary Search Apporach
+*For all `i`, binary search and find `k + A[i]`.*
+
+- **Time Complexity:**
+O(N * log(N)), as we need to apply binary search for every element in the worst case.
+- **Space Complexity:**
+O(1), as no additional space is required.
+
+
+
+---
+
+### Question
+Given an array A is **[5, 4, 2, 12, 1, 6]** and K is 10.
+
+Find any pair `(i, j)` such that
+* A[j] - A[i] = k
+* i != j
+
+Note: 0-based indexing
+**Choices**
+- [x] (2, 3)
+- [ ] (5, 5)
+- [ ] (0, 0)
+- [ ] (3, 2)
+
+**Explanation:**
+
+The answer is (2, 3).
+
+Since (2, 3) satisfies both the condition:
+* A[3] - A[2] = 10
+* 3 != 2
+
+
+---
+### Pair Difference K Two Pointers Apporach
+
+We have, A[] =
+| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
+|-------|---|---|---|---|---|---|---|
+| Value | -5 | -2 | 1 | 8 | 10 | 12 | 15 |
+
+and k = 11
+
+*Where should we keep the pointers?*
+
+**Option 1:**
+Let's start with keeping the pointers, `i` and `j` at the beginning and end of the array respectively, i.e., `i` = 0 and `j` = `N - 1` = 6.
+
+Observations:
+- A[j] - A[i] = 15 - (-5) = 20 > k(11). So, to decrease the difference we need to either decrease A[j] or increase A[i].
+- We know that, either we can increase pointer `i` or decrease pointer `j`. Increasing pointer `i` will increase the `A[i]` and similarly, decreasing pointer `j` will decrease the `A[j]`.
+- Since we do not have a single direction to move, we cannot eliminate any element. Therefore, placing the pointers at the beginning and the end isn't helpful.
+
+
+**Option 2:**
+Let's now place the pointers at (N - 2) and (N - 1) indices, i.e., i = N - 2 = 5 and j = N - 1 = 6.
+
+Observations:
+- A[i] = A[5] = 12 and A[j] = A[6] = 15. A[j] - A[i] = A[6] - A[5] = 15 - 12 = 3. Therefore, **A[j] - A[i] < k**
+- Here, we either need to increase A[j] or decrease A[i]. To increase A[j], j should be increased but it isn't possible as j is already pointing to the last element. So, we can decrease i.
+- Doing so will eliminate the 12 to be possible second value of the pair. This is true because from here, we can conclude that the `largest element - A[i] < k`. So, `any element - A[i] < k` because the array is sorted.
+- Thus, N - 2 and N - 1 are the correct possible initial values of pointers.
+
+
+Similary result can be obtained by starting with index 0 and 1.
+So, let's place the pointers at 0 and 1 indices, i.e., i = 0 and j = 1.
+
+**Step 1: i = 0, j = 1**
+- A[i] = A[0] = -5 and A[j] = A[1] = -2. A[j] - A[i] = A[1] - A[0] = -2 - (-5) = 3. Therefore, **A[j] - A[i] < k**
+- Here, we either need to increase A[j] or decrease A[i]. To decrease A[i], i should be decreased but it isn't possible as i is already pointing to the first element. So, we can increase j.
+
+**Step 2: i = 0, j = 2**
+- A[i] = A[0] = -5 and A[j] = A[2] = 1. A[j] - A[i] = A[2] - A[0] = 1 - (-5) = 6. Therefore, **A[j] - A[i] < k**
+- Similarly, increasing j.
+
+**Step 3: i = 0, j = 3**
+- A[i] = A[0] = -5 and A[j] = A[3] = 8. A[j] - A[i] = A[3] - A[0] = 8 - (-5) = 13. Therefore, **A[j] - A[i] > k**.
+- Since difference is greater than k, we need to decrease A[j] or increase A[i]. Hence, increasing i to increase A[i].
+
+**Step 4: i = 1, j = 3**
+- A[i] = A[1] = -2 and A[j] = A[3] = 8. A[j] - A[i] = A[3] - A[0] = 8 - (-2) = 10. Therefore, **A[j] - A[i] < k**.
+- Since difference is less than k, we need to increase A[j] or decrease A[i]. Hence, increasing j to increase A[j].
+
+**Step 5: i = 1, j = 4**
+- A[i] = A[1] = -2 and A[j] = A[4] = 10. A[j] - A[i] = A[4] - A[0] = 10 - (-2) = 12. Therefore, **A[j] - A[i] > k**.
+- Since difference is greater than k, we need to decrease A[j] or increase A[i]. Hence, increasing i to increase A[i].
+
+**Step 6: i = 2, j = 4**
+- A[i] = A[2] = 1 and A[j] = A[4] = 10. A[j] - A[i] = A[4] - A[0] = 10 - 1 = 9. Therefore, **A[j] - A[i] < k**.
+- Since difference is less than k, we need to increase A[j] or decrease A[i]. Hence, increasing j to increase A[j].
+
+**Step 7: i = 2, j = 5**
+- A[i] = A[2] = 1 and A[j] = A[5] = 12. A[j] - A[i] = A[5] - A[0] = 12 - 1 = 11. Finally, **A[j] - A[i] = k**.
+- Required pair: (i, j) = (2, 5).
+
+#### Pseudocode:
+```java
+i = 0, j = 1
+while (j < n) {
+ diff = A[j] - A[i];
+ if (diff == k) {
+ return (i, j);
+ } else if (diff < k) {
+ j++;
+ } else {
+ i--;
+ }
+}
+```
+
+*Why the `while` loop condition should be `j < n` and not `i < n`?*
+
+It is based on assumption that `i` will always be <= `j`.
+Proof:
+Suppose we start with `i = 0`, `j = 1` and after some steps `j` reaches `x`.
+To `i` cross `j`, `i` should first reach `j`. When `i` reaches `j`, then `diff = 0`. It is given that `k > 0`, so in order to achieve this, `j` should be increased, and hence `i` can never exceed `j`.
+
+
+- **Time Complexity:**
+O(N), as we need to traverse the complete array once in the worst case.
+- **Space Complexity:**
+O(1), as no additional space is required.
+
+---
+### Problem 4 Check subarray with sum k
+
+Given an integer array `A` and an integer `k`. Check if there exists a subarray with sum `k`
+
+**Example:**
+A = {1, 3, 15, 10, 20, 3, 23}; k = 33
+
+**Ans:** True, because {10, 20, 3} sums upto 33.
+
+A = {1, 3, 15, 10, 20, 3, 23}; k = 43
+
+**Ans:** False, because no subarray exists that sums upto 43
+
+> Number of subarrays in an array of length n is `n * (n + 1) / 2`.
+
+
+#### Brute Force Apporach:
+*Check every subarray sum (with carry forward approach)*
+
+- **Time Complexity:**
+ , as we need to use two for loops.
+- **Space Complexity:**
+O(1), as no additional space is required.
+
+
+
+---
+### Question
+If the given array is [1, 2, 5, 4, 3] and k is 9, does there exist a subarray with sum k?
+
+**Choices**
+- [ ] Not Exist
+- [x] Exist
+
+**Explanation:**
+
+Exist. The subarray is [5, 4].
+
+---
+
+:::warning
+Please take some time to think about the optimised approach on your own before reading further.....
+:::
+
+### Check subarray with sum k Two Pointers Approach
+
+Given A = {1, 3, 15, 10, 20, 3, 23}, k = 33. Let's create prefix sum array for this: Pf = {1, 4, 19, 29, 49, 52, 75}.
+
+> `sum(i, j)` =
+> `Pf[j] - Pf[i - 1]`, if `i > 0`
+> `Pf[j]`, if `i = 0`
+- To find the subarray with sum `k`, we can utilize the prefix sum array.
+- For all `j`, if we check `Pf[j]`, essentially, we have checked all the subarrays starting from 0. On the same line, if we check for `Pf[j] - Pf[i - 1]`, we checked for every other subarray which doesn't starts with 0 in the array.
+- Hence, we need to find the values of `i` and `j` for which `Pf[j] - Pf[i - 1] = k`. This is equivalent to *finding a pair in a sorted array whose difference is `k`*.
+
+> Prefix sum array is always sorted for positive integer array as the sum of every next subarray is increasing.
+
+
+- **Time Complexity:** O(N)
+ - Creating prefix sum array takes O(N) time.
+ - Using two pointers approach to find the pair having diff as `k` also takes O(N).
+
+- **Space Complexity:**
+O(1), as no additional space is required if we use same array to create prefix sum array.
+
+
+#### Dynamic Sliding Window Approach:
+*We can maintain a running sum based on the pointers position and check if it is equal to `k`.*
+
+Example:
+
+ A = {1, 3, 15, 10, 20, 3, 23, 33, 43}, k = 33
+
+**Step 1:** i = 0, j = 0
+- `sum(i, j) = sum(0, 0) = A[0] = 1 < k`. To increase the sum, we need to increase the length of subarray, so `j++`.
+
+**Step 2:** i = 0, j = 1
+- `sum(i, j) = sum(0, 1) = A[0] + A[1] = 1 + 3 = 4 < k`. To increase the sum, we need to increase the length of subarray, so `j++`.
+
+**Step 3:** i = 0, j = 2
+- `sum(i, j) = sum(0, 2) = A[0] + A[1] + A[2] = 1 + 3 + 15 = 19 < k`. To increase the sum, we need to increase the length of subarray, so `j++`.
+
+**Step 4:** i = 0, j = 3
+- `sum(i, j) = sum(0, 3) = A[0] + A[1] + A[2] + A[3] = 1 + 3 + 15 + 10 = 29 < k`. To increase the sum, we need to increase the length of subarray, so `j++`.
+
+**Step 5:** i = 0, j = 4
+- `sum(i, j) = sum(0, 4) = A[0] + A[1] + A[2] + A[3] + A[4] = 1 + 3 + 15 + 10 + 20 = 49 > k`. To decrease the sum, we need to decrease the length of subarray. This can either be done by `i++` or `j--`. If we do `j--`, we will be at the same stage at step 4, which isn't helpful. So, we need to do `i++` to decrease the length and effectively the sum.
+
+**Step 6:** i = 1, j = 4
+- `sum(i, j) = sum(1, 4) = A[1] + A[2] + A[3] + A[4] = 3 + 15 + 10 + 20 = 48 > k`. Again, we need to decrease the length to decrease the sum.
+
+*What shall we do here: `i++` or `j--`?*
+We know that, sum (0, 3) < k. Therefore, sum(1, 3) will definitely be less than k. Therefore, `i++` is correct way out here.
+
+**Step 7:** i = 2, j = 4
+- `sum(i, j) = sum(2, 4) = A[2] + A[3] + A[4] = 15 + 10 + 20 = 45 > k`. Again, we need to decrease the length to decrease the sum. As discussed above, do `i++`.
+
+**Step 8:** i = 3, j = 4
+- `sum(i, j) = sum(3, 4) = A[3] + A[4] = 10 + 20 = 30 < k`. To increase the array length, do `j++`.
+
+**Step 9:** i = 3, j = 5
+- `sum(i, j) = sum(3, 5) = A[3] + A[4] + A[5] = 10 + 20 + 3 = 33 = k`. We have found the required subarray.
+
+
+#### Pseudocode
+```java
+i = 0, j = 0, sum = A[0]
+
+while (j < n) {
+ if (sum == k) {
+ return true;
+ } else if (sum < k) {
+ j++;
+ if (j == n) { // To make sure index is not out of bounds
+ break;
+ }
+
+ sum += A[j];
+ } else {
+ sum -= A[i];
+ i++;
+ if (i > j) { // To make sure i never exceeds j
+ break;
+ }
+ }
+}
+
+return false;
+```
+
+- **Time Complexity:**
+O(N), as in the worst case, complete array will be traversed.
+- **Space Complexity:**
+O(1), as no additional space is required if we use same array to create prefix array.
+
+---
+### Problem 5 Container with most Water
+
+Given an integer array `A` where array elements represent the height of the wall. Find any two walls that can form a container to store the maximum amount of water.
+
+**Example:**
+A = {4, 2, 10, 6, 8, 2, 6, 2}
+
+
, as we need to use two for loops.
+- **Space Complexity:**
+O(1), as no additional space is required.
+
+
+
+---
+### Question
+If the given array is [1, 2, 5, 4, 3] and k is 9, does there exist a subarray with sum k?
+
+**Choices**
+- [ ] Not Exist
+- [x] Exist
+
+**Explanation:**
+
+Exist. The subarray is [5, 4].
+
+---
+
+:::warning
+Please take some time to think about the optimised approach on your own before reading further.....
+:::
+
+### Check subarray with sum k Two Pointers Approach
+
+Given A = {1, 3, 15, 10, 20, 3, 23}, k = 33. Let's create prefix sum array for this: Pf = {1, 4, 19, 29, 49, 52, 75}.
+
+> `sum(i, j)` =
+> `Pf[j] - Pf[i - 1]`, if `i > 0`
+> `Pf[j]`, if `i = 0`
+- To find the subarray with sum `k`, we can utilize the prefix sum array.
+- For all `j`, if we check `Pf[j]`, essentially, we have checked all the subarrays starting from 0. On the same line, if we check for `Pf[j] - Pf[i - 1]`, we checked for every other subarray which doesn't starts with 0 in the array.
+- Hence, we need to find the values of `i` and `j` for which `Pf[j] - Pf[i - 1] = k`. This is equivalent to *finding a pair in a sorted array whose difference is `k`*.
+
+> Prefix sum array is always sorted for positive integer array as the sum of every next subarray is increasing.
+
+
+- **Time Complexity:** O(N)
+ - Creating prefix sum array takes O(N) time.
+ - Using two pointers approach to find the pair having diff as `k` also takes O(N).
+
+- **Space Complexity:**
+O(1), as no additional space is required if we use same array to create prefix sum array.
+
+
+#### Dynamic Sliding Window Approach:
+*We can maintain a running sum based on the pointers position and check if it is equal to `k`.*
+
+Example:
+
+ A = {1, 3, 15, 10, 20, 3, 23, 33, 43}, k = 33
+
+**Step 1:** i = 0, j = 0
+- `sum(i, j) = sum(0, 0) = A[0] = 1 < k`. To increase the sum, we need to increase the length of subarray, so `j++`.
+
+**Step 2:** i = 0, j = 1
+- `sum(i, j) = sum(0, 1) = A[0] + A[1] = 1 + 3 = 4 < k`. To increase the sum, we need to increase the length of subarray, so `j++`.
+
+**Step 3:** i = 0, j = 2
+- `sum(i, j) = sum(0, 2) = A[0] + A[1] + A[2] = 1 + 3 + 15 = 19 < k`. To increase the sum, we need to increase the length of subarray, so `j++`.
+
+**Step 4:** i = 0, j = 3
+- `sum(i, j) = sum(0, 3) = A[0] + A[1] + A[2] + A[3] = 1 + 3 + 15 + 10 = 29 < k`. To increase the sum, we need to increase the length of subarray, so `j++`.
+
+**Step 5:** i = 0, j = 4
+- `sum(i, j) = sum(0, 4) = A[0] + A[1] + A[2] + A[3] + A[4] = 1 + 3 + 15 + 10 + 20 = 49 > k`. To decrease the sum, we need to decrease the length of subarray. This can either be done by `i++` or `j--`. If we do `j--`, we will be at the same stage at step 4, which isn't helpful. So, we need to do `i++` to decrease the length and effectively the sum.
+
+**Step 6:** i = 1, j = 4
+- `sum(i, j) = sum(1, 4) = A[1] + A[2] + A[3] + A[4] = 3 + 15 + 10 + 20 = 48 > k`. Again, we need to decrease the length to decrease the sum.
+
+*What shall we do here: `i++` or `j--`?*
+We know that, sum (0, 3) < k. Therefore, sum(1, 3) will definitely be less than k. Therefore, `i++` is correct way out here.
+
+**Step 7:** i = 2, j = 4
+- `sum(i, j) = sum(2, 4) = A[2] + A[3] + A[4] = 15 + 10 + 20 = 45 > k`. Again, we need to decrease the length to decrease the sum. As discussed above, do `i++`.
+
+**Step 8:** i = 3, j = 4
+- `sum(i, j) = sum(3, 4) = A[3] + A[4] = 10 + 20 = 30 < k`. To increase the array length, do `j++`.
+
+**Step 9:** i = 3, j = 5
+- `sum(i, j) = sum(3, 5) = A[3] + A[4] + A[5] = 10 + 20 + 3 = 33 = k`. We have found the required subarray.
+
+
+#### Pseudocode
+```java
+i = 0, j = 0, sum = A[0]
+
+while (j < n) {
+ if (sum == k) {
+ return true;
+ } else if (sum < k) {
+ j++;
+ if (j == n) { // To make sure index is not out of bounds
+ break;
+ }
+
+ sum += A[j];
+ } else {
+ sum -= A[i];
+ i++;
+ if (i > j) { // To make sure i never exceeds j
+ break;
+ }
+ }
+}
+
+return false;
+```
+
+- **Time Complexity:**
+O(N), as in the worst case, complete array will be traversed.
+- **Space Complexity:**
+O(1), as no additional space is required if we use same array to create prefix array.
+
+---
+### Problem 5 Container with most Water
+
+Given an integer array `A` where array elements represent the height of the wall. Find any two walls that can form a container to store the maximum amount of water.
+
+**Example:**
+A = {4, 2, 10, 6, 8, 2, 6, 2}
+
+ +
+
+**Ans:** 24. (Maximum amount of water stored between walls at idx (1 and 7) or between idx (3 and 7))
+
+Since `area = height * width`, therefore
+Amount of water stored between any two walls `A[i]` and `A[j]` = `min(A[i], A[j]) * (j - i)`, where height = `min(A[i], A[j])` and width = `(j - i)`.
+
+> **Note:** height = `min(A[i], A[j])`, as water can be stored upto minimum height of the wall, and width = `(j - i)`, i.e., the difference between the position of walls.
+
+#### Brute Force Apporach:
+*Choose all the pair of walls, calculate the amount of water stored between them and find the maximum.*
+
+- **Time Complexity:**
+O(N$^2$), as we need to use two for loops.
+- **Space Complexity:**
+O(1), as no additional space is required.
+
+
+---
+### Question
+What is the water trapped between 2 walls at index L and R.
+Array A gives the heights of buildings
+Chose the correct answer
+
+
+**Choices**
+- [x] (R - L) * min(A[L], A[r])
+- [ ] (R - L)* max(A[L], A[r])
+- [ ] (R - L + 1) * min(A[L], A[r])
+- [ ] (R - L + 1) * max(A[L], A[r])
+
+
+**Explanation:**
+
+The answer is **(R - L) * min(A[L], A[r])**.
+
+* Amount of water stored between any two walls A[L] and A[R] = min(A[L], A[R]) * (R - L)
+
+where height = min(A[L], A[R])
+width = (R - L).
+
+
+---
+
+:::warning
+Please take some time to think about the optimised approach on your own before reading further.....
+:::
+
+### Container with most Water Two Pointer Approach
+
+
+- Since `area = height * width`. To achieve the maximum area, we should find the maximum values for height and width.
+- Let's start with maximum width, so keep i = 0 and j = n - 1.
+- `height = min(A[i], A[j])`. So, in order to increase the height, we should move in the direction of increasing the minimum height.
+
+**Example:**
+A[] =
+
+| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
+|-------|---|---|---|---|---|---|---|---|
+| Value | 4 | 2 | 10 | 6 | 8 | 2 | 6 | 2 |
+
+
+**Step 1:** i = 0, j = 7, max_area = -1 (Initially)
+- `height = min(A[0], A[7]) = min(4, 2) = 2`.
+ `width = j - i = 7 - 0 = 7`.
+ `area = height * width = 2 * 7 = 14`.
+ `max_area = max(max_area, area) = max(-1, 14) = 14`.
+ To increase the area, we need to move in direction of increasing the minimum height. Since min height is 2, this can be increased by doing `j--`.
+
+**Step 2:** i = 0, j = 6, max_area = 14
+- `height = min(A[0], A[6]) = min(4, 6) = 4`.
+ `width = j - i = 6 - 0 = 6`.
+ `area = height * width = 4 * 6 = 24`.
+ `max_area = max(max_area, area) = max(14, 24) = 24`.
+ To increase the area, we need to move in direction of increasing the minimum height. Since min height is 4, this can be increased by doing `i++`.
+
+**Step 3:** i = 1, j = 6, max_area = 24
+- `height = min(A[1], A[6]) = min(2, 6) = 2`.
+ `width = j - i = 6 - 1 = 5`.
+ `area = height * width = 2 * 5 = 10`.
+ `max_area = max(max_area, area) = max(24, 10) = 24`.
+ To increase the area, we need to move in direction of increasing the minimum height. Since min height is 2, this can be increased by doing `i++`.
+
+**Step 4:** i = 2, j = 6, max_area = 24
+- `height = min(A[2], A[6]) = min(10, 6) = 6`.
+ `width = j - i = 6 - 2 = 4`.
+ `area = height * width = 6 * 4 = 24`.
+ `max_area = max(max_area, area) = max(24, 24) = 24`.
+ To increase the area, we need to move in direction of increasing the minimum height. Since min height is 6, this can be increased by doing `j--`.
+
+**Step 5:** i = 2, j = 5, max_area = 24
+- `height = min(A[2], A[5]) = min(10, 2) = 2`.
+ `width = j - i = 5 - 2 = 3`.
+ `area = height * width = 2 * 3 = 6`.
+ `max_area = max(max_area, area) = max(24, 6) = 24`.
+ To increase the area, we need to move in direction of increasing the minimum height. Since min height is 2, this can be increased by doing `j--`.
+
+**Step 6:** i = 2, j = 4, max_area = 24
+- `height = min(A[2], A[4]) = min(10, 8) = 8`.
+ `width = j - i = 4 - 2 = 2`.
+ `area = height * width = 8 * 2 = 16`.
+ `max_area = max(max_area, area) = max(24, 16) = 24`.
+ To increase the area, we need to move in direction of increasing the minimum height. Since min height is 2, this can be increased by doing `j--`.
+
+**Step 7:** i = 2, j = 3, max_area = 24
+- `height = min(A[2], A[3]) = min(10, 6) = 6`.
+ `width = j - i = 3 - 2 = 1`.
+ `area = height * width = 6 * 1 = 6`.
+ `max_area = max(max_area, area) = max(24, 6) = 6`.
+ After this, moving any of i or j will yield width as 0. Hence, we stop the execution and final ans is 24.
+
+
+#### Pseudocode:
+```java
+i = 0, j = n - 1;
+while (i < j) {
+ area = min(A[i], A[j]) * (j - 1);
+ if (A[i] < A[j]) {
+ i++;
+ } else if (A[i] > A[j]) {
+ j--;
+ } else {
+ i++, j--; // Doesn't matter if we move only i or j or both
+ }
+}
+return area;
+```
+
+- **Time Complexity:**
+O(N), as we are traversing the complete array only once.
+- **Space Complexity:**
+O(1), as no additional space is required.
diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner Data Types 2 + Reading .md b/Academy DSA Typed Notes/Beginner Language/Beginner Data Types 2 + Reading .md
new file mode 100644
index 0000000..ce7eda0
--- /dev/null
+++ b/Academy DSA Typed Notes/Beginner Language/Beginner Data Types 2 + Reading .md
@@ -0,0 +1,1070 @@
+# Beginner : Data Types 2 + Reading Inputs
+
+---
+
+Recap: Start the class with Revising the previous session rules:
+
+:::success
+There are a lot of quizzes in this session, please take some time to think about the solution on your own before reading further.....
+:::
+
+## Revision: Type Casting Rules
+
+1. Int data can be stored in long and there wont be any loss of data, so there wont be any issues.
+Ex:
+int a = 10;
+long b = a;
+System.out.print(b); --> 10
+
+2. Long data cannot be stored in int, there can be a loss of data so we will get an error
+Ex:
+long a = 100;
+int b = a;
+System.out.print(b); Error
+
+3. If we want to still force we need to keep explicitly type cast it
+Ex :
+long a = 100;
+int b = (int)a;
+System.out.print(b) --> 100
+
+---
+
+# Question
+
+
+```
+int a = 10000;
+long b = a;
+System.out.print(b);
+```
+
+# Choices
+
+- [x] 10000
+
+- [ ] Compilation Error
+
+- [ ] 100000.0
+
+- [ ] 10000L
+
+---
+
+**Explanation:**
+First line we create a variable of type int then we are creating a long type variable "b" and trying to store the value of "a" in it. This is Implicit Typecasting.
+Ans= 10000
+
+
+---
+
+# Question
+
+
+```
+long x = 10000;
+System.out.print(x);
+```
+
+# Choices
+
+- [ ] 10000L
+
+- [ ] Compilation Error
+
+- [x] 10000
+
+- [ ] None of the above
+
+---
+
+**Explanation:**
+First line automatic typecasting is happening between Int and Long.
+Ans= 10000
+
+---
+
+# Question
+
+
+```
+long x = 10000;
+int y = x;
+System.out.print(y);
+```
+# Choices
+
+- [ ] 10000L
+
+- [x] Compilation Error
+
+- [ ] 10000
+
+- [ ] None of the above
+
+
+---
+
+**Explanation:**
+First line we create a variable of type long then we are creating a int type variable "y" and trying to store the value of "x" in it. In this acse there is a possiblilty of Data Loss.
+Error- Possible lossy conversion from long to int.
+
+---
+
+# Question
+
+
+```
+long x = 1000;
+int y = (int)x;
+System.out.print(y);
+```
+
+# Choices
+
+- [x] 1000
+
+- [ ] Compilation Error
+
+- [ ] 1000L
+
+- [ ] None of the above
+
+---
+
+**Explanation:**
+`int y = (int)x;` Now with this line we are forcing the compiler to typecast it to int.
+It is explicit Typecasting.
+Ans= 1000.
+
+---
+
+# Question
+
+
+```
+long a = 10000000000L;
+int b = (int)a;
+System.out.print(b);
+```
+
+# Choices
+
+- [ ] 10000000000
+
+- [x] Random Value
+
+- [ ] 10
+
+- [ ] None of the above
+
+---
+
+**Explanation:**
+`int b = (int)a;` Here we are forcing the compiler to store the value 10^10 into int. Because of that overflow will happen.
+Ans= Some random value.
+
+
+---
+
+## Taking input from the user:
+
+Tool to take input from the user: Scanner.
+
+**Syntax of Scanner:**
+```
+Scanner scn = new Scanner(System. in);
+```
+
+> We dont need to know what is this scanner. Just exactly follow the syntax to take input from the user.
+
+Now in order to use scanner also we need to write one line:
+
+```
+import java.util.*;
+```
+
+> Consider this like in order to play pubg we need to import some files, some packages similarly to use scanner we need to import java files.
+
+
+### Take Input and print the output:
+```
+int x = scn.nextInt();
+System.out.print(x);
+```
+**Explanation:**
+Here we are taking the help of scanner by using its name scn and asking the user for an integer value which we will store in "x" varaible.
+
+> Just try to give different integer values in the custom input and explain how it got printed.
+
+**Take input and print twice the number:**
+
+```
+int y = scn.nextInt();
+System.out.print(2 * y);
+```
+
+---
+
+# Question
+
+Predict the output for given input:
+Input: 100
+
+```
+scanner sc = new scanner(System.in);
+int xyz = sc.nextInt();
+System.out.print(xyz);
+```
+
+# Choices
+- [ ] xyz
+- [x] Error
+- [ ] 100
+- [ ] Goodnight :)
+
+---
+
+**Explanation:**
+At line 1, scanner is in small letter. Because Java is case sensitive.
+
+
+---
+
+# Question
+
+Predict the output for given input:
+Input: 594
+
+```
+Scanner sc = new Scanner(system.in);
+int abc = sc.nextInt();
+System.out.print(abc);
+```
+
+# Choices
+- [ ] 594
+- [x] Error
+- [ ] abc
+- [ ] Only here to watch!
+
+---
+
+**Explanation:**
+Error: S in System should be capital.
+
+---
+
+# Question
+
+Predict the output for given input:
+Input: 5000
+
+```
+Scanner scn = new Scanner(System.in);
+int a = scn.nextInt();
+System.out.print(a);
+```
+
+# Choices
+- [ ] Error
+- [x] 5000
+- [ ] Watching Netflix on the side!
+
+---
+
+
+**Explanation:**
+Here we are creating a variable "a" and taking integer from the user.
+
+
+---
+
+# Question
+
+Predict the output for given input:
+Input: 24 30
+```
+Scanner sc = new Scanner(System.in);
+int a = sc.nextInt();
+int b = sc.nextInt();
+System.out.print(a);
+```
+# Choices
+- [x] 24
+- [ ] 30
+- [ ] Error
+
+---
+
+
+**Explanation:**
+
+The first value will be stored in first variable and second value will be stored in second variable.
+
+
+---
+
+# Question
+
+Predict the output for given input:
+Input: 33 11
+
+```
+Scanner sc = new Scanner(System.in);
+int c = sc.nextInt();
+int d = sc.nextInt();
+System.out.print(c + d);
+```
+# Choices
+- [ ] 3311
+- [ ] c + d
+- [x] 44
+- [ ] Error
+
+---
+
+
+**Explanation:**
+
+"c" variable will have value 33, and "d" variablle will have value 11.
+
+
+---
+
+# Question
+
+What will be the output for the following input?
+```
+Input: 15 21
+Scanner sc = new Scanner(System.in);
+int a = sc.nextInt();
+int b = sc.nextInt();
+int c = sc.nextInt();
+System.out.print(a + b + c);
+```
+# Choices
+- [ ] 36
+- [ ] a + b + c
+- [ ] 36c
+- [x] Error
+
+---
+
+
+**Explanation:**
+"a" variable will have value 15, then variable "b" will have value 21, but for "c" variable user is not giving any input.
+Ans = Error, No such element exception.
+
+---
+
+
+### Input for long data type:
+```
+Scanner scn = new Scanner(System .in);
+long c = scn.nextLong();
+```
+
+---
+
+# Question
+How to take input for a long variable?
+
+# Choices
+- [ ] sc.nextlong()
+- [ ] sc.nextint()
+- [x] sc.nextLong()
+- [ ] sc.nextInt()
+
+---
+
+# Question
+
+Predict the output for the following input:
+Input: 10000000000
+```
+Scanner scn = new Scanner(System.in);
+long N = scn.nextLong();
+System.out.println(N);
+```
+# Choices
+- [x] 10000000000
+- [ ] Error
+- [ ] 10000000000L
+
+---
+
+# Question
+
+Predict the output for the following input:
+Input: 10000000000L
+
+```
+Scanner scn = new Scanner(System.in):
+long N = scn.nextLong();
+System.out.println(N);
+```
+# Choices
+- [ ] 10000000000
+- [x] Error
+- [ ] 10000000000L
+
+---
+
+**Explanation:**
+
+Here, when we give L in the input, then the whole input is not a number anymore.
+Ans = Error, Input Mismatch.
+
+> Do not write L in the input section to give a long value.
+
+---
+
+# Question
+```
+Input: 2500
+long x = scn.nextInt();
+System.out.print(x);
+```
+# Choices
+- [x] 2500
+- [ ] Error
+- [ ] 2500L
+
+---
+
+**Explanation:**
+
+First 2500 is considered an integer value, ans we can store an integer value into long. It is implicit typecasting.
+
+
+---
+
+# Question
+```
+Input: 2500
+int x = scn.nextLong();
+System.out.print(x);
+```
+# Choices
+- [ ] 2500
+- [x] Error
+- [ ] 2500L
+
+---
+
+**Explanation:**
+Now here from long to int, it cannot happen automatically.
+Ans = Error, possible lossy conversion from long to int.
+
+**Correct**
+```
+Input: 2500
+int x = (int)scn.nextLong();
+System.out.print(x);
+```
+
+Ans = 2500.
+
+---
+
+## Float vs Double
+
+1. Non Decimal{Integers} --> Datatypes : int long
+2. Decimal --> float double
+Ex : 1.24 , 1.56 , 20.0,and soon...
+
+
+**Declare a variable of any Type
+Syntax: type name = value;**
+
+---
+
+# Question
+
+```
+double d = 6.17;
+System.out.print(d);
+```
+
+# Choices
+
+- [ ] Compilation Error
+- [ ] 6
+- [x] 6.17
+- [ ] None of the above
+
+---
+
+**Explanation:**
+We are creating a variable of type double.
+Ans= 6.17
+
+---
+
+# Question
+
+```
+float x = 3.14;
+System.out.print(x);
+```
+
+# Choices
+
+- [x] Compilation Error
+- [ ] 3.14f
+- [ ] 3.1400001
+- [ ] 3.14
+
+---
+
+**Explanation:**
+Error-> Possible lossy conversion from double to float.
+
+> Rule : In JAVA, Any decimal number is considered as double
+
+
+---
+
+# Question
+
+
+```
+float a = 3.14f;
+System.out.print(a);
+```
+
+# Choices
+
+- [ ] 3.1400001
+- [x] 3.14
+- [ ] Compilation Error
+- [ ] None of the above
+
+---
+
+**Explanation:**
+Now when we add "f" in front of it, Basically we are trying to tell compiler, consider this as float.
+Ans= 3.14
+
+---
+
+### Difference Between Float and Double?
+
+```
+float a = 10.0f;
+float b = 3.0f;
+float c = (a/b);
+System.out.println(c);
+```
+
+```
+double x = 10.0;
+double y = 3.0;
+double z = x/y;
+System.out.println(z);
+```
+**Output:**
+```plaintext
+3.3333333
+3.3333333333333335
+```
+**Explanation:**
+* float -> can have upto 6 to 7 digits after decimal point.
+* double -> can have upto 15 to 16 digits after decimal point.
+* double is more precise [more digits after decimal point]
+
+---
+
+## Type Casting Float vs Double
+**Rules:**
+
+Same Rules of int vs long apply here,
+
+1. When we store float to double no loss of data hence no issue
+{Implicit Type Casting}.
+
+2. When we store double to float there can be a loss of data, complier will raise an error.
+```
+double d = 3.14
+float f = d // Error
+```
+3. If we want to still force we need to keep explicitly type cast it.
+```
+double d = 3.14
+float f = (float)d; // doubtle --> Explicilty --> float
+System.out.print(f); // 3.14
+```
+
+---
+# Question
+
+
+```
+double x = 3.14;
+float y = x;
+System.out.print(y);
+```
+
+# Choices
+
+- [ ] 3.14f
+- [ ] 3.14
+- [x] Compilation Error
+- [ ] None of the above
+
+---
+
+**Explanation:**
+Here we are trying to store a double type value into float.
+Error- Possible lossy conversion from double to float.
+
+---
+
+# Question
+
+
+```
+double x = 17.67;
+float y = (float)x;
+System.out.print(y);
+```
+
+# Choices
+
+- [x] 17.67
+- [ ] 17.669999999999998
+- [ ] Compilation Error
+- [ ] None of the above
+
+---
+
+**Explanation:**
+In this case, we are forcing the compiler to convert double to float.
+This is known as Explicit Typecasting.
+Ans= 17.67
+
+**No data loss -> No error**
+* int (45) -> double -> No error
+* double (45.6) -> int -> Error
+
+---
+
+## Type Casting Decimal vs Non Decimal
+For typecasting just remember 2 rules:
+1. If there is is no loss of data then no error : Implicit from non-decimal to decimal : Implicit.
+2. If there is chance for loss of data then error but We can still do this type casting forcefully : Explicit from decimal to non - decimal : Explicilty.
+
+
+---
+
+# Question
+
+
+```
+double x = 3.45;
+int y = x;
+System.out.print(y);
+```
+
+# Choices
+
+- [ ] 3
+- [ ] 3.45
+- [x] Compilation Error
+- [ ] None of the above
+
+---
+**Output:**
+```
+Error- Possible lossy conversion from double to int.
+```
+
+---
+
+# Question
+
+
+```
+double x = 3.45;
+int y = (int)x;
+System.out.print(y);
+```
+
+# Choices
+
+- [x] 3
+- [ ] 3.45
+- [ ] Compilation Error
+- [ ] None of the above
+
+
+---
+
+**Explanation:**
+Here we are forcing the compiler to convert 3.14 to int, We will only get the integer part.
+Ans= 3.
+
+---
+
+# Question
+
+Quiz 24:
+```
+int x = 40;
+double y = x;
+System.out.print(y);
+```
+
+# Choices
+
+- [ ] 40
+- [x] 40.0
+- [ ] Compilation Error
+- [ ] None of the above
+
+
+---
+
+**Explanation:**
+In this example, we are trying to store a int type value into double.
+Double stores decimal values, and here we can easily convert 40 to 40.0, therefore it is called Implicit Typecasting.
+Ans= 40.0
+
+
+---
+
+
+## Reading Inputs for Float and Double
+
+```
+How to take input for a float variable?
+```
+```
+Scanner scn = new Scanner(System.in);
+float a = scn.nextFloat();
+```
+
+
+```
+How to take input for a double variable?
+```
+```
+Scanner scn = new Scanner(System.in);
+double a = scn.nextDouble();
+```
+
+#Ques 1:
+```
+float x = sc.nextFloat();
+System.out.println(x);
+```
+
+ Explain we don't need to write "f" while taking inputs for float.
+
+---
+
+# Question
+
+
+```
+Input : 3.14
+
+Scanner sc = new Scanner(System.in);
+float a = sc.nextFloat();
+System.out.print(2 * a);
+```
+
+# Choices
+
+- [ ] 2.0
+- [ ] 3.14
+- [x] 6.28
+- [ ] 1.57
+
+---
+
+**Explanation:**
+Now this 3.14 is stored on variable "a", Then we are trying to print 2*a-> 2* 3.14.
+Ans= 6.28
+
+---
+
+# Question
+
+
+```
+Input : 3.14 20
+
+Scanner sc = new Scanner(System.in);
+int a = sc.nextInt();
+int b = sc.nextInt();
+System.out.print(a + b);
+```
+
+# Choices
+
+- [ ] 17
+- [ ] 3
+- [ ] 14
+- [x] Error
+
+---
+
+**Explanation:**
+In the first line, we are trying to take an integer type input, But the user is not giving an integer value for the first time.
+Error-> Input mismatch.
+
+---
+
+# Question
+
+
+```
+Input : 3.14
+
+Scanner sc = new Scanner(System.in);
+float a = sc.nextFloat();
+float b = sc.nextFloat()
+System.out.print(2 * a);
+```
+
+# Choices
+
+- [ ] 6.28
+- [ ] 3.14
+- [x] Error
+- [ ] None of the above
+
+
+---
+
+**Explanation:**
+There are 2 errors,
+In line `float b = sc.nextFloat()` semicolon is missing.
+We are only giving one input.
+Error- No such element exeception.
+
+---
+
+# Ques 1
+
+**Code:**
+```
+Input: 3.45
+int x = sc.nextDouble();
+System.out.println(x);
+```
+Explanation:
+
+According to rules of typecasting, we cannot do it there is a chance of data loss.
+Ans=Error
+
+
+**Correct Code:**
+```
+Input: 3.45
+int x = (int)sc.nextDouble();
+System.out.println(x);
+```
+Explanation:
+
+In this case, we are forcing the compiler to do it, But int can only store integer value, so we will only get the integer part as output.
+Ans=3
+
+
+# Ques 2
+```
+Input: 3
+double y = sc.nextInt();
+System.out.println(y);
+```
+
+Explanation:
+
+We can easily Typecast from integer to decimal.
+Ans=3.0
+
+---
+## Dividing numbers by zero
+
+```
+System.out.println(4 / 0);
+```
+Output:
+```
+Error
+```
+
+```
+System.out.println(4.0 / 0);
+```
+Output:
+```plaintext
+Infinity
+```
+```
+System.out.println(4.0f / 0);
+```
+Output:
+```plaintext
+infinity
+```
+
+```
+System.out.println(0 / 0);
+```
+
+Output:
+```plaintext
+Error.
+```
+
+```
+System.out.println(0.0 / 0);
+```
+Output:
+```plaintext
+NAN[Not A Number].
+```
+
+
+
+---
+## Boolean Input
+
+
+ Ques1:
+```
+boolean x = false;
+System.out.println(x);
+````
+
+Output:
+```
+false.
+```
+
+boolean -> true / false only, it will work on True/False, but give answer in lowercase only.
+
+Ques2:
+```
+
+Input: true
+Scanner sc = new Scanner(System.in);
+boolean y = sc.nextBoolean();
+System.out.println(y);
+```
+
+Output:
+```
+true
+```
+### Take inputs like True/False/false also.
+
+---
+## Arithmetic Operators
+
++, -, *, / are very basic arithmetic operators. Confirm whether the students know about them. And directly give the below quiz.
+
+---
+
+
+# Question
+What will be the output?
+```
+int a = 10;
+int b = 24;
+System.out.println(a+b);
+System.out.println(a-b);
+System.out.println(a*b);
+System.out.println(b/a);
+```
+
+# Choices
+- [ ] 34
+
+
+**Ans:** 24. (Maximum amount of water stored between walls at idx (1 and 7) or between idx (3 and 7))
+
+Since `area = height * width`, therefore
+Amount of water stored between any two walls `A[i]` and `A[j]` = `min(A[i], A[j]) * (j - i)`, where height = `min(A[i], A[j])` and width = `(j - i)`.
+
+> **Note:** height = `min(A[i], A[j])`, as water can be stored upto minimum height of the wall, and width = `(j - i)`, i.e., the difference between the position of walls.
+
+#### Brute Force Apporach:
+*Choose all the pair of walls, calculate the amount of water stored between them and find the maximum.*
+
+- **Time Complexity:**
+O(N$^2$), as we need to use two for loops.
+- **Space Complexity:**
+O(1), as no additional space is required.
+
+
+---
+### Question
+What is the water trapped between 2 walls at index L and R.
+Array A gives the heights of buildings
+Chose the correct answer
+
+
+**Choices**
+- [x] (R - L) * min(A[L], A[r])
+- [ ] (R - L)* max(A[L], A[r])
+- [ ] (R - L + 1) * min(A[L], A[r])
+- [ ] (R - L + 1) * max(A[L], A[r])
+
+
+**Explanation:**
+
+The answer is **(R - L) * min(A[L], A[r])**.
+
+* Amount of water stored between any two walls A[L] and A[R] = min(A[L], A[R]) * (R - L)
+
+where height = min(A[L], A[R])
+width = (R - L).
+
+
+---
+
+:::warning
+Please take some time to think about the optimised approach on your own before reading further.....
+:::
+
+### Container with most Water Two Pointer Approach
+
+
+- Since `area = height * width`. To achieve the maximum area, we should find the maximum values for height and width.
+- Let's start with maximum width, so keep i = 0 and j = n - 1.
+- `height = min(A[i], A[j])`. So, in order to increase the height, we should move in the direction of increasing the minimum height.
+
+**Example:**
+A[] =
+
+| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
+|-------|---|---|---|---|---|---|---|---|
+| Value | 4 | 2 | 10 | 6 | 8 | 2 | 6 | 2 |
+
+
+**Step 1:** i = 0, j = 7, max_area = -1 (Initially)
+- `height = min(A[0], A[7]) = min(4, 2) = 2`.
+ `width = j - i = 7 - 0 = 7`.
+ `area = height * width = 2 * 7 = 14`.
+ `max_area = max(max_area, area) = max(-1, 14) = 14`.
+ To increase the area, we need to move in direction of increasing the minimum height. Since min height is 2, this can be increased by doing `j--`.
+
+**Step 2:** i = 0, j = 6, max_area = 14
+- `height = min(A[0], A[6]) = min(4, 6) = 4`.
+ `width = j - i = 6 - 0 = 6`.
+ `area = height * width = 4 * 6 = 24`.
+ `max_area = max(max_area, area) = max(14, 24) = 24`.
+ To increase the area, we need to move in direction of increasing the minimum height. Since min height is 4, this can be increased by doing `i++`.
+
+**Step 3:** i = 1, j = 6, max_area = 24
+- `height = min(A[1], A[6]) = min(2, 6) = 2`.
+ `width = j - i = 6 - 1 = 5`.
+ `area = height * width = 2 * 5 = 10`.
+ `max_area = max(max_area, area) = max(24, 10) = 24`.
+ To increase the area, we need to move in direction of increasing the minimum height. Since min height is 2, this can be increased by doing `i++`.
+
+**Step 4:** i = 2, j = 6, max_area = 24
+- `height = min(A[2], A[6]) = min(10, 6) = 6`.
+ `width = j - i = 6 - 2 = 4`.
+ `area = height * width = 6 * 4 = 24`.
+ `max_area = max(max_area, area) = max(24, 24) = 24`.
+ To increase the area, we need to move in direction of increasing the minimum height. Since min height is 6, this can be increased by doing `j--`.
+
+**Step 5:** i = 2, j = 5, max_area = 24
+- `height = min(A[2], A[5]) = min(10, 2) = 2`.
+ `width = j - i = 5 - 2 = 3`.
+ `area = height * width = 2 * 3 = 6`.
+ `max_area = max(max_area, area) = max(24, 6) = 24`.
+ To increase the area, we need to move in direction of increasing the minimum height. Since min height is 2, this can be increased by doing `j--`.
+
+**Step 6:** i = 2, j = 4, max_area = 24
+- `height = min(A[2], A[4]) = min(10, 8) = 8`.
+ `width = j - i = 4 - 2 = 2`.
+ `area = height * width = 8 * 2 = 16`.
+ `max_area = max(max_area, area) = max(24, 16) = 24`.
+ To increase the area, we need to move in direction of increasing the minimum height. Since min height is 2, this can be increased by doing `j--`.
+
+**Step 7:** i = 2, j = 3, max_area = 24
+- `height = min(A[2], A[3]) = min(10, 6) = 6`.
+ `width = j - i = 3 - 2 = 1`.
+ `area = height * width = 6 * 1 = 6`.
+ `max_area = max(max_area, area) = max(24, 6) = 6`.
+ After this, moving any of i or j will yield width as 0. Hence, we stop the execution and final ans is 24.
+
+
+#### Pseudocode:
+```java
+i = 0, j = n - 1;
+while (i < j) {
+ area = min(A[i], A[j]) * (j - 1);
+ if (A[i] < A[j]) {
+ i++;
+ } else if (A[i] > A[j]) {
+ j--;
+ } else {
+ i++, j--; // Doesn't matter if we move only i or j or both
+ }
+}
+return area;
+```
+
+- **Time Complexity:**
+O(N), as we are traversing the complete array only once.
+- **Space Complexity:**
+O(1), as no additional space is required.
diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner Data Types 2 + Reading .md b/Academy DSA Typed Notes/Beginner Language/Beginner Data Types 2 + Reading .md
new file mode 100644
index 0000000..ce7eda0
--- /dev/null
+++ b/Academy DSA Typed Notes/Beginner Language/Beginner Data Types 2 + Reading .md
@@ -0,0 +1,1070 @@
+# Beginner : Data Types 2 + Reading Inputs
+
+---
+
+Recap: Start the class with Revising the previous session rules:
+
+:::success
+There are a lot of quizzes in this session, please take some time to think about the solution on your own before reading further.....
+:::
+
+## Revision: Type Casting Rules
+
+1. Int data can be stored in long and there wont be any loss of data, so there wont be any issues.
+Ex:
+int a = 10;
+long b = a;
+System.out.print(b); --> 10
+
+2. Long data cannot be stored in int, there can be a loss of data so we will get an error
+Ex:
+long a = 100;
+int b = a;
+System.out.print(b); Error
+
+3. If we want to still force we need to keep explicitly type cast it
+Ex :
+long a = 100;
+int b = (int)a;
+System.out.print(b) --> 100
+
+---
+
+# Question
+
+
+```
+int a = 10000;
+long b = a;
+System.out.print(b);
+```
+
+# Choices
+
+- [x] 10000
+
+- [ ] Compilation Error
+
+- [ ] 100000.0
+
+- [ ] 10000L
+
+---
+
+**Explanation:**
+First line we create a variable of type int then we are creating a long type variable "b" and trying to store the value of "a" in it. This is Implicit Typecasting.
+Ans= 10000
+
+
+---
+
+# Question
+
+
+```
+long x = 10000;
+System.out.print(x);
+```
+
+# Choices
+
+- [ ] 10000L
+
+- [ ] Compilation Error
+
+- [x] 10000
+
+- [ ] None of the above
+
+---
+
+**Explanation:**
+First line automatic typecasting is happening between Int and Long.
+Ans= 10000
+
+---
+
+# Question
+
+
+```
+long x = 10000;
+int y = x;
+System.out.print(y);
+```
+# Choices
+
+- [ ] 10000L
+
+- [x] Compilation Error
+
+- [ ] 10000
+
+- [ ] None of the above
+
+
+---
+
+**Explanation:**
+First line we create a variable of type long then we are creating a int type variable "y" and trying to store the value of "x" in it. In this acse there is a possiblilty of Data Loss.
+Error- Possible lossy conversion from long to int.
+
+---
+
+# Question
+
+
+```
+long x = 1000;
+int y = (int)x;
+System.out.print(y);
+```
+
+# Choices
+
+- [x] 1000
+
+- [ ] Compilation Error
+
+- [ ] 1000L
+
+- [ ] None of the above
+
+---
+
+**Explanation:**
+`int y = (int)x;` Now with this line we are forcing the compiler to typecast it to int.
+It is explicit Typecasting.
+Ans= 1000.
+
+---
+
+# Question
+
+
+```
+long a = 10000000000L;
+int b = (int)a;
+System.out.print(b);
+```
+
+# Choices
+
+- [ ] 10000000000
+
+- [x] Random Value
+
+- [ ] 10
+
+- [ ] None of the above
+
+---
+
+**Explanation:**
+`int b = (int)a;` Here we are forcing the compiler to store the value 10^10 into int. Because of that overflow will happen.
+Ans= Some random value.
+
+
+---
+
+## Taking input from the user:
+
+Tool to take input from the user: Scanner.
+
+**Syntax of Scanner:**
+```
+Scanner scn = new Scanner(System. in);
+```
+
+> We dont need to know what is this scanner. Just exactly follow the syntax to take input from the user.
+
+Now in order to use scanner also we need to write one line:
+
+```
+import java.util.*;
+```
+
+> Consider this like in order to play pubg we need to import some files, some packages similarly to use scanner we need to import java files.
+
+
+### Take Input and print the output:
+```
+int x = scn.nextInt();
+System.out.print(x);
+```
+**Explanation:**
+Here we are taking the help of scanner by using its name scn and asking the user for an integer value which we will store in "x" varaible.
+
+> Just try to give different integer values in the custom input and explain how it got printed.
+
+**Take input and print twice the number:**
+
+```
+int y = scn.nextInt();
+System.out.print(2 * y);
+```
+
+---
+
+# Question
+
+Predict the output for given input:
+Input: 100
+
+```
+scanner sc = new scanner(System.in);
+int xyz = sc.nextInt();
+System.out.print(xyz);
+```
+
+# Choices
+- [ ] xyz
+- [x] Error
+- [ ] 100
+- [ ] Goodnight :)
+
+---
+
+**Explanation:**
+At line 1, scanner is in small letter. Because Java is case sensitive.
+
+
+---
+
+# Question
+
+Predict the output for given input:
+Input: 594
+
+```
+Scanner sc = new Scanner(system.in);
+int abc = sc.nextInt();
+System.out.print(abc);
+```
+
+# Choices
+- [ ] 594
+- [x] Error
+- [ ] abc
+- [ ] Only here to watch!
+
+---
+
+**Explanation:**
+Error: S in System should be capital.
+
+---
+
+# Question
+
+Predict the output for given input:
+Input: 5000
+
+```
+Scanner scn = new Scanner(System.in);
+int a = scn.nextInt();
+System.out.print(a);
+```
+
+# Choices
+- [ ] Error
+- [x] 5000
+- [ ] Watching Netflix on the side!
+
+---
+
+
+**Explanation:**
+Here we are creating a variable "a" and taking integer from the user.
+
+
+---
+
+# Question
+
+Predict the output for given input:
+Input: 24 30
+```
+Scanner sc = new Scanner(System.in);
+int a = sc.nextInt();
+int b = sc.nextInt();
+System.out.print(a);
+```
+# Choices
+- [x] 24
+- [ ] 30
+- [ ] Error
+
+---
+
+
+**Explanation:**
+
+The first value will be stored in first variable and second value will be stored in second variable.
+
+
+---
+
+# Question
+
+Predict the output for given input:
+Input: 33 11
+
+```
+Scanner sc = new Scanner(System.in);
+int c = sc.nextInt();
+int d = sc.nextInt();
+System.out.print(c + d);
+```
+# Choices
+- [ ] 3311
+- [ ] c + d
+- [x] 44
+- [ ] Error
+
+---
+
+
+**Explanation:**
+
+"c" variable will have value 33, and "d" variablle will have value 11.
+
+
+---
+
+# Question
+
+What will be the output for the following input?
+```
+Input: 15 21
+Scanner sc = new Scanner(System.in);
+int a = sc.nextInt();
+int b = sc.nextInt();
+int c = sc.nextInt();
+System.out.print(a + b + c);
+```
+# Choices
+- [ ] 36
+- [ ] a + b + c
+- [ ] 36c
+- [x] Error
+
+---
+
+
+**Explanation:**
+"a" variable will have value 15, then variable "b" will have value 21, but for "c" variable user is not giving any input.
+Ans = Error, No such element exception.
+
+---
+
+
+### Input for long data type:
+```
+Scanner scn = new Scanner(System .in);
+long c = scn.nextLong();
+```
+
+---
+
+# Question
+How to take input for a long variable?
+
+# Choices
+- [ ] sc.nextlong()
+- [ ] sc.nextint()
+- [x] sc.nextLong()
+- [ ] sc.nextInt()
+
+---
+
+# Question
+
+Predict the output for the following input:
+Input: 10000000000
+```
+Scanner scn = new Scanner(System.in);
+long N = scn.nextLong();
+System.out.println(N);
+```
+# Choices
+- [x] 10000000000
+- [ ] Error
+- [ ] 10000000000L
+
+---
+
+# Question
+
+Predict the output for the following input:
+Input: 10000000000L
+
+```
+Scanner scn = new Scanner(System.in):
+long N = scn.nextLong();
+System.out.println(N);
+```
+# Choices
+- [ ] 10000000000
+- [x] Error
+- [ ] 10000000000L
+
+---
+
+**Explanation:**
+
+Here, when we give L in the input, then the whole input is not a number anymore.
+Ans = Error, Input Mismatch.
+
+> Do not write L in the input section to give a long value.
+
+---
+
+# Question
+```
+Input: 2500
+long x = scn.nextInt();
+System.out.print(x);
+```
+# Choices
+- [x] 2500
+- [ ] Error
+- [ ] 2500L
+
+---
+
+**Explanation:**
+
+First 2500 is considered an integer value, ans we can store an integer value into long. It is implicit typecasting.
+
+
+---
+
+# Question
+```
+Input: 2500
+int x = scn.nextLong();
+System.out.print(x);
+```
+# Choices
+- [ ] 2500
+- [x] Error
+- [ ] 2500L
+
+---
+
+**Explanation:**
+Now here from long to int, it cannot happen automatically.
+Ans = Error, possible lossy conversion from long to int.
+
+**Correct**
+```
+Input: 2500
+int x = (int)scn.nextLong();
+System.out.print(x);
+```
+
+Ans = 2500.
+
+---
+
+## Float vs Double
+
+1. Non Decimal{Integers} --> Datatypes : int long
+2. Decimal --> float double
+Ex : 1.24 , 1.56 , 20.0,and soon...
+
+
+**Declare a variable of any Type
+Syntax: type name = value;**
+
+---
+
+# Question
+
+```
+double d = 6.17;
+System.out.print(d);
+```
+
+# Choices
+
+- [ ] Compilation Error
+- [ ] 6
+- [x] 6.17
+- [ ] None of the above
+
+---
+
+**Explanation:**
+We are creating a variable of type double.
+Ans= 6.17
+
+---
+
+# Question
+
+```
+float x = 3.14;
+System.out.print(x);
+```
+
+# Choices
+
+- [x] Compilation Error
+- [ ] 3.14f
+- [ ] 3.1400001
+- [ ] 3.14
+
+---
+
+**Explanation:**
+Error-> Possible lossy conversion from double to float.
+
+> Rule : In JAVA, Any decimal number is considered as double
+
+
+---
+
+# Question
+
+
+```
+float a = 3.14f;
+System.out.print(a);
+```
+
+# Choices
+
+- [ ] 3.1400001
+- [x] 3.14
+- [ ] Compilation Error
+- [ ] None of the above
+
+---
+
+**Explanation:**
+Now when we add "f" in front of it, Basically we are trying to tell compiler, consider this as float.
+Ans= 3.14
+
+---
+
+### Difference Between Float and Double?
+
+```
+float a = 10.0f;
+float b = 3.0f;
+float c = (a/b);
+System.out.println(c);
+```
+
+```
+double x = 10.0;
+double y = 3.0;
+double z = x/y;
+System.out.println(z);
+```
+**Output:**
+```plaintext
+3.3333333
+3.3333333333333335
+```
+**Explanation:**
+* float -> can have upto 6 to 7 digits after decimal point.
+* double -> can have upto 15 to 16 digits after decimal point.
+* double is more precise [more digits after decimal point]
+
+---
+
+## Type Casting Float vs Double
+**Rules:**
+
+Same Rules of int vs long apply here,
+
+1. When we store float to double no loss of data hence no issue
+{Implicit Type Casting}.
+
+2. When we store double to float there can be a loss of data, complier will raise an error.
+```
+double d = 3.14
+float f = d // Error
+```
+3. If we want to still force we need to keep explicitly type cast it.
+```
+double d = 3.14
+float f = (float)d; // doubtle --> Explicilty --> float
+System.out.print(f); // 3.14
+```
+
+---
+# Question
+
+
+```
+double x = 3.14;
+float y = x;
+System.out.print(y);
+```
+
+# Choices
+
+- [ ] 3.14f
+- [ ] 3.14
+- [x] Compilation Error
+- [ ] None of the above
+
+---
+
+**Explanation:**
+Here we are trying to store a double type value into float.
+Error- Possible lossy conversion from double to float.
+
+---
+
+# Question
+
+
+```
+double x = 17.67;
+float y = (float)x;
+System.out.print(y);
+```
+
+# Choices
+
+- [x] 17.67
+- [ ] 17.669999999999998
+- [ ] Compilation Error
+- [ ] None of the above
+
+---
+
+**Explanation:**
+In this case, we are forcing the compiler to convert double to float.
+This is known as Explicit Typecasting.
+Ans= 17.67
+
+**No data loss -> No error**
+* int (45) -> double -> No error
+* double (45.6) -> int -> Error
+
+---
+
+## Type Casting Decimal vs Non Decimal
+For typecasting just remember 2 rules:
+1. If there is is no loss of data then no error : Implicit from non-decimal to decimal : Implicit.
+2. If there is chance for loss of data then error but We can still do this type casting forcefully : Explicit from decimal to non - decimal : Explicilty.
+
+
+---
+
+# Question
+
+
+```
+double x = 3.45;
+int y = x;
+System.out.print(y);
+```
+
+# Choices
+
+- [ ] 3
+- [ ] 3.45
+- [x] Compilation Error
+- [ ] None of the above
+
+---
+**Output:**
+```
+Error- Possible lossy conversion from double to int.
+```
+
+---
+
+# Question
+
+
+```
+double x = 3.45;
+int y = (int)x;
+System.out.print(y);
+```
+
+# Choices
+
+- [x] 3
+- [ ] 3.45
+- [ ] Compilation Error
+- [ ] None of the above
+
+
+---
+
+**Explanation:**
+Here we are forcing the compiler to convert 3.14 to int, We will only get the integer part.
+Ans= 3.
+
+---
+
+# Question
+
+Quiz 24:
+```
+int x = 40;
+double y = x;
+System.out.print(y);
+```
+
+# Choices
+
+- [ ] 40
+- [x] 40.0
+- [ ] Compilation Error
+- [ ] None of the above
+
+
+---
+
+**Explanation:**
+In this example, we are trying to store a int type value into double.
+Double stores decimal values, and here we can easily convert 40 to 40.0, therefore it is called Implicit Typecasting.
+Ans= 40.0
+
+
+---
+
+
+## Reading Inputs for Float and Double
+
+```
+How to take input for a float variable?
+```
+```
+Scanner scn = new Scanner(System.in);
+float a = scn.nextFloat();
+```
+
+
+```
+How to take input for a double variable?
+```
+```
+Scanner scn = new Scanner(System.in);
+double a = scn.nextDouble();
+```
+
+#Ques 1:
+```
+float x = sc.nextFloat();
+System.out.println(x);
+```
+
+ Explain we don't need to write "f" while taking inputs for float.
+
+---
+
+# Question
+
+
+```
+Input : 3.14
+
+Scanner sc = new Scanner(System.in);
+float a = sc.nextFloat();
+System.out.print(2 * a);
+```
+
+# Choices
+
+- [ ] 2.0
+- [ ] 3.14
+- [x] 6.28
+- [ ] 1.57
+
+---
+
+**Explanation:**
+Now this 3.14 is stored on variable "a", Then we are trying to print 2*a-> 2* 3.14.
+Ans= 6.28
+
+---
+
+# Question
+
+
+```
+Input : 3.14 20
+
+Scanner sc = new Scanner(System.in);
+int a = sc.nextInt();
+int b = sc.nextInt();
+System.out.print(a + b);
+```
+
+# Choices
+
+- [ ] 17
+- [ ] 3
+- [ ] 14
+- [x] Error
+
+---
+
+**Explanation:**
+In the first line, we are trying to take an integer type input, But the user is not giving an integer value for the first time.
+Error-> Input mismatch.
+
+---
+
+# Question
+
+
+```
+Input : 3.14
+
+Scanner sc = new Scanner(System.in);
+float a = sc.nextFloat();
+float b = sc.nextFloat()
+System.out.print(2 * a);
+```
+
+# Choices
+
+- [ ] 6.28
+- [ ] 3.14
+- [x] Error
+- [ ] None of the above
+
+
+---
+
+**Explanation:**
+There are 2 errors,
+In line `float b = sc.nextFloat()` semicolon is missing.
+We are only giving one input.
+Error- No such element exeception.
+
+---
+
+# Ques 1
+
+**Code:**
+```
+Input: 3.45
+int x = sc.nextDouble();
+System.out.println(x);
+```
+Explanation:
+
+According to rules of typecasting, we cannot do it there is a chance of data loss.
+Ans=Error
+
+
+**Correct Code:**
+```
+Input: 3.45
+int x = (int)sc.nextDouble();
+System.out.println(x);
+```
+Explanation:
+
+In this case, we are forcing the compiler to do it, But int can only store integer value, so we will only get the integer part as output.
+Ans=3
+
+
+# Ques 2
+```
+Input: 3
+double y = sc.nextInt();
+System.out.println(y);
+```
+
+Explanation:
+
+We can easily Typecast from integer to decimal.
+Ans=3.0
+
+---
+## Dividing numbers by zero
+
+```
+System.out.println(4 / 0);
+```
+Output:
+```
+Error
+```
+
+```
+System.out.println(4.0 / 0);
+```
+Output:
+```plaintext
+Infinity
+```
+```
+System.out.println(4.0f / 0);
+```
+Output:
+```plaintext
+infinity
+```
+
+```
+System.out.println(0 / 0);
+```
+
+Output:
+```plaintext
+Error.
+```
+
+```
+System.out.println(0.0 / 0);
+```
+Output:
+```plaintext
+NAN[Not A Number].
+```
+
+
+
+---
+## Boolean Input
+
+
+ Ques1:
+```
+boolean x = false;
+System.out.println(x);
+````
+
+Output:
+```
+false.
+```
+
+boolean -> true / false only, it will work on True/False, but give answer in lowercase only.
+
+Ques2:
+```
+
+Input: true
+Scanner sc = new Scanner(System.in);
+boolean y = sc.nextBoolean();
+System.out.println(y);
+```
+
+Output:
+```
+true
+```
+### Take inputs like True/False/false also.
+
+---
+## Arithmetic Operators
+
++, -, *, / are very basic arithmetic operators. Confirm whether the students know about them. And directly give the below quiz.
+
+---
+
+
+# Question
+What will be the output?
+```
+int a = 10;
+int b = 24;
+System.out.println(a+b);
+System.out.println(a-b);
+System.out.println(a*b);
+System.out.println(b/a);
+```
+
+# Choices
+- [ ] 34-14
240
2.4 +- [ ] 34
14
240
2 +- [x] 34
-14
240
2 +- [ ] None of them + +--- + + +# Explanation + +a + b -> 10 + 24 = 34 +a - b -> 10 - 24 = -14 +a * b -> 10 * 24 = 240 +b / a -> 24 / 10 = 2 (Because both are integers, so the result should be an integer.) + +--- + +One more arithmetic operator: +% -> Modulus Operator (Gives remainder of divison of two numbers as output) + +### Examples +12 % 4 = 0 +9 % 7 = 2 +24 % 5 = 4 + +Now, give the following quiz. + + +--- + + +# Question +What will be the output? +``` +System.out.print(36 % 6); +``` + +# Choices +- [ ] 3 +- [ ] 6 +- [x] 0 +- [ ] Error + + +--- + + +# Question +What will be the output? +``` +System.out.print(5 % 3); +``` + +# Choices +- [ ] 1 +- [x] 2 +- [ ] 3 +- [ ] Error + +If necessary, take some more examples. + + +--- + + +**Q.** What are Relational operators? +**A.** Relational operators are used to check the relations between two operands. After comparison, the relational operators return a boolean value. + +**Syntax:** +``` +operand1 relational_operator operand2 +``` + + +| Relation between a and b | Syntax | a = 45, b = 16 | a = 5, b = 5 | +|:-------------------------------:|:------:|:--------------:|:------------:| +| a is greater than b | a > b | True | False | +| a is less than b | a < b | False | False | +| a is greater than or equal to b | a >= b | True | True | +| a is less than or equal to b | a <= b | False | True | +| a is equal to b | a == b | False | True | +| a is not equal to b | a != b | True | False | + + +**Note:** Explain the difference between assignment operator (=) and equality operator (==). + diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner Data Types.md b/Academy DSA Typed Notes/Beginner Language/Beginner Data Types.md new file mode 100644 index 0000000..2d4d118 --- /dev/null +++ b/Academy DSA Typed Notes/Beginner Language/Beginner Data Types.md @@ -0,0 +1,722 @@ +# Beginner: Data Types + +--- + +# Agenda + +* Quizes to revise the previous session +* Rules of Naming a variable +* Different categories of Data + * Why we need multiple datatype under one category + * Int Vs Long +* TypeCasting + +:::success +There are a lot of quizzes in this session, please take some time to think about the solution on your own before reading further..... +::: + +--- + +# Question + +What will be output for this ? +``` +System.out.print(12 + 4 + "try" + 3 * 4); +``` +# Choices +- [ ] Error +- [ ] 124try34 +- [ ] 16try34 +- [x] 16try12 + + +--- + +# Question + +``` +Declare a int variable with name x and intialize with value 10 +``` + +# Choices +- [ ] x int = 10; +- [ ] int x = 20 +- [x] int x = 10; +- [ ] None of them + +--- + + +# Question +``` +int x = 10; +int y = 20; +System.out.print(x + y); +``` + +# Choices +- [ ] Error +- [ ] x + y +- [x] 30 +- [ ] 1020 + + +--- + + +# Question +``` +int x = 10; +int y = 20; +System.out.print(x + " " + y); +``` + +# Choices + +- [ ] 1020 +- [ ] Error +- [x] 10 20 +- [ ] 30 + + +--- + +# Question +``` +int try = 10; +System.out.print(Try); +``` +# Choices + +- [ ] 10 +- [ ] Try +- [x] Error + +--- + + +# Question +``` +System.out.print(x); +int x = 10; +``` +# Choices +- [ ] x +- [ ] 10 +- [x] Error +- [ ] None of the above + +--- + + +**Rule:** In order to use a variable we need to declare and initialise it first. + +--- + + +# Question +``` +int x = 10; +System.out.print(x + y); +int y = 20; +``` +# Choices +- [ ] 30 +- [ ] 10y +- [x] Error +- [ ] None of them + + +--- + + +# Question +``` +int x = 10; +int x = 20; +System.out.print(x); +``` +# Choices +- [ ] 10 +- [ ] 20 +- [x] Error +- [ ] None of them + +--- + + +**Explanation:** +Here, when we write `int x = 10;`, we are declaring and initialising a variable "x". +Now when we write this statement, `int x = 20;`, again a variable is created of type int, and name x with value 20. +But this is not possible, we cannot have 2 variables with same name. + + +## **Rule:** We cannot have 2 variables with same name. + +--- + + +# Question +``` +int x = 20; +System.out.println(x); +x = 40; +System.out.print(x); +``` +# Choices +- [ ] 2040 +- [ ] Error +- [x] 20 40 + +--- + +**Explanation:** +Here, when we write `int x = 20;` , a variable is created of type int and name x. +But `x= 40` means we are not creating the variable, instead changing the value of the variable. This line will change the value of x to 40. + + +--- + + +# Question +``` +int x = 20; +int y = 40; +x = y + 10; +System.out.print(x); +``` + +# Choices + +- [ ] 70 +- [ ] 60 +- [x] 50 + +--- + + +**Explanation:** + +With very first line,
 +
+All of them store water.
+Difference lies in their storage capacity.
+
+
+
+| category | small | medium | large |
+|:--------:|:----------:|:------:|:-----:|
+| 500ml | yes [ideal] | yes | yes |
+| 15L | no | no | yes |
+
+
+---
+
+### Int Vs Long:
+They both have different range.
+
+**int:**
+
+All of them store water.
+Difference lies in their storage capacity.
+
+
+
+| category | small | medium | large |
+|:--------:|:----------:|:------:|:-----:|
+| 500ml | yes [ideal] | yes | yes |
+| 15L | no | no | yes |
+
+
+---
+
+### Int Vs Long:
+They both have different range.
+
+**int:**  +
+**approx:**
+
+**approx:**  +
+
+**long:**
+
+
+**long:** +
+
+**approx:**
+
+
+**approx:**  +
+1. We can easily transfer water from 5L bucket to 20; bucket.
+From smaller storage to higher storage, we can easily do it.
+
+
+
+1. We can easily transfer water from 5L bucket to 20; bucket.
+From smaller storage to higher storage, we can easily do it.
+
+ +
+2. We can again transfer water from 20L bucket to 5L bucket, if the water level is less than 5L.
+
+
+
+2. We can again transfer water from 20L bucket to 5L bucket, if the water level is less than 5L.
+
+ +
+3. We have 8L of water in 20l bucket, now this time when we try to transfer it to 5L bucket, overflow will happen. Water will flow outside of the bucket as well. It will spill.
+
+**Replicate the example with data types:**
+5L bucket: int
+20L bucket: long.
+
+4. Easily transfer data from int(smaller) to long(bigger).
+
+---
+
+# Question
+```
+int a = 1000;
+long b = a;
+System.out.print(b);
+```
+# Choices
+- [x] 1000
+- [ ] Error
+
+---
+
+**Explanation:**
+Here,`int a = 1000;` we are trying to create a int type variable of name a, value 1000.
+Now `long b = a;` with this we create a long type variable, name b.
+b = 1000.
+And we can easily store 1000 in long.
+
+**It is Implicit/Widening TypeCasting(automatic).**
+
+---
+
+# Question
+```
+long x = 10000;
+System.out.print(x);
+```
+
+# Choices
+- [x] 1000
+- [ ] Error
+
+---
+
+**Explanation:**
+Java considers non decimal number as int.
+Therefore, the value 10000 is considered as int and we are trying to store int value into long which is possible.
+Int to Long is implicit typecasting.
+
+---
+
+# Question
+
+```
+long x = 10000;
+int y = x;
+System.out.print(y);
+```
+
+# Choices
+- [ ] 1000
+- [x] Error
+
+---
+
+**Explanation:**
+`long x = 10000` It is implicit typecasting.
+But, `int y = x;` Here we are trying to store long value into int container.
+Error: Possible lossy conversion.
+
+---
+
+# Question
+```
+long x = 1000;
+int y = (int)x;
+System.out.print(y);
+```
+
+# Choices
+- [x] 1000
+- [ ] Error
+
+---
+
+**Explanation:**
+
+Here we are doing Explicit/Narrowing Typecasting from long to int.
+
+
+---
+
+# Question
+
+```
+long a = 10^10;
+int b = (int)a;
+System.out.print(b);
+```
+
+# Choices
+- [ ] 10^10
+- [ ] 10^10L
+- [x] Error
+- [ ] Some random value
+
+---
+
+**Explanation:**
+
+Here, value 10^10 is too large for int.
+Ans = Error, Integer number too large.
+
+
+---
+
+# Question
+```
+long a = 10^10L;
+int b = (int)a;
+System.out.print(b);
+```
+
+
+# Choices
+- [ ] 10^10
+- [ ] 10^10L
+- [ ] Error
+- [x] Some random value
+
+---
+**Explanation:**
+
+Here, We are specifying L so compiler considers 10^10 as long only and then we are trying to store in a long container only which is possible.
+After that in next line we are doing explicit typecasting, but then also we know that this number is out of range of int.
+We are actually forcing the compiler to do it, data loss will happen.
+
+---
+Some quizzes to revise
+
+---
+
+# Question
+
+```
+int a = (int)10000000000L;
+System.out.print(a);
+```
+
+# Choices
+- [x] Some Random Value
+- [ ] Error
+- [ ] Very Complicated
+
+---
+
+
+# Question
+
+```
+int a = (int)10000000000;
+System.out.print(a);
+```
+
+# Choices
+- [ ] Some Random Value
+- [x] Error
+- [ ] 10000000000
+
diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner Patterns 1.md b/Academy DSA Typed Notes/Beginner Language/Beginner Patterns 1.md
new file mode 100644
index 0000000..4b66446
--- /dev/null
+++ b/Academy DSA Typed Notes/Beginner Language/Beginner Patterns 1.md
@@ -0,0 +1,597 @@
+# Patterns Introduction
+---
+
+## Agenda
+
+**Some abbreviations that will be used in this class:**
+* System.out.print - SOP
+* System.out.println - SOPln
+
+
+
+We will work with patterns today. After this class, the students will feel very comfortable with loops.
+1. Print stars in a single row
+2. Print a square
+3. Print a rectangle
+4. Print staircase
+5. Print reverse staircase
+6. Print special pattern
+
+
+
+---
+
+# Question
+Loop to print " * " N times in a single row?
+Ex: N = 5, print *****
+N = 9, print *********
+
+# Choices
+- [x] for(int i = 1; i <= N; i++) {
+SOP(" * ");
+}
+- [ ] for(int i = 1; i < N; i++) {
+SOP(" * ");
+}
+- [ ] for(int i = 0; i <= N; i++) {
+SOP(" * ");
+}
+
+
+
+---
+
+## Explanation
+
+```java
+for(int i = 1; i <= N; i++) {
+ SOP(" * ");
+}
+```
+This choice is correct. The code uses a loop to iterate from `i = 1` to `i = N` (both inclusive). In each iteration, it prints the "*" character using the `SOP("*");` statement. This loop will print "*" N times in a single row, as desired.
+
+
+Certainly, let's take a look at why the other two choices are incorrect:
+
+1. **Incorrect Choice 2:**
+ ```java
+ for (int i = 1; i < N; i++) {
+ SOP(" * ");
+ }
+ ```
+ **Explanation:** This code uses a loop that starts from `i = 1` and continues until `i` is less than `N`. In each iteration, it prints an asterisk. However, this loop only iterates `N - 1` times, which means it will print one less asterisk than the desired value. For example, if `N` is 5, this loop will print `****` (4 asterisks) instead of `*****`.
+
+2. **Incorrect Choice 3:**
+ ```java
+ for (int i = 0; i <= N; i++) {
+ SOP(" * ");
+ }
+ ```
+ **Explanation:** This code uses a loop that starts from `i = 0` and continues until `i` is less than or equal to `N`. In each iteration, it prints an asterisk. However, this loop iterates `N + 1` times, which means it will print one more asterisk than the desired value. For example, if `N` is 5, this loop will print `******` (6 asterisks) instead of `*****`.
+
+
+---
+
+
+### Example 1
+
+This is the quiz question.
+Print N starts " * " in a single row.
+N = 5, *****
+N = 4, ****
+N = 2, **
+
+**Q.** What should be the number of iterations?
+**A.** "N"
+
+
+**Code:**
+
+```
+ public static void main() {
+ Scanner sc = new Scanner(System.in);
+ int n = sc.nextInt();
+ for (int i = 1; i <= n; i++) {
+ System.out.print(" * ");
+ }
+ }
+```
+Dry run the codes and justify why Option 1 is correct for some values of N.
+
+---
+
+### Example 2
+Print a square (N * N) of stars.
+
+For example,
+
+N = 4
+```plaintext
+****
+****
+****
+****
+```
+
+N = 5
+```plaintext
+*****
+*****
+*****
+*****
+*****
+```
+
+**Q.** If you have to repeat a single task N number of tasks, how to do that?
+**A.** We can write a loop.
+
+
+Now, this questions is similar to repeating 1st task N number of times.
+So, the code can be:
+
+```
+for (int i = 1; i <= N; i++) {
+ for (int i = 1; i <= N; i++) {
+ SOP(" * ");
+ }
+ SOPln();
+}
+```
+
+Ask students if this code is correct. It's not, because we cannot repeat variable 'i' in java.
+So, the final correct code is:
+
+```
+for (int i = 1; i <= N; i++) {
+ for (int j = 1; j <= N; j++) {
+ SOP(" * ");
+ }
+ SOPln();
+}
+```
+
+Explain why we need `SOPln()` after the 2nd for loop.
+
+**Explanation:**
+Without the `SOPln()` statement after the inner loop, all the asterisks would be printed in a single continuous line, and the pattern would not be formed with rows and columns. The `SOPln()` call ensures that each row of asterisks is printed on a new line, creating the desired pattern.
+
+Dry run the above code for N = 3.
+
+
+
+3. We have 8L of water in 20l bucket, now this time when we try to transfer it to 5L bucket, overflow will happen. Water will flow outside of the bucket as well. It will spill.
+
+**Replicate the example with data types:**
+5L bucket: int
+20L bucket: long.
+
+4. Easily transfer data from int(smaller) to long(bigger).
+
+---
+
+# Question
+```
+int a = 1000;
+long b = a;
+System.out.print(b);
+```
+# Choices
+- [x] 1000
+- [ ] Error
+
+---
+
+**Explanation:**
+Here,`int a = 1000;` we are trying to create a int type variable of name a, value 1000.
+Now `long b = a;` with this we create a long type variable, name b.
+b = 1000.
+And we can easily store 1000 in long.
+
+**It is Implicit/Widening TypeCasting(automatic).**
+
+---
+
+# Question
+```
+long x = 10000;
+System.out.print(x);
+```
+
+# Choices
+- [x] 1000
+- [ ] Error
+
+---
+
+**Explanation:**
+Java considers non decimal number as int.
+Therefore, the value 10000 is considered as int and we are trying to store int value into long which is possible.
+Int to Long is implicit typecasting.
+
+---
+
+# Question
+
+```
+long x = 10000;
+int y = x;
+System.out.print(y);
+```
+
+# Choices
+- [ ] 1000
+- [x] Error
+
+---
+
+**Explanation:**
+`long x = 10000` It is implicit typecasting.
+But, `int y = x;` Here we are trying to store long value into int container.
+Error: Possible lossy conversion.
+
+---
+
+# Question
+```
+long x = 1000;
+int y = (int)x;
+System.out.print(y);
+```
+
+# Choices
+- [x] 1000
+- [ ] Error
+
+---
+
+**Explanation:**
+
+Here we are doing Explicit/Narrowing Typecasting from long to int.
+
+
+---
+
+# Question
+
+```
+long a = 10^10;
+int b = (int)a;
+System.out.print(b);
+```
+
+# Choices
+- [ ] 10^10
+- [ ] 10^10L
+- [x] Error
+- [ ] Some random value
+
+---
+
+**Explanation:**
+
+Here, value 10^10 is too large for int.
+Ans = Error, Integer number too large.
+
+
+---
+
+# Question
+```
+long a = 10^10L;
+int b = (int)a;
+System.out.print(b);
+```
+
+
+# Choices
+- [ ] 10^10
+- [ ] 10^10L
+- [ ] Error
+- [x] Some random value
+
+---
+**Explanation:**
+
+Here, We are specifying L so compiler considers 10^10 as long only and then we are trying to store in a long container only which is possible.
+After that in next line we are doing explicit typecasting, but then also we know that this number is out of range of int.
+We are actually forcing the compiler to do it, data loss will happen.
+
+---
+Some quizzes to revise
+
+---
+
+# Question
+
+```
+int a = (int)10000000000L;
+System.out.print(a);
+```
+
+# Choices
+- [x] Some Random Value
+- [ ] Error
+- [ ] Very Complicated
+
+---
+
+
+# Question
+
+```
+int a = (int)10000000000;
+System.out.print(a);
+```
+
+# Choices
+- [ ] Some Random Value
+- [x] Error
+- [ ] 10000000000
+
diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner Patterns 1.md b/Academy DSA Typed Notes/Beginner Language/Beginner Patterns 1.md
new file mode 100644
index 0000000..4b66446
--- /dev/null
+++ b/Academy DSA Typed Notes/Beginner Language/Beginner Patterns 1.md
@@ -0,0 +1,597 @@
+# Patterns Introduction
+---
+
+## Agenda
+
+**Some abbreviations that will be used in this class:**
+* System.out.print - SOP
+* System.out.println - SOPln
+
+
+
+We will work with patterns today. After this class, the students will feel very comfortable with loops.
+1. Print stars in a single row
+2. Print a square
+3. Print a rectangle
+4. Print staircase
+5. Print reverse staircase
+6. Print special pattern
+
+
+
+---
+
+# Question
+Loop to print " * " N times in a single row?
+Ex: N = 5, print *****
+N = 9, print *********
+
+# Choices
+- [x] for(int i = 1; i <= N; i++) {
+SOP(" * ");
+}
+- [ ] for(int i = 1; i < N; i++) {
+SOP(" * ");
+}
+- [ ] for(int i = 0; i <= N; i++) {
+SOP(" * ");
+}
+
+
+
+---
+
+## Explanation
+
+```java
+for(int i = 1; i <= N; i++) {
+ SOP(" * ");
+}
+```
+This choice is correct. The code uses a loop to iterate from `i = 1` to `i = N` (both inclusive). In each iteration, it prints the "*" character using the `SOP("*");` statement. This loop will print "*" N times in a single row, as desired.
+
+
+Certainly, let's take a look at why the other two choices are incorrect:
+
+1. **Incorrect Choice 2:**
+ ```java
+ for (int i = 1; i < N; i++) {
+ SOP(" * ");
+ }
+ ```
+ **Explanation:** This code uses a loop that starts from `i = 1` and continues until `i` is less than `N`. In each iteration, it prints an asterisk. However, this loop only iterates `N - 1` times, which means it will print one less asterisk than the desired value. For example, if `N` is 5, this loop will print `****` (4 asterisks) instead of `*****`.
+
+2. **Incorrect Choice 3:**
+ ```java
+ for (int i = 0; i <= N; i++) {
+ SOP(" * ");
+ }
+ ```
+ **Explanation:** This code uses a loop that starts from `i = 0` and continues until `i` is less than or equal to `N`. In each iteration, it prints an asterisk. However, this loop iterates `N + 1` times, which means it will print one more asterisk than the desired value. For example, if `N` is 5, this loop will print `******` (6 asterisks) instead of `*****`.
+
+
+---
+
+
+### Example 1
+
+This is the quiz question.
+Print N starts " * " in a single row.
+N = 5, *****
+N = 4, ****
+N = 2, **
+
+**Q.** What should be the number of iterations?
+**A.** "N"
+
+
+**Code:**
+
+```
+ public static void main() {
+ Scanner sc = new Scanner(System.in);
+ int n = sc.nextInt();
+ for (int i = 1; i <= n; i++) {
+ System.out.print(" * ");
+ }
+ }
+```
+Dry run the codes and justify why Option 1 is correct for some values of N.
+
+---
+
+### Example 2
+Print a square (N * N) of stars.
+
+For example,
+
+N = 4
+```plaintext
+****
+****
+****
+****
+```
+
+N = 5
+```plaintext
+*****
+*****
+*****
+*****
+*****
+```
+
+**Q.** If you have to repeat a single task N number of tasks, how to do that?
+**A.** We can write a loop.
+
+
+Now, this questions is similar to repeating 1st task N number of times.
+So, the code can be:
+
+```
+for (int i = 1; i <= N; i++) {
+ for (int i = 1; i <= N; i++) {
+ SOP(" * ");
+ }
+ SOPln();
+}
+```
+
+Ask students if this code is correct. It's not, because we cannot repeat variable 'i' in java.
+So, the final correct code is:
+
+```
+for (int i = 1; i <= N; i++) {
+ for (int j = 1; j <= N; j++) {
+ SOP(" * ");
+ }
+ SOPln();
+}
+```
+
+Explain why we need `SOPln()` after the 2nd for loop.
+
+**Explanation:**
+Without the `SOPln()` statement after the inner loop, all the asterisks would be printed in a single continuous line, and the pattern would not be formed with rows and columns. The `SOPln()` call ensures that each row of asterisks is printed on a new line, creating the desired pattern.
+
+Dry run the above code for N = 3.
+
+ +
+
+
+---
+
+### Example 3
+Print rectangle of N * M having stars.
+N rows having M stars in each row.
+
+For example,
+
+N = 4, M = 3
+```plaintext
+***
+***
+***
+***
+```
+N = 2, M = 4
+```plaintext
+****
+****
+```
+
+Outer loop -> N times
+Inner loop -> M times
+
+The correct code is:
+```
+for (int i = 1; i <= N; i++) {
+ for (int j = 1; j <= M; j++) {
+ SOP(" * ");
+ }
+ SOPln();
+}
+```
+
+**Note:** Mention that the starting values does not matter. Just that the number of iterations should be N.
+
+Dry run for N = 2, M = 3.
+
+
+
+
+
+---
+
+### Example 3
+Print rectangle of N * M having stars.
+N rows having M stars in each row.
+
+For example,
+
+N = 4, M = 3
+```plaintext
+***
+***
+***
+***
+```
+N = 2, M = 4
+```plaintext
+****
+****
+```
+
+Outer loop -> N times
+Inner loop -> M times
+
+The correct code is:
+```
+for (int i = 1; i <= N; i++) {
+ for (int j = 1; j <= M; j++) {
+ SOP(" * ");
+ }
+ SOPln();
+}
+```
+
+**Note:** Mention that the starting values does not matter. Just that the number of iterations should be N.
+
+Dry run for N = 2, M = 3.
+
+ +
+
+**Observation Table:**
+
+| Row | Stars |
+|:---:|:-----:|
+| 1 | 3 |
+| 2 | 3 |
+
+
+ith row => M stars
+and a total N rows
+
+
+---
+
+### Example 4
+Print staircase pattern.
+For example,
+
+N = 4
+```plaintext
+*
+**
+***
+****
+```
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+Observe for each row number i, we have i stars in that row.
+
+Outer Loop -> N times
+Inner Loop -> i times
+Inner loop does not work for constant number of times.
+
+**Observation Table:**
+
+| Row | Stars |
+|:---:|:-----:|
+| 1 | 1 |
+| 2 | 2 |
+| 3 | 3 |
+| 4 | 4 |
+| 5 | 5 |
+
+
+ith row => i stars
+
+
+The correct code is:
+```
+for (int i = 1; i <= N; i++) {
+
+ // Loop to print i stars.
+ for (int j = 1; j <= i; j++) {
+ SOP(" * ");
+ }
+ SOPln();
+}
+```
+
+Dry run this code for N = 4 (Given image is incomplete).
+You may complete the dry run or stop in-between according to the batch.
+
+
+
+
+**Observation Table:**
+
+| Row | Stars |
+|:---:|:-----:|
+| 1 | 3 |
+| 2 | 3 |
+
+
+ith row => M stars
+and a total N rows
+
+
+---
+
+### Example 4
+Print staircase pattern.
+For example,
+
+N = 4
+```plaintext
+*
+**
+***
+****
+```
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+Observe for each row number i, we have i stars in that row.
+
+Outer Loop -> N times
+Inner Loop -> i times
+Inner loop does not work for constant number of times.
+
+**Observation Table:**
+
+| Row | Stars |
+|:---:|:-----:|
+| 1 | 1 |
+| 2 | 2 |
+| 3 | 3 |
+| 4 | 4 |
+| 5 | 5 |
+
+
+ith row => i stars
+
+
+The correct code is:
+```
+for (int i = 1; i <= N; i++) {
+
+ // Loop to print i stars.
+ for (int j = 1; j <= i; j++) {
+ SOP(" * ");
+ }
+ SOPln();
+}
+```
+
+Dry run this code for N = 4 (Given image is incomplete).
+You may complete the dry run or stop in-between according to the batch.
+
+ +
+
+---
+
+
+### Example 5
+
+> **Note for instructor:** Give some context of why we are learning this approach. Like, as similar approach will work in majority of pattern questions
+
+Print reverse staircase pattern.
+For example,
+N = 4
+```plaintext
+****
+***
+**
+*
+```
+
+N = 5
+```plaintext
+*****
+****
+***
+**
+*
+```
+
+For N = 5, we are printing stars in the following manner.
+
+
+
+
+---
+
+
+### Example 5
+
+> **Note for instructor:** Give some context of why we are learning this approach. Like, as similar approach will work in majority of pattern questions
+
+Print reverse staircase pattern.
+For example,
+N = 4
+```plaintext
+****
+***
+**
+*
+```
+
+N = 5
+```plaintext
+*****
+****
+***
+**
+*
+```
+
+For N = 5, we are printing stars in the following manner.
+
+ +
+Row + star = N + 1
+So, star = N + 1 - Row
+Observe for each row number i, we have N - i + 1 stars in that row.
+
+Outer Loop -> N times
+Inner Loop -> N - i + 1 times
+Inner loop does not work for constant number of times.
+
+The correct code is:
+```java
+for (int i = 1; i <= N; i++) {
+
+ // Loop to print N - i + 1 stars.
+ for (int j = 1; j <= N - i + 1; j++) {
+ SOP(" * ");
+ }
+ SOPln();
+}
+```
+
+Dry run the code for N = 3.
+
+
+
+Row + star = N + 1
+So, star = N + 1 - Row
+Observe for each row number i, we have N - i + 1 stars in that row.
+
+Outer Loop -> N times
+Inner Loop -> N - i + 1 times
+Inner loop does not work for constant number of times.
+
+The correct code is:
+```java
+for (int i = 1; i <= N; i++) {
+
+ // Loop to print N - i + 1 stars.
+ for (int j = 1; j <= N - i + 1; j++) {
+ SOP(" * ");
+ }
+ SOPln();
+}
+```
+
+Dry run the code for N = 3.
+
+ +
+---
+
+
+#### Another Approach
+
+
+
+---
+
+
+#### Another Approach
+
+ +
+In this approach, we will change the starting value of i itself.
+
+The correct code is:
+```
+for (int i = N; i >= 1; i--) {
+
+ // Loop to print i stars.
+ for (int j = 1; j <= i; j++) {
+ SOP(" * ");
+ }
+ SOPln();
+}
+```
+
+
+---
+
+### Example 6
+Print the diamond pattern.
+
+For example,
+N = 5
+
+```plaintext
+**********
+****--****
+***----***
+**------**
+*--------*
+*--------*
+**------**
+***----***
+****--****
+**********
+```
+
+
+
+In this approach, we will change the starting value of i itself.
+
+The correct code is:
+```
+for (int i = N; i >= 1; i--) {
+
+ // Loop to print i stars.
+ for (int j = 1; j <= i; j++) {
+ SOP(" * ");
+ }
+ SOPln();
+}
+```
+
+
+---
+
+### Example 6
+Print the diamond pattern.
+
+For example,
+N = 5
+
+```plaintext
+**********
+****--****
+***----***
+**------**
+*--------*
+*--------*
+**------**
+***----***
+****--****
+**********
+```
+
+ +
+You are only supposed to print star " * ", but not underscores (they should be spaces).
+
+If N = 5, so 10 rows are needed.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+The pattern can be broken into two halves.
+
+
+
+You are only supposed to print star " * ", but not underscores (they should be spaces).
+
+If N = 5, so 10 rows are needed.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+The pattern can be broken into two halves.
+
+ +
+Again, we can break this pattern into halves again.
+
+
+
+Again, we can break this pattern into halves again.
+
+ +
+For the right quarter, we need to print some spaces first and then stars.
+The table shows for each row, how many spaces and stars need to be printed.
+
+
+
+For the right quarter, we need to print some spaces first and then stars.
+The table shows for each row, how many spaces and stars need to be printed.
+
+ +
+Combining everything for the first half, we have the following table.
+
+
+
+Combining everything for the first half, we have the following table.
+
+ +
+In one single row,
+
+print (N + 1 - i) stars + (i - 1) spaces + (i - 1) spaces + (N + 1 - i) stars
+
+So, print (N + 1 - i) stars + 2 * (i - 1) spaces + (N + 1 - i) stars
+So, let's write the code for the upper half using the above facts.
+
+```
+for (int i = 1; i <= N; i++) {
+
+ // In each row, print N + 1 - i stars.
+ for (int j = 1; j <= N + 1 - i; j++) {
+ SOP(" * ");
+ }
+
+ // In each row, (i - 1) spaces.
+ for (int j = 1; j <= 2 * (i - 1); j++) {
+ SOP(" _ ");
+ }
+
+ // In each row, print N + 1 - i stars.
+ for (int j = 1; j <= N + 1 - i; j++) {
+ SOP(" * ");
+ }
+ SOPln();
+}
+```
+
+**Lower Half:**
+
+
+
+In one single row,
+
+print (N + 1 - i) stars + (i - 1) spaces + (i - 1) spaces + (N + 1 - i) stars
+
+So, print (N + 1 - i) stars + 2 * (i - 1) spaces + (N + 1 - i) stars
+So, let's write the code for the upper half using the above facts.
+
+```
+for (int i = 1; i <= N; i++) {
+
+ // In each row, print N + 1 - i stars.
+ for (int j = 1; j <= N + 1 - i; j++) {
+ SOP(" * ");
+ }
+
+ // In each row, (i - 1) spaces.
+ for (int j = 1; j <= 2 * (i - 1); j++) {
+ SOP(" _ ");
+ }
+
+ // In each row, print N + 1 - i stars.
+ for (int j = 1; j <= N + 1 - i; j++) {
+ SOP(" * ");
+ }
+ SOPln();
+}
+```
+
+**Lower Half:**
+
+ +
+For lower part, we can directly write the following table:
+
+
+
+For lower part, we can directly write the following table:
+
+ +
+
+In one single row,
+print i stars + print (N - i) spaces + print (N - i) spaces + i stars
+
+So, print i stars + print 2 * (N - i) spaces + i stars
+So, let's write the code for the upper half using the above facts.
+
+```
+for (int i = 1; i <= N; i++) {
+
+ // In each row, print N + 1 - i stars.
+ for (int j = 1; j <= i; j++) {
+ SOP(" * ");
+ }
+
+ // In each row, (i - 1) spaces.
+ for (int j = 1; j <= 2 * (N - i); j++) {
+ SOP(" _ ");
+ }
+
+ // In each row, print N + 1 - i stars.
+ for (int j = 1; j <= i; j++) {
+ SOP(" * ");
+ }
+ SOPln();
+}
+```
+
+Combining these 2 codes we get, the diamond pattern.
+
+
+---
+
+
+### Example 7
+Print the following pattern:
+
+For example,
+
+N = 5
+```plaintext
+1
+2 3
+4 5 6
+7 8 9 10
+11 12 13 14 15
+```
+
+N = 4
+```plaintext
+1
+2 3
+4 5 6
+7 8 9 10
+```
+
+We will create a variable and print that variable. After printing, we increment it.
+
+```
+int val = 1;
+for (int i = 1; i <= N; i++) {
+ for (int j = 1; j <= i; j++) {
+ SOP(val);
+ val++;
+ }
+ SOPln();
+}
+```
+
+
+**Explanation:**
+
+In the given approach we have initialized a variable `val` to 1. It employs an outer loop that iterates from 1 to N, governing the rows. Within this loop, an inner loop runs from 1 to the current value of the outer loop index, controlling the values within each row. It prints the value of `val`, increments it, and then proceeds with the next iteration of the inner loop. This structure creates a pattern where each row holds an increasing sequence of numbers. The `SOPln()` statement at the end of the outer loop iteration ensures a new line for the subsequent row. By iteratively printing values and managing rows through nested loops, the code systematically generates the desired pattern of numbers.
+
+
+---
+
+
+### Example 8
+Print the following pattern:
+For example,
+
+N = 5
+```plaintext
+1
+1 2
+1 2 3
+1 2 3 4
+1 2 3 4 5
+```
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+**Approach 1:**
+```
+for (int i = 1; i <= N; i++) {
+
+ int val = 1;
+ for (int j = 1; j <= i; j++) {
+ SOP(val);
+ val++;
+ }
+ SOPln();
+}
+```
+
+**Approach 2:**
+In this approach instead of taking an extra variable we can directly print j.
+```
+for (int i = 1; i <= N; i++) {
+ for (int j = 1; j <= i; j++) {
+ SOP(j);
+ }
+ SOPln();
+}
+```
+
+---
+
+
+### Example 9
+
+Print the following pattern.
+For example,
+
+N = 5
+```plaintext
+1
+2 3
+3 4 5
+4 5 6 7
+5 6 7 8 9
+```
+
+The pattern now starts at each row with that row number. So, only 1 change is required i.e, in the initial value of val.
+
+The correct code for this pattern is:
+```
+for (int i = 1; i <= N; i++) {
+
+ int val = i;
+ for (int j = 1; j <= i; j++) {
+ SOP(val);
+ val++;
+ }
+ SOPln();
+}
+```
+
+---
\ No newline at end of file
diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner Patterns 2 & Introduction to Strings.md b/Academy DSA Typed Notes/Beginner Language/Beginner Patterns 2 & Introduction to Strings.md
new file mode 100644
index 0000000..9149d7b
--- /dev/null
+++ b/Academy DSA Typed Notes/Beginner Language/Beginner Patterns 2 & Introduction to Strings.md
@@ -0,0 +1,550 @@
+# Beginner: Patterns 2 & Introduction to Strings
+
+---
+
+### Agenda
+
+1. Print reverse triangle V
+2. Print numeric triangle /\
+3. Strings
+4. next() vs nextLine()
+5. How to deal with different type of inputs
+6. Character Pattern
+
+---
+
+### Problem Statement
+Print the following pattern:
+
+For example,
+
+N = 5
+```
+* * * * *
+ * * * *
+ * * *
+ * *
+ *
+```
+
+N = 4
+```
+* * * *
+ * * *
+ * *
+ *
+```
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Observation
+Lets consider the spaces as "_"
+```
+* _ * _ * _ * _ * _
+_ * _ * _ * _ * _
+_ _ * _ * _ * _
+_ _ _ * _ * _
+_ _ _ _ * _
+```
+
+Now lets assume we are removing the spaces after every '*', then
+```
+* * * * *
+_ * * * *
+_ _ * * *
+_ _ _ * *
+_ _ _ _ *
+```
+
+
+
+In one single row,
+print i stars + print (N - i) spaces + print (N - i) spaces + i stars
+
+So, print i stars + print 2 * (N - i) spaces + i stars
+So, let's write the code for the upper half using the above facts.
+
+```
+for (int i = 1; i <= N; i++) {
+
+ // In each row, print N + 1 - i stars.
+ for (int j = 1; j <= i; j++) {
+ SOP(" * ");
+ }
+
+ // In each row, (i - 1) spaces.
+ for (int j = 1; j <= 2 * (N - i); j++) {
+ SOP(" _ ");
+ }
+
+ // In each row, print N + 1 - i stars.
+ for (int j = 1; j <= i; j++) {
+ SOP(" * ");
+ }
+ SOPln();
+}
+```
+
+Combining these 2 codes we get, the diamond pattern.
+
+
+---
+
+
+### Example 7
+Print the following pattern:
+
+For example,
+
+N = 5
+```plaintext
+1
+2 3
+4 5 6
+7 8 9 10
+11 12 13 14 15
+```
+
+N = 4
+```plaintext
+1
+2 3
+4 5 6
+7 8 9 10
+```
+
+We will create a variable and print that variable. After printing, we increment it.
+
+```
+int val = 1;
+for (int i = 1; i <= N; i++) {
+ for (int j = 1; j <= i; j++) {
+ SOP(val);
+ val++;
+ }
+ SOPln();
+}
+```
+
+
+**Explanation:**
+
+In the given approach we have initialized a variable `val` to 1. It employs an outer loop that iterates from 1 to N, governing the rows. Within this loop, an inner loop runs from 1 to the current value of the outer loop index, controlling the values within each row. It prints the value of `val`, increments it, and then proceeds with the next iteration of the inner loop. This structure creates a pattern where each row holds an increasing sequence of numbers. The `SOPln()` statement at the end of the outer loop iteration ensures a new line for the subsequent row. By iteratively printing values and managing rows through nested loops, the code systematically generates the desired pattern of numbers.
+
+
+---
+
+
+### Example 8
+Print the following pattern:
+For example,
+
+N = 5
+```plaintext
+1
+1 2
+1 2 3
+1 2 3 4
+1 2 3 4 5
+```
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+**Approach 1:**
+```
+for (int i = 1; i <= N; i++) {
+
+ int val = 1;
+ for (int j = 1; j <= i; j++) {
+ SOP(val);
+ val++;
+ }
+ SOPln();
+}
+```
+
+**Approach 2:**
+In this approach instead of taking an extra variable we can directly print j.
+```
+for (int i = 1; i <= N; i++) {
+ for (int j = 1; j <= i; j++) {
+ SOP(j);
+ }
+ SOPln();
+}
+```
+
+---
+
+
+### Example 9
+
+Print the following pattern.
+For example,
+
+N = 5
+```plaintext
+1
+2 3
+3 4 5
+4 5 6 7
+5 6 7 8 9
+```
+
+The pattern now starts at each row with that row number. So, only 1 change is required i.e, in the initial value of val.
+
+The correct code for this pattern is:
+```
+for (int i = 1; i <= N; i++) {
+
+ int val = i;
+ for (int j = 1; j <= i; j++) {
+ SOP(val);
+ val++;
+ }
+ SOPln();
+}
+```
+
+---
\ No newline at end of file
diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner Patterns 2 & Introduction to Strings.md b/Academy DSA Typed Notes/Beginner Language/Beginner Patterns 2 & Introduction to Strings.md
new file mode 100644
index 0000000..9149d7b
--- /dev/null
+++ b/Academy DSA Typed Notes/Beginner Language/Beginner Patterns 2 & Introduction to Strings.md
@@ -0,0 +1,550 @@
+# Beginner: Patterns 2 & Introduction to Strings
+
+---
+
+### Agenda
+
+1. Print reverse triangle V
+2. Print numeric triangle /\
+3. Strings
+4. next() vs nextLine()
+5. How to deal with different type of inputs
+6. Character Pattern
+
+---
+
+### Problem Statement
+Print the following pattern:
+
+For example,
+
+N = 5
+```
+* * * * *
+ * * * *
+ * * *
+ * *
+ *
+```
+
+N = 4
+```
+* * * *
+ * * *
+ * *
+ *
+```
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Observation
+Lets consider the spaces as "_"
+```
+* _ * _ * _ * _ * _
+_ * _ * _ * _ * _
+_ _ * _ * _ * _
+_ _ _ * _ * _
+_ _ _ _ * _
+```
+
+Now lets assume we are removing the spaces after every '*', then
+```
+* * * * *
+_ * * * *
+_ _ * * *
+_ _ _ * *
+_ _ _ _ *
+```
+ +
+While printing stars, remember to print a space after every star, to get the our required reverse triangle pattern.
+
+### Code
+
+```java
+for (int i = 0; i < N; i++) {
+
+ //loop to print i spaces
+ for (int j = 1; j <= i; j++) {
+ System.out.print(" ");
+ }
+
+ //loop to print n-i stars
+ for (int j = 1; j <= n - i; j++) {
+ System.out.print("* ");
+ }
+
+ System.out.println();
+}
+```
+
+
+---
+
+### Problem Statement
+Print the following pattern:
+
+For example,
+
+N = 5
+```
+0 0 0 0 1 0 0 0 0
+0 0 0 2 3 2 0 0 0
+0 0 3 4 5 4 3 0 0
+0 4 5 6 7 6 5 4 0
+5 6 7 8 9 8 7 6 5
+```
+N = 4
+```
+0 0 0 1 0 0 0
+0 0 2 3 2 0 0
+0 3 4 5 4 3 0
+4 5 6 7 6 5 4
+```
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Approach
+
+Lets divide the pattern into two halfs,
+
+
+
+While printing stars, remember to print a space after every star, to get the our required reverse triangle pattern.
+
+### Code
+
+```java
+for (int i = 0; i < N; i++) {
+
+ //loop to print i spaces
+ for (int j = 1; j <= i; j++) {
+ System.out.print(" ");
+ }
+
+ //loop to print n-i stars
+ for (int j = 1; j <= n - i; j++) {
+ System.out.print("* ");
+ }
+
+ System.out.println();
+}
+```
+
+
+---
+
+### Problem Statement
+Print the following pattern:
+
+For example,
+
+N = 5
+```
+0 0 0 0 1 0 0 0 0
+0 0 0 2 3 2 0 0 0
+0 0 3 4 5 4 3 0 0
+0 4 5 6 7 6 5 4 0
+5 6 7 8 9 8 7 6 5
+```
+N = 4
+```
+0 0 0 1 0 0 0
+0 0 2 3 2 0 0
+0 3 4 5 4 3 0
+4 5 6 7 6 5 4
+```
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Approach
+
+Lets divide the pattern into two halfs,
+
+ +
+Lets consider the 2 halves separately,
+
+### First Half
+
+| **0** | **0** | **0** | **0** | **1** |
+|-------|-------|-------|-------|-------|
+| **0** | **0** | **0** | **2** | **3** |
+| **0** | **0** | **3** | **4** | **5** |
+| **0** | **4** | **5** | **6** | **7** |
+| **5** | **6** | **7** | **8** | **9** |
+
+Lets create a table, on observing the pattern.
+| row | zeros | start | end |
+|-----|---------|-------|-----------|
+| 1 | 4 [5-1] | 1 | 1 [2\*1-1] |
+| 2 | 3 [5-2] | 2 | 3 [2\*2-1] |
+| 3 | 2 [5-3] | 3 | 5 [2\*3-1] |
+| 4 | 1 [5-4] | 4 | 7 [2\*4-1] |
+| 5 | 0 [5-5] | 5 | 9 [2\*5-1] |
+
+We can come up with an generalized pattern on observing the values of the table based on the value i.
+
+| ith row | (n - i) zeros | starts with i | ends with 2 * i - 1 |
+|---|---|---|---|
+
+### Psuedo code for First Half
+
+```java
+// Printing (n - i) zeros
+for (int j = 1; j <= n - i; j++){
+ System.out.print(0 + " ");
+}
+
+int lim = 2 *i - 1;
+// Printing the increasing numbers from i to 2*i-1
+for (int j = i; j <= lim; j++){
+ System.out.print(j + " ");
+}
+```
+
+### Second Half
+
+| **0** | **0** | **0** | **0** |
+|-------|-------|-------|-------|
+| **2** | **0** | **0** | **0** |
+| **4** | **3** | **0** | **0** |
+| **6** | **5** | **4** | **0** |
+| **8** | **7** | **6** | **5** |
+
+Lets create a table, on observing the pattern.
+
+| row | start | end | zeros |
+|-----|-----------|-----|-------|
+| 1 | | | 4 |
+| 2 | 2 [2\*2-2] | 2 | 3 |
+| 3 | 4 [2\*3-2] | 3 | 2 |
+| 4 | 6 [2\*4-2] | 4 | 1 |
+| 5 | 8 [2\*5-2] | 5 | 0 |
+
+We can come up with an generalized pattern on observing the values of the table based on the value i.
+
+| ith row | starts with (i * 2 - 2) | ends with i | (n i) zeros |
+|---|---|---|---|
+
+Here **starts with (i * 2 - 2)** can be even simplified, by using the end value of the previous calculation as **end - 1**.
+
+
+### Psuedo code for Second Half
+
+```java
+// For the Second Half
+// Printing the decreasing numbers
+int lim = 2 *i - 1;
+for (int j = lim - 1; j >= i; j--){
+ System.out.print(j + " ");
+}
+
+//loop to print n - i zeros
+for (int j = 1; j <= n - i; j++){
+ System.out.print(0 + " ");
+}
+```
+
+
+
+
+### Overall Code
+
+``` java
+for (int i = 1; i <= n; i++){
+
+ // For the First Half
+ //loop to print n - i zeros
+ for (int j = 1; j <= n - i; j++){
+ System.out.print(0 + " ");
+ }
+
+ int lim = 2 *i - 1;
+ // Printing the increasing numbers from i to 2*i-1
+ for (int j = i; j <= lim; j++){
+ System.out.print(j + " ");
+ }
+
+ // For the Second Half
+ // Printing the decreasing numbers
+ for (int j = lim - 1; j >= i; j--){
+ System.out.print(j + " ");
+ }
+
+ //loop to print n - i zeros
+ for (int j = 1; j <= n - i; j++){
+ System.out.print(0 + " ");
+ }
+
+ System.out.println();
+}
+```
+
+
+
+---
+
+### Reading Inputs for Strings
+
+**1. sc.next()-> cannot take spaces as input**
+
+Ques1:
+```java
+Input: "Hello World"
+String s1 = sc.next();
+System.out.println(s1);
+
+String s2 = sc.next();
+System.out.println(s2);
+```
+Output:
+```plaintext
+Hello
+World
+```
+
+Explanation:
+
+s1 will have first word, Hello
+s2 will have next word, World
+
+
+
+
+**2. sc.nextLine() -> can take spaces as well, until next line is encountered.**
+
+Ques1:
+```java
+Input: Hello World
+String s3 = sc.nextLine();
+System.out.println(s3);
+```
+
+Output:
+```plaintext
+Hello World
+```
+
+---
+
+# Question
+Input :
+
+```
+Hello World
+```
+```
+Scanner scn = new Scanner(System.in);
+String str1 = scn.next();
+String str2 = scn.next();
+System.out.println(str1);
+System.out.println(str2);
+```
+
+# Choices
+
+- [x] Hello
+
+Lets consider the 2 halves separately,
+
+### First Half
+
+| **0** | **0** | **0** | **0** | **1** |
+|-------|-------|-------|-------|-------|
+| **0** | **0** | **0** | **2** | **3** |
+| **0** | **0** | **3** | **4** | **5** |
+| **0** | **4** | **5** | **6** | **7** |
+| **5** | **6** | **7** | **8** | **9** |
+
+Lets create a table, on observing the pattern.
+| row | zeros | start | end |
+|-----|---------|-------|-----------|
+| 1 | 4 [5-1] | 1 | 1 [2\*1-1] |
+| 2 | 3 [5-2] | 2 | 3 [2\*2-1] |
+| 3 | 2 [5-3] | 3 | 5 [2\*3-1] |
+| 4 | 1 [5-4] | 4 | 7 [2\*4-1] |
+| 5 | 0 [5-5] | 5 | 9 [2\*5-1] |
+
+We can come up with an generalized pattern on observing the values of the table based on the value i.
+
+| ith row | (n - i) zeros | starts with i | ends with 2 * i - 1 |
+|---|---|---|---|
+
+### Psuedo code for First Half
+
+```java
+// Printing (n - i) zeros
+for (int j = 1; j <= n - i; j++){
+ System.out.print(0 + " ");
+}
+
+int lim = 2 *i - 1;
+// Printing the increasing numbers from i to 2*i-1
+for (int j = i; j <= lim; j++){
+ System.out.print(j + " ");
+}
+```
+
+### Second Half
+
+| **0** | **0** | **0** | **0** |
+|-------|-------|-------|-------|
+| **2** | **0** | **0** | **0** |
+| **4** | **3** | **0** | **0** |
+| **6** | **5** | **4** | **0** |
+| **8** | **7** | **6** | **5** |
+
+Lets create a table, on observing the pattern.
+
+| row | start | end | zeros |
+|-----|-----------|-----|-------|
+| 1 | | | 4 |
+| 2 | 2 [2\*2-2] | 2 | 3 |
+| 3 | 4 [2\*3-2] | 3 | 2 |
+| 4 | 6 [2\*4-2] | 4 | 1 |
+| 5 | 8 [2\*5-2] | 5 | 0 |
+
+We can come up with an generalized pattern on observing the values of the table based on the value i.
+
+| ith row | starts with (i * 2 - 2) | ends with i | (n i) zeros |
+|---|---|---|---|
+
+Here **starts with (i * 2 - 2)** can be even simplified, by using the end value of the previous calculation as **end - 1**.
+
+
+### Psuedo code for Second Half
+
+```java
+// For the Second Half
+// Printing the decreasing numbers
+int lim = 2 *i - 1;
+for (int j = lim - 1; j >= i; j--){
+ System.out.print(j + " ");
+}
+
+//loop to print n - i zeros
+for (int j = 1; j <= n - i; j++){
+ System.out.print(0 + " ");
+}
+```
+
+
+
+
+### Overall Code
+
+``` java
+for (int i = 1; i <= n; i++){
+
+ // For the First Half
+ //loop to print n - i zeros
+ for (int j = 1; j <= n - i; j++){
+ System.out.print(0 + " ");
+ }
+
+ int lim = 2 *i - 1;
+ // Printing the increasing numbers from i to 2*i-1
+ for (int j = i; j <= lim; j++){
+ System.out.print(j + " ");
+ }
+
+ // For the Second Half
+ // Printing the decreasing numbers
+ for (int j = lim - 1; j >= i; j--){
+ System.out.print(j + " ");
+ }
+
+ //loop to print n - i zeros
+ for (int j = 1; j <= n - i; j++){
+ System.out.print(0 + " ");
+ }
+
+ System.out.println();
+}
+```
+
+
+
+---
+
+### Reading Inputs for Strings
+
+**1. sc.next()-> cannot take spaces as input**
+
+Ques1:
+```java
+Input: "Hello World"
+String s1 = sc.next();
+System.out.println(s1);
+
+String s2 = sc.next();
+System.out.println(s2);
+```
+Output:
+```plaintext
+Hello
+World
+```
+
+Explanation:
+
+s1 will have first word, Hello
+s2 will have next word, World
+
+
+
+
+**2. sc.nextLine() -> can take spaces as well, until next line is encountered.**
+
+Ques1:
+```java
+Input: Hello World
+String s3 = sc.nextLine();
+System.out.println(s3);
+```
+
+Output:
+```plaintext
+Hello World
+```
+
+---
+
+# Question
+Input :
+
+```
+Hello World
+```
+```
+Scanner scn = new Scanner(System.in);
+String str1 = scn.next();
+String str2 = scn.next();
+System.out.println(str1);
+System.out.println(str2);
+```
+
+# Choices
+
+- [x] Hello World +- [ ] Hello +- [ ] World +- [ ] None of the above + +--- + +Output: +```plaintext +Hello +World +``` + + +Explanation: + +str1 will have, Hello +str2 will have next word, World + + +--- + +# Question + +Input: +``` +Hello Welcome in Scaler +``` + +``` +Scanner scn = new Scanner(System.in); +String str1 = scn.next(); +String str2 = scn.nextLine(); +System.out.println(str1); +System.out.println(str2); +``` + +# Choices + +- [ ] Hello +- [ ] Error +- [x] Hello
Welcome in Scaler +- [ ] None of the above + +--- + +Output: +```plaintext +Hello +Welcome in Scaler +``` + +Explanation: + +str1 will have first word, Hello +str2 will have complete line after hello, Welcome in scaler(including space before welcome). + +--- + +**Rule:** When the inputs are given in separate lines, and we take a String input using nextLine() after taking number input[nextInt(), nextLong(), nextFloat(), nextDouble()] or a single word [next()] then we get a empty String. + +### Example + +### Input +``` +45 +Hello World! +``` +``` java +Scanner sc = new Scanner(System.in); +int x = sc.nextInt(); // x[45] +String st = sc.nextLine(); // st -> Empty String +String st2 = sc.nextLine(); // st2 -> "Hello World!" +System.out.println(st); +System.out.println(s2); +``` + +### Output +``` + +Hello World! +``` +--- + + +# Question + +Predict the output : +``` +Input- +11 +Super Excited! +``` +``` +Scanner scn = new Scanner(System.in); +int x = scn.nextInt(); +String str = scn.nextLine(); +System.out.println(x); +System.out.println(str); +``` + +# Choices + +- [ ] 11 Super Excited! +- [ ] Error +- [ ] 11
Super Excited! +- [x] 11 + +--- + + + +# Question + +Predict the output : +``` +Input- +11 +Super Excited! +``` +``` +Scanner scn = new Scanner(System.in); +int x = scn.nextInt(); +String str = scn.nextLine(); +System.out.println(x); +System.out.println(str); +System.out.println("The End"); +``` + +# Choices + +- [ ] 11 Super Excited! The End +- [x] 11
The End +- [ ] Error +- [ ] 11
Super Excited!
The End + + +--- + + +### Character: +A character represent a single symbol. + +There are different types of characters: +* Uppercase characters : ['A' - 'Z'] +* Lowercase characters : ['a' - 'z'] +* Numeric characters: ['0' - '9'] +* Special characters: ['@', '#', '\$', '%', '&'...] + +There are a total of 128 characters. + + +### Syntax + +**Example 1:** +```java +char ch = 'a'; +System.out.println(ch); +``` +**Output:** +```plaintext +a +``` + +**Example 2:** +```java +char ch = 'ab'; +System.out.println(ch); +``` +**Output:** +```plaintext +Error: Only a single symbol is a character. +``` + +--- + + +### Problem Statement +Write a program to print all characters from A to Z. + + + +### Code +```java +public static void printCharacters(String str) { + for(char i = 'A'; i <= 'Z'; i++) { + System.out.println(i); + } +} +``` +--- + + +### Character Stairacase Pattern + +N = 5 +``` +A +A B +A B C +A B C D +A B C D E +``` + +N = 3 +``` +A +A B +A B C +``` + +:::warning +Please take some time to think about the solution approach on your own before reading further..... +::: + +### Approach +Consider the spaces as underscores (for better visualization). + +Lets take N = 5, +``` +A _ +A _ B _ +A _ B _ C _ +A _ B _ C _ D _ +A _ B _ C _ D _ E _ +``` + +Lets assume we are printing the standard stair case pattern, + +``` +1 +1 2 +1 2 3 +1 2 3 4 +1 2 3 4 5 +``` + +Now both the patterns is similar. So, instead of printing numbers, we just create a new variable, which starts with **A**, then increment inside the innerloop. + + +### Code + +``` java +for (int i = 1; i <= N; ++i) { + char ch = 'A'; + for (char j = 1; j <= i; j++) { + System.out.print(ch + " "); + ch++; + } + System.out.println(); +} +``` +--- diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner 1D Array - 1.md b/Academy DSA Typed Notes/Beginner Language/Beginner 1D Array - 1.md new file mode 100644 index 0000000..bd2f2ff --- /dev/null +++ b/Academy DSA Typed Notes/Beginner Language/Beginner 1D Array - 1.md @@ -0,0 +1,688 @@ +# 1D Arrays 1 + +--- +## Agenda + +1. Introduction to Arrays +2. Reading Input +3. Indexing and Properties +4. Sum of all elements +5. Frequency of k in array +6. Max of all elements + + +--- + +### Example +Let's say we need to read four inputs for our programme. We can use the below approach. + +#### Code +```java +public static void main(String[] args) { + int a, b, c, d; + Scanner scanner = new Scanner(System.in); + a = scanner.nextInt(); + b = scanner.nextInt(); + c = scanner.nextInt(); + d = scanner.nextInt(); +} +``` +Some one can suggest that we should use loop to get all four values like :- + +#### Code +```cpp +public static void main(){ + for(int i = 1; i <= 4;i ++ ){ + int a = sc.nextInt(); + } +} + +``` +The above provided approach is wrong because what we are doing is updating the value of variable `a` in each iteration due this a would be set to the last input value provided. + +--- + + + +### Concept of Arrays +* In above example what is instead of four there are hundreds of value to store. It would be manually infeasible to declare and set hundreds of variables. +* Therefore to overcome above problem we use **arrays** + +#### Array +It is a data structure that can hold fixed number of values of same data type. + +#### Syntax +```cpp +datatype name[] = new datatype[size] + +// example +float f[] = new float[10] +int arr[] = new int[10] + +// Various ways +datatype[] name = new datatype[size] +datatype []name = new datatype[size] +``` + +--- + + + +# Question + +Correct way to create an Array containing 5 int values in Java? + +# Choices + +- [x] int[] ar = new int[5] +- [ ] int[] ar = new int[4] +- [ ] int[] ar = int new[5] + +--- + + + +## Explanation + +Since size is 5 and datatype is int using above provided syntax rules: +int[] ar = new int[5] + +--- + + + +### Indexing and Properties + +* Indexing in array starts from **0**. + + +| index | 0 | 1 | 2 | 3 | +|:-----:|:---:|:---:|:---:|:---:| + +* Accessing an element at **ith** index in an array can be done as follows:- +```cpp + nameOfArray[i] +``` + +
 +
+
+
+---
+
+# Question
+
+`int[] ar = new int[6];`
+
+How can we access last position element ?
+
+# Choices
+- [x] ar[5]
+- [ ] ar[6]
+- [ ] ar[4]
+- [ ] ar[7]
+
+
+---
+
+
+## Explanation
+
+Since size is 6 indexing would be like :-
+
+| index | 0 | 1 | 2 | 3 | 4 | 5 |
+|:-----:|:---:|:---:|:---:|:---:|:---:|:---:|
+| arr | 0 | 0 | 3 | 0 | 0 | 0 |
+
+last element would be at index 5
+
+---
+
+
+# Question
+`int[] ar = new int[10];`
+
+How can we access last position element ?
+
+# Choices
+- [x] ar[9]
+- [ ] ar[10]
+- [ ] ar[7]
+- [ ] ar[8]
+
+---
+
+## Explanation
+
+Since size is 10 indexing would be like :-
+
+| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
+|:-----:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|
+| ar | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
+
+last element would be at index 9
+
+---
+
+
+
+# Question
+Say int[] ar = new int[N]
+How to access first element and last element ?
+
+# Choices
+- [x] ar[0] ar[N-1]
+- [ ] ar[0] ar[N]
+- [ ] ar[1] ar[N]
+
+---
+
+
+## Explanation
+By observing previous questions we can generalize the idea that :-
+* Last element in array 'arr' of size 'N' is accessed as `arr[N-1]`.
+* First element in array 'arr' of size 'N' is accessed as `arr[0]`.
+
+
+
+---
+
+
+# Question
+What is the Output of
+```java
+public static void main(String args[]) {
+ int[] arr = new int[10];
+ int n = arr.length;
+ System.out.println(n);
+}
+```
+
+# Choices
+- [x] 10
+- [ ] 9
+- [ ] 8
+
+
+---
+
+* By default values in an array of type `int` are intialized with **'0'**
+
+
+
+---
+
+# Question
+
+What will be the output?
+```java
+public static void main(String args[]) {
+ int[] arr = new int[5];
+ arr[0] = 10;
+ arr[1] = 20;
+
+ int sum = 0;
+ for(int i = 0; i < 5;i ++ ) {
+ sum += arr[i];
+ }
+
+ System.out.println(sum);
+}
+```
+
+# Choices
+- [x] 30
+- [ ] error
+- [ ] 20
+- [ ] 43
+
+---
+
+
+## Explanation
+By observing previous questions we can generalize the idea that :-
+* Last element in array 'arr' of size 'N' is accessed as `arr[N-1]`.
+* First element in array 'arr' of size 'N' is accessed as `arr[0]`.
+
+
+#### Solution
+
+
+
+
+---
+
+# Question
+
+`int[] ar = new int[6];`
+
+How can we access last position element ?
+
+# Choices
+- [x] ar[5]
+- [ ] ar[6]
+- [ ] ar[4]
+- [ ] ar[7]
+
+
+---
+
+
+## Explanation
+
+Since size is 6 indexing would be like :-
+
+| index | 0 | 1 | 2 | 3 | 4 | 5 |
+|:-----:|:---:|:---:|:---:|:---:|:---:|:---:|
+| arr | 0 | 0 | 3 | 0 | 0 | 0 |
+
+last element would be at index 5
+
+---
+
+
+# Question
+`int[] ar = new int[10];`
+
+How can we access last position element ?
+
+# Choices
+- [x] ar[9]
+- [ ] ar[10]
+- [ ] ar[7]
+- [ ] ar[8]
+
+---
+
+## Explanation
+
+Since size is 10 indexing would be like :-
+
+| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
+|:-----:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|
+| ar | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
+
+last element would be at index 9
+
+---
+
+
+
+# Question
+Say int[] ar = new int[N]
+How to access first element and last element ?
+
+# Choices
+- [x] ar[0] ar[N-1]
+- [ ] ar[0] ar[N]
+- [ ] ar[1] ar[N]
+
+---
+
+
+## Explanation
+By observing previous questions we can generalize the idea that :-
+* Last element in array 'arr' of size 'N' is accessed as `arr[N-1]`.
+* First element in array 'arr' of size 'N' is accessed as `arr[0]`.
+
+
+
+---
+
+
+# Question
+What is the Output of
+```java
+public static void main(String args[]) {
+ int[] arr = new int[10];
+ int n = arr.length;
+ System.out.println(n);
+}
+```
+
+# Choices
+- [x] 10
+- [ ] 9
+- [ ] 8
+
+
+---
+
+* By default values in an array of type `int` are intialized with **'0'**
+
+
+
+---
+
+# Question
+
+What will be the output?
+```java
+public static void main(String args[]) {
+ int[] arr = new int[5];
+ arr[0] = 10;
+ arr[1] = 20;
+
+ int sum = 0;
+ for(int i = 0; i < 5;i ++ ) {
+ sum += arr[i];
+ }
+
+ System.out.println(sum);
+}
+```
+
+# Choices
+- [x] 30
+- [ ] error
+- [ ] 20
+- [ ] 43
+
+---
+
+
+## Explanation
+By observing previous questions we can generalize the idea that :-
+* Last element in array 'arr' of size 'N' is accessed as `arr[N-1]`.
+* First element in array 'arr' of size 'N' is accessed as `arr[0]`.
+
+
+#### Solution
+ +
+
+
+
+---
+
+
+# Question
+
+```java
+public static void main(String args[]) {
+ int[] arr = new int[5];
+ System.out.println(arr[0]);
+}
+```
+
+# Choices
+- [x] 0
+- [ ] error
+- [ ] random number
+- [ ] 43
+
+
+
+
+---
+
+
+# Question
+
+```java
+public static void main(String args[]) {
+ int[] ar = new int[3];
+ ar[0] = 10;
+ ar[1] = 20;
+ ar[2] = 30;
+ System.out.print(ar[0] + ar[3]);
+}
+```
+
+# Choices
+- [x] error
+- [ ] 0
+- [ ] 40
+- [ ] 60
+
+
+
+---
+
+# Question
+
+```java
+public static void main(String args[]) {
+ int[] ar = new int[3];
+ ar[0] = 10;
+ ar[1] = 20;
+ ar[2] = 30;
+ System.out.print(ar[0] + ar[2]);
+}
+```
+
+# Choices
+- [x] 40
+- [ ] 0
+- [ ] error
+- [ ] 60
+
+
+
+---
+
+# Question
+
+```java
+public static void main(String args[]) {
+ int[] ar = new int[3];
+ ar[0] = 10;
+ ar[1] = 20;
+ ar[2] = 30;
+ System.out.print(ar[-1] + ar[3]);
+}
+
+```
+
+# Choices
+- [x] error
+- [ ] 0
+- [ ] 40
+- [ ] 60
+
+---
+
+
+We can reassign an array to replace the previous value it was referencing.
+
+
+**Code:**
+```java
+public static void main(){
+ int[] ar = new int[6];
+ ar= new int[2];
+ S.O.Pln(arr.length);
+}
+```
+**Output:**
+```plaintext
+2
+```
+
+
+
+---
+
+* We can directly store elements into an array
+
+**Code:**
+```java
+int ar[] = {10,20,30};
+```
+
+
+---
+
+### Creating and Reading an array
+
+#### Create an array of size 4 and print sum of all it's element :-
+
+* Let's create an array of size 4 and take input.
+
+```java
+public static void main(String[] args) {
+ Scanner sc = new Scanner(System.in);
+
+ int[] arr = new int[4];
+ arr[0] = sc.nextInt();
+ arr[1] = sc.nextInt();
+ arr[2] = sc.nextInt();
+ arr[3] = sc.nextInt();
+}
+```
+
+* In above approach we have to take input for each index manually which is not a good idea.
+* So **How can we take inputs efficiently ?**
+ * **Solution** :- We use a loop.
+ * But **how to apply loop to take array input ?**
+* On observing above approach we will find that only index changes each time we take an input.
+ * **In each iteration we change the index number.**
+ * We iterate starting from 0 till last index i.e. array size -1.
+
+```java
+public static void main(String[] args) {
+ Scanner sc = new Scanner(System.in);
+
+ int[] arr = new int[4];
+ for (int i = 0; i < 4; i ++ ) {
+ arr[i] = sc.nextInt();
+ }
+}
+```
+
+
+---
+
+
+
+### Passing Array to Functions
+
+#### Create a Function Which Takes arr[] as A Parameter and Print the Array
+
+* We need to declare a function which takes array as parameter to function.
+ * It can be done like :-
+ `Function nameOfFunction(dataType anyName[]){}`
+ * '`[]`' are important for distinguishing array type parameter from other variable type parameters.
+* **How can we access the length of array from function ?**
+ * We use `array.length` for this purpose.
+* We can pass array parameter to function call like:
+ `functionName(arrayName)`
+ * **We only need to pass array name.**
+
+```java
+static void printArray(int[] ar) {
+ int n = ar.length;
+ for (int i = 0; i < n; i ++ ) {
+ System.out.print(ar[i] + " ");
+ }
+ System.out.println();
+}
+
+public static void main(String[] args) {
+ Scanner sc = new Scanner(System.in);
+
+ int[] arr = new int[4];
+ for (int i = 0; i < 4; i ++ ) {
+ arr[i] = sc.nextInt();
+ }
+ printArray(arr);
+}
+```
+We take the sum of all elements of array as follows :-
+
+```java
+public static void main(String[] args) {
+ int[] arr = new int[4]; // creates an array of size 4
+ Scanner scanner = new Scanner(System.in);
+
+ for (int i = 0; i < 4; i ++ ) {
+ arr[i] = scanner.nextInt();
+ }
+ int sum = 0;
+ for (int i = 0; i < 4; i ++ ) {
+ sum += arr[i]; // add element at ith index to sum variable
+ }
+
+ System.out.println(sum);
+ }
+
+```
+
+---
+
+
+### Problem 1
+
+Given an array and k. Write a function to return the frequency of k in array?
+
+#### Testcase
+
+```java
+arr[7] = [3,6,7,6,11,6,14]
+
+k = 6
+```
+
+#### solution
+
+```plaintext
+ans = 4
+```
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+#### Approach
+* We need to create a function and pass array and k as parameters to the function.
+* Inside the function :-
+ * Maintain a count variable which is intialised to 0.
+ * Iterate over the array:-
+ * If element at current index equals k increament count by 1.
+ * Return count.
+
+#### Trace
+
+![]()
+
+
+#### Solution
+
+
+
+
+
+---
+
+
+# Question
+
+```java
+public static void main(String args[]) {
+ int[] arr = new int[5];
+ System.out.println(arr[0]);
+}
+```
+
+# Choices
+- [x] 0
+- [ ] error
+- [ ] random number
+- [ ] 43
+
+
+
+
+---
+
+
+# Question
+
+```java
+public static void main(String args[]) {
+ int[] ar = new int[3];
+ ar[0] = 10;
+ ar[1] = 20;
+ ar[2] = 30;
+ System.out.print(ar[0] + ar[3]);
+}
+```
+
+# Choices
+- [x] error
+- [ ] 0
+- [ ] 40
+- [ ] 60
+
+
+
+---
+
+# Question
+
+```java
+public static void main(String args[]) {
+ int[] ar = new int[3];
+ ar[0] = 10;
+ ar[1] = 20;
+ ar[2] = 30;
+ System.out.print(ar[0] + ar[2]);
+}
+```
+
+# Choices
+- [x] 40
+- [ ] 0
+- [ ] error
+- [ ] 60
+
+
+
+---
+
+# Question
+
+```java
+public static void main(String args[]) {
+ int[] ar = new int[3];
+ ar[0] = 10;
+ ar[1] = 20;
+ ar[2] = 30;
+ System.out.print(ar[-1] + ar[3]);
+}
+
+```
+
+# Choices
+- [x] error
+- [ ] 0
+- [ ] 40
+- [ ] 60
+
+---
+
+
+We can reassign an array to replace the previous value it was referencing.
+
+
+**Code:**
+```java
+public static void main(){
+ int[] ar = new int[6];
+ ar= new int[2];
+ S.O.Pln(arr.length);
+}
+```
+**Output:**
+```plaintext
+2
+```
+
+
+
+---
+
+* We can directly store elements into an array
+
+**Code:**
+```java
+int ar[] = {10,20,30};
+```
+
+
+---
+
+### Creating and Reading an array
+
+#### Create an array of size 4 and print sum of all it's element :-
+
+* Let's create an array of size 4 and take input.
+
+```java
+public static void main(String[] args) {
+ Scanner sc = new Scanner(System.in);
+
+ int[] arr = new int[4];
+ arr[0] = sc.nextInt();
+ arr[1] = sc.nextInt();
+ arr[2] = sc.nextInt();
+ arr[3] = sc.nextInt();
+}
+```
+
+* In above approach we have to take input for each index manually which is not a good idea.
+* So **How can we take inputs efficiently ?**
+ * **Solution** :- We use a loop.
+ * But **how to apply loop to take array input ?**
+* On observing above approach we will find that only index changes each time we take an input.
+ * **In each iteration we change the index number.**
+ * We iterate starting from 0 till last index i.e. array size -1.
+
+```java
+public static void main(String[] args) {
+ Scanner sc = new Scanner(System.in);
+
+ int[] arr = new int[4];
+ for (int i = 0; i < 4; i ++ ) {
+ arr[i] = sc.nextInt();
+ }
+}
+```
+
+
+---
+
+
+
+### Passing Array to Functions
+
+#### Create a Function Which Takes arr[] as A Parameter and Print the Array
+
+* We need to declare a function which takes array as parameter to function.
+ * It can be done like :-
+ `Function nameOfFunction(dataType anyName[]){}`
+ * '`[]`' are important for distinguishing array type parameter from other variable type parameters.
+* **How can we access the length of array from function ?**
+ * We use `array.length` for this purpose.
+* We can pass array parameter to function call like:
+ `functionName(arrayName)`
+ * **We only need to pass array name.**
+
+```java
+static void printArray(int[] ar) {
+ int n = ar.length;
+ for (int i = 0; i < n; i ++ ) {
+ System.out.print(ar[i] + " ");
+ }
+ System.out.println();
+}
+
+public static void main(String[] args) {
+ Scanner sc = new Scanner(System.in);
+
+ int[] arr = new int[4];
+ for (int i = 0; i < 4; i ++ ) {
+ arr[i] = sc.nextInt();
+ }
+ printArray(arr);
+}
+```
+We take the sum of all elements of array as follows :-
+
+```java
+public static void main(String[] args) {
+ int[] arr = new int[4]; // creates an array of size 4
+ Scanner scanner = new Scanner(System.in);
+
+ for (int i = 0; i < 4; i ++ ) {
+ arr[i] = scanner.nextInt();
+ }
+ int sum = 0;
+ for (int i = 0; i < 4; i ++ ) {
+ sum += arr[i]; // add element at ith index to sum variable
+ }
+
+ System.out.println(sum);
+ }
+
+```
+
+---
+
+
+### Problem 1
+
+Given an array and k. Write a function to return the frequency of k in array?
+
+#### Testcase
+
+```java
+arr[7] = [3,6,7,6,11,6,14]
+
+k = 6
+```
+
+#### solution
+
+```plaintext
+ans = 4
+```
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+#### Approach
+* We need to create a function and pass array and k as parameters to the function.
+* Inside the function :-
+ * Maintain a count variable which is intialised to 0.
+ * Iterate over the array:-
+ * If element at current index equals k increament count by 1.
+ * Return count.
+
+#### Trace
+
+![]()
+
+
+#### Solution
+ +
+
+#### Pseudeocode
+```cpp
+static int frequencyK(int[] ar, int k) {
+ int n = ar.length;
+ int count = 0;
+ for (int i = 0; i < n; i ++ ) {
+ if (ar[i] == k) {
+ count ++ ;
+ }
+ }
+ return count;
+}
+```
+
+---
+
+
+### Problem 2
+
+Given an array . Write a function to return the maximum element present in array?
+
+#### Testcase 1
+
+```cpp
+arr[6] = [3,1,7,6,9,11]
+
+```
+
+#### solution
+
+```plaintext
+ans = 11
+```
+#### Testcase 2
+
+```plaintext
+arr[6] = [4,2,7,9,12,3]
+
+```
+
+#### solution
+
+```plaintext
+ans = 12
+```
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+#### Approach 1
+* We need to create a function and pass array as parameters to the function.
+* Inside the function :-
+ * Maintain a max variable which is intialised to 0.
+ * Iterate over the array:-
+ * If element at current index is greater than max then set max to current element.
+ * Return max.
+
+#### Trace 1
+
+
+
+
+#### Pseudeocode
+```cpp
+static int frequencyK(int[] ar, int k) {
+ int n = ar.length;
+ int count = 0;
+ for (int i = 0; i < n; i ++ ) {
+ if (ar[i] == k) {
+ count ++ ;
+ }
+ }
+ return count;
+}
+```
+
+---
+
+
+### Problem 2
+
+Given an array . Write a function to return the maximum element present in array?
+
+#### Testcase 1
+
+```cpp
+arr[6] = [3,1,7,6,9,11]
+
+```
+
+#### solution
+
+```plaintext
+ans = 11
+```
+#### Testcase 2
+
+```plaintext
+arr[6] = [4,2,7,9,12,3]
+
+```
+
+#### solution
+
+```plaintext
+ans = 12
+```
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+#### Approach 1
+* We need to create a function and pass array as parameters to the function.
+* Inside the function :-
+ * Maintain a max variable which is intialised to 0.
+ * Iterate over the array:-
+ * If element at current index is greater than max then set max to current element.
+ * Return max.
+
+#### Trace 1
+
+ +
+
+![]()
+
+#### Trace 2
+
+
+
+
+![]()
+
+#### Trace 2
+
+ +
+
+
+
+#### Code
+```java
+ static int maxElement(int array[]) {
+ int n = array.length;
+ int max = Integer.MIN_VALUE; // Initialize max with the smallest possible integer value
+ for (int i = 0; i < n; i ++ ) {
+ if (array[i] > max) {
+ max = array[i];
+ }
+ }
+ return max;
+}
+```
+
+**There is a flaw in above code.** Let's see it with help of an testcase.
+
+#### Testcase 3
+
+```cpp
+arr[4] = [ - 8, - 4, - 3, - 5]
+
+```
+
+#### solution
+
+```cpp
+ans = - 3
+```
+
+* Let' apply approach 1 to testcase 3
+
+
+
+
+
+
+#### Code
+```java
+ static int maxElement(int array[]) {
+ int n = array.length;
+ int max = Integer.MIN_VALUE; // Initialize max with the smallest possible integer value
+ for (int i = 0; i < n; i ++ ) {
+ if (array[i] > max) {
+ max = array[i];
+ }
+ }
+ return max;
+}
+```
+
+**There is a flaw in above code.** Let's see it with help of an testcase.
+
+#### Testcase 3
+
+```cpp
+arr[4] = [ - 8, - 4, - 3, - 5]
+
+```
+
+#### solution
+
+```cpp
+ans = - 3
+```
+
+* Let' apply approach 1 to testcase 3
+
+ +
+
+
+
+* In trace we get the answer as 0 whereas the correact answer is -3. **Why ?**
+
+#### Issue
+
+**Since max/ans variable is intialised to 0 which is already greater than all elements in array therefore max/ans is not updated.**
+
+
+---
+# Question
+
+
+For taking sum of N numbers we initialise our sum variable with =
+
+# Choices
+- [x] 0
+- [ ] 9
+- [ ] 1
+
+
+
+---
+title: Quiz 13
+description:
+duration: 30
+card_type : quiz_card
+---
+# Question
+
+For taking product of N numbers we initialise our product variable with `=`
+
+
+# Choices
+- [ ] 0
+- [ ] 9
+- [x] 1
+
+
+
+---
+
+* Based upon observations from above questions we need to intialize max/ans in such a manner that it won't affect the answer.
+* We intialize the ans/max variable to **- ∞**(negative infinity) so that it does not affect the final answer.
+ * We do this by **Integer.MIN_VALUE**
+
+
+
+
+
+
+
+* In trace we get the answer as 0 whereas the correact answer is -3. **Why ?**
+
+#### Issue
+
+**Since max/ans variable is intialised to 0 which is already greater than all elements in array therefore max/ans is not updated.**
+
+
+---
+# Question
+
+
+For taking sum of N numbers we initialise our sum variable with =
+
+# Choices
+- [x] 0
+- [ ] 9
+- [ ] 1
+
+
+
+---
+title: Quiz 13
+description:
+duration: 30
+card_type : quiz_card
+---
+# Question
+
+For taking product of N numbers we initialise our product variable with `=`
+
+
+# Choices
+- [ ] 0
+- [ ] 9
+- [x] 1
+
+
+
+---
+
+* Based upon observations from above questions we need to intialize max/ans in such a manner that it won't affect the answer.
+* We intialize the ans/max variable to **- ∞**(negative infinity) so that it does not affect the final answer.
+ * We do this by **Integer.MIN_VALUE**
+
+
+ +
+
+
+#### Code
+
+```java
+static int maxElement(int[] ar) {
+ int n = ar.length;
+ int max = Integer.MIN_VALUE;
+
+ for (int i = 0; i < n; i ++ ) {
+ if (ar[i] > max) {
+ max = ar[i];
+ }
+ }
+ return max;
+}
+```
\ No newline at end of file
diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner 1D Array - 2.md b/Academy DSA Typed Notes/Beginner Language/Beginner 1D Array - 2.md
new file mode 100644
index 0000000..823999f
--- /dev/null
+++ b/Academy DSA Typed Notes/Beginner Language/Beginner 1D Array - 2.md
@@ -0,0 +1,606 @@
+# 1D Array - 2
+
+# Agenda
+
+1. Revision
+2. Implement Function
+3. Increasing Order [increasing and non-decreasing]
+4. Drawbacks of Array
+5. Right shift of the array
+6. Array List introduction
+7. Functions [add, get, set, remove, size, sort]
+8. ArrayList functions via code
+9. Write a function which takes arrayList as input and update all values by 1
+10. Return an arraylist with all even numbers
+
+
+---
+
+
+## Revision
+
+Let us revise what we discussed in the last class wit the help of quizzes.
+
+---
+
+
+# Question
+What will be output for this program ?
+```java
+int[] myArray = {1, 2, 3, 4, 5};
+System.out.println(myArray[2]);
+```
+
+
+# Choices
+- [ ] 2
+- [x] 3
+- [ ] 4
+
+---
+
+
+# Question
+What will be output for this program ?
+
+```java
+int[] myArray = new int[3];
+System.out.println(myArray[1]);
+```
+
+
+
+# Choices
+- [x] 0
+- [ ] Null
+- [ ] Error
+
+
+---
+
+# Question
+What will be output for this program ?
+```java
+int[] myArray = {1, 2, 3, 4, 5};
+System.out.println(myArray.length);
+```
+
+
+
+# Choices
+- [ ] 4
+- [ ] 0
+- [x] 5
+
+---
+
+
+# Question
+What will be output for this program ?
+```java
+int[] myArray = {1, 2, 3, 4, 5};
+myArray[2] = 6;
+System.out.println(myArray[2]);
+```
+
+
+# Choices
+- [x] 6
+- [ ] 3
+- [ ] 3
+- [ ] Error
+
+
+
+---
+
+
+## Return arr[] Syntax
+
+### Implement Function
+
+Given N, create an array of size N, which should contain all elements in increasing order from 1 to N.
+
+## Example
+
+```plaintext
+N = 3
+arr[3] = { 1, 2, 3 }
+
+N = 5
+arr[5] = { 1, 2, 3, 4, 5 }
+```
+
+---
+
+
+
+# Question
+
+Given N = 6, create an array of size N containing all elements in increasing order from 1 to N.
+
+
+
+# Choices
+- [ ] 0 1 2 3 4 5 6
+- [x] 1 2 3 4 5 6
+- [ ] 6 5 4 3 2 1
+
+
+---
+
+
+
+# Implement Function Code
+
+
+
+## Pseudocode
+```java
+static int[] num(int N){
+ int arr = new int[N];
+ for(int i = 0; i < N; i++){
+ arr[i] = i + 1;
+ }
+ return arr;
+}
+```
+
+---
+
+## Increasing Order
+
+Numbers arranged from smallest to largest.
+**Note:** If elements are equal then no issues
+
+## Scritly Increasing Order
+Arrangement of numbers such that the next number is always greater than the previous number.
+
+---
+
+
+# Question
+
+Check whether the given numbers are in increasing order?
+`3, 4, 4, 4, 4, 5, 5, 7, 9, 18, 18, 26`
+
+# Choices
+- [x] yes
+- [ ] no
+- [ ] maybe
+
+
+---
+
+
+
+# Question
+
+Check whether the given numbers are in increasing order?
+`-1, -2, -3, -4, -5`
+
+# Choices
+- [ ] Yes
+- [x] No
+- [ ] Maybe
+
+
+---
+
+
+
+# Question
+
+Check whether the given numbers are in strictly increasing order?
+
+`3, 9, 16, 24, 29, 29, 34, 50`
+
+# Choices
+
+- [ ] Yes
+- [x] No
+- [ ] Maybe
+
+---
+
+
+### Checking Strictly Increasing Array
+
+Given an integer N, create an array of size N containing elements in increasing order from 1 to N. Check if the created array is strictly increasing (each element is greater than the previous element).
+
+#### Example
+For N = 5, the array `arr` will be `{1, 2, 3, 4, 5}`, and it is strictly increasing.
+
+For N = 5, the array `arr` will be `{1, 2, 2, 4, 5}`, and it is not strictly increasing.
+
+---
+
+# Question
+
+Check whether the given numbers are in strictly increasing order?
+
+`21, 39, 46, 97, 105`
+
+
+# Choices
+- [x] Yes
+- [ ] No
+- [ ] Maybe
+
+---
+
+
+## If Array Is Strictly Increasing Code
+
+**Note to instructor:** Explain logic of implementing this in code format here
+
+
+### Pseudocode
+```java
+static boolean isStrictlyIncreasing(int N) {
+ int[] arr = new int[N];
+ for (int i = 0; i < N; i++) {
+ arr[i] = i + 1;
+ }
+
+ for (int i = 1; i < N; i++) {
+ if (arr[i] < arr[i - 1]) {
+ return false; // Array is not strictly increasing
+ }
+ }
+
+ return true; // Array is strictly increasing
+}
+```
+
+---
+
+
+## Right Shift of An Array
+Given an array of size N, shift all the elements to the right by 1 and move the last element to the beginning of array
+
+
+## Example 1
+
+```plaintext
+N = 10
+arr[10] = { 7, 4, 9, 11, 2, 24, -5, 17, 1, 8 }
+Ans =
+arr[10] = { 8, 7, 4, 9, 11, 2, 24, -5, 17, 1}
+```
+
+
+
+
+---
+
+
+
+# Question
+
+Right shift the given array
+
+arr[] = {10, 20, 30, 40, 50, 60}
+
+
+# Choices
+- [ ] 60, 50, 40, 30, 20, 10
+- [ ] 0, 10, 20, 30, 40, 50, 60
+- [x] 60, 10, 20, 30, 40, 50
+
+
+---
+
+
+## Right Shift of An Array Idea and Code
+
+
+## Idea
+1. Store last element of original array in a temp variable for future use (`temp = arr[n - 1]`)
+2. Traverse from end to first index and do
+`arr[i] = arr[i - 1]`
+3. Till here all indexes are updated with their new value except 0th index. Finally do
+`arr[0] = temp`
+
+
+## Pseudocode
+```java
+static int[] rotateByone(int arr[]){
+ int n = arr.length
+ int temp = arr[n - 1]
+ for(int i = n - 1; i >= 1; i--){
+ arr[i] = arr[i - 1]
+ }
+ arr[0] = temp;
+ return ans;
+}
+```
+---
+## Drawbacks of Arrays
+
+Once array size is fixed, it cannot be changed.
+If we want to change, we need to create a new array.
+
+int[] ar=new int[4];
+This can only store 4 elements, if we want to store 1 more element we cannot update the size. We have to create a new array only.
+
+---
+
+
+### Arraylist
+
+#### Definition
+
+ArrayList is a class that provides a resizable array implementation that is similar to an ordinary array, but with the added benefit of being able to resize dynamically as elements are added or removed. An ArrayList can store objects of any type, including primitives.
+
+#### Syntax
+
+The general syntax for creating an ArrayList in Java is as follows:
+```java
+ArrayList
+
+
+
+#### Code
+
+```java
+static int maxElement(int[] ar) {
+ int n = ar.length;
+ int max = Integer.MIN_VALUE;
+
+ for (int i = 0; i < n; i ++ ) {
+ if (ar[i] > max) {
+ max = ar[i];
+ }
+ }
+ return max;
+}
+```
\ No newline at end of file
diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner 1D Array - 2.md b/Academy DSA Typed Notes/Beginner Language/Beginner 1D Array - 2.md
new file mode 100644
index 0000000..823999f
--- /dev/null
+++ b/Academy DSA Typed Notes/Beginner Language/Beginner 1D Array - 2.md
@@ -0,0 +1,606 @@
+# 1D Array - 2
+
+# Agenda
+
+1. Revision
+2. Implement Function
+3. Increasing Order [increasing and non-decreasing]
+4. Drawbacks of Array
+5. Right shift of the array
+6. Array List introduction
+7. Functions [add, get, set, remove, size, sort]
+8. ArrayList functions via code
+9. Write a function which takes arrayList as input and update all values by 1
+10. Return an arraylist with all even numbers
+
+
+---
+
+
+## Revision
+
+Let us revise what we discussed in the last class wit the help of quizzes.
+
+---
+
+
+# Question
+What will be output for this program ?
+```java
+int[] myArray = {1, 2, 3, 4, 5};
+System.out.println(myArray[2]);
+```
+
+
+# Choices
+- [ ] 2
+- [x] 3
+- [ ] 4
+
+---
+
+
+# Question
+What will be output for this program ?
+
+```java
+int[] myArray = new int[3];
+System.out.println(myArray[1]);
+```
+
+
+
+# Choices
+- [x] 0
+- [ ] Null
+- [ ] Error
+
+
+---
+
+# Question
+What will be output for this program ?
+```java
+int[] myArray = {1, 2, 3, 4, 5};
+System.out.println(myArray.length);
+```
+
+
+
+# Choices
+- [ ] 4
+- [ ] 0
+- [x] 5
+
+---
+
+
+# Question
+What will be output for this program ?
+```java
+int[] myArray = {1, 2, 3, 4, 5};
+myArray[2] = 6;
+System.out.println(myArray[2]);
+```
+
+
+# Choices
+- [x] 6
+- [ ] 3
+- [ ] 3
+- [ ] Error
+
+
+
+---
+
+
+## Return arr[] Syntax
+
+### Implement Function
+
+Given N, create an array of size N, which should contain all elements in increasing order from 1 to N.
+
+## Example
+
+```plaintext
+N = 3
+arr[3] = { 1, 2, 3 }
+
+N = 5
+arr[5] = { 1, 2, 3, 4, 5 }
+```
+
+---
+
+
+
+# Question
+
+Given N = 6, create an array of size N containing all elements in increasing order from 1 to N.
+
+
+
+# Choices
+- [ ] 0 1 2 3 4 5 6
+- [x] 1 2 3 4 5 6
+- [ ] 6 5 4 3 2 1
+
+
+---
+
+
+
+# Implement Function Code
+
+
+
+## Pseudocode
+```java
+static int[] num(int N){
+ int arr = new int[N];
+ for(int i = 0; i < N; i++){
+ arr[i] = i + 1;
+ }
+ return arr;
+}
+```
+
+---
+
+## Increasing Order
+
+Numbers arranged from smallest to largest.
+**Note:** If elements are equal then no issues
+
+## Scritly Increasing Order
+Arrangement of numbers such that the next number is always greater than the previous number.
+
+---
+
+
+# Question
+
+Check whether the given numbers are in increasing order?
+`3, 4, 4, 4, 4, 5, 5, 7, 9, 18, 18, 26`
+
+# Choices
+- [x] yes
+- [ ] no
+- [ ] maybe
+
+
+---
+
+
+
+# Question
+
+Check whether the given numbers are in increasing order?
+`-1, -2, -3, -4, -5`
+
+# Choices
+- [ ] Yes
+- [x] No
+- [ ] Maybe
+
+
+---
+
+
+
+# Question
+
+Check whether the given numbers are in strictly increasing order?
+
+`3, 9, 16, 24, 29, 29, 34, 50`
+
+# Choices
+
+- [ ] Yes
+- [x] No
+- [ ] Maybe
+
+---
+
+
+### Checking Strictly Increasing Array
+
+Given an integer N, create an array of size N containing elements in increasing order from 1 to N. Check if the created array is strictly increasing (each element is greater than the previous element).
+
+#### Example
+For N = 5, the array `arr` will be `{1, 2, 3, 4, 5}`, and it is strictly increasing.
+
+For N = 5, the array `arr` will be `{1, 2, 2, 4, 5}`, and it is not strictly increasing.
+
+---
+
+# Question
+
+Check whether the given numbers are in strictly increasing order?
+
+`21, 39, 46, 97, 105`
+
+
+# Choices
+- [x] Yes
+- [ ] No
+- [ ] Maybe
+
+---
+
+
+## If Array Is Strictly Increasing Code
+
+**Note to instructor:** Explain logic of implementing this in code format here
+
+
+### Pseudocode
+```java
+static boolean isStrictlyIncreasing(int N) {
+ int[] arr = new int[N];
+ for (int i = 0; i < N; i++) {
+ arr[i] = i + 1;
+ }
+
+ for (int i = 1; i < N; i++) {
+ if (arr[i] < arr[i - 1]) {
+ return false; // Array is not strictly increasing
+ }
+ }
+
+ return true; // Array is strictly increasing
+}
+```
+
+---
+
+
+## Right Shift of An Array
+Given an array of size N, shift all the elements to the right by 1 and move the last element to the beginning of array
+
+
+## Example 1
+
+```plaintext
+N = 10
+arr[10] = { 7, 4, 9, 11, 2, 24, -5, 17, 1, 8 }
+Ans =
+arr[10] = { 8, 7, 4, 9, 11, 2, 24, -5, 17, 1}
+```
+
+
+
+
+---
+
+
+
+# Question
+
+Right shift the given array
+
+arr[] = {10, 20, 30, 40, 50, 60}
+
+
+# Choices
+- [ ] 60, 50, 40, 30, 20, 10
+- [ ] 0, 10, 20, 30, 40, 50, 60
+- [x] 60, 10, 20, 30, 40, 50
+
+
+---
+
+
+## Right Shift of An Array Idea and Code
+
+
+## Idea
+1. Store last element of original array in a temp variable for future use (`temp = arr[n - 1]`)
+2. Traverse from end to first index and do
+`arr[i] = arr[i - 1]`
+3. Till here all indexes are updated with their new value except 0th index. Finally do
+`arr[0] = temp`
+
+
+## Pseudocode
+```java
+static int[] rotateByone(int arr[]){
+ int n = arr.length
+ int temp = arr[n - 1]
+ for(int i = n - 1; i >= 1; i--){
+ arr[i] = arr[i - 1]
+ }
+ arr[0] = temp;
+ return ans;
+}
+```
+---
+## Drawbacks of Arrays
+
+Once array size is fixed, it cannot be changed.
+If we want to change, we need to create a new array.
+
+int[] ar=new int[4];
+This can only store 4 elements, if we want to store 1 more element we cannot update the size. We have to create a new array only.
+
+---
+
+
+### Arraylist
+
+#### Definition
+
+ArrayList is a class that provides a resizable array implementation that is similar to an ordinary array, but with the added benefit of being able to resize dynamically as elements are added or removed. An ArrayList can store objects of any type, including primitives.
+
+#### Syntax
+
+The general syntax for creating an ArrayList in Java is as follows:
+```java
+ArrayList20,15
30,18 +- [ ] 10,20
30,14
15,18 +- [ ] I am confused about what is transpose :( + +--- + + +#### Observations :- + +* if we observe example 1 + * Element at row 0 and column 1 in matrix mat becomes Element at column 0 and row 1 in transpose. + * similarly mat[2][3] ---> newMat[3][2] + * mat[1][4] ---> newMat[4][1] +* Is there any pattern between the position of element in intial matrix and tranpose matrix ? +* On observing we can say that :- + +
+ Transpose[i][j] = Mat[j][i]
+
+
+
+
+**If dimensions of Mat are MxN then dimensions of transpose would be NxM**
+
+
+#### Code
+```java
+static int[][] transposeMatrix(int[][] Mat) {
+ int m = Mat.length;
+ int n = Mat[0].length;
+ int[][] ans = new int[n][m];
+ for (int i = 0; i < m; i++) {
+ for (int j = 0; j < n; j++) {
+ ans[j][i] = Mat[i][j];
+ }
+ }
+ return ans;
+}
+```
+
+---
+
+
+### Reverse every row
+Given a matrix reverse every row of matrix and return the same matrix
+
+#### Example 1
+
+`mat[3][5]`
+
+| 3 | 2 | 6 | 1 | 9 |
+|:---:|:---:|:---:|:---:|:---:|
+| 14 | 18 | 2 | 4 | 10 |
+| 5 | 6 | 3 | 9 | 8 |
+
+#### Explanation and solution
+
+Initial matrix :-
+
+`mat[3][5]`
+
+| 3 | 2 | 6 | 1 | 9 |
+|:---:|:---:|:---:|:---:|:---:|
+| 14 | 18 | 2 | 4 | 10 |
+| 5 | 6 | 3 | 9 | 8 |
+
+
+Step 1 :- Reverse row 1 of matrix
+
+| 9 | 1 | 6 | 2 | 3 |
+|:---:|:---:|:---:|:---:|:---:|
+| 14 | 18 | 2 | 4 | 10 |
+| 5 | 6 | 3 | 9 | 8 |
+
+
+Step 2 :- Reverse row 2 of matrix
+
+| 9 | 1 | 6 | 2 | 3 |
+|:---:|:---:|:---:|:---:|:---:|
+| 10 | 4 | 2 | 18 | 14 |
+| 5 | 6 | 3 | 9 | 8 |
+
+
+
+Step 4 :- Reverse row 3 of matrix
+
+
+| 9 | 1 | 6 | 2 | 3 |
+|:---:|:---:|:---:|:---:|:---:|
+| 10 | 4 | 2 | 18 | 14 |
+| 8 | 9 | 3 | 6 | 5 |
+
+
+#### Example 2
+
+`mat[3][4]`
+
+| 1 | 2 | 3 | 4 |
+|:---:|:---:|:---:|:---:|
+| 6 | 7 | 8 | 9 |
+| 11 | 12 | 13 | 14 |
+
+#### Explanation and solution
+
+| 4 | 3 | 2 | 1 |
+|:---:|:---:|:---:|:---:|
+| 9 | 8 | 7 | 6 |
+| 14 | 13 | 12 | 11 |
+
+---
+
+
+# Question
+
+ What will be result if we reverse each row of this matrix?
+
+```java
+10, 20, 30
+14, 15, 18
+```
+
+# Choices
+- [ ] 10, 20, 3014, 15, 18 + +- [ ] 20, 10, 30
14, 15, 18 + +- [ ] 10, 20, 30
18, 15, 14 + +- [x] 30, 20, 10
18, 15, 14 + +--- + + +#### Approach +* Our approach should be to traverse each row reverse it. +* But how to reverse a row ? +**Reversing a single row:-** +* First element of the row is swapped with the last element of the row. Similarly, the second element of the array is swapped with the second last element of the array and so on. +* 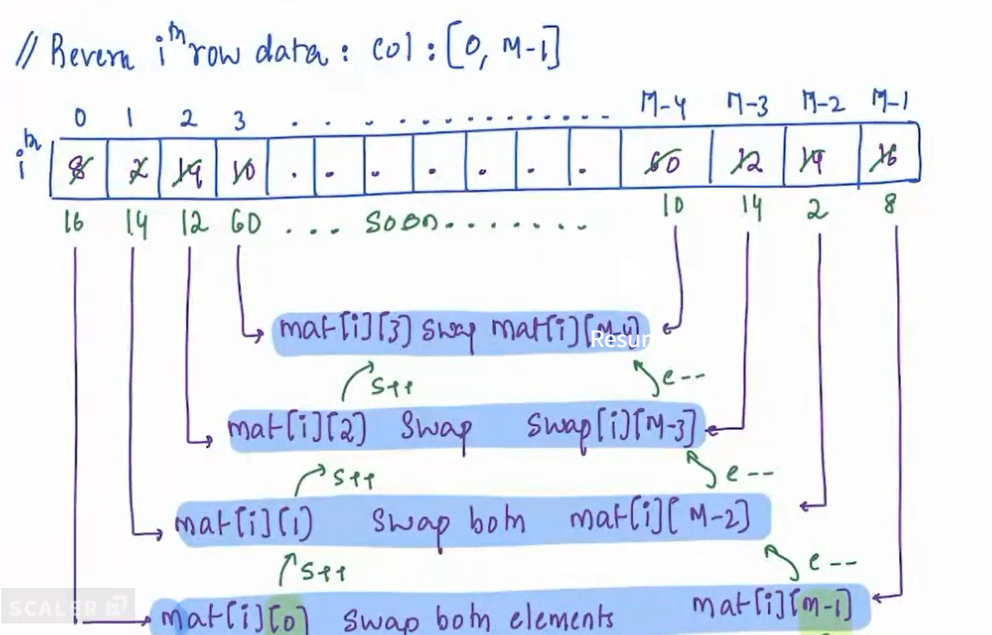 +* But if keep on swapping we would end up with intial configuartion again +* So **we swap till e>s** +This way at the end of traversal, we will have the entire row reversed. + +### Code + +```java + static int[][] reverseEachRow(int[][] Mat) { + int m = Mat[0].length; + int n = Mat.length; + + for (int i = 0; i < n; i++) { + int s = 0; + int e = m - 1; + + while (e > s) { + // Swap elements in the current row + int temp = Mat[i][s]; + Mat[i][s] = Mat[i][e]; + Mat[i][e] = temp; + + e--; + s++; + } + } + + return Mat; +} +``` + +--- + + +### Rotate by 90 + +Given a matrix rotate it by 90o in clockwise direction ? +#### Testcase + + + +#### Solution + + + +#### Example + + + +#### Approach +* **First we take transpose of matrix. On taking transpose:-** +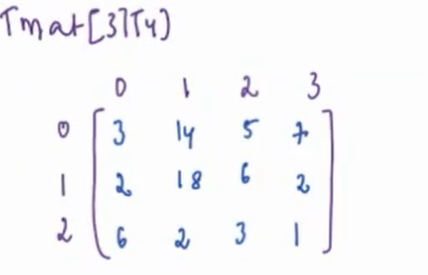 + +* **Reverse each row of transpose to get the solution**. +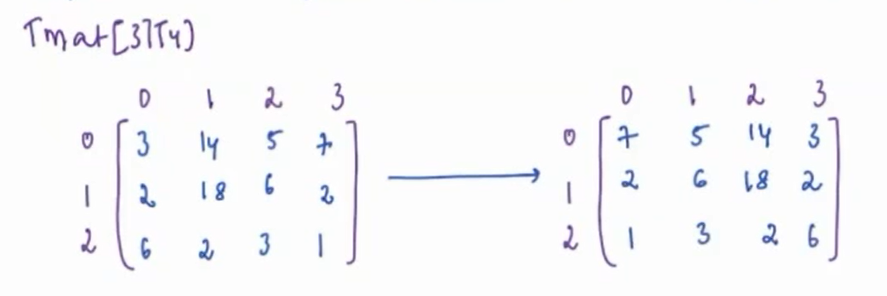 + + + + +**Code** +```java +import java.util.*; + +public class Main { + static int[][] transposeMatrix(int Mat[][]) { + int m = Mat.length; + int n = Mat[0].length; + int transposeMat[][] = new int[n][m]; + for (int i = 0; i < m; i++) { + for (int j = 0; j < n; j++) { + transposeMat[j][i] = Mat[i][j]; + } + } + return transposeMat; + } + + static int[][] reverseEachRow(int Mat[][]) { + int m = Mat[0].length; + int n = Mat.length; + + for (int i = 0; i < n; i++) { + int s = 0; + int e = m - 1; + + while (e > s) { + int temp = Mat[i][s]; + Mat[i][s] = Mat[i][e]; + Mat[i][e] = temp; + + e--; + s++; + } + } + + return Mat; + } + + public static void main(String[] args) { + Scanner sc = new Scanner(System.in); + int Mat[][] = new int[3][4]; + for (int i = 0; i < 3; i++) { + for (int j = 0; j < 4; j++) { + Mat[i][j] = sc.nextInt(); + } + } + int transpose[][] = transposeMatrix(Mat); + int matRotatedClockwise90Degree[][] = reverseEachRow(transpose); + } +} + +``` + + +--- + + +### Syntax +```java +ArrayList
 +
+
+
+
+**Q2.** Eligibility criteria for voting.
+
+---
+
+# Question
+Correct logic to check whether you are eligible to vote.
+
+# Choices
+- [ ] age > 180
+- [ ] age != 17
+- [ ] age == 18
+- [x] age >= 18
+
+---
+
+# Explanation
+
+Look at the following diagram.
+
+
+
+
+
+**Q2.** Eligibility criteria for voting.
+
+---
+
+# Question
+Correct logic to check whether you are eligible to vote.
+
+# Choices
+- [ ] age > 180
+- [ ] age != 17
+- [ ] age == 18
+- [x] age >= 18
+
+---
+
+# Explanation
+
+Look at the following diagram.
+ +
+
+
+**Note:** Some students may ask why are we drawing diagrams. Just mention that it's easy to visualize.
+
+---
+**Q3.** Check person is senior citizen or not.
+If age >= 65, then they can collect pension.
+
+**A.** Look at the following diagram.
+
+
+
+
+
+**Note:** Some students may ask why are we drawing diagrams. Just mention that it's easy to visualize.
+
+---
+**Q3.** Check person is senior citizen or not.
+If age >= 65, then they can collect pension.
+
+**A.** Look at the following diagram.
+
+ +
+
+
+**Q4.** Check whether person is suffering from fever or not.
+
+**A.**
+
+
+
+
+**Q4.** Check whether person is suffering from fever or not.
+
+**A.**
+ +
+
+
+
+### Syntax of If
+**Idea:** When we want to do something when condition is True.
+
+**Syntax:**
+```
+if (condition) {
+ // Statements we want to be executed
+ // if above condition is True.
+}
+```
+
+**Imp point:** `condition` should be a boolean expression. A boolean expression is an expression whose value can only be true or false.
+
+
+---
+
+# Question
+Which of the following is NOT a boolean expression?
+
+# Choices
+- [ ] true
+- [ ] 4 == 5
+- [x] 4 + 5
+- [ ] 4 < 5
+- [ ] false
+
+
+---
+
+1. Read a number and If person is eligible, print "eligible to vote".
+
+Run the below code on IDE and explain.
+```
+public static void main() {
+ Scanner sc = new Scanner(System.in);
+ int age = sc.nextInt();
+ if (age >= 18) {
+ System.out.print("Eligible to vote");
+ }
+}
+```
+
+
+---
+
+# Question
+Which data type should be used to store temperature of a patient?
+
+# Choices
+- [ ] int
+- [x] double
+- [ ] boolean
+- [ ] String
+
+---
+
+# Explanation
+Explain with the following code:
+
+```
+psv main() {
+ Scanner sc = new Scanner(System.in);
+ double temp = sc.nextDouble();
+ if (temp >= 98.6) {
+ System.out.print("Go to doctor!");
+ }
+}
+```
+
+
+
+---
+
+# Question
+Predict the output:
+```
+int a = 10;
+if(a >= 10){
+ System.out.println("Yo");
+}
+System.out.println("Yo");
+```
+
+# Choices
+- [ ] YoYo
+- [x] Yo
+
+
+
+
+### Syntax of If
+**Idea:** When we want to do something when condition is True.
+
+**Syntax:**
+```
+if (condition) {
+ // Statements we want to be executed
+ // if above condition is True.
+}
+```
+
+**Imp point:** `condition` should be a boolean expression. A boolean expression is an expression whose value can only be true or false.
+
+
+---
+
+# Question
+Which of the following is NOT a boolean expression?
+
+# Choices
+- [ ] true
+- [ ] 4 == 5
+- [x] 4 + 5
+- [ ] 4 < 5
+- [ ] false
+
+
+---
+
+1. Read a number and If person is eligible, print "eligible to vote".
+
+Run the below code on IDE and explain.
+```
+public static void main() {
+ Scanner sc = new Scanner(System.in);
+ int age = sc.nextInt();
+ if (age >= 18) {
+ System.out.print("Eligible to vote");
+ }
+}
+```
+
+
+---
+
+# Question
+Which data type should be used to store temperature of a patient?
+
+# Choices
+- [ ] int
+- [x] double
+- [ ] boolean
+- [ ] String
+
+---
+
+# Explanation
+Explain with the following code:
+
+```
+psv main() {
+ Scanner sc = new Scanner(System.in);
+ double temp = sc.nextDouble();
+ if (temp >= 98.6) {
+ System.out.print("Go to doctor!");
+ }
+}
+```
+
+
+
+---
+
+# Question
+Predict the output:
+```
+int a = 10;
+if(a >= 10){
+ System.out.println("Yo");
+}
+System.out.println("Yo");
+```
+
+# Choices
+- [ ] YoYo
+- [x] YoYo +- [ ] Error + + +--- + +# Question +Predict the output: +``` +int a = 18,b = 16; +if(a >= 18){ + System.out.println("a is major"); +} +if(b >= 18){ + System.out.println("b is major"); +} +System.out.println("Blab"); +``` + +# Choices +- [ ] a is major
b is major
Blab +- [ ] a is major
b is major +- [ ] b is major
Blab +- [x] a is major
Blab + + +--- + +# Question +Predict the output: +``` +int a = 50,b = 50; +if(a >= 50){ + System.out.println("a scored half"); + a = a + 1; +} +if(b >= 50){ + System.out.println("b scored half"); + b = b + 1; +} +System.out.print(a + b); +``` + +# Choices +- [ ] a scored half
101 +- [ ] a scored half
b scored half
101 +- [ ] b scored half
102 +- [x] a scored half
b scored half
102 + + + +--- + +# Question +Predict the output: +``` +if(5 > 4) { + System.out.println("First if"); +} +if(10 >= 6) { + System.out.println("Second if"); +} +``` + +# Choices +- [x] First if
Second if +- [ ] First if +- [ ] Second if +- [ ] Error + + + + +--- + +# Question +Predict the output: +``` +if(5 > 10) { + System.out.println("First if"); +} +if(10 >= 16) { + System.out.println("Second if"); +} +System.out.println("Oops!! Nothing will get printed.."); +``` + + +# Choices +- [ ] First if +- [ ] Second if +- [ ] First if
Second if
Oops!! Nothing will get printed.. +- [x] Oops!! Nothing will get printed.. + + +--- + +# Question +Predict the output: +``` +if(true) { + System.out.println("1"); +} +if(true) { + System.out.println("2"); +} +if(true) { + System.out.println("3"); +} +``` + + +# Choices +- [x] 1
2
3 +- [ ] 1 +- [ ] 2 +- [ ] Error + + +--- + +Check if someone has normal temperature: Normal temp = [98.0 to 98.9] + +Ex: +* 98.1 -> Normal temperature +* 99 -> Not normal temperature +* 97.9 -> Not normal temperature + +Explain -> _______98.0________98.9_______ +* 96.8 -> Not normal temperature +* 98.5 -> Normal temperature + +**Q.** What is the Java code for this? + + + +``` +Scanner sc = new Scanner(System.in); +double temp = sc.nextDouble(); +if (temp >= 98.0 && temp >= 98.9) { + System.out.println("Normal temperature"); +} +``` + +**Note:** Logical operators are used to combine conditions. + + +--- + +Now, we want to do something or the other accordingly when the condition is true or false. + +### Syntax of If / Else +``` +if (condition) { + // Statements to run, when above condition True +} +else { + // Statements to run, when above condition False +} +``` + +### Flow 1 +``` +if (condition) { + Statement 1 +}else{ + Statement 2 +} +``` +Q1: Condition True: Statement 1 +Q2: Condition False: Statement 2 + +### Flow 2 +``` +Statement 1 +if (condition) { + Statement 2 +}else{ + Statement 3 +} +Statement 4 +``` +**Q.** What all statements will be executed? +**A.** Condition True: Statement 1, 2 4 +Condition False: Statement 1, 3, 4 + +--- + + +### Example 1 +Read age of a person, check if person is at retirement age, or still have few years left to work. Retirement age is 65. + +``` +Scanner sc = new Scanner(System.in); +int age = sc.nextInt(); +if (age > 65) { + System.out.println("Retired"); +}else{ + System.out.println("Few more years of service."); +} +``` + +--- + + +# Question +Predict the output: +``` +if(9 > 5){ + System.out.println("If block"); +} +else{ + System.out.println("Else block"); +} +``` + +# Choices +- [x] If block +- [ ] If block
Else block +- [ ] Error + + + +--- + + +# Question +Predict the output: +``` +if(false){ + System.out.println("Line 1"); +} else { + System.out.println("Line 2"); +} +``` + +# Choices +- [ ] Line 1 +- [x] Line 2 +- [ ] Line 1
Line 2 +- [ ] Error + + +--- + + +### Modulus Operator + +Modulus operator (%) -> Gives remainder + +``` +System.out.println(17 % 4) -> Remainder = 1 +System.out.println(24 % 2) -> Remainder = 0 +System.out.println(97 % 2) -> Remainder = 1 +System.out.println(82 % 2) -> Remainder = 0 +``` + +Explain even and odd numbers. +**Even numbers:** Numbers which are divisible by 2. +Eg: 2, 4, 6, 8, 10, 12.. +When we divide the number with 2, remainder = 0 +**Odd numbers:** Numbers which are not divisible 2. +Eg: 1, 3, 5, 7, 9, 11.. +When we divide the number with 2, remainder = 1 + + +--- + +### Example 1 + +Read a number and check if number is odd or even. + +``` +Scanner sc = new Scanner(System.in); +int a = sc.nextInt(); +if (a % 2 == 0) { + System.out.println("Number is even"); +}else{ + System.out.println("Number is odd"); +} +``` + +--- + +### Example 2 + +Check if a number is divisible by 5. + +``` +Scanner sc = new Scanner(System.in); +int a = sc.nextInt(); +if (a % 5 == 0) { + System.out.println("Number is divisible by 5"); +}else{ + System.out.println("Number is not divisible by 5"); +} +``` + +--- + +### Example 3 + +Check if a number is divisible by 2 or 3. + +```java +Scanner sc = new Scanner(System.in); +int a = sc.nextInt(); +if (a % 2 == 0 || a % 3 == 0) { + System.out.println("Number is divisible by 2 or 3"); +}else{ + System.out.println("Number is not divisible by 2 and 3 both"); +} +``` + + + + +# Question +Can we have if without an else block? + +# Choices +- [x] Yup!! +- [ ] Nope!! +- [ ] Don't know + + + + +# Question +Can we have else without an if block? + +# Choices +- [ ] Yup!! +- [x] Nooo!! +- [ ] Maybe + +--- + +Read 2 numbers and print max of 2 numbers. + +**Examples:** +```plaintext +a = 5 , b = 10 +Max of a and b = 10 +``` + + +```plaintext +a = 15 , b = 10 +Max of a and b = 15 +``` + + +``` +Scanner sc = new Scanner(System.in); +int a = sc.nextInt(); +int b = sc.nextInt(); +if (a > b) { + System.out.println(a); +}else{ + System.out.println(b); +} + +``` + + + + + +# Question +Predict the output: +For input: 45 45 + +``` +Scanner sc = new Scanner(System.in); +int a = sc.nextInt(); +int b = sc.nextInt(); +if(a > b){ + System.out.print(a); +} +else{ + System.out.print(b); +} +``` + +# Choices +- [ ] Error +- [ ] 45
45 +- [x] 45 + + + + +### Categorize Number +Given an integer n0, categorize it into positive, negative or zero. + +Category: +n = 10: n > 0: print "positive number" +n = -27: n < 0: print "negative number" +n = 0: n == 0: print "zero" + +Give some more examples. + +Idea: +``` +public static void main() { + Scanner sc = new Scanner(System.in); + int a = scn.nextInt(); + if (a > 0) { + System.out.println("positive number"); + } + if (a < 0) { + System.out.println("negative number"); + } + if (a == 0) { + System.out.println("zero"); + } +} +``` + +**Q.** Is the above logic correct? +**A.** Yes + +Dry run the above code for some examples. + +Explain the problem in the above approach. +It's the wastage of comparisions. + + + +**Syntax:** + +``` +if (cond_1) { + // Statements if cond_1 is true +} +else if (cond_2) { + // Statements if cond_1 is false and cond_2 is true +}else{ + // Statements if cond_1 is false and cond_2 is false +} +``` + +**Note:** "else" is optional. + +### Flow +``` +Statement 1 +if (cond_1) { + Statement 2 +} +else if (cond_2) { + Statement 3 +} +else{ + Statement 4 +} +Statement 5 +``` + +Explain the above flow according to below table. +| Conditions which are true | Statements executed | +|:-------------------------:|:-------------------:| +| 1 | 1 2 5 | +| 2 | 1 3 5 | +| All false | 1 4 5 | +| 1 2 | 1 2 4 | + +**Note:** If a condition is true, it will execute and will come out of If/Else block and execute remaining statements. +**Note:** We can have multiple "else if()" blocks. + +Back to Categorize number problem, + + +``` +public static void main() { + Scanner sc = new Scanner(System.in); + int a = scn.nextInt(); + if (a > 0) { + System.out.println("positive number"); + } + else if (a < 0) { + System.out.println("negative number"); + } + else{ + System.out.println("zero"); + } +} +``` + +### Example + +Is the below code correct or not? +``` +int a = 10; +else if (a > 5) { + System.out.println("Number is more than 5"); +} +else{ + System.out.println("Number is not more than 5"); +} +``` +Correct Answer: Compilation error. + +We cannot write any `else if()` without `if()` block. + + + + +--- + +# Question +What will be the output of the following: +``` +if(true) { + System.out.println("1"); +} +else if(true) { + System.out.println("2"); +} +else if(true) { + System.out.println("3"); +} +``` + + +# Choices +- [x] 1 +- [ ] 1
2
3 +- [ ] 2 +- [ ] 3 + +--- + +# Question +Can there be an else if block without a if block + + + +# Choices +- [ ] Yes +- [x] No +- [ ] Maybe + + +--- + +# Question +Can there be an else if block without an else block + + + +# Choices +- [x] Yes +- [ ] No +- [ ] Maybe + + + + +--- diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner If-Else 2.md b/Academy DSA Typed Notes/Beginner Language/Beginner If-Else 2.md new file mode 100644 index 0000000..7513df9 --- /dev/null +++ b/Academy DSA Typed Notes/Beginner Language/Beginner If-Else 2.md @@ -0,0 +1,666 @@ +### If Else : 2 + +--- + + +# Content +- Revision Quizzes +- Categorize triangle +- Max of three +- Fizz Buzz +- Nested If Else +- Categorize into positive, negative and zero + +:::success +There are a lot of quizzes in this session, please take some time to think about the solution on your own before reading further..... +::: + +--- + +## Recap +**Some abbreviations that will be used in this class:** +* System.out.print - SOP +* System.out.println - SOPln + + +--- + +# Question +What will be the output of the following code? +```java +int a = 10,b = 10; +if(a >= 10 && b >= 10){ + System.out.print(a+b); +} +``` + +# Choices +- [ ] 10 +- [x] 20 +- [ ] 30 +- [ ] None + + +--- + +# Question +What will be the output of the following code? +```java +int a = 10; +int b = 10; +if( ++ a >= 12 && ++ b >= 12 ){ + System.out.println("Hello"); +} +System.out.println(a + b); +``` + +# Choices +- [ ] Hello
10 +- [ ] 22 +- [x] 21 +- [ ] None + + +--- + +# Question +What will be the output of the following code? +```java +int a = 10; +int b = 10; +if( ++ a >= 11 || ++ b >= 12 ){ + System.out.println("Hello"); +} +System.out.println(a + b) +``` + +# Choices +- [ ] 20 +- [ ] 22 +- [x] Hello
21 +- [ ] None + +--- + +# Question +What will be the output of the following code? +```java +int a = 10; +int b = 10; +if( ++ a >= 12 || ++ b >= 12 ){ + System.out.println("Hello"); +} +System.out.println(a + b); +``` + +# Choices +- [ ] 20 +- [ ] 21 +- [x] 22 +- [ ] None + + +--- + +# Question +What will be the output of the following code? +```java +int N = 5; +if(N > 2) + System.out.println("Yayay"); +else + System.out.println("Blahblah!!"); +``` + +# Choices +- [x] Yayay +- [ ] Blahblah!! + + +--- + +# Question +What will be the output of the following code? +```java +int N = 5; +if(N > 2) + System.out.println("Yayay"); + System.out.println("Hmmmm"); +else + System.out.println("Blahblah!!"); + System.out.println("Blahblah!!"); +``` + +# Choices +- [x] Error :( +- [ ] No Error, this code rocks! :D +- [ ] Yayay Hmmmm +- [ ] Blahblah!! + +--- + +# Question +What will be the output of the following code? +```java +int marks = 80; +if(marks > 70) { + System.out.print("Distinction "); + System.out.print("Congrats "); +} else if(marks > 35) { + System.out.print("Pass "); +} else + System.out.print("Fail "); +System.out.print("Good luck"); +``` + +# Choices +- [x] Distinction Congrats Good luck +- [ ] Good luck +- [ ] Error +- [ ] Distinction Congrats + + +--- +# Categorize Triangles + +Categorize triangle on the basis of the length of the sides + +**Equilateral:** When the length of the all the sides are equal. +**Isosceles:** When the length of any two sides are equal. +**Scalene:** When the length of all sides are different. + +Let `a`, `b`, `c` be the length of the three sides of a triangle. Given in each case they take some values, tell the category of the triangle. It is the given that the input values for a, b, c are positive integer values. + +```plaintext +a = 20, b = 20, c = 20 +-- Output = Equilaterial +``` + +```plaintext +a = 7, b = 12, c = 9 +-- Output = Scalene +``` + +```plaintext +a = 5, b = 13, c = 5 +-- Output = Isosceles +``` + +```plaintext +a = 12, b = 7, c = 7 +-- Output = Isosceles +``` + +The equivalent code for implementing the above logic is as follows: + +```java +if(a == b && b == c){ + SOPln("Equilateral"); +} +else if(a == b || b == c || a == c){ + SOPln("Isosceles"); +} +else{ + SOPln("Scalene"); +} +``` + + +--- +# Max of three +**Ques:** Given three numbers, print the maximum among them. + +
 +
+
+
+ Note that `a`, `b`, `c` can take any integer values.
+ Stress on the point that `a`, `b`, `c` can also take equal values. The three test case demonstrates this point.
+
+For example,
+* a = 7, b = 20, c = 50 ==> max = 50
+* a = 10, b = 9, c = 10 ==> max = 10
+* a = 3, b = 3, c = 3 ==> max = 3
+
+The equivalent code for implementing the above logic is as follows:
+
+```java
+if(a >= b && a >= c){
+ SOPln("a");
+}
+else if(b >= c){
+ SOPln("b");
+}
+else{
+ SOPln("c");
+}
+```
+
+
+---
+# Fizz-Buzz
+**Ques:** Given a number,
+* print "Fizz" if the number is divisible by 3.
+* print "Buzz" if the number is divisible by 5.
+* print "Fizz-Buzz" if the number is divisble by both 3 and 5.
+
+For example,
+
+* n = 39, O/p = Fizz
+* n = 25, O/p = Buzz
+* n = 15, O/p = Fizz-Buzz
+* n = 13, O/p = `No output`
+
+**How to implement this? **
+
+The following code shows a **wrong implementation** of the above logic:
+
+```java
+if(n % 3 == 0){
+ SOPln("Fizz");
+}
+else if(n % 5 == 0){
+ SOPln("Buzz");
+}
+else{
+ SOPln("Fizz-Buzz");
+}
+```
+
+The above code prints "Fizz-Buzz" for n = 11, but this is wrong as n is neither divisble by 3 nor 5. So there should have no output for this number.
+
+**Another wrong implementation is as follows:**
+
+```java
+if(n % 3 == 0){
+ SOPln("Fizz");
+}
+else if(n % 5 == 0){
+ SOPln("Buzz");
+}
+else if(n % 3 == 0 && n % 5 == 0){
+ SOPln("Fizz-Buzz");
+}
+```
+
+The above code prints "Fizz" for n = 15, but this is wrong as n is divisble by 3 and 5 both. So the correct output should be "Fizz-Buzz".
+
+So finally, the **correct implementation** of this logic is as follows:
+
+```java
+if(n % 3 == 0 && n % 5 == 0){
+ SOPln("Fizz-Buzz");
+}
+else if(n % 3 == 0){
+ SOPln("Fizz");
+}
+else if(n % 5 == 0){
+ SOPln("Buzz");
+}
+```
+
+
+---
+# Nested If Else
+**Syntax:**
+```java
+
+Statement 1
+if(cond1){
+ Statement 2
+ if(cond2){
+ Statement 3
+ }
+ else{
+ Statement 4
+ }
+ Statement 5
+}
+else{
+ Statement 6
+ if(cond3){
+ Statement 7
+ }
+ else{
+ Statement 8
+ }
+ Statement 9
+}
+```
+
+
+
+
+ Note that `a`, `b`, `c` can take any integer values.
+ Stress on the point that `a`, `b`, `c` can also take equal values. The three test case demonstrates this point.
+
+For example,
+* a = 7, b = 20, c = 50 ==> max = 50
+* a = 10, b = 9, c = 10 ==> max = 10
+* a = 3, b = 3, c = 3 ==> max = 3
+
+The equivalent code for implementing the above logic is as follows:
+
+```java
+if(a >= b && a >= c){
+ SOPln("a");
+}
+else if(b >= c){
+ SOPln("b");
+}
+else{
+ SOPln("c");
+}
+```
+
+
+---
+# Fizz-Buzz
+**Ques:** Given a number,
+* print "Fizz" if the number is divisible by 3.
+* print "Buzz" if the number is divisible by 5.
+* print "Fizz-Buzz" if the number is divisble by both 3 and 5.
+
+For example,
+
+* n = 39, O/p = Fizz
+* n = 25, O/p = Buzz
+* n = 15, O/p = Fizz-Buzz
+* n = 13, O/p = `No output`
+
+**How to implement this? **
+
+The following code shows a **wrong implementation** of the above logic:
+
+```java
+if(n % 3 == 0){
+ SOPln("Fizz");
+}
+else if(n % 5 == 0){
+ SOPln("Buzz");
+}
+else{
+ SOPln("Fizz-Buzz");
+}
+```
+
+The above code prints "Fizz-Buzz" for n = 11, but this is wrong as n is neither divisble by 3 nor 5. So there should have no output for this number.
+
+**Another wrong implementation is as follows:**
+
+```java
+if(n % 3 == 0){
+ SOPln("Fizz");
+}
+else if(n % 5 == 0){
+ SOPln("Buzz");
+}
+else if(n % 3 == 0 && n % 5 == 0){
+ SOPln("Fizz-Buzz");
+}
+```
+
+The above code prints "Fizz" for n = 15, but this is wrong as n is divisble by 3 and 5 both. So the correct output should be "Fizz-Buzz".
+
+So finally, the **correct implementation** of this logic is as follows:
+
+```java
+if(n % 3 == 0 && n % 5 == 0){
+ SOPln("Fizz-Buzz");
+}
+else if(n % 3 == 0){
+ SOPln("Fizz");
+}
+else if(n % 5 == 0){
+ SOPln("Buzz");
+}
+```
+
+
+---
+# Nested If Else
+**Syntax:**
+```java
+
+Statement 1
+if(cond1){
+ Statement 2
+ if(cond2){
+ Statement 3
+ }
+ else{
+ Statement 4
+ }
+ Statement 5
+}
+else{
+ Statement 6
+ if(cond3){
+ Statement 7
+ }
+ else{
+ Statement 8
+ }
+ Statement 9
+}
+```
+ +
+
+
+---
+
+# Question
+Predict the output of the following code?
+```java
+int a = 10, b = 15;
+if(a > 8) {
+ if(a < b || b == 9) {
+ System.out.println("Hi");
+ }
+ else {
+ System.out.println("Bye");
+ }
+}
+else {
+ System.out.println("Good Bye");
+}
+```
+
+# Choices
+- [x] Hi
+- [ ] Bye
+- [ ] Good Bye
+- [ ] None
+
+
+
+
+---
+
+# Question
+Predict the output of the following code?
+```java
+int a = 10, b = 15;
+if(a > 8) {
+ if(a == b || b < a) {
+ System.out.println("Hi");
+ }
+ else {
+ System.out.println("Bye");
+ }
+}
+else {
+ System.out.println("Got it");
+}
+```
+
+# Choices
+- [ ] Hi
+- [x] Bye
+- [ ] Got it
+- [ ] None
+
+
+
+---
+
+# Question
+Predict the output of the following code?
+```java
+if(true) {
+ if(true) {
+ if(false) {
+ System.out.println("Hey there");
+ }
+ }
+ else {
+ System.out.println("Hello");
+ }
+}
+else {
+ System.out.println(10 / 0);
+}
+```
+
+# Choices
+- [ ] Hey there
+- [ ] Hello
+- [x] No output
+- [ ] Error
+
+
+
+---
+
+**Explanation:**
+We are not getting an error because the inner if statement with the false condition is not executed due to the if condition being false. Therefore, the else block following it is also not executed. The program simply moves on to the next line, which is outside of any control structures and executes the statement `System.out.println("Hello");` as expected.
+
+The else block following the outer if statement is also not executed since the condition of the outer if statement is true, and the program again moves to the next line and executes the statement `System.out.println("Hello");`
+
+
+---
+## Categorise the number
+**Ques:** Given a number, classify it as follows:
+
+* +ve and even
+* +ve and odd
+* -ve and even
+* -ve and odd
+
+## Example :
+
+**Input:**
+
+
+
+```java
+public static void main(){
+ Scanner scn = new Scanner(System.in);
+ int n = scn.nextInt();
+ if(num > 0){
+ if(num % 2 == 0){
+ SOPln("Positive and even");
+ }
+ else{
+ SOPln("Positive and odd");
+ }
+ }
+ else{
+ if(num % 2 == 0){
+ SOPln("Negative and even");
+ }
+ else{
+ SOPln("Negative and odd");
+ }
+ }
+}
+```
+
+
+
+---
+
+## Scope of a Variable
+
+It defines the point till where you can use the variable. You can only use a variable till the closing bracket of the block in which it was created.
+
+**Example 1:**
+
+```java=
+public static void main(){
+
+
+ int x;
+ x = 5;
+
+ int y;
+ y = 20
+
+}
+```
+
+Scope of variable `x`: Line 4 to 10
+Scope of variable `y`: Line 7 to 10
+
+**Example 2:**
+
+```java=
+public static void main(){
+
+ int x = 10;
+ if(x == 10){
+ int y = 5;
+ SOP(y);
+ }
+ int z = 9;
+
+}
+```
+
+Scope of variable `x`: Line 3 to 10
+Scope of variable `y`: Line 5 to 7
+Scope of variable `z`: Line 8 to 10
+
+**Example 3:**
+
+```java=
+public static void main(){
+ int a = 10;
+ {
+ a = 20;
+ }
+ SOP(a);
+
+}
+```
+
+Scope of variable `a`: Line 2 to 8
+Also the code will print 20 as the changes done in the variable values are not restricted to that block in which the change is done. But the life of the variable is restricted to the block in which it was created.
+
+**Example 4:**
+
+```java=
+public static void main(){
+ int x = 10;
+ {
+ int y = 20;
+ SOP(x + " " + y);
+ }
+ {
+ SOP(x + " " + y); // This line will give error as y is not present in its scope
+ }
+
+}
+```
+
+**Example 5:** Redefining variable error
+
+```java=
+public static void main(){
+ int a = 90;
+ {
+ int a = 7; // This line will give error as variable a is already defined in this scope
+ SOPln(a);
+ }
+
+}
+```
+
+---
+
+# Question
+Predict the output of the following code:
+```java
+public static void main(String args[]) {
+ int x = 10;
+ {
+ int y = 20;
+ System.out.println(x + " " + y);
+ }
+ {
+ System.out.println(x + " " + y);
+ }
+ System.out.println(x + " " + y);
+}
+```
+
+# Choices
+- [x] Error
+- [ ] 10 20
+
+
+
+---
+
+# Question
+Predict the output of the following code?
+```java
+int a = 10, b = 15;
+if(a > 8) {
+ if(a < b || b == 9) {
+ System.out.println("Hi");
+ }
+ else {
+ System.out.println("Bye");
+ }
+}
+else {
+ System.out.println("Good Bye");
+}
+```
+
+# Choices
+- [x] Hi
+- [ ] Bye
+- [ ] Good Bye
+- [ ] None
+
+
+
+
+---
+
+# Question
+Predict the output of the following code?
+```java
+int a = 10, b = 15;
+if(a > 8) {
+ if(a == b || b < a) {
+ System.out.println("Hi");
+ }
+ else {
+ System.out.println("Bye");
+ }
+}
+else {
+ System.out.println("Got it");
+}
+```
+
+# Choices
+- [ ] Hi
+- [x] Bye
+- [ ] Got it
+- [ ] None
+
+
+
+---
+
+# Question
+Predict the output of the following code?
+```java
+if(true) {
+ if(true) {
+ if(false) {
+ System.out.println("Hey there");
+ }
+ }
+ else {
+ System.out.println("Hello");
+ }
+}
+else {
+ System.out.println(10 / 0);
+}
+```
+
+# Choices
+- [ ] Hey there
+- [ ] Hello
+- [x] No output
+- [ ] Error
+
+
+
+---
+
+**Explanation:**
+We are not getting an error because the inner if statement with the false condition is not executed due to the if condition being false. Therefore, the else block following it is also not executed. The program simply moves on to the next line, which is outside of any control structures and executes the statement `System.out.println("Hello");` as expected.
+
+The else block following the outer if statement is also not executed since the condition of the outer if statement is true, and the program again moves to the next line and executes the statement `System.out.println("Hello");`
+
+
+---
+## Categorise the number
+**Ques:** Given a number, classify it as follows:
+
+* +ve and even
+* +ve and odd
+* -ve and even
+* -ve and odd
+
+## Example :
+
+**Input:**
+
+
+
+```java
+public static void main(){
+ Scanner scn = new Scanner(System.in);
+ int n = scn.nextInt();
+ if(num > 0){
+ if(num % 2 == 0){
+ SOPln("Positive and even");
+ }
+ else{
+ SOPln("Positive and odd");
+ }
+ }
+ else{
+ if(num % 2 == 0){
+ SOPln("Negative and even");
+ }
+ else{
+ SOPln("Negative and odd");
+ }
+ }
+}
+```
+
+
+
+---
+
+## Scope of a Variable
+
+It defines the point till where you can use the variable. You can only use a variable till the closing bracket of the block in which it was created.
+
+**Example 1:**
+
+```java=
+public static void main(){
+
+
+ int x;
+ x = 5;
+
+ int y;
+ y = 20
+
+}
+```
+
+Scope of variable `x`: Line 4 to 10
+Scope of variable `y`: Line 7 to 10
+
+**Example 2:**
+
+```java=
+public static void main(){
+
+ int x = 10;
+ if(x == 10){
+ int y = 5;
+ SOP(y);
+ }
+ int z = 9;
+
+}
+```
+
+Scope of variable `x`: Line 3 to 10
+Scope of variable `y`: Line 5 to 7
+Scope of variable `z`: Line 8 to 10
+
+**Example 3:**
+
+```java=
+public static void main(){
+ int a = 10;
+ {
+ a = 20;
+ }
+ SOP(a);
+
+}
+```
+
+Scope of variable `a`: Line 2 to 8
+Also the code will print 20 as the changes done in the variable values are not restricted to that block in which the change is done. But the life of the variable is restricted to the block in which it was created.
+
+**Example 4:**
+
+```java=
+public static void main(){
+ int x = 10;
+ {
+ int y = 20;
+ SOP(x + " " + y);
+ }
+ {
+ SOP(x + " " + y); // This line will give error as y is not present in its scope
+ }
+
+}
+```
+
+**Example 5:** Redefining variable error
+
+```java=
+public static void main(){
+ int a = 90;
+ {
+ int a = 7; // This line will give error as variable a is already defined in this scope
+ SOPln(a);
+ }
+
+}
+```
+
+---
+
+# Question
+Predict the output of the following code:
+```java
+public static void main(String args[]) {
+ int x = 10;
+ {
+ int y = 20;
+ System.out.println(x + " " + y);
+ }
+ {
+ System.out.println(x + " " + y);
+ }
+ System.out.println(x + " " + y);
+}
+```
+
+# Choices
+- [x] Error
+- [ ] 10 2010 20
10 20 +- [ ] 10 20 10 20 10 20 + + +--- + +# Question +Predict the output of the following code: +```java +public static void main(){ + int x = 10, y = 20; + { + SOP(x + " " + y); + } + { + x = 15; + SOPln(x + " " + y); + } + SOPln(x + " " + y); +} +``` + +# Choices +- [ ] 10 20
15 20
10 20 +- [ ] Error +- [x] 10 20
15 20
15 20 +- [ ] inky pinky ponky + + +--- + +# Question +Predict the output of the following code: +```java +if(true){ + int x = 10; + SOPln("Value of x is " + x); + x ++ ; +} +SOPln("Value of x is " + x); +``` + +# Choices +- [ ] Value of x is 10
Value of x is 11 +- [ ] Value of x is 10
Value of x is 0 +- [ ] Value of x is 10
Value of x is 10 +- [x] Error + + +--- + + +# Question +Predict the output of the following code: +```java +int a = 0; +{ + int b = 10; + SOPln("b = " + b); + int c = a + b; + SOPln("c = " + c); +} +a = c + b; +SOPln("a = " + a); +``` + +# Choices +- [ ] a = 20
b = 10
c = 10 +- [ ] b = 10
c = 10
a = 20 +- [x] Error +--- +**Explanation:** Error b and c are out of the scope + + +--- + + +# Question +Predict the output of the following code: +```java +int a = 10, b = 5; +if(true){ + int c = a * b; +} +SOPln(c); +``` + +# Choices +- [ ] 50 +- [x] Error +- [ ] Need Coffee!! + +--- +**Explanation:** Error the variable c is out of the scope diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner Introduction to Beginner Module.pdf b/Academy DSA Typed Notes/Beginner Language/Beginner Introduction to Beginner Module.pdf new file mode 100644 index 0000000..63c42ea Binary files /dev/null and b/Academy DSA Typed Notes/Beginner Language/Beginner Introduction to Beginner Module.pdf differ diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner Loop - 1.md b/Academy DSA Typed Notes/Beginner Language/Beginner Loop - 1.md new file mode 100644 index 0000000..a12fefe --- /dev/null +++ b/Academy DSA Typed Notes/Beginner Language/Beginner Loop - 1.md @@ -0,0 +1,628 @@ +# While Loop + + +--- + +## Agenda +- Intro of Loops +- Print numbers from 1 to 5 +- Structure and Syntax of while loop +- Even numbers from 1 to n +- Print multiples of 4 +- Print numbers from n to 1 +- Find last digit +- Remove last digit + + +:::success +There are a lot of quizzes in this session, please take some time to think about the solution on your own before reading further..... +::: + +--- + +**Ques:** Print natural numbers from 1 to 5. + +**Method 1:** +``` +System.out.println(1); +System.out.println(2); +System.out.println(3); +System.out.println(4); +System.out.println(5); +``` + +**Method 2:** +``` +int i = 1; +System.out.println(i); +i ++ ; +System.out.println(i); +i ++ ; +System.out.println(i); +i ++ ; +System.out.println(i); +i ++ ; +System.out.println(i); +``` + +**Comparison of Method 1 and Method 2:** +Both **Method 1** and **Method 2** output the numbers 1, 2, 3, 4, and 5 in order. The only difference between the two methods is the way the code is written. +* Issues In **Method 1** : Since we are updating the values as well along with copy pasting the lines. +Possibility of Human Error +* Issues In **Method 2** : We are repeating the same lines again and again. + +## Loops +Repeat a task multiple times + +- For Loop +- While Loop +- Do while Loop + +**Method 3:** +``` +int i = 1; +while(i <= 5){ + SOPln(i); + i = i + 1; +} +``` + +| i | i<=5 | Output | i + 1 | +|:---:|:-----:|:------:|:---------:| +| 1 | true | 1 | 2 | +| 2 | true | 2 | 3 | +| 3 | true | 3 | 4 | +| 4 | true | 4 | 5 | +| 5 | true | 5 | 6 | +| 6 | false | | **Break** | + + +--- + +## Structure of While loop + +**Step 1:** Initialization of a loop variable. +**Step 2:** Write while with condition. +**Step 3:** Write the task you want to repeat. +**Step 4:** Updation of loop variable. + +## Syntax of while loop + +``` +initialize +while(condition){ + // task to be repeated + // updation +} +``` + +**Flow chart of while loop:** + + +
 +
+---
+
+# Question
+What is the output of the following code?
+```
+int i = 5;
+while(i <= 10){
+ System.out.println(i);
+ i = i * 2;
+}
+```
+
+# Choices
+- [x] 5
+
+---
+
+# Question
+What is the output of the following code?
+```
+int i = 5;
+while(i <= 10){
+ System.out.println(i);
+ i = i * 2;
+}
+```
+
+# Choices
+- [x] 510 +- [ ] 0 +- [ ] Error + + + + +--- + +# Question +What is the output of the following code? +``` +int i = 1; +while(i < 5){ + System.out.print(i + " "); + i = i + 1; +} +``` + +# Choices +- [ ] 1 2 3 4 5 +- [x] 1 2 3 4 +- [ ] 5 4 3 2 1 + + + +--- + + +# Question +What is the output of the following code? +``` +int i = 0; +while(i <= 10){ + System.out.print(i + " "); + i++; +} +``` + +# Choices +- [x] 0 1 2 3 4 5 6 7 8 9 10 +- [ ] 1 2 3 4 5 6 7 8 9 10 +- [ ] Error + + + + +--- + +# Question +What is the output of the following code? + +``` +int i = 1; +while(i >= 10){ + System.out.print(i + " "); + i = i + 1; +} +``` + +# Choices +- [ ] Error +- [ ] 1 2 3 4 5 6 7 8 9 10 +- [x] Nothing will get printed +- [ ] 10 9 8 7 6 5 4 3 2 1 + + +--- + + +# Question +What is the output of the following code? + +``` +int i = 1; +while(i <= 10){ + System.out.print(i + " "); +} +``` + +# Choices +- [ ] 1 2 3 4 5 6 7 8 9 10 +- [x] 1 1 1 1 1 1 ... Infinite times + + + +--- + + +# Question +What is the output of the following code? + +``` +int i = 0; +while(i <= 10){ + System.out.print(i + " "); + i = i * 2; +} +``` + +# Choices +- [ ] 5 10 +- [ ] 0 +- [x] Infinite loop +- [ ] 0 2 4 + + + +--- + + +# Question +What is the output of the following code? + +``` +int i = 1; +while(i <= 5){ + System.out.print(i + " "); + i = i - 1; +} +``` + +# Choices +- [ ] 1 2 3 4 5 +- [ ] 5 4 3 2 1 +- [x] Infinite loop +- [ ] Inki pinky ponky + + +--- + + +# Question +How many times `Hi` will be printed in the output? + +``` +int i = 0; +while(i <= 5){ + System.out.println("Hi"); + i = i + 1; +} +``` + +# Choices +- [ ] 5 +- [x] 6 +- [ ] 4 +- [ ] Infinite times + +--- + + +# Question +How many times `Inki Pinki Ponki` will be printed in the output? + +``` +int i = 1; +while(i <= n){ + System.out.println("Inki Pinki Ponki"); + i = i + 1; +} +``` + +# Choices +- [x] n +- [ ] (n+1) +- [ ] Only once +- [ ] Too many times + + + +--- + + +**Ques:** Print even numbers from 1 to n + +``` +int n = scn.nextInt(); +int i = 1; +while(i <= n){ + if(i % 2 == 0){ + System.out.println(i); + } + i = i + 1; +} +``` + +> Explain dry run of the above code for more clarity +> Example of how to dry run the above code: + +
 +
+
+
+Another way to implement the above task is as follows:
+
+```
+int i = 2;
+while(i <= n){
+ System.out.println(i);
+ i = i + 2;
+}
+```
+
+
+
+
+
+Another way to implement the above task is as follows:
+
+```
+int i = 2;
+while(i <= n){
+ System.out.println(i);
+ i = i + 2;
+}
+```
+
+ +
+
+Note that the number of iterations are reduced from 6 to 3.
+
+Let us take some test cases to test our code.
+Consider `n = 17`
+The output should be `2 4 6 8 10 12 14 16`
+> **Instruction for Instructor:** Run the code on editor to verify the same and show to the students.
+
+
+In the range 1 - 17, the total number of even numbers are 8.
+
+In the range 1 - 10, the total number of even numbers are 5.
+
+> Based on the above observation, ask the following question to the students?
+**How to calculate the total number of multiples of x between 1 and n?**
+**Ans:** `n/x`
+
+Total number of multiples of 2 from 1 to 40 is = 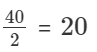
+
+Total number of multiples of 2 from 1 to 51 is = 
+
+---
+
+
+
+
+
+# Question
+What will be the total number of iterations in the following code?
+
+```
+int i = 1;
+while(i <= 20){
+ System.out.println(i);
+ i = i + 1;
+}
+```
+
+# Choices
+- [x] 20
+- [ ] 10
+- [ ] 15
+- [ ] No clue
+
+
+---
+
+
+# Question
+What will be the total number of iterations in the following code?
+
+```
+int i = 2;
+while(i <= n){
+ System.out.println(i);
+ i = i + 2;
+}
+```
+
+# Choices
+- [ ] n
+- [x] n/2
+- [ ] n+1
+- [ ] Infinite
+
+
+---
+
+
+# Question
+What will be the total number of iterations in the following code?
+
+```
+int i = 3;
+while(i <= n){
+ System.out.println(i);
+ i = i + 3;
+}
+```
+
+# Choices
+- [x] n / 3
+- [ ] 3 * n
+- [ ] n+3
+- [ ] n
+
+---
+
+
+# Question
+What are all the multiples of 4 between 1 to 18 ?
+
+# Choices
+- [ ] 4 8 12 16 20 24
+- [ ] 4 6 8 10 12 14
+- [x] 4 8 12 16
+- [ ] 1 4 8 12 16
+
+
+---
+
+**Ques:** Print multiples of 4 till n.
+
+**Approach 1:**
+In this approach, the code takes an input from the user and stores it in the variable n. Then, it uses a `while` loop to iterate from 1 to n. During each iteration, if the value of i is divisible by 4, it prints the value of i using `System.out.println()`.
+
+```
+int n = scn.nextInt();
+int i = 1;
+while(i <= n){
+ if(i % 4 == 0){
+ System.out.println(i);
+ }
+ i++;
+}
+```
+
+If n is taken as 10, the output of the above code would be: `4 8`
+
+
+**Approach 2:** **Number of instructions executed are reduced**
+In this approach, the code initializes the variable $i$ to $4$ and then uses a `while` loop to print the value of $i$ in each iteration. The value of $i$ is incremented by $4$ during each iteration until it becomes greater than $n$.
+
+**Code:**
+```
+int i = 4;
+while(i <= n){
+ System.out.println(i);
+ i = i + 4;
+}
+```
+
+> Explain using dry run as follows:
+
+
+
+
+Note that the number of iterations are reduced from 6 to 3.
+
+Let us take some test cases to test our code.
+Consider `n = 17`
+The output should be `2 4 6 8 10 12 14 16`
+> **Instruction for Instructor:** Run the code on editor to verify the same and show to the students.
+
+
+In the range 1 - 17, the total number of even numbers are 8.
+
+In the range 1 - 10, the total number of even numbers are 5.
+
+> Based on the above observation, ask the following question to the students?
+**How to calculate the total number of multiples of x between 1 and n?**
+**Ans:** `n/x`
+
+Total number of multiples of 2 from 1 to 40 is = 
+
+Total number of multiples of 2 from 1 to 51 is = 
+
+---
+
+
+
+
+
+# Question
+What will be the total number of iterations in the following code?
+
+```
+int i = 1;
+while(i <= 20){
+ System.out.println(i);
+ i = i + 1;
+}
+```
+
+# Choices
+- [x] 20
+- [ ] 10
+- [ ] 15
+- [ ] No clue
+
+
+---
+
+
+# Question
+What will be the total number of iterations in the following code?
+
+```
+int i = 2;
+while(i <= n){
+ System.out.println(i);
+ i = i + 2;
+}
+```
+
+# Choices
+- [ ] n
+- [x] n/2
+- [ ] n+1
+- [ ] Infinite
+
+
+---
+
+
+# Question
+What will be the total number of iterations in the following code?
+
+```
+int i = 3;
+while(i <= n){
+ System.out.println(i);
+ i = i + 3;
+}
+```
+
+# Choices
+- [x] n / 3
+- [ ] 3 * n
+- [ ] n+3
+- [ ] n
+
+---
+
+
+# Question
+What are all the multiples of 4 between 1 to 18 ?
+
+# Choices
+- [ ] 4 8 12 16 20 24
+- [ ] 4 6 8 10 12 14
+- [x] 4 8 12 16
+- [ ] 1 4 8 12 16
+
+
+---
+
+**Ques:** Print multiples of 4 till n.
+
+**Approach 1:**
+In this approach, the code takes an input from the user and stores it in the variable n. Then, it uses a `while` loop to iterate from 1 to n. During each iteration, if the value of i is divisible by 4, it prints the value of i using `System.out.println()`.
+
+```
+int n = scn.nextInt();
+int i = 1;
+while(i <= n){
+ if(i % 4 == 0){
+ System.out.println(i);
+ }
+ i++;
+}
+```
+
+If n is taken as 10, the output of the above code would be: `4 8`
+
+
+**Approach 2:** **Number of instructions executed are reduced**
+In this approach, the code initializes the variable $i$ to $4$ and then uses a `while` loop to print the value of $i$ in each iteration. The value of $i$ is incremented by $4$ during each iteration until it becomes greater than $n$.
+
+**Code:**
+```
+int i = 4;
+while(i <= n){
+ System.out.println(i);
+ i = i + 4;
+}
+```
+
+> Explain using dry run as follows:
+
+ +
+
+> Contrast both the dry runs and stress on the fact that the number of iterations are reduced from 10 to 2.
+
+
+---
+
+
+# Question
+What are the total number of iterations of the following code?
+```
+int i = 4;
+while(i <= n){
+ System.out.println(i);
+ i = i + 4;
+}
+```
+
+# Choices
+- [ ] n
+- [ ] n + 4
+- [x] n / 4
+- [ ] Easy Peesy
+
+---
+
+
+**Ques:** Print numbers from n to 1.
+
+```
+int n = 5;
+while(i >= 1){
+ System.out.println(i);
+ i--;
+}
+```
+
+> Explain using dry run as follows:
+
+
+
+
+> Contrast both the dry runs and stress on the fact that the number of iterations are reduced from 10 to 2.
+
+
+---
+
+
+# Question
+What are the total number of iterations of the following code?
+```
+int i = 4;
+while(i <= n){
+ System.out.println(i);
+ i = i + 4;
+}
+```
+
+# Choices
+- [ ] n
+- [ ] n + 4
+- [x] n / 4
+- [ ] Easy Peesy
+
+---
+
+
+**Ques:** Print numbers from n to 1.
+
+```
+int n = 5;
+while(i >= 1){
+ System.out.println(i);
+ i--;
+}
+```
+
+> Explain using dry run as follows:
+
+ +
+
+
+---
+
+
+# Question
+Predict the output:
+
+```
+int i = 10;
+while(i >= 0){
+ System.out.print(i + " ");
+ i = i - 2;
+}
+```
+
+# Choices
+- [ ] 10 9 8 7 6 5 4 3 2 1 0
+- [ ] 10 8 6 4 2
+- [x] 10 8 6 4 2 0
+- [ ] 0 2 4 6 8 10
+
+---
+
+**Dry Run:**
+
+
+
+
+---
+
+
+# Question
+Predict the output:
+
+```
+int i = 10;
+while(i >= 0){
+ System.out.print(i + " ");
+ i = i - 2;
+}
+```
+
+# Choices
+- [ ] 10 9 8 7 6 5 4 3 2 1 0
+- [ ] 10 8 6 4 2
+- [x] 10 8 6 4 2 0
+- [ ] 0 2 4 6 8 10
+
+---
+
+**Dry Run:**
+ +
+
+---
+
+
+## Modulus operator (%)
+It is used to find the remainder. When we take modulus by 10, we get the last digit of that number.
+
+
+---
+
+
+# Question
+Predict the output of the following code:
+
+```
+int x = 7185;
+System.out.println(x % 10);
+```
+
+# Choices
+- [ ] 8
+- [ ] 578
+- [ ] 718.5
+- [x] 5
+
+---
+
+
+# Question
+Predict the output of the following code:
+
+```
+int x = 4578;
+System.out.println(x % 10);
+```
+
+# Choices
+- [x] 8
+- [ ] 578
+- [ ] 78
+- [ ] None
+
+
+---
+
+
+# Question
+Predict the output of the following code:
+
+```
+int x = 99576;
+System.out.println(x % 10);
+```
+
+# Choices
+- [x] 6
+- [ ] 576
+- [ ] 995
+- [ ] None
+
+
+---
+
+
+# Question
+Predict the output of the following code:
+
+```
+int x = 7248;
+System.out.println(x / 10);
+```
+
+# Choices
+- [ ] 724.8
+- [ ] 725
+- [x] 724
+- [ ] Inky pinky ponky
+
+---
+
+
+**Ques:** Given a positive integer, write code to find it's last digit.
+
+**Code:**
+```
+int n = scn.nextInt();
+System.out.println(n % 10);
+```
+
+---
+
+
+**Ques:** Given a positive integer, write code to remove it's last digit.
+
+**Code:**
+```
+int n = scn.nextInt();
+n = n / 10;
+System.out.println(n);
+```
+---
+
diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner Loop - 2.md b/Academy DSA Typed Notes/Beginner Language/Beginner Loop - 2.md
new file mode 100644
index 0000000..1b81eab
--- /dev/null
+++ b/Academy DSA Typed Notes/Beginner Language/Beginner Loop - 2.md
@@ -0,0 +1,599 @@
+# Loops 2
+
+---
+
+> Quick revision
+
+**Step 1:** Initialization of a loop variable.
+**Step 2:** Write while with condition.
+**Step 3:** Write the task you want to repeat.
+**Step 4:** Updation of loop variable.
+
+## Syntax of while loop
+
+```
+initialize
+while(condition){ // loop stops when the condition fails
+ // task to be repeated
+ // updation
+}
+```
+
+**Flow chart of while loop:**
+
+
+
+---
+
+
+## Modulus operator (%)
+It is used to find the remainder. When we take modulus by 10, we get the last digit of that number.
+
+
+---
+
+
+# Question
+Predict the output of the following code:
+
+```
+int x = 7185;
+System.out.println(x % 10);
+```
+
+# Choices
+- [ ] 8
+- [ ] 578
+- [ ] 718.5
+- [x] 5
+
+---
+
+
+# Question
+Predict the output of the following code:
+
+```
+int x = 4578;
+System.out.println(x % 10);
+```
+
+# Choices
+- [x] 8
+- [ ] 578
+- [ ] 78
+- [ ] None
+
+
+---
+
+
+# Question
+Predict the output of the following code:
+
+```
+int x = 99576;
+System.out.println(x % 10);
+```
+
+# Choices
+- [x] 6
+- [ ] 576
+- [ ] 995
+- [ ] None
+
+
+---
+
+
+# Question
+Predict the output of the following code:
+
+```
+int x = 7248;
+System.out.println(x / 10);
+```
+
+# Choices
+- [ ] 724.8
+- [ ] 725
+- [x] 724
+- [ ] Inky pinky ponky
+
+---
+
+
+**Ques:** Given a positive integer, write code to find it's last digit.
+
+**Code:**
+```
+int n = scn.nextInt();
+System.out.println(n % 10);
+```
+
+---
+
+
+**Ques:** Given a positive integer, write code to remove it's last digit.
+
+**Code:**
+```
+int n = scn.nextInt();
+n = n / 10;
+System.out.println(n);
+```
+---
+
diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner Loop - 2.md b/Academy DSA Typed Notes/Beginner Language/Beginner Loop - 2.md
new file mode 100644
index 0000000..1b81eab
--- /dev/null
+++ b/Academy DSA Typed Notes/Beginner Language/Beginner Loop - 2.md
@@ -0,0 +1,599 @@
+# Loops 2
+
+---
+
+> Quick revision
+
+**Step 1:** Initialization of a loop variable.
+**Step 2:** Write while with condition.
+**Step 3:** Write the task you want to repeat.
+**Step 4:** Updation of loop variable.
+
+## Syntax of while loop
+
+```
+initialize
+while(condition){ // loop stops when the condition fails
+ // task to be repeated
+ // updation
+}
+```
+
+**Flow chart of while loop:**
+ +
+
+**Question:**
+
+How to find the last digit of a number N?
+
+**Answer:** Use the modulus operator as `N%10`.
+
+> Give an example
+
+**Question:** How to delete the last digit of N?
+
+**Answer:**
+```
+N = N / 10;
+SOP(N);
+```
+
+---
+title: Printing all digits
+description: Print all the digits of that number from right to left
+duration: 480
+card_type: cue_card
+---
+
+**Ques:** Given a integer number, print all the digits of that number from right to left.
+
+Example, if `n = 6397` the correct output should be `7 9 3 6`
+
+> Give the students, an intuition to solve the problem as follows:
+
+
+
+**Question:**
+
+How to find the last digit of a number N?
+
+**Answer:** Use the modulus operator as `N%10`.
+
+> Give an example
+
+**Question:** How to delete the last digit of N?
+
+**Answer:**
+```
+N = N / 10;
+SOP(N);
+```
+
+---
+title: Printing all digits
+description: Print all the digits of that number from right to left
+duration: 480
+card_type: cue_card
+---
+
+**Ques:** Given a integer number, print all the digits of that number from right to left.
+
+Example, if `n = 6397` the correct output should be `7 9 3 6`
+
+> Give the students, an intuition to solve the problem as follows:
+ +
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+**Approach:**
+* Find the last digit.
+* Print the digit.
+* Remove last digit.
+
+**Code:**
+```
+int n = scn.nextInt();
+while(n > 0){
+ int digit = n % 10;
+ SOPln(digit);
+ n = n / 10;
+}
+```
+
+> To figure out the condition in the while loop expression (i.e., `n > 0`), give the students an intuition as follows:
+
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+**Approach:**
+* Find the last digit.
+* Print the digit.
+* Remove last digit.
+
+**Code:**
+```
+int n = scn.nextInt();
+while(n > 0){
+ int digit = n % 10;
+ SOPln(digit);
+ n = n / 10;
+}
+```
+
+> To figure out the condition in the while loop expression (i.e., `n > 0`), give the students an intuition as follows:
+ +
+**How to handle negative numbers?**
+**Ans:** Convert negative numbers to positive numbers.
+
+> Take an example of a negative number, dry run the code. Tell the students that the code exits from the while loop condition since `n < 0`. Then give the solution.
+
+**The updated code is as follows:**
+```
+int n = scn.nextInt();
+if(n < 0){
+ n = n * -1;
+}
+while(n > 0){
+ int digit = n % 10;
+ SOPln(digit);
+ n = n / 10;
+}
+```
+
+**Next corner test case:** What if `n == 0`?
+In this case, the output should be $0$, but according to the code this will print nothing. So we need to handle this case as well.
+
+**The updated code is as follows:**
+```
+int n = scn.nextInt();
+if(n < 0){
+ n = n * -1;
+ return;
+}
+else if(n == 0){
+ SOPln(0);
+ return;
+}
+while(n > 0){
+ int digit = n % 10;
+ SOPln(digit);
+ n = n / 10;
+}
+```
+
+
+**Dry Run:**
+
+
+
+**How to handle negative numbers?**
+**Ans:** Convert negative numbers to positive numbers.
+
+> Take an example of a negative number, dry run the code. Tell the students that the code exits from the while loop condition since `n < 0`. Then give the solution.
+
+**The updated code is as follows:**
+```
+int n = scn.nextInt();
+if(n < 0){
+ n = n * -1;
+}
+while(n > 0){
+ int digit = n % 10;
+ SOPln(digit);
+ n = n / 10;
+}
+```
+
+**Next corner test case:** What if `n == 0`?
+In this case, the output should be $0$, but according to the code this will print nothing. So we need to handle this case as well.
+
+**The updated code is as follows:**
+```
+int n = scn.nextInt();
+if(n < 0){
+ n = n * -1;
+ return;
+}
+else if(n == 0){
+ SOPln(0);
+ return;
+}
+while(n > 0){
+ int digit = n % 10;
+ SOPln(digit);
+ n = n / 10;
+}
+```
+
+
+**Dry Run:**
+
+ +
+
+---
+title: Find sum of digits of a given number
+description: Take examples to explain how to use while loops
+duration: 900
+card_type: cue_card
+---
+
+## Find Sum of Digits of A Given Number
+**Question:**
+
+Find the sum of digits of a given number.
+
+Give examples -> 1274, 1004, -512
+
+```
+1274 -> 1 + 2 + 7 + 4 = 14
+1004 -> 1 + 0 + 0 + 4 = 5
+-512 -> 5 + 1 + 2 = 8
+```
+
+
+Note: Negative sign (**-**) is not a digit.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+**Approach:**
+To discuss the approach take an example.
+
+```
+// Initialization
+n = 2748
+s = 0
+```
+
+| n | n > 0 | d = n % 10 | s = s + d | n = n / 10 |
+|:----:|:-----:|:----------:|:---------:|:----------:|
+| 2748 | true | 8 | 8 | 274 |
+| 274 | true | 4 | 12 | 27 |
+| 27 | true | 7 | 19 | 2 |
+| 2 | true | 2 | 21 | 0 |
+| 0 | false | - | - | - |
+
+```
+int n = scn.nextInt();
+
+if (n < 0) {
+ n = n * - 1;
+}
+
+int s = 0;
+while (n > 0) {
+ int d = n % 10;
+ s = s + d;
+ n = n / 10;
+}
+
+SOPln(s);
+```
+
+---
+title: Add a given digit to the back of a given number N.
+description: Take examples to explain how to use while loops
+duration: 800
+card_type: cue_card
+---
+
+### Example 1
+**Question:**
+
+Given a positive integer N and a single digit d, add d to the back of N.
+
+**Example:**
+
+
+
+---
+title: Find sum of digits of a given number
+description: Take examples to explain how to use while loops
+duration: 900
+card_type: cue_card
+---
+
+## Find Sum of Digits of A Given Number
+**Question:**
+
+Find the sum of digits of a given number.
+
+Give examples -> 1274, 1004, -512
+
+```
+1274 -> 1 + 2 + 7 + 4 = 14
+1004 -> 1 + 0 + 0 + 4 = 5
+-512 -> 5 + 1 + 2 = 8
+```
+
+
+Note: Negative sign (**-**) is not a digit.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+**Approach:**
+To discuss the approach take an example.
+
+```
+// Initialization
+n = 2748
+s = 0
+```
+
+| n | n > 0 | d = n % 10 | s = s + d | n = n / 10 |
+|:----:|:-----:|:----------:|:---------:|:----------:|
+| 2748 | true | 8 | 8 | 274 |
+| 274 | true | 4 | 12 | 27 |
+| 27 | true | 7 | 19 | 2 |
+| 2 | true | 2 | 21 | 0 |
+| 0 | false | - | - | - |
+
+```
+int n = scn.nextInt();
+
+if (n < 0) {
+ n = n * - 1;
+}
+
+int s = 0;
+while (n > 0) {
+ int d = n % 10;
+ s = s + d;
+ n = n / 10;
+}
+
+SOPln(s);
+```
+
+---
+title: Add a given digit to the back of a given number N.
+description: Take examples to explain how to use while loops
+duration: 800
+card_type: cue_card
+---
+
+### Example 1
+**Question:**
+
+Given a positive integer N and a single digit d, add d to the back of N.
+
+**Example:**
+ +
+Formula to add d to the back of N:
+
+```
+n = n * 10 + d;
+```
+
+---
+title: Find the reverse of a given number
+description: Take examples to explain how to use while loops
+duration: 1100
+card_type: cue_card
+---
+
+### Example 2
+**Question:**
+
+Given a number N, store it's reverse in another variable and print it.
+
+**Examples:**
+
+
+Formula to add d to the back of N:
+
+```
+n = n * 10 + d;
+```
+
+---
+title: Find the reverse of a given number
+description: Take examples to explain how to use while loops
+duration: 1100
+card_type: cue_card
+---
+
+### Example 2
+**Question:**
+
+Given a number N, store it's reverse in another variable and print it.
+
+**Examples:**
+ +
+**Idea/Approach:**
+Initialize a variable rev = 0 and one by one take the last digit of N and add it to rev as shown below.
+
+
+
+**Idea/Approach:**
+Initialize a variable rev = 0 and one by one take the last digit of N and add it to rev as shown below.
+
+ +
+**Steps:**
+* Get last digit
+* Add last digit to the back of rev
+* Remove last digit
+* Repeat the above three steps till the number is greater than zero
+
+**Dry run:**
+| n | n > 0 | d = n % 10 | rev = rev * 10 + d | n = n / 10 |
+|:----:|:-----:|:----------:|:------------------:|:----------:|
+| 1456 | true | 6 | 6 | 145 |
+| 145 | true | 5 | 65 | 14 |
+| 14 | true | 4 | 654 | 1 |
+| 1 | true | 1 | 6541 | 0 |
+| 0 | false | - | - | - |
+
+```
+int n = scn.nextInt();
+int copy = n;
+
+if (n < 0) {
+ n = n * - 1;
+}
+
+int rev = 0;
+while (n > 0) {
+ int d = n % 10;
+ rev = rev * 10 + d;
+ n = n / 10;
+}
+
+if (copy < 0) {
+ rev = rev * - 1;
+}
+
+SOPln(s);
+```
+
+> Dry run with n = 2400 and show that the output will be 42 and not 0042.
+
+Tell them that if you want to print 0042, print the digits of n from right to left. It is not possible for an integer variable to store 0042.
+
+
+
+**Steps:**
+* Get last digit
+* Add last digit to the back of rev
+* Remove last digit
+* Repeat the above three steps till the number is greater than zero
+
+**Dry run:**
+| n | n > 0 | d = n % 10 | rev = rev * 10 + d | n = n / 10 |
+|:----:|:-----:|:----------:|:------------------:|:----------:|
+| 1456 | true | 6 | 6 | 145 |
+| 145 | true | 5 | 65 | 14 |
+| 14 | true | 4 | 654 | 1 |
+| 1 | true | 1 | 6541 | 0 |
+| 0 | false | - | - | - |
+
+```
+int n = scn.nextInt();
+int copy = n;
+
+if (n < 0) {
+ n = n * - 1;
+}
+
+int rev = 0;
+while (n > 0) {
+ int d = n % 10;
+ rev = rev * 10 + d;
+ n = n / 10;
+}
+
+if (copy < 0) {
+ rev = rev * - 1;
+}
+
+SOPln(s);
+```
+
+> Dry run with n = 2400 and show that the output will be 42 and not 0042.
+
+Tell them that if you want to print 0042, print the digits of n from right to left. It is not possible for an integer variable to store 0042.
+
+ +
+> Show dry run with - 417 as n.
+
+---
+title: Check if a given number is palindrome or not
+description: Take examples to explain how to use while loops
+duration: 720
+card_type: cue_card
+---
+
+### Example 3
+**Question:**
+
+Given a number N, check if number if palindrome or not.
+A number is said to a palindrome if it remains the same when its digits are reversed. Ex- 1221, 1551, 131, etc.
+
+**Exercise for students:**
+
+
+> Show dry run with - 417 as n.
+
+---
+title: Check if a given number is palindrome or not
+description: Take examples to explain how to use while loops
+duration: 720
+card_type: cue_card
+---
+
+### Example 3
+**Question:**
+
+Given a number N, check if number if palindrome or not.
+A number is said to a palindrome if it remains the same when its digits are reversed. Ex- 1221, 1551, 131, etc.
+
+**Exercise for students:**
+ +
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+**Approach:**
+Find the reverse of the number using what we discussed in the last quiz and compare it with the original number. It it is the same, then the number is palindromic, otherwise not.
+
+```
+int n = scn.nextInt();
+int copy = n;
+
+if (n < 0) {
+ n = n * - 1;
+}
+
+int rev = 0;
+while (n > 0) {
+ int d = n % 10;
+ rev = rev * 10 + d;
+ n = n / 10;
+}
+
+if (copy < 0) {
+ rev = rev * - 1;
+}
+
+if (rev == copy) {
+ SOPln("PALINDROME");
+}
+else {
+ SOPln("NOT PALINDROME")
+}
+```
+
+---
+title: For loop basics
+description: Quick recap of the syntax and flow of for loops
+duration: 120
+card_type: cue_card
+---
+
+## For loop Basics
+
+Every for loop question can be done using a while loop. The difference lies in the syntax.
+
+**Syntax:**
+```
+for(Initialization; Condition; update) {
+ // Statements to be executed
+}
+```
+
+> Explain the syntax.
+
+
+**Flow:**
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+**Approach:**
+Find the reverse of the number using what we discussed in the last quiz and compare it with the original number. It it is the same, then the number is palindromic, otherwise not.
+
+```
+int n = scn.nextInt();
+int copy = n;
+
+if (n < 0) {
+ n = n * - 1;
+}
+
+int rev = 0;
+while (n > 0) {
+ int d = n % 10;
+ rev = rev * 10 + d;
+ n = n / 10;
+}
+
+if (copy < 0) {
+ rev = rev * - 1;
+}
+
+if (rev == copy) {
+ SOPln("PALINDROME");
+}
+else {
+ SOPln("NOT PALINDROME")
+}
+```
+
+---
+title: For loop basics
+description: Quick recap of the syntax and flow of for loops
+duration: 120
+card_type: cue_card
+---
+
+## For loop Basics
+
+Every for loop question can be done using a while loop. The difference lies in the syntax.
+
+**Syntax:**
+```
+for(Initialization; Condition; update) {
+ // Statements to be executed
+}
+```
+
+> Explain the syntax.
+
+
+**Flow:**
+ +
+---
+title: Print numbers from 1 to 5 using for loops
+description: Take examples to explain how to use for loops
+duration: 180
+card_type: cue_card
+---
+### Example 4
+**Question:**
+
+Print all numbers from 1 to 5.
+
+```
+for(int i = 1; i <= 5; i ++ ) {
+ SOPln(i);
+}
+```
+
+> Explain the logic behind initialization, condition and update statements.
+
+**Dry Run:**
+| i | i <= 5 | print(i) | i++ |
+|:---:|:------:|:--------:|:---:|
+| 1 | true | 1 | 2 |
+| 2 | true | 2 | 3 |
+| 3 | true | 3 | 4 |
+| 4 | true | 4 | 5 |
+| 5 | true | 5 | 6 |
+| 6 | false | - | - |
+
+---
+title: Quiz 1
+description: Quiz 1
+duration: 60
+card_type: quiz_card
+---
+
+# Question
+Expected output for following code :
+
+```
+for(int i = 1; i <= 10; i = i + 2) {
+ System.out.println(i);
+}
+```
+
+# Choices
+- [ ] All Numbers from 1 to 10
+- [ ] All Even Numbers from 1 to 10
+- [x] All Odd Numbers from 1 to 10
+- [ ] All Numbers from 1 to 9
+
+---
+title: Explain the quiz answer
+description: Perform a dry run to explain the quiz question
+duration: 240
+card_type: cue_card
+---
+
+### Explaination
+
+**Dry Run:**
+| i | i <= 10 | print(i) | i += 2 |
+|:---:|:-------:|:--------:|:------:|
+| 1 | true | 1 | 3 |
+| 3 | true | 3 | 5 |
+| 5 | true | 5 | 7 |
+| 7 | true | 7 | 9 |
+| 9 | true | 9 | 11 |
+| 11 | false | - | - |
+
+---
+title: Print the count of digits of a number
+description: Take examples to explain how to use for loops
+duration: 600
+card_type: cue_card
+---
+
+### Example 5
+**Question:**
+
+Given a positive number, print the count of digits.
+
+> Give examples such as 5164, 121700, 9, etc.
+
+**Approach/Intuition:**
+
+
+---
+title: Print numbers from 1 to 5 using for loops
+description: Take examples to explain how to use for loops
+duration: 180
+card_type: cue_card
+---
+### Example 4
+**Question:**
+
+Print all numbers from 1 to 5.
+
+```
+for(int i = 1; i <= 5; i ++ ) {
+ SOPln(i);
+}
+```
+
+> Explain the logic behind initialization, condition and update statements.
+
+**Dry Run:**
+| i | i <= 5 | print(i) | i++ |
+|:---:|:------:|:--------:|:---:|
+| 1 | true | 1 | 2 |
+| 2 | true | 2 | 3 |
+| 3 | true | 3 | 4 |
+| 4 | true | 4 | 5 |
+| 5 | true | 5 | 6 |
+| 6 | false | - | - |
+
+---
+title: Quiz 1
+description: Quiz 1
+duration: 60
+card_type: quiz_card
+---
+
+# Question
+Expected output for following code :
+
+```
+for(int i = 1; i <= 10; i = i + 2) {
+ System.out.println(i);
+}
+```
+
+# Choices
+- [ ] All Numbers from 1 to 10
+- [ ] All Even Numbers from 1 to 10
+- [x] All Odd Numbers from 1 to 10
+- [ ] All Numbers from 1 to 9
+
+---
+title: Explain the quiz answer
+description: Perform a dry run to explain the quiz question
+duration: 240
+card_type: cue_card
+---
+
+### Explaination
+
+**Dry Run:**
+| i | i <= 10 | print(i) | i += 2 |
+|:---:|:-------:|:--------:|:------:|
+| 1 | true | 1 | 3 |
+| 3 | true | 3 | 5 |
+| 5 | true | 5 | 7 |
+| 7 | true | 7 | 9 |
+| 9 | true | 9 | 11 |
+| 11 | false | - | - |
+
+---
+title: Print the count of digits of a number
+description: Take examples to explain how to use for loops
+duration: 600
+card_type: cue_card
+---
+
+### Example 5
+**Question:**
+
+Given a positive number, print the count of digits.
+
+> Give examples such as 5164, 121700, 9, etc.
+
+**Approach/Intuition:**
+ +
+```
+int count = 0;
+for(int i = n; i > 0; i = i / 10) {
+ count += 1;
+}
+
+SOPln(count);
+```
+
+> Show that the above code does not work for n = 0 and make the following change.
+
+```
+int count = 0;
+if (n == 0) count = 1;
+
+for(int i = n; i > 0; i = i / 10) {
+ count += 1;
+}
+
+SOPln(count);
+```
+
+---
+title: Read 5 numbers and for every number print last digit of the number.
+description: Explain the need of for loops
+duration: 780
+card_type: cue_card
+---
+### Example 6
+
+**Question:**
+
+Read 5 numbers and for every number print last digit of the number.
+
+**Example:**
+Input:
+34
+45
+378
+980
+456
+
+**Output:**
+4
+5
+8
+0
+6
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+**Approach 1:**
+
+```
+int a = scn.nextInt();
+int b = scn.nextInt();
+int c = scn.nextInt();
+int d = scn.nextInt();
+int e = scn.nextInt();
+
+SOPln(a % 10);
+SOPln(b % 10);
+SOPln(c % 10);
+SOPln(d % 10);
+SOPln(e % 10);
+```
+
+**Approach 2:**
+```
+for(int i = 0; i < 5; i ++ ) {
+ int n = scn.nextInt();
+ SOPln(n % 10);
+}
+```
+
+---
+title: Read T numbers and for every number print last digit of the number.
+description: Show examples to explain how to use for loops
+duration: 360
+card_type: cue_card
+---
+### Example 7
+
+**Question:**
+
+Read T numbers and for every number print the last digit.
+
+**Input Format:**
+1st Line: Contains T
+Followed by T lines containing the T numbers
+
+```
+int T = scn.nextInt();
+
+for(int i = 0; i < T; i ++ ) {
+ int n = scn.nextInt();
+ SOPln(n % 10);
+}
+```
+
+---
+title: Read T numbers and for every number print the sum of digits of the number.
+description: Show examples to explain how to use for loops
+duration: 420
+card_type: cue_card
+---
+### Example 8
+**Question:**
+
+Read T numbers and for each number, print the sum of digits of the number.
+
+**Input:**
+3
+566
+4130
+162
+
+**Output:**
+17
+8
+9
+
+```
+int T = scn.nextInt();
+
+for(int i = 0; i < T; i ++ ) {
+ int n = scn.nextInt();
+
+ if (n < 0) {
+ n = n * - 1;
+ }
+
+ int s = 0;
+ while (n > 0) {
+ int d = n % 10;
+ s = s + d;
+ n = n / 10;
+ }
+
+ SOPln(s);
+}
+```
+
+> Show dry run for the example above.
+
+Same question using for loop -
+```
+int T = scn.nextInt();
+
+for(int i = 0; i < T; i ++ ) {
+ int n = scn.nextInt();
+
+ if (n < 0) {
+ n = n * -1;
+ }
+
+ int s = 0;
+ for(int x = n; x > 0; x ++ ) {
+ int d = x % 10;
+ s = s + d;
+ }
+
+ SOPln(s);
+}
+```
+
diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner Maths Basics & Calculate Iterations.pdf b/Academy DSA Typed Notes/Beginner Language/Beginner Maths Basics & Calculate Iterations.pdf
new file mode 100644
index 0000000..0f49dfd
Binary files /dev/null and b/Academy DSA Typed Notes/Beginner Language/Beginner Maths Basics & Calculate Iterations.pdf differ
diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner Operators.md b/Academy DSA Typed Notes/Beginner Language/Beginner Operators.md
new file mode 100644
index 0000000..753e26b
--- /dev/null
+++ b/Academy DSA Typed Notes/Beginner Language/Beginner Operators.md
@@ -0,0 +1,958 @@
+# Beginner: Operators
+---
+## Agenda
+
+* Typecasting Revision
+* Rules doing basic operations
+* Integer Overflow
+* Operators (Logical, Unary)
+
+:::success
+There are a lot of quizzes in this session, please take some time to think about the solution on your own before reading further.....
+:::
+
+---
+
+## Rules
+1. While type casting, if no chance of data loss, then we get no error -> Implicit / Widening Typecasting (Happens automatically).
+2. If there may be a data loss, then we will get some error. If we still want to typecast, we forcefully have to do it -> Explicit / Narrowing (forcefully).
+
+**Note:** If students are not able to understand, run the corresponding quiz code in IDE, and then clarify any questions.
+
+
+---
+
+
+# Question
+Predict the output:
+```
+int abc = 400;
+long x = abc;
+System.out.print(x);
+```
+
+# Choices
+- [x] 400
+- [ ] Error
+- [ ] Random Value
+- [ ] Good Morning!
+
+---
+
+
+# Explanation
+When we store int into long, there is no data loss, hence 400 is the answer. Explain more if necessary.
+
+
+
+---
+
+
+# Question
+
+Predict the output:
+```
+long a = 100000; // 10^5
+System.out.print(a);
+```
+
+# Choices
+- [ ] Error
+- [x] 100000
+- [ ] a
+
+---
+
+
+# Explanation
+**Mistake:** Some students may think that we need a L after the number but its not necessary. Because implicity typecasting is going on. Explain more, if needed.
+
+
+---
+
+
+# Question
+
+Predict the output:
+```
+long x = 500000;
+int y = x;
+System.out.print(y);
+```
+
+# Choices
+- [x] Error
+- [ ] 500000
+- [ ] Some random value
+---
+
+
+# Explanation
+
+```
+long x = 500000; // This line is correct (Implcity typecasting)
+int y = x; // Possible data loss.
+System.out.print(y);
+```
+We cannot store a long into int, because of possible data loss. Hence, the error.
+
+**Q.** Ask students on how to correct this?
+**A.** Explicit typecasting
+
+Move on to the next quiz which is based on this.
+
+
+
+---
+
+
+# Question
+Predict the output:
+```
+long n = 60000;
+int a = (int)n;
+System.out.print(a);
+```
+
+# Choices
+- [ ] Random Value
+- [ ] Error
+- [x] 60000
+- [ ] How would I know?
+
+---
+
+
+# Explanation
+The 2nd line is forcing the compiler to change the long to int which is correct.
+
+**Mistake:** Some students may ask why we won't get any random value. Because, 60000 is within the range of int data type, and hence no loss.
+
+Range of int -> -2 * 10^9 to 2 * 10^9
+
+Give the following example:
+long x = 100000000000 // 10^11
+This number is too large and so we need to mention explicity that:
+long x = 100000000000L.
+
+
+---
+
+
+# Question
+Predict the output:
+```
+long a = 100000000000L; // 10^11
+int b = (int)a;
+System.out.println(b);
+```
+
+# Choices
+- [ ] 100000000000
+- [ ] Error
+- [x] Random Value
+- [ ] Too many zeroes
+
+---
+
+
+# Explanation
+
+Since 10^11 cannot be stored in int, and we are forcing. So, data loss (Overflow) is happening, and some value is getting lost, we are getting random value.
+
+
+---
+title: Quiz 6
+description: Quiz 6
+duration: 30
+card_type: quiz_card
+---
+
+# Question
+Predict the output:
+```
+double x = 7.89;
+System.out.print(x);
+```
+
+# Choices
+- [ ] 7
+- [x] 7.89
+- [ ] Error
+- [ ] Ex is not texting back.
+
+---
+
+# Explanation
+
+Since the right value is of type double. We can store double into double without any issues.
+
+
+---
+
+# Question
+Predict the output:
+```
+float val = 10.78;
+System.out.print(val);
+```
+
+# Choices
+- [ ] 10.78
+- [ ] 10
+- [x] Error
+- [ ] I am sleeping
+
+---
+
+# Explanation
+
+Any decimal number is of double type, while the type of val is float.
+**Q.** Can we store double into float type?
+**A.** No, as there can be possible data loss.
+
+Hence, we get an error.
+**Q.** Ask students into how to fix this?
+**A.** Explicit typecasting to float.
+
+
+---
+
+# Question
+
+Predict the output:
+```
+float x = 15.88f;
+System.out.print(x);
+```
+
+# Choices
+- [x] 15.88
+- [ ] 15
+- [ ] Error
+
+---
+
+# Explanation
+Since, we explicitly typecasted to float, hence we will not get any error.
+
+---
+
+# Question
+
+Predict the output:
+```java
+double y = 4.78;
+float a = y;
+System.out.println(a);
+```
+
+# Choices
+- [ ] 4.78
+- [x] Error
+- [ ] Missed the lectures
+
+---
+
+# Explanation
+
+Since, we are storing a double type into float, we have possible data loss. Hence, we get an error.
+
+
+---
+## Rules doing Basic Operations
+
+
+## Rule 1
+When we do operation between a decimal and a non-decimal number, the output is always decimal.
+
+* int op double --> double
+* long op float --> float
+
+**Note:** Run each of the following example codes in the compiler, and show the output to students.
+
+## Example 1
+
+### Incorrect Code
+Don't let the students know that the code is incorrect. Ask them if it's correct and if not, how is it violating the Rule 1.
+
+```
+class Scaler {
+ public static void main(String[] args) {
+ int x = 10;
+ double y = 10.25;
+ int z = x + y;
+ System.out.println(z);
+ }
+}
+```
+
+### Output
+```
+error: incompatible types: possible lossy conversion from double to int
+ int z = x + y;
+ ^
+1 error
+```
+
+Explain why their is a possible lossy conversion if we store the sum in an integer.
+A. (x + y) is of double type.
+
+Ask students on how to remove the error?
+
+### Correct Code
+```
+class Scaler {
+ public static void main(String[] args) {
+ int x = 10;
+ double y = 10.25;
+ double z = x + y;
+ System.out.println(z);
+ }
+}
+```
+
+### Output
+```
+20.25
+```
+
+Q. Ask students on how to store the result into an integer i.e, we don't want to store into a double.
+
+A. Typecasting
+
+### Correct Code
+```
+class Scaler {
+ public static void main(String[] args) {
+ int x = 10;
+ double y = 10.25;
+ int z = (int)(x + y);
+ System.out.println(z);
+ }
+}
+```
+
+
+
+## Rule 2
+When we do operation between two operands of same category, the result is of bigger type.
+
+* int op long --> long
+* float op double --> double
+* int op int --> int
+* long op long --> long
+
+**Note:** Run each of the following example codes in the compiler, and show the output to students.
+
+## Example 1
+
+### Incorrect Code
+Don't let the students know that the code is incorrect. Ask them if it's correct and if not, how is it violating the Rule 2.
+
+```
+class Scaler {
+ public static void main(String[] args) {
+ int x = 20;
+ long y = 150L;
+ int z = x + y;
+ System.out.println(z);
+ }
+}
+```
+
+### Output
+```
+/tmp/thqSRPUchr/Scaler.java:6: error: incompatible types: possible lossy conversion from long to int
+int z = x + y;
+^
+1 error
+```
+
+Explain why their is a possible lossy conversion if we store the sum in an integer.
+A. (x + y) is of long type.
+
+Ask students on how to remove the error?
+
+### Correct Code
+
+```
+class Scaler {
+ public static void main(String[] args) {
+ int x = 20;
+ long y = 150L;
+ long z = x + y;
+ System.out.println(z);
+ }
+}
+```
+
+### Output
+```
+170
+```
+
+---
+## Integer Overflow
+
+
+**Note:** For better clarity of quizzes, please run the codes in the compiler as well.
+Explain the integer overflow concept after giving the following quiz.
+
+
+---
+
+
+# Question
+
+Predict the output:
+```
+int a = 100000;
+int b = 400000;
+int c = a * b;
+System.out.print(c);
+```
+
+# Choices
+- [ ] 40000000000
+- [x] Some random Value
+- [ ] Error
+
+
+---
+## CPU and its components
+
+
+Before explaining the quiz's answer, we need to understand some more information.
+
+**Q.** Where are these variables stored and where are these operations carried out?
+
+We have two major components:
+* Central Processing Unit (CPU)
+ * ALU - Arithmetic Logic Unit
+ * Control Unit
+ * Registers
+* Random Access Memory (RAM)
+
+Look at the following diagram.
+
+
+```
+int count = 0;
+for(int i = n; i > 0; i = i / 10) {
+ count += 1;
+}
+
+SOPln(count);
+```
+
+> Show that the above code does not work for n = 0 and make the following change.
+
+```
+int count = 0;
+if (n == 0) count = 1;
+
+for(int i = n; i > 0; i = i / 10) {
+ count += 1;
+}
+
+SOPln(count);
+```
+
+---
+title: Read 5 numbers and for every number print last digit of the number.
+description: Explain the need of for loops
+duration: 780
+card_type: cue_card
+---
+### Example 6
+
+**Question:**
+
+Read 5 numbers and for every number print last digit of the number.
+
+**Example:**
+Input:
+34
+45
+378
+980
+456
+
+**Output:**
+4
+5
+8
+0
+6
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+**Approach 1:**
+
+```
+int a = scn.nextInt();
+int b = scn.nextInt();
+int c = scn.nextInt();
+int d = scn.nextInt();
+int e = scn.nextInt();
+
+SOPln(a % 10);
+SOPln(b % 10);
+SOPln(c % 10);
+SOPln(d % 10);
+SOPln(e % 10);
+```
+
+**Approach 2:**
+```
+for(int i = 0; i < 5; i ++ ) {
+ int n = scn.nextInt();
+ SOPln(n % 10);
+}
+```
+
+---
+title: Read T numbers and for every number print last digit of the number.
+description: Show examples to explain how to use for loops
+duration: 360
+card_type: cue_card
+---
+### Example 7
+
+**Question:**
+
+Read T numbers and for every number print the last digit.
+
+**Input Format:**
+1st Line: Contains T
+Followed by T lines containing the T numbers
+
+```
+int T = scn.nextInt();
+
+for(int i = 0; i < T; i ++ ) {
+ int n = scn.nextInt();
+ SOPln(n % 10);
+}
+```
+
+---
+title: Read T numbers and for every number print the sum of digits of the number.
+description: Show examples to explain how to use for loops
+duration: 420
+card_type: cue_card
+---
+### Example 8
+**Question:**
+
+Read T numbers and for each number, print the sum of digits of the number.
+
+**Input:**
+3
+566
+4130
+162
+
+**Output:**
+17
+8
+9
+
+```
+int T = scn.nextInt();
+
+for(int i = 0; i < T; i ++ ) {
+ int n = scn.nextInt();
+
+ if (n < 0) {
+ n = n * - 1;
+ }
+
+ int s = 0;
+ while (n > 0) {
+ int d = n % 10;
+ s = s + d;
+ n = n / 10;
+ }
+
+ SOPln(s);
+}
+```
+
+> Show dry run for the example above.
+
+Same question using for loop -
+```
+int T = scn.nextInt();
+
+for(int i = 0; i < T; i ++ ) {
+ int n = scn.nextInt();
+
+ if (n < 0) {
+ n = n * -1;
+ }
+
+ int s = 0;
+ for(int x = n; x > 0; x ++ ) {
+ int d = x % 10;
+ s = s + d;
+ }
+
+ SOPln(s);
+}
+```
+
diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner Maths Basics & Calculate Iterations.pdf b/Academy DSA Typed Notes/Beginner Language/Beginner Maths Basics & Calculate Iterations.pdf
new file mode 100644
index 0000000..0f49dfd
Binary files /dev/null and b/Academy DSA Typed Notes/Beginner Language/Beginner Maths Basics & Calculate Iterations.pdf differ
diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner Operators.md b/Academy DSA Typed Notes/Beginner Language/Beginner Operators.md
new file mode 100644
index 0000000..753e26b
--- /dev/null
+++ b/Academy DSA Typed Notes/Beginner Language/Beginner Operators.md
@@ -0,0 +1,958 @@
+# Beginner: Operators
+---
+## Agenda
+
+* Typecasting Revision
+* Rules doing basic operations
+* Integer Overflow
+* Operators (Logical, Unary)
+
+:::success
+There are a lot of quizzes in this session, please take some time to think about the solution on your own before reading further.....
+:::
+
+---
+
+## Rules
+1. While type casting, if no chance of data loss, then we get no error -> Implicit / Widening Typecasting (Happens automatically).
+2. If there may be a data loss, then we will get some error. If we still want to typecast, we forcefully have to do it -> Explicit / Narrowing (forcefully).
+
+**Note:** If students are not able to understand, run the corresponding quiz code in IDE, and then clarify any questions.
+
+
+---
+
+
+# Question
+Predict the output:
+```
+int abc = 400;
+long x = abc;
+System.out.print(x);
+```
+
+# Choices
+- [x] 400
+- [ ] Error
+- [ ] Random Value
+- [ ] Good Morning!
+
+---
+
+
+# Explanation
+When we store int into long, there is no data loss, hence 400 is the answer. Explain more if necessary.
+
+
+
+---
+
+
+# Question
+
+Predict the output:
+```
+long a = 100000; // 10^5
+System.out.print(a);
+```
+
+# Choices
+- [ ] Error
+- [x] 100000
+- [ ] a
+
+---
+
+
+# Explanation
+**Mistake:** Some students may think that we need a L after the number but its not necessary. Because implicity typecasting is going on. Explain more, if needed.
+
+
+---
+
+
+# Question
+
+Predict the output:
+```
+long x = 500000;
+int y = x;
+System.out.print(y);
+```
+
+# Choices
+- [x] Error
+- [ ] 500000
+- [ ] Some random value
+---
+
+
+# Explanation
+
+```
+long x = 500000; // This line is correct (Implcity typecasting)
+int y = x; // Possible data loss.
+System.out.print(y);
+```
+We cannot store a long into int, because of possible data loss. Hence, the error.
+
+**Q.** Ask students on how to correct this?
+**A.** Explicit typecasting
+
+Move on to the next quiz which is based on this.
+
+
+
+---
+
+
+# Question
+Predict the output:
+```
+long n = 60000;
+int a = (int)n;
+System.out.print(a);
+```
+
+# Choices
+- [ ] Random Value
+- [ ] Error
+- [x] 60000
+- [ ] How would I know?
+
+---
+
+
+# Explanation
+The 2nd line is forcing the compiler to change the long to int which is correct.
+
+**Mistake:** Some students may ask why we won't get any random value. Because, 60000 is within the range of int data type, and hence no loss.
+
+Range of int -> -2 * 10^9 to 2 * 10^9
+
+Give the following example:
+long x = 100000000000 // 10^11
+This number is too large and so we need to mention explicity that:
+long x = 100000000000L.
+
+
+---
+
+
+# Question
+Predict the output:
+```
+long a = 100000000000L; // 10^11
+int b = (int)a;
+System.out.println(b);
+```
+
+# Choices
+- [ ] 100000000000
+- [ ] Error
+- [x] Random Value
+- [ ] Too many zeroes
+
+---
+
+
+# Explanation
+
+Since 10^11 cannot be stored in int, and we are forcing. So, data loss (Overflow) is happening, and some value is getting lost, we are getting random value.
+
+
+---
+title: Quiz 6
+description: Quiz 6
+duration: 30
+card_type: quiz_card
+---
+
+# Question
+Predict the output:
+```
+double x = 7.89;
+System.out.print(x);
+```
+
+# Choices
+- [ ] 7
+- [x] 7.89
+- [ ] Error
+- [ ] Ex is not texting back.
+
+---
+
+# Explanation
+
+Since the right value is of type double. We can store double into double without any issues.
+
+
+---
+
+# Question
+Predict the output:
+```
+float val = 10.78;
+System.out.print(val);
+```
+
+# Choices
+- [ ] 10.78
+- [ ] 10
+- [x] Error
+- [ ] I am sleeping
+
+---
+
+# Explanation
+
+Any decimal number is of double type, while the type of val is float.
+**Q.** Can we store double into float type?
+**A.** No, as there can be possible data loss.
+
+Hence, we get an error.
+**Q.** Ask students into how to fix this?
+**A.** Explicit typecasting to float.
+
+
+---
+
+# Question
+
+Predict the output:
+```
+float x = 15.88f;
+System.out.print(x);
+```
+
+# Choices
+- [x] 15.88
+- [ ] 15
+- [ ] Error
+
+---
+
+# Explanation
+Since, we explicitly typecasted to float, hence we will not get any error.
+
+---
+
+# Question
+
+Predict the output:
+```java
+double y = 4.78;
+float a = y;
+System.out.println(a);
+```
+
+# Choices
+- [ ] 4.78
+- [x] Error
+- [ ] Missed the lectures
+
+---
+
+# Explanation
+
+Since, we are storing a double type into float, we have possible data loss. Hence, we get an error.
+
+
+---
+## Rules doing Basic Operations
+
+
+## Rule 1
+When we do operation between a decimal and a non-decimal number, the output is always decimal.
+
+* int op double --> double
+* long op float --> float
+
+**Note:** Run each of the following example codes in the compiler, and show the output to students.
+
+## Example 1
+
+### Incorrect Code
+Don't let the students know that the code is incorrect. Ask them if it's correct and if not, how is it violating the Rule 1.
+
+```
+class Scaler {
+ public static void main(String[] args) {
+ int x = 10;
+ double y = 10.25;
+ int z = x + y;
+ System.out.println(z);
+ }
+}
+```
+
+### Output
+```
+error: incompatible types: possible lossy conversion from double to int
+ int z = x + y;
+ ^
+1 error
+```
+
+Explain why their is a possible lossy conversion if we store the sum in an integer.
+A. (x + y) is of double type.
+
+Ask students on how to remove the error?
+
+### Correct Code
+```
+class Scaler {
+ public static void main(String[] args) {
+ int x = 10;
+ double y = 10.25;
+ double z = x + y;
+ System.out.println(z);
+ }
+}
+```
+
+### Output
+```
+20.25
+```
+
+Q. Ask students on how to store the result into an integer i.e, we don't want to store into a double.
+
+A. Typecasting
+
+### Correct Code
+```
+class Scaler {
+ public static void main(String[] args) {
+ int x = 10;
+ double y = 10.25;
+ int z = (int)(x + y);
+ System.out.println(z);
+ }
+}
+```
+
+
+
+## Rule 2
+When we do operation between two operands of same category, the result is of bigger type.
+
+* int op long --> long
+* float op double --> double
+* int op int --> int
+* long op long --> long
+
+**Note:** Run each of the following example codes in the compiler, and show the output to students.
+
+## Example 1
+
+### Incorrect Code
+Don't let the students know that the code is incorrect. Ask them if it's correct and if not, how is it violating the Rule 2.
+
+```
+class Scaler {
+ public static void main(String[] args) {
+ int x = 20;
+ long y = 150L;
+ int z = x + y;
+ System.out.println(z);
+ }
+}
+```
+
+### Output
+```
+/tmp/thqSRPUchr/Scaler.java:6: error: incompatible types: possible lossy conversion from long to int
+int z = x + y;
+^
+1 error
+```
+
+Explain why their is a possible lossy conversion if we store the sum in an integer.
+A. (x + y) is of long type.
+
+Ask students on how to remove the error?
+
+### Correct Code
+
+```
+class Scaler {
+ public static void main(String[] args) {
+ int x = 20;
+ long y = 150L;
+ long z = x + y;
+ System.out.println(z);
+ }
+}
+```
+
+### Output
+```
+170
+```
+
+---
+## Integer Overflow
+
+
+**Note:** For better clarity of quizzes, please run the codes in the compiler as well.
+Explain the integer overflow concept after giving the following quiz.
+
+
+---
+
+
+# Question
+
+Predict the output:
+```
+int a = 100000;
+int b = 400000;
+int c = a * b;
+System.out.print(c);
+```
+
+# Choices
+- [ ] 40000000000
+- [x] Some random Value
+- [ ] Error
+
+
+---
+## CPU and its components
+
+
+Before explaining the quiz's answer, we need to understand some more information.
+
+**Q.** Where are these variables stored and where are these operations carried out?
+
+We have two major components:
+* Central Processing Unit (CPU)
+ * ALU - Arithmetic Logic Unit
+ * Control Unit
+ * Registers
+* Random Access Memory (RAM)
+
+Look at the following diagram.
+ +
+Explain the use of the two components using the code for the quiz.
+
+int a = 100000;
+int b = 400000;
+Populate the RAM with these two variables.
+int c = a * b;
+We want to store c into RAM. But we need to compute a * b first.
+
+**Q.** Where will the computation happen?
+**A.** ALU
+Values will be transferred to CPU's registers via buses, and then computation will be performed. The values are then written back to c's location in RAM.
+
+The result would look something like this:
+
+
+Explain the use of the two components using the code for the quiz.
+
+int a = 100000;
+int b = 400000;
+Populate the RAM with these two variables.
+int c = a * b;
+We want to store c into RAM. But we need to compute a * b first.
+
+**Q.** Where will the computation happen?
+**A.** ALU
+Values will be transferred to CPU's registers via buses, and then computation will be performed. The values are then written back to c's location in RAM.
+
+The result would look something like this:
+ +
+
+If the inputs are integers, the ALU will assume that the output is also integer, which cannot be stored.
+**Note:** The compiler has no control over this.
+
+So, the output will be some random value.
+
+Now, formally define what is **Integer Overflow**?
+* When we attempt to store a value that cannot be represented correctly by a data type, an Integer Overflow.
+* Integer Overflow occurs when the value is more than the maximum representable value
+
+
+
+---
+
+
+# Question
+
+Predict the output:
+```
+int a = 100000;
+int b = 400000;
+long c = a * b;
+System.out.print(c);
+```
+
+# Choices
+- [ ] 40000000000
+- [ ] 2147483647
+- [x] Some random Value
+- [ ] Error: product of integers can't be stored in long
+
+# Explanation
+
+Explain why this is the correct answer. If we store an integer in a long, we don't have any issues. So, according to the compiler, there's nothing wrong.
+
+Explain it in the following way:
+
+
+
+
+
+If the inputs are integers, the ALU will assume that the output is also integer, which cannot be stored.
+**Note:** The compiler has no control over this.
+
+So, the output will be some random value.
+
+Now, formally define what is **Integer Overflow**?
+* When we attempt to store a value that cannot be represented correctly by a data type, an Integer Overflow.
+* Integer Overflow occurs when the value is more than the maximum representable value
+
+
+
+---
+
+
+# Question
+
+Predict the output:
+```
+int a = 100000;
+int b = 400000;
+long c = a * b;
+System.out.print(c);
+```
+
+# Choices
+- [ ] 40000000000
+- [ ] 2147483647
+- [x] Some random Value
+- [ ] Error: product of integers can't be stored in long
+
+# Explanation
+
+Explain why this is the correct answer. If we store an integer in a long, we don't have any issues. So, according to the compiler, there's nothing wrong.
+
+Explain it in the following way:
+
+
+ +
+
+---
+
+
+# Question
+
+Predict the output:
+```
+long a = 100000;
+long b = 400000;
+int c = a * b;
+System.out.print(c);
+```
+
+# Choices
+- [ ] 40000000000
+- [ ] Some random Value
+- [x] Error
+
+---
+
+
+# Explanation
+Explain why we are getting error in this case.
+long * long --> long
+Q. Can we store long into an integer?
+A. No, we can't. So, there is a possible lossy conversion.
+
+**Reminder:** Remind the students to focus on the two rules, and all the questions would be easy.
+
+
+---
+
+
+# Question
+Predict the output:
+```
+long a = 100000;
+int b = 400000;
+long c = a * b;
+System.out.print(c);
+```
+
+# Choices
+- [x] 40000000000
+- [ ] Compilation Error
+- [ ] Some random Value
+
+---
+
+# Explanation
+long * int --> long
+Q. Can we store long into a long type?
+A. Yes.
+
+Explain this again in RAM and ALU in the following way:
+
+
+
+---
+
+
+# Question
+
+Predict the output:
+```
+long a = 100000;
+long b = 400000;
+int c = a * b;
+System.out.print(c);
+```
+
+# Choices
+- [ ] 40000000000
+- [ ] Some random Value
+- [x] Error
+
+---
+
+
+# Explanation
+Explain why we are getting error in this case.
+long * long --> long
+Q. Can we store long into an integer?
+A. No, we can't. So, there is a possible lossy conversion.
+
+**Reminder:** Remind the students to focus on the two rules, and all the questions would be easy.
+
+
+---
+
+
+# Question
+Predict the output:
+```
+long a = 100000;
+int b = 400000;
+long c = a * b;
+System.out.print(c);
+```
+
+# Choices
+- [x] 40000000000
+- [ ] Compilation Error
+- [ ] Some random Value
+
+---
+
+# Explanation
+long * int --> long
+Q. Can we store long into a long type?
+A. Yes.
+
+Explain this again in RAM and ALU in the following way:
+ +
+
+---
+
+
+# Question
+
+Predict the output:
+```
+int a = 100000;
+int b = 400000;
+long c = (long)(a * b);
+System.out.println(c);
+```
+
+# Choices
+- [ ] 40000000000
+- [ ] Compilation Error
+- [x] Some random Value
+
+---
+
+
+# Explanation
+
+int * int --> int
+Q. Ask if we are typecasting individual variables or (a * b)?
+A. We are typecasting (a * b) which is a random value to long.
+
+Explain this again in RAM and ALU in the following way:
+
+
+
+---
+
+
+# Question
+
+Predict the output:
+```
+int a = 100000;
+int b = 400000;
+long c = (long)(a * b);
+System.out.println(c);
+```
+
+# Choices
+- [ ] 40000000000
+- [ ] Compilation Error
+- [x] Some random Value
+
+---
+
+
+# Explanation
+
+int * int --> int
+Q. Ask if we are typecasting individual variables or (a * b)?
+A. We are typecasting (a * b) which is a random value to long.
+
+Explain this again in RAM and ALU in the following way:
+ +
+Let the students know that this is not the correct way to multiply two integers.
+
+
+---
+
+
+# Question
+What will be the output?
+```
+int a = 100000;
+int b = 400000;
+long c = (long)a * b;
+System.out.println(c);
+```
+
+# Choices
+- [x] 40000000000
+- [ ] Compilation Error
+- [ ] Some random Value
+
+---
+
+
+# Explanation
+
+Typecast the value of a to long, and then multiply it with the integer b.
+Q. What will be the output of the multiplication of a long and an integer?
+A. According to Rule 2, it will be long.
+
+We can store a long into a long variable.
+Explain this again in RAM and ALU in the following way:
+
+
+Let the students know that this is not the correct way to multiply two integers.
+
+
+---
+
+
+# Question
+What will be the output?
+```
+int a = 100000;
+int b = 400000;
+long c = (long)a * b;
+System.out.println(c);
+```
+
+# Choices
+- [x] 40000000000
+- [ ] Compilation Error
+- [ ] Some random Value
+
+---
+
+
+# Explanation
+
+Typecast the value of a to long, and then multiply it with the integer b.
+Q. What will be the output of the multiplication of a long and an integer?
+A. According to Rule 2, it will be long.
+
+We can store a long into a long variable.
+Explain this again in RAM and ALU in the following way:
+ +
+
+**Clarification:**
+
+Some students get confused between the following 2 things:
+* long c = (long) (a * b)
+* long c = (long)a * b
+
+Explain that in the 1st case, we are typecasting the product of two integers to a long, and in the 2nd case, we are first typecasting a into long, and then multiplying it with an integer.
+
+---
+
+In this section, we will study different types of operators namely:
+* Arithmetic Operators
+* Relational Operators
+* Logical Operators
+* Unary Operators
+* Assignment Operators
+
+---
+
+
+**Q.** What are Logical Operators?
+**A.** Logical operators can be defined as a type of operators that help us to combine multiple conditional statements. There are three types of logical operators: **AND (&&), OR (||) and Logical NOT (!) operators**.
+
+To better understand AND(&&) operator, give the students the following analogy.
+
+1. Driver's License
+ * age >= 18
+ * Know how to drive
+
+In which of the following 4 scenarios the person should get their driver's license.
+
+
+
+$\begin{array}{|c:c:c:c:c:c|}
+ \hline
+age >= 18 & Know\ how\ to\ drive & Driver's\ License\ received \\ \hline
+True & True & True \\ \hline
+True & False & False \\ \hline
+False & True & False \\ \hline
+False & False & False \\ \hline
+\end{array}$
+
+
+So, we get the drivers's license when both the conditions are true.
+AND [&&] -> Both conditions need to be true to get true as answer.
+
+To better understand Logical OR (||) operator, give the students the following analogy.
+
+2. Eligibility Criterion for Exam
+ * Should have a diploma
+ * Should have a degree
+
+If they have either diploma or degree, they will be allowed to sit in the exam.
+
+In which of the following 4 scenarios the person should be allowed to sit in the exam.
+
+
+
+$\begin{array}{|c:c:c:c:c:c|}
+ \hline
+Have\ a\ diploma? & Have\ a\ degree? &Allowed\ to\ sit\ in\ exam \\ \hline
+True & True & True \\ \hline
+True & False & True \\ \hline
+False & True & True \\ \hline
+False & False & False \\ \hline
+\end{array}$
+
+
+
+
+
+OR [||] -> Even if one of the conditions is true, we get true as an answer.
+
+### Important Observation of AND and OR Operator
+
+* In case of AND, if the 1st condition is false, does the 2nd value have any effect? No, so the compiler would skip the 2nd check if the 1st condition is false.
+* Similarly, if the 1st condition is true, does the 2nd value have any effect? No, so the compiler would skip the 2nd check if the 1st condition is true.
+
+
+To better understand Logical Not (!) operator, let us look into following analogy.
+
+3. To purchase milk, it shouldn't be raining outside. How to check for this condition?
+
+If it's not raining outside, purchase milk.
+
+
+
+$\begin{array}{|c:c:c:c:c:c|}
+ \hline
+Raining\ outside & Can\ purchase\ Milk? \\ \hline
+True & False \\ \hline
+False & True \\ \hline
+\end{array}$
+
+
+Meaning, whatever is the case, just invert it.
+
+### Examples
+
+Discuss the following examples related to both arithmetic and logical operators.
+1. Given two scores, check if they made a 50 partnership i.e, their combined score is 50 or not.
+ * a = 15, b = 30 -> False
+ * a = 25, b = 25 -> True
+ * a = 10, b = 60 -> False
+How to write the code for it in java?
+```
+a + b == 50
+```
+
+Q. What type of operator are we using here?
+A. Relational Operator
+
+2. Read 2 scores, check if both of them passes. The passing score is 35.
+ * a = 35, b = 40 -> True
+ * a = 34, b = 40 -> False
+ * a = 50, b = 14 -> False
+
+Q. How to check if a score is passed?
+A. Use the >= operator.
+
+Q. How to check if both the scores are passed?
+A. Use the AND (&&) operator.
+
+How to write the code for it in java?
+```
+a >= 35 && b >= 35
+```
+
+3. Read 2 scores and check if atleast one of them passed. The passing score is 35.
+
+Ask students to do it themselves.
+**Answer:**
+```
+a >= 35 || b >= 35
+```
+
+**Note:** If students ask about the Logical NOT (!) operator, let them know that this will be discussed in unary operators section.
+
+---
+
+
+# Assignment Operators
+
+It is used to assign value.
+They are : =, +=, -=, * =, /= etc.
+
+```java
+int a = 10;
+a = a+5;
+System.out.println(a);
+```
+>Explanation: This will increase the value of a by 5.
+
+Same thing can be done using "+=".
+```java
+int b = 10;
+b += 5; // increment the value of b by 5
+System.out.println(b);
+```
+
+```java
+int c = 20;
+c -= 4; // decrement the value of c by 4
+System.out.println(b);
+```
+Similarly, /= and * = works
+
+
+
+---
+
+
+Q. What are unary operators?
+A. Unary operators work on a single operand only.
+
+Give them a little bit idea of the following:
+* What are Pre operators -> ++a, --a
+* What are Post operators -> a++, a--
+
+Run the following codes on IDE:
+```
+int a = 10;
+a ++ ;
+System.out.println(a);
+```
+
+```
+int b = 10;
+++ b;
+System.out.println(b);
+```
+
+Both the codes give 11 as output.
+Ask the students what is happening here, and why are we getting the same result.
+
+Now, to show the difference, use the following codes.
+
+```
+int a = 10;
+System.out.println(a ++ );
+```
+
+```
+int b = 10;
+System.out.println( ++ b);
+```
+
+The first code will give 10 as output, while the 2nd code gives 11 as output.
+To explain the reason for this behaviour, show them the following table and ask them to focus on the first 4 rows.
+
+
+$\begin{array}{|c:c:c:c:c:c|}
+ \hline
+Operator & Name \\ \hline
+a++ & Post-Increment\ Operator \\ \hline
+++a & Pre-Increment\ Operator \\ \hline
+a-- & Post-Decrement\ Operator \\ \hline
+--a & Pre-Decrement\ Operator \\ \hline
+! & Logical\ Not\ Operator \\ \hline
+\end{array}$
+
+
+
+
+
+
+
+
+Coming back to the original question,
+
+**Post-Increment**
+```
+int a = 10;
+System.out.println(a ++ );
+```
+
+The last line is broken down into the following two lines.
+```
+System.out.println(a);
+a ++ ;
+```
+
+**Pre-Increment**
+```
+int a = 10;
+System.out.println(++ a);
+```
+
+The last line is broken down into the following two lines.
+```
+++a;
+System.out.println(a);
+```
+
+Now, ask students if they can figure out the reason why the 1st code is printing 10, while the 2nd code is printing 11.
+
+
+Mention that similar is the case with pre-decrement and post-decrement operators.
+
+# Examples
+
+## Example 1
+```
+int a = 10;
+int b = 20;
+int c = a ++ + b ++ ;
+System.out.println(a + b + c);
+```
+
+Ask the following questions along with explanation, wherever necessary.
+**Q.** What is the value of c?
+**A.** 30
+
+**Q.** What is the current value of a after 3rd line?
+**A.** 11
+
+**Q.** What is the current value of b after 3rd line?
+**A.** 21
+
+**Q.** What will be the output?
+**A.** 62
+
+
+## Example 2
+```
+int a = 10;
+int b = a ++ + a ++ ;
+System.out.println(a);
+System.out.println(b);
+```
+
+**Output:**
+```
+12
+21
+```
+
+Explanation: First we will solve left "a++", that will give b = 10 + a++, and now a will be 11.
+Then again, we solve 2nd "a++", b = 10 + 11, and now a will be 12 after this.
+So, finally a = 12, b = 21.
+
+Q. Suppose, we add the following statement in the above code, what would be the value of c?
+
+```
+int c = b ++ ;
+```
+
+A. There are 2 things happening -> Assignment and Post-Increment.
+But since its post-increment, we will use the value of b first, and then increment the value of b.
+So, value of c = 21.
+
+Q. What if we add the following statement instead?
+
+```
+int c = ++ b;
+```
+A. There are 2 things happening -> Assignment and Pre-Increment.
+But since its pre-increment, we will increment the value of b and then use the value of b.
+So, value of c = 22.
+
+
+## Example 3
+```
+int a = 10;
+int b = a-- ;
+System.out.println(a);
+System.out.println(b);
+```
+
+**Output:**
+```plaintext
+9
+10
+```
+
+Explain the reason for the above output accordingly if the students understood or not.
+
diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner Output & Basic Data Types.md b/Academy DSA Typed Notes/Beginner Language/Beginner Output & Basic Data Types.md
new file mode 100644
index 0000000..d79574b
--- /dev/null
+++ b/Academy DSA Typed Notes/Beginner Language/Beginner Output & Basic Data Types.md
@@ -0,0 +1,1056 @@
+# Output and Basic Data Types
+
+---
+
+## Agenda
+
+- Revise Initial Rules
+- Evaluating Expression
+- Quizzes
+- Concatenation
+- Intro to variable
+
+---
+# Section 2.1 (Revision)
+
+
+
+1. end statements with a **semicolon ( ; )**
+2. JAVA is **case sensitive.** -> System, system are considered different
+3. In order to print text, we use **double quotes ( " " )**
+4. {}, (), " " --> All of these are in pairs.
+5. Comments →
+ * **Single-line comments** start with two forward slashes ( // ). Any text between // and the end of the line is ignored by Java (will not be executed).
+ * **Multi-line comments** start with /* and ends with \*/. Any text between /* and */ will be ignored by Java.
+6. **System.out.print(); →** Just type the output
+7. **System.out.println(); →** Just type the output and press Enter [cursor moves to the next line]
+
+
+Now, let's check how much they remember from the last class with the help of quizzes.
+
+
+---
+
+
+# Question
+
+What will be output for this ?
+```
+System.out.print("Welcome in playground")
+```
+# Choices
+
+- [ ] Welcome Home
+- [ ] Welcome in playground
+- [x] Error
+- [ ] All the options are correct
+
+
+---
+
+
+# Question
+
+What will be output for this ?
+```
+system.out.print("Hi Everyone");
+```
+
+# Choices
+
+- [ ] Hi Everyone
+- [ ] Bye Everyone
+- [x] Error
+- [ ] Welcome Everyone
+
+
+---
+
+
+# Question
+What will be output for this ?
+```
+System.ouT.print("Hi Guys");
+```
+
+# Choices
+- [ ] Hi Guys
+- [ ] Bye Guys
+- [x] Error
+- [ ] Welcome Guys
+
+
+---
+
+
+# Question
+What will be output for this ?
+```
+System.out.print(Good Morning Everyone);
+```
+
+# Choices
+
+- [ ] Good Morning Everyone
+- [ ] Good Afternoon Everyone
+- [x] Error
+- [ ] Good Night Everyone
+
+
+
+---
+
+
+# Question
+
+What will be output for this ?
+```
+System.out.print('Happy Thursday');
+```
+
+# Choices
+
+- [ ] Happy Thursday
+- [ ] Sad Thursday
+- [x] Error
+- [ ] All the options are correct
+
+
+
+---
+
+
+# Question
+What will be output for this ?
+
+```
+System.out.print(10 + 20);
+```
+
+
+# Choices
+
+- [x] 30
+- [ ] 10+20
+- [ ] Error
+
+
+---
+
+
+# Question
+
+What will be output for this ?
+```
+System.out.print(10 - 25);
+```
+
+# Choices
+- [x] -15
+- [ ] 15
+- [ ] 10
+- [ ] Error
+
+---
+
+
+# Question
+
+What will be output for this ?
+```
+System.out.println("Hello");
+System.out.print("World);
+```
+
+# Choices
+
+- [ ] Hello
+
+
+**Clarification:**
+
+Some students get confused between the following 2 things:
+* long c = (long) (a * b)
+* long c = (long)a * b
+
+Explain that in the 1st case, we are typecasting the product of two integers to a long, and in the 2nd case, we are first typecasting a into long, and then multiplying it with an integer.
+
+---
+
+In this section, we will study different types of operators namely:
+* Arithmetic Operators
+* Relational Operators
+* Logical Operators
+* Unary Operators
+* Assignment Operators
+
+---
+
+
+**Q.** What are Logical Operators?
+**A.** Logical operators can be defined as a type of operators that help us to combine multiple conditional statements. There are three types of logical operators: **AND (&&), OR (||) and Logical NOT (!) operators**.
+
+To better understand AND(&&) operator, give the students the following analogy.
+
+1. Driver's License
+ * age >= 18
+ * Know how to drive
+
+In which of the following 4 scenarios the person should get their driver's license.
+
+
+
+$\begin{array}{|c:c:c:c:c:c|}
+ \hline
+age >= 18 & Know\ how\ to\ drive & Driver's\ License\ received \\ \hline
+True & True & True \\ \hline
+True & False & False \\ \hline
+False & True & False \\ \hline
+False & False & False \\ \hline
+\end{array}$
+
+
+So, we get the drivers's license when both the conditions are true.
+AND [&&] -> Both conditions need to be true to get true as answer.
+
+To better understand Logical OR (||) operator, give the students the following analogy.
+
+2. Eligibility Criterion for Exam
+ * Should have a diploma
+ * Should have a degree
+
+If they have either diploma or degree, they will be allowed to sit in the exam.
+
+In which of the following 4 scenarios the person should be allowed to sit in the exam.
+
+
+
+$\begin{array}{|c:c:c:c:c:c|}
+ \hline
+Have\ a\ diploma? & Have\ a\ degree? &Allowed\ to\ sit\ in\ exam \\ \hline
+True & True & True \\ \hline
+True & False & True \\ \hline
+False & True & True \\ \hline
+False & False & False \\ \hline
+\end{array}$
+
+
+
+
+
+OR [||] -> Even if one of the conditions is true, we get true as an answer.
+
+### Important Observation of AND and OR Operator
+
+* In case of AND, if the 1st condition is false, does the 2nd value have any effect? No, so the compiler would skip the 2nd check if the 1st condition is false.
+* Similarly, if the 1st condition is true, does the 2nd value have any effect? No, so the compiler would skip the 2nd check if the 1st condition is true.
+
+
+To better understand Logical Not (!) operator, let us look into following analogy.
+
+3. To purchase milk, it shouldn't be raining outside. How to check for this condition?
+
+If it's not raining outside, purchase milk.
+
+
+
+$\begin{array}{|c:c:c:c:c:c|}
+ \hline
+Raining\ outside & Can\ purchase\ Milk? \\ \hline
+True & False \\ \hline
+False & True \\ \hline
+\end{array}$
+
+
+Meaning, whatever is the case, just invert it.
+
+### Examples
+
+Discuss the following examples related to both arithmetic and logical operators.
+1. Given two scores, check if they made a 50 partnership i.e, their combined score is 50 or not.
+ * a = 15, b = 30 -> False
+ * a = 25, b = 25 -> True
+ * a = 10, b = 60 -> False
+How to write the code for it in java?
+```
+a + b == 50
+```
+
+Q. What type of operator are we using here?
+A. Relational Operator
+
+2. Read 2 scores, check if both of them passes. The passing score is 35.
+ * a = 35, b = 40 -> True
+ * a = 34, b = 40 -> False
+ * a = 50, b = 14 -> False
+
+Q. How to check if a score is passed?
+A. Use the >= operator.
+
+Q. How to check if both the scores are passed?
+A. Use the AND (&&) operator.
+
+How to write the code for it in java?
+```
+a >= 35 && b >= 35
+```
+
+3. Read 2 scores and check if atleast one of them passed. The passing score is 35.
+
+Ask students to do it themselves.
+**Answer:**
+```
+a >= 35 || b >= 35
+```
+
+**Note:** If students ask about the Logical NOT (!) operator, let them know that this will be discussed in unary operators section.
+
+---
+
+
+# Assignment Operators
+
+It is used to assign value.
+They are : =, +=, -=, * =, /= etc.
+
+```java
+int a = 10;
+a = a+5;
+System.out.println(a);
+```
+>Explanation: This will increase the value of a by 5.
+
+Same thing can be done using "+=".
+```java
+int b = 10;
+b += 5; // increment the value of b by 5
+System.out.println(b);
+```
+
+```java
+int c = 20;
+c -= 4; // decrement the value of c by 4
+System.out.println(b);
+```
+Similarly, /= and * = works
+
+
+
+---
+
+
+Q. What are unary operators?
+A. Unary operators work on a single operand only.
+
+Give them a little bit idea of the following:
+* What are Pre operators -> ++a, --a
+* What are Post operators -> a++, a--
+
+Run the following codes on IDE:
+```
+int a = 10;
+a ++ ;
+System.out.println(a);
+```
+
+```
+int b = 10;
+++ b;
+System.out.println(b);
+```
+
+Both the codes give 11 as output.
+Ask the students what is happening here, and why are we getting the same result.
+
+Now, to show the difference, use the following codes.
+
+```
+int a = 10;
+System.out.println(a ++ );
+```
+
+```
+int b = 10;
+System.out.println( ++ b);
+```
+
+The first code will give 10 as output, while the 2nd code gives 11 as output.
+To explain the reason for this behaviour, show them the following table and ask them to focus on the first 4 rows.
+
+
+$\begin{array}{|c:c:c:c:c:c|}
+ \hline
+Operator & Name \\ \hline
+a++ & Post-Increment\ Operator \\ \hline
+++a & Pre-Increment\ Operator \\ \hline
+a-- & Post-Decrement\ Operator \\ \hline
+--a & Pre-Decrement\ Operator \\ \hline
+! & Logical\ Not\ Operator \\ \hline
+\end{array}$
+
+
+
+
+
+
+
+
+Coming back to the original question,
+
+**Post-Increment**
+```
+int a = 10;
+System.out.println(a ++ );
+```
+
+The last line is broken down into the following two lines.
+```
+System.out.println(a);
+a ++ ;
+```
+
+**Pre-Increment**
+```
+int a = 10;
+System.out.println(++ a);
+```
+
+The last line is broken down into the following two lines.
+```
+++a;
+System.out.println(a);
+```
+
+Now, ask students if they can figure out the reason why the 1st code is printing 10, while the 2nd code is printing 11.
+
+
+Mention that similar is the case with pre-decrement and post-decrement operators.
+
+# Examples
+
+## Example 1
+```
+int a = 10;
+int b = 20;
+int c = a ++ + b ++ ;
+System.out.println(a + b + c);
+```
+
+Ask the following questions along with explanation, wherever necessary.
+**Q.** What is the value of c?
+**A.** 30
+
+**Q.** What is the current value of a after 3rd line?
+**A.** 11
+
+**Q.** What is the current value of b after 3rd line?
+**A.** 21
+
+**Q.** What will be the output?
+**A.** 62
+
+
+## Example 2
+```
+int a = 10;
+int b = a ++ + a ++ ;
+System.out.println(a);
+System.out.println(b);
+```
+
+**Output:**
+```
+12
+21
+```
+
+Explanation: First we will solve left "a++", that will give b = 10 + a++, and now a will be 11.
+Then again, we solve 2nd "a++", b = 10 + 11, and now a will be 12 after this.
+So, finally a = 12, b = 21.
+
+Q. Suppose, we add the following statement in the above code, what would be the value of c?
+
+```
+int c = b ++ ;
+```
+
+A. There are 2 things happening -> Assignment and Post-Increment.
+But since its post-increment, we will use the value of b first, and then increment the value of b.
+So, value of c = 21.
+
+Q. What if we add the following statement instead?
+
+```
+int c = ++ b;
+```
+A. There are 2 things happening -> Assignment and Pre-Increment.
+But since its pre-increment, we will increment the value of b and then use the value of b.
+So, value of c = 22.
+
+
+## Example 3
+```
+int a = 10;
+int b = a-- ;
+System.out.println(a);
+System.out.println(b);
+```
+
+**Output:**
+```plaintext
+9
+10
+```
+
+Explain the reason for the above output accordingly if the students understood or not.
+
diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner Output & Basic Data Types.md b/Academy DSA Typed Notes/Beginner Language/Beginner Output & Basic Data Types.md
new file mode 100644
index 0000000..d79574b
--- /dev/null
+++ b/Academy DSA Typed Notes/Beginner Language/Beginner Output & Basic Data Types.md
@@ -0,0 +1,1056 @@
+# Output and Basic Data Types
+
+---
+
+## Agenda
+
+- Revise Initial Rules
+- Evaluating Expression
+- Quizzes
+- Concatenation
+- Intro to variable
+
+---
+# Section 2.1 (Revision)
+
+
+
+1. end statements with a **semicolon ( ; )**
+2. JAVA is **case sensitive.** -> System, system are considered different
+3. In order to print text, we use **double quotes ( " " )**
+4. {}, (), " " --> All of these are in pairs.
+5. Comments →
+ * **Single-line comments** start with two forward slashes ( // ). Any text between // and the end of the line is ignored by Java (will not be executed).
+ * **Multi-line comments** start with /* and ends with \*/. Any text between /* and */ will be ignored by Java.
+6. **System.out.print(); →** Just type the output
+7. **System.out.println(); →** Just type the output and press Enter [cursor moves to the next line]
+
+
+Now, let's check how much they remember from the last class with the help of quizzes.
+
+
+---
+
+
+# Question
+
+What will be output for this ?
+```
+System.out.print("Welcome in playground")
+```
+# Choices
+
+- [ ] Welcome Home
+- [ ] Welcome in playground
+- [x] Error
+- [ ] All the options are correct
+
+
+---
+
+
+# Question
+
+What will be output for this ?
+```
+system.out.print("Hi Everyone");
+```
+
+# Choices
+
+- [ ] Hi Everyone
+- [ ] Bye Everyone
+- [x] Error
+- [ ] Welcome Everyone
+
+
+---
+
+
+# Question
+What will be output for this ?
+```
+System.ouT.print("Hi Guys");
+```
+
+# Choices
+- [ ] Hi Guys
+- [ ] Bye Guys
+- [x] Error
+- [ ] Welcome Guys
+
+
+---
+
+
+# Question
+What will be output for this ?
+```
+System.out.print(Good Morning Everyone);
+```
+
+# Choices
+
+- [ ] Good Morning Everyone
+- [ ] Good Afternoon Everyone
+- [x] Error
+- [ ] Good Night Everyone
+
+
+
+---
+
+
+# Question
+
+What will be output for this ?
+```
+System.out.print('Happy Thursday');
+```
+
+# Choices
+
+- [ ] Happy Thursday
+- [ ] Sad Thursday
+- [x] Error
+- [ ] All the options are correct
+
+
+
+---
+
+
+# Question
+What will be output for this ?
+
+```
+System.out.print(10 + 20);
+```
+
+
+# Choices
+
+- [x] 30
+- [ ] 10+20
+- [ ] Error
+
+
+---
+
+
+# Question
+
+What will be output for this ?
+```
+System.out.print(10 - 25);
+```
+
+# Choices
+- [x] -15
+- [ ] 15
+- [ ] 10
+- [ ] Error
+
+---
+
+
+# Question
+
+What will be output for this ?
+```
+System.out.println("Hello");
+System.out.print("World);
+```
+
+# Choices
+
+- [ ] HelloWorld +- [ ] HelloWorld +- [x] Error +- [ ] inky pinky po + + + +--- + + +# Question +What will be output for this ? +``` +System.out.print("Hello"); +System.out.println("World"); +``` + +# Choices +- [ ] Hello
World +- [x] HelloWorld +- [ ] Error +- [ ] inky pinky po + +--- + + +# Question +What will be output for this ? +``` +System.out.println("Hello"); +System.out.print("World"); +System.out.println("Welcome") +``` + +# Choices + +- [ ] Hello
World
Welcome +- [ ] HelloWorldWelcome +- [x] Error +- [ ] Hello
WorldWelcome + + + +--- + + +# Question + +What will be output for this ? +``` +System.out.printLN("Hello"); +System.out.println("World); +``` + +# Choices +- [ ] Hello
World +- [ ] HelloWorld +- [x] Error +- [ ] inky-pinky-po + + + +--- + + +# Question +What will be output for this ? +``` +Which of the follwing are operators? +``` + +# Choices +- [ ] ( + ) +- [ ] ( - ) +- [ ] ( * ) +- [ ] ( / ) +- [x] All of them + + +--- + + +# Question + +``` +10+30 +In the given expression choose the operands. +``` + +# Choices +- [ ] (+) +- [ ] 10 +- [ ] 30 +- [x] Both 10 and 30 +--- + +**Explanation of Quiz :** +Operator : + +Operands : 10 and 30 + +Explain using one more example if needed. + +Numbers -> 2 types +1. Decimal -> Numbers that have Decimal point +Ex. 4.67, 0.986, 20.73, 2.0 +2. Non Decimal / Integer -> Any +ve, -ve or 0 +Ex. 7, -30, 0, -7 + +- Note: In today's class, we will only discuss Integers. + + +Very Basic expression on simple maths. Time of the quiz is 20sec. + + +--- + + +# Question +What will be output for this ? +``` +System.out.print(5 + 8); +``` + +# Choices +- [ ] 11 +- [ ] 12 +- [x] 13 +- [ ] 14 + +--- + + +# Question +What will be output for this ? +``` +System.out.print(5 - 8); +``` + +# Choices +- [ ] -1 +- [ ] -2 +- [x] -3 +- [ ] -4 + +--- + + +# Question +What will be output for this ? +``` +System.out.print(5 * 8); +``` + +# Choices + +- [ ] 30 +- [ ] 32 +- [x] 40 +- [ ] 42 + +--- + + +# Question +What will be output for this ? +``` +System.out.print(8 / 2); +``` + +# Choices +- [ ] 3 +- [x] 4 +- [ ] 5 +- [ ] 6 + + +--- + + +# Question + +What will be output for this ? +``` +System.out.print(10 / 3); +``` + +# Choices + +- [ ] 3.3333 +- [x] 3 +- [ ] Error +- [ ] None of them +--- + +**Explanation :** +In calculator, 10 / 3 = 3.33333 +But in JAVA, we get 3 + + +**Rule :** In JAVA, when you divide (/) integers we only get quotient. + +--- + + +# Question + +What will be output for this ? +``` +System.out.print(24 / 9); +``` + +# Choices + +- [ ] 1 +- [ ] 2.54 +- [x] 2 +- [ ] 3 + +--- + + +# Question + +What will be output for this ? +``` +System.out.print(3 / 6); +``` + +# Choices +- [ ] 1 +- [x] 0 +- [ ] Error + +--- + + +# Question +What will be output for this ? +``` +System.out.print(24 / 0); +``` + +# Choices +- [ ] Infinite +- [ ] 24 +- [ ] 0 +- [x] Error + +--- + + +## **Rule:** +Division of integers by zero is not possible in JAVA + +--- + + +# Question +What will be output for this ? +``` +System.out.print(6 * 7 / 6); +``` + +# Choices +- [x] 7 +- [ ] 6 +- [ ] None of them +- [ ] All of them + +--- + + +**Explanation:** +
If we have same priority operators, whichever comes first from left to right that will be evaluated first. +* **Rule 2 :**
If we have different priority operators, whichever has highest priority that will be evaluated first. + +**Explanation:** +Here, * and / have same priority. Because * comes first we will evaluate 6 * 7 will be evaluated first. +=> 6 * 7 / 6 +=> 42 / 6 +=> 7 + +--- + + +# Question + +What will be output for this ? +``` +System.out.print(4 + 3 * 6 - 7 / 2); +``` + +# Choices +- [ ] 16 +- [ ] 17 +- [ ] 18 +- [x] 19 +--- +**Explanation:** +Between * and / we will be evaluating multiply first and then divide. +=> 4 + 3 * 6 - 7 / 2 +=> 4 + 18 - 7 / 2 +=> 4 + 18 - 3 +=> 22 - 3 +=> 19 + +--- + +# Question +What will be output for this ? + +``` +System.out.print(5 + 2 * 3); +``` + +# Choices +- [ ] 21 +- [ ] 17 +- [x] 11 +- [ ] Error +--- +**Explanation:** +Here, * has higher priority. +=> 5 + 2 * 3 +=> 5 + 6 +=> 11 + +--- + +# Question +What will be output for this ? +``` +System.out.print(5 + 15 / 5 + 6 * 3); +``` + +# Choices +- [ ] 30 +- [x] 26 +- [ ] 11 +- [ ] Error +--- +**Explanation:** +=> 5 + 15 / 5 + 6 * 3 +=> 5 + 3 + 6 * 3 +=> 5 + 3 + 18 +=> 8 + 18 +=> 26 + +--- + +# Question + +What will be output for this ? +``` +System.out.print(7 - 2 * 4 + 18 / 3); +``` + +# Choices +- [ ] 15 +- [x] 5 +- [ ] 30 +- [ ] Error +--- +**Explanation:** +=> 7 - 2 * 4 + 18 / 3 +=> 7 - 8 + 18 / 3 +=> 7 - 8 + 6 +=> -1 + 6 +=> 5 + +--- + +# Question +What will be output for this ? +``` +System.out.print(3 * 4 / 2 + 7 + 3 - 4 / 2); +``` + +# Choices +- [ ] 21 +- [x] 14 +- [ ] 11 +- [ ] Error +--- +**Explanation:** +=> 3 * 4 / 2 + 7 + 3 - 4 / 2 +=> 12 / 2 + 7 + 3 - 4 / 2 +=> 6 + 7 + 3 - 4 / 2 +=> 6 + 7 + 3 - 2 +=> 13 + 3 - 2 +=> 16 - 2 +=> 14 + +--- + +# Question +What will be output for this ? +``` +System.out.print(5 + 2 * 4 + 8 - 6 + 12 / 4); +``` + +# Choices +- [ ] 25 +- [x] 18 +- [ ] 16 +- [ ] Error +--- +**Explanation:** +=> 5 + 2 * 4 + 8 - 6 + 12 / 4 +=> 5 + 8 + 8 - 6 + 12 / 4 +=> 5 + 8 + 8 - 6 + 3 +=> 13 + 8 - 6 + 3 +=> 21 - 6 + 3 +=> 15 + 3 +=> 18 + +--- + +# Question +What will be output for this ? +``` +System.out.print( (5 + 2) * 3 ); +``` + +# Choices +- [x] 21 +- [ ] 17 +- [ ] 11 +- [ ] Error +--- +**Explanation:** +=> (5 + 2) * 3) +=> 7 * 3 +=> 21 + +--- + +# Question +What will be output for this ? +```java +System.out.print("Hello" + "World"); +``` +# Choices +- [ ] Hello
World +- [x] HelloWorld +- [ ] Error +- [ ] I'm sleeping, Don't Disturb +--- +**Explanation:** + +
 +
+**Rule:** With + operator, If one Operand is text then we concatenate both Operands
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print("Hi" + "Students" + "Namaste");
+```
+
+# Choices
+- [x] HiStudentsNamaste
+- [ ] HelloEveryone
+- [ ] Error
+- [ ] I'm Angry :(
+---
+**Explanation:**
+=> "Hi" + "Students" + "Namaste"
+=> "HiStudents" + "Namaste"
+=> "HiStudentsNamaste"
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print("Hi" + " " + "Namaste");
+```
+
+# Choices
+- [x] Hi Namaste
+- [ ] HiNamaste
+- [ ] Error
+- [ ] Namaste Hi
+---
+**Explanation:**
+=> "Hi" + " " + "Namaste"
+=> "Hi " + "Namaste"
+=> "Hi Namaste"
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print("Hi" * "Guys");
+```
+
+# Choices
+- [ ] HiGuys HiGuys HiGuys
+- [x] Error
+- [ ] abcdefghijklmnopqrstuvwxyz
+- [ ] Hi Guys
+---
+**Explanation:**
+We cannot use * with text operand.
+
+
+## **Rule:**
+With text operand, only + operator can be used. Any other operator gives error.
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print("WelcomeHome" - "Home");
+```
+
+# Choices
+- [ ] Welcome
+- [ ] WelcomeHome-Home
+- [ ] Home
+- [x] Error
+---
+**Explanation:**
+We cannot use - with text operand.
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print("Hello" + 3);
+```
+
+# Choices
+- [ ] Hello
+- [x] Hello3
+- [ ] Error
+- [ ] HelloHelloHello
+---
+**Explanation:**
+Operator: +
+Operands:
+"Hello" -> text
+3 -> number
+ Since, one operand is text, we concatenate both operands.
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print("Hello" + 3 + 4);
+```
+
+# Choices
+- [ ] Hello
+- [x] Hello34
+- [ ] Hello7
+- [ ] Error
+---
+**Explanation:**
+Since, both operators are + and have same priority we will evaluate from left to right
+=> "Hello" + 3 + 4
+=> "Hello3" + 4
+=> "Hello34"
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print("Hello" + 10 + "World");
+```
+
+# Choices
+- [ ] HelloWorld
+- [x] Hello10World
+- [ ] Hello10
+- [ ] Error
+---
+**Explanation:**
+=> "Hello" + 10 + "World"
+=> "Hello10" + "World"
+=> "Hello10World"
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print(10 + "Welcome");
+```
+# Choices
+- [ ] Welcome10
+- [x] 10Welcome
+- [ ] Welcome 10 times
+- [ ] inky pinky po
+---
+**Explanation:**
+=> 10 + "Welcome"
+=> "10Welcome"
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print(10 + 20 + "WakeUp" + 3 + 2);
+```
+
+# Choices
+- [ ] 1020WakeUp32
+- [ ] 1020WakeUp5
+- [ ] 30WakeUp5
+- [x] 30WakeUp32
+---
+**Explanation:**
+=> 10 + 20 + "WakeUp" + 3 + 2
+=> 30 + "WakeUp" + 3 + 2
+=> "30WakeUp" + 3 + 2
+=> "30WakeUp3" + 2
+=> "30WakeUp32"
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print("HiGuys" * 2);
+```
+
+# Choices
+- [ ] HiGuys*2
+- [ ] HiGuys2
+- [ ] HiGuysHiGuys
+- [x] Error
+---
+**Explanation:**
+We cannot use * operator with text operand
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print(10 + 20 + "WakeUp" + 3 * 2);
+```
+
+# Choices
+- [ ] 1020WakeUp32
+- [ ] 30WakeUp32
+- [ ] Error
+- [x] 30WakeUp6
+---
+**Explanation:**
+
+=> 10 + 20 + "WakeUp" + 3 * 2
+=> 10 + 20 + "WakeUp" + 6
+=> 30 + "WakeUp" + 6
+=> "30WakeUp" + 6
+=> "30WakeUp6"
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print(10 + "Hello" * "World" + 3);
+```
+
+# Choices
+- [ ] 10HelloWorld3
+- [ ] 10HelloWorldWorldWorld3
+- [x] Error
+- [ ] Good Morning :)
+---
+**Explanation:**
+We cannot use * operator with text operand
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print(10 + "WelcomeHome" - "Home" + 3);
+```
+# Choices
+- [ ] 10Welcome3
+- [ ] 10WelcomeHomeHome3
+- [x] Error
+- [ ] Good Morning :)
+---
+**Explanation:**
+We cannot use - operator with text operand
+
+
+---
+
+# Question
+Predict the output for the following code:
+```
+System.out.println(10 + 20 + "Hello");
+```
+
+# Choices
+- [ ] 1020Hello
+- [x] 30Hello
+- [ ] Hello1020
+- [ ] Hello Hello Hello
+---
+**Explanation**
+10 + 20 = 30,
+ Now when string is concatenated then 30 becomes as string "30" so the answer is "30Hello".
+
+
+---
+# Section 2.3 (Introduction to Variables)
+
+> Start with that numbers are of two types:
+1. **Non-Decimal / Integers**
+2. Decimals
+
+**Story :** Assume we have a container storing water in it. And then explain the three factors of container that are : Type, Name and Value
+
+After that take a container to store integers and explain the same three factors.
+
+
+
+
+**Rule:** With + operator, If one Operand is text then we concatenate both Operands
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print("Hi" + "Students" + "Namaste");
+```
+
+# Choices
+- [x] HiStudentsNamaste
+- [ ] HelloEveryone
+- [ ] Error
+- [ ] I'm Angry :(
+---
+**Explanation:**
+=> "Hi" + "Students" + "Namaste"
+=> "HiStudents" + "Namaste"
+=> "HiStudentsNamaste"
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print("Hi" + " " + "Namaste");
+```
+
+# Choices
+- [x] Hi Namaste
+- [ ] HiNamaste
+- [ ] Error
+- [ ] Namaste Hi
+---
+**Explanation:**
+=> "Hi" + " " + "Namaste"
+=> "Hi " + "Namaste"
+=> "Hi Namaste"
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print("Hi" * "Guys");
+```
+
+# Choices
+- [ ] HiGuys HiGuys HiGuys
+- [x] Error
+- [ ] abcdefghijklmnopqrstuvwxyz
+- [ ] Hi Guys
+---
+**Explanation:**
+We cannot use * with text operand.
+
+
+## **Rule:**
+With text operand, only + operator can be used. Any other operator gives error.
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print("WelcomeHome" - "Home");
+```
+
+# Choices
+- [ ] Welcome
+- [ ] WelcomeHome-Home
+- [ ] Home
+- [x] Error
+---
+**Explanation:**
+We cannot use - with text operand.
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print("Hello" + 3);
+```
+
+# Choices
+- [ ] Hello
+- [x] Hello3
+- [ ] Error
+- [ ] HelloHelloHello
+---
+**Explanation:**
+Operator: +
+Operands:
+"Hello" -> text
+3 -> number
+ Since, one operand is text, we concatenate both operands.
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print("Hello" + 3 + 4);
+```
+
+# Choices
+- [ ] Hello
+- [x] Hello34
+- [ ] Hello7
+- [ ] Error
+---
+**Explanation:**
+Since, both operators are + and have same priority we will evaluate from left to right
+=> "Hello" + 3 + 4
+=> "Hello3" + 4
+=> "Hello34"
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print("Hello" + 10 + "World");
+```
+
+# Choices
+- [ ] HelloWorld
+- [x] Hello10World
+- [ ] Hello10
+- [ ] Error
+---
+**Explanation:**
+=> "Hello" + 10 + "World"
+=> "Hello10" + "World"
+=> "Hello10World"
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print(10 + "Welcome");
+```
+# Choices
+- [ ] Welcome10
+- [x] 10Welcome
+- [ ] Welcome 10 times
+- [ ] inky pinky po
+---
+**Explanation:**
+=> 10 + "Welcome"
+=> "10Welcome"
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print(10 + 20 + "WakeUp" + 3 + 2);
+```
+
+# Choices
+- [ ] 1020WakeUp32
+- [ ] 1020WakeUp5
+- [ ] 30WakeUp5
+- [x] 30WakeUp32
+---
+**Explanation:**
+=> 10 + 20 + "WakeUp" + 3 + 2
+=> 30 + "WakeUp" + 3 + 2
+=> "30WakeUp" + 3 + 2
+=> "30WakeUp3" + 2
+=> "30WakeUp32"
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print("HiGuys" * 2);
+```
+
+# Choices
+- [ ] HiGuys*2
+- [ ] HiGuys2
+- [ ] HiGuysHiGuys
+- [x] Error
+---
+**Explanation:**
+We cannot use * operator with text operand
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print(10 + 20 + "WakeUp" + 3 * 2);
+```
+
+# Choices
+- [ ] 1020WakeUp32
+- [ ] 30WakeUp32
+- [ ] Error
+- [x] 30WakeUp6
+---
+**Explanation:**
+
+=> 10 + 20 + "WakeUp" + 3 * 2
+=> 10 + 20 + "WakeUp" + 6
+=> 30 + "WakeUp" + 6
+=> "30WakeUp" + 6
+=> "30WakeUp6"
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print(10 + "Hello" * "World" + 3);
+```
+
+# Choices
+- [ ] 10HelloWorld3
+- [ ] 10HelloWorldWorldWorld3
+- [x] Error
+- [ ] Good Morning :)
+---
+**Explanation:**
+We cannot use * operator with text operand
+
+---
+
+# Question
+What will be output for this ?
+```
+System.out.print(10 + "WelcomeHome" - "Home" + 3);
+```
+# Choices
+- [ ] 10Welcome3
+- [ ] 10WelcomeHomeHome3
+- [x] Error
+- [ ] Good Morning :)
+---
+**Explanation:**
+We cannot use - operator with text operand
+
+
+---
+
+# Question
+Predict the output for the following code:
+```
+System.out.println(10 + 20 + "Hello");
+```
+
+# Choices
+- [ ] 1020Hello
+- [x] 30Hello
+- [ ] Hello1020
+- [ ] Hello Hello Hello
+---
+**Explanation**
+10 + 20 = 30,
+ Now when string is concatenated then 30 becomes as string "30" so the answer is "30Hello".
+
+
+---
+# Section 2.3 (Introduction to Variables)
+
+> Start with that numbers are of two types:
+1. **Non-Decimal / Integers**
+2. Decimals
+
+**Story :** Assume we have a container storing water in it. And then explain the three factors of container that are : Type, Name and Value
+
+After that take a container to store integers and explain the same three factors.
+
+
+ +
+In programming, containers are known as variables.
+
+## Creating a variable:
+
+
+
+In programming, containers are known as variables.
+
+## Creating a variable:
+
+ +
+---
+
+# Question
+What will be output for this ?
+```java
+Create a variable of type int and give name as num and assign 34 in it.
+```
+
+# Choices
+- [ ] num = 34
+- [x] int num = 34;
+- [ ] int 34 num
+- [ ] num int = 34
+
+
+
+---
+
+# Question
+What will be output for this ?
+```
+int val = 30;
+System.out.println(val);
+```
+
+# Choices
+- [ ] val
+- [x] 30
+- [ ] Error
+- [ ] Don't Select me, I'm wrong option
+---
+**Explanation:**
+The value of variable val is 30.
+
+**Rule :** Whenever we use variable name, the value of that variable is used.
+
+---
+
+# Question
+What will be output for this ?
+```
+int a = 10;
+int b = 20;
+System.out.println(a + b);
+```
+
+# Choices
+- [ ] ab
+- [x] 30
+- [ ] Error
+- [ ] Keep focus on the above option, I am wrong
+
+
+
+
+---
+
+# Question
+What will be output for this ?
+```
+int a = 10;
+int b = 20;
+System.out.println("Sum of Number is " + a + b);
+ ```
+
+# Choices
+- [ ] Sum of Number is 30
+- [x] Sum of Number is 1020
+- [ ] Error
+- [ ] Above Options, Not me :)
+---
+**Explanation:**
+
+Here, both operators are + and have same priority. Hence, the exppression will be evaluated from left to right.
+=> "Sum of Number is " + a + b
+=> "Sum of Number is " + 10 + 20
+=> "Sum of Number is 10" + 20
+=> "Sum of Number is 1020"
+
+
+---
+
+# Question
+What will be output for this ?
+```
+int a = 10;
+int b = 20;
+System.out.println("Product of Number is " + a * b);
+```
+
+# Choices
+- [ ] Product of Number is 1020
+- [x] Product of Number is 200
+- [ ] Error
+- [ ] Again Above Options, Not me :)
+---
+**Explanation:**
+Here, * has highest priority. So, a * b will be evaluated first.
+=> "Product of Number is " + a * b
+=> "Product of Number is " + 10 * 20
+=> "Product of Number is " + 200
+=> "Product of Number is 200"
+
+---
+# Section 2.4 (Summary)
+1. In Java, when we divide ( / ) integers we only get quotient.
+2. We cannot divide integers by 0, we get error.
+3. Priority of Operators :
+ * Rank 1 : **()**
+ * Rank 2 : __*__ , __/__
+ * Rank 3 : __+__ , __-__
+4. When two operators of different priority are there, we evaluate the one with higher priority first.
+5. When two operators of same priority are there, we evaluate the one which comes first from left to right.
+6. With + operator, if one of the operand is text then we concatenate both the operands.
+7. Creating a variable:
+ * type name = value;
+ * Way 1 :
+ * int x = 30;
+ * Way 2 :
+ * int y;
+ y = 40;
+8. When we use variable name, we use its value.
+
+
+
+
+
+
+
+
diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner Problems on Arrays.md b/Academy DSA Typed Notes/Beginner Language/Beginner Problems on Arrays.md
new file mode 100644
index 0000000..27bd2f2
--- /dev/null
+++ b/Academy DSA Typed Notes/Beginner Language/Beginner Problems on Arrays.md
@@ -0,0 +1,412 @@
+# Problems on Arrays:
+
+---
+
+## Agenda
+
+1. Count of Pairs with sum = K
+2. Elements having at least 1 element greater than it
+3. Given a mat[][] and row num, return sum of that row
+4. Given a mat[][] and col num, return sum of that col"
+5. Given two matrices and return sum of mat[][]
+6. Return an arraylist with all unique element
+7. Return unique of elements from every row
+
+---
+
+
+#### Problem Statement
+Given an array arr and a value k, find the count of pairs (i, j) such that `arr[i] + arr[j] == k` where i != j.
+**Note 1:** i & j are indices of array.
+**Note 2:** (i, j) is the same as (j, i).
+
+#### Example 1
+```cpp
+Input: arr = [2, 4, 2, 5, 1, 3], k = 6
+Output: 3
+```
+**Explanation:** Following pairs satisfy the condition-
+(0, 1) -> arr[0] + arr[1] = 2 + 4 = 6
+(1, 2) -> arr[1] + arr[2] = 4 + 2 = 6
+(3, 4) -> arr[3] + arr[4] = 5 + 1 = 6
+Hence, the answer is 3.
+
+---
+
+# Question
+Given ar[5] = {5 3 2 3 6} k = 8
+no of pairs (i , j) are there such that ar[i] + ar[j] = k ?
+
+# Choices
+- [x] 3
+- [ ] 4
+- [ ] 5
+- [ ] 6
+
+---
+
+
+### Explanation
+
+Following pairs satisfy the condition-
+(0, 1) -> arr[0] + arr[1] = 5 + 3 = 8
+(0, 3) -> arr[0] + arr[3] = 5 + 3 = 8
+(2, 4) -> arr[2] + arr[4] = 2 + 6 = 8
+Hence, the answer is 3.
+
+---
+
+
+#### Solution 1
+
+
+
+One way to solve this problem is to use a brute force approach, which involves checking every possible pair of elements in the array to see if their sum is equal to k. Here are the steps involved in this approach:
+* Initialize a variable count to 0 to keep track of the count of pairs.
+* Traverse the array arr using two nested loops, comparing each pair of elements in the array to see if their sum is equal to k.
+* Return count/2, since (i, j) & (j, i) are considered as same.
+
+#### Pseudocode
+```java
+public static int countPairs(int[] arr, int k) {
+ int count = 0;
+
+ for (int i = 0; i < arr.length; i++) {
+ for (int j = 0; j < arr.length; j++) {
+ if (i!=j && arr[i] + arr[j] == k) {
+ count++;
+ }
+ }
+ }
+
+ return count / 2;
+}
+```
+
+#### Solution 2
+
+
+
+If we notice, in the above solution we are counting (i, j) & (j, i) both. If we not consider one of the pair initially only, then it will not get added to the count. To achieve this, we will always start the inner loop from one index greater than the outer loop.
+
+#### Pseudocode
+```java
+public static int countPairs(int[] arr, int k){
+ int count = 0;
+
+ for (int i = 0; i < arr.length; i++){
+ for (int j = i+1; j < arr.length; j++){
+ if (arr[i] + arr[j] == k){
+ count++;
+ }
+ }
+ }
+
+ return count;
+}
+```
+
+---
+
+
+### Problem:
+Given a 2D array and a row index, return sum of that particular row.
+
+
+| 0 | 1 | 2 | 3 |
+|:--- | --- | --- | --- |
+| 1 | 2 | 3 | 4 |
+| 5 | 6 | 7 | 8 |
+| 9 | 10 | 11 | 12 |
+
+row index =1,
+5 + 6 + 7 + 8, output=26
+
+---
+
+
+# Question
+Given a matrix, row index =0, return sum of that particular row.
+
+```plaintext
+1 2 3 4
+5 6 7 8
+9 10 11 12
+```
+# Choices
+- [x] 10
+- [ ] 4
+- [ ] 26
+- [ ] 6
+
+---
+
+
+#### Pseudocode
+```java
+static int rowSum(int[] mat, int i){
+ int n = mat.length;
+ int m = mat[0].length;
+
+ int sum=0;
+ for (int j = 0; j < m; j++){
+ sum=sum+mar[i][j];
+ }
+
+ return sum;
+}
+```
+---
+
+
+### Problem:
+Given a 2D array and a column index, return sum of that particular column.
+
+
+| 0 | 1 | 2 | 3 |
+|:--- | --- | --- | --- |
+| 1 | 2 | 3 | 4 |
+| 5 | 6 | 7 | 8 |
+| 9 | 10 | 11 | 12 |
+
+column index =2,
+3 + 7 + 11, output=21
+
+Ask the students to do it yourself.
+
+---
+
+
+### Add two matrices
+Write a function to add two matrix of same dimension and return the resultant
+
+#### Testcase 1
+
+
+#### Solution with explaination
+
+
+
+* Matrix are of same dimension i.e. they have same number of rows and columns.
+* The values that are present at same row number and same column number in both matrix are to be added together inorder to get the resultant.
+* In above solution number with same colors are present at same row number and same column number in both matrix.
+* So inorder to get element at c[0][0] we add A[0][0] i.e 7 and B[0][0] i.e. 3 and so on.
+
+#### Testcase 2
+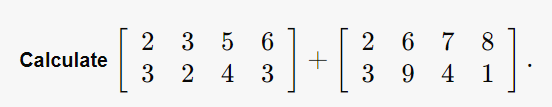
+#### Solution
+
+
+
+---
+
+
+# Question
+
+Can we add a 3x4 matrix with a 3x4 matrix?
+
+# Choices
+- [x] Yes
+- [ ] No
+- [ ] Maybe
+
+---
+
+
+# Question
+
+Can we add a 3x4 matrix with a 3x3 matrix ?
+
+# Choices
+- [ ] Yes
+- [x] No
+- [ ] Maybe
+
+---
+
+
+#### Observation
+* On oberserving both the cases we can give generalized formula for sum of matrix having same dimensions as:-
+
+
+
+---
+
+# Question
+What will be output for this ?
+```java
+Create a variable of type int and give name as num and assign 34 in it.
+```
+
+# Choices
+- [ ] num = 34
+- [x] int num = 34;
+- [ ] int 34 num
+- [ ] num int = 34
+
+
+
+---
+
+# Question
+What will be output for this ?
+```
+int val = 30;
+System.out.println(val);
+```
+
+# Choices
+- [ ] val
+- [x] 30
+- [ ] Error
+- [ ] Don't Select me, I'm wrong option
+---
+**Explanation:**
+The value of variable val is 30.
+
+**Rule :** Whenever we use variable name, the value of that variable is used.
+
+---
+
+# Question
+What will be output for this ?
+```
+int a = 10;
+int b = 20;
+System.out.println(a + b);
+```
+
+# Choices
+- [ ] ab
+- [x] 30
+- [ ] Error
+- [ ] Keep focus on the above option, I am wrong
+
+
+
+
+---
+
+# Question
+What will be output for this ?
+```
+int a = 10;
+int b = 20;
+System.out.println("Sum of Number is " + a + b);
+ ```
+
+# Choices
+- [ ] Sum of Number is 30
+- [x] Sum of Number is 1020
+- [ ] Error
+- [ ] Above Options, Not me :)
+---
+**Explanation:**
+
+Here, both operators are + and have same priority. Hence, the exppression will be evaluated from left to right.
+=> "Sum of Number is " + a + b
+=> "Sum of Number is " + 10 + 20
+=> "Sum of Number is 10" + 20
+=> "Sum of Number is 1020"
+
+
+---
+
+# Question
+What will be output for this ?
+```
+int a = 10;
+int b = 20;
+System.out.println("Product of Number is " + a * b);
+```
+
+# Choices
+- [ ] Product of Number is 1020
+- [x] Product of Number is 200
+- [ ] Error
+- [ ] Again Above Options, Not me :)
+---
+**Explanation:**
+Here, * has highest priority. So, a * b will be evaluated first.
+=> "Product of Number is " + a * b
+=> "Product of Number is " + 10 * 20
+=> "Product of Number is " + 200
+=> "Product of Number is 200"
+
+---
+# Section 2.4 (Summary)
+1. In Java, when we divide ( / ) integers we only get quotient.
+2. We cannot divide integers by 0, we get error.
+3. Priority of Operators :
+ * Rank 1 : **()**
+ * Rank 2 : __*__ , __/__
+ * Rank 3 : __+__ , __-__
+4. When two operators of different priority are there, we evaluate the one with higher priority first.
+5. When two operators of same priority are there, we evaluate the one which comes first from left to right.
+6. With + operator, if one of the operand is text then we concatenate both the operands.
+7. Creating a variable:
+ * type name = value;
+ * Way 1 :
+ * int x = 30;
+ * Way 2 :
+ * int y;
+ y = 40;
+8. When we use variable name, we use its value.
+
+
+
+
+
+
+
+
diff --git a/Academy DSA Typed Notes/Beginner Language/Beginner Problems on Arrays.md b/Academy DSA Typed Notes/Beginner Language/Beginner Problems on Arrays.md
new file mode 100644
index 0000000..27bd2f2
--- /dev/null
+++ b/Academy DSA Typed Notes/Beginner Language/Beginner Problems on Arrays.md
@@ -0,0 +1,412 @@
+# Problems on Arrays:
+
+---
+
+## Agenda
+
+1. Count of Pairs with sum = K
+2. Elements having at least 1 element greater than it
+3. Given a mat[][] and row num, return sum of that row
+4. Given a mat[][] and col num, return sum of that col"
+5. Given two matrices and return sum of mat[][]
+6. Return an arraylist with all unique element
+7. Return unique of elements from every row
+
+---
+
+
+#### Problem Statement
+Given an array arr and a value k, find the count of pairs (i, j) such that `arr[i] + arr[j] == k` where i != j.
+**Note 1:** i & j are indices of array.
+**Note 2:** (i, j) is the same as (j, i).
+
+#### Example 1
+```cpp
+Input: arr = [2, 4, 2, 5, 1, 3], k = 6
+Output: 3
+```
+**Explanation:** Following pairs satisfy the condition-
+(0, 1) -> arr[0] + arr[1] = 2 + 4 = 6
+(1, 2) -> arr[1] + arr[2] = 4 + 2 = 6
+(3, 4) -> arr[3] + arr[4] = 5 + 1 = 6
+Hence, the answer is 3.
+
+---
+
+# Question
+Given ar[5] = {5 3 2 3 6} k = 8
+no of pairs (i , j) are there such that ar[i] + ar[j] = k ?
+
+# Choices
+- [x] 3
+- [ ] 4
+- [ ] 5
+- [ ] 6
+
+---
+
+
+### Explanation
+
+Following pairs satisfy the condition-
+(0, 1) -> arr[0] + arr[1] = 5 + 3 = 8
+(0, 3) -> arr[0] + arr[3] = 5 + 3 = 8
+(2, 4) -> arr[2] + arr[4] = 2 + 6 = 8
+Hence, the answer is 3.
+
+---
+
+
+#### Solution 1
+
+
+
+One way to solve this problem is to use a brute force approach, which involves checking every possible pair of elements in the array to see if their sum is equal to k. Here are the steps involved in this approach:
+* Initialize a variable count to 0 to keep track of the count of pairs.
+* Traverse the array arr using two nested loops, comparing each pair of elements in the array to see if their sum is equal to k.
+* Return count/2, since (i, j) & (j, i) are considered as same.
+
+#### Pseudocode
+```java
+public static int countPairs(int[] arr, int k) {
+ int count = 0;
+
+ for (int i = 0; i < arr.length; i++) {
+ for (int j = 0; j < arr.length; j++) {
+ if (i!=j && arr[i] + arr[j] == k) {
+ count++;
+ }
+ }
+ }
+
+ return count / 2;
+}
+```
+
+#### Solution 2
+
+
+
+If we notice, in the above solution we are counting (i, j) & (j, i) both. If we not consider one of the pair initially only, then it will not get added to the count. To achieve this, we will always start the inner loop from one index greater than the outer loop.
+
+#### Pseudocode
+```java
+public static int countPairs(int[] arr, int k){
+ int count = 0;
+
+ for (int i = 0; i < arr.length; i++){
+ for (int j = i+1; j < arr.length; j++){
+ if (arr[i] + arr[j] == k){
+ count++;
+ }
+ }
+ }
+
+ return count;
+}
+```
+
+---
+
+
+### Problem:
+Given a 2D array and a row index, return sum of that particular row.
+
+
+| 0 | 1 | 2 | 3 |
+|:--- | --- | --- | --- |
+| 1 | 2 | 3 | 4 |
+| 5 | 6 | 7 | 8 |
+| 9 | 10 | 11 | 12 |
+
+row index =1,
+5 + 6 + 7 + 8, output=26
+
+---
+
+
+# Question
+Given a matrix, row index =0, return sum of that particular row.
+
+```plaintext
+1 2 3 4
+5 6 7 8
+9 10 11 12
+```
+# Choices
+- [x] 10
+- [ ] 4
+- [ ] 26
+- [ ] 6
+
+---
+
+
+#### Pseudocode
+```java
+static int rowSum(int[] mat, int i){
+ int n = mat.length;
+ int m = mat[0].length;
+
+ int sum=0;
+ for (int j = 0; j < m; j++){
+ sum=sum+mar[i][j];
+ }
+
+ return sum;
+}
+```
+---
+
+
+### Problem:
+Given a 2D array and a column index, return sum of that particular column.
+
+
+| 0 | 1 | 2 | 3 |
+|:--- | --- | --- | --- |
+| 1 | 2 | 3 | 4 |
+| 5 | 6 | 7 | 8 |
+| 9 | 10 | 11 | 12 |
+
+column index =2,
+3 + 7 + 11, output=21
+
+Ask the students to do it yourself.
+
+---
+
+
+### Add two matrices
+Write a function to add two matrix of same dimension and return the resultant
+
+#### Testcase 1
+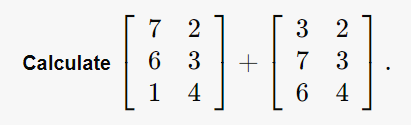
+
+#### Solution with explaination
+
+
+
+* Matrix are of same dimension i.e. they have same number of rows and columns.
+* The values that are present at same row number and same column number in both matrix are to be added together inorder to get the resultant.
+* In above solution number with same colors are present at same row number and same column number in both matrix.
+* So inorder to get element at c[0][0] we add A[0][0] i.e 7 and B[0][0] i.e. 3 and so on.
+
+#### Testcase 2
+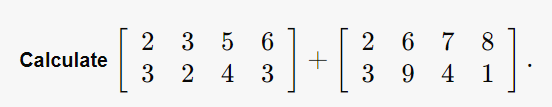
+#### Solution
+
+
+
+---
+
+
+# Question
+
+Can we add a 3x4 matrix with a 3x4 matrix?
+
+# Choices
+- [x] Yes
+- [ ] No
+- [ ] Maybe
+
+---
+
+
+# Question
+
+Can we add a 3x4 matrix with a 3x3 matrix ?
+
+# Choices
+- [ ] Yes
+- [x] No
+- [ ] Maybe
+
+---
+
+
+#### Observation
+* On oberserving both the cases we can give generalized formula for sum of matrix having same dimensions as:-
+
+
+ SumMat[i][j] = Mat1[i][j] + Mat2[i][j]
+
+
+
+#### Code
+```java
+static int[][] addMatrix(int[][] A, int[][] B) {
+ int m = A.length;
+ int n = A[0].length;
+ int[][] ans = new int[m][n];
+
+ for (int i = 0; i < m; i++) {
+ for (int j = 0; j < n; j++) {
+ ans[i][j] = A[i][j] + B[i][j];
+ }
+ }
+
+ return ans;
+}
+```
+
+---
+
+
+#### Problem Statement
+Given an ArrayList of integers, return all the unique numbers in the ArrayList.
+
+**Note:** An element with frequency 1 is known as unique element.
+
+#### Example 1
+```java
+Input = 10 7 32 10 32 48 56 12 48 19 11 32
+Output = 7 56 12 19 11
+```
+
+---
+
+# Question
+ar[] = {6 10 8 2 8 10 11}
+Return all unique elements
+
+# Choices
+- [x] 6 2 11
+- [ ] 6 2 10
+- [ ] 10 8 11
+- [ ] None of the above
+
+---
+
+
+#### Solution
+Iterate on each element, check if frequency is 1 then add element to ans arrayList.
+
+
+
+
+
+#### Pseudocode
+
+```java
+static ArrayList5 uppercase +- [x] 3 uppercase
5 lowercase +- [ ] 5 uppercase
9 lowercase +- [ ] I dont know + +--- + + +```java +public static void main(String args[]) { + Scanner scn = new Scanner(System.in); + String str = scn.next(); + + int c1 = 0; + int c2 = 0; + + for (int i = 0; i < str.length(); i++) { + char ch = str.charAt(i); + + if (ch >= 'A' && ch <= 'Z') { + c1++; + } else if (ch >= 'a' && ch <= 'z') { + c2++; + } + } + + System.out.println(c1); + System.out.println(c2); + + } +``` + +--- + +### Problem: + +Count number of characters of first string present in the second string. + +### Example: +String A=abbd +String B=aabb + +Output: +Number of common characters: 3(a,b,b) + +### Pseudo Code + +```java +static int countCommonCharacters(String str1, String str2) { + int count = 0; + + for (int i = 0; i < str1.length(); i++) { + char currentChar = str1.charAt(i); + + for (int j = 0; j < str2.length(); j++) { + if (currentChar == str2.charAt(j)) { + count++; + break; // Break the inner loop once a common character is found + } + } + } + + return count; + } +``` + +------ diff --git a/Academy DSA Typed Notes/Intermediate/Intermediate DSA Arrays 2D Matrices.md b/Academy DSA Typed Notes/Intermediate/Intermediate DSA Arrays 2D Matrices.md new file mode 100644 index 0000000..c7afb37 --- /dev/null +++ b/Academy DSA Typed Notes/Intermediate/Intermediate DSA Arrays 2D Matrices.md @@ -0,0 +1,480 @@ +# 2D Matrices + +### Definition +A 2D matrix is a specific type of 2D array that has a rectangular grid of numbers, where each number is called an element. It is a mathematical structure that consists of a set of numbers arranged in rows and columns. +2D matrix can be declared as: + +``` +int mat[N][M]; +``` +*int* is the datatype. +*mat* is the matrix name. +*N* is the number of rows in matrix. +*M* is the number of columns in matrix. + +*mat[i][j]* represents the element present in the *i-th* row of *j-th* column. + +Below is the pictorial representation of 2D matrix. + + + + +**Note:** A matrix having *N* rows and *M* columns can store **N*M** elements. + + + +### Question + +Given a matrix of size NxM. What will be the index of the top right cell? +Choose the correct answer + +**Choices** +- [ ] 0,0 +- [ ] 0,M +- [ ] M-1,0 +- [x] 0,M-1 + + +### Question + +Given a matrix of size NxM. What will be the index of the bottom right cell? +Choose the correct answer + +**Choices** +- [ ] N,M +- [ ] M,N +- [x] N-1,M-1 +- [ ] M-1,N-1 + +### Question 1 : Given a matrix print row-wise sum + +**Problem Statement** +Given a 2D matrix mat[N][M], print the row-wise sum. + +#### TestCase + +**Input:** + +``` +mat[3][4] = { + {1,2,3,4}, + {5,6,7,8}, + {9,10,11,12} +} +``` + +**Output:** + +``` +10 +26 +42 +``` + +### Approach + +The approach is to traverse each row and while traversing take the sum of all the elements present in that row. + +### Pseudocode: +```cpp +function SumRow(int mat[N][M]) { + for (int i = 0; i < N; i++) { + int sum = 0; + for (int j = 0; j < M; j++) { + sum = sum + mat[i][j]; + } + print(sum); + } +} +``` + + +### Question + +What is the time and space complexity of to calculate row-wise sum for a matrix of size N*M? +Choose the correct answer + +**Choices** +- [ ] TC: O(N^2), SC: O(n) +- [ ] TC: O(N^2), SC: O(1) +- [ ] TC: O(N^M), SC: O(n) +- [x] TC: O(N*M), SC: O(1) + + +Since we are iterating over all the elements just once, hence +Time Complexity: **O(N*M)**. + +We are not using any extra space, +Space Complextiy: **O(1)**. + +### Question 2 : Given a matrix print col-wise sum + +Given a 2D matrix mat[N][M], print the column-wise sum. + +**TestCase** + +``` +mat[3][4] = { + {1,2,3,4}, + {5,6,7,8}, + {9,10,11,12} +} +``` + +**Output** + +``` +15 18 21 24 +``` + +:::warning +Please take some time to think about the solution approach on your own before reading further..... +::: + +### Approach + +While traversing each column, we can calculate sum of all the elements present in that column. + +### Pseudocode +```cpp +function SumColumn(int mat[N][M]) { + for (int j = 0; j < M; j++) { + int sum = 0; + for (int i = 0; i < N; i++) { + sum = sum + mat[i][j]; + } + print(sum); + } +} +``` + +#### Complexity +Time Complexity: **O(N*M)**. +Space Complextiy: **O(1)**. + +### Question 3 : Given a square matrix print diagonals + +Given a matrix 2D square matrix mat[N][N], print diagonals. + +How many main Diagonals are there in a square matrix? +$2.$ + +1. **Principal Diagonal:** From top left to bottom right. +3. **Anti Diagonal:** From top right to bottom left. + + + + +First, let's print **Principal Diagonal** + +**TestCase** + +``` +mat[3][3] = { + {1,2,3}, + {5,6,7}, + {9,10,11} +} +``` + +**Output:** + +``` +1 6 11 +``` +### Question 3 Approach + +#### Pseudocode: +```cpp +function PrintDiagonal(int mat[N][N]) { + int i = 0; + while (i < N) { + print(mat[i][i]); + i = i + 1; + } +} +``` + + +### Question + +Given a matrix of size NxN. What will be the time complexity to print the diagonal elements? +Chose the correct answer + +**Choices** +- [ ] O(N*sqrt(N)) +- [x] O(N) +- [ ] O(N^2) +- [ ] O(NlogN) + + +Since i starts at 0 and goes till N-1, hence there are total N iterations. + +Time Complexity: **O(N)**. +Space Complextiy: **O(1)**. + +### Given square matrix, print **Anti-diagonal** + +**TestCase** +``` +mat[3][3] = { + {1,2,3}, + {5,6,7}, + {9,10,11} +} +``` + +**Output:** + +``` +3 6 9 +``` + +### Pseudocode: +```cpp +function PrintDiagonal(int mat[N][N]) { + int i = 0, j = N - 1; + while (i < N) { + print(mat[i][j]); + i++; + j--; + } +} +``` + +### Complexity +Time Complexity: **O(N)**. +Space Complextiy: **O(1)**. + +### Question 4 Print diagonals in a matrix (right to left) + + +**Problem Statement** +Given a 2D matrix mat print all the elements diagonally from right to left + +**TestCase** + +``` +mat[3][4] = { + {1,2,3,4}, + {5,6,7,8}, + {9,10,11,12} +} +``` + +**Output:** + +``` +1 +2 5 +3 6 9 +4 7 10 +8 11 +12 +``` + + +### Question + +Given a matrix of size N*M, how many Right to Left diagonals will be there? + +Choose the correct Options + +**Choices** +- [ ] N*M +- [ ] N+M +- [x] N+M-1 +- [ ] N+M+1 + + +1. M diagonals are starting from first row. +2. N diagonals start from last column. +3. There is a common diagonal at index 0, M-1. + +So, total count = N+M-1 Let's take an example as shown below: + + + +### Question + +Given a matrix of size 4x5, how many Right to Left diagonals will be there? +Choose the correct answer + +**Choices** +- [x] 8 +- [ ] 11 +- [ ] 9 +- [ ] 10 + +### Question 4 Approach + +:::warning +Please take some time to think about the solution approach on your own before reading further..... +::: + +* For every start of the diagonal, how do the indices change when we iterate over it? +Row number increments by 1 and column number decrements by 1 as shown in the diagram. + + +### Pseudocode +```cpp +function print_diagonal_elements(A[N][M]) { + //print all diagonals starting from 0th row + i = 0 + for (j = 0; j < M; j++) { + s = i; + e = j; + while (s < N && e >= 0) { + print(A[s][e]) + s++ + e— + } + print(“\n”) + } + + //print all diagonals starting from last column + j = M - 1 + for (i = 1; i < N; i++) { + s = i; + e = j; + while (s < N && e >= 0) { + print(A[s][e]) + s++ + e— + } + print(“\n”) + } +} +``` +### Question + +Time Complexity of printing all the diagonals of a matrix of dimensions N X M? +Choose the correct answer + +**Choices** +- [ ] O(N^2 * M^2) +- [ ] O(N^2 + M^2) +- [ ] O(N + M) +- [x] O(N * M) + +### Question 5 : Transpose of a square matrix + +**Problem Statement** +Given a square 2D matrix mat[N][N], find transpose. + +**Transpose of matrix** +The transpose of a matrix is a new matrix obtained by interchanging the rows and columns of the original matrix. + + +**TestCase** + +``` +mat[3][3] = { + {1,2,3}, + {5,6,7}, + {9,10,11} +} +``` + +**Output:** + +``` +{ +{1,5,9}, +{2,6,10}, +{3,7,11} +} +``` + +:::warning +Please take some time to think about the solution approach on your own before reading further..... +::: + +### Question 5 Approach + +#### Observation +* After performing the transpose, what is same in the original matix and its transpose ? +The diagonal that starts from (0,0) is same. + +* Along the diagonals, the elements have swapped their positions with corresponding elements. + +#### PseudoCode +```cpp +function find_transpose(matrix[N][N]){ + for(int i = 0; i < N; i++){ + for(int j = i + 1; j < N; j++){ + swap(matrix[i][j],matrix[j][i]); + } + } +} +``` +**Note:** If we start j at 0, the matrix will come back to its original position. + +### Question +What is the time and space complexity to find transpose of a square matrix? +Chose the correct answer + +**Choices** +- [ ] TC: O(N), SC: O(n) +- [ ] TC: O(N^2), SC: O(n) +- [x] TC: O(N^2), SC: O(1) +- [ ] O(N), SC: O(1) + +**Complexity** +Time Complexity: **O(N^2)**. +Space Complextiy: **O(1)**. + +### Question 6 Rotate a matrix to 90 degree clockwise + + +**Problem Statement** +Given a matrix mat[N][N], rotate it to 90 degree clockwise. + +**TestCase** +``` +{ +{1,2,3}, +{4,5,6}, +{7,8,9} +} +``` +**Output** +``` +{ +{7,4,1}, +{8,5,2}, +{9,6,3} +} +``` +### Question 6 Approach + +### Hint: +* What if we first find the transpose of the matrix? +* Is there any relation between rotated matrix and transposed matrix ? + +:::warning +Using the Hints, please take some time to think about the solution approach on your own before reading further..... +::: + +### Observation: +Yes, if we reverse all the rows, then it will become rotated matrix. +The rotated matrix looks like: + + +**Transpose and rotated matrix:** + + +#### PseudoCode +```cpp +Function rotate(int mat[N][N]) { + mat = transpose(mat); + for (int i = 0; i < N; i++) { + reverse(mat[i]); + } + return mat; +} +``` +#### Complexity +Time Complexity: **O(N*N)**. +Space Complextiy: **O(1)**. + diff --git a/Academy DSA Typed Notes/Intermediate/Intermediate DSA Arrays Sliding Window & Contribution Technique.md b/Academy DSA Typed Notes/Intermediate/Intermediate DSA Arrays Sliding Window & Contribution Technique.md new file mode 100644 index 0000000..f9d2557 --- /dev/null +++ b/Academy DSA Typed Notes/Intermediate/Intermediate DSA Arrays Sliding Window & Contribution Technique.md @@ -0,0 +1,393 @@ +# Sliding Window & Contribution Technique + +## Problem 1 : Find the max sum out of all possible subarray of the array + +### Problem Statement +Given an array of integers, find the total sum of all possible subarrays. +**#Note:** This question has been previously asked in *Google* and *Facebook*. + +### Solution +* We can use the previous approach, where we calculated all sum subarray using Carry Forward technique. +* Instead of keeping track of maximum, we can simply add the sums in a variable. + +### Pseudocode +```cpp +int sumOfAllSubarraySums(int arr[], int n) { + int total_sum = 0; + for (int i = 0; i < n; i++) { + int subarray_sum = 0; + for (int j = i; j < n; j++) { + subarray_sum += arr[j]; + total_sum += subarray_sum; + } + } + return total_sum; +} +``` +### Time and Space Complexity +* TC - O(n^2) +* SC - O(1) + +## Problem 2 : Contribution Technique + +We can optimize the above solution further by observing a pattern in the subarray sums. +Let's take the example array ``[1, 2, 3]``. The subarrays and their sums are: + +``` +[1] -> 1 +[1, 2] -> 3 +[1, 2, 3] -> 6 +[2] -> 2 +[2, 3] -> 5 +[3] -> 3 +Total Sum = 1+3+6+2+5+3 = 20 +``` + +Instead of generating all subarrays, we can check that a particular element appears in how many subarrays and add its contribution that many times to the answer. + +* the first element 1 appears in 3 subarrays: [1], [1, 2], and [1, 2, 3]. +* the second element 2 appears in 4 subarrays: [2], [1, 2], [2, 3], and [1, 2, 3]. +* the third element 3 appears in 3 subarrays: [3], [2, 3], and [1, 2, 3]. + +Total = $(1*3) + (2*4) + (3*3) = 20$ + + + +:::warning +Please take some time to think about "How to calculate the number of subarrays in which A[i] appears?" on your own before reading further..... +::: + + +### Question +In how many subarrays, the element at index 1 will be present? +A: [3, -2, 4, -1, 2, 6 ] + +**Choices** +- [ ] 6 +- [ ] 3 +- [x] 10 +- [ ] 8 + +**Explanation:** The subarrays in which the element at index 1 is present are - +[3, -2], [3, -2, 4], [3, -2, 4, -1], [3, -2, 4, -1, 2], [3, -2, 4, -1, 2, 6], [-2], [-2, 4], [-2, 4, -1], [-2, 4, -1, 2], [-2, 4, -1, 2, 6 ]. There are total 10 such subarrays. + +### Question +In how many subarrays, the element at index 2 will be present? +A: [3, -2, 4, -1, 2, 6 ] + +**Choices** +- [ ] 6 +- [x] 12 +- [ ] 10 +- [ ] 8 + +**Explanation:** The subarrays in which the element at index 1 is present are - +[3, -2, 4], [3, -2, 4, -1], [3, -2, 4, -1, 2], [3, -2, 4, -1, 2, 6], [-2, 4], [-2, 4, -1], [-2, 4, -1, 2], [-2, 4, -1, 2, 6], [4], [4, -1], [4, -1, 2], [4, -1, 2, 6 ]. There are total 12 such subarrays. + +### Find sum of all Subarrays sums continued +**Generalized Calculation -** +The start of such subarrays can be $0, 1, ..i$ +The end of such subarrays can be $i, i+1, i+2, ...n-1$ + +Elements in range [0 i] = $i+1$ +Elements in range [i n-1] = $n-1-i+1 = n-i$ +Thus, the total number of subarrays containing arr[i] is i+1 multiplied by n-i. + +This gives us the expression `(i+1) * (n-i)`. + +We can use this pattern to compute the total sum of all subarrays in O(n) time complexity. The steps are as follows: +* Initialize a variable total_sum to zero. +* Iterate over all elements of the input array arr. For each element arr[i], compute `arr[i] * (i+1) * (n-i)` and add it to total_sum. +* Return total_sum as the output of the function. + +#### Pseudocode +```cpp +int sumOfAllSubarraySums(arr[]) { + int n = arr.size(); + int total_sum = 0; + + // Iterate over all elements of the array and compute the sum of all subarrays containing that element + for (int i = 0; i < n; i++) { + total_sum += arr[i] * (i + 1) * (n - i); + } + + return total_sum; +} +``` +#### Time and Space Complexity +* TC - O(n) +* SC - O(1) + +### Total number of subarrays of length K + + +Number of subarrays of length K = Total number of start indices of subarrays of length K. + + + +| length (K) | start of first window | start of last window | +| -------- | -------- | -------- | +| 1 | 0 | N-1 | +| 2 | 0 | N-2 | +| 3 | 0 | N-3 | +| 4 | 0 | N-4 | +| K | 0 | N-K | + +All start positions for length K, will be within range **[0 N-K]**. Therefore total is N-K+1. + +Hence, total number of subarrays of length K = **N-K+1**. + + + + +### Question +Given N=7, K=4, what will be the total number of subarrays of len K? + +**Choices** +- [ ] 3 +- [x] 4 +- [ ] 5 +- [ ] 6 + + +## Problem 3 Given an array, print start and end indices of subarrays of length K. + + +Given an array of size N, print start and end indices of subarrays of length K. + +**Example** + +If N=8, K=3 +All start and end indices are + + +| start | end | +| ----- | ----- | +| 0 | 2 | +| 1 | 3 | +| 2 | 4 | +| 3 | 5 | +| 4 | 6 | +| 5 | 7 | + +[start end] = K +end - start + 1 = K +end = K + start - 1 + +#### Pseudocode +```cpp= +//Iterate over all the start indices +for (int i = 0; i <= N - K; i++) { + int j = K + i - 1; + + print(i, j); +} +``` + +> Note: Now we know how to iterate over windows of length K. + +## Problem 4 : Given an array, print maximum subarray sum with length K + + +Given an array of N elements. Print maximum subarray sum for subarrays with length = K. + +**Example** +``` +N=10 K=5 +``` + +| -3 | 4 | -2 | 5 | 3 | -2 | 8 | 2 | -1 | 4 | +| --- | --- | --- | --- | --- | --- | --- | --- | --- |:---:| + +**Explanation** + + + +| s | e | sum | +| -------- | -------- | -------- | +| 0 | 4 | 7 | +| 1 | 5 | 8 | +| 2 | 6 | 12 | +| 3 | 7 | 16 | +| 4 | 8 | 10 | +| 5 | 9 | 11 | + +Maximum: **16** + +:::warning +Please take some time to think about the solution approach on your own before reading further..... +::: + +### Problem 4 : Bruteforce Approach + + +We have to calculate the sum of all subarrays of size k and find the maximum out of them + +#### Pseudeocode + +```cpp +function maxSubarrayOfLengthK(A[], N, K) { + ans = INT_MIN + + //first window + i = 0 + j = k - 1 + + while (j < N) { + sum = 0 + for (idx = start; idx <= end; idx++) { + sum += A[idx] + } + ans = max(sum, ans) + + //going to next subarray of length k + i++ + j++ + } + print(ans) + +} +``` + +#### Complexity + +For what value of k will the iterations be highest ? + + + +:::warning +Please take some time to think about the optimised solution approach on your own before reading further..... +::: + +## Problem 4 : Optimized Approach using Prefix Sum Array + + +We can use **Prefix Sum Array** since we have to find sum within a range. + +### Pseudeocode + +```cpp +function maxSubarrayOfLengthK(A[], N, K) { + // calculate prefix sum array + pf[N] + pf[0] = A[0] + for (idx = 1; idx < N; idx++) { + pf[idx] = pf[idx - 1] + A[idx]; + + } + + ans = INT_MIN + i = 0 + j = K - 1 + + // calculate for each pair of indicies + while (j < N) { + sum = pf[j] - (i == 0 ? 0 : pf[i - 1]) + + ans = max(sum, ans) + i++ + j++ + } + print(ans) + +} +``` + + + +### Question + +What is Time Complexity and Space Complexity respectively? + +**Choices** +- [ ] O(N^2) and O(N) +- [x] O(N) and O(N) +- [ ] O(N) and O(N^2) +- [ ] O(1) and O(N) + +--- + +### Problem 4 Optimized Approach : using Sliding Window + + +We want to reduce the space complexity without modifying the given array, but how? + +#### Observations +* We can get sum of next subarray using current subarray sum as follows:- + * By adding a new element to current sum. + * By subtracting the first element of current subarray. + +Given array :- +| -3 | 4 | -2 | 5 | 3 | -2 | 8 | 2 | -1 | 4 | +| --- | --- | --- | --- | --- | --- | --- | --- | --- |:---:| + +First subarray from 0 to 4:- +| -3 | 4 | -2 | 5 | 3 | +| --- | --- | --- | --- | --- | + +Converting first to second subarray :- + +| ~~-3~~ | 4 | -2 | 5 | 3 | -2 | +| --- | --- | --- | --- | --- | --- | + +Based upon above observation can we say:- +
+sum of all elements of next subarray = sum of elements of current subarray - first element of current subarray + new element
+
+
+This approach is known as **Sliding window approach**.
+
+#### Dry Run
+
+
+
+**We can clearly observe the window sliding in above run.**
+
+#### Pseudeocode
+
+```cpp
+function maxSubarrayOfLengthK(A[], N, K) {
+ ans = INT_MIN
+ i = 0
+ j = K - 1
+
+ sum = 0 // here k iterations
+ for (int idx = i; idx <= j; idx++) {
+ sum += A[idx]
+ }
+ ans = max(sum, ans)
+
+ j++
+ i++
+
+ while (j < N) {
+ sum = sum + A[j] - A[i - 1]
+
+ ans = max(sum, ans)
+ // here N-k iterations
+ i++
+ j++
+ }
+ print(ans)
+
+}
+
+```
+***Time Complexity : O(N)**
+**Space Complexity : O(1)***
+
+
+
+## Observations for solving problems on Subarrays.
+
+### Observations
+Following are the observations that can be useful when solving problems related to subarrays:
+* Subarrays can be visualized as contiguous part of an array, where the starting and ending indices determine the subarray.
+
+* The total number of subarrays in an array of length n is n*(n+1)/2.
+* To print all possible subarrays, O(n^3) time complexity is required.
+* The sum of all subarrays can be computed in O(n^2) time complexity and O(1) space complexity by using Carry Forward technique.
+* The sum of all subarrays can be computed in O(n^2) time complexity and O(n) space complexity using the prefix sum technique.
+* The number of subarrays containing a particular element arr[i] can be computed in O(n) time complexity and O(1) space complexity using the formula (i+1)*(n-i). This method is called `Contribution Technique`.
+
+
diff --git a/Academy DSA Typed Notes/Intermediate/Intermediate DSA Arrays - Carry Forward & Subarrays.md b/Academy DSA Typed Notes/Intermediate/Intermediate DSA Arrays - Carry Forward & Subarrays.md
new file mode 100644
index 0000000..9200d23
--- /dev/null
+++ b/Academy DSA Typed Notes/Intermediate/Intermediate DSA Arrays - Carry Forward & Subarrays.md
@@ -0,0 +1,400 @@
+# Carry Forward & Subarrays
+
+
+## Problem 1 : Count of Pairs ag
+
+Given a string **s** of lowercase characters, return the **count of pairs (i,j)** such that **i < j** and **s[ i ] is 'a'** and **s[ j ] is 'g'**.
+
+### Example 1
+
+```plaintext
+String s = "abegag"
+Ans = 3
+```
+
+### Explanation:
+Here, [i,j] such that i
+ PSe[i] = PSe[i-1] + A[i]
+
+
+If **i is odd** we will use the following equation :-
+
+ PSe[i] = PSe[i-1]
+
+
+
+### Question
+Construct the Prefix Sum for even indexed elements for the given array
+[2, 4, 3, 1, 5]
+
+**Choices**
+- [ ] 1, 6, 9, 10, 15
+- [x] 2, 2, 5, 5, 10
+- [ ] 0, 4, 4, 5, 5
+- [ ] 0, 4, 7, 8, 8
+
+
+
+We will assume elements at odd indices to be 0 and create a prefix sum array taking this assumption.
+So ```2 2 5 5 10``` will be the answer.
+
+
+### Problem 1 : Pseudocode
+
+
+```cpp
+void sum_of_even_indexed(int A[], int queries[][], int N) {
+ // prefix sum for even indexed elements
+ int PSe[N];
+
+ if (A[0] % 2 == 0) PSe[0] = A[0];
+ else PSe[0] = 0;
+
+ for (int i = 0; i < N; i++) {
+ if (i % 2 == 0) {
+ PSe[i] = PSe[i - 1] + A[i];
+ } else {
+ PSe[i] = PSe[i - 1];
+ }
+ }
+ for (int i = 0; i < queries.size(); i++) {
+ s = queries[i][0]
+ e = queries[i][1]
+ if (s == 0) {
+ print(PSe[e])
+ } else {
+ print(PSe[e] - PSe[s - 1])
+ }
+
+ }
+
+}
+```
+### Complexity
+-- TC - $O(n)$
+-- SC - $O(n)$
+
+### Problem 1 Extension : Sum of all odd indexed elements
+
+
+
+If we have to calculate the sum of all ODD indexed elements from index **s** to **e**, then Prefix Sum array will be created as follows -
+
+> if i is odd
+
+ PSo[i] = PSo[i-1] + array[i]
+
+
+> and if i is even :-
+
+ PSo[i] = PSo[i-1]
+
+
+### Problem 2 : Special Index
+
+Given an array of size N, count the number of special index in the array.
+**Note:** **Special Indices** are those after removing which, sum of all **EVEN** indexed elements is equal to sum of all **ODD** indexed elements.
+
+**Example**
+
+```plaintext
+A[ ] = { 4, 3, 2, 7, 6, -2 }
+Ans = 2
+```
+
+We can see that after removing 0th and 2nd index **Se** and **So** are equal.
+
+| i | A[i] | Se | So |
+| --- |------------------| ----- | ----- |
+| 0 | { 3, 2, 7, 6, -2 } | 8 | 8 |
+| 1 | { 4, 2, 7, 6, -2 } | 9 | 8 |
+| 2 | { 4, 3, 7, 6, -2 } | 9 | 9 |
+| 3 | { 4, 3, 2, 6, -2 } | 4 | 9 |
+| 4 | { 4, 3, 2, 7, -2 } | 4 | 10 |
+| 5 | { 4, 3, 2, 7, 6 } | 12 | 10 |
+
+**Note: Please keep a pen and paper with you for solving quizzes.**
+
+
+
+### Question
+What will be the sum of elements at **ODD indices** in the resulting array after removal of **index 2** ?
+A[ ] = [ 4, 1, 3, 7, 10 ]
+
+**Choices**
+- [ ] 8
+- [ ] 14
+- [x] 11
+- [ ] 9
+
+
+After removal of element at **index 2**, elements after index 2 has changed their positions:
+Sum of elements at **ODD** indices from **[0 to 1]** + Sum of elements at **EVEN** indices from **[3 to 4]** =
+ 1 + 10 = 11
+
+
+
+### Question
+What will be the sum of elements at **ODD indices** in the resulting array after removal of **index 3** ?
+A[ ] = { 2, 3, 1, 4, 0, -1, 2, -2, 10, 8 }
+
+**Choices**
+- [ ] 8
+- [x] 15
+- [ ] 12
+- [ ] 21
+
+
+**Explanation:**
+
+After removal of element at index 3, elements after index 3 has changed their positions:
+Sum of elements at **ODD** indices from **[0 to 2]** index + Sum of elements at **EVEN** indices from **[4 to 9]** = A[1]+A[4]+A[6]+A[8] = **3+0+2+10 = 15**
+
+
+
+
+### Question
+What will be the sum of elements at EVEN indices in the resulting array after removal of index 3 ?
+[2, 3, 1, 4, 0, -1, 2, -2, 10, 8]
+
+**Choices**
+- [ ] 15
+- [x] 8
+- [ ] 10
+- [ ] 12
+
+
+
+After removal of element at index 3, elements are after index 3 has changed their positions:
+Sum of elements at **EVEN** indices from **[0 to 2]** index + Sum of elements at **ODD** indices from **[4 to 9]** = A[0]+A[2]+A[5]+A[7]+A[9] = 2+1+(-1)+(-2)+8 = 8
+
+:::warning
+Please take some time to think about the optimised solution approach on your own before reading further.....
+:::
+
+### Problem 2 : Observation for Optimised Approach
+
+
+* Suppose, we want to check if **i** is a **Special Index**.
+* Indices of elements present on the left side of i will remain intact while indices of elements present on the right side of element i will get changed.
+* Elements which were placed on odd indices will shift on even indices and vice versa.
+
+For example:
+```plaintext
+A[ ] = { 2, 3, 1, 4, 0, -1, 2, -2, 10, 8 }
+```
+Sum of **ODD** indexed elements after removing element at index 3 =
+
+ +
+Sum of **EVEN** indexed elements after removing element at index 3 =
+
+
+
+Sum of **EVEN** indexed elements after removing element at index 3 =
+
+ +
+
+### Approach
+* Create **Prefix Sum** arrays for **ODD** and **EVEN** indexed elements.
+* Run a loop for $i$ from 0 to n – 1, where n is the size of the array.
+* For every element check whether **So** is equal to **Se** or not using the above equations.
+* Increment the count if Se is equal to So.
+
+**NOTE:** Handle the case of $i=0$.
+### Pseudocode
+```cpp
+int count_special_index(int arr[], int n) {
+ // prefix sum for even indexed elements
+ int PSe[n];
+ // prefix sum for odd indexed elements
+ int PSo[n];
+
+ //Say we have already calculated PSe and PSo
+
+ //Code to find Special Indices
+
+ int count = 0;
+ for (int i = 0; i < n; i++) {
+
+ int Se, So;
+
+ if (i == 0) {
+ Se = PSo[n - 1] - PSo[i]; //sum from [i+1 n-1]
+ So = PSe[n - 1] - PSe[i]; //sum from [i+1 n-1]
+ } else {
+ Se = PSe[i - 1] + PSo[n - 1] - PSo[i]; //sum even from [0 to i-1] and odd from [i+1 n-1]
+ So = PSo[i - 1] + PSe[n - 1] - PSe[i]; //sum odd from [0 to i] and even from [i+1 n-1]
+ }
+
+ if (Se == So) {
+ count++;
+ }
+
+ }
+
+ return count;
+}
+```
+
+### Complexity
+
+-- TC - $O(n)$
+-- SC - $O(n)$
+
diff --git a/Academy DSA Typed Notes/Intermediate/Intermediate DSA Bit Manipulations Basics.md b/Academy DSA Typed Notes/Intermediate/Intermediate DSA Bit Manipulations Basics.md
new file mode 100644
index 0000000..c425753
--- /dev/null
+++ b/Academy DSA Typed Notes/Intermediate/Intermediate DSA Bit Manipulations Basics.md
@@ -0,0 +1,484 @@
+
+# Bit Manipulation Basics
+
+## Decimal Number System
+* The decimal system, also known as the base-10 system, is the number system we use in our everyday lives.
+* It is called base-10 because a single digit can take 10 values from 0 to 9.
+
+The position of each digit in a decimal number represents a different power of 10.
+
+For example,
+```cpp
+342 = 300 + 40 + 2 = 3*10^2 + 4*10^1 + 2*10^0
+```
+```cpp
+2563 = 2000 + 500 + 60 + 3 = 2*10^3 + 5*10^2 + 6*10^1 + 3*10^0
+```
+
+---
+## Binary Number System
+* The binary system, also known as the base-2 system, is used in digital electronics and computing.
+* It has only two digits, which are 0 and 1.
+
+In the binary system, each digit represents a different power of 2.
+
+For example,
+```cpp
+110 = 1*2^2 + 1*2^1 + 0*2^0 = 4 + 2 + 0 = 6
+```
+```cpp
+1011 = 1*2^3 + 0*2^2 1*2^1 + 1*2^0 = 8 + 0 + 2 + 1 = 11
+```
+
+---
+### Binary to Decimal Conversion
+For this conversion, we need to multiply each digit of the binary number by the corresponding power of 2, and then add up the results.
+
+**Example 1:**
+Convert binary number 1101 to decimal number.
+
+```
+Starting from the rightmost digit, we have:
+
+1 * 2^0 = 1
+0 * 2^1 = 0
+1 * 2^2 = 4
+1 * 2^3 = 8
+
+Adding up the results, we get:
+
+1 + 0 + 4 + 8 = 13
+
+Therefore, the decimal equivalent of the binary number 1101 is 13.
+```
+
+**Example 2:**
+Convert binary number 10101 to decimal number.
+
+- Starting from the rightmost digit, we have:
+```
+1 * 2^0 = 1
+0 * 2^1 = 0
+1 * 2^2 = 4
+0 * 2^3 = 0
+1 * 2^4 = 16
+```
+- Adding up the results, we get:
+
+```
+1 + 0 + 4 + 0 + 16 = 21
+```
+
+Therefore, the decimal equivalent of the binary number 10101 is 21.
+
+---
+### Question
+What is the decimal representation of this binary number: 1011010
+
+**Choices**
+
+- [ ] 45
+- [x] 90
+- [ ] 94
+- [ ] 130
+
+
+**Explanation:**
+
+Starting from the rightmost digit, we have:
+0 * 2^0 = 0
+1 * 2^1 = 2
+0 * 2^2 = 0
+1 * 2^3 = 8
+1 * 2^4 = 16
+0 * 2^5 = 0
+1 * 2^6 = 64
+Adding up the results, we get: 0 + 2 + 0 + 8 + 16 + 0 + 64 = 90
+Therefore, the decimal representation of the binary number 1011010 is 90.
+
+---
+### Decimal to Binary Conversion
+We can solve it using long division method, for which we need to repeatedly divide the decimal number by 2 and record the remainder until the quotient becomes 0.
+
+**Example:**
+Convert decimal number 20 to binary number.
+
+
+
+### Approach
+* Create **Prefix Sum** arrays for **ODD** and **EVEN** indexed elements.
+* Run a loop for $i$ from 0 to n – 1, where n is the size of the array.
+* For every element check whether **So** is equal to **Se** or not using the above equations.
+* Increment the count if Se is equal to So.
+
+**NOTE:** Handle the case of $i=0$.
+### Pseudocode
+```cpp
+int count_special_index(int arr[], int n) {
+ // prefix sum for even indexed elements
+ int PSe[n];
+ // prefix sum for odd indexed elements
+ int PSo[n];
+
+ //Say we have already calculated PSe and PSo
+
+ //Code to find Special Indices
+
+ int count = 0;
+ for (int i = 0; i < n; i++) {
+
+ int Se, So;
+
+ if (i == 0) {
+ Se = PSo[n - 1] - PSo[i]; //sum from [i+1 n-1]
+ So = PSe[n - 1] - PSe[i]; //sum from [i+1 n-1]
+ } else {
+ Se = PSe[i - 1] + PSo[n - 1] - PSo[i]; //sum even from [0 to i-1] and odd from [i+1 n-1]
+ So = PSo[i - 1] + PSe[n - 1] - PSe[i]; //sum odd from [0 to i] and even from [i+1 n-1]
+ }
+
+ if (Se == So) {
+ count++;
+ }
+
+ }
+
+ return count;
+}
+```
+
+### Complexity
+
+-- TC - $O(n)$
+-- SC - $O(n)$
+
diff --git a/Academy DSA Typed Notes/Intermediate/Intermediate DSA Bit Manipulations Basics.md b/Academy DSA Typed Notes/Intermediate/Intermediate DSA Bit Manipulations Basics.md
new file mode 100644
index 0000000..c425753
--- /dev/null
+++ b/Academy DSA Typed Notes/Intermediate/Intermediate DSA Bit Manipulations Basics.md
@@ -0,0 +1,484 @@
+
+# Bit Manipulation Basics
+
+## Decimal Number System
+* The decimal system, also known as the base-10 system, is the number system we use in our everyday lives.
+* It is called base-10 because a single digit can take 10 values from 0 to 9.
+
+The position of each digit in a decimal number represents a different power of 10.
+
+For example,
+```cpp
+342 = 300 + 40 + 2 = 3*10^2 + 4*10^1 + 2*10^0
+```
+```cpp
+2563 = 2000 + 500 + 60 + 3 = 2*10^3 + 5*10^2 + 6*10^1 + 3*10^0
+```
+
+---
+## Binary Number System
+* The binary system, also known as the base-2 system, is used in digital electronics and computing.
+* It has only two digits, which are 0 and 1.
+
+In the binary system, each digit represents a different power of 2.
+
+For example,
+```cpp
+110 = 1*2^2 + 1*2^1 + 0*2^0 = 4 + 2 + 0 = 6
+```
+```cpp
+1011 = 1*2^3 + 0*2^2 1*2^1 + 1*2^0 = 8 + 0 + 2 + 1 = 11
+```
+
+---
+### Binary to Decimal Conversion
+For this conversion, we need to multiply each digit of the binary number by the corresponding power of 2, and then add up the results.
+
+**Example 1:**
+Convert binary number 1101 to decimal number.
+
+```
+Starting from the rightmost digit, we have:
+
+1 * 2^0 = 1
+0 * 2^1 = 0
+1 * 2^2 = 4
+1 * 2^3 = 8
+
+Adding up the results, we get:
+
+1 + 0 + 4 + 8 = 13
+
+Therefore, the decimal equivalent of the binary number 1101 is 13.
+```
+
+**Example 2:**
+Convert binary number 10101 to decimal number.
+
+- Starting from the rightmost digit, we have:
+```
+1 * 2^0 = 1
+0 * 2^1 = 0
+1 * 2^2 = 4
+0 * 2^3 = 0
+1 * 2^4 = 16
+```
+- Adding up the results, we get:
+
+```
+1 + 0 + 4 + 0 + 16 = 21
+```
+
+Therefore, the decimal equivalent of the binary number 10101 is 21.
+
+---
+### Question
+What is the decimal representation of this binary number: 1011010
+
+**Choices**
+
+- [ ] 45
+- [x] 90
+- [ ] 94
+- [ ] 130
+
+
+**Explanation:**
+
+Starting from the rightmost digit, we have:
+0 * 2^0 = 0
+1 * 2^1 = 2
+0 * 2^2 = 0
+1 * 2^3 = 8
+1 * 2^4 = 16
+0 * 2^5 = 0
+1 * 2^6 = 64
+Adding up the results, we get: 0 + 2 + 0 + 8 + 16 + 0 + 64 = 90
+Therefore, the decimal representation of the binary number 1011010 is 90.
+
+---
+### Decimal to Binary Conversion
+We can solve it using long division method, for which we need to repeatedly divide the decimal number by 2 and record the remainder until the quotient becomes 0.
+
+**Example:**
+Convert decimal number 20 to binary number.
+ +
+
+---
+### Question
+
+What is the binary representation of 45 ?
+
+**Choices**
+
+- [ ] 101100
+- [ ] 101110
+- [ ] 101111
+- [x] 101101
+
+
+**Explanation:** Here are the steps to convert decimal number 45 to binary:
+
+
+
+---
+### Question
+
+What is the binary representation of 45 ?
+
+**Choices**
+
+- [ ] 101100
+- [ ] 101110
+- [ ] 101111
+- [x] 101101
+
+
+**Explanation:** Here are the steps to convert decimal number 45 to binary:
+ +
+---
+### Addition of Decimal Numbers
+**Example -**
+```cpp
+Calculate => (368 + 253)
+```
+
+
+---
+### Addition of Decimal Numbers
+**Example -**
+```cpp
+Calculate => (368 + 253)
+```
+ +
+
+### Stack
+
+
+
+
+
+### Stack
+
+
+ +
+:::success
+There are a lot of quizzes in this session, please take some time to think about the solution on your own before reading further.....
+:::
+
+---
+### Introduction to call stack
+
+#### Example 1
+Consider the below code:
+```java
+int add(int x, int y) {
+ return x + y;
+}
+
+int product(int x, int y) {
+ return x * y;
+}
+
+int subtract(int x, int y) {
+ return x - y;
+}
+
+public static void main() {
+ int x = 10;
+ int y = 20;
+ int temp1 = add(x, y);
+ int temp2 = product(x, y);
+ int temp3 = subtract(x, y);
+ System.out.println(temp1 + temp2 + temp3);
+}
+```
+
+Following is the call stack execution for above code:
+
+
+
+
+:::success
+There are a lot of quizzes in this session, please take some time to think about the solution on your own before reading further.....
+:::
+
+---
+### Introduction to call stack
+
+#### Example 1
+Consider the below code:
+```java
+int add(int x, int y) {
+ return x + y;
+}
+
+int product(int x, int y) {
+ return x * y;
+}
+
+int subtract(int x, int y) {
+ return x - y;
+}
+
+public static void main() {
+ int x = 10;
+ int y = 20;
+ int temp1 = add(x, y);
+ int temp2 = product(x, y);
+ int temp3 = subtract(x, y);
+ System.out.println(temp1 + temp2 + temp3);
+}
+```
+
+Following is the call stack execution for above code:
+
+
+ +
+
+**Ouput:** 220
+
+#### Example 2
+Consider the below code:
+```java
+int add(int x, int y) {
+ return x + y;
+}
+
+public static void main() {
+ int x = 10;
+ int y = 20;
+ int temp1 = add(x, y);
+ int temp2 = add(temp1, 30);
+ int temp3 = add(temp2, 40);
+ System.out.println(temp3);
+}
+```
+Following is the call stack execution for above code:
+
+
+
+
+
+**Ouput:** 220
+
+#### Example 2
+Consider the below code:
+```java
+int add(int x, int y) {
+ return x + y;
+}
+
+public static void main() {
+ int x = 10;
+ int y = 20;
+ int temp1 = add(x, y);
+ int temp2 = add(temp1, 30);
+ int temp3 = add(temp2, 40);
+ System.out.println(temp3);
+}
+```
+Following is the call stack execution for above code:
+
+
+ +
+
+**Output:** 100
+
+#### Example 3
+Consider the below code:
+```java
+int add(int x, int y) {
+ return x + y;
+}
+
+static int fun(int a, int b) {
+ int sum = add(a, b);
+ int ans = sum * 10;
+ return ans;
+}
+static void extra(int w){
+ System.out.println("Hello");
+ System.out.println(w);
+}
+public static void main() {
+ int x = 10;
+ int y = 20;
+ int z = fun(x, y);
+ System.out.println(z);
+ extra(z);
+}
+```
+
+Following is the call stack execution for above code:
+
+
+
+**Output:** 100
+
+#### Example 3
+Consider the below code:
+```java
+int add(int x, int y) {
+ return x + y;
+}
+
+static int fun(int a, int b) {
+ int sum = add(a, b);
+ int ans = sum * 10;
+ return ans;
+}
+static void extra(int w){
+ System.out.println("Hello");
+ System.out.println(w);
+}
+public static void main() {
+ int x = 10;
+ int y = 20;
+ int z = fun(x, y);
+ System.out.println(z);
+ extra(z);
+}
+```
+
+Following is the call stack execution for above code:
+ +
+
+
+**Output:**
+```plaintext
+300
+Hello
+310
+```
+
+---
+
+### Types of Memory in Java
+Following are the types of memory present in Java -
+1. **Stack** -
+
+
+
+**Output:**
+```plaintext
+300
+Hello
+310
+```
+
+---
+
+### Types of Memory in Java
+Following are the types of memory present in Java -
+1. **Stack** -All the primitive data type and reference will be stored in stack. +2. **Heap** -
Container of that reference is stored in heap. Arrays, ArrayList, Objects are created inside heap. + +**Example 1** +Consider the below code: +```java +public static void main() { + int x = 10; + int[] ar = new int[3]; + System.out.println(ar); // #ad1 + System.out.println(ar[2]); // 0 + ar[1] = 7; +} +``` +Now, lets analyze the given code - + +
 +
+
+
+**Note**:
+1. **Primitive data types:** [int, float, double, char, boolean, long] memory will be assigned in stack.
+2. **Reference/ address of the container:** will be stored in stack.
+3. **Container:** [Array/ Arraylist] will be stored in heap.
+
+**Example 2**
+Consider the below code:
+```java
+public static void main() {
+ int x = 10;
+ int[] ar = new int[3];
+ int[] ar2 = ar;
+ System.out.println(ar); // 4k
+ System.out.println(ar2); // 4k
+}
+```
+Now, lets analyze the given code -
+
+
+
+
+
+**Note**:
+1. **Primitive data types:** [int, float, double, char, boolean, long] memory will be assigned in stack.
+2. **Reference/ address of the container:** will be stored in stack.
+3. **Container:** [Array/ Arraylist] will be stored in heap.
+
+**Example 2**
+Consider the below code:
+```java
+public static void main() {
+ int x = 10;
+ int[] ar = new int[3];
+ int[] ar2 = ar;
+ System.out.println(ar); // 4k
+ System.out.println(ar2); // 4k
+}
+```
+Now, lets analyze the given code -
+
+ +
+
+
+
+**Example 3**
+Consider the below code:
+```java
+public static void main() {
+ int[] ar = new int[3];
+ System.out.println(ar); // 5k
+ ar[1] = 9;
+ ar[2] = 5;
+
+ ar = new int[5];
+ System.out.println(ar); // 7k
+}
+```
+Now, lets analyze the given code -
+
+
+
+
+
+
+**Example 3**
+Consider the below code:
+```java
+public static void main() {
+ int[] ar = new int[3];
+ System.out.println(ar); // 5k
+ ar[1] = 9;
+ ar[2] = 5;
+
+ ar = new int[5];
+ System.out.println(ar); // 7k
+}
+```
+Now, lets analyze the given code -
+
+ +
+
+**Example 4**
+Consider the below code:
+```java
+static void fun(int[] a){
+ System.out.println(a); // 9k
+ a[1] = 5;
+}
+public static void main() {
+ int[] ar = new int[3];
+ System.out.println(ar); // 9k
+ ar[0] = 90;
+ ar[1] = 50;
+ fun(ar);
+ System.out.println(ar[1]); // 5
+}
+```
+Now, lets analyze the given code -
+
+
+
+
+**Example 4**
+Consider the below code:
+```java
+static void fun(int[] a){
+ System.out.println(a); // 9k
+ a[1] = 5;
+}
+public static void main() {
+ int[] ar = new int[3];
+ System.out.println(ar); // 9k
+ ar[0] = 90;
+ ar[1] = 50;
+ fun(ar);
+ System.out.println(ar[1]); // 5
+}
+```
+Now, lets analyze the given code -
+
+ +
+
+**Example 5**
+Consider the below code:
+```java
+public static void main() {
+ float y = 7.84f;
+ int[][] mat = new int[3][4];
+ System.out.println(mat); // 9k
+ System.out.println(mat[1]); // 3k
+ System.out.println(mat[1][3]); // 0
+}
+```
+Now, lets analyze the given code -
+
+
+
+
+
+**Example 5**
+Consider the below code:
+```java
+public static void main() {
+ float y = 7.84f;
+ int[][] mat = new int[3][4];
+ System.out.println(mat); // 9k
+ System.out.println(mat[1]); // 3k
+ System.out.println(mat[1][3]); // 0
+}
+```
+Now, lets analyze the given code -
+
+
+ +
+
+
+**Example 6**
+Consider the below code:
+```java
+static void sum(int[][] mat){
+ System.out.println(mat); // 2k
+ System.out.println(mat[0][0] + mat[1][0]); // 40
+}
+public static void main() {
+ int[][] mat = new int[2][3];
+ mat[0][0] = 15;
+ mat[1][0] = 25;
+ sum(mat);
+}
+```
+Now, lets analyze the given code -
+
+
+
+
+
+
+**Example 6**
+Consider the below code:
+```java
+static void sum(int[][] mat){
+ System.out.println(mat); // 2k
+ System.out.println(mat[0][0] + mat[1][0]); // 40
+}
+public static void main() {
+ int[][] mat = new int[2][3];
+ mat[0][0] = 15;
+ mat[1][0] = 25;
+ sum(mat);
+}
+```
+Now, lets analyze the given code -
+
+
+ +
+
+
+
+**Example 7**
+
+Consider the below code:
+```java
+static int sumOfRow(int[] arr){
+ System.out.println(arr); // 7k
+ int sum = 0;
+ for (int i = 0; i < arr.length; i++){
+ sum = sum + arr[i];
+ }
+ return sum;
+}
+
+public static void main() {
+ int[][] mat = new int[2][3];
+ mat[0][0] = 9;
+ mat[0][1] = 5;
+ mat[0][2] = 1;
+ int ans = sumOfRow(mat[0]); // 7k
+ System.out.println(ans); // 15
+}
+```
+Now, lets analyze the given code -
+
+
+
+
+
+
+**Example 7**
+
+Consider the below code:
+```java
+static int sumOfRow(int[] arr){
+ System.out.println(arr); // 7k
+ int sum = 0;
+ for (int i = 0; i < arr.length; i++){
+ sum = sum + arr[i];
+ }
+ return sum;
+}
+
+public static void main() {
+ int[][] mat = new int[2][3];
+ mat[0][0] = 9;
+ mat[0][1] = 5;
+ mat[0][2] = 1;
+ int ans = sumOfRow(mat[0]); // 7k
+ System.out.println(ans); // 15
+}
+```
+Now, lets analyze the given code -
+
+ +
+### Question
+Predict the Output :
+```Java
+static void change(int a) {
+ a = 50;
+}
+
+public static void main(String args[]) {
+ int a = 10;
+ change(a);
+ System.out.println(a);
+}
+```
+
+
+**Choices**
+- [x] 10
+- [ ] 50
+- [ ] Error
+
+
+
+**Explanation**
+
+
+
+
+### Question
+Predict the Output :
+```Java
+static void change(int a) {
+ a = 50;
+}
+
+public static void main(String args[]) {
+ int a = 10;
+ change(a);
+ System.out.println(a);
+}
+```
+
+
+**Choices**
+- [x] 10
+- [ ] 50
+- [ ] Error
+
+
+
+**Explanation**
+
+
+ +
+
+
+* The parameter variable 'a' of change function is reassigned to the value of 50, because both the functions have their own variables, so the variable "a" of main function is different than of variable "a" in change function.
+* Stack changes are temporary.
+
+---
+### Question
+Predict the output :
+```java
+static void change(int[]a) {
+ a[0] = 50;
+}
+
+public static void main(String args[]) {
+ int[]a = {10};
+ change(a);
+ System.out.println(a[0]);
+}
+```
+
+**Choices**
+- [ ] 10
+- [x] 50
+- [ ] Error
+
+---
+
+**Explanation:**
+
+* The array a in change method and main method both refer to the same array object in the heap.
+* Heap changes are permanent changes.
+
+
+
+
+
+
+* The parameter variable 'a' of change function is reassigned to the value of 50, because both the functions have their own variables, so the variable "a" of main function is different than of variable "a" in change function.
+* Stack changes are temporary.
+
+---
+### Question
+Predict the output :
+```java
+static void change(int[]a) {
+ a[0] = 50;
+}
+
+public static void main(String args[]) {
+ int[]a = {10};
+ change(a);
+ System.out.println(a[0]);
+}
+```
+
+**Choices**
+- [ ] 10
+- [x] 50
+- [ ] Error
+
+---
+
+**Explanation:**
+
+* The array a in change method and main method both refer to the same array object in the heap.
+* Heap changes are permanent changes.
+
+
+ +
+
+
+---
+### Question
+Predict the output :
+```java
+static void test(int[]a) {
+ a = new int[1];
+ a[0] = 50;
+}
+
+public static void main(String args[]) {
+ int[]a = {10};
+ test(a);
+ System.out.println(a[0]);
+}
+```
+
+
+**Choices**
+- [x] 10
+- [ ] 50
+- [ ] Error
+
+---
+**Explanation:**
+Inside the test method, a new integer array with length 1 is allocated on the heap memory, and the reference to this array is assigned to the parameter variable a. Hence, now the variable 'a' inside test function and main function point to different references.Heap changes are permanent.
+
+
+
+
+
+---
+### Question
+Predict the output :
+```java
+static void test(int[]a) {
+ a = new int[1];
+ a[0] = 50;
+}
+
+public static void main(String args[]) {
+ int[]a = {10};
+ test(a);
+ System.out.println(a[0]);
+}
+```
+
+
+**Choices**
+- [x] 10
+- [ ] 50
+- [ ] Error
+
+---
+**Explanation:**
+Inside the test method, a new integer array with length 1 is allocated on the heap memory, and the reference to this array is assigned to the parameter variable a. Hence, now the variable 'a' inside test function and main function point to different references.Heap changes are permanent.
+
+ +
+
+
+
+---
+### Question
+
+Predict the output:
+```java
+static void fun(int[] a) {
+ a = new int[1];
+ a[0] = 100;
+}
+public static void main() {
+ int[] a = {10, 20, 30};
+ fun(a);
+ System.out.println(a[0]);
+}
+
+```
+
+**Choices**
+- [x] 10
+- [ ] 100
+- [ ] Error
+- [ ] inky pinky po
+
+**Explanation:**
+
+Inside the fun method, a new integer array with length 1 is allocated on the heap memory, and the reference to this array is assigned to the parameter variable a. Hence, now the variable 'a' inside test function and main function point to different references.
+
+
+
+
+
+
+---
+### Question
+
+Predict the output:
+```java
+static void fun(int[] a) {
+ a = new int[1];
+ a[0] = 100;
+}
+public static void main() {
+ int[] a = {10, 20, 30};
+ fun(a);
+ System.out.println(a[0]);
+}
+
+```
+
+**Choices**
+- [x] 10
+- [ ] 100
+- [ ] Error
+- [ ] inky pinky po
+
+**Explanation:**
+
+Inside the fun method, a new integer array with length 1 is allocated on the heap memory, and the reference to this array is assigned to the parameter variable a. Hence, now the variable 'a' inside test function and main function point to different references.
+
+ +
+
+
+
+---
+
+### Question
+Predict the output :
+```java
+static void swap(int a,int b) {
+ int temp = a;
+ a = b;
+ b = temp;
+}
+
+public static void main(String args[]) {
+ int a = 10;
+ int b = 20;
+ swap(a,b);
+ System.out.println(a + " " + b);
+}
+```
+
+
+**Choices**
+- [x] 10 20
+- [ ] 20 10
+- [ ] 10 10
+- [ ] Error
+
+**Explanation:**
+
+* Swap function is called by value not by reference.
+* So, the changes made in the swap function are temporary in the memory stack.
+* Once we got out of the swap function, the changes will go because they are made in temporary variables.
+* Hence no swapping is done and variable have the same value as previous.
+
+
+
+
+
+
+---
+
+### Question
+Predict the output :
+```java
+static void swap(int a,int b) {
+ int temp = a;
+ a = b;
+ b = temp;
+}
+
+public static void main(String args[]) {
+ int a = 10;
+ int b = 20;
+ swap(a,b);
+ System.out.println(a + " " + b);
+}
+```
+
+
+**Choices**
+- [x] 10 20
+- [ ] 20 10
+- [ ] 10 10
+- [ ] Error
+
+**Explanation:**
+
+* Swap function is called by value not by reference.
+* So, the changes made in the swap function are temporary in the memory stack.
+* Once we got out of the swap function, the changes will go because they are made in temporary variables.
+* Hence no swapping is done and variable have the same value as previous.
+
+ +
+
+
+
+---
+### Question
+Predict the output :
+```java
+static void swap(int[]a,int[]b) {
+ int temp = a[0];
+ a[0] = b[0];
+ b[0] = temp;
+}
+
+public static void main(String args[]) {
+ int[]a = {10};
+ int[]b = {20};
+ swap(a,b);
+ System.out.println(a[0] + " " + b[0]);
+}
+```
+**Choices**
+- [ ] 10 20
+- [x] 20 10
+- [ ] 10 10
+- [ ] Error
+
+**Explanation:**
+Inside swap function, the array variables 'a' & 'b' are passed by reference, so they are pointing to same references in the heap memory as of 'a' & 'b' variables inside main function.
+
+
+
+
+
+
+---
+### Question
+Predict the output :
+```java
+static void swap(int[]a,int[]b) {
+ int temp = a[0];
+ a[0] = b[0];
+ b[0] = temp;
+}
+
+public static void main(String args[]) {
+ int[]a = {10};
+ int[]b = {20};
+ swap(a,b);
+ System.out.println(a[0] + " " + b[0]);
+}
+```
+**Choices**
+- [ ] 10 20
+- [x] 20 10
+- [ ] 10 10
+- [ ] Error
+
+**Explanation:**
+Inside swap function, the array variables 'a' & 'b' are passed by reference, so they are pointing to same references in the heap memory as of 'a' & 'b' variables inside main function.
+
+ +
+
+
+---
+### Question
+Predict the output :
+```java
+static int[] fun(int[]a) {
+ a = new int[2];
+ a[0] = 50; a[1] = 60;
+ return a;
+}
+
+public static void main(String args[]) {
+ int[]a = {10,20,30};
+ a = fun(a);
+ System.out.println(a[0]);
+}
+```
+
+**Choices**
+- [ ] 10
+- [x] 50
+- [ ] Error
+
+
+
+**Explanation:**
+* When fun method is called on array a, then a new integer array is allocated on the heap memory.
+* But since, we are returning the new array in the main method, so now the changes done in fun method persists.
+
+
+
+
+
+---
+### Question
+Predict the output :
+```java
+static int[] fun(int[]a) {
+ a = new int[2];
+ a[0] = 50; a[1] = 60;
+ return a;
+}
+
+public static void main(String args[]) {
+ int[]a = {10,20,30};
+ a = fun(a);
+ System.out.println(a[0]);
+}
+```
+
+**Choices**
+- [ ] 10
+- [x] 50
+- [ ] Error
+
+
+
+**Explanation:**
+* When fun method is called on array a, then a new integer array is allocated on the heap memory.
+* But since, we are returning the new array in the main method, so now the changes done in fun method persists.
+
+ +
+
+
+---
+### Question
+Predict the output :
+```java
+static void test(int[]a) {
+ a = new int[2];
+ a[0] = 94;
+}
+
+public static void main(String args[]) {
+ int[]a = {10,20,30};
+ test(a);
+ System.out.println(a[0]);
+}
+```
+
+
+**Choices**
+- [x] 10
+- [ ] 94
+- [ ] Error
+
+**Explanation:**
+
+Inside the test function, a new integer array with length 2 is allocated on the heap memory, and the reference to this array is assigned to the parameter variable a. Hence, now the variable 'a' inside test function and main function point to different references.
+
+
+
+
+
+---
+### Question
+Predict the output :
+```java
+static void test(int[]a) {
+ a = new int[2];
+ a[0] = 94;
+}
+
+public static void main(String args[]) {
+ int[]a = {10,20,30};
+ test(a);
+ System.out.println(a[0]);
+}
+```
+
+
+**Choices**
+- [x] 10
+- [ ] 94
+- [ ] Error
+
+**Explanation:**
+
+Inside the test function, a new integer array with length 2 is allocated on the heap memory, and the reference to this array is assigned to the parameter variable a. Hence, now the variable 'a' inside test function and main function point to different references.
+
+ +
diff --git a/Academy DSA Typed Notes/Intermediate/Intermediate DSA Sorting Basics.md b/Academy DSA Typed Notes/Intermediate/Intermediate DSA Sorting Basics.md
new file mode 100644
index 0000000..f48ace7
--- /dev/null
+++ b/Academy DSA Typed Notes/Intermediate/Intermediate DSA Sorting Basics.md
@@ -0,0 +1,454 @@
+# Sorting
+
+## Introduction
+
+
+**Sorting** is an arrangement of data in particular order on the basis of some parameter
+
+### Example 1:
+```
+ A[ ] = { 2, 3, 9, 12, 17, 19 }
+```
+
+The above example is sorted in ascending order on the basis of magnitude.
+
+### Example 2:
+```
+ A[ ] = { 19, 6, 5, 2, -1, -19 }
+```
+
+The above example is sorted in descending order on the basis of magnitude.
+
+
+
+### Question
+Is the array { 1, 13, 9 , 6, 12 } sorted ?
+
+**Choices**
+- [x] Yes
+- [ ] No
+
+
+In the above quiz, array is sorted in ascending order on the basis of count of factors. Count of factors for the above array is { 1, 2, 3, 4, 6 }.
+
+
+
+**Sorting** is essential for organizing, analyzing, searching, and presenting data efficiently and effectively in various applications and contexts.
+
+### Problem 1 : Minimize the cost to empty array
+
+
+Given an array of **n** integers, minimize the cost to empty given array where cost of removing an element is equal to **sum of all elements left in an array**.
+
+### Example 1
+
+```plaintext
+A[ ] = { 2, 1, 4 }
+Ans = 11
+```
+
+**Explanation**
+After removing 4 cost = 4+2+1 = 7
+After removing 2 cost = 2+1 = 3
+After removing 1 cost = 1 = 1
+
+Total cost = 11
+
+
+### Question
+Minimum cost to remove all elements from array {4, 6, 1} ?
+
+**Choices**
+- [ ] 11
+- [ ] 15
+- [x] 17
+- [ ] 21
+
+
+
+After removing 6 cost = 4+6+1 = 11
+After removing 4 cost = 4+1 = 5
+After removing 1 cost = 1 = 1
+
+Total cost = 17
+
+
+### Question
+Minimum cost to remove all elements from array[] = {3, 5, 1, -3}
+
+**Choices**
+- [ ] 4
+- [x] 2
+- [ ] 0
+- [ ] 18
+
+
+
+After removing 5 cost = 5+3+1+(-3) = 6
+After removing 3 cost = 3+1+(-3) = 1
+After removing 1 cost = 1+(-3) = -2
+After removing -3 cost = -3) = -3
+
+Total cost = 2
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Problem 1 Solution Approach
+
+**Observation**
+* Start removing from the largest element.
+
+
+
+Here we can see if we have to minimise the cost we should add the largest number minimum number of times, that implies it should be the first one to be removed.
+The formula would be **$\sum$(i+1)\*arr[i]** where **i** is the index.
+
+Follow the below steps to solve the problem.
+* **Sort** the data in descending order.
+* Initialise the **ans** equal to 0.
+* Run a loop for i from 0 to **n** – 1, where **n** is the size of the array.
+* For every element add **arr[i]\*i** to the ans.
+
+#### Pseudocode
+```cpp
+int calculate_cost(int arr[], int n) {
+ reverse_sort(arr);
+ int ans = 0;
+ for (int i = 0; i < n; i++) {
+ ans += i * arr[i];
+ }
+
+ return ans;
+}
+```
+
+#### Time and Space Complexity
+
+-- TC - O(nlogn)
+-- SC - O(n)
+
+### Problem 2 : Find count of Noble Integers
+
+
+Given an array of distinct elements of size n, find the count of **noble integers**.
+
+> Note: arr[i] is **noble** if count of elements smaller than arr[i] is equal to arr[i] where arr[i] is element at index i.
+
+**Example 1**
+
+```plaintext
+A[ ] = { 1, -5, 3, 5, -10, 4}
+Ans = 3
+```
+
+**Explanation**
+For arr[2] there are three elements less than 3 that is 1, -5 and -10. So arr[0] is noble integer.
+For arr[3] there are five elements less than 5 that is 1, 3, 4, 5, -5 and -10. So arr[3] is noble integer.
+For arr[5] there are four elements less than 4 that is 1, 3, -5 and -10. So arr[5] is noble integer.
+
+In total there are 3 noble elements.
+
+
+### Question
+Count the number of noble integers in the array. A = { -3, 0, 2 , 5 }
+
+**Choices**
+- [ ] 0
+- [x] 1
+- [ ] 2
+- [ ] 3
+
+
+
+**Explanation:**
+For arr[2] there are two elements less than 2 that is -3 and 0. So arr[2] is noble integer.
+In total there are 2 noble elements.
+
+:::warning
+Please take some time to think about the Brute Force solution approach on your own before reading further.....
+:::
+
+### Problem 2 : Bruteforce Solution
+
+#### Observation
+Iterate through every element in the array, for every element count the number of smaller elements.
+
+#### Pseudocode
+```cpp
+int find_nobel_integers(int arr[], int n) {
+ int ans = 0;
+ for (int i = 0; i < n; i++) {
+ int count = 0;
+ for (int j = 0; j < n; j++) {
+ if (arr[j] < arr[i])
+ count++;
+ }
+ if (count == arr[i]) {
+ ans++;
+ }
+ }
+ return ans;
+}
+```
+
+#### Time and Space Complexity
+-- TC - O(N^2)
+-- SC - O(1)
+
+### Problem 1 Optimised Solution
+
+#### Optimised Solution - 1
+
+* Hint 1: What is the extra work being done?
+Expected: For every element, we are using an extra loop for calculating the count of smaller elements.
+* Hint 2: Can sorting the array help here?
+
+#### Observation:
+ If we sort the data all elements smaller than the element at index i will be on from index **0 to i-1**. So total number of smaller elements will be equal to **i**.
+
+#### Pseudocode
+```cpp
+
+int find_nobel_integers(int arr[], int n) {
+ sort(arr);
+ int ans = 0;
+ for (int i = 0; i < n; i++) {
+ if (arr[i] == i) {
+ ans = ans + 1;
+ }
+ }
+ return ans;
+}
+```
+
+#### Time and Space Complexity
+-- TC - O(nlogn)
+-- SC - O(1)
+
+### Problem 3 Find count of nobel integers (Not Distinct)
+
+Given an array of size n, find the count of noble integers.
+> Note: Same as previous question, but all elements need not to be distinct
+
+### Question
+
+Count the no of noble integers in the array. A = { -10, 1, 1, 3, 100 }
+
+**Choices**
+- [ ] 1
+- [x] 3
+- [ ] 2
+- [ ] 4
+
+
+**Explanation:**
+For arr[1] and arr[2] there is one element less than 1. So arr[1] and arr[2] are noble integers.
+Similarly arr[3] will be the npble lement as there are 3 elements less than 3.
+So in total 3 elements are noble integers.
+
+### Question
+Count the no of noble integers in the array
+A = { -10, 1, 1, 2, 4, 4, 4, 8, 10 }
+
+**Choices**
+- [ ] 4
+- [x] 5
+- [ ] 6
+- [ ] 7
+
+
+
+**Explanation:**
+arr[1], arr[2], arr[4], arr[5], arr[6] are the noble elements here.
+
+
+### Question
+Count the no of noble integers in the array
+A = { -3, 0, 2, 2, 5, 5, 5, 5, 8, 8, 10, 10, 10, 14 }
+
+**Choices**
+- [ ] 4
+- [ ] 5
+- [ ] 6
+- [x] 7
+
+
+**Explanation:**
+For arr[8] and arr[9] there are eight elements less than 8 that is -3, 0, 2, 5. So arr[8] and arr[9] are noble integers.
+Similarly arr[9], arr[10], arr[11], ar[12] are noble elements.
+So in total 6 elements are noble integers.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Problem 3 Solution
+#### Observation
+* If the current element is same as previous element then the total number of smaller elements will be same as previous element.
+* If current element is not equal to previous element then the total number of smaller elements is equal to its index.
+
+#### Pseudocode
+```cpp
+
+int find_nobel_integers(int arr[], int n) {
+ sort(arr);
+ int count = 0, ans = 0;
+ if (arr[0] == 0) ans++;
+
+ for (int i = 1; i < n; i++) {
+ if (arr[i] != arr[i - 1])
+ count = i;
+
+ if (count == arr[i])
+ ans++;
+ }
+ return ans;
+}
+```
+
+#### Time and Space Complexity
+-- TC - O(nlogn)
+-- SC - O(1)
+
+## Sorting Algorithm - Selection Sort
+
+
+A sorting algorithm is a method of reorganizing the elements in a meaningful order.
+
+> Imagine this. You are asked to arrange students according to their increasing heights.
+
+**Divide the queue of students into two parts – arranged and unarranged.**
+
+1. To begin with, place all the students in the unarranged queue.
+2. From this unarranged queue, search for the shortest student and place him/her in the list of arranged students.
+3. Again, from the unarranged queue, select the second-shortest student. Place this student in the arranged queue, just after the smallest student.
+4. Repeat the above-given steps until all the students are placed into the arranged queue.
+
+**Did you see what we just did here?**
+We used the selection sort algorithm to arrange all the students in a height-wise order.
+
+
+**To better understand selection sort, let's consider a list of Integers 5, 6, 4, 2.**
+
+
+The steps to sort this list would involve –
+
+
+
+
+#### Pseudocode:
+
+```cpp
+void selectionSort(int arr[], int size) {
+ int i, j, minIndex;
+
+ for (i = 0; i < size - 1; i++) {
+
+ // set minIndex equal to the first unsorted element
+ minIndex = i;
+
+ //iterate over unsorted sublist and find the minimum element
+ for (j = i + 1; j < size; j++) {
+
+ if (arr[j] < arr[minIndex]) {
+ minIndex = j;
+ }
+
+ }
+
+ // swapping the minimum element with the element at minIndex to place it at its correct position
+ swap(arr[minIndex], arr[i]);
+ }
+}
+```
+
+#### TC & SC
+
+**Time Complexity:** O(N2) since we have to iterate entire list to search for a minimum element everytime.
+For 1 element, N iterations,
+For N elements, N2 iterations.
+
+**Space Complexity:** O(1)
+
+## Sorting Algorithm - Insertion Sort
+
+**Insertion Sort** is one of the simplest sorting techniques which you might have used in your daily lives while arranging a deck of cards.
+
+> So without going into how this algorithm works, let’s think about how you would usually go about arranging the deck of cards?
+
+**Say you are given 10 cards, 1 to 10 of spades, all shuffled, and you want to sort these cards.**
+
+1. You would basically pick any random card(e.g. 7), and place it into your left hand, assuming the left hand is meant to carry the sorted cards.
+2. Then you would pick another random card, say 2, and place 2 in the correct position on your left hand, i.e. before 7.
+3. Then again if you pick 5, you would place it between 2 and 7 on your left hand, and this way we know we are able to sort our deck of cards. Since we insert one element at a time in its correct position, hence its name “Insertion Sort”.
+
+#### Dry Run
+
+E.g. if elements were in order:
+
+```3, 5, 2```
+
+You can start by picking 3, and since there is no element to the left of 3, we can assume it is in the correct place.
+Array:
+
+```3, 5, 2```
+
+You can pick 5, you compare 5 with 3, and you find 5 is in the correct order amongst the array of [3, 5].
+Array:
+
+```3, 5, 2```
+
+Then you pick 2, you find the place in the left side array of [3,5] to place this 2. Since 2 must come before 3, we insert 2 before 3.
+Array:
+
+```2, 3, 5 →```
+
+Which is a sorted order.
+
+
+#### Approach
+
+Line 2: We don’t process the first element, as it has nothing to compare against.
+Line 3: Loop from i=1 till the end, to process each element.
+Line 4: Extract the element at position i i.e. array[i]. Let it be called E.
+Line 5: To compare E with its left elements, loop j from i-1 to 0
+Line 6, 7: Compare E with the left element, if E is lesser, then move array[j] to right by 1.
+Line 8: Once we have found the position for E, place it there.
+
+#### Pseudocode
+
+```cpp
+void insertionSort(int arr[], int n) {
+ for (int i = 1; i < n; i++) { // Start from 1 as arr[0] is always sorted
+ Int currentElement = arr[i];
+ Int j = i - 1;
+ // Move elements of arr[0..i-1], that are greater than key,
+ // to one position ahead of their current position
+ while (j >= 0 && arr[j] > currentElement) {
+ arr[j + 1] = arr[j];
+ j = j - 1;
+ }
+ // Finally place the Current element at its correct position.
+ arr[j + 1] = currentElement;
+ }
+}
+```
+
+#### TC & SC
+
+**Time Complexity:**
+
+**Worst Case:** O(N^2), when the array is sorted in reverse order.
+
+**Best Case:** O(N), when the data is already sorted in desied order, in that case there will be no swap.
+
+Space Complexity: O(1)
+
+**Note**
+
+1. Both Selection & Insertion are in-place sorting algorithms, means they don't need extra space.
+2. Since the time complexity of both can go to O(N^2), it is only useful when we have a lesser number of elements to sort in an array.
+
+
diff --git a/Academy DSA Typed Notes/Intermediate/Intermediate DSA Strings.md b/Academy DSA Typed Notes/Intermediate/Intermediate DSA Strings.md
new file mode 100644
index 0000000..52942f7
--- /dev/null
+++ b/Academy DSA Typed Notes/Intermediate/Intermediate DSA Strings.md
@@ -0,0 +1,382 @@
+
+# String
+
+A string can be defined as a sequence of characters or in other words we can say that it is an array of characters.
+
+**Example**
+Below are the examples of string:
+```
+"Welcome to Scaler"
+"Hello World!"
+```
+**Note:** String is represented using double quote i.e, `""`. All the characters of string must be inside this quote.
+
+**Character**
+A character is a single symbol that represents a letter, number, or other symbol in a computer's character set. Characters are used to represent textual data, and they are typically represented using its ASCII value.
+
+**Example**
+```
+'a'
+'B'
+'1'
+'_'
+```
+
+Computer store everything in binary. So, how do we store strings in computer?
+
+Each character has corresponding decimal value associated to it which is known as ASCII value.
+
+**'A' to 'Z'** have ASCII from **65 to 90**
+**'a' to 'z'** have ASCII from **97 to 122**
+**'0' to '9'** have ASCII from **48 to 57**
+
+Each character '?', '!', '\*', ... has a corresponding ASCII associated with it.
+
+### Some Operations:
+**Note:** Characters can also be printed using its ascii value. for example, the ascii value of 'A' is 65, so it can be printed as
+```CPP
+char ch = (char)65;
+print(ch);
+/*
+character 'A' gets printed; we are assigning Integer to Char,hence in some languages typecasting will be required.
+*/
+```
+
+```cpp=
+char ch = (char)('a' + 1);
+/*
+When we do arithmetic operations on characters, automatically computations happen on their ASCII values.
+ */
+print(ch); //'b' will get printed
+```
+
+```cpp=
+int x = 'a';
+/*
+No need to typecast since we are assigning Char to Int (smaller data type to bigger, so it will not overflow)
+*/
+print(x); //97 will be printed
+
+```
+
+
+
+## Question 1 : Switch cases
+
+
+Given a string consisting of only alphabets(either lowercase or uppercase). Print all the characters of string in such a way that for all lowercase character, print its uppercase character and for all uppercase character, print its lowercase character.
+
+**TestCase**
+**Input**
+```
+"Hello"
+```
+**Output**
+```
+"hELLO"
+```
+**Explanation**
+
+Here, there is only one uppercase character present in the string i.e, 'H' so convert it to lowercase character. All other characters are in lowercase, hence they are converted into uppercase characters.
+
+
+
+### Question
+What is the output for String = "aDgbHJe" ?
+
+**Choices**
+- [ ] ADGBHJE
+- [ ] aDgbHJe
+- [x] AdGBhjE
+- [ ] adgbhje
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+**Observation**
+The key observations are:
+* Lowercase characters can be changed into uppercase by subtracting 32 from its ASCII values.
+* Uppercase charactes can be changed into lowercase by adding 32 from its ASCII values.
+
+The above points are derived from the fact that for every alphabet, the difference between its ascii value in lowercase and uppercase is 32.
+
+#### Pseudocode
+```cpp
+Function toggle(char s[]) {
+ int n = s.size();
+ for (int i = 0; i < n; i++) {
+ if (s[i] >= 65 and s[i] <= 91) {
+ print(s[i] + 32);
+ } else {
+ print(s[i] - 32);
+ }
+ }
+}
+```
+#### Complexity
+Time Complexity- **O(N)**.
+Space Complexity- **O(1)**.
+
+
+## Substring
+A substring is a contiguous sequence of characters within a string. A substring concept in string is similar to subarray concept in array.
+
+**A substring can be:**
+1. Continous part of string.
+2. Full string can be a substring.
+3. A single character can also be a subsring.
+
+**Example**
+
+Suppose, we have a string as
+```
+"abc"
+```
+There are total 6 substring can be formed from the above string. All substrings are
+```
+"a"
+"b"
+"c"
+"ab"
+"bc"
+"abc"
+```
+### Question
+How many total substrings will be there for the String "bxcd" ?
+
+**Choices**
+- [ ] 7
+- [ ] 8
+- [x] 10
+- [ ] 9
+---
+
+**Explanation:**
+All the substrings are as follows-
+```
+"b", "x", "c", "d", "bx", "xc", "cd", "bxc", "xcd", "bxcd"
+```
+We can also find the count using n*(n+1)/2.
+
+### Question 2 Check Palindrome
+
+
+Check whether the given substring of string **s** is palindrome or not.
+A palindrome is the sequence of characters that reads the same forward and backward.for example, "nayan", "madam", etc.
+
+**TestCase**
+
+**Input**
+```
+s = "anamadamspe"
+start = 3
+end = 7
+```
+**Output**
+```
+true
+```
+**Explanation**
+The substring formed from index 3 to 7 is "madam" which is palindrome.
+
+### Question 2 Approach
+
+#### Approach
+Below is the simple algorithm to check whether the substring is palindrome or not:
+* Initialize two indices *start* and *end* to point to the beginning and *end* of the string, respectively.
+* While *start* is less than *end*, do the following:
+ * If the character at index *start* is not equal to the character at index *end*, the string is not a palindrome. Return false.
+ * Else, increment *start* and decrement *end*.
+* If the loop completes without finding a non-matching pair, the string is a palindrome. Return true.
+
+#### Pseudocode
+```cpp
+function ispalindrome(char s[], int start, int end) {
+ while (start < end) {
+ if (s[start] != s[end]) {
+ return false;
+ } else {
+ start++;
+ end--;
+ }
+ }
+ return true;
+}
+```
+
+
+#### Complexity
+
+Time Complexity- **O(N)**.
+Space Complexity- **O(1)**.
+
+
+## Question 3 : Longest Palindromic substring
+Given a string **s**, calculate the length of longest palindromic substring in **s**.
+
+**TestCase**
+**Input**
+```
+"anamadamm"
+```
+**Output**
+```
+5
+```
+**Explanation**
+The substring "madam" of size 5 is the longest palindromic substring that can be formed from given string.
+
+
+
+### Question
+What is the length of longest palindromic substring within string "feacabacabgf" ?
+
+**Choices**
+- [ ] 6
+- [ ] 3
+- [x] 7
+- [ ] 10
+
+
+### Question
+What is the length of longest palindromic substring within string "a d a e b c d f d c b e t g g t e" ?
+
+**Choices**
+- [ ] 6
+- [ ] 3
+- [x] 9
+- [ ] 10
+
+
+:::warning
+Please take some time to think about the brute force solution approach on your own before reading further.....
+:::
+
+
+### Question 4 Brute Force Approach
+
+
+The naive approach is to for all the substring check whether the string is palindrome or not. if it is palindrome and its size is greater than the previous answer(which is initially 0), then update the answer.
+
+#### Pseudocode
+
+```cpp
+function longestPalindrome(char s[]) {
+ int N = s.size();
+ int ans = 0;
+ for (int i = 0; i < N; i++) {
+ for (int j = i; j < N; j++) {
+ if (ispalindrome(s, i, j)) {
+ ans = max(ans, j - i + 1);
+ }
+ }
+ }
+ return ans;
+}
+```
+
+#### Complexity
+
+Time Complexity- **O(N^3)**.
+Space Complexity- **O(1)**.
+
+
+#### Idea
+The key idea here is that:
+* For odd length substring, take every character as a center and expand its center and gets maximum size palindromic substring.
+* For even length substring, take every adjacent character as a center and expand its center and get maximum size palindromic substring.
+
+
+#### Pseudocode
+```cpp
+function longestpalindrome(char s[]) {
+ int maxlength = 0;
+ int N = s.size();
+ for (int c = 0; c < N; c++) {
+
+ //odd length string
+ int left = c, right = c;
+ while (left >= 0 and right < N) {
+ if (s[left] != s[right]) {
+ break;
+ }
+ left--;
+ right++;
+ }
+ maxlength = max(maxlength, right - left - 1);
+
+ //even length string
+ left = c;
+ right = c + 1;
+ while (left >= 0 and right < N) {
+ if (s[left] != s[right]) {
+ break;
+ }
+ left--;
+ right++;
+ }
+ maxlength = max(maxlength, right - left - 1);
+ }
+ return maxlength;
+}
+```
+
+#### Complexity
+
+Time Complexity- **O(N^2)**.
+Space Complexity- **O(1)**.
+
+### Immutability of Strings
+
+In languages like **Java, C#, JavaScript, Python and Go**, strings are immutable, which means it's **value can't be changed**.
+
+```cpp=
+String s1 = "Hello"; // String literal
+String s2 = "Hello"; // String literal
+String s3 = s1; // same reference
+```
+
+
+
+* As seen above, because strings with the same content share storage in a single pool, this minimize creating a copy of the same value.
+* That is to say, once a String is generated, its content cannot be changed and hence changing content will lead to the creation of a new String.
+
+```cpp=
+//Changing the value of s1
+s1 = "Java";
+
+//Updating with concat() operation
+s2.concat(" World");
+
+//The concatenated String will be created as a new instance and an object should refer to that instance to get the concatenated value.
+String newS3 = s3.concat(" Scaler");
+
+System.out.println("s1 refers to " + s1);
+System.out.println("s2 refers to " + s2);
+System.out.println("s3 refers to " + s3);
+System.out.println("newS3 refers to " + newS3);
+```
+
+**Output**
+
+```cpp=
+s1 refers to Java
+s2 refers to Hello
+s3 refers to Hello
+news3 refers to Hello Scaler
+```
+
+
+
+As shown above, considering the example:
+
+* String s1 is updated with a new value and that's why a new instance is created. Hence, s1 reference changes to that newly created instance "Java".
+* String s2 and s3 remain unchanged as their references were not changed to a new instance created after performing concat() operation.
+* "Hello World" remains unreferenced to any object and lost in the pool as s2.concat() operation (in line number 5) is not assigned to any object. That's why there is a reference to its result.
+* String newS3 refers to the instance of s3.concat() operation that is "Hello Scaler" as it is referenced to new object newS3.
+
+**Hence, Strings are immutable and whenever we change the string only its reference is changed to the new instance.**
+
diff --git a/Academy DSA Typed Notes/Intermediate/Intermediate DSA Time Complexity.md b/Academy DSA Typed Notes/Intermediate/Intermediate DSA Time Complexity.md
new file mode 100644
index 0000000..4596399
--- /dev/null
+++ b/Academy DSA Typed Notes/Intermediate/Intermediate DSA Time Complexity.md
@@ -0,0 +1,565 @@
+# Time Complexity
+
+**Topics covered :**
+
+1. Log Basics + Iteration Problems
+2. Comparing Iterations using Graph
+3. Time Complexity - Definition and Notations (Asymptotic Analysis - Big O)
+6. TLE
+7. Importance of Constraints
+
+:::success
+There are a lot of quizzes in this session, please take some time to think about the solution on your own before reading further.....
+:::
+
+## Basics of Logarithm
+
+Q. What is the meaning of LOG ?
+A. Logarithm is the inverse of exponential function.
+
+
+Q. How to read the statement "logb(a)"?
+A. To what value we need to raise b, such that we get a.
+
+If logb(a) = c, then it means bc = a.
+
+**Examples**
+
+1. log2(64) = 6
+**How?** 2 raise to the power what is 64? It's 6 since 26 = 64
+
+2. log3(27) = 3
+3. log5(25) = 2
+4. log2(32) = 5
+
+Now, calculate the floor values of the following logarithms.
+5. log2(10) = 3
+6. log2(40) = 5
+
+**Note:**
+If 2k = N => log2(N) = k
+
+Let's look at one more formula:
+1. What is log2(2^6)?
+A. 6
+Explanation: To what power you should raise 2, such that it equates to 2^6.
+
+2. What is log3(3^5)?
+A. 5
+Explanation: To what power you should raise 3, such that it equates to 3^5.
+
+**Note:**
+In general, loga(a^N) = N
+
+**Question**:
+
+Given a positive integer N, how many times do we need to divide it by 2 (Consider only integer part) until it reaches 1.
+
+For example, N = 100
+100 -> 50 -> 25 -> 12 -> 6 -> 3 -> 1
+Hence, 6 times.
+
+What if N = 324?
+324 -> 162 -> 81 -> 40 -> 20 -> 10 -> 5 -> 2 -> 1
+Hence, 8 times.
+
+
+### **Question**
+How many times we need to divide 9 by 2 till it reaches 1 ?
+
+**Choices**
+- [ ] 4
+- [x] 3
+- [ ] 5
+- [ ] 2
+
+**Explanation:**
+N --> N/2 --> N/4 --> N/8 --> ...... 1
+N/2^0 --> N/2^1 --> N/2^2 --> N/2^3 --> ...... N/2^K
+
+N/2^K = 1
+K = log2(N)
+
+### **Question**
+How many times we need to divide 27 by 2 till reaches 1 ?
+
+**Choices**
+- [ ] 5
+- [x] 4
+- [ ] 3
+- [ ] 6 -->
+
+
+
+### **Question**
+How many iterations will be there in this loop ?
+```pseudocode
+N > 0
+i = N;
+while (i > 1) {
+ i = i / 2;
+}
+```
+
+**Choices**
+- [ ] N
+- [ ] N/2
+- [ ] sqrt(N)
+- [x] log(N)
+
+
+
+**Explanation:**
+
+The given loop starts with the initial value of i as N and continues until i becomes less than or equal to 1, by repeatedly dividing i by 2 in each iteration.
+
+Hence, Iterations are log(N)
+
+
+### **Question**
+How many iterations will be there in this loop
+```
+for(i=1; i
+
diff --git a/Academy DSA Typed Notes/Intermediate/Intermediate DSA Sorting Basics.md b/Academy DSA Typed Notes/Intermediate/Intermediate DSA Sorting Basics.md
new file mode 100644
index 0000000..f48ace7
--- /dev/null
+++ b/Academy DSA Typed Notes/Intermediate/Intermediate DSA Sorting Basics.md
@@ -0,0 +1,454 @@
+# Sorting
+
+## Introduction
+
+
+**Sorting** is an arrangement of data in particular order on the basis of some parameter
+
+### Example 1:
+```
+ A[ ] = { 2, 3, 9, 12, 17, 19 }
+```
+
+The above example is sorted in ascending order on the basis of magnitude.
+
+### Example 2:
+```
+ A[ ] = { 19, 6, 5, 2, -1, -19 }
+```
+
+The above example is sorted in descending order on the basis of magnitude.
+
+
+
+### Question
+Is the array { 1, 13, 9 , 6, 12 } sorted ?
+
+**Choices**
+- [x] Yes
+- [ ] No
+
+
+In the above quiz, array is sorted in ascending order on the basis of count of factors. Count of factors for the above array is { 1, 2, 3, 4, 6 }.
+
+
+
+**Sorting** is essential for organizing, analyzing, searching, and presenting data efficiently and effectively in various applications and contexts.
+
+### Problem 1 : Minimize the cost to empty array
+
+
+Given an array of **n** integers, minimize the cost to empty given array where cost of removing an element is equal to **sum of all elements left in an array**.
+
+### Example 1
+
+```plaintext
+A[ ] = { 2, 1, 4 }
+Ans = 11
+```
+
+**Explanation**
+After removing 4 cost = 4+2+1 = 7
+After removing 2 cost = 2+1 = 3
+After removing 1 cost = 1 = 1
+
+Total cost = 11
+
+
+### Question
+Minimum cost to remove all elements from array {4, 6, 1} ?
+
+**Choices**
+- [ ] 11
+- [ ] 15
+- [x] 17
+- [ ] 21
+
+
+
+After removing 6 cost = 4+6+1 = 11
+After removing 4 cost = 4+1 = 5
+After removing 1 cost = 1 = 1
+
+Total cost = 17
+
+
+### Question
+Minimum cost to remove all elements from array[] = {3, 5, 1, -3}
+
+**Choices**
+- [ ] 4
+- [x] 2
+- [ ] 0
+- [ ] 18
+
+
+
+After removing 5 cost = 5+3+1+(-3) = 6
+After removing 3 cost = 3+1+(-3) = 1
+After removing 1 cost = 1+(-3) = -2
+After removing -3 cost = -3) = -3
+
+Total cost = 2
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Problem 1 Solution Approach
+
+**Observation**
+* Start removing from the largest element.
+
+
+
+Here we can see if we have to minimise the cost we should add the largest number minimum number of times, that implies it should be the first one to be removed.
+The formula would be **$\sum$(i+1)\*arr[i]** where **i** is the index.
+
+Follow the below steps to solve the problem.
+* **Sort** the data in descending order.
+* Initialise the **ans** equal to 0.
+* Run a loop for i from 0 to **n** – 1, where **n** is the size of the array.
+* For every element add **arr[i]\*i** to the ans.
+
+#### Pseudocode
+```cpp
+int calculate_cost(int arr[], int n) {
+ reverse_sort(arr);
+ int ans = 0;
+ for (int i = 0; i < n; i++) {
+ ans += i * arr[i];
+ }
+
+ return ans;
+}
+```
+
+#### Time and Space Complexity
+
+-- TC - O(nlogn)
+-- SC - O(n)
+
+### Problem 2 : Find count of Noble Integers
+
+
+Given an array of distinct elements of size n, find the count of **noble integers**.
+
+> Note: arr[i] is **noble** if count of elements smaller than arr[i] is equal to arr[i] where arr[i] is element at index i.
+
+**Example 1**
+
+```plaintext
+A[ ] = { 1, -5, 3, 5, -10, 4}
+Ans = 3
+```
+
+**Explanation**
+For arr[2] there are three elements less than 3 that is 1, -5 and -10. So arr[0] is noble integer.
+For arr[3] there are five elements less than 5 that is 1, 3, 4, 5, -5 and -10. So arr[3] is noble integer.
+For arr[5] there are four elements less than 4 that is 1, 3, -5 and -10. So arr[5] is noble integer.
+
+In total there are 3 noble elements.
+
+
+### Question
+Count the number of noble integers in the array. A = { -3, 0, 2 , 5 }
+
+**Choices**
+- [ ] 0
+- [x] 1
+- [ ] 2
+- [ ] 3
+
+
+
+**Explanation:**
+For arr[2] there are two elements less than 2 that is -3 and 0. So arr[2] is noble integer.
+In total there are 2 noble elements.
+
+:::warning
+Please take some time to think about the Brute Force solution approach on your own before reading further.....
+:::
+
+### Problem 2 : Bruteforce Solution
+
+#### Observation
+Iterate through every element in the array, for every element count the number of smaller elements.
+
+#### Pseudocode
+```cpp
+int find_nobel_integers(int arr[], int n) {
+ int ans = 0;
+ for (int i = 0; i < n; i++) {
+ int count = 0;
+ for (int j = 0; j < n; j++) {
+ if (arr[j] < arr[i])
+ count++;
+ }
+ if (count == arr[i]) {
+ ans++;
+ }
+ }
+ return ans;
+}
+```
+
+#### Time and Space Complexity
+-- TC - O(N^2)
+-- SC - O(1)
+
+### Problem 1 Optimised Solution
+
+#### Optimised Solution - 1
+
+* Hint 1: What is the extra work being done?
+Expected: For every element, we are using an extra loop for calculating the count of smaller elements.
+* Hint 2: Can sorting the array help here?
+
+#### Observation:
+ If we sort the data all elements smaller than the element at index i will be on from index **0 to i-1**. So total number of smaller elements will be equal to **i**.
+
+#### Pseudocode
+```cpp
+
+int find_nobel_integers(int arr[], int n) {
+ sort(arr);
+ int ans = 0;
+ for (int i = 0; i < n; i++) {
+ if (arr[i] == i) {
+ ans = ans + 1;
+ }
+ }
+ return ans;
+}
+```
+
+#### Time and Space Complexity
+-- TC - O(nlogn)
+-- SC - O(1)
+
+### Problem 3 Find count of nobel integers (Not Distinct)
+
+Given an array of size n, find the count of noble integers.
+> Note: Same as previous question, but all elements need not to be distinct
+
+### Question
+
+Count the no of noble integers in the array. A = { -10, 1, 1, 3, 100 }
+
+**Choices**
+- [ ] 1
+- [x] 3
+- [ ] 2
+- [ ] 4
+
+
+**Explanation:**
+For arr[1] and arr[2] there is one element less than 1. So arr[1] and arr[2] are noble integers.
+Similarly arr[3] will be the npble lement as there are 3 elements less than 3.
+So in total 3 elements are noble integers.
+
+### Question
+Count the no of noble integers in the array
+A = { -10, 1, 1, 2, 4, 4, 4, 8, 10 }
+
+**Choices**
+- [ ] 4
+- [x] 5
+- [ ] 6
+- [ ] 7
+
+
+
+**Explanation:**
+arr[1], arr[2], arr[4], arr[5], arr[6] are the noble elements here.
+
+
+### Question
+Count the no of noble integers in the array
+A = { -3, 0, 2, 2, 5, 5, 5, 5, 8, 8, 10, 10, 10, 14 }
+
+**Choices**
+- [ ] 4
+- [ ] 5
+- [ ] 6
+- [x] 7
+
+
+**Explanation:**
+For arr[8] and arr[9] there are eight elements less than 8 that is -3, 0, 2, 5. So arr[8] and arr[9] are noble integers.
+Similarly arr[9], arr[10], arr[11], ar[12] are noble elements.
+So in total 6 elements are noble integers.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+### Problem 3 Solution
+#### Observation
+* If the current element is same as previous element then the total number of smaller elements will be same as previous element.
+* If current element is not equal to previous element then the total number of smaller elements is equal to its index.
+
+#### Pseudocode
+```cpp
+
+int find_nobel_integers(int arr[], int n) {
+ sort(arr);
+ int count = 0, ans = 0;
+ if (arr[0] == 0) ans++;
+
+ for (int i = 1; i < n; i++) {
+ if (arr[i] != arr[i - 1])
+ count = i;
+
+ if (count == arr[i])
+ ans++;
+ }
+ return ans;
+}
+```
+
+#### Time and Space Complexity
+-- TC - O(nlogn)
+-- SC - O(1)
+
+## Sorting Algorithm - Selection Sort
+
+
+A sorting algorithm is a method of reorganizing the elements in a meaningful order.
+
+> Imagine this. You are asked to arrange students according to their increasing heights.
+
+**Divide the queue of students into two parts – arranged and unarranged.**
+
+1. To begin with, place all the students in the unarranged queue.
+2. From this unarranged queue, search for the shortest student and place him/her in the list of arranged students.
+3. Again, from the unarranged queue, select the second-shortest student. Place this student in the arranged queue, just after the smallest student.
+4. Repeat the above-given steps until all the students are placed into the arranged queue.
+
+**Did you see what we just did here?**
+We used the selection sort algorithm to arrange all the students in a height-wise order.
+
+
+**To better understand selection sort, let's consider a list of Integers 5, 6, 4, 2.**
+
+
+The steps to sort this list would involve –
+
+
+
+
+#### Pseudocode:
+
+```cpp
+void selectionSort(int arr[], int size) {
+ int i, j, minIndex;
+
+ for (i = 0; i < size - 1; i++) {
+
+ // set minIndex equal to the first unsorted element
+ minIndex = i;
+
+ //iterate over unsorted sublist and find the minimum element
+ for (j = i + 1; j < size; j++) {
+
+ if (arr[j] < arr[minIndex]) {
+ minIndex = j;
+ }
+
+ }
+
+ // swapping the minimum element with the element at minIndex to place it at its correct position
+ swap(arr[minIndex], arr[i]);
+ }
+}
+```
+
+#### TC & SC
+
+**Time Complexity:** O(N2) since we have to iterate entire list to search for a minimum element everytime.
+For 1 element, N iterations,
+For N elements, N2 iterations.
+
+**Space Complexity:** O(1)
+
+## Sorting Algorithm - Insertion Sort
+
+**Insertion Sort** is one of the simplest sorting techniques which you might have used in your daily lives while arranging a deck of cards.
+
+> So without going into how this algorithm works, let’s think about how you would usually go about arranging the deck of cards?
+
+**Say you are given 10 cards, 1 to 10 of spades, all shuffled, and you want to sort these cards.**
+
+1. You would basically pick any random card(e.g. 7), and place it into your left hand, assuming the left hand is meant to carry the sorted cards.
+2. Then you would pick another random card, say 2, and place 2 in the correct position on your left hand, i.e. before 7.
+3. Then again if you pick 5, you would place it between 2 and 7 on your left hand, and this way we know we are able to sort our deck of cards. Since we insert one element at a time in its correct position, hence its name “Insertion Sort”.
+
+#### Dry Run
+
+E.g. if elements were in order:
+
+```3, 5, 2```
+
+You can start by picking 3, and since there is no element to the left of 3, we can assume it is in the correct place.
+Array:
+
+```3, 5, 2```
+
+You can pick 5, you compare 5 with 3, and you find 5 is in the correct order amongst the array of [3, 5].
+Array:
+
+```3, 5, 2```
+
+Then you pick 2, you find the place in the left side array of [3,5] to place this 2. Since 2 must come before 3, we insert 2 before 3.
+Array:
+
+```2, 3, 5 →```
+
+Which is a sorted order.
+
+
+#### Approach
+
+Line 2: We don’t process the first element, as it has nothing to compare against.
+Line 3: Loop from i=1 till the end, to process each element.
+Line 4: Extract the element at position i i.e. array[i]. Let it be called E.
+Line 5: To compare E with its left elements, loop j from i-1 to 0
+Line 6, 7: Compare E with the left element, if E is lesser, then move array[j] to right by 1.
+Line 8: Once we have found the position for E, place it there.
+
+#### Pseudocode
+
+```cpp
+void insertionSort(int arr[], int n) {
+ for (int i = 1; i < n; i++) { // Start from 1 as arr[0] is always sorted
+ Int currentElement = arr[i];
+ Int j = i - 1;
+ // Move elements of arr[0..i-1], that are greater than key,
+ // to one position ahead of their current position
+ while (j >= 0 && arr[j] > currentElement) {
+ arr[j + 1] = arr[j];
+ j = j - 1;
+ }
+ // Finally place the Current element at its correct position.
+ arr[j + 1] = currentElement;
+ }
+}
+```
+
+#### TC & SC
+
+**Time Complexity:**
+
+**Worst Case:** O(N^2), when the array is sorted in reverse order.
+
+**Best Case:** O(N), when the data is already sorted in desied order, in that case there will be no swap.
+
+Space Complexity: O(1)
+
+**Note**
+
+1. Both Selection & Insertion are in-place sorting algorithms, means they don't need extra space.
+2. Since the time complexity of both can go to O(N^2), it is only useful when we have a lesser number of elements to sort in an array.
+
+
diff --git a/Academy DSA Typed Notes/Intermediate/Intermediate DSA Strings.md b/Academy DSA Typed Notes/Intermediate/Intermediate DSA Strings.md
new file mode 100644
index 0000000..52942f7
--- /dev/null
+++ b/Academy DSA Typed Notes/Intermediate/Intermediate DSA Strings.md
@@ -0,0 +1,382 @@
+
+# String
+
+A string can be defined as a sequence of characters or in other words we can say that it is an array of characters.
+
+**Example**
+Below are the examples of string:
+```
+"Welcome to Scaler"
+"Hello World!"
+```
+**Note:** String is represented using double quote i.e, `""`. All the characters of string must be inside this quote.
+
+**Character**
+A character is a single symbol that represents a letter, number, or other symbol in a computer's character set. Characters are used to represent textual data, and they are typically represented using its ASCII value.
+
+**Example**
+```
+'a'
+'B'
+'1'
+'_'
+```
+
+Computer store everything in binary. So, how do we store strings in computer?
+
+Each character has corresponding decimal value associated to it which is known as ASCII value.
+
+**'A' to 'Z'** have ASCII from **65 to 90**
+**'a' to 'z'** have ASCII from **97 to 122**
+**'0' to '9'** have ASCII from **48 to 57**
+
+Each character '?', '!', '\*', ... has a corresponding ASCII associated with it.
+
+### Some Operations:
+**Note:** Characters can also be printed using its ascii value. for example, the ascii value of 'A' is 65, so it can be printed as
+```CPP
+char ch = (char)65;
+print(ch);
+/*
+character 'A' gets printed; we are assigning Integer to Char,hence in some languages typecasting will be required.
+*/
+```
+
+```cpp=
+char ch = (char)('a' + 1);
+/*
+When we do arithmetic operations on characters, automatically computations happen on their ASCII values.
+ */
+print(ch); //'b' will get printed
+```
+
+```cpp=
+int x = 'a';
+/*
+No need to typecast since we are assigning Char to Int (smaller data type to bigger, so it will not overflow)
+*/
+print(x); //97 will be printed
+
+```
+
+
+
+## Question 1 : Switch cases
+
+
+Given a string consisting of only alphabets(either lowercase or uppercase). Print all the characters of string in such a way that for all lowercase character, print its uppercase character and for all uppercase character, print its lowercase character.
+
+**TestCase**
+**Input**
+```
+"Hello"
+```
+**Output**
+```
+"hELLO"
+```
+**Explanation**
+
+Here, there is only one uppercase character present in the string i.e, 'H' so convert it to lowercase character. All other characters are in lowercase, hence they are converted into uppercase characters.
+
+
+
+### Question
+What is the output for String = "aDgbHJe" ?
+
+**Choices**
+- [ ] ADGBHJE
+- [ ] aDgbHJe
+- [x] AdGBhjE
+- [ ] adgbhje
+
+---
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+**Observation**
+The key observations are:
+* Lowercase characters can be changed into uppercase by subtracting 32 from its ASCII values.
+* Uppercase charactes can be changed into lowercase by adding 32 from its ASCII values.
+
+The above points are derived from the fact that for every alphabet, the difference between its ascii value in lowercase and uppercase is 32.
+
+#### Pseudocode
+```cpp
+Function toggle(char s[]) {
+ int n = s.size();
+ for (int i = 0; i < n; i++) {
+ if (s[i] >= 65 and s[i] <= 91) {
+ print(s[i] + 32);
+ } else {
+ print(s[i] - 32);
+ }
+ }
+}
+```
+#### Complexity
+Time Complexity- **O(N)**.
+Space Complexity- **O(1)**.
+
+
+## Substring
+A substring is a contiguous sequence of characters within a string. A substring concept in string is similar to subarray concept in array.
+
+**A substring can be:**
+1. Continous part of string.
+2. Full string can be a substring.
+3. A single character can also be a subsring.
+
+**Example**
+
+Suppose, we have a string as
+```
+"abc"
+```
+There are total 6 substring can be formed from the above string. All substrings are
+```
+"a"
+"b"
+"c"
+"ab"
+"bc"
+"abc"
+```
+### Question
+How many total substrings will be there for the String "bxcd" ?
+
+**Choices**
+- [ ] 7
+- [ ] 8
+- [x] 10
+- [ ] 9
+---
+
+**Explanation:**
+All the substrings are as follows-
+```
+"b", "x", "c", "d", "bx", "xc", "cd", "bxc", "xcd", "bxcd"
+```
+We can also find the count using n*(n+1)/2.
+
+### Question 2 Check Palindrome
+
+
+Check whether the given substring of string **s** is palindrome or not.
+A palindrome is the sequence of characters that reads the same forward and backward.for example, "nayan", "madam", etc.
+
+**TestCase**
+
+**Input**
+```
+s = "anamadamspe"
+start = 3
+end = 7
+```
+**Output**
+```
+true
+```
+**Explanation**
+The substring formed from index 3 to 7 is "madam" which is palindrome.
+
+### Question 2 Approach
+
+#### Approach
+Below is the simple algorithm to check whether the substring is palindrome or not:
+* Initialize two indices *start* and *end* to point to the beginning and *end* of the string, respectively.
+* While *start* is less than *end*, do the following:
+ * If the character at index *start* is not equal to the character at index *end*, the string is not a palindrome. Return false.
+ * Else, increment *start* and decrement *end*.
+* If the loop completes without finding a non-matching pair, the string is a palindrome. Return true.
+
+#### Pseudocode
+```cpp
+function ispalindrome(char s[], int start, int end) {
+ while (start < end) {
+ if (s[start] != s[end]) {
+ return false;
+ } else {
+ start++;
+ end--;
+ }
+ }
+ return true;
+}
+```
+
+
+#### Complexity
+
+Time Complexity- **O(N)**.
+Space Complexity- **O(1)**.
+
+
+## Question 3 : Longest Palindromic substring
+Given a string **s**, calculate the length of longest palindromic substring in **s**.
+
+**TestCase**
+**Input**
+```
+"anamadamm"
+```
+**Output**
+```
+5
+```
+**Explanation**
+The substring "madam" of size 5 is the longest palindromic substring that can be formed from given string.
+
+
+
+### Question
+What is the length of longest palindromic substring within string "feacabacabgf" ?
+
+**Choices**
+- [ ] 6
+- [ ] 3
+- [x] 7
+- [ ] 10
+
+
+### Question
+What is the length of longest palindromic substring within string "a d a e b c d f d c b e t g g t e" ?
+
+**Choices**
+- [ ] 6
+- [ ] 3
+- [x] 9
+- [ ] 10
+
+
+:::warning
+Please take some time to think about the brute force solution approach on your own before reading further.....
+:::
+
+
+### Question 4 Brute Force Approach
+
+
+The naive approach is to for all the substring check whether the string is palindrome or not. if it is palindrome and its size is greater than the previous answer(which is initially 0), then update the answer.
+
+#### Pseudocode
+
+```cpp
+function longestPalindrome(char s[]) {
+ int N = s.size();
+ int ans = 0;
+ for (int i = 0; i < N; i++) {
+ for (int j = i; j < N; j++) {
+ if (ispalindrome(s, i, j)) {
+ ans = max(ans, j - i + 1);
+ }
+ }
+ }
+ return ans;
+}
+```
+
+#### Complexity
+
+Time Complexity- **O(N^3)**.
+Space Complexity- **O(1)**.
+
+
+#### Idea
+The key idea here is that:
+* For odd length substring, take every character as a center and expand its center and gets maximum size palindromic substring.
+* For even length substring, take every adjacent character as a center and expand its center and get maximum size palindromic substring.
+
+
+#### Pseudocode
+```cpp
+function longestpalindrome(char s[]) {
+ int maxlength = 0;
+ int N = s.size();
+ for (int c = 0; c < N; c++) {
+
+ //odd length string
+ int left = c, right = c;
+ while (left >= 0 and right < N) {
+ if (s[left] != s[right]) {
+ break;
+ }
+ left--;
+ right++;
+ }
+ maxlength = max(maxlength, right - left - 1);
+
+ //even length string
+ left = c;
+ right = c + 1;
+ while (left >= 0 and right < N) {
+ if (s[left] != s[right]) {
+ break;
+ }
+ left--;
+ right++;
+ }
+ maxlength = max(maxlength, right - left - 1);
+ }
+ return maxlength;
+}
+```
+
+#### Complexity
+
+Time Complexity- **O(N^2)**.
+Space Complexity- **O(1)**.
+
+### Immutability of Strings
+
+In languages like **Java, C#, JavaScript, Python and Go**, strings are immutable, which means it's **value can't be changed**.
+
+```cpp=
+String s1 = "Hello"; // String literal
+String s2 = "Hello"; // String literal
+String s3 = s1; // same reference
+```
+
+
+
+* As seen above, because strings with the same content share storage in a single pool, this minimize creating a copy of the same value.
+* That is to say, once a String is generated, its content cannot be changed and hence changing content will lead to the creation of a new String.
+
+```cpp=
+//Changing the value of s1
+s1 = "Java";
+
+//Updating with concat() operation
+s2.concat(" World");
+
+//The concatenated String will be created as a new instance and an object should refer to that instance to get the concatenated value.
+String newS3 = s3.concat(" Scaler");
+
+System.out.println("s1 refers to " + s1);
+System.out.println("s2 refers to " + s2);
+System.out.println("s3 refers to " + s3);
+System.out.println("newS3 refers to " + newS3);
+```
+
+**Output**
+
+```cpp=
+s1 refers to Java
+s2 refers to Hello
+s3 refers to Hello
+news3 refers to Hello Scaler
+```
+
+
+
+As shown above, considering the example:
+
+* String s1 is updated with a new value and that's why a new instance is created. Hence, s1 reference changes to that newly created instance "Java".
+* String s2 and s3 remain unchanged as their references were not changed to a new instance created after performing concat() operation.
+* "Hello World" remains unreferenced to any object and lost in the pool as s2.concat() operation (in line number 5) is not assigned to any object. That's why there is a reference to its result.
+* String newS3 refers to the instance of s3.concat() operation that is "Hello Scaler" as it is referenced to new object newS3.
+
+**Hence, Strings are immutable and whenever we change the string only its reference is changed to the new instance.**
+
diff --git a/Academy DSA Typed Notes/Intermediate/Intermediate DSA Time Complexity.md b/Academy DSA Typed Notes/Intermediate/Intermediate DSA Time Complexity.md
new file mode 100644
index 0000000..4596399
--- /dev/null
+++ b/Academy DSA Typed Notes/Intermediate/Intermediate DSA Time Complexity.md
@@ -0,0 +1,565 @@
+# Time Complexity
+
+**Topics covered :**
+
+1. Log Basics + Iteration Problems
+2. Comparing Iterations using Graph
+3. Time Complexity - Definition and Notations (Asymptotic Analysis - Big O)
+6. TLE
+7. Importance of Constraints
+
+:::success
+There are a lot of quizzes in this session, please take some time to think about the solution on your own before reading further.....
+:::
+
+## Basics of Logarithm
+
+Q. What is the meaning of LOG ?
+A. Logarithm is the inverse of exponential function.
+
+
+Q. How to read the statement "logb(a)"?
+A. To what value we need to raise b, such that we get a.
+
+If logb(a) = c, then it means bc = a.
+
+**Examples**
+
+1. log2(64) = 6
+**How?** 2 raise to the power what is 64? It's 6 since 26 = 64
+
+2. log3(27) = 3
+3. log5(25) = 2
+4. log2(32) = 5
+
+Now, calculate the floor values of the following logarithms.
+5. log2(10) = 3
+6. log2(40) = 5
+
+**Note:**
+If 2k = N => log2(N) = k
+
+Let's look at one more formula:
+1. What is log2(2^6)?
+A. 6
+Explanation: To what power you should raise 2, such that it equates to 2^6.
+
+2. What is log3(3^5)?
+A. 5
+Explanation: To what power you should raise 3, such that it equates to 3^5.
+
+**Note:**
+In general, loga(a^N) = N
+
+**Question**:
+
+Given a positive integer N, how many times do we need to divide it by 2 (Consider only integer part) until it reaches 1.
+
+For example, N = 100
+100 -> 50 -> 25 -> 12 -> 6 -> 3 -> 1
+Hence, 6 times.
+
+What if N = 324?
+324 -> 162 -> 81 -> 40 -> 20 -> 10 -> 5 -> 2 -> 1
+Hence, 8 times.
+
+
+### **Question**
+How many times we need to divide 9 by 2 till it reaches 1 ?
+
+**Choices**
+- [ ] 4
+- [x] 3
+- [ ] 5
+- [ ] 2
+
+**Explanation:**
+N --> N/2 --> N/4 --> N/8 --> ...... 1
+N/2^0 --> N/2^1 --> N/2^2 --> N/2^3 --> ...... N/2^K
+
+N/2^K = 1
+K = log2(N)
+
+### **Question**
+How many times we need to divide 27 by 2 till reaches 1 ?
+
+**Choices**
+- [ ] 5
+- [x] 4
+- [ ] 3
+- [ ] 6 -->
+
+
+
+### **Question**
+How many iterations will be there in this loop ?
+```pseudocode
+N > 0
+i = N;
+while (i > 1) {
+ i = i / 2;
+}
+```
+
+**Choices**
+- [ ] N
+- [ ] N/2
+- [ ] sqrt(N)
+- [x] log(N)
+
+
+
+**Explanation:**
+
+The given loop starts with the initial value of i as N and continues until i becomes less than or equal to 1, by repeatedly dividing i by 2 in each iteration.
+
+Hence, Iterations are log(N)
+
+
+### **Question**
+How many iterations will be there in this loop
+```
+for(i=1; i +
+**Ans: 8**
+
+#### Hint:
+If we get units of water stored over every building, then we can get the overall water by summing individual answers.
+
+#### Observations
+1. How much water is stored over **building 2** ? **-> 4 units**
+
+
+
+
+**Ans: 8**
+
+#### Hint:
+If we get units of water stored over every building, then we can get the overall water by summing individual answers.
+
+#### Observations
+1. How much water is stored over **building 2** ? **-> 4 units**
+
+
+ +
+2. Now, how much water is stored over **building 2** ? **still -> 4 units**
+
+
+
+2. Now, how much water is stored over **building 2** ? **still -> 4 units**
+
+ +
+3. Now, how much water is stored over **building 2** ? **still -> 4 units**
+
+
+
+3. Now, how much water is stored over **building 2** ? **still -> 4 units**
+
+ +
+4. Now, how much water is stored over **building 2** ? **Now it is 6**
+
+
+4. Now, how much water is stored over **building 2** ? **Now it is 6**
+ +
+5. Now, how much water is stored over **building 2** ? **Now it is 8**
+
+
+5. Now, how much water is stored over **building 2** ? **Now it is 8**
+ +
+#### Conclusion:
+It depends on the height of the minimum of the largest buildings on either sides.
+
+**Example:**
+Water stored over building 5 depends on minimum of the largest building on either sides.
+**i.e, min(10, 12) = 10**
+**Water stored over 5 is 10 - 5 = 5 units.**
+
+
+
+#### Conclusion:
+It depends on the height of the minimum of the largest buildings on either sides.
+
+**Example:**
+Water stored over building 5 depends on minimum of the largest building on either sides.
+**i.e, min(10, 12) = 10**
+**Water stored over 5 is 10 - 5 = 5 units.**
+
+ +
+
+---
+### Question
+Given N buildings with height of each building, find the rain water trapped between the buildings.
+
+`A = [1, 2, 3, 2, 1]`
+
+**Choices**
+- [ ] 2
+- [ ] 9
+- [x] 0
+- [ ] 3
+
+
+
+**Explanation:**
+
+No water is trapped, Since the building is like a mountain.
+
+
+
+
+
+
+---
+### Question
+Given N buildings with height of each building, find the rain water trapped between the buildings.
+
+`A = [1, 2, 3, 2, 1]`
+
+**Choices**
+- [ ] 2
+- [ ] 9
+- [x] 0
+- [ ] 3
+
+
+
+**Explanation:**
+
+No water is trapped, Since the building is like a mountain.
+
+
+
+ +
+
+
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+---
+### Rain Water Trapping Brute Force Approach
+
+For **ith** building,
+We need to find maximum heights on both the left and right sides of **ith** building.
+
+NOTE: For **0th** and **(N-1)th** building, no water will be stored on top.
+
+#### Pseudocode (Wrong)
+```cpp
+ans = 0
+
+for (int i = 1; i < N - 1; i++) {
+ maxL = max(0 to i - 1); //loop O(N)
+ maxR = max(i + 1 to N - 1); //loop O(N)
+
+ water = min(maxL, maxR) - A[i];
+ ans += water;
+}
+```
+
+#### Edge Case
+
+
+
+
+
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+---
+### Rain Water Trapping Brute Force Approach
+
+For **ith** building,
+We need to find maximum heights on both the left and right sides of **ith** building.
+
+NOTE: For **0th** and **(N-1)th** building, no water will be stored on top.
+
+#### Pseudocode (Wrong)
+```cpp
+ans = 0
+
+for (int i = 1; i < N - 1; i++) {
+ maxL = max(0 to i - 1); //loop O(N)
+ maxR = max(i + 1 to N - 1); //loop O(N)
+
+ water = min(maxL, maxR) - A[i];
+ ans += water;
+}
+```
+
+#### Edge Case
+
+) +
+For building with height 4, the Lmax = 3 and Rmax = 3
+min(3, 3) = 3
+water = **3 - 4 < 0**
+
+So, for such case, we'll take water stored as 0.
+
+#### Pseudocode (Correct)
+```cpp
+ans = 0
+
+for (int i = 1; i < N - 1; i++) {
+ maxL = max(0 to i - 1); //loop O(N)
+ maxR = max(i + 1 to N - 1); //loop O(N)
+
+ water = min(maxL, maxR) - A[i];
+
+ if (water > 0) {
+ ans += water;
+ }
+}
+```
+
+#### Complexity
+**Time Complexity:** O(N^2) {Since for every element, we'll loop to find max on left and right}
+**Space Complexity:** O(N)
+
+---
+### Rain Water Trapping Optimised Approach
+
+We can store the max on right & left using carry forward approach.
+
+* We can take 2 arrays, lmax[] & rmax[].
+* Below is the calculation for finding max on left & right using carry forward approach.
+* This way, we don't have to find max for every element, as it has been pre-calculated.
+
+
+
+For building with height 4, the Lmax = 3 and Rmax = 3
+min(3, 3) = 3
+water = **3 - 4 < 0**
+
+So, for such case, we'll take water stored as 0.
+
+#### Pseudocode (Correct)
+```cpp
+ans = 0
+
+for (int i = 1; i < N - 1; i++) {
+ maxL = max(0 to i - 1); //loop O(N)
+ maxR = max(i + 1 to N - 1); //loop O(N)
+
+ water = min(maxL, maxR) - A[i];
+
+ if (water > 0) {
+ ans += water;
+ }
+}
+```
+
+#### Complexity
+**Time Complexity:** O(N^2) {Since for every element, we'll loop to find max on left and right}
+**Space Complexity:** O(N)
+
+---
+### Rain Water Trapping Optimised Approach
+
+We can store the max on right & left using carry forward approach.
+
+* We can take 2 arrays, lmax[] & rmax[].
+* Below is the calculation for finding max on left & right using carry forward approach.
+* This way, we don't have to find max for every element, as it has been pre-calculated.
+
+ +
+#### Pseudocode
+
+```cpp
+ans = 0;
+
+int lmax[N] = {
+ 0
+};
+for (int i = 1; i < N; i++) {
+ lmax[i] = max(lmax[i - 1], A[i - 1]);
+}
+
+int rmax[N] = {
+ 0
+};
+for (int i = N - 2; i >= 0; i--) {
+ rmax[i] = max(rmax[i + 1], A[i + 1]);
+}
+
+for (int i = 1; i < N - 1; i++) {
+ water = min(lmax[i], rmax[i]) - A[i];
+
+ if (water > 0) {
+ ans += water;
+ }
+}
+```
+
+#### Complexity
+**Time Complexity:** O(N) {Since we have precalculated lmax & rmax}
+**Space Complexity:** O(N)
+
+
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Arrays 2 Two Dimensional.md b/Academy DSA Typed Notes/Advanced/DSA Arrays 2 Two Dimensional.md
new file mode 100644
index 0000000..b8e1967
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Arrays 2 Two Dimensional.md
@@ -0,0 +1,568 @@
+# Advanced DSA : Arrays 2: Two Dimensional
+
+---
+## Problem 1 Find in rowise and colwise sorted matrix
+
+### Problem Statement
+Given a row wise and column wise sorted matrix, find out whether element **k** is present or not.
+
+**Example**
+Observe that rows and columns are both sorted.
+
+
+#### Pseudocode
+
+```cpp
+ans = 0;
+
+int lmax[N] = {
+ 0
+};
+for (int i = 1; i < N; i++) {
+ lmax[i] = max(lmax[i - 1], A[i - 1]);
+}
+
+int rmax[N] = {
+ 0
+};
+for (int i = N - 2; i >= 0; i--) {
+ rmax[i] = max(rmax[i + 1], A[i + 1]);
+}
+
+for (int i = 1; i < N - 1; i++) {
+ water = min(lmax[i], rmax[i]) - A[i];
+
+ if (water > 0) {
+ ans += water;
+ }
+}
+```
+
+#### Complexity
+**Time Complexity:** O(N) {Since we have precalculated lmax & rmax}
+**Space Complexity:** O(N)
+
+
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Arrays 2 Two Dimensional.md b/Academy DSA Typed Notes/Advanced/DSA Arrays 2 Two Dimensional.md
new file mode 100644
index 0000000..b8e1967
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Arrays 2 Two Dimensional.md
@@ -0,0 +1,568 @@
+# Advanced DSA : Arrays 2: Two Dimensional
+
+---
+## Problem 1 Find in rowise and colwise sorted matrix
+
+### Problem Statement
+Given a row wise and column wise sorted matrix, find out whether element **k** is present or not.
+
+**Example**
+Observe that rows and columns are both sorted.
+ +
+**Test Case 1**
+
+13 => Present (true)
+
+**Test Case 2**
+
+2 => Present (true)
+
+**Test Case 3**
+15 => Not Present (false)
+
+---
+
+### Question
+What is the brute force approach and the time complexity of it?
+
+**Choices**
+- [ ] Iterate over first row; T.C - O(M)
+- [ ] Iterate over last col; T.C - O(N)
+- [x] Iterate over all rows & cols; T.C - O(N * M)
+- [ ] Iterate over first col; T.C - O(N)
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+#### Idea
+* We shall exploit the property of the matrix being sorted.
+* Start with the cell from where we can decide the next step.
+**Example:**
+
+
+**Test Case 1**
+
+13 => Present (true)
+
+**Test Case 2**
+
+2 => Present (true)
+
+**Test Case 3**
+15 => Not Present (false)
+
+---
+
+### Question
+What is the brute force approach and the time complexity of it?
+
+**Choices**
+- [ ] Iterate over first row; T.C - O(M)
+- [ ] Iterate over last col; T.C - O(N)
+- [x] Iterate over all rows & cols; T.C - O(N * M)
+- [ ] Iterate over first col; T.C - O(N)
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+#### Idea
+* We shall exploit the property of the matrix being sorted.
+* Start with the cell from where we can decide the next step.
+**Example:**
+ +Search for: 0
+
+Say we stand at **top left cell i.e, -5**.
+Now, **-5 < 0**, can we determined the direction to search based on this?
+No, because on rightside as well as downwards, the elements are in increasing order, so 0 can be present anywhere.
+
+Now, say we stand at **top right cell i.e, 13**.
+Now,**13 > 0**, should we go left or down ? Can we decide ?
+Yes, if we move down the elements are > 13, but we are looking for an element < 13, so we should move left.
+
+It means, all elements below 13, can be neglected.
+
+
+Search for: 0
+
+Say we stand at **top left cell i.e, -5**.
+Now, **-5 < 0**, can we determined the direction to search based on this?
+No, because on rightside as well as downwards, the elements are in increasing order, so 0 can be present anywhere.
+
+Now, say we stand at **top right cell i.e, 13**.
+Now,**13 > 0**, should we go left or down ? Can we decide ?
+Yes, if we move down the elements are > 13, but we are looking for an element < 13, so we should move left.
+
+It means, all elements below 13, can be neglected.
+
+ +
+**Move Left**
+
+
+
+**Move Left**
+
+ +
+Now, where shall we move ?
+
+---
+
+### Question
+Say we are at 1 and want to find 0, where should we move ?
+
+
+
+
+Now, where shall we move ?
+
+---
+
+### Question
+Say we are at 1 and want to find 0, where should we move ?
+
+
+ +
+**Move Left**
+
+
+**Move Left**
+) +
+Now, **-2 < 0**, all elements on left of -2 are lesser than -2, hence can be neglected.
+
+
+
+Now, **-2 < 0**, all elements on left of -2 are lesser than -2, hence can be neglected.
+
+ +
+**Move Down**
+
+
+
+**Move Down**
+
+ +
+#### Approach
+
+* We can start at top right cell.
+* If A[i][j] < K, move down, else move left.
+* Repeat until the element is found, our the search space is exhausted.
+
+**NOTE:** We could have also started at bottom left cell.
+
+
+#### Pseudocode
+
+```cpp
+int i = 0, j = M - 1
+while (i < N && j >= 0) {
+ if (arr[i][j] == K) {
+ return true;
+ } else if (arr[i][j] < K) {
+ i++; //move down; next row
+ } else {
+ j--; //move left; previous column
+ }
+}
+return false;
+```
+#### Time & Space Complexity
+**Time Complexity:** O(M+N) since at every step, we are either discarding a row or a column. Since total rows+columns are N+M, hence Iterations will be N+M.
+**Space Complexity:** O(1)
+
+---
+### Problem 2 Row with maximum number of 1s
+
+
+Given a binary sorted matrix A of size N x N. Find the row with the maximum number of 1.
+
+NOTE:
+
+* If two rows have the maximum number of 1 then return the row which has a lower index.
+* Assume each row to be sorted by values.
+
+
+**Example 1:**
+
+
+#### Approach
+
+* We can start at top right cell.
+* If A[i][j] < K, move down, else move left.
+* Repeat until the element is found, our the search space is exhausted.
+
+**NOTE:** We could have also started at bottom left cell.
+
+
+#### Pseudocode
+
+```cpp
+int i = 0, j = M - 1
+while (i < N && j >= 0) {
+ if (arr[i][j] == K) {
+ return true;
+ } else if (arr[i][j] < K) {
+ i++; //move down; next row
+ } else {
+ j--; //move left; previous column
+ }
+}
+return false;
+```
+#### Time & Space Complexity
+**Time Complexity:** O(M+N) since at every step, we are either discarding a row or a column. Since total rows+columns are N+M, hence Iterations will be N+M.
+**Space Complexity:** O(1)
+
+---
+### Problem 2 Row with maximum number of 1s
+
+
+Given a binary sorted matrix A of size N x N. Find the row with the maximum number of 1.
+
+NOTE:
+
+* If two rows have the maximum number of 1 then return the row which has a lower index.
+* Assume each row to be sorted by values.
+
+
+**Example 1:**
+ +
+**Output 1:** 0th row
+
+
+**Example 2:**
+
+
+**Output 1:** 0th row
+
+
+**Example 2:**
+ +
+**Output 2:** 3th row
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+#### Brute Force
+
+We can iterate over each row and maintain the max number of 1s.
+
+
+#### Complexity
+**Time Complexity:** O(N * N)
+
+
+
+---
+### Question
+Find the row with the maximum number of 1.
+Note : If there are two rows with same no. of 1, consider the smaller row.
+| **0** | **1** | **1** | **1** |
+|---|---|---|---|
+| **0** | **0** | **0** | **1** |
+| **1** | **1** | **1** | **1** |
+| **1** | **1** | **1** | **1** |
+
+**Choices**
+- [ ] 0th Row
+- [ ] 1st Row
+- [x] 2nd Row
+- [ ] 3rd Row
+
+
+
+---
+
+### Optimisation Approach
+
+We know that rows are sorted, how can we utilise this property of the matrix ?
+
+#### Idea
+
+Say we start from top right of first row and saw that there are 2 ones.
+Now, in the next row, we don't want to see 2 1s, rather we'll check if 3rd 1 is present or not?
+
+
+
+**Output 2:** 3th row
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+#### Brute Force
+
+We can iterate over each row and maintain the max number of 1s.
+
+
+#### Complexity
+**Time Complexity:** O(N * N)
+
+
+
+---
+### Question
+Find the row with the maximum number of 1.
+Note : If there are two rows with same no. of 1, consider the smaller row.
+| **0** | **1** | **1** | **1** |
+|---|---|---|---|
+| **0** | **0** | **0** | **1** |
+| **1** | **1** | **1** | **1** |
+| **1** | **1** | **1** | **1** |
+
+**Choices**
+- [ ] 0th Row
+- [ ] 1st Row
+- [x] 2nd Row
+- [ ] 3rd Row
+
+
+
+---
+
+### Optimisation Approach
+
+We know that rows are sorted, how can we utilise this property of the matrix ?
+
+#### Idea
+
+Say we start from top right of first row and saw that there are 2 ones.
+Now, in the next row, we don't want to see 2 1s, rather we'll check if 3rd 1 is present or not?
+
+ +
+If yes, it means we have three 1s, but then we want to check if more 1s are there, so we'll move towards left in the same row and check.
+
+
+
+If yes, it means we have three 1s, but then we want to check if more 1s are there, so we'll move towards left in the same row and check.
+
+ +
+Now, in the subsequent rows, we'll proceed in the same manner.
+
+In 2nd and 3rd rows, 1 is not present at 1st index.
+
+In 4th row, it is present. So, we check on left if more 1s are present.
+
+In 4th row, we found the maximum 1s, i.e 5 in total. Hence that is our answer.
+
+#### Algorithm
+
+1. Start at i = 0, j = M - 1
+2. If 1 is present, decrement j i.e, move towards the left column.
+ * Whenever j is decremented, it means that row has more 1s, so we can update our answer to that particular row number
+4. If 0 is present, then we want to check in next row that if 1 is present, so we increment i
+
+
+
+#### Pseudocode
+```cpp
+i = 0, j = N - 1
+
+while (i < N && j >= 0) {
+ while (j >= 0 && arr[i][j] == 1) {
+ j--;
+ ans = i;
+ }
+ i++;
+}
+return ans;
+
+```
+
+#### Complexity
+**Time Complexity:** O(M + N) since at every step, we are either discarding a row or a column. Since total rows+columns are N+M, hence Iterations will be N+M.
+**Space Complexity:** O(1)
+
+
+
+---
+### Problem 3 Print Boundary Elements
+
+
+Given an matrix of N X N i.e. Mat[N][N], print boundary elements in clockwise direction.
+
+**Example:**
+```cpp
+N = 5
+```
+
+
+Now, in the subsequent rows, we'll proceed in the same manner.
+
+In 2nd and 3rd rows, 1 is not present at 1st index.
+
+In 4th row, it is present. So, we check on left if more 1s are present.
+
+In 4th row, we found the maximum 1s, i.e 5 in total. Hence that is our answer.
+
+#### Algorithm
+
+1. Start at i = 0, j = M - 1
+2. If 1 is present, decrement j i.e, move towards the left column.
+ * Whenever j is decremented, it means that row has more 1s, so we can update our answer to that particular row number
+4. If 0 is present, then we want to check in next row that if 1 is present, so we increment i
+
+
+
+#### Pseudocode
+```cpp
+i = 0, j = N - 1
+
+while (i < N && j >= 0) {
+ while (j >= 0 && arr[i][j] == 1) {
+ j--;
+ ans = i;
+ }
+ i++;
+}
+return ans;
+
+```
+
+#### Complexity
+**Time Complexity:** O(M + N) since at every step, we are either discarding a row or a column. Since total rows+columns are N+M, hence Iterations will be N+M.
+**Space Complexity:** O(1)
+
+
+
+---
+### Problem 3 Print Boundary Elements
+
+
+Given an matrix of N X N i.e. Mat[N][N], print boundary elements in clockwise direction.
+
+**Example:**
+```cpp
+N = 5
+```
+ +
+**Output:** [1, 2, 3, 4, 5, 10, 15, 20, 25, 24, 23, 22, 21, 16, 11, 6]
+
+
+---
+### Question
+Given N and matrix mat, select the correct order of boundary elements traversed in clockwise direction.
+```cpp
+N = 3
+```
+mat :-
+| 1 | 2 | 3 |
+|:---:|:---:|:---:|
+| **4** | **5** | **6** |
+| **7** | **8** | **9** |
+
+
+**Choices**
+- [x] [1, 2, 3, 6, 9, 8, 7, 4]
+- [ ] [1, 4, 7, 8, 9, 6, 3, 2]
+- [ ] [1, 2, 3, 4, 5, 6, 7, 8]
+- [ ] [2, 3, 4, 5, 6, 7, 8, 9]
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Approach
+* Print N - 1 elements of first row from left to right
+* Print N - 1 elements of last column from top to bottom
+* Print N - 1 elements of last row from right to left
+* Print N - 1 elements of first column from bottom to top
+
+#### Pseudocode
+
+```cpp
+function printBoundaryElements(Mat[][], N) {
+ i = 0 j = 0
+
+ // Print N - 1 elements of first row from left to right
+
+ for (idx = 1; idx < N; idx++) {
+ print(Mat[i][j] + ",")
+ j++
+ }
+
+ // Print N - 1 elements of last column from top to bottom
+ // i and j will already be 0 and 4 respectively after above loop ends
+
+ for (idx = 1; idx < N; idx++) {
+ print(Mat[i][j] + ",")
+ i++
+ }
+
+ // Print N - 1 elements of last row from right to left
+ // i and j will already be 4 and 4 respectively after above loop ends
+
+ for (idx = 1; idx < N; idx++) {
+ print(Mat[i][j] + ",")
+ j--
+ }
+
+ // Print N - 1 elements of first column from bottom to top
+ // i and j will already be 4 and 0 respectively after above loop ends
+
+ for (idx = 1; idx < N; idx++) {
+ print(Mat[i][j] + ",")
+ i--
+ }
+}
+```
+#### Complexity
+**Time Complexity : O(N)**
+**Space Complexity : O(1)**
+
+---
+### Problem 4 Spiral Matrix
+
+
+Given an matrix of N X N i.e. Mat[N][N]. Print elements in spiral order in clockwise direction.
+
+**Example**
+
+```cpp
+N = 5
+```
+
+
+**Output:** [1, 2, 3, 4, 5, 10, 15, 20, 25, 24, 23, 22, 21, 16, 11, 6]
+
+
+---
+### Question
+Given N and matrix mat, select the correct order of boundary elements traversed in clockwise direction.
+```cpp
+N = 3
+```
+mat :-
+| 1 | 2 | 3 |
+|:---:|:---:|:---:|
+| **4** | **5** | **6** |
+| **7** | **8** | **9** |
+
+
+**Choices**
+- [x] [1, 2, 3, 6, 9, 8, 7, 4]
+- [ ] [1, 4, 7, 8, 9, 6, 3, 2]
+- [ ] [1, 2, 3, 4, 5, 6, 7, 8]
+- [ ] [2, 3, 4, 5, 6, 7, 8, 9]
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Approach
+* Print N - 1 elements of first row from left to right
+* Print N - 1 elements of last column from top to bottom
+* Print N - 1 elements of last row from right to left
+* Print N - 1 elements of first column from bottom to top
+
+#### Pseudocode
+
+```cpp
+function printBoundaryElements(Mat[][], N) {
+ i = 0 j = 0
+
+ // Print N - 1 elements of first row from left to right
+
+ for (idx = 1; idx < N; idx++) {
+ print(Mat[i][j] + ",")
+ j++
+ }
+
+ // Print N - 1 elements of last column from top to bottom
+ // i and j will already be 0 and 4 respectively after above loop ends
+
+ for (idx = 1; idx < N; idx++) {
+ print(Mat[i][j] + ",")
+ i++
+ }
+
+ // Print N - 1 elements of last row from right to left
+ // i and j will already be 4 and 4 respectively after above loop ends
+
+ for (idx = 1; idx < N; idx++) {
+ print(Mat[i][j] + ",")
+ j--
+ }
+
+ // Print N - 1 elements of first column from bottom to top
+ // i and j will already be 4 and 0 respectively after above loop ends
+
+ for (idx = 1; idx < N; idx++) {
+ print(Mat[i][j] + ",")
+ i--
+ }
+}
+```
+#### Complexity
+**Time Complexity : O(N)**
+**Space Complexity : O(1)**
+
+---
+### Problem 4 Spiral Matrix
+
+
+Given an matrix of N X N i.e. Mat[N][N]. Print elements in spiral order in clockwise direction.
+
+**Example**
+
+```cpp
+N = 5
+```
+ +
+Here is the depiction to understand the problem better
+
+
+
+Here is the depiction to understand the problem better
+
+ +
+```cpp
+Solution = [1,2,3,4,5,6,12,18,24,30,36,35,34,33,32,31,25,19,13,7,8,9,10,11,17,23,29,28,27,26,20,14,15,16,22,21]
+```
+
+The red arrow represents direction of traversal(clockwise) and fashion in which elements are traversed.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+#### Approach
+* We can break the problem into several boundary printing problem discussed above
+* So first print boundary of matrix of N x N
+* Then we print boundary of next submatrix with top left element being (1,1) and Bottom right element being (N - 2 , N - 2).
+* After every boundary, to print the next boundary, N will be reduced by 2 and i & j will be incremented by 1.
+* We do this till matrix of size least size is reached.
+
+
+
+```cpp
+Solution = [1,2,3,4,5,6,12,18,24,30,36,35,34,33,32,31,25,19,13,7,8,9,10,11,17,23,29,28,27,26,20,14,15,16,22,21]
+```
+
+The red arrow represents direction of traversal(clockwise) and fashion in which elements are traversed.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+#### Approach
+* We can break the problem into several boundary printing problem discussed above
+* So first print boundary of matrix of N x N
+* Then we print boundary of next submatrix with top left element being (1,1) and Bottom right element being (N - 2 , N - 2).
+* After every boundary, to print the next boundary, N will be reduced by 2 and i & j will be incremented by 1.
+* We do this till matrix of size least size is reached.
+
+ +
+
+Boundaries of submatricies are highlighted in different color.
+
+#### Edge Case
+Will the above code work if matrix size is 1 ?
+No, since the loops run N-1 times, therefore we have to handle it separately.
+
+---
+### Question
+Print elements in spiral order in clockwise direction.
+
+|**13**|**14**|**12**|**8**|
+|-----|-----|-----|-----|
+|**9**|**1**|**2**|**7**|
+|**0**|**4**|**3**|**0**|
+|**10**|**5**|**6**|**11**|
+
+
+**Choices**
+- [ ] [13, 9, 0, 10, 5, 6, 11, 0, 7, 8, 12, 14, 1, 4, 2, 3]
+- [ ] [13, 14, 12, 8, 9, 1, 2, 7, 0, 4, 3, 0, 10, 5, 6, 11]
+- [x] [13, 14, 12, 8, 7, 0, 11, 6, 5, 10, 0, 9, 1, 2, 3, 4]
+- [ ] [13, 14, 12, 8, 10, 5, 6, 11, 9, 1, 2, 7, 0, 4, 3, 0]
+
+
+#### Pseudocode
+
+```cpp
+Function printBoundaryElements(Mat[][], N) {
+ i = 0 j = 0
+ while (N > 1) {
+
+ // Print N-1 elements of first row from left to right
+ for (idx = 1; idx < N; idx++) {
+ print(Mat[i][j] + ",")
+ j++
+ }
+
+ // Print N-1 elements of last column from top to bottom
+ for (idx = 1; idx < N; idx++) {
+ print(Mat[i][j] + ",")
+ i++
+ }
+
+ // Print N-1 elements of last row from right to left
+ for (idx = 1; idx < N; idx++) {
+ print(Mat[i][j] + ",")
+ j--
+ }
+
+ // Print N-1 elements of first column from bottom to top
+ for (idx = 1; idx < N; idx++) {
+ print(Mat[i][j] + ",")
+ i--
+ }
+
+ N = N - 2
+ i++
+ j++
+ }
+
+ if (N == 1) {
+ print(Mat[i][j] + ",")
+ }
+}
+
+```
+#### Complexity
+**Time Complexity : $O(N^2)$**
+**Space Complexity : O(1)**
+
+---
+## What is a submatrices and how can we uniquely identify it
+
+
+### What is a submatrix?
+
+Same as how a subarray is continuous part of an Array, a submatrix is continuous sub-matrix of a matrix.
+
+Example,
+
+
+| 11 | 12 |
+|:------:|:------:|
+| **15** | **16** |
+
+is submatrix of the below matrix.
+
+
+
+
+Boundaries of submatricies are highlighted in different color.
+
+#### Edge Case
+Will the above code work if matrix size is 1 ?
+No, since the loops run N-1 times, therefore we have to handle it separately.
+
+---
+### Question
+Print elements in spiral order in clockwise direction.
+
+|**13**|**14**|**12**|**8**|
+|-----|-----|-----|-----|
+|**9**|**1**|**2**|**7**|
+|**0**|**4**|**3**|**0**|
+|**10**|**5**|**6**|**11**|
+
+
+**Choices**
+- [ ] [13, 9, 0, 10, 5, 6, 11, 0, 7, 8, 12, 14, 1, 4, 2, 3]
+- [ ] [13, 14, 12, 8, 9, 1, 2, 7, 0, 4, 3, 0, 10, 5, 6, 11]
+- [x] [13, 14, 12, 8, 7, 0, 11, 6, 5, 10, 0, 9, 1, 2, 3, 4]
+- [ ] [13, 14, 12, 8, 10, 5, 6, 11, 9, 1, 2, 7, 0, 4, 3, 0]
+
+
+#### Pseudocode
+
+```cpp
+Function printBoundaryElements(Mat[][], N) {
+ i = 0 j = 0
+ while (N > 1) {
+
+ // Print N-1 elements of first row from left to right
+ for (idx = 1; idx < N; idx++) {
+ print(Mat[i][j] + ",")
+ j++
+ }
+
+ // Print N-1 elements of last column from top to bottom
+ for (idx = 1; idx < N; idx++) {
+ print(Mat[i][j] + ",")
+ i++
+ }
+
+ // Print N-1 elements of last row from right to left
+ for (idx = 1; idx < N; idx++) {
+ print(Mat[i][j] + ",")
+ j--
+ }
+
+ // Print N-1 elements of first column from bottom to top
+ for (idx = 1; idx < N; idx++) {
+ print(Mat[i][j] + ",")
+ i--
+ }
+
+ N = N - 2
+ i++
+ j++
+ }
+
+ if (N == 1) {
+ print(Mat[i][j] + ",")
+ }
+}
+
+```
+#### Complexity
+**Time Complexity : $O(N^2)$**
+**Space Complexity : O(1)**
+
+---
+## What is a submatrices and how can we uniquely identify it
+
+
+### What is a submatrix?
+
+Same as how a subarray is continuous part of an Array, a submatrix is continuous sub-matrix of a matrix.
+
+Example,
+
+
+| 11 | 12 |
+|:------:|:------:|
+| **15** | **16** |
+
+is submatrix of the below matrix.
+
+ +
+
+### How can we uniquely indentify a rectangle ?
+
+A rectangle is made up of 4 coordinates.
+1. Top Left (TL)
+2. Top Right (TR)
+3. Bottom Left (BL)
+4. Bottom Right (BR)
+
+**If we pick any two diagonal coordinates, we can uniquely identify a rectangle.**
+
+
+
+
+### How can we uniquely indentify a rectangle ?
+
+A rectangle is made up of 4 coordinates.
+1. Top Left (TL)
+2. Top Right (TR)
+3. Bottom Left (BL)
+4. Bottom Right (BR)
+
+**If we pick any two diagonal coordinates, we can uniquely identify a rectangle.**
+
+ +
+So, let's say we pick TL and BR.
+
+**Example -**
+
+If TL = (3,2) and BR = (2,3)
+Then we know which rectangle we are talking about(shown below).
+
+
+
+So, let's say we pick TL and BR.
+
+**Example -**
+
+If TL = (3,2) and BR = (2,3)
+Then we know which rectangle we are talking about(shown below).
+
+ +
+So, with the help of TL and BR coordinates(or TR & BL), we can uniquely identify a submatrices.
+
+---
+### Problem 5 Sum of all Submatrices Sum
+
+
+Given a matrix of N rows and M columns determine the sum of all the possible submatrices.
+
+**Example:**
+
+
+
+So, with the help of TL and BR coordinates(or TR & BL), we can uniquely identify a submatrices.
+
+---
+### Problem 5 Sum of all Submatrices Sum
+
+
+Given a matrix of N rows and M columns determine the sum of all the possible submatrices.
+
+**Example:**
+
+) +
+All Possible sub-matrices are -
+
+
+All Possible sub-matrices are -
+) +
+Total Sum = 166
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Approach
+
+This question sounds same as "Sum of all Subarray Sums". We did that question is Intermediate - Subarrays. The technique used was Contribution Technique, where for every element we had to find that in how many subarrays it was part of.
+
+In "Sum of all Submatrices Sums", we have to find that in how many submatrices a particular element is part of.
+
+If we are able to find that, then we just have to add up the individual results.
+
+#### In what all submatrices, a particular element is part of ?
+
+Let's look at the red cell in below figure.
+If we combine all the top left cells(marked with green color) with all the bottom right cells(marked with blue color), then in all those submatrices, the red cell will be present.
+
+
+
+Total Sum = 166
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+#### Approach
+
+This question sounds same as "Sum of all Subarray Sums". We did that question is Intermediate - Subarrays. The technique used was Contribution Technique, where for every element we had to find that in how many subarrays it was part of.
+
+In "Sum of all Submatrices Sums", we have to find that in how many submatrices a particular element is part of.
+
+If we are able to find that, then we just have to add up the individual results.
+
+#### In what all submatrices, a particular element is part of ?
+
+Let's look at the red cell in below figure.
+If we combine all the top left cells(marked with green color) with all the bottom right cells(marked with blue color), then in all those submatrices, the red cell will be present.
+
+) +
+#### How to find the number of TL cells and BR cells in which (i,j) is part of.
+
+
+
+#### How to find the number of TL cells and BR cells in which (i,j) is part of.
+
+) +
+**TOP LEFT:**
+rows: [0 i]
+cols: [0 j]
+total cells = (i+1) * (j+1)
+
+**BOTTOM RIGHT:**
+rows: [i N-1]
+cols: [j M-1]
+total cells = (N-i) * (M-j)
+
+#### Now, to find the total submatrices of whish (i,j) is part of -
+
+**contribution of (i,j) = TOP LEFT * BOTTOM RIGHT**
+Every top left cell can be combined with every bottom right cell.
+
+**Example**
+
+
+
+**TOP LEFT:**
+rows: [0 i]
+cols: [0 j]
+total cells = (i+1) * (j+1)
+
+**BOTTOM RIGHT:**
+rows: [i N-1]
+cols: [j M-1]
+total cells = (N-i) * (M-j)
+
+#### Now, to find the total submatrices of whish (i,j) is part of -
+
+**contribution of (i,j) = TOP LEFT * BOTTOM RIGHT**
+Every top left cell can be combined with every bottom right cell.
+
+**Example**
+
+) +
+For (2,2)
+
+TOP LEFT:
+3 * 3 = 9
+
+BOTTOM RIGHT
+(5-2) * (6-2) = 3 * 4 = 12
+
+Total matrices of which (2,2) is part of 9 * 12.
+
+---
+### Question
+
+
+For (2,2)
+
+TOP LEFT:
+3 * 3 = 9
+
+BOTTOM RIGHT
+(5-2) * (6-2) = 3 * 4 = 12
+
+Total matrices of which (2,2) is part of 9 * 12.
+
+---
+### Question
+ +
+In a matrix of size 4 * 5, in how many submatrices (1,2) is part of ?
+
+**Choices**
+- [ ] 56
+- [x] 54
+- [ ] 15
+- [ ] 16
+
+#### Pseudocode
+
+```cpp
+total = 0
+for (int i = 0; i < N; i++) {
+ for (int j = 0; j < M; j++) {
+
+ top_left = (i + 1) * (j + 1);
+ bottom_right = (N - i) * (M - j);
+
+ contribution = A[i][j] * top_left * bottom_right;
+
+ total += contribution
+ }
+}
+return total
+```
\ No newline at end of file
diff --git a/Academy DSA Typed Notes/Advanced/DSA Arrays 3 Interview Problems.md b/Academy DSA Typed Notes/Advanced/DSA Arrays 3 Interview Problems.md
new file mode 100644
index 0000000..42af631
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Arrays 3 Interview Problems.md
@@ -0,0 +1,456 @@
+# Lecture | Advanced DSA: Arrays 3 - Interview Problems
+
+---
+## Merge Intervals
+
+An Interval is defined by start and end time, where start <= end.
+
+Say we are given a list of Intervals, we will have to merge them if they overlap.
+
+Let's look at them below -
+
+
+
+In a matrix of size 4 * 5, in how many submatrices (1,2) is part of ?
+
+**Choices**
+- [ ] 56
+- [x] 54
+- [ ] 15
+- [ ] 16
+
+#### Pseudocode
+
+```cpp
+total = 0
+for (int i = 0; i < N; i++) {
+ for (int j = 0; j < M; j++) {
+
+ top_left = (i + 1) * (j + 1);
+ bottom_right = (N - i) * (M - j);
+
+ contribution = A[i][j] * top_left * bottom_right;
+
+ total += contribution
+ }
+}
+return total
+```
\ No newline at end of file
diff --git a/Academy DSA Typed Notes/Advanced/DSA Arrays 3 Interview Problems.md b/Academy DSA Typed Notes/Advanced/DSA Arrays 3 Interview Problems.md
new file mode 100644
index 0000000..42af631
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Arrays 3 Interview Problems.md
@@ -0,0 +1,456 @@
+# Lecture | Advanced DSA: Arrays 3 - Interview Problems
+
+---
+## Merge Intervals
+
+An Interval is defined by start and end time, where start <= end.
+
+Say we are given a list of Intervals, we will have to merge them if they overlap.
+
+Let's look at them below -
+
+) +
+### Non-Overlapping Condition
+
+Say there are two Intervals, I1 {s1 e1} & I2 {s2 e2}
+Then the condition for them to not overlap is -
+
+
+
+
+### Non-Overlapping Condition
+
+Say there are two Intervals, I1 {s1 e1} & I2 {s2 e2}
+Then the condition for them to not overlap is -
+
+
+) +
+```javascript
+if(s2 > e1 || s1 > e2)
+```
+
+So, if above condition is not followed, it says that Intervals are overlapping!
+
+
+### How to merge overlapping Intervals ?
+
+
+**[I1.start , I1.end] & [I2.start , I2.end]**
+After merging -
+**[min(I1.start, I2.start) , max(I1.end, I2.end)]**
+
+---
+### Question
+If the intervals [3, 8] and [5, 12] are given, do they overlap?
+
+**Choices**
+- [x] Yes
+- [ ] No
+
+
+### Explanation:
+
+Answer: Yes
+
+The intervals [3, 8] and [5, 12] overlap because 8 is greater than 5. The overlapping area is [5, 8]
+
+---
+### Question
+What is the correct way to represent the merged result of intervals [6, 10] and [8, 15]?
+
+**Choices**
+- [x] [6, 15]
+- [ ] [6, 8, 10, 15]
+- [ ] [6, 10] and [8, 15]
+- [ ] [8, 10]
+
+### Explanation:
+
+[6, 15]
+
+This is because the merging of intervals involves combining overlapping intervals into a single, continuous interval
+
+
+---
+### Problem 1 : Merge sorted Overlapping Intervals
+
+**Problem Statement**
+Given a sorted list of overlapping intervals, sorted based on start time, merge all overlapping intervals and return sorted list.
+
+**Input:**
+Interval[] = {(0,2), (1,4), (5,6), (6,8), (7,10), (8,9), (12,14)}
+
+**Output:**
+
+{(0,4), (5,10), (12,14)}
+
+#### Explanation:
+
+
+| Interval 1 | Interval 2 | | Answer Interval List |
+|:----------:|:----------:|:---------------:|:--------------------:|
+| 0-2 | 1-4 | Overlapping | 0-4 |
+| 0-4 | 5-6 | Not Overlapping | 0-4, 5-6 |
+| 5-6 | 6-8 | Overlapping | 0-4, 5-8 |
+| 5-8 | 7-10 | Overlapping | 0-4, 5-10 |
+| 5-10 | 8-9 | Overlapping | 0-4, 5-10 |
+| 5-10 | 12-14 | Not Overlapping | 0-4, 5-10, 12-14 |
+
+
+#### The Array Is Sorted Based on Start Time. What Is the Overlapping Condition?
+Say start time of A < start time of B
+
+
+
+```javascript
+if(s2 > e1 || s1 > e2)
+```
+
+So, if above condition is not followed, it says that Intervals are overlapping!
+
+
+### How to merge overlapping Intervals ?
+
+
+**[I1.start , I1.end] & [I2.start , I2.end]**
+After merging -
+**[min(I1.start, I2.start) , max(I1.end, I2.end)]**
+
+---
+### Question
+If the intervals [3, 8] and [5, 12] are given, do they overlap?
+
+**Choices**
+- [x] Yes
+- [ ] No
+
+
+### Explanation:
+
+Answer: Yes
+
+The intervals [3, 8] and [5, 12] overlap because 8 is greater than 5. The overlapping area is [5, 8]
+
+---
+### Question
+What is the correct way to represent the merged result of intervals [6, 10] and [8, 15]?
+
+**Choices**
+- [x] [6, 15]
+- [ ] [6, 8, 10, 15]
+- [ ] [6, 10] and [8, 15]
+- [ ] [8, 10]
+
+### Explanation:
+
+[6, 15]
+
+This is because the merging of intervals involves combining overlapping intervals into a single, continuous interval
+
+
+---
+### Problem 1 : Merge sorted Overlapping Intervals
+
+**Problem Statement**
+Given a sorted list of overlapping intervals, sorted based on start time, merge all overlapping intervals and return sorted list.
+
+**Input:**
+Interval[] = {(0,2), (1,4), (5,6), (6,8), (7,10), (8,9), (12,14)}
+
+**Output:**
+
+{(0,4), (5,10), (12,14)}
+
+#### Explanation:
+
+
+| Interval 1 | Interval 2 | | Answer Interval List |
+|:----------:|:----------:|:---------------:|:--------------------:|
+| 0-2 | 1-4 | Overlapping | 0-4 |
+| 0-4 | 5-6 | Not Overlapping | 0-4, 5-6 |
+| 5-6 | 6-8 | Overlapping | 0-4, 5-8 |
+| 5-8 | 7-10 | Overlapping | 0-4, 5-10 |
+| 5-10 | 8-9 | Overlapping | 0-4, 5-10 |
+| 5-10 | 12-14 | Not Overlapping | 0-4, 5-10, 12-14 |
+
+
+#### The Array Is Sorted Based on Start Time. What Is the Overlapping Condition?
+Say start time of A < start time of B
+
+) +
+Overlapping Condition -
+**If start of B <= end of A**
+
+
+---
+### Question
+Given a sorted list of overlapping intervals, sorted based on start time, merge all overlapping intervals and return sorted list.
+
+**Input:**
+Interval[] = { (1,10), (2, 3), (4, 5), (9, 12)}
+
+**Choices**
+- [x] (1, 12)
+- [ ] (1, 10), (9, 12)
+- [ ] (1, 9), (9, 12)
+- [ ] No Change
+
+
+#### Problem 1 Approach
+
+* Create an array to store the merged intervals.
+* If the current and ith intervals overlaps, merge them. In this case update the current interval with the merged interval.
+* Else, insert the current interval to answer array since it doesn't overlap with any other interval and update the current Interval to ith Interval.
+
+#### Dry Run
+
+**Input:**
+Interval[] = {(0,2), (1,4), (5,6), (6,8), (7,10), (8,9), (12,14)}
+
+#### Explanation:
+
+
+| current | ith | | After merging | answer list |
+|:-------:|:-----:|:---------------:|:-------------:|:-----------:|
+| 0-2 | 1-4 | Overlapping | 0-4 | |
+| 0-4 | 5-6 | Not Overlapping | Not needed | 0-4 |
+| 5-6 | 6-8 | Overlapping | 5-8 | 0-4 |
+| 5-8 | 7-10 | Overlapping | 5-10 | 0-4 |
+| 5-10 | 8-9 | Overlapping | 5-10 | 0-4 |
+| 5-10 | 12-14 | Not Overlapping | Not needed | 0-4, 5-10 |
+| 12-14 | end | | | |
+
+At the end, we are left with the last interval, so add it to the list.
+
+#### Pseudocode
+```cpp
+//Already a class/structure will be present for Interval
+//We will only need to create an answer array of type Interval
+
+list < Interval > ans;
+
+// Current Segment
+int cur_start = A[0].start, cur_end = A[0].end;
+
+for (int i = 1; i < A.size(); i++) {
+
+ // if i'th interval overlaps with current interval
+ if (A[i].start <= cur_end) {
+ // merging them
+ cur_end = max(cur_end, A[i].end);
+ } else {
+ //adding current interval to answer.
+ //create a new Interval
+ Interval temp(cur_start, cur_end); //if struct is declared, otherwise if class is declared then we can simply use new keyword
+ ans.push_back(temp);
+
+ // update cur Interval to ith
+ cur_start = A[i].start;
+ cur_end = A[i].end;
+ }
+}
+Interval temp(cur_start, cur_end);
+ans.push_back(temp);
+return ans;
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(1)
+
+---
+### Problem 2 Sorted Set of Non Overlapping Intervals
+
+Given a sorted list of overlapping intervals based on start time, insert a new interval such that the final list of intervals is also sorted and non-overlapping.
+Print the Intervals.
+
+**Example 1:**
+**N = 9**
+(1,3)
+(4,7)
+(10,14)
+(16,19)
+(21,24)
+(27,30)
+(32,35)
+(38,41)
+(43,50)
+
+New Interval
+**(12, 22)**
+
+**Explanation:**
+
+| ith | new Interval | Overlaps? | Print |
+|-------|----------|----------|-----------------|
+| (1,3) | (12,22) | No | (1,3) |
+| (4,7) | (12,22) | No | (4,7) |
+| (10,14) | (12,22) | Yes; merged: (10,22) ||
+| (16,19) | (10,22) | Yes; merged: (10,22) ||
+| (21,24) | (10,22) | Yes; merged: (10,24) ||
+| (27,30) | (10,22) | No; small new Interval gets printed first |(10,22)|
+| (32,35)| | |(32,35)|
+| (38,41)| | |(38,41) |
+| (43,50)| | | (43,50)|
+
+**Please Note:** Once the new Interval gets printed, all the Intervals following it also gets printed.
+
+**More Examples**
+
+**Example 2:**
+**N = 5**
+(1,5)
+(8,10)
+(11,14)
+(15,20)
+(21,24)
+
+New Interval
+**(12, 24)**
+
+| ith | new Interval | Overlaps? | Print |
+|:-------:|:------------:|:--------------------:|:------:|
+| (1,5) | (12, 24) | No | (1,5) |
+| (8,10) | (12, 24) | No | (8,10) |
+| (11,14) | (12, 24) | Yes; merged:(11, 24) | |
+| (15,20) | (11, 24) | Yes; merged:(11, 24) | |
+| (21,24) | (11, 24) | Yes; merged:(11, 24) | |
+
+We are done with all the intervals but left the new Interval at the end; in this case we have to print the new Interval.
+
+**Example 3:**
+
+
+
+Overlapping Condition -
+**If start of B <= end of A**
+
+
+---
+### Question
+Given a sorted list of overlapping intervals, sorted based on start time, merge all overlapping intervals and return sorted list.
+
+**Input:**
+Interval[] = { (1,10), (2, 3), (4, 5), (9, 12)}
+
+**Choices**
+- [x] (1, 12)
+- [ ] (1, 10), (9, 12)
+- [ ] (1, 9), (9, 12)
+- [ ] No Change
+
+
+#### Problem 1 Approach
+
+* Create an array to store the merged intervals.
+* If the current and ith intervals overlaps, merge them. In this case update the current interval with the merged interval.
+* Else, insert the current interval to answer array since it doesn't overlap with any other interval and update the current Interval to ith Interval.
+
+#### Dry Run
+
+**Input:**
+Interval[] = {(0,2), (1,4), (5,6), (6,8), (7,10), (8,9), (12,14)}
+
+#### Explanation:
+
+
+| current | ith | | After merging | answer list |
+|:-------:|:-----:|:---------------:|:-------------:|:-----------:|
+| 0-2 | 1-4 | Overlapping | 0-4 | |
+| 0-4 | 5-6 | Not Overlapping | Not needed | 0-4 |
+| 5-6 | 6-8 | Overlapping | 5-8 | 0-4 |
+| 5-8 | 7-10 | Overlapping | 5-10 | 0-4 |
+| 5-10 | 8-9 | Overlapping | 5-10 | 0-4 |
+| 5-10 | 12-14 | Not Overlapping | Not needed | 0-4, 5-10 |
+| 12-14 | end | | | |
+
+At the end, we are left with the last interval, so add it to the list.
+
+#### Pseudocode
+```cpp
+//Already a class/structure will be present for Interval
+//We will only need to create an answer array of type Interval
+
+list < Interval > ans;
+
+// Current Segment
+int cur_start = A[0].start, cur_end = A[0].end;
+
+for (int i = 1; i < A.size(); i++) {
+
+ // if i'th interval overlaps with current interval
+ if (A[i].start <= cur_end) {
+ // merging them
+ cur_end = max(cur_end, A[i].end);
+ } else {
+ //adding current interval to answer.
+ //create a new Interval
+ Interval temp(cur_start, cur_end); //if struct is declared, otherwise if class is declared then we can simply use new keyword
+ ans.push_back(temp);
+
+ // update cur Interval to ith
+ cur_start = A[i].start;
+ cur_end = A[i].end;
+ }
+}
+Interval temp(cur_start, cur_end);
+ans.push_back(temp);
+return ans;
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(1)
+
+---
+### Problem 2 Sorted Set of Non Overlapping Intervals
+
+Given a sorted list of overlapping intervals based on start time, insert a new interval such that the final list of intervals is also sorted and non-overlapping.
+Print the Intervals.
+
+**Example 1:**
+**N = 9**
+(1,3)
+(4,7)
+(10,14)
+(16,19)
+(21,24)
+(27,30)
+(32,35)
+(38,41)
+(43,50)
+
+New Interval
+**(12, 22)**
+
+**Explanation:**
+
+| ith | new Interval | Overlaps? | Print |
+|-------|----------|----------|-----------------|
+| (1,3) | (12,22) | No | (1,3) |
+| (4,7) | (12,22) | No | (4,7) |
+| (10,14) | (12,22) | Yes; merged: (10,22) ||
+| (16,19) | (10,22) | Yes; merged: (10,22) ||
+| (21,24) | (10,22) | Yes; merged: (10,24) ||
+| (27,30) | (10,22) | No; small new Interval gets printed first |(10,22)|
+| (32,35)| | |(32,35)|
+| (38,41)| | |(38,41) |
+| (43,50)| | | (43,50)|
+
+**Please Note:** Once the new Interval gets printed, all the Intervals following it also gets printed.
+
+**More Examples**
+
+**Example 2:**
+**N = 5**
+(1,5)
+(8,10)
+(11,14)
+(15,20)
+(21,24)
+
+New Interval
+**(12, 24)**
+
+| ith | new Interval | Overlaps? | Print |
+|:-------:|:------------:|:--------------------:|:------:|
+| (1,5) | (12, 24) | No | (1,5) |
+| (8,10) | (12, 24) | No | (8,10) |
+| (11,14) | (12, 24) | Yes; merged:(11, 24) | |
+| (15,20) | (11, 24) | Yes; merged:(11, 24) | |
+| (21,24) | (11, 24) | Yes; merged:(11, 24) | |
+
+We are done with all the intervals but left the new Interval at the end; in this case we have to print the new Interval.
+
+**Example 3:**
+
+) +
+
+---
+### Question
+If the sorted set of non-overlapping intervals is [1, 5], [6, 10], and [12, 15], what happens if you add the interval `[4, 7]` such that the final list of intervals is also sorted and non-overlapping.?
+
+**Choices**
+- [x] [1, 10] and [12, 15]
+- [ ] [1, 5], [4, 7], [6, 10], [12, 15]
+- [ ] [1, 5] and [6, 10] only
+- [ ] No change
+
+
+#### Explanation:
+(1,5)
+(6,10)
+(12,15)
+
+New Interval
+**(4, 7)**
+
+| ith | new Interval | Overlaps? | Print |
+|:-------:|:------------:|:--------------------:|:------:|
+| (1,5) | (4, 7) | Yes; merged:(1, 7) | |
+| (6,10) | (1, 7) | Yes; merged:(1, 10) | |
+| (12,15) | (1, 10) | No; small new Interval gets printed first | (1, 10) |
+| (12,15) | | | (12, 15) |
+
+Thus after merging, the intervals are [1, 10] and [12, 15]
+
+#### Problem 2 Pseudocode
+
+```cpp
+
+void merge(int Interval[], int nS, int nE) {
+ for (int i = 0; i < N; i++) {
+ int L = Interval[i].start, R = Interval[i].end;
+
+ //Not Overlapping
+ if (nS > R) {
+ print({
+ L,
+ R
+ });
+ }
+ // new Interval is not overlapping and is smaller
+ // print new Interval and then all the remaining Intervals
+ else if (L > nE) {
+ print({
+ nS,
+ nE
+ });
+
+ for (int j = i; j < N; j++) {
+ print({
+ Interval[j].start,
+ Interval[j].end
+ })
+ }
+ return;
+ } else {
+ nS = min(L, nS);
+ nE = max(R, nE);
+ }
+ }
+ print({
+ nS,
+ nE
+ });
+}
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(1)
+
+---
+### Problem 3 Find First Missing Natural Number
+
+Given an unsorted array of integers, Find first missing Natural Number.
+
+**Examples**
+
+
+
+---
+### Question
+If the sorted set of non-overlapping intervals is [1, 5], [6, 10], and [12, 15], what happens if you add the interval `[4, 7]` such that the final list of intervals is also sorted and non-overlapping.?
+
+**Choices**
+- [x] [1, 10] and [12, 15]
+- [ ] [1, 5], [4, 7], [6, 10], [12, 15]
+- [ ] [1, 5] and [6, 10] only
+- [ ] No change
+
+
+#### Explanation:
+(1,5)
+(6,10)
+(12,15)
+
+New Interval
+**(4, 7)**
+
+| ith | new Interval | Overlaps? | Print |
+|:-------:|:------------:|:--------------------:|:------:|
+| (1,5) | (4, 7) | Yes; merged:(1, 7) | |
+| (6,10) | (1, 7) | Yes; merged:(1, 10) | |
+| (12,15) | (1, 10) | No; small new Interval gets printed first | (1, 10) |
+| (12,15) | | | (12, 15) |
+
+Thus after merging, the intervals are [1, 10] and [12, 15]
+
+#### Problem 2 Pseudocode
+
+```cpp
+
+void merge(int Interval[], int nS, int nE) {
+ for (int i = 0; i < N; i++) {
+ int L = Interval[i].start, R = Interval[i].end;
+
+ //Not Overlapping
+ if (nS > R) {
+ print({
+ L,
+ R
+ });
+ }
+ // new Interval is not overlapping and is smaller
+ // print new Interval and then all the remaining Intervals
+ else if (L > nE) {
+ print({
+ nS,
+ nE
+ });
+
+ for (int j = i; j < N; j++) {
+ print({
+ Interval[j].start,
+ Interval[j].end
+ })
+ }
+ return;
+ } else {
+ nS = min(L, nS);
+ nE = max(R, nE);
+ }
+ }
+ print({
+ nS,
+ nE
+ });
+}
+```
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(1)
+
+---
+### Problem 3 Find First Missing Natural Number
+
+Given an unsorted array of integers, Find first missing Natural Number.
+
+**Examples**
+ +
+
+---
+### Question
+In the array [5, 3, 1, -1, -2, -4, 7, 2], what is the first missing natural number?
+
+**Choices**
+- [x] 4
+- [ ] 6
+- [ ] -3
+- [ ] 8
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+---
+### Find First Missing Natural Number Solution Approach
+#### Approach 1: Brute Force
+Check for all the numbers from 1 till we get the answer
+**T.C -** O(N * ans)
+
+Here, in the worst case answer can go uptil N+1, in case if all numbers from 1 to N are present in the array.
+
+**Example -** {4, 1, 3, 2}
+Here we will have to iterate till 5, ie. N+1.
+
+#### Idea
+**Can we utilise the fact that answer can be out of 1 to N+1?**
+If any number other than 1 to N is present, then missing is out of 1 to N only.
+If all elements from 1 to N are present, then it will be N+1.
+
+Say we start checking if 1 is present or not, we somehow want to mark the presence of 1.
+Now, since we can't use extra space, so we can use indices to mark the presence of a number.
+
+Index 0 can be used to mark presence of 1.
+Index 1 can be used to mark presence of 2.
+Index 2 can be used to mark presence of 3.
+so on....
+
+**Now how do we mark the presence ?**
+
+**One Solution:**
+```plaintext
+We can set element at that index as negative.
+```
+
+*But what if negative number is part of the input?*
+
+**Let's assume only positive numbers are present**
+We can use indices to mark the presence of a number.
+We can set element at that index as negative.
+
+**A[ ] = {8, 1, 4, 2, 6, 3}**
+
+```plaintext
+N = 6
+Answer can be from [1 7]
+So, if any number is beyond this range, we don't care!
+```
+
+| index | element | presence marked at index | state of the array |
+|:-----:|:-------:|:-------------------------------------:|:-----------------------:|
+| 0 | 8 | don't care, since out of answer range | |
+| 1 | 1 | 0 | {-8, 1, 4, 2, 6, 3} |
+| 2 | 4 | 3 | {-8, 1, 4, -2, 6, 3} |
+| 3 | 2 | 1 | {-8, -1, 4, -2, 6, 3} |
+| 4 | 6 | 5 | {-8, -1, 4, -2, 6, -3} |
+| 5 | 3 | 2 | {-8, -1, -4, -2, 6, -3} |
+
+Now, we can just iterate from left to right and whichever element is not ve-, we can return i+1 as the answer.
+**Example: {-8, -1, -4, -2, 6, -3}**
+Here, index: 4 is +ve, hence 5 is the answer.
+
+**NOTE:** Since we are marking elements as negative, so when checking presence of a certain number, we'll have to consider the absolute value of it.
+
+#### Pseudocode
+```cpp
+for (int i = 0; i < N; i++) {
+ int ele = abs(A[i]);
+
+ if (ele >= 1 && ele <= N) {
+ int idx = ele - 1;
+ A[idx] = -1 * abs(A[i]);
+ }
+}
+```
+
+---
+### Find First Missing Natural Number For Negative Numbers
+#### How to resolve for negative numbers ?
+
+Will negatives ever be our answer?
+**NO!**
+So, we don't have to care about them!
+
+Should we change them to ve+ ?
+**NO!** They may fall in our answer range.
+
+Should we mark them 0?
+**NO!** Then we will not be able to mark the presence of a number!
+
+***We can just change negative number to a number that is out of our answer range. **It can be N+2**.***
+
+```cpp
+for (int i = 0; i < N; i++) {
+ if (A[i] <= 0) {
+ A[i] = N + 2;
+ }
+}
+
+for (int i = 0; i < N; i++) {
+ int ele = abs(A[i]);
+
+ if (ele >= 1 && ele <= N) {
+ int idx = ele - 1;
+ A[idx] = -1 * abs(A[i]);
+ }
+}
+
+for (int i = 0; i < N; i++) {
+ if (A[i] > 0) return i + 1;
+}
+return N + 1;
+```
+>Please show a dry run on - {4, 0, 1, -5, -10, 8, 2, 6}
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(1)
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Backtracking.md b/Academy DSA Typed Notes/Advanced/DSA Backtracking.md
new file mode 100644
index 0000000..1c234ba
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Backtracking.md
@@ -0,0 +1,482 @@
+# Backtracking
+
+---
+### Question
+What is the output of below code for N = 7 ?
+```
+int magicfun( int N) {
+ if ( N == 0)
+ return 0;
+ else
+ return magicfun(N/2) * 10 + (N % 2);
+}
+```
+
+**Choices**
+
+- [ ] 100
+- [x] 111
+- [ ] 99
+- [ ] 112
+
+**Explanation**
+```cpp
+ magicfun(7)
+
+ magicfun(3) * 10 + 1
+
+ magicfun(1) * 10 + 1
+
+ magicfun(0) * 10 + 1
+
+ 0
+```
+
+
+---
+### Question
+
+Time complexity of below code is?
+```
+int magicfun( int N) {
+ if ( N == 0)
+ return 0;
+ else
+ return magicfun(N/2) * 10 + (N % 2);
+}
+```
+
+**Choices**
+
+- [x] O(log N)
+- [ ] O(1)
+- [ ] O(N)
+- [ ] O(N/2)
+
+
+Everytime we are dividing N by 2. Hence complexity will be log N.
+
+---
+### Question
+
+Output of below code is?
+```
+void fun(char s[], int x) {
+ print(s)
+ char temp
+ if(x < s.length/2) {
+ temp=s[x]
+ s[x] = s[s.length-x-1]
+ s[s.length-x-1]=temp
+ fun(s, x+1)
+ }
+}
+```
+
+Run for fun("SCROLL", 0)
+
+**Choices**
+
+- [ ] SCROLL
+ SCROLL
+ SCROLL
+ SCROLL
+- [x] SCROLL
+ LCROLS
+ LLROCS
+ LLORCS
+- [ ] LLORCS
+ SCROLL
+ LCROLS
+ LLROCS
+
+
+We start with
+(SCROLL, 0); line 2 runs; print => SCROLL
+since 0 < 6/2, we run the if block and index 0 gets swapped with 5
+
+(LCROLS, 1); line 2 runs; print => LCROLS
+since 1 < 6/2, we run the if block and index 1 gets swapped with 4
+
+(LLROCS, 2); line 2 runs; print => LLROCS
+since 2 < 6/2, we run the if block and index 2 gets swapped with 3
+
+(LLORCS, 3); line 2 runs; print => LLORCS
+since 3 not less than 6/2, we skip if block and come back from recursion
+
+---
+### Question
+
+Time Complexity of below code is?
+```
+void fun(char s[], int x) {
+ print(s)
+ char temp
+ if(x < s.length/2) {
+ temp=s[x]
+ s[x] = s[s.length-x-1]
+ s[s.length-x-1]=temp
+ fun(s, x+1)
+ }
+}
+```
+
+**Choices**
+
+- [ ] O(N^2)
+- [ ] O(1)
+- [x] O(N)
+- [ ] O(N/2)
+
+
+
+We are only iterating till half of the string. In the worst case, we can start at 0th index.
+
+Therefore, #iterations = N/2
+Hence, T.C = O(N)
+S.C is also O(N) since call will be made for half of the string.
+
+---
+## What is Backtracking
+
+
+The above process is known as **Backtracking**.
+
+Let's try to understand the concept of backtracking by a very basic example. We are given a set of words represented in the form of a tree. The tree is formed such that every branch ends in a word.
+
+
+
+
+---
+### Question
+In the array [5, 3, 1, -1, -2, -4, 7, 2], what is the first missing natural number?
+
+**Choices**
+- [x] 4
+- [ ] 6
+- [ ] -3
+- [ ] 8
+
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+---
+### Find First Missing Natural Number Solution Approach
+#### Approach 1: Brute Force
+Check for all the numbers from 1 till we get the answer
+**T.C -** O(N * ans)
+
+Here, in the worst case answer can go uptil N+1, in case if all numbers from 1 to N are present in the array.
+
+**Example -** {4, 1, 3, 2}
+Here we will have to iterate till 5, ie. N+1.
+
+#### Idea
+**Can we utilise the fact that answer can be out of 1 to N+1?**
+If any number other than 1 to N is present, then missing is out of 1 to N only.
+If all elements from 1 to N are present, then it will be N+1.
+
+Say we start checking if 1 is present or not, we somehow want to mark the presence of 1.
+Now, since we can't use extra space, so we can use indices to mark the presence of a number.
+
+Index 0 can be used to mark presence of 1.
+Index 1 can be used to mark presence of 2.
+Index 2 can be used to mark presence of 3.
+so on....
+
+**Now how do we mark the presence ?**
+
+**One Solution:**
+```plaintext
+We can set element at that index as negative.
+```
+
+*But what if negative number is part of the input?*
+
+**Let's assume only positive numbers are present**
+We can use indices to mark the presence of a number.
+We can set element at that index as negative.
+
+**A[ ] = {8, 1, 4, 2, 6, 3}**
+
+```plaintext
+N = 6
+Answer can be from [1 7]
+So, if any number is beyond this range, we don't care!
+```
+
+| index | element | presence marked at index | state of the array |
+|:-----:|:-------:|:-------------------------------------:|:-----------------------:|
+| 0 | 8 | don't care, since out of answer range | |
+| 1 | 1 | 0 | {-8, 1, 4, 2, 6, 3} |
+| 2 | 4 | 3 | {-8, 1, 4, -2, 6, 3} |
+| 3 | 2 | 1 | {-8, -1, 4, -2, 6, 3} |
+| 4 | 6 | 5 | {-8, -1, 4, -2, 6, -3} |
+| 5 | 3 | 2 | {-8, -1, -4, -2, 6, -3} |
+
+Now, we can just iterate from left to right and whichever element is not ve-, we can return i+1 as the answer.
+**Example: {-8, -1, -4, -2, 6, -3}**
+Here, index: 4 is +ve, hence 5 is the answer.
+
+**NOTE:** Since we are marking elements as negative, so when checking presence of a certain number, we'll have to consider the absolute value of it.
+
+#### Pseudocode
+```cpp
+for (int i = 0; i < N; i++) {
+ int ele = abs(A[i]);
+
+ if (ele >= 1 && ele <= N) {
+ int idx = ele - 1;
+ A[idx] = -1 * abs(A[i]);
+ }
+}
+```
+
+---
+### Find First Missing Natural Number For Negative Numbers
+#### How to resolve for negative numbers ?
+
+Will negatives ever be our answer?
+**NO!**
+So, we don't have to care about them!
+
+Should we change them to ve+ ?
+**NO!** They may fall in our answer range.
+
+Should we mark them 0?
+**NO!** Then we will not be able to mark the presence of a number!
+
+***We can just change negative number to a number that is out of our answer range. **It can be N+2**.***
+
+```cpp
+for (int i = 0; i < N; i++) {
+ if (A[i] <= 0) {
+ A[i] = N + 2;
+ }
+}
+
+for (int i = 0; i < N; i++) {
+ int ele = abs(A[i]);
+
+ if (ele >= 1 && ele <= N) {
+ int idx = ele - 1;
+ A[idx] = -1 * abs(A[i]);
+ }
+}
+
+for (int i = 0; i < N; i++) {
+ if (A[i] > 0) return i + 1;
+}
+return N + 1;
+```
+>Please show a dry run on - {4, 0, 1, -5, -10, 8, 2, 6}
+
+#### Complexity
+**Time Complexity:** O(N)
+**Space Complexity:** O(1)
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Backtracking.md b/Academy DSA Typed Notes/Advanced/DSA Backtracking.md
new file mode 100644
index 0000000..1c234ba
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Backtracking.md
@@ -0,0 +1,482 @@
+# Backtracking
+
+---
+### Question
+What is the output of below code for N = 7 ?
+```
+int magicfun( int N) {
+ if ( N == 0)
+ return 0;
+ else
+ return magicfun(N/2) * 10 + (N % 2);
+}
+```
+
+**Choices**
+
+- [ ] 100
+- [x] 111
+- [ ] 99
+- [ ] 112
+
+**Explanation**
+```cpp
+ magicfun(7)
+
+ magicfun(3) * 10 + 1
+
+ magicfun(1) * 10 + 1
+
+ magicfun(0) * 10 + 1
+
+ 0
+```
+
+
+---
+### Question
+
+Time complexity of below code is?
+```
+int magicfun( int N) {
+ if ( N == 0)
+ return 0;
+ else
+ return magicfun(N/2) * 10 + (N % 2);
+}
+```
+
+**Choices**
+
+- [x] O(log N)
+- [ ] O(1)
+- [ ] O(N)
+- [ ] O(N/2)
+
+
+Everytime we are dividing N by 2. Hence complexity will be log N.
+
+---
+### Question
+
+Output of below code is?
+```
+void fun(char s[], int x) {
+ print(s)
+ char temp
+ if(x < s.length/2) {
+ temp=s[x]
+ s[x] = s[s.length-x-1]
+ s[s.length-x-1]=temp
+ fun(s, x+1)
+ }
+}
+```
+
+Run for fun("SCROLL", 0)
+
+**Choices**
+
+- [ ] SCROLL
+ SCROLL
+ SCROLL
+ SCROLL
+- [x] SCROLL
+ LCROLS
+ LLROCS
+ LLORCS
+- [ ] LLORCS
+ SCROLL
+ LCROLS
+ LLROCS
+
+
+We start with
+(SCROLL, 0); line 2 runs; print => SCROLL
+since 0 < 6/2, we run the if block and index 0 gets swapped with 5
+
+(LCROLS, 1); line 2 runs; print => LCROLS
+since 1 < 6/2, we run the if block and index 1 gets swapped with 4
+
+(LLROCS, 2); line 2 runs; print => LLROCS
+since 2 < 6/2, we run the if block and index 2 gets swapped with 3
+
+(LLORCS, 3); line 2 runs; print => LLORCS
+since 3 not less than 6/2, we skip if block and come back from recursion
+
+---
+### Question
+
+Time Complexity of below code is?
+```
+void fun(char s[], int x) {
+ print(s)
+ char temp
+ if(x < s.length/2) {
+ temp=s[x]
+ s[x] = s[s.length-x-1]
+ s[s.length-x-1]=temp
+ fun(s, x+1)
+ }
+}
+```
+
+**Choices**
+
+- [ ] O(N^2)
+- [ ] O(1)
+- [x] O(N)
+- [ ] O(N/2)
+
+
+
+We are only iterating till half of the string. In the worst case, we can start at 0th index.
+
+Therefore, #iterations = N/2
+Hence, T.C = O(N)
+S.C is also O(N) since call will be made for half of the string.
+
+---
+## What is Backtracking
+
+
+The above process is known as **Backtracking**.
+
+Let's try to understand the concept of backtracking by a very basic example. We are given a set of words represented in the form of a tree. The tree is formed such that every branch ends in a word.
+
+ +
+To ensure that the current string is always valid during the backtracking process, we need two variables `left_count` and `right_count` that record the number of left and right parentheses in it, respectively.
+
+Therefore, we can define our recursive function as `solve(cur_string, left_count, right_count)` that takes the current string, the number of left parentheses, and the number of right parentheses as arguments. This function will build valid combinations of parentheses of length 2n recursively.
+
+The function adds more parentheses to cur_string only when certain conditions are met:
+
+* If **`left_count < n`**, it suggests that a left parenthesis can still be added, so we add one left parenthesis to cur_string, creating a new string new_string = cur_string + (, and then call `solve(new_string, left_count + 1, right_count)`.
+
+* If **`left_count > right_count`**, it suggests that a right parenthesis can be added to match a previous unmatched left parenthesis, so we add one right parenthesis to cur_string, creating a new string new_string = cur_string + ), and then call solve(new_string, left_count, right_count + 1).
+
+This function ensures that the generated string of length 2n is valid, and adds it directly to the answer. By only generating valid strings, we can avoid wasting time checking invalid strings.
+
+
+#### Dry Run for N = 2, means overall length will be 4.
+
+
+
+To ensure that the current string is always valid during the backtracking process, we need two variables `left_count` and `right_count` that record the number of left and right parentheses in it, respectively.
+
+Therefore, we can define our recursive function as `solve(cur_string, left_count, right_count)` that takes the current string, the number of left parentheses, and the number of right parentheses as arguments. This function will build valid combinations of parentheses of length 2n recursively.
+
+The function adds more parentheses to cur_string only when certain conditions are met:
+
+* If **`left_count < n`**, it suggests that a left parenthesis can still be added, so we add one left parenthesis to cur_string, creating a new string new_string = cur_string + (, and then call `solve(new_string, left_count + 1, right_count)`.
+
+* If **`left_count > right_count`**, it suggests that a right parenthesis can be added to match a previous unmatched left parenthesis, so we add one right parenthesis to cur_string, creating a new string new_string = cur_string + ), and then call solve(new_string, left_count, right_count + 1).
+
+This function ensures that the generated string of length 2n is valid, and adds it directly to the answer. By only generating valid strings, we can avoid wasting time checking invalid strings.
+
+
+#### Dry Run for N = 2, means overall length will be 4.
+
+ +
+- Here **"(())" and "()()"** are valid answers.
+
+#### PseudoCode
+```cpp
+void solve(str, N, opening, closing) { //also taking given N value in parameter
+ // base case
+ if (str.length() == 2 N) {
+ print(str);
+ return;
+ }
+ if (opening < N) {
+ solve(N, str + '(', opening + 1, closing)
+ }
+ if (closing < opening) {
+ solve(N, str + ')', opening, closing + 1)
+ }
+}
+```
+
+#### Complexity
+- **Time Complexity:** O(2N)
+- **Space Complexity:** O(N)
+
+---
+### Definition of Subset and Subsequences
+
+
+#### Definition of Subset and Example
+A subset is often confused with subarray and subsequence but a subset is nothing but any possible combination of the original array (or a set).
+
+For example, the subsets of array arr = [1, 2, 3, 4, 5] can be:
+
+[3, 1]
+[2, 5]
+[1, 2], etc.
+So, we can conclude that subset is the superset of subarrays i.e. all the subarrays are subsets but vice versa is not true.
+
+#### Definition of Subsequence and Example
+As the name suggests, a subsequence is a sequence of the elements of the array obtained by deleting some elements of the array. One important thing related to the subsequence is that even after deleting some elements, the sequence of the array elements is not changed. Both the string and arrays can have subsequences.
+
+The subsequence should not be confused with the subarray or substring. The subarray or substring is contiguous but a subsequence need not to be contiguous.
+
+For example, the subsequences of the array arr : [1, 2, 3, 4] can be:
+
+[1, 3]
+[2, 3, 4]
+[1, 2, 3, 4], etc.
+
+Note: A subarray is a subsequence, a subsequence is a subset but the reverse order is not correct.
+
+---
+### Problem 2 Subsets
+
+Given an array with distinct integers. Print all the subsets using recursion.
+
+**Example**
+
+**Input:** [1, 2, 3]
+**Output:** {[], [1], [2], [3], [1, 2], [1, 3], [2, 3], [1, 2, 3]}
+
+Total Subsets possible are **2^N**
+For every element, there can be two options:
+- It is **considered** as part of a subset
+- It is **not considered** as part of a subset
+
+Say there are **3 elements**, for each of them we have above two options, hence **2 * 2 * 2 = 2^N^** are the total options.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+#### Approach
+
+The approach to solve the problem is to use backtracking.
+
+For each element, I have two choices whether to keep it or not, I execute my choice and then ask recursion to do the remaining work.
+
+Let us take an example of `[1, 2, 3]`.
+
+
+
+- Here **"(())" and "()()"** are valid answers.
+
+#### PseudoCode
+```cpp
+void solve(str, N, opening, closing) { //also taking given N value in parameter
+ // base case
+ if (str.length() == 2 N) {
+ print(str);
+ return;
+ }
+ if (opening < N) {
+ solve(N, str + '(', opening + 1, closing)
+ }
+ if (closing < opening) {
+ solve(N, str + ')', opening, closing + 1)
+ }
+}
+```
+
+#### Complexity
+- **Time Complexity:** O(2N)
+- **Space Complexity:** O(N)
+
+---
+### Definition of Subset and Subsequences
+
+
+#### Definition of Subset and Example
+A subset is often confused with subarray and subsequence but a subset is nothing but any possible combination of the original array (or a set).
+
+For example, the subsets of array arr = [1, 2, 3, 4, 5] can be:
+
+[3, 1]
+[2, 5]
+[1, 2], etc.
+So, we can conclude that subset is the superset of subarrays i.e. all the subarrays are subsets but vice versa is not true.
+
+#### Definition of Subsequence and Example
+As the name suggests, a subsequence is a sequence of the elements of the array obtained by deleting some elements of the array. One important thing related to the subsequence is that even after deleting some elements, the sequence of the array elements is not changed. Both the string and arrays can have subsequences.
+
+The subsequence should not be confused with the subarray or substring. The subarray or substring is contiguous but a subsequence need not to be contiguous.
+
+For example, the subsequences of the array arr : [1, 2, 3, 4] can be:
+
+[1, 3]
+[2, 3, 4]
+[1, 2, 3, 4], etc.
+
+Note: A subarray is a subsequence, a subsequence is a subset but the reverse order is not correct.
+
+---
+### Problem 2 Subsets
+
+Given an array with distinct integers. Print all the subsets using recursion.
+
+**Example**
+
+**Input:** [1, 2, 3]
+**Output:** {[], [1], [2], [3], [1, 2], [1, 3], [2, 3], [1, 2, 3]}
+
+Total Subsets possible are **2^N**
+For every element, there can be two options:
+- It is **considered** as part of a subset
+- It is **not considered** as part of a subset
+
+Say there are **3 elements**, for each of them we have above two options, hence **2 * 2 * 2 = 2^N^** are the total options.
+
+:::warning
+Please take some time to think about the solution approach on your own before reading further.....
+:::
+
+
+#### Approach
+
+The approach to solve the problem is to use backtracking.
+
+For each element, I have two choices whether to keep it or not, I execute my choice and then ask recursion to do the remaining work.
+
+Let us take an example of `[1, 2, 3]`.
+
+ +
+
+#### Psuedocode
+
+```cpp
+list < list < int >> ans;
+void subsets(list < int > A, list < int > currset, int idx) {
+
+ //base case
+ if (idx == A.size()) {
+ ans.add(currset);
+ return;
+ }
+
+ //for every ele in A, we have 2 choices
+
+ //choice 1 : keep it in currset
+ currset.add(A[idx]);
+ subsets(A, currset, idx + 1);
+
+ //choice 2 : Don't keep it in currset
+ currset.remove_back();
+ subsets(A, currset, idx + 1);
+}
+```
+
+NOTE: For producing individual sorted subsets, we need to sort the given array first. We will get the desired result with this since elements are being processed in sequence.
+
+#### Dry Run
+A = {2, 6, 9}
+
+
+
+
+#### Psuedocode
+
+```cpp
+list < list < int >> ans;
+void subsets(list < int > A, list < int > currset, int idx) {
+
+ //base case
+ if (idx == A.size()) {
+ ans.add(currset);
+ return;
+ }
+
+ //for every ele in A, we have 2 choices
+
+ //choice 1 : keep it in currset
+ currset.add(A[idx]);
+ subsets(A, currset, idx + 1);
+
+ //choice 2 : Don't keep it in currset
+ currset.remove_back();
+ subsets(A, currset, idx + 1);
+}
+```
+
+NOTE: For producing individual sorted subsets, we need to sort the given array first. We will get the desired result with this since elements are being processed in sequence.
+
+#### Dry Run
+A = {2, 6, 9}
+
+ +
+Continued
+
+
+
+Continued
+
+ +
+#### Complexity
+- **Time Complexity:** O(2^N^)
+- **Space Complexity:** O(N)
+
+---
+### Question
+What is the count of total permutations of a string with unique characters? (N=String length)
+
+**Choices**
+
+- [ ] N$^2$
+- [ ] N + (N + 1) / 2
+- [ ] N * (N - 1) / 2
+- [x] N!
+
+---
+### Problem 3 : Permutation
+
+Given a character array with distinct elements. Print all permutations of it without modifying it.
+
+**Example**
+For string **abc**, of length 3, we have total 3! = 6 permutations:
+- abc
+- acb
+- bac
+- bca
+- cab
+- cba
+
+**Input:** abc
+**Output:** abc acb bac bca cab cba
+
+
+**Constraint**
+We don't have duplicate characters in a string.
+
+---
+## Permutations Idea
+
+- Every permutation has n number of characters, where n is the length of the original string.
+- So initially we have n number of empty spots.
+`_ _ _`
+- And we need to fill these empty spots one by one.
+- Let us start with the first empty spot, which means from the 0th index.
+- For the 0th index we have three options, `a, b, and c`, any of the three characters can occupy this position.
+
+
+
+#### Complexity
+- **Time Complexity:** O(2^N^)
+- **Space Complexity:** O(N)
+
+---
+### Question
+What is the count of total permutations of a string with unique characters? (N=String length)
+
+**Choices**
+
+- [ ] N$^2$
+- [ ] N + (N + 1) / 2
+- [ ] N * (N - 1) / 2
+- [x] N!
+
+---
+### Problem 3 : Permutation
+
+Given a character array with distinct elements. Print all permutations of it without modifying it.
+
+**Example**
+For string **abc**, of length 3, we have total 3! = 6 permutations:
+- abc
+- acb
+- bac
+- bca
+- cab
+- cba
+
+**Input:** abc
+**Output:** abc acb bac bca cab cba
+
+
+**Constraint**
+We don't have duplicate characters in a string.
+
+---
+## Permutations Idea
+
+- Every permutation has n number of characters, where n is the length of the original string.
+- So initially we have n number of empty spots.
+`_ _ _`
+- And we need to fill these empty spots one by one.
+- Let us start with the first empty spot, which means from the 0th index.
+- For the 0th index we have three options, `a, b, and c`, any of the three characters can occupy this position.
+
+ +
+- If `a` will occupy 0th index, then we have `a _ _`, and if `b` will occupy 0th index, then we have `b _ _`, and if `c` will occupy 0th index, then we have `c _ _`,
+
+
+
+- If `a` will occupy 0th index, then we have `a _ _`, and if `b` will occupy 0th index, then we have `b _ _`, and if `c` will occupy 0th index, then we have `c _ _`,
+
+ +
+- Now the first spot is occupied, now we have to think about the second spot.
+- Now for a second spot we have only options left.
+
+
+
+- Now the first spot is occupied, now we have to think about the second spot.
+- Now for a second spot we have only options left.
+
+ +
+- Now when the character occupies the second spot, then we get.
+
+
+
+- Now when the character occupies the second spot, then we get.
+
+ +
+- Now for the last spot, every string has left with a single character, like in `a b _`, we are only left with the character `c`.
+
+
+
+- Now for the last spot, every string has left with a single character, like in `a b _`, we are only left with the character `c`.
+
+ +
+
+- Now this character will occupy the last spot.
+
+
+
+
+
+- Now this character will occupy the last spot.
+
+
+ +
+We are setting characters at positions one by one. So **We need to keep track of visited/used characters.**
+
+---
+### Permutations PsuedoCode
+
+```cpp
+void permutations1(char[] arr, idx, ans[N], visited[N]) {
+ if (idx == arr.length) {
+ print(ans[])
+ return
+ }
+ for (i = 0; i < N; i++) { // All possibilities
+ if (visited[i] == false) { // valid possibilities
+ visited[i] = true;
+ ans[idx] = arr[i];
+ permutations1(arr, idx + 1, ans, visited); // recursive call for next index
+ visited[i] = false; //undo changes
+ }
+ }
+}
+```
+
+### Permutations - Dry Run
+Let us suppose we have the string `arr[] = a b c` , and initially ans array is empty, `ans[] = _ _ _`.
+
+
+
+We are setting characters at positions one by one. So **We need to keep track of visited/used characters.**
+
+---
+### Permutations PsuedoCode
+
+```cpp
+void permutations1(char[] arr, idx, ans[N], visited[N]) {
+ if (idx == arr.length) {
+ print(ans[])
+ return
+ }
+ for (i = 0; i < N; i++) { // All possibilities
+ if (visited[i] == false) { // valid possibilities
+ visited[i] = true;
+ ans[idx] = arr[i];
+ permutations1(arr, idx + 1, ans, visited); // recursive call for next index
+ visited[i] = false; //undo changes
+ }
+ }
+}
+```
+
+### Permutations - Dry Run
+Let us suppose we have the string `arr[] = a b c` , and initially ans array is empty, `ans[] = _ _ _`.
+
+ +
+
+- Initially, we are at index 0,
+
+
+
+
+- Initially, we are at index 0,
+
+ +
+- Now i vary from 0 to `n-1`, so it will go from 0 to 2, as here the length of the string is 3.
+
+
+
+- Now i vary from 0 to `n-1`, so it will go from 0 to 2, as here the length of the string is 3.
+
+ +
+- Now when `i = 0`, we will check that `visited[i] == false`, so this condition is true, we mark `visited[i] == true` and `ans[0] = arr[0] = a`.
+
+
+
+- Now when `i = 0`, we will check that `visited[i] == false`, so this condition is true, we mark `visited[i] == true` and `ans[0] = arr[0] = a`.
+
+ +
+- Now it makes a recursive call for the next index, `permutations1(arr, 1, ans, visited)`
+
+
+
+- Now it makes a recursive call for the next index, `permutations1(arr, 1, ans, visited)`
+
+ +
+- Inside this call, `idx != arr.length`, so we will continue further, now inside this call, the loop will go from 0 to 2.
+
+
+
+- Inside this call, `idx != arr.length`, so we will continue further, now inside this call, the loop will go from 0 to 2.
+
+ +
+- But in case `i = 0`, now `visited[0] != false`, so in this iteration we will not enter inside the if condition, i will simply get incremented.
+
+
+- Now `i = 1`, we will check that `visited[i] == false`, so this condition is true, we mark `visited[1] == true` and `ans[1] = arr[1] = b`.
+
+
+
+- But in case `i = 0`, now `visited[0] != false`, so in this iteration we will not enter inside the if condition, i will simply get incremented.
+
+
+- Now `i = 1`, we will check that `visited[i] == false`, so this condition is true, we mark `visited[1] == true` and `ans[1] = arr[1] = b`.
+
+ +
+- Now it will make recussive call for `idx + 1`, `permutations1(arr, 2, ans, visited)`
+
+
+
+- Now it will make recussive call for `idx + 1`, `permutations1(arr, 2, ans, visited)`
+
+ +
+- Now inside this new recursive again loop will run from 0 to 2.
+
+
+
+- Now inside this new recursive again loop will run from 0 to 2.
+
+ +
+- Now when `i = 0`, now `visited[0] != false`, so in this iteration, we will not enter inside the if condition, i will simply get incremented.
+- Now `i = 1`, again `visited[1] != false`, so in this iteration, we will not enter inside the if condition, i will simply get incremented.
+
+
+
+- Now when `i = 0`, now `visited[0] != false`, so in this iteration, we will not enter inside the if condition, i will simply get incremented.
+- Now `i = 1`, again `visited[1] != false`, so in this iteration, we will not enter inside the if condition, i will simply get incremented.
+
+ +
+- Now `i = 2`, we will check that `visited[i] == false`, so this condition is true, we mark `visited[2] == true` and `ans[2] = arr[2] = c`.
+
+
+
+- Now `i = 2`, we will check that `visited[i] == false`, so this condition is true, we mark `visited[2] == true` and `ans[2] = arr[2] = c`.
+
+ +
+- Now it will make recussive call for `idx + 1`, `permutations1(arr, 3, ans, visited)`
+
+
+
+- Now it will make recussive call for `idx + 1`, `permutations1(arr, 3, ans, visited)`
+
+ +
+- Inside this call, our `idx == arr.length`, so print `ans`, so **abc will be printed**, and it will return. And after returning `visited[2] = false`.
+
+
+
+- Inside this call, our `idx == arr.length`, so print `ans`, so **abc will be printed**, and it will return. And after returning `visited[2] = false`.
+
+ +
+
+
+
+
+ +
+
+- Now for `arr, 2, ans, visited`, all iterations are completed. So it will also return and `visited[1] = false`
+
+
+
+
+- Now for `arr, 2, ans, visited`, all iterations are completed. So it will also return and `visited[1] = false`
+
+ +
+
+
+ +
+
+- Now for `arr, 1, ans, visited`, we are left for the iteration `i = 2`, so it will check for `visited[i] == false`, as `visited[2] = false`, so go inside the if condition and `visited[2] == true` and `ans[1] = arr[2] = c`
+
+
+
+
+- Now for `arr, 1, ans, visited`, we are left for the iteration `i = 2`, so it will check for `visited[i] == false`, as `visited[2] = false`, so go inside the if condition and `visited[2] == true` and `ans[1] = arr[2] = c`
+
+ +
+- Now it will make the recursive call for `arr, 2, ans, visited`. And inside this call again loop will run from 0 to 2. Now `visited[0] == true`, so it will for `i = 1`, and so it will check for `visited[i] == false`, as `visited[1] = false`, so go inside the if condition and `visited[1] == true` and `ans[2] = arr[1] = b`
+
+
+
+
+- Now it will make the recursive call for `arr, 2, ans, visited`. And inside this call again loop will run from 0 to 2. Now `visited[0] == true`, so it will for `i = 1`, and so it will check for `visited[i] == false`, as `visited[1] = false`, so go inside the if condition and `visited[1] == true` and `ans[2] = arr[1] = b`
+
+
+ +
+- Now it will make recussive call for `idx + 1`, `permutations1(arr, 3, ans, visited)`
+
+
+
+- Now it will make recussive call for `idx + 1`, `permutations1(arr, 3, ans, visited)`
+
+ +
+- Now inside this call `idx == arr.length`, so it will print `ans`, so **acb will be printed**, and it will return.
+
+In this way, all the permutations will be printed.
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Bit Manipulation 1.md b/Academy DSA Typed Notes/Advanced/DSA Bit Manipulation 1.md
new file mode 100644
index 0000000..b9bddbc
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Bit Manipulation 1.md
@@ -0,0 +1,455 @@
+# Bit Manipulation 1
+
+## Truth Table for Bitwise Operators
+
+
+Below is the truth table for bitwise operators.
+
+
+- Now inside this call `idx == arr.length`, so it will print `ans`, so **acb will be printed**, and it will return.
+
+In this way, all the permutations will be printed.
+
diff --git a/Academy DSA Typed Notes/Advanced/DSA Bit Manipulation 1.md b/Academy DSA Typed Notes/Advanced/DSA Bit Manipulation 1.md
new file mode 100644
index 0000000..b9bddbc
--- /dev/null
+++ b/Academy DSA Typed Notes/Advanced/DSA Bit Manipulation 1.md
@@ -0,0 +1,455 @@
+# Bit Manipulation 1
+
+## Truth Table for Bitwise Operators
+
+
+Below is the truth table for bitwise operators.
+ +
+## Basic AND XOR OR Properties
+
+### Basic AND Properties
+1. **Even/Odd Number**
+In binary representation, if a number is even, then its least significant bit (LSB) is 0.
+Conversely, if a number is odd, then its LSB is 1.
+
+ * **A & 1 = 1** (if A is odd)
+ ```cpp
+ 181 = 10110101 //181 is odd, therefore LSB is 1
+
+ 10110101 & 1 = 1 // Performing Bitwise AND Operation
+
+ Since, 181 is odd, Bitwise AND with 1 gave 1.
+ ```
+ * **A & 1 = 0** (if A is even)
+ ```cpp
+ 180 = 10110100 //180 is even, therefore LSB is 0
+
+ 10110100 & 1 = 0 // Performing Bitwise AND Operation
+
+ Since, 180 is even, Bitwise AND with 1 gave 0.
+ ```
+2. **A & 0 = 0** (for all values of A)
+3. **A & A = A** (for all values of A)
+
+### Basic OR Properties
+1. **A | 0 = A** (for all values of A)
+2. **A | A = A** (for all values of A)
+
+### Basic XOR Properties
+1. **A ^ 0 = A** (for all values of A)
+2. **A ^ A = 0** (for all values of A)
+
+### Commutative Property
+The order of the operands does not affect the result of a bitwise operation.
+
+```cpp
+A & B = B & A // Bitwise AND
+A | B = B | A // Bitwise OR
+A ^ B = B ^ A // Bitwise XOR
+```
+
+### Associative Property
+* It states that the grouping of operands does not affect the result of the operation.
+* In other words, if we have three or more operands that we want to combine using a bitwise operation, we can group them in any way we want, and the final result will be the same.
+
+```cpp
+(A & B) & C = A & (B & C) // Bitwise AND
+(A | B) | C = A | (B | C) // Bitwise OR
+(A ^ B) ^ C = A ^ (B ^ C) // Bitwise XOR
+```
+
+---
+### Question
+
+Evaluate the expression: a ^ b ^ a ^ d ^ b
+
+**Choices**
+
+- [ ] a ^ b ^ a ^ b
+- [ ] b
+- [ ] b ^ d
+- [x] d
+
+
+We can evaluate the expression as follows:
+```cpp
+a ^ b ^ a ^ d ^ b = (a ^ a) ^ (b ^ b) ^ d // grouping the a's and the b's
+= 0 ^ 0 ^ d // since a ^ a and b ^ b are both 0
+= d // the result is d
+```
+Therefore, the expression a ^ b ^ a ^ d ^ b simplifies to d.
+
+### Question
+
+Evaluate the expression: 1 ^ 3 ^ 5 ^ 3 ^ 2 ^ 1 ^ 5
+
+**Choices**
+
+- [ ] 5
+- [ ] 3
+- [x] 2
+- [ ] 1
+
+
+We can evaluate the expression as follows:
+```cpp
+1 ^ 3 ^ 5 ^ 3 ^ 2 ^ 1 ^ 5 = ((1 ^ 1) ^ (3 ^ 3) ^ (5 ^ 5)) ^ 2 // grouping the pairs of equal values and XORing them
+= (0 ^ 0 ^ 0) ^ 2 // since x ^ x is always 0
+= 0 ^ 2 // since 0 ^ y is always y
+= 2 // the result is 2
+```
+Therefore, the expression 1 ^ 3 ^ 5 ^ 3 ^ 2 ^ 1 ^ 5 simplifies to 2.
+
+
+### Left Shift Operator (<<)
+* The left shift operator (<<) shifts the bits of a number to the left by a specified number of positions.
+* The left shift operator can be used to multiply a number by 2 raised to the power of the specified number of positions.
+
+Example: a = 10
+Let's see a dry run on smaller bit representation(say 8)
+Binary Representation of 10 in 8 bits: 00001010
+```cpp
+(a << 0) = 00001010 = 10
+(a << 1) = 00010100 = 20 (mutiplied by 2)
+(a << 2) = 00101000 = 40 (mutiplied by 2)
+(a << 3) = 01010000 = 80 (mutiplied by 2)
+(a << 4) = 10100000 = 160 (mutiplied by 2)
+(a << 5) = 01000000 = 64 (overflow, significant bit is lost)
+```
+
+In general, it can be formulated as:
+```cpp
+a << n = a * 2^n
+1 << n = 2^n
+```
+However, it's important to note that left shifting a number beyond the bit capacity of its data type can cause an **overflow** condition.
+
+In above case, if we shift the number 10 more than 4 positions to the left an overflow will occur.
+
+
+```cpp
+(a << 5) = 01000000 = 64
+//(incorrect ans due to overflow)
+// correct was 320 but it is too large to get stored in 8 bits
+```
+
+**Note:** We can increase the number of bits, but after a certain point it will reach limit and overflow will occur.
+
+
+
+### Right Shift Operator (>>)
+* The right shift operator (>>) shifts the bits of a number to the right by a specified number of positions.
+* When we right shift a binary number, the most significant bit (the leftmost bit) is filled with 0.
+* Right shift operator can also be used for division by powers of 2.
+
+Let’s take the example of the number 20, which is represented in binary as 00010100. Lets suppose, it can be represented just by 8 bits.
+```cpp
+(a >> 0) = 00010100 = 20
+(a >> 1) = 00001010 = 10 (divided by 2)
+(a >> 2) = 00000101 = 5 (divided by 2)
+(a >> 3) = 00000010 = 2 (divided by 2)
+(a >> 4) = 00000001 = 1 (divided by 2)
+(a >> 5) = 00000000 = 0 (divided by 2)
+```
+In general, it can be formulated as:
+```cpp
+a >> n = a/2^n
+1 >> n = 1/2^n
+```
+Here, overflow condition doesn't arise.
+
+
+### Question
+
+What will we get if we do 1 << 3 ?
+
+**Choices**
+
+- [ ] 1
+- [x] 8
+- [ ] 3
+- [ ] 4
+
+
+---
+### Power of Left Shift Operator
+
+### OR( | ) Operator
+**Left Shift Operator** can be used with the **OR** operator to **SET** the **ith** bit in the number.
+
+```
+N = (N | (1<
+
+## Basic AND XOR OR Properties
+
+### Basic AND Properties
+1. **Even/Odd Number**
+In binary representation, if a number is even, then its least significant bit (LSB) is 0.
+Conversely, if a number is odd, then its LSB is 1.
+
+ * **A & 1 = 1** (if A is odd)
+ ```cpp
+ 181 = 10110101 //181 is odd, therefore LSB is 1
+
+ 10110101 & 1 = 1 // Performing Bitwise AND Operation
+
+ Since, 181 is odd, Bitwise AND with 1 gave 1.
+ ```
+ * **A & 1 = 0** (if A is even)
+ ```cpp
+ 180 = 10110100 //180 is even, therefore LSB is 0
+
+ 10110100 & 1 = 0 // Performing Bitwise AND Operation
+
+ Since, 180 is even, Bitwise AND with 1 gave 0.
+ ```
+2. **A & 0 = 0** (for all values of A)
+3. **A & A = A** (for all values of A)
+
+### Basic OR Properties
+1. **A | 0 = A** (for all values of A)
+2. **A | A = A** (for all values of A)
+
+### Basic XOR Properties
+1. **A ^ 0 = A** (for all values of A)
+2. **A ^ A = 0** (for all values of A)
+
+### Commutative Property
+The order of the operands does not affect the result of a bitwise operation.
+
+```cpp
+A & B = B & A // Bitwise AND
+A | B = B | A // Bitwise OR
+A ^ B = B ^ A // Bitwise XOR
+```
+
+### Associative Property
+* It states that the grouping of operands does not affect the result of the operation.
+* In other words, if we have three or more operands that we want to combine using a bitwise operation, we can group them in any way we want, and the final result will be the same.
+
+```cpp
+(A & B) & C = A & (B & C) // Bitwise AND
+(A | B) | C = A | (B | C) // Bitwise OR
+(A ^ B) ^ C = A ^ (B ^ C) // Bitwise XOR
+```
+
+---
+### Question
+
+Evaluate the expression: a ^ b ^ a ^ d ^ b
+
+**Choices**
+
+- [ ] a ^ b ^ a ^ b
+- [ ] b
+- [ ] b ^ d
+- [x] d
+
+
+We can evaluate the expression as follows:
+```cpp
+a ^ b ^ a ^ d ^ b = (a ^ a) ^ (b ^ b) ^ d // grouping the a's and the b's
+= 0 ^ 0 ^ d // since a ^ a and b ^ b are both 0
+= d // the result is d
+```
+Therefore, the expression a ^ b ^ a ^ d ^ b simplifies to d.
+
+### Question
+
+Evaluate the expression: 1 ^ 3 ^ 5 ^ 3 ^ 2 ^ 1 ^ 5
+
+**Choices**
+
+- [ ] 5
+- [ ] 3
+- [x] 2
+- [ ] 1
+
+
+We can evaluate the expression as follows:
+```cpp
+1 ^ 3 ^ 5 ^ 3 ^ 2 ^ 1 ^ 5 = ((1 ^ 1) ^ (3 ^ 3) ^ (5 ^ 5)) ^ 2 // grouping the pairs of equal values and XORing them
+= (0 ^ 0 ^ 0) ^ 2 // since x ^ x is always 0
+= 0 ^ 2 // since 0 ^ y is always y
+= 2 // the result is 2
+```
+Therefore, the expression 1 ^ 3 ^ 5 ^ 3 ^ 2 ^ 1 ^ 5 simplifies to 2.
+
+
+### Left Shift Operator (<<)
+* The left shift operator (<<) shifts the bits of a number to the left by a specified number of positions.
+* The left shift operator can be used to multiply a number by 2 raised to the power of the specified number of positions.
+
+Example: a = 10
+Let's see a dry run on smaller bit representation(say 8)
+Binary Representation of 10 in 8 bits: 00001010
+```cpp
+(a << 0) = 00001010 = 10
+(a << 1) = 00010100 = 20 (mutiplied by 2)
+(a << 2) = 00101000 = 40 (mutiplied by 2)
+(a << 3) = 01010000 = 80 (mutiplied by 2)
+(a << 4) = 10100000 = 160 (mutiplied by 2)
+(a << 5) = 01000000 = 64 (overflow, significant bit is lost)
+```
+
+In general, it can be formulated as:
+```cpp
+a << n = a * 2^n
+1 << n = 2^n
+```
+However, it's important to note that left shifting a number beyond the bit capacity of its data type can cause an **overflow** condition.
+
+In above case, if we shift the number 10 more than 4 positions to the left an overflow will occur.
+
+
+```cpp
+(a << 5) = 01000000 = 64
+//(incorrect ans due to overflow)
+// correct was 320 but it is too large to get stored in 8 bits
+```
+
+**Note:** We can increase the number of bits, but after a certain point it will reach limit and overflow will occur.
+
+
+
+### Right Shift Operator (>>)
+* The right shift operator (>>) shifts the bits of a number to the right by a specified number of positions.
+* When we right shift a binary number, the most significant bit (the leftmost bit) is filled with 0.
+* Right shift operator can also be used for division by powers of 2.
+
+Let’s take the example of the number 20, which is represented in binary as 00010100. Lets suppose, it can be represented just by 8 bits.
+```cpp
+(a >> 0) = 00010100 = 20
+(a >> 1) = 00001010 = 10 (divided by 2)
+(a >> 2) = 00000101 = 5 (divided by 2)
+(a >> 3) = 00000010 = 2 (divided by 2)
+(a >> 4) = 00000001 = 1 (divided by 2)
+(a >> 5) = 00000000 = 0 (divided by 2)
+```
+In general, it can be formulated as:
+```cpp
+a >> n = a/2^n
+1 >> n = 1/2^n
+```
+Here, overflow condition doesn't arise.
+
+
+### Question
+
+What will we get if we do 1 << 3 ?
+
+**Choices**
+
+- [ ] 1
+- [x] 8
+- [ ] 3
+- [ ] 4
+
+
+---
+### Power of Left Shift Operator
+
+### OR( | ) Operator
+**Left Shift Operator** can be used with the **OR** operator to **SET** the **ith** bit in the number.
+
+```
+N = (N | (1<